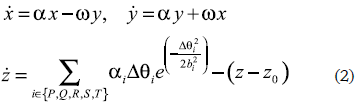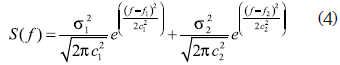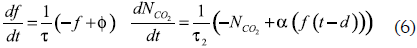Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.16 Envigado July/Dec. 2011
SIMULATION OF A NEONATAL MONITOR FOR MEDICAL TRAINING PURPOSES
SIMULACIÓN DE UN MONITOR NEONATAL PARA ENTRENAMIENTO MÉDICO
SIMULAÇÃO DE UM MONITOR NEONATAL PARA TREINAMENTO MÉDICO
Jenny Cifuentes*, Flavio Prieto**, Luis Carlos Méndez***
*Ingeniera Mecatrónica, Magíster en Automatización Industrial y Doctora (c) en Ingeniería Mecánica y Mecatrónica, Universidad Nacional de Colombia. Bogotá, Colombia. jacifuentesq@unal.edu.co
**Ingeniero Electrónico, Universidad Distrital Francisco José de Caldas; Físico, Universidad Nacional de Colombia Sede Bogotá; Magíster en Ingeniería Eléctrica, Doctor en Automática Industrial, Institut National des Sciences Appliquées (INSA), Lyon, Francia. Profesor Titular, Universidad Nacional de Colombia. Bogotá, Colombia. faprietoo@unal.edu.co
***Médico General y Cirujano, Universidad del Quindío. Especialista en Pediatría, Perinatología y Neonatología, Universidad Nacional de Colombia. lcmendezc@unal.edu.co
Artículo recibido 13-I-2011. Aprobado 15-IX-2011
Discusión abierta hasta junio de 2012
ABSTRACT
The design of a neonatal monitor for medical training purposes is hereby presented. In order to do that, the following main vital signs were modeled and simulated: ECG, pulse, blood pressure, CO2 level, among others. The signals were integrated to a graphic interface that generates different scenarios showing signals of patients with or without pathologies. Simulated signals were validated against real ones and, in general, the error is less than 5%; in addition, the neonatal monitor was assessed by 16 specialists; those doctors stated that simulated signals are of "excellent quality", "truthful" and that the interface is "user friendly".
KEY WORDS: monitor neonatal; vital signs; medical training; signal modeling.
RESUMEN
Se presenta el desarrollo de un monitor neonatal orientado al entrenamiento médico. Para esto se modelaron y simularon los principales signos vitales como son: señal ECG, señal de pulso, presión arterial, nivel de CO2, entre otros. Las señales fueron integradas en una interfaz gráfica, la cual permite generar diferentes escenarios de pacientes, no solo normales sino también con patologías. Las señales simuladas fueron validadas contra señales reales y, en general, el error es inferior al 5%. El monitor neonatal fue evaluado por 16 médicos especialistas quienes manifestaron que las señales simuladas son "de excelente calidad", "fidedignas" y que la interfaz es "amigable al usuario".
PALABRAS CLAVE: monitor neonatal; signos vitales; entrenamiento médico; modelado de señales.
RESUMO
Apresenta-se o desenvolvimento de um monitor neonatal orientado ao treinamento médico. Para isto se modelaram e simularam os principais signos vitais: sinal ECG, sinal de premo, pressão arterial, nível de CO2, entre outros. Os sinais foram integrados em uma interface gráfica, a qual permite gerar diferentes cenários de pacientes, não só normais senão também com patologias. Os sinais simulados foram validados contra sinais reais e, em geral, o erro é inferior a 5%. O monitor neonatal foi avaliado por 16 médicos especialistas que manifestaram que os sinais simulados são "de excelente qualidade", "fidedignos" e que a interface é "amigável ao usuario".
PALAVRAS-CÓDIGO: monitor neonatal; signos vitais; treinamento médico; modelado de sinais.
1. INTRODUCTION
Around 100 million babies are born worldwide every year; approximately 10% requires any assistance to start breathing and around 1% requires intensive resuscitation efforts, such as endotracheal intubation and thoracic massages (Murphy and Halamek, 2005). Hence, the learning and training medical personnel receive becomes a decisive factor when saving lives and guaranteeing adequate diagnosis. The traditional method of learning comprises two stages: theoretical knowledge and clinical experience; the problem lies in how this latter training is oriented; that is, even though apprentices at some point have to refine their skills with live patients, it is also true that safety and optimal treatment to patients need to be ensured (Lynõe et al., 1998; Howells and Madar, 2002). Balancing these latter needs, among other limitations, represents an ethical tension in medical education that has led to a new way of teaching based on medical simulation (Murphy and Halamek, 2005; Alinier et al., 2006; Ziv et al., 2006; Halamek, 2008).
In general terms, simulation has been structured into five categories according to a scheme proposed by Small, Wuerz and Simon (1999) as follows: verbal, standardized patients, body parts usage, computerized patients and electronic patients. In summary, verbal simulation is learning based on role playing games; standardized patients are actors used to teach and evaluate the way of acquiring the clinic history and the skills to perform physical checkups, to communicate and to act professionally; training using body parts is the use of anatomic models showing normal or abnormal health conditions; computerized patients are interactive patients that can be software based or part of a virtual world based on Internet; lastly, electronic patients are based on software, virtual reality or mannequins as well as the integral replica of the clinical environment.
The first simulation-based training on neonatal resuscitation was developed at Stanford University in mid-90's (Halamek et al., 2000). Then the simulator of Gaumard Scientific Company (Gaumard, 2010) was developed; it was a mannequin of a newborn capable of mimicking cyanosis symptoms; years later, a computer program would allow observation and remote control of the most relevant signals to assess the neonate such as cardiac frequency and skin color (Halamek et al., 2000); likewise, a virtual model of the patient was developed in which vital signs could be controlled from an external application (Korocsec et al., 2005). In year 2000, Laerdal presented Sim Man, the first mannequin which was portable and of human scale and designed to practice trainees skills and to present resuscitation scenarios. The mannequin also generates heartbeat sounds and shows breathing and blood pressure; it also allows the instructor to develop and edit his or her own scenarios as well as to use pre-programmed scenarios (Perkins, 2007). Later on, SIMA adopted a new approach and added a personal computer, software, a monitor and 8 training scenarios (Rosen, 2008). Nowadays, the most used simulator for training on neonatal reanimation is SimBaby and now is SimNewBaby, which includes the software and a technological advanced and interactive mannequin.
These commercial simulators are of excellent quality, but have some shortcomings; first of all, its cost is very high (Alinier et al., 2006; Halamek, 2008) and special training centers are required along with monitors, mannequins and equipment enabled to control and supervise the training (Korocsec et al., 2005). The latter reasons make it difficult for the educational institutions to acquire the number of simulators to satisfy the needs of the medical training. Secondly, but more important, teaching the adaptation or reanimation of neonatal in Colombian context and other countries of the region requires a personalization level not available in commercial levels (Currea, 2004; Minproteccion Social, 2000), causing confusions at the moment of illustrating the medical techniques on the simulator. Due to those reasons, it is necessary to develop, as an initial stage, a virtual environment of a neonatal simulator adequate to the clinical history, approach, reasoning and procedures of the Perinatal and Neonatology School of the region (Currea, 2004; Minproteccion Social, 2000).
Seeking to resolve this need, the present work introduces the development of a system that simulates the main biomedical signals and possible pathologies of a newborn patient. The referenced tool shows the results (analytically and graphically) that emerge from generating and adjusting mathematical models that describe vital signs of a neonate patient experiencing pathological and non-pathological scenarios. The mentioned vital signs are: ECG, pulse, cardiac frequencies, CO2 saturation, and pressure. The system is interactive and it allows generating different scenarios to assist both professors and students during the training on medical diagnosis. The initial evaluation of the tool was carried out by 16 medicine doctors; among them, there were doctors in general medicine doing their residence term of a post graduate in Pediatrics as well as specialists in fields such as pediatrics, anesthesiology, perinatology and neonatology. The results were satisfactory according to the objectives and promising in the process of integration and complexity. Nevertheless, in a subsequent stage of the present work, it becomes necessary to execute more rigorous validation experiments that include medicine students to achieve statistical significance so the tool can be validated as a training tool suitable for General and Specialized Medicine.
The document is structured as follows: in Section 2, vital signals are briefly described; in Section 3, the modeling of some vital signals and some pathology is presented; in Section 4 it is presented the integration of the simulations on a graphical interface; finally, in Section 5 the conclusion is presented along with some future developments.
2. VITAL SIGNALS
Vital signals are generally defined as indicators that reflect the physiological status of vital organs such as brain, heart and lungs. Indicators express instantly the functional changes that take place in the body.
2.1 Electrocardiograph -ECG-
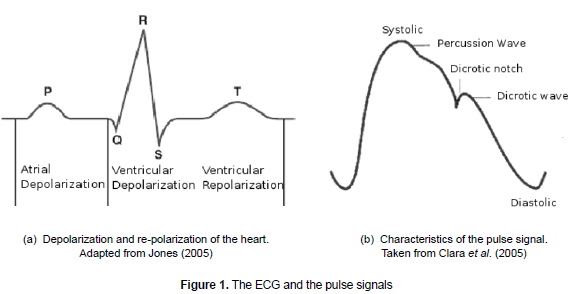
The heart is the central structure of the cardiovascular system. The contraction of any muscle is associated to electric changes called "depolarization". Those changes can be detected by electrodes located on the body. Even though the heart has four chambers, it has only two from the electrical perspective as the two auricles contract simultaneously as do the two ventricles. Contraction of auricles is associated to the "P" wave of the ECG signal. On the other hand, the ventricular mass, due to its bigger size, generates a great deflection of the ECG signal when ventricles are depolarized; the wave is called QSR complex. The T wave of the ECG signal is associated to the return of the ventricular mass to its electric status or re-polarization (see figure 1a).
2.2 Pulse signal
The pulse wave is generated when the heart beats and it is caused by the expansion of the arteries as the blood circulates. In this wave, the initial peak is rounded and descends smoothly until a hollow called "dicrotic notch" or "incisures" that results from the sudden closure of the aortic valve, finally it descents until the diastole occurs (see figure 1b). This particular shape results from the overlapping of an incident wave that starts from the heart to the peripheral area with other wave that reflects itself on the aortic bifurcation. Hence, the characteristic parameters of each arterial pulse are the incident wave and the amplitude of the reflected wave (Fuster et al., 2004).
2.3 Blood pressure
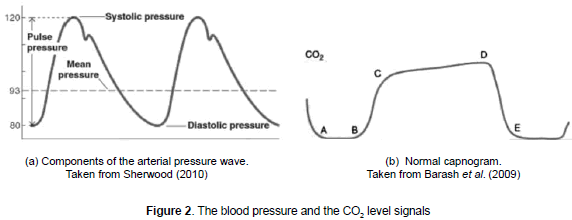
Blood pressure is the strength that blood applies against the artery walls. This variable depends on the volume contained in the blood vessels and the flexibility of the walls themselves. During the ventricular systole, a great amount of blood enters the arteries whereas only a third of it is expelled towards the arterioles. During the diastole there is no blood entering the arteries; nevertheless, there is a flow back due to backward movement of the vessel walls. The maximum pressure applied on the artery walls while the blood is expelled during systole is called "systolic pressure". The minimum pressure within the arteries takes place when the blood flows to the rest of the vessels during the diastole and it is called "diastolic pressure". The pulse pressure is the difference between the systolic and diastolic pressure; the mean pressure is the average during the whole cardiac cycle (see figure 2a).
2.4 CO2 level and respiratory frequency
Capnography is the graphic record of the instant concentration of CO2 in the gases breathed during a respiratory cycle. It has four basic phases shown in figure 2b (Barash et al., 2009). The first A-B phase represents the initial stage of the expiration, in this phase the gas occupies the empty space (dead space), normally containing CO2. At B point, a strong movement occurs in the capnogram which is the B-C phase. The slope of the graph of this movement is determined by the uniformity of the alveolar ventilation and the expiratory emptying. The C-D phase represents the alveolar or expiratory plateau. Normally this part of the wave is almost horizontal; the D point is the highest value of CO2, at the end of the expiration. When the patient starts inspiration, fresh gas enters and the sharp decline of the curve takes place down until the baseline; unless there is a re-inhalation of CO2 the line of the base is close to zero. The frequency of this graph is called "respiratory frequency" and represents the number of breathings (inhalation and exhalation) in a period.
2.5 Other signs
Temperature. The center for temperature regulation in human beings is the hypothalamus; it is an area above the pituitary gland that acts as a thermostat to maintain the inner body temperature within a range of 36.1 to 37.7 Celsius grades (Simmers, 1988).
Cardiac output. It is determined by measuring the amount of blood pumped to the lungs. The technique requires measuring O2 consumption (VO2) of the patient, the contents of O2 in arterial blood ContO2,a and the mixed venous blood ContO2,v (McArdle, Katch and Katch, 2009).
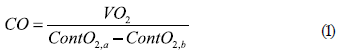
Oxygen saturation (SO2). It indicates the amount of oxygen that it is being transported by the hemoglobin in the blood and it is defined as the ratio between the oxygen in the hemoglobin present in a setting and the maximum amount of oxygen that could be combined with hemoglobin in a similar setting: SO2 (%)= (Oxi-hemoglobin/Total hemoglobin) x 100 (Ahrens and Rutherford, 1993).
3. MODELING SIGNALS
The fundamental importance of the medical mathematics lies in the effectiveness of the models applied to describe and study diverse health problems. This section presents the implementation of mathematical models to describe vital signs and the parameter adjustment process in order to present a set of characteristic signals in newborns. Likewise, values were adjusted to obtain signals that represent a wide set of pathologies of common occurrence in newborns.
3.1 ECG signal
3.1.1 Dynamic model
The model applied in this work is a modification to the one presented by McSharry et al. (2003); although this model was originally proposed for adult patients, in this work it was adapted to newborn patients. The model generates a trajectory in a tridimensional (3D) space in (x, y, z) coordinates. The quasi-periodicity of the ECG signal is reflected in the movement of the graph throughout a limit cycle of unitary radio on the plane (x, y). Each revolution of this cycle corresponds to one heartbeat. The points of the ECG signal (P, Q, R, S and T, see figure 1a) are described as attractors or repulsors, positive or negative on the z axis. These are placed with fixed angles throughout the unitary circle given by θP, θQ, θR, θS and θT. The dynamic equations of movement are given by the following set of ordinary differential equations:
where α=1-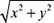 , Δθi= (θ-θi)mod{2π}, θ= tan-1(y/x) and w is the angular speed of the trajectory (McSharry et al., 2003). The respiratory frequency f2 is described by equation 3:
, Δθi= (θ-θi)mod{2π}, θ= tan-1(y/x) and w is the angular speed of the trajectory (McSharry et al., 2003). The respiratory frequency f2 is described by equation 3:
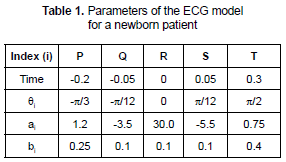
In this case, the frequency was adjusted to obtain a range acceptable for newborns (100-160 Lpm). ai and bi values as well as the times and angles for a normal child can be seen in table 1.
The angular speed is obtained from the power signal spectrum given by the addition of two Gaussian distributions as shown in equation 4.
with mean f1=0.1, f2=0.25 and standard deviation c1=0.01 and c2=0.01 (McSharry et al., 2003). In this way, the angular speed w(t) is given by, where T(t) represents the time series generated by the spectrum S(f).
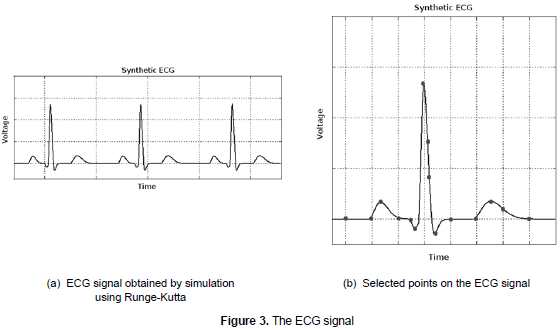
These equations of movement are numerically integrated in Phyton by using a fourth order method Runge-Kutta, with fixed time elapsed At=1/fs, where fs is the sampling frequency, 360 Hz in this case. The result of the implementation is shown in figure 3a.
3.1.2 Validating the simulation
To validate this model, 25 images of ECG signals were obtained; the images are common in newborn patients and come from literature and databases available on the web (PhysioBank Archive Index, 2010). Subsequently, real and synthetic ECG signals were adjusted to the same scale, and 15 significant points in the signal were chosen; this selection was based on relevant points in the signal morphology, such as maximum and minimum locals and crossings on zero values present in the P, Q, R, S, T and U waves and the PR, QRS, QT and ST intervals (see figure 3b).
Following this approach, 20 samples of ECG signals were taken and a mean square error between each point was obtained. The average error was 0.05 or 5% and the variance had a value of 0.012. This magnitude is normally less than 6% considering the number of samples taken and the variability of actual signals from patient to patient; it can be concluded that this model is an adequate tool to practice skills necessary in medical diagnostic. Preliminarily, we can say that the result is adequate and promising. In order to have conclusive results a more comprehensive validation is needed so the tool can be considered for training purposes.
3.1.3 Variation of the model to obtain pathologies
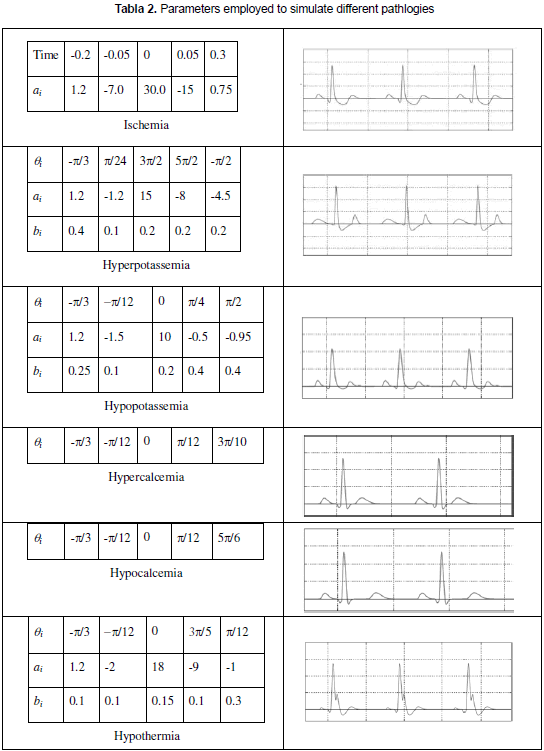
The variation of the model results from the implementation of an algorithm that modifies the model parameters allowing the representation of diverse pathologies (Cifuentes, Prieto and Méndez, 2010); the algorithm is based on the digitalization of actual electrocardiograms of newborn patients who had diverse fenotypical characteristics and were obtained from the literature and from the MIT's database (PhysioBank Archive Index, 2010). The algorithm reduces the mean square error of the points shown in figure 3b. In Cifuentes, Prieto and Méndez (2010) the implementation of six pathologies is shown: ischemia, hyperpotassemia, hypopotassemia, hypercalcemia, hypocalcemia and hypothermia; the hypopotassemia was presented with four degrees of intensity. The parameters employed to simulate those pathologies can be seen in table 2.
Likewise, the variation of the parameters can generate a wide range of scenarios that allows training of medical personnel.
3.2 Pulse signal
3.2.1 Dynamic model
This wave in particular results from the overlapping of a pressure wave that goes from the heart to the periphery and another that is reflected on the bifurcation of the descendent aorta. The model generates a trajectory in 3D space with coordinates (x, y, z). The frequency of the pulse signal is reflected in the graph movement throughout the limit cycle of unitary radio on the (x, y) plane. The two waves that make the pulse signal are described as positive attractors in "z" direction. These latter are located, with fixed angles, along the unitary circle. The dynamic equations of the movement are given by a set of ordinary differential equations:
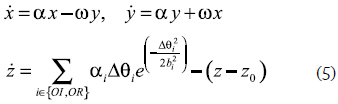
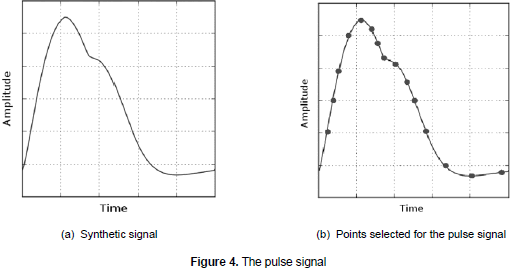
where α=1-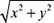 , Δθi= (θ-θi)mod{2π}, θ= tan-1(y/x), OI is the incident wave, OR it is the reflected wave and ω is the angular speed of the trajectory. These equations of movement are numerically integrated on Phyton using the Runge- Kutta method of fourth order with fixed time elapsed Δt= l/fs, where fs is the sampling frequency. The result of the implementation is shown in figure 4a.
, Δθi= (θ-θi)mod{2π}, θ= tan-1(y/x), OI is the incident wave, OR it is the reflected wave and ω is the angular speed of the trajectory. These equations of movement are numerically integrated on Phyton using the Runge- Kutta method of fourth order with fixed time elapsed Δt= l/fs, where fs is the sampling frequency. The result of the implementation is shown in figure 4a.
3.2.2 Validating the simulation
To validate the model, images of pulse signals from normal newborns were obtained mainly from the literature; then, the signals of the testing and the synthetic pulses were adjusted to the same scale. Subsequently, 15 significant points of the signal's morphology were chosen; that selection was based on the time span values which are important in the diagnostic of both the incident wave and the reflected wave that make up the signal (see figure 4b). 15 samples of pulse signals were used and the mean square error between each point was obtained. The mean error was 0,037 or 3,7% and the variance was 0,008. As shown, the error is smaller than 5% considering the sample size and the variability of the real signals from patient to patient. The obtained result is promising and shows potential of its application in the training process of health sciences.
3.3 Arterial pressure
The linearized cardiovascular physiology model presented by Beneken (1965) was used for the dynamic model to represent the cardiovascular model. This hydraulic analog model of 10 compartments describes the systemic circulation and makes a distinction between arteries and veins both intra- thoracic and extra-thoracic as well as the pulmonary circulation make a distinction between pulmonary veins and arteries. The model allows as input the changes of blood volume and the intra-thoracic and extra-thoracic pressures, and it generates as output both pulmonary and systemic arterial pressures.
To build the model of each compartment, blood pressure, incoming blood flow and volume changes are calculated and validated as in Sá Couto, Van Meurs and Goodwin (2006). The equations of the compartments keep coordination among themselves as the entry flow of a compartment depends on the pressure of the previous one; likewise, the volume changes depend on the entry and outlet flows. The expressions use elastance, resistance and unforced volume variables UV The elastance E establishes the relationship between the pressure and the volume and it reflexes the heart contraction process. The entry flow of each compartment f(t) is proportional to the pressure of the previous compartment (pi(t) and p(t)). The change of the volume in each compartment equals the difference between the flow f(t) and the outlet flow fout(t). For a more detailed analysis of this model refer to Sá Couto, Van Meurs and Goodwin (2006).
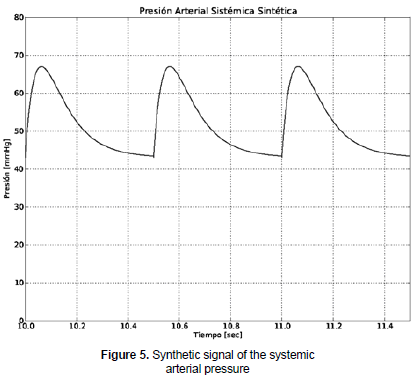
Figure 5 shows the signal of the systemic arterial pressure that was obtained by using the present simulation. The model was not validated as it has been already reported in the literature. Systolic and diastolic pressures data were modified in order to obtain and include different pathologies in the simulator; such variation is carried out directly from the neonatal simulator.
3.4 CO2 Level
3.4.1 Dynamic model
As mentioned the capnogram is divided into four fundamental phases (see figure 2b). This type of wave can be described by decreasing exponentials that model both the inspiration and expiration processes; in turn, periodicity of the pulse signal is given by the respiratory frequency. The dynamic process was modeled with two first-order differential equations; the first expression describes inspiration and the second describes all the cycle (inspiration and expiration):
where τ and τ2 define the time constants of the exponentials that represent the inspiration and expiration, respectively. Likewise, φ and α define the baseline and the maximum level of the CO2 of the respiratory cycle. Again, these equations of movement are numerically integrated in Phyton, using the fourth-order Runge-Kutta method with a fixed time elapsed Δt= 1/fs, where fs is the sampling frequency. The result of the implementation is shown in figure 6a.
3.4.2 Validating the simulation
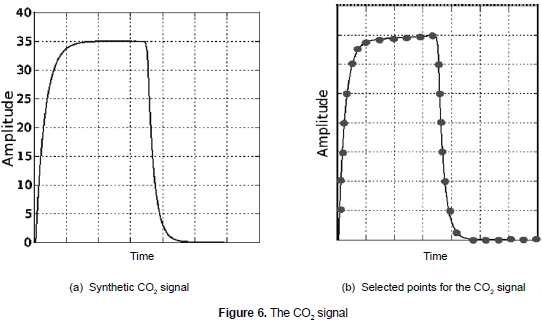
To validate this model, 30 images corresponding to capnograms common in newborns patients were obtained; these images are mainly from the literature and international databases (CapnoBase, 2010). Subsequently, CO2 testing and synthetic signals were adjusted to the same scale and 26 significant points of the signal's morphology were chosen. The selection of these points was based on the amplitude and time values which are relevant in the diagnostic for the inspiration and expiration cycles (see figure 6b). The average error was 0.019 or 1.9% and the variance was 0.005. As shown, the error is generally smaller than 3% taking into consideration both the number of samples used and the variability of the real signals from patient to patient. As in the previous cases result are promising, but a more comprehensive validation is needed.
3.4.3 Generating pathologies
An algorithm that modifies the parameters and permits the representation of diverse pathologies was implemented; such implementation was carried out by means of digitalization of real capno-grams obtained in the literature and corresponding to multiple pathologies. The algorithm 1 varies the different parameters of the differential equation and finds the set of parameters that minimizes the mean quadratic error of the chosen points between the synthetic signal and the real one. The algorithm minimizes the mean square error of the points shown in figure 6b. Even though a few pathologies were presented in the present work, the software lets the user to create an ample range of scenarios useful in the medical diagnostic.
τ, τ2, φ, α are the parameters of the differential equation, Vs is the amplitude of the simulated signal with these parameters and Vd is the digitized amplitude values obtained from the website and literature.
3.4.4 Muscle relaxants and dents in graphs
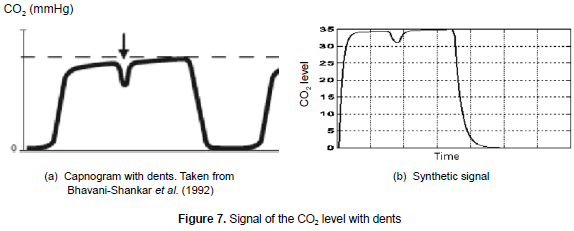
The dents can be seen on the capnogram plateau (see figure 7a); they show up when the action of the muscle relaxants ceases and the muscle returns to spontaneous ventilation. The main characteristic of the dent in the graph are: depth, which is inversely proportional to the relaxant activity and the location, generally constant for the same patient. For representing the scenario (see figure 7b), it was modified the a parameter of the differential equation that represents the expiration (see equation 6) in a short period with an amplitude value that depends on the dent size. For this pathology, the mean square error obtained was 0.032 and the variance of 0.007. These results indicate the relevance of this model in the representation of this type of signals.
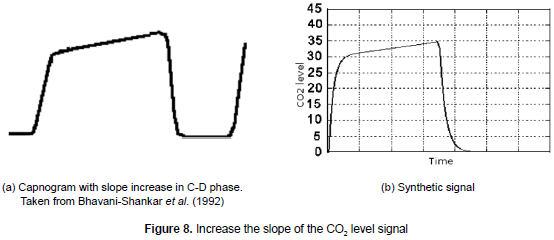
Increase of the slope in C-D phase. In this pathology, the slope of C-D phase of the capnogram increases (see figure 8a). This feature may be the result of the obstruction of the respiratory ways. To represent this pathology (see figure 8b), the a variable is parameterized in a way that it varies throughout time. The slope depends on the severity of the respiratory obstruction. The mean square error obtained for this representation was 0.04 and the variance was 0.012.
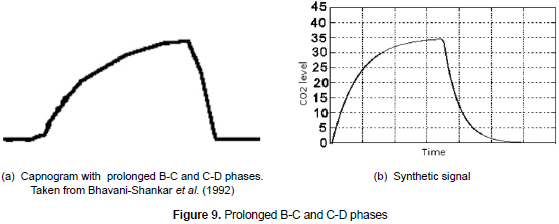
Prolonged B-C and C-D phases. The existence of prolonged B-C and C-D phases (see figure 9a) is a characteristic of pathologies such as bronchospasm or the obstruction of airways. In order to represent this pathology (see figure 9b), the time constant t2 is increased in equation 6.
3.5 Other variables
Other variables included in the simulator are constants of relevance for medical diagnosis; they include cardiac and respiratory frequencies, skin and rectal temperatures, oxygen saturation and cardiac output. In general, these signals are static unless a scenario with a medical condition needs to be represented; in such case, the simulator allows the trainer the variation of both amplitude and time interval at which the change is carried out. Thus, the interpolation between the present value and the one proposed by the trainer can be carried out in two possible ways:
- Linear. It is about drawing a straight line that crosses on the points of interest, calculating the intermediate values by using a function y = f(x).
- Sigmoid. It is about using a Bezier curve with the following shape:
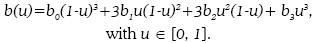
The use of those types of interpolation is carried out with the normal behavior of the variables of a neonate patient.
4. RESULTS: GRAPHIC INTERFACE
This section shows the interface corresponding to the vital signs and the interaction obtained in a simulator of a neonatal monitor. The interface was developed in Python. Python is a multiplatform open source language that is easy to install along with every one of its extensions; in addition, it has a very visual syntax thanks its mandatory indentation; since Python is an interpreted language, it does not require code compilation prior execution.
4.1 ECG signal
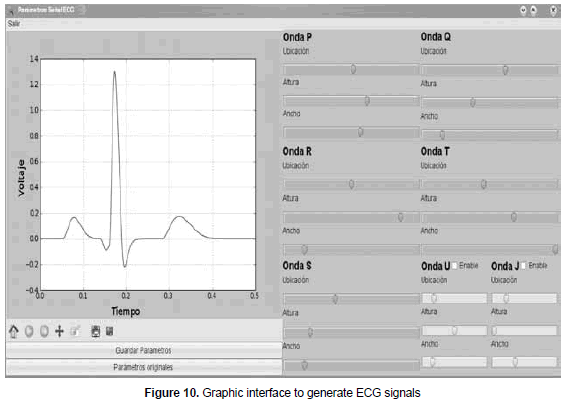
Taking into account the model described in Section 3.1, the interface shown in figure 10 was implemented. The interface allows, in a transparent way for the user, to modify the values of the amplitude, location and width of each wave of the ECG signal (P, Q, R, S, T); such process is carried out by modifying a, b and q values within certain limits restricted by the signal morphology (see equation 2).
The interface allows saving all the modified parameters for all signals and pathologies of the dynamic system into a text file with its own extension. This file can be opened only by the neonatal simulator in order to create either a pathologic or a non-pathologic scenario; likewise, it allows resetting to the default values of a non-pathological signal.
4.2 Pulse signal
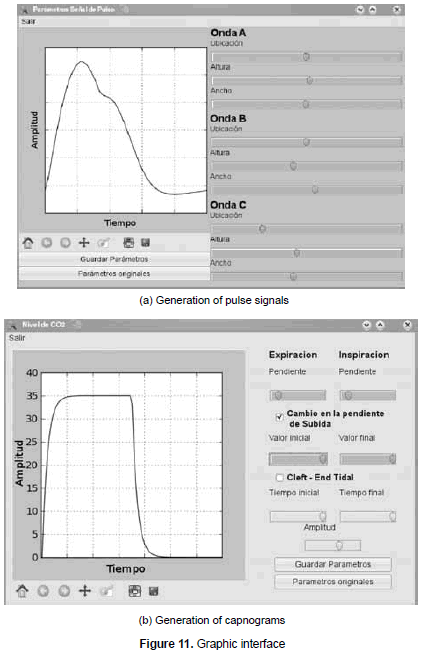
The interface allows modifying the dynamics of the model described in Section 3.2 by varying height, position and width of the incident and the reflected waves (see figure 11a). Similarly, it is possible to add and reconfigure the wave of a particular pathology.
4.3. CO2 level
Likewise, the interface allows creating pathologic and non-pathologic signals in relation to the CO2 level (see figure 11b). This tool enables the modification of time constants of the differential equations described in Section 3.3. In order to describe non-pathologic scenarios on the interface, sudden changes and holes can be added to the exponential that represents the expiration. These modifications can be obtained by changing the reference of each differential equation, that is, the interest points.
4.4 Other variables
For each constant included in the simulator, a graphic interface was created; it allows, in general terms, to modify the constant value within a time interval. The interpolation in this period is carried out in linear or sigmoidal forms, according to the user's preferences.
Cardiac and respiratory frequencies. The interface for these constants is very similar; it allows varying the cardiac frequency from 0 until 300 bpm (beats per minute) and the respiratory frequency from 0 to 140 brpm (breathings per minute). In addition, the time interval can fluctuate from 0 to 11 min.
Skin and rectal temperatures. Similarly to the previous features, the interface for skin and rectal temperatures is the same. The variation can range from 0 to 45 degrees and the time interval, from 0 to 11 min.
Blood pressure. The system offers the possibility to change values of systolic and diastolic pressures within a range from 0 to 300 mmHg.
Oxygen saturation. The simulator allows the variation of the oxygen saturation within a range from 0 to 100%. The time interval can vary continually from 0 to 11 min. It also allows the modification of the cyanosis detection threshold (bluish coloring of skin or mucous membranes due to lack of oxygen in the blood).
CO2 level. The interface allows the modification of a maximum value of CO2 and the corresponding baseline within a range from 0 to 35.
Cardiac output. The user can create scenarios whose cardiac output varies from 0 to 1000 L/min/kg in time intervals from 0 to 11 minutes.
4.5 Simulating signals for a newborn patient
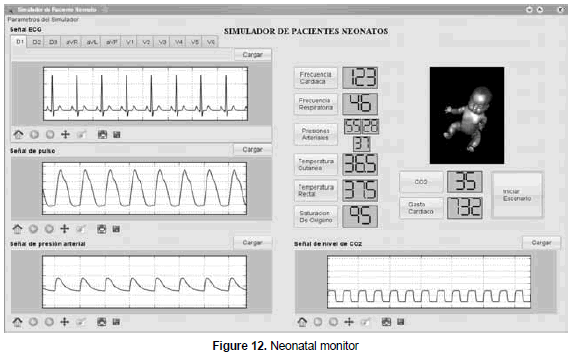
The simulator of a neonate patient or neonatal monitor is shown in figure 12. The tool allows the direct access to the interfaces, described in sections 4.1, 4.2 and 4.3, in order to generate ECG, pulse and CO2 level signals. Likewise, each variable has a button that leads to the interfaces described in Section 4.4.
Each graph (ECG, pulse, pressure and CO2 level) allows, by clicking on a button, to load up saved parameters from the interfaces described in sections 4.1, 4.2 and 4.3 in order to generate the corresponding signals. It is relevant to highlight that it is possible to load up ECG signals to create a full electrocardiogram, that is, interfaces are included for both standard and precordial derivatives. The Start button allows the simulation of each variable in the interface.
In order to show how the interface works, a scenario that mimics the vital signs of a patient with tachycardia and fever was created; similarly, the values of a 3 kg patient and that shows no pathology condition was defined as follows (Crocetti and Barone, 1998; D'Harlingue and Durand, 2001; Gomella, Cunningham and Eyal, 2009): cardiac frequency 123 bpm; respiratory frequency: 46 brpm; skin temperature: 36.0 °C; rectal temperature 36.5 °C; oxygen saturation: 92%; CO2 level: 35 mmHg; and cardiac output: 732 L/min/kg.
In order to mimic fever and tachycardia, a scenario was created in which each of the following values is modified: cardiac frequency: 190 bpm; respiratory frequency: 92 brpm; skin temperature: 38.3 °C; rectal temperature: 38.5 °C ; oxygen saturation: 92%; CO2 level: 35 mmHg and cardiac output: 842 L/min/kg.
The interface refreshes the values every half a second. Although the change of values is allowed for up to 11 minutes, the simulation was carried out for 4 seconds for illustration purposes; this approach was carried out to obtain 9 screenshots to show the dynamics in this type of pathology. These scenarios can be seen on the website http://www.youtube.com/watch?v=hla1gLvZQoM.
4.6 Medical validation
In order to validate the usefulness of the neonatal monitor in the training process, particularly in the Neonatology and Pediatric areas, a study of the accuracy of the signals was conducted.
The initial validation approach took into account the assessment criteria provided for educational software (Geissinger, 2011) (see table 3).
Based on these criteria, the interface was presented to a group of 16 doctors, specialists in Anesthesiology (3), Neonatology and Perinatology (3), Pediatric Intensive Care (3), Pediatric (3), Perinatology and Neonatology Fellow (2) and Pediatric Resident (2) for its evaluation; then, an ECG signal showing hyperpotassemia was selected and the signals to the 12 derivations based on the interface were obtained.
For the CO2 level signal, three signals were obtained (normal, without muscular relaxants and with obstruction in respiratory airways). Finally and in order to test all the variables, two full scenarios were generated: one that mimics fever, tachypnea and tachycardia and other that mimics hypothermia, bradypnea and bradycardia. The constants for normal patients were selected based on a 3 kg weight patient and with no specific pathology (Crocetti, and Barone, 1998; Gomella, Cunningham and Eyal, 2009; D'Harlingue and Durand, 2001). Constants for patients with pathologies were selected on the expert advice that the present work receives.
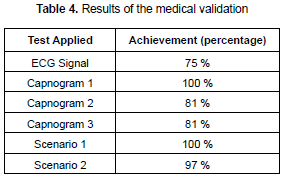
Scenarios and signals obtained from the neonatal simulator were evaluated by using multiple choice questions. Resulting electrocardiographic signals, simulated capnograms, and two scenarios generated are presented in table 4. The signals and scenarios generated in this first part evaluate the first criterion in table 3. These results were satisfactory with a high percentage of approval.
In order to evaluate the other criteria, the evaluators described the tool regarding to engagement, interactivity and tailorability. Signals as well as the neonatal monitor were considered by the specialists as "of excellent quality", "truthful" and "user friendly".
Based on these results, it is necessary to do a study with two variants to obtain more conclusive results in the validation. In this case, first we will consider a greater number of specialists and residents and second we will make the evaluation of the last 3 criteria in table 3 in more depth. Based on other evaluation criteria (Yildiz and Atkins, 1993; Reiser and Kegelmann, 1994); evaluators will assign a score (between 1 and 5) for each of the linguistic variables that will be evaluated (engagement, interactivity, tailorability, etc.). This will provide a greater statistical analysis and conclusive results from the application of the tool.
5. CONCLUSIONS AND FUTURE WORK
A neonatal simulator was presented with the possibility of generating synthetic signals that illustrate fundamental characteristics of diverse pathologies, such as ECG, pulse, blood pressure and CO2 level. The results of validating the dynamics in models of neonate patients were satisfactory, showing an error smaller than 5% when comparing real data with signals obtained from the simulator.
If the current scenario is considered as a preliminary phase intended to achieve future integration between real and virtual, the results can be considered satisfactory and encouraging when evaluating the fidelity of each one of the represented signals. However, for it to be validated as a tool for medical training, it is necessary to make a more rigorous evaluation that includes a greater number of specialists and residents and a clearer analysis of the linguistic variables associated with the validation of the tool. Such validation will provide the work the statistical validation so the tool can be used for learning purposes in the health area.
The graphic interface is an educational tool of great importance to students in the health area, as its handling is practical and intuitive. This application allows generating diverse scenarios by varying properties of signals such as frequency, minimum and maximum values, as well as other medical variables such as temperature, cardiac output and oxygen saturation.
As a future development, the present neonatal monitor should be integrated to a physical simulator such as a mannequin to emulate the signals present in the virtual simulator.
REFERENCES
Ahrens, Thomas and Rutherford, Kim. Essentials of oxygenation: Implication for clinical practice. Boston: Jones and Bartlett, 1993. 40 p. [ Links ]
Alinier, Guillaume; Hunt, Barry; Gordon, Ray and Harwood, Colin (2006). "Effectiveness of intermediate- fidelity simulation training technology in undergraduate nursing education". Journal of Advanced Nursing, vol. 54, No. 3 (May), pp. 359-369. [ Links ]
Barash, Paul; Cullen, Bruce; Stoelting, Robert and Cahalan, Michael. Clinical anesthesia. 6th ed. Philadelphia: Lippincott Williams & Wilkins, 2009. [ Links ]
Beneken, William (1965). "A mathematical approach to cardiovascular function. The uncontrolled human system". Ph. D. dissertation. Institute of Medical Physics. Utrecht, The Netherlands. [ Links ]
Bhavani-Shankar, K.; Moseley, H.; Kumar, A. Y. and Delph, Y. (1992). "Capnometry and anaesthesia". Canadian Journal of Anaesthesia, vol. 39, No. 6 (July), pp. 617-632. [ Links ]
CapnoBase Database. (consulted on January 10, 2010) Available in: <http://www.capnobase.org> [ Links ]
Cifuentes, Jenny; Prieto, Flavio y Méndez, Luis Carlos. Simulador de señales ECG de pacientes neonatos para entrenamiento médico. Bogotá. XV Simposio de Tratamiento de Señales, Imágenes y Visión Artificial. 2010. [ Links ]
Clara, Fernando M.; Cayrol, María L.; Scandurra, Adriana G.; Meschino, Gustavo J.; Garzillo, Miriam G.; Moyano, Eduardo e Introzzi, Aníbal R. (2005). "La técnica de análisis de onda de pulso en la determinación del riesgo cardiovascular". Revista de la Federación Argentina de Cardiología, vol. 34, No. 2 (abril-junio), pp. 213-220. [ Links ]
Colombia. Ministerio de Salud. Resolución 00412 de 2000. Norma técnica para la atención al recién nacido. [ Links ]
Crocetti, Michael and Barone, Michael A. Oski's essential pediatrics. 2nd ed. Philadelphia: Lippincott Williams & Wilkins, 1998. [ Links ]
Currea, Santiago. La adaptación neonatal inmediata. La reanimación neonatal. Bogotá: Unibiblos, 2004. [ Links ]
D'Harlingue, Arthur E. and Durand, David J. Recognition, stabilization, and transport of the highrisk newborn. In: Care of the high-risk neonate. 5th ed. 2001. [ Links ]
Fuster, Valentin; Alexander, Wayne; O'Rourke, Robert A.; Roberts, Robert; King, Spencer B.; Nash, Ira and Prystowsky, Eric N. Hurst's the heart. Book 1. New York: McGraw-Hill, 2004. 11th ed. 1100 p. [ Links ]
Gaumard Scientific Company. Simulators for Health Care Education. (consulted on December 6, 2010) Available in: http://www.gaumard.com/. [ Links ]
Geissinger, H. Educational software: Criteria for evaluation. (Consulted on January 11, 2011) Available in: <http://www.ascilite.org.au.conferences/perth97/papers/Geissinger/Geissinger.html> [ Links ]
Gomella, Tricial L.; Cunningham, M. Douglas and Eyal, Fabien G. Neonatology: Management, procedures, on-call problems, diseases, and drugs. 6th ed. New York: Lange Medical Books/McGraw-Hill, 2009, 894 p. [ Links ]
Halamek, Louis (2008). "The simulated delivery-room environment as the future for acquiring and maintaining skills in fetal and neonatal resuscitation". Seminars in Fetal and Neonatal Medicine, vol. 13, No. 6 (December), pp. 448-453. [ Links ]
Halamek, Louis; Kaegi, David; Gaba, David; Sowb, Yasser; Smith, Bradford; Smith, Brian and Howard, Steven (2000). "Time for a new paradigm in pediatric medical education: Teaching neonatal resuscitation in a simulated delivery room environment". Pediatrics, vol. 106, No. 4 (October), pp. 106-110. [ Links ]
Howells, Rachel and Madar, John (2002). "Newborn resuscitation training - which manikin". Resuscitation, vol. 54, No. 2 (August), pp. 175-181. [ Links ]
Jones, Shirley. ECG notes: Interpretation and management guide. 1st ed. Philadelphia: F. A. Davis, 2005. [ Links ]
Korocsec, Dean; Holobar, Ales; Divjak, Matjaz and Zazula, Damjan (2005). "Building interactive virtual environments for simulation training in medicine using VRML and Java/JavaScript". Computer Methods and Programs in Biomedicine, vol. 80. Supplement 1 (December), pp. S61-S70. [ Links ]
Lynõe, Niels; Sandlund, Mikael; Westberg, Katarina and Duchek, Milos (1998). "Informed consent in clinical training: Patient experiences and motives for participating". Medical Education, vol. 32, No. 5 (September). pp. 465-471. [ Links ]
McArdle, William D.; Katch, Frank L. and Katch, Victor L. Exercise physiology: Nutrition, energy, and human performance. United States of America: J. B. Lippincott, 2009. 341 p. [ Links ]
McSharry, Patrick; Clifford, Gari; Tarassenko, Lionel and Smith, Leonard (2003). "A dynamical model for generating synthetic electrocardiogram signals". IEEE Transactions on Biomedical Enginering, vol. 50, No. 3 (March), pp. 289-294. [ Links ]
Murphy, Allison and Halamek, Louis (2005). "Simulation-based training in neonatal resuscitation". Neo Reviews, vol. 6, No. 11 (November), pp. 489-492. [ Links ]
Perkins, Gavin (2007). "Simulation in resuscitation training". Resuscitation, vol. 73, No. 2 (May), pp. 202-211. [ Links ]
PhysioBank Archive Index, Physiologic Signal Archives for Biomedical Research. (consulted on January 10, 2010) Available in: <http://www.physionet.org/physiobank/database/> [ Links ]
Reiser, R. A. and Kegelmann, H. W. (1994). Evaluating instructional software: A review and critique of current methods". Educational Technology Research and Development, vol. 42, No. 3, pp. 63-69. [ Links ]
Rosen, Kathleen (2008). "The history of medical simulation". Journal of Critical Care, vol. 23, No. 2 (June), pp. 157-166. [ Links ]
Sá Couto, Carla D.; van Meurs, Willem; Goodwin, Jan and Andriessen, Peter (2006). "A model for educational simulation of neonatal cardiovascular pathophysiology". Simulation in Healthcare, vol. 1, No. 1 (January), pp. 4-9. [ Links ]
Sherwood, Lauralee. Human physiology: From cells to systems. 7th ed. Belmont, CA: Brooks/Cole, 2010. 928 p. [ Links ]
Simmers, Louise. Diversified health occupations. 2nd ed. Canada: Delmar, 1988. pp. 150-151. [ Links ]
Small, Steven; Wuerz, Richard and Simon, Richard (1999). "Demonstration of high-fidelity simulation team training for emergency medicine". Academic Emergency Medicine, vol. 6, No. 4 (April), pp. 312-323. [ Links ]
Yildiz, Rauf and Atkins, Madelene J. (1993). "Evaluating multimedia applications". Computers & Education, vol. 21, No.1-2, pp. 133-139. [ Links ]
Ziv, Amitai; Wolpe, Paul Root; Small, Stephen D. and Glick, Shimon (2006). "Simulation-based medical education: An ethical imperative". Simulation in Healthcare, vol. 1, No. 4, (Winter), pp. 252-256. [ Links ]