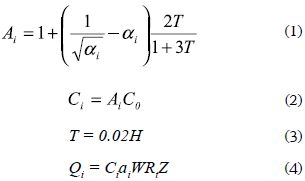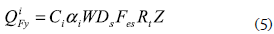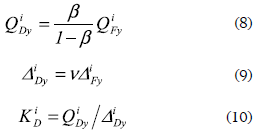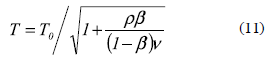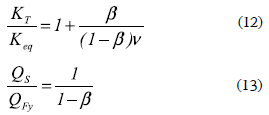Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237On-line version ISSN 2463-0950
Rev.EIA.Esc.Ing.Antioq no.17 Envigado Jan./June 2012
INFLUENCE OF THE STORY STIFFNESS OF REINFORCED CONCRETE FRAME WITH PROPORTIONAL HYSTERETIC DAMPERS ON THE SEISMIC RESPONSE
INFLUENCIA DE LA RIGIDEZ DE PISO DE PÓRTICOS DE CONCRETO REFORZADO CON DISIPADORES HISTERÉTICOS PROPORCIONALES SOBRE LA RESPUESTA SÍSMICA
INFLUÊNCIA DA RIGIDEZ DE ANDAR DE PÓRTICOS DE CONCRETO REFORÇADO COM DISIPADORES HISTERÉTICOS PROPORCIONAIS SOBRE A RESPOSTA SÍSMICA
Juan Andrés Oviedo*
*Ingeniero Civil, Escuela de Ingeniería de Antioquia; Doctor en Ingeniería, Universidad de Hokkaido, Japón. Ingeniero Asociado f'c Control y Diseño de Estructuras S. A. S. Profesor e integrante del Grupo de Investigación Estructuras y Construcción, Escuela de Ingeniería de Antioquia. Medellín, Colombia. joviedo@controldiseno.com.
Artículo recibido 15-XII-2011. Aprobado 29-V-2012
Discusión abierta hasta diciembre de 2012
ABSTRACT
This paper investigates the influence of the story stiffness of reinforced concrete (R/C) frame on the seismic response of R/C buildings with proportional hysteretic dampers. For this purpose, non-linear time-history analyses were conducted on a series of multi-degree-of-freedom system models that include a wide range of structural parameters and vertical distributions of story stiffnesses and strengths of R/C main frame and dampers. Although the basic purpose of damper installation is to reduce deformation demands, the results of analyses indicate that the story-drift demand on an entire system could be larger than that of the structure without dampers, depending highly on the stiffness and response period of R/C main frame. Moreover, dampers are shown to be more efficient in reducing the story-drift demand when installed into a flexible R/C main frame.
KEY WORDS: hysteretic dampers; reinforced concrete frames; seismic response; story-drift demand.
RESUMEN
Este artículo investiga la influencia de la rigidez de piso del pórtico de concreto reforzado sobre la respuesta sísmica de edificaciones de concreto equipadas con disipadores histeréticos proporcionales. Para esto, fueron llevados a cabo análisis cronológicos no lineales sobre una serie de modelos de sistemas de múltiples grados de libertad. Los modelos incluyen un amplio rango de parámetros estructurales y diferentes distribuciones en altura de rigideces y resistencias de piso del pórtico principal de concreto y de los disipadores. Aunque el objetivo básico de instalar disipadores sea reducir la demanda de deformación en la estructura, los resultados de los análisis indican que la demanda de deriva de piso del sistema completo puede ser incluso más grande que la de la edificación sin disipadores, dependiendo en gran medida de la rigidez y del período de respuesta del pórtico principal de concreto. Por otra parte, se muestra que los disipadores son más eficientes para reducir la demanda de deriva de piso cuando se instalan en pórticos flexibles de concreto.
PALABRAS CLAVE: disipadores de energía; pórticos de concreto reforzado; respuesta sísmica; demanda de deriva de piso.
RESUMO
Este artigo pesquisa a influência da rigidez de andar do pórtico de concreto reforçado sobre a resposta sísmica de edificações de concreto equipadas com dissipadores histeréticos proporcionais. Para isto, foram levadas a cabo análises cronológicas não lineares sobre uma série de modelos de sistemas de múltiplos graus de liberdade. Os modelos incluem uma ampla faixa de parâmetros estruturais e diferentes distribuições em altura de rigidezes e resistências de andar do pórtico principal de concreto e dos dissipadores. Ainda que o objetivo básico de instalar dissipadores seja reduzir a demanda de deformação na estrutura, os resultados das análises indicam que a demanda de deriva de andar do sistema completo pode ser inclusive maior do que a edificação sem dissipadores, dependendo em grande parte da rigidez e do período de resposta do pórtico principal de concreto. Por outra parte, mostra-se que os dissipadores são mais eficientes para reduzir a demanda de deriva de andar quando são instalados em pórticos flexíveis de concreto.
PALAVRAS-CÓDIGO: dissipadores de energia; pórticos de concreto reforçado; resposta sísmica; demanda de deriva de andar.
1. INTRODUCTION
The engineering community worldwide is well aware of the damaging effects of strong earthquake motions on building structures. For this reason, there has been a growing interest in developing techniques and devices for improving the seismic performance of building structures. Among the numerous devices that have been developed (e.g., Soong and Spencer, 2002; Bozorgnia and Bertero, 2004; Higashino and Okamoto, 2006), deformation-dependent hysteretic dampers (hysteretic dampers) have wide applicability in the structural engineering practice. The basic goal of damper installation is to limit the lateral deformation (e.g., story-drift response) and absorb most of the damaging vibration energy imposed by ground motions on a structure. As a result, the seismic damage in structural elements of a main structural system (main frame) is reduced.
The widespread use of energy dissipation systems has led researchers to investigate not only different configurations of energy-dissipating devices (e.g., Whittaker, Bertero and Alonso, 1989; Tsai and Hong, 1992; Wada and Nakashima, 2004; Iwata and Murai, 2006), but also their optimal mechanical properties so that the seismic performance of a structure is improved with the installation of such devices (e.g., Cherry and Filiatrault, 1993; McNamara, 1995; Nakashima, Saburi and Tsuji, 1996; Inoue and Kuwahara, 1998; Yamaguchi and El-Abd, 2003; Kim and Choi 2004; Oviedo, Midorikawa and Asari, 2008a, 2008b, 2009; Takewaki, 2009; Teran-Gilmore and Virto-Cambray, 2009). Most previous studies, however, have been limited in terms of the influence of the stiffness of main frame on the seismic performance of the entire system, particularly in the case of reinforced concrete (R/C) buildings. In the retrofit of an existing building using hysteretic dampers, whose structural properties are fixed before installing the dampers, the stiffness of the existing building could become a decisive factor for the selection of an adequate set of mechanical properties of dampers so as to achieve a given retrofit target.
Recently, the author introduced a scheme for defining the mechanical properties of hysteretic dampers, in such a way that the yield story drift and strength of dampers are proportional to those of the R/C main frame (Oviedo, Midorikawa and Asari, 2010). This scheme was shown to lead to a relatively constant distribution over the building height of the ratio of the maximum story-drift response to that of the building without dampers. It was pointed out the range of applicability for dampers under this scheme might depend on the stiffness of R/C main frame. Consequently, a parametric study was carried out to examine the influence of the range of stiffness of R/C frame on the seismic performance of R/C building structures with proportional hysteretic dampers. This study also aims to search for parameters that could lead to an increase in the story-drift response after the installation of dampers, compared with that of the R/C frame. The building models comprise a wide range of structural characteristics, such as the number of stories, story-drift angle limit at the design phase, vertical distribution of story stiffnesses and shear strengths, and mechanical properties of hysteretic dampers.
2. ANALYTICAL BUILDING MODEL
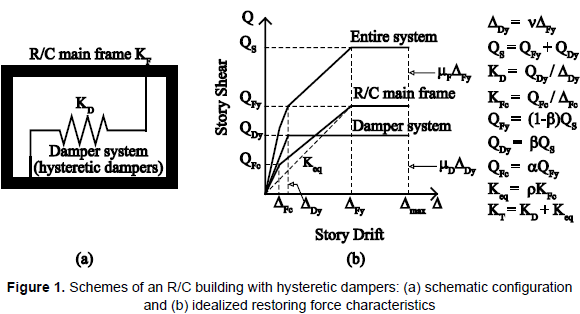
From a general standpoint, hysteretic dampers (damper system) link the story shear Q and the story drift Δ of the story at which they are installed. Figure 1a depicts a schematic of the resistance behavior of an R/C main frame combined with a damper system (entire system), and figure 1b illustrates the idealized restoring forces. In figure 1b, QS, QFy and QDy are the yield shear strength of the entire system, R/C main frame and damper system, respectively. ΔFc, ΔFy, ΔDy, Δmax, µF, µD are the cracking story drift, the yield story drift of the main frame, the yield story drift of the damper system, the maximum story drift, the story-drift ductility of the R/C main frame and the story-drift ductility of the damper system, respectively. α and ρ define the shear at the cracking point QFc and the equivalent stiffness Keq for the R/C main frame, respectively. KT is the stiffness of the entire system. The factors β and ν are discussed in the following section.
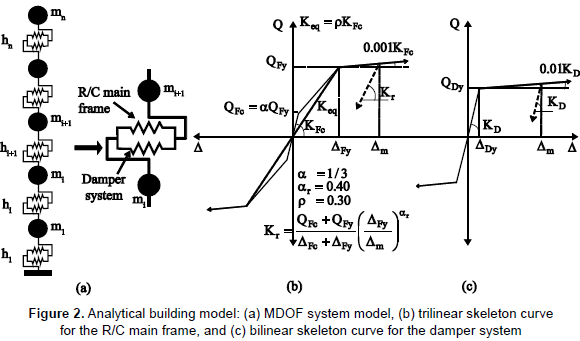
Based on figure 1, the structural model used in this study is a multi-degree-of-freedom (MDOF) system model, as shown in figure 2a. The mass is assumed to be the same and concentrated at the floor levels and the story height is the same for all stories. The model comprises a set of two non-linear shear springs at each story to represent the restoring force characteristics of the entire system at the i-th story. Here, one spring represents the R/C main frame and the other spring represents the damper system. In this study, two hysteresis models are used to describe the force-displacement (story shear-story drift) relationship of each story. For the R/C main frame, the degrading Takeda hysteresis model (Takeda, Sozen and Nielsen, 1970) was used; figure 2b shows the parameters used to define the trilinear skeleton curve. Figure 2c shows the bilinear hysteresis model used for the damper system.
3. DESCRIPTION OF ANALYZED BUILDING MODELS
This study considers MDOF system models with 5, 10 and 20 stories as representative of low-, mid-, and high-rise buildings. Based on a study on R/C frames with hysteretic dampers previously done by the authors (Oviedo, Midorikawa and Asari, 2010), the story height and floor mass are set at 3.50 m and 601 kN-s2/m, respectively. Before installing hysteretic dampers, the story shear strengths and stiffnesses of R/C main frame were established based on the Building Standard Law of Japan (BSLJ) (BCJ, 2000). Here, it should be noted that the R/C main frame is kept unchanged while the mechanical properties of the damper system -yield strength and yield story drift- are changed. The BSLJ stipulates the lateral strength of the i-th story based on the story shear distribution factor Ai and the story shear coefficient Ci defined by
where C0 is the standard shear coefficient, T is the natural period, H is the building height, Qi is the shear strength of the i-th story, αi is the normalized weight above the i-th story, W is the total weight, Rt is the vibration characteristic factor as function of the natural period T and soil type (II), and Z is the seismic zone factor (Z=1.0).
3.1 Strength and stiffness of R/C main frame
To generate a representative set of stiffness variations for the R/C main frame, this study considers the following two cases: (i) variation of the overall stiffness and (ii) variation of the vertical distribution of story stiffnesses and strengths. For the case (i), under the design seismic force Qi with C0 = 0.2 in equations 2 and 4, the equivalent lateral stiffness of the R/C main frame at the i-th story Kieq (see figure 2b) was determined for four different story-drift angle limits: 1/50, 1/100, 1/200 and 1/300, covering from flexible to rigid structures. In accordance with the BSLJ, the ultimate shear strength of the R/C main frame at the i-th story, QiFy, was determined by setting C0 = 1.0, Fes=1.0 and Ds=0.3 in
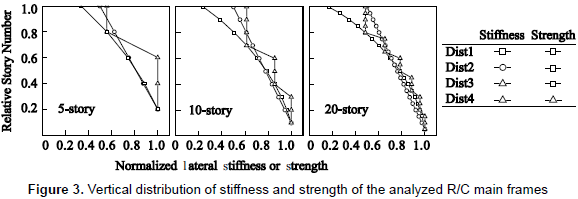
In equation 5, Ds is the structural characteristic factor and Fes is the shape factor which considers rigidity and eccentricity factors. For the case (ii), the values of Kieq and QiFy of the R/C main frame at the i-th story were determined for four different vertical distribution patterns: Dist1 to Dist4, as explained in table 1. Figure 3 shows the vertical distribution patterns of stiffness and strength normalized by the corresponding values for the first story.
3.2 Strength and stiffness of damper system
As previously mentioned, the structural characteristics of the damper system are assumed to be proportional to those of the R/C main frame. Thus, this study utilizes the yield strength ratio β (ratio of the yield strength of the damper system to that of the entire system, hereafter the strength ratio) and the yield drift ratio v (ratio of the yield story drift of the damper system to that of the R/C main frame, hereafter the drift ratio) (Oviedo, Midorikawa and Asari, 2010). The yield shear strengthQiFy and yield story drift ΔiFy at the i-th story of each R/C main frame have been determined according to the cases (i) and (ii), as explained in the previous section. Thus, referring to figure 1b, the yield strengths of the R/C main frame, damper system and entire system at each story are related by
The value of β varied from 0.1 to 0.9 with an interval of 0.1 to define the total yield shear strength of the damper system QDy. Thus, for each value of β , the yield shear strength of the damper system at the i-th story QiDy was determined by Equation 8. The yield story drift is determined by using the ‘constant yield story-drift ratio' scheme previously introduced by the authors (Oviedo, Midorikawa and Asari, 2010). This scheme uses the drift ratio v to define the yield story drift of the damper system from the structural characteristics of the primary structure (R/C main frame). The value of v varied from 0.1 to 1.0 with an interval of 0.1 to define the yield story drift ΔiDy and lateral stiffness KiD of the damper system at the i-th story.
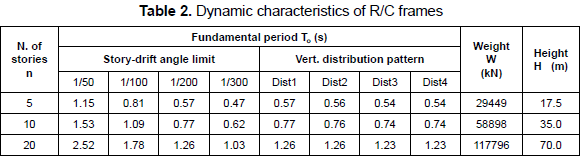
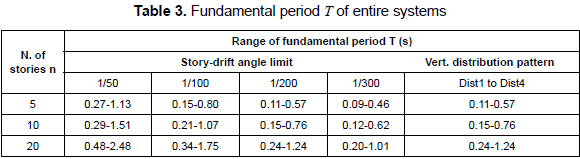
3.3 Dynamic characteristics of analyzed building models
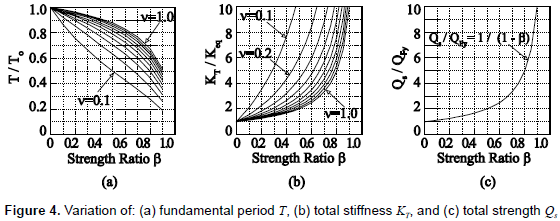
The dynamic characteristics of the series of R/C main frames and the range of fundamental period of analyzed building models are shown in tables 2 and 3, respectively. Figure 4 shows the variation of the fundamental period T, stiffness KT and strength Qs of the entire system of analyzed models after installing hysteretic dampers. From figure 1b, the variation of fundamental period T can be expressed in terms of the fundamental period of the building without dampers To, β and v by
Similarly, the variation of stiffness KT and Qs is given by
In general, the fundamental period T shortens with increasing values of β and decreasing values of v, due to the additional stiffness and strength given by dampers. However, this change in T is more noticeable when β changes, as clearly shown in figure 4a. Equations 12 and 13 shown in figures 4b and 4c, respectively, suggest that the capacity (strength and stiffness) of the entire system increases significantly for β > 0.5. Here, it should be noted that, although the use of a large value of β might not represent realistic conditions of structures, especially for new buildings, large values of β are considered in this study because they may represent the case of the retrofit of old buildings, and for the robustness of the results.
4. PARAMETERS AND INPUT GROUND MOTIONS
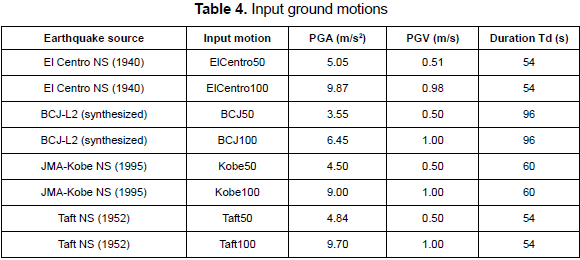
The numerical analyses correspond to the following parameters: (i) three numbers of stories (n = 5, 10 and 20), (ii) ten strength ratios (β = 0 to 0.9), (iii) ten drift ratios (v = 0.1 to 1.0), (iv) four storydrift angle limits at the design phase (1/50, 1/100, 1/200, 1/300), (v) four vertical distribution patterns of story stiffness and shear strength (Dist1 to Dist4), and (vi) different input ground motions, as shown in table 4. Four different source acceleration records were selected: two well-known earthquake ground motion records in the United States, El Centro NS (1940) and Taft NS (1952), and two earthquake records widely used in Japan, BCJ-L2 and JMAKobe NS (1995). In table 4, all ground motions have been scaled to meet two different levels of seismic intensity: peak ground velocity (PGV) of 0.50 m/s and 1.00 m/s. The selection of the acceleration records listed in table 4 corresponds to their very frequent use in the structural design practice in Japan. In the numerical analyses, the Rayleigh damping matrix was used with a viscous damping ratio of 3 % of the critical for the first two modes. For numerical step-by-step integration, the unconditionally stable Newmark's average acceleration method (Chopra, 1995) was used with a time step of 0.005 s. In total, over 15200 non-linear time-history analyses were performed.
5. ANALYSIS RESULTS AND DISCUSION
5.1 Influence of the story-drift limit at the design phase
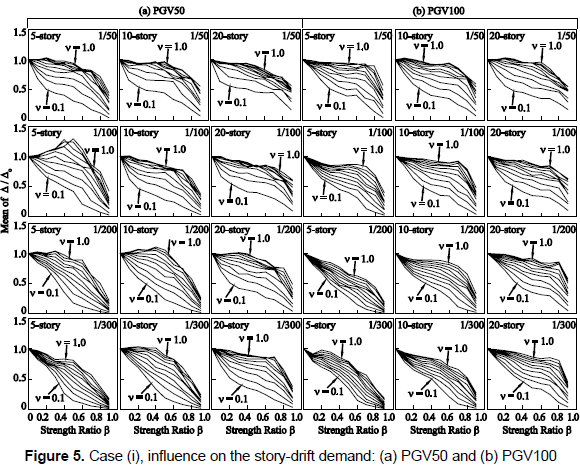
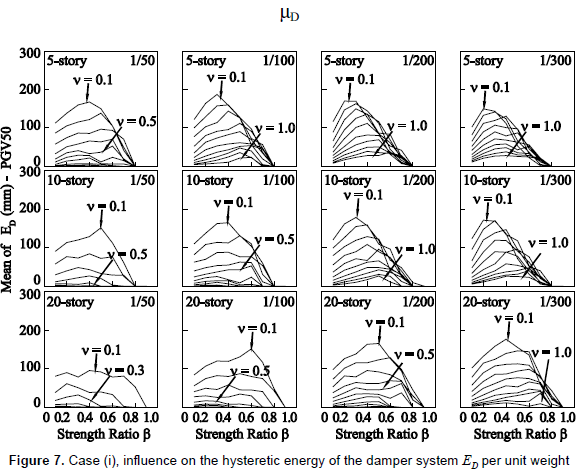
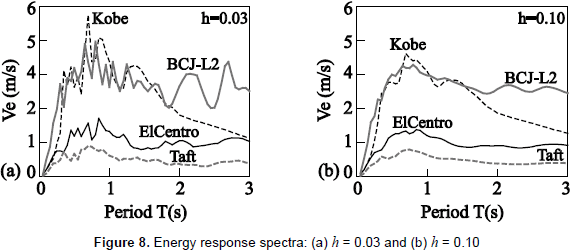
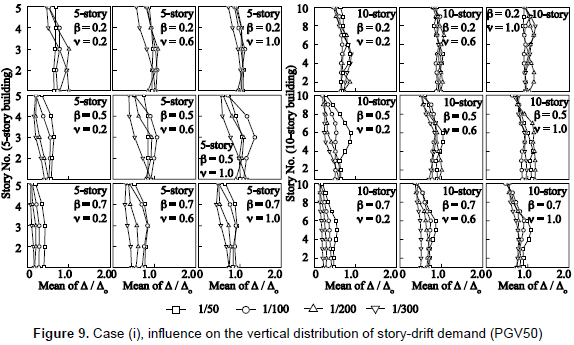
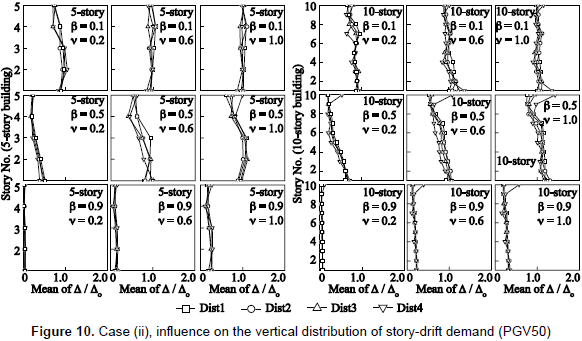
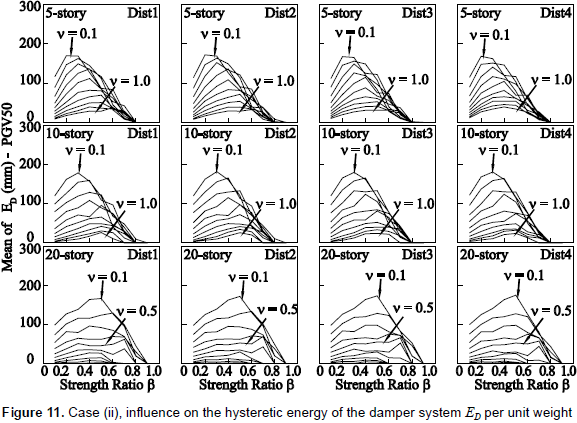
Results hereafter are divided into two groups of seismic intensity: PGV50 and PGV100. In figure 5, the vertical axis denotes the mean value of the ratio of story-drift demand Δ to that of the building without dampers Δo. Figure 6 shows the extent of inelasticity by means of the mean value of the storydrift ductility demand of the damper system µD. In figure 7, the vertical axis denotes the mean value of hysteretic energy of the damper system ED per unit weight. In figures 5 to 7, the mean values for a number of stories are computed from the response of all stories and under input motions of each PGV group. Figure 8 shows the elastic energy response spectra in terms of an equivalent velocity Ve of the source records for damping ratios of h = 0.03 and h = 0.1. Here, it should be mentioned that an elastic energy spectrum with a damping ratio of 0.1 may describe an envelope of the input energy of an inelastic system (Akiyama, 1985); especially for the long period range. Figure 9 shows the vertical distribution of the mean value of the Δ/Δo ratio.
From the analysis results shown in this group of figures, the following aspects are identified:
(1) The story-drift demand tends to decrease (Δ/Δo < 1.0) as β increases and v decreases, regardless of the value of the story-drift angle limit; however, an increase in the story-drift demand (Δ/Δo > 1.0) is clearly observed, especially for the 5- and 10-story models of the PGV50 group. It can also be observed that for a higher seismic intensity of PGV100, there is almost no increasing effect to the story-drift demand after installing dampers to the R/C main frame; this is a desirable performance when installing dampers. An increase in the storydrift demand is particularly observed for the case of 5- and 10-story models under a seismic intensity of PGV50 with a story-drift angle limit of 1/100 and 1/200, respectively, and with values of β smaller than 0.5 and values of v larger than 0.6. This increase is attributed to the increase in the input energy and to a large extent of inelasticity for analysis cases whose response period fell within the range of periods near to the corner period between the short and the long period range, as can be inferred from figure 8. In this context, it is worth mentioning that for the short period range, the input energy increases due to plastification and to a larger period which dominates the response, and for the long period range, the energy response spectra shape softens for a large damping ratio (i.e., large extent of inelasticity) (Akiyama, 1985). The latter phenomenon can be clearly identified in figure 8.
(2) After installing dampers, the following response patterns are identified based on the fundamental period of R/C main frame: (i) in R/C main frames whose fundamental periods fell in the short period range (i.e., 5-story [1/300]), the input energy tends to be slightly larger or smaller than that of the R/C main frame regardless of the extent of inelasticity. Moreover, for an entire system with a large capacity (β > 0.5 and v < 0.5), its fundamental period shortens significantly compared with that of the R/C main frame, resulting in a larger reduction in the input energy (as can be inferred from figure 8). (ii) In R/C main frames whose fundamental periods fell in the long period range (i.e., 10-story [1/50] and 20-story [1/50 and 1/100]), the story-drift demand tends to decrease despite larger energy inputs because the damper system responded inelastically while the R/C main frame remained essentially elastic. (iii) In R/C main frames whose fundamental periods fell in the vicinity of the corner period between the long and short period range (i.e., 5-story [1/50, 1/100 and 1/200], 10-story [1/100, 1/200 and 1/300] and 20-story [1/200 and 1/300]), there is a high fluctuation in the input energy which might bring an increase in the story-drift demand.
(3) Regardless of the seismic intensity or an increase in the input energy after installing dampers, for an entire system in which the strength of the damper system is larger than that of the R/C main frame (i.e., β > 0.5), the story-drift demand is almost unlikely to be amplified as the capacity of the entire system increases significantly (see figures 4b and 4c). The storydrift demand also seems unlikely to be amplified for β < 0.5 and under a strong ground motion (PGV100), because the input energy is almost the same as that of the R/C main frame (due to a smooth fluctuation in the input energy) while the capacity of the structure increases, as seen in figures 4b and 4c. Here, it should be noted that the possibility of an increase in the storydrift demand decreases with decreasing values of v.
(4) With regard to the influence on the hysteretic energy dissipated by the damper system ED as shown in figure 7, it can be observed that a damper system installed to an R/C main frame whose fundamental period fall in the short period range contributes to the hysteretic energy dissipation, regardless of the values of v. On the other hand, a loss of efficiency in contributing to dissipating hysteretic energy is observed for a damper system with a value of v larger than 0.5 and installed into a flexible R/C main frame. Another important aspect is that there is a tendency of the value of β that maximizes ED (i.e., an optimum β ) to decrease with the decrease of the story-drift angle limit, especially for the 5- and 10-story models. This indicates that an optimum value of β is dependent not only on the relative stiffness between the main frame and damper system, expressed by the stiffness ratio k, as proposed by Inoue and Kuwahara (1998), but also somewhat on the overall stiffness of the main frame. With the maximization of ED, a higher protection of the R/C main frame is assured. The results in figure 7 provide additional support to what has been reported in previous investigations (e.g., Nakashima, Saburi and Tsuji, 1996; Inoue and Kuwahara, 1998); it is advisable to keep the yield strength of dampers low, i.e., low values of β , so that energy dissipation occurs in the damper system before the main frame goes beyond its elastic range.
(5) According to figure 9, the Δ/Δo ratio remains relatively constant throughout all stories, which suggests a uniform control of the story-drift demand regardless of the number of stories and the value of β or v. Oviedo, Midorikawa and Asari (2010) reported a similar behavior for the case of R/C frames. It is also observed that the tendency of the Δ/Δo ratio to remain constant over the building height is stronger in the case of a damper system installed into a flexible R/C main frame. Another important point to note is that a damper system with a low value of v and β and installed into a flexible R/C main frame tends to produce a larger reduction in the story-drift demand than that when installed into a rigid R/C main frame.
Finally, it should be noted that the results shown in this section and subsequent one correspond to response trends after installing dampers rather than to an extent of reduction or increase in the seismic response, compared with that of the building without dampers.
5.2 Influence of the vertical distribution of stiffness and strength
Figures 10 and 11 summarize some analysis results of the study of the influence of the vertical distribution of story stiffnesses of R/C main frame. Figure 10 shows the influence on the vertical distribution of the story-drift demand, and figure 11 shows the influence on the hysteretic energy dissipated by the damper system. From figure 11, it is evident that the amount of reduction or increase in the hysteretic energy of dampers is scarcely affected by the vertical distribution of stiffness or strength. Moreover, the input energy response was found to be practically not affected by either the vertical distribution of strength or stiffness. This is mainly because there is no change in the response period, as shown in table 3. On the other hand, the story-drift response depicted in figure 10 reveals a slight difference in the response of Dist4 pattern. Here, the story-drift response is more influenced by the vertical distribution of strength (Dist4) than by that of stiffness (Dist1 to Dist3). Although the difference in the response among all four distribution patterns is not significant, it seems to increase with increasing values of v. Moreover, although not shown here, the results indicate that the difference in the response between Dist1 to Dist 3 and Dist4 patterns is mainly because the response of the R/C main frame in most analysis cases for the Dist4 pattern was essentially elastic, whereas inelastic for Dist1 to Dist3 patterns (i.e., responses of the R/C main frame in Dist4 pattern shifted from the inelastic (µF > 1.0) to the elastic range (µF < 1.0)). This shift is due to story shear strengths larger than those of Dist1 to Dist3 patterns.
6. CONCLUSIONS
The influence of the range of stiffness of R/C main frame on the earthquake response of R/C buildings with proportional hysteretic dampers was investigated. The influence of overall stiffness of R/C main frame was studied by using different story-drift angle limits at the design phase, from flexible to rigid structures. The influence of the vertical distribution of story stiffnesses and strengths was studied by using different distribution patterns that represent those often used in the design practice.
The results indicate that the range of overall stiffness of R/C main frame has an important role in the earthquake response. This role is understood as a contributing factor to the possibility of story drift demands larger than those on the structure without dampers. This is clearly contrary to a desirable reduction in the deformation demand when installing hysteretic dampers to a building structure. Thus, the mechanical properties of dampers should be selected so that the response period of an entire system (R/C main frame and damper system) does not fall in the vicinity of the corner period between the short and long period range of the response spectrum of an input ground motion or around the natural period where the input energy takes the maximum value; if so, the yield story drift of dampers should be small enough compared with that of the R/C main frame. By using a small yield story drift for dampers, for instance 50 % of that of the R/C main frame or smaller, not only the possibility of an increase in the story drift demand is reduced, but also the damper system contributes to the hysteretic energy dissipation.
The efficiency of the damper system in reducing story drift demands, due to the additional stiffness, strength and energy dissipation capacity given by dampers, is dependent on the overall stiffness of R/C main frame. A damper system with a yield story drift smaller or equal than half of that of the R/C frame, and with a yield shear strength smaller than that of the R/C main frame, is shown to be more efficient in reducing the story drift demand when installed into a flexible R/C main frame. Moreover, when installing a damper system whose yield story drift is proportional to that of the R/C main frame, the ratio of the maximum story drift to that of the building without dampers tends to remain relatively constant over the building height, regardless of the overall stiffness of R/C main frame. However, this tendency becomes stronger in the case of a damper system installed into a flexible R/C main frame. The vertical distribution of stiffness and strength of R/C main frame has a minor effect as well.
Finally, further study will certainly strengthen the results herein presented. For instance, it is appropriate to consider the effect of global flexural deformation and a much larger population of ground motions along with their statistics. However, response trends obtained from the results provide a valuable insight on the influence of the story stiffness and strength of R/C main frame on the seismic response of R/C buildings with proportional hysteretic dampers, and are expected to contribute to ongoing efforts toward the seismic response control of this type of building structures.
ACKNOWLEDGEMENTS
The author would like to acknowledge the financial support given by the Ministry of Education, Culture, Sports, Science and Technology of Japan. The author would also like to express his gratitude to Professor Mitsumasa Midorikawa and Assistant Professor Tetsuhiro Asari for their support during the stay at Hokkaido etsuhiro University.
REFERENCES
Akiyama, H. Earthquake-resistant limit-state design for buildings. Tokyo: University of Tokyo Press, 1985. 372 p. [ Links ]
Bozorgnia, Y. and Bertero, V. V. Earthquake engineering: From engineering seismology to performance-based engineering. Florida: The International Code Council and CRC Press, 2004. 1268 p. [ Links ]
Cherry, S. and Filiatrault, A. (1993). "Seismic response control of buildings using friction dampers". Earthquake Spectra, vol. 3, No. 7, pp. 447-466. [ Links ]
Chopra, A. K. Dynamics of structures: Theory and applications to earthquake engineering. New Jersey: Prentice-Hall, 1995. 844 p. [ Links ]
Higashino, M. and Okamoto, S. Response control and seismic isolation of buildings. London and New York: Taylor and Francis, 2006. 400 p. [ Links ]
Inoue, K. and Kuwahara, S. (1998). "Optimum strength ratio of hysteretic damper". Earthquake Engineering and Structural Dynamics, vol. 27, No. 6 (June), pp. 577-588. [ Links ]
Iwata, M. and Murai, M. (2006). "Buckling-restrained brace using steel mortar planks; performance evaluation as a hysteretic damper". Earthquake Engineering and Structural Dynamics, vol. 35, No. 14 (November), pp. 1807-1826. [ Links ]
Kim, J. and Choi, H. (2004). "Behavior and design of structures with buckling-restrained braces". Engineering Structures, vol. 26, No. 6, pp. 693-706. [ Links ]
McNamara, R. J. (1995). "Seismic damage control with passive energy devices: A case study". Earthquake Spectra, vol. 11, No. 2, pp. 217-232. [ Links ]
Nakashima, M.; Saburi, K. and Tsuji, B. (1996). "Energy input and dissipation behaviour of structures with hysteretic dampers". Earthquake Engineering and Structural Dynamics, vol. 25, No. 5 (May), pp. 483-496. [ Links ]
Oviedo, J. A.; Midorikawa, M. and Asari, T. (2008a). Optimum strength ratio of buckling-restrained braces as hysteretic energy dissipation devices installed in R/C frames. Proceedings of the 14th World Conference on Earthquake Engineering, Beijing, China, Paper No. 05-03-0235. [ Links ]
Oviedo, J. A.; Midorikawa, M. and Asari, T. (2008b). "Optimum strength ratio of hysteretic energy dissipating devices in R/C frames - Case of buckling-restrained braces". Journal of Structural Engineering and Construction (Transactions of AIJ), vol. 54B, pp. 571-580. [ Links ]
Oviedo, J. A.; Midorikawa, M. and Asari, T. (2009). Story drift response of R/C buildings with hysteretic dampers. Proceedings of the 33rd IABSE Symposium, Bangkok, Thailand, Paper No. 240-02-01. [ Links ]
Oviedo, J. A.; Midorikawa, M., and Asari, T. (2010). "Earthquake response of ten-story story-drift-controlled reinforced concrete frames with hysteretic dampers". Engineering Structures, vol. 32, No. 6, pp. 1735-1746. [ Links ]
Soong, T. T. and Spencer, Jr. B. F. (2002). "Supplemental energy dissipation: State-of-the-art and state-of-thepractice". Engineering Structures, vol. 24, No. 3, (March), pp. 243-259. [ Links ]
Takeda, T.; Sozen, M. A. and Nielsen, N. N. (1970). "Reinforced concrete response to simulated earthquakes". Journal of Structural Division (ASCE), vol. 96, No. 12 (December), pp. 2557-2573. [ Links ]
Takewaki, I. Building control with passive dampers: optimal performance-based design for earthquakes. Singapore: John Wiley and Sons (Asia), 2009. 306 p. [ Links ]
Teran-Gilmore, A. and Virto-Cambray, N. (2009). "Preliminary design of low-rise buildings stiffened with bucklingrestrained braces by a displacement-based approach". Earthquake Spectra, vol. 25, No.1, pp. 185-211. [ Links ]
The Building Center of Japan (BCJ). The building standard law of Japan, 2000. [ Links ]
Tsai, K. C. and Hong, C. P. (1992). Steel triangular plate energy absorber for earthquake resistant buildings. Proceedings of the 1st World Conference on Constructional Steel Design, Acapulco, Mexico (6-9 December). [ Links ]
Wada, A. and Nakashima, M. (2004). From infancy to maturity of buckling-restrained braces research. Proceedings of the 13th World Conference on Earthquake Engineering, Vancouver, Canada, Paper No. 1732. [ Links ]
Whittaker, A. S.; Bertero, V. V. and Alonso, J. (1989). "Earthquake simulator testing of steel plate added damping and stiffness elements", Report No. UCB/ EERC-89/02, Earthquake Engineering Research Center, University of California, Berkeley, California. [ Links ]
Yamaguchi, H. and El-Abd, A. (2003). "Effect of earthquake energy input characteristics on hysteretic damper efficiency". Earthquake Engineering and Structural Dynamics, vol. 32, pp. 827-843. [ Links ]