A SYSTEMATIC REVIEW ON IDENTIFICATION OF EXCITATION SYSTEMS FOR SYNCHRONOUS GENERATORS

REVISIÓN SISTEMÁTICA EN IDENTIFICACIÓN DE SISTEMAS DE EXCITACIÓN PARA GENERADORES SINCRÓNICOS

REVISÃO SISTEMÁTICA EM IDENTIFICAÇÃO DE SISTEMAS DE EXCITAÇÃO PARA GERADORES SINCRÓNICOS

Andrés Julián Saavedra-Montes^*, Carlos Andrés Ramos-Paja^** y José Miguel Ramírez^***

^*Ingeniero Electricista, Magíster en Sistemas de Generación de Energía Eléctrica y Doctor en Ingeniería Eléctrica, Universidad del Valle. Profesor Asociado, Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. ajsaaved@unal.edu.co.
^**Ingeniero Electrónico y Magíster en Ingeniería, Universidad del Valle; Doctor en Ingeniería Electrónica, Automática y Comunicaciones, Universitat Rovira i Virgili. Profesor Asociado, Departamento de Energía Eléctrica y Automática, Facultad de Minas, Universidad Nacional de Colombia. Medellín, Colombia. caramosp@unal.edu.co.
^***Ingeniero Electricista y Magíster en Sistemas de Generación de Energía, Universidad del Valle; Doctor en Automática, Université Joseph Fourier, Grenoble, Francia. Profesor Titular, Escuela de Ingeniería Eléctrica y Electrónica, Facultad de Ingeniería, Universidad del Valle. Cali, Colombia. jose.ramirez@correounivalle.edu.co.

Artículo recibido 16-VI-2011. Aprobado 24-VII-2012
Discusión abierta hasta junio de 2013

ABSTRACT

This paper presents the state of the art on system identification applied to excitation systems. First, general overviews about system identification and excitation systems for synchronous generators are presented, highlighting the unique characteristics imposed by the excitation systems in an identification process. Then, a bibliographic classification method based on the excitation system characteristics was designed, which provides a results matrix condensing the topics addressed by more than 40 reviewed publications. From the results analysis the state of the art in excitation system identification was established, and open research areas in the topic were recognized.

KEY WORDS: excitation system; synchronous generator; system identification; literature systematization.

RESUMEN

Este artículo presenta el estado del tema en identificación de sistemas aplicada a sistemas de excitación. Primero se presenta una visión general de identificación de sistemas y de los sistemas de excitación de generadores sincrónicos, resaltando las características impuestas por los sistemas de excitación en un proceso de identificación. Luego se presenta el diseño de un método de clasificación basado en las características de los sistemas de excitación. El resultado del método es una matriz que condensa los asuntos discutidos en más de 40 publicaciones. El estado se establece desde el análisis de los resultados y adicionalmente se reconocen áreas abiertas de investigación en la identificación de sistemas de excitación.

PALABRAS CLAVE: Sistema de excitación; generador sincrónico; identificación de sistemas; revisión sistemática.

RESUMO

Este artigo apresenta o estado do tema em identificação de sistemas aplicada a sistemas de excitação. Primeiro apresenta-se uma visão geral de identificação de sistemas e dos sistemas de excitação de geradores sincrónicos, realçando as características impostas pelos sistemas de excitação em um processo de identificação. Depois se apresenta o desenho de um método de classificação baseado nas características dos sistemas de excitação. O resultado do método é uma matriz que condensa os assuntos discutidos em mais de 40 publicações. O estado estabelece-se desde a análise dos resultados e adicionalmente reconhecem-se áreas abertas de investigação na identificação de sistemas de excitação.

PALAVRAS-CÓDIGO: Sistema de excitação; gerador sincrónico; identificação de sistemas; revisão sistemática.

1. INTRODUCTION

The stability analyses support the planning and operation of power systems. The accuracy of stability studies depends on the model structures and parameters of the power system elements such as synchronous generators, excitation systems, turbines, and speed governors. A large number of generation companies around the world do not have appropriate models for these studies, particularly because they have no precise parameter values.

Nowadays there is renewed interest on the identification of excitation systems. This renewed interest is because regulators have recommended testing and verifying models of the elements in power generating units, among these excitation system models, as reported by Karl and Schaefer (2004) and Veloza and Cespedes (2006). The excitation system identification is a research topic well explored, i.e. there are a large number of publications about this subject, creating a challenge for those who want to research in the topic because open research issues are not evident.

To investigate in fields in which there is no previous knowledge or experience, it is possible to collect articles on the topic and try to identify open research issues. The success of this task is often associated with the researcher’s experience. However, for those who start as young researchers and for those who choose to work in unfamiliar areas, tools to detect open research issues will be useful.

This paper presents the state of the art on system identification applied to excitation systems. First, general overviews about system identification and excitation systems for synchronous generators are given. Then, a bibliographic classification method is presented, which is used to review the publications in excitation system identification, to establish the state of the art, and to detect open research issues in the topic. The paper is organized as follows: a general description of system identification is presented in section 2, where a flow chart showing the four basic identification stages and some important aspects about each identification stage are discussed. Section 3 deals with the excitation systems for synchronous generators. The elements and signals that shape the excitation system and the excitation system classification according to the power source used for excitation are presented in this section. The modeling of excitation systems published and standardized by IEEE, and the characteristics of excitation system models are also presented. The state of the art in system identification applied to excitation systems is provided in section 4. To establish the state of the art, a bibliographic classification method was designed. The method was also used to review the publications in excitation system identification and to detect open research issues in the topic. In addition, the steps to develop the classification method are presented in this section. Finally, the conclusions are given in section 5.

2. BACKGROUND ON SYSTEM IDENTIFICATION

This section gives a general background on system identification to contextualize the analysis and results given in this paper. The background is mainly based on traditional references for system identification such as Eykhoff (1974), Söderström and Stoica (1989), and Ljung (1999), providing the required knowledge to extract the particular requirements for excitation system identification.

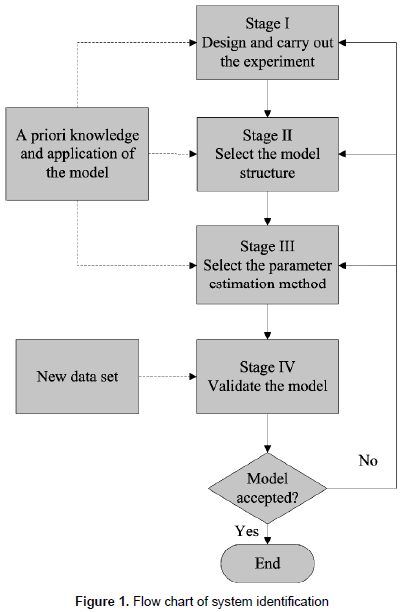
Figure 1 presents a flow chart that describes a general identification process. To identify a system, an experiment to collect input/output data of the system should be designed and carried out. The intended application and the previous knowledge about the model are used to design the experiment. The experiment consists in applying some perturbation signal, e.g. a step signal, sinusoidal signals, rich in frequency binary signals, etc., and sampling the input/output signals with a data acquisition system. The input/output data are recorded and stored for their pre-processing.

The next step is to select a model structure taking into account the knowledge about the system behavior to increase the possibilities of a successful identification. Then, the method to estimate the parameters of the chosen model is selected. These steps take into account the prior knowledge and the future use of the model. Among the criteria to select the estimation method are the model structure and the system operating conditions. Once the structure and the estimation method have been selected, a simulation is done in which the estimation algorithm adjusts the structure parameters until the output signal meets a previously defined criterion.

The model can be validated comparing its output against the system output to the same input and/or comparing a parameter set of reference with the estimated parameters. Also, there are several indexes to validate the model, which are chosen depending on the intended application. If validation criteria are met, the identification process concludes; otherwise previous steps must be revised looking for possible sources of error until a proper representation of the system is obtained.

To provide a background on the identification process given in figure 1, important aspects at each stage such as the input or excitation signals, the structure of linear models, the methods to estimate parameters and to validate models are discussed.

2.1 Input or excitation signals

At the design of the experiment stage, the most important aspects are the perturbation signal or input signal and the sampling time. Some input signals are the step signal, the sum of sinusoids, the chirp signal, and the pseudo-random binary signals. Detailed information of previous signals is found in Söderström and Stoica (1989) and Ljung (1999). A list of available programs on the Internet to generate some excitation signals in addition to its classification is found in Godfrey et al. (2005).

2.2 The model structure

There are several ways to classify dynamic models and therefore their structures. Based on the number of inputs and outputs, the model can be: single input, single output; single input, multiple outputs; multiple inputs, single output; or multiple inputs, multiple outputs. Based on the input-output dependency, the models can be linear and nonlinear; they are linear when the output or outputs depend linearly on the input or inputs. Also there are parametric and non-parametric models, the former are described by a set of parameters and the latter can consist of a curve or graph.

There is another classification based on the domain model. There are time domain and frequency domain models. Differential and difference equations are examples of time domain models, which can be discrete or continuous. Particularly a continuous time model can be fitted to a discrete time data.

2.3 Methods to estimate parameters

The methods to estimate parameters are classified as parametric and non-parametric. The nonparametric method results are curves or functions from which parameters must be obtained; among these, the transient analysis of a step response and the frequency response analysis are found. The parametric method results are parameter vectors. The least square (LS) method is used to estimate static models of linear regression. An extension of this method allows estimating dynamic models. An LS generalization is the prediction error method (PEM), and another LS generalization is the instrumental variable (IV) method. There are instances in which PEM is known as the generalized minimum square (GLS) method. In other cases PEM could be interpreted as the maximum likelihood (ML) method. When the LS, IV, and PEM methods are applied to estimate parameters on line, they are known as recursive estimation methods or online estimation methods.

2.4 Methods to validate models

Validating a model can be compared with the larger amount of information on the real system as much as practical. There are several methods of validation that could clear the doubts about the model and could create confidence in its use. A natural validation method is to solve the problem that inspired the modeling exercise. If the model succeeds in solving the problem set forth, then this model can be considered valid, but this method can be expensive and not practical. There are other methods that help create confidence in using the model.

When the model structures are based in physical parameters, i.e., the excitation system models, an important method of validation is to compare the estimated values with their estimated variances. Some knowledge of possible values must exist. Another method of validation is to compare the response from the model and the real system to the same input. This method shows which characteristics of the real system the model reproduces and which it does not.

The residual analysis is based on the residues that are part of the data that the model can not reproduce. Applying basic statistics on the residues some information can be had in regard to the model, but nothing convincing. The covariance between the residues and past inputs gives convincing information. For example, if the covariance is small, there are some reasons to believe that the data is relevant. The correlation of the residues between themselves also gives convincing information; for example, if the residues correlation is small, this is a sign of a deficient model.

3. EXCITATION SYSTEMS FOR SYNCHRONOUS GENERATORS

The excitation system is a control system associated with synchronous machines. When it works associated with a synchronous generator connected to the grid, its functions are to supply direct current to the generator field windings, regulate the generator terminal voltage, control the reactive power flow between the generator and the power grid, improve the stability of the power system, and provide limiting and control functions to the generator.

3.1 Elements and signals of excitation systems

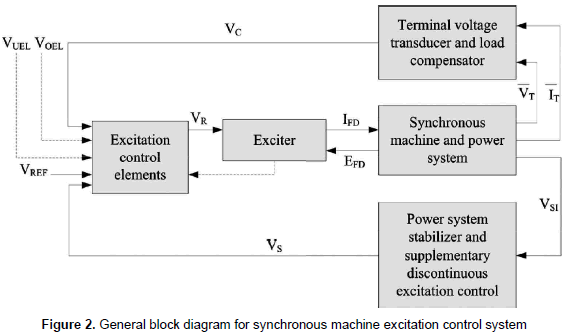
Commonly, excitation systems are composed of a terminal voltage transducer, an automatic voltage regulator, an exciter and compensators. Sometimes, it also includes limitation and protection circuits, and a power system stabilizer as reported in IEEE (2006); see figure 2.

Terminal voltage transducer conditions the terminal voltage to introduce it to the automatic voltage regulator (AVR). The AVR processes and amplifies the input signal to an appropriate level and form in order to control the exciter, which provides the power of direct current to the field winding of the generator. Protective and limiting systems include a wide number of control and protection circuits that guarantee the operation within the capability limits of the exciter and the generator. Power system stabilizer introduces damping to mitigate the oscillations of the power system. Additional compensators could be introduced to deal with load transients, line drops, and reactive current. Finally, the excitation control system is composed by the excitation system and the synchronous generator. The description of the excitation system signals depicted in figure 2 is given in table 1.

3.2 Excitation systems classification

Excitation systems are classified in three groups according to the power source used for excitation (IEEE, 2006). Direct current (DC) excitation systems use direct current generators to feed the field windings of the synchronous machine. Alternate current (AC) excitation systems use alternate current generators in sets with rotary or static rectifiers to feed the field winding of the generator. Static (ST) excitation systems can be composed by transformers and rectifiers that feed with direct current the generator field winding.

In each one of the previous categories there are systems with distinctive characteristics that differentiate them, producing new subcategories. For almost each subcategory there is a model that represents the system (IEEE, 2006).

3.3 Modeling of excitation systems

In 1968 IEEE Power Engineering Society released a report about most widely known excitation system models in the USA and Canada (IEEE, 1968). The purpose of that document was to normalize nomenclature and structure of models existing at that time. The scope of the models is limited to studies of power systems. The parameters of those models are presented in per-unit system. Some nonlinearities, such as the magnetic saturation of rotating exciters and limits of the regulator signals, are presented. The models in IEEE (1968) were not the first models of excitation systems, but they were the first normalized models.

In 1981 the IEEE Working Group on Computer Modeling of Excitation System extended the work presented in IEEE (1968) in a new publication, IEEE (1981). The proposed models, which have been widely used by the industry, were improved for the new excitation systems that were not properly represented by the older models. In 1992 the recommended practice of the excitation system models for power systems stability studies is consolidated by IEEE. In this standard, models for the load compensator and the voltage transducer are presented. Per unit system, and the representation of the magnetic saturation, the regulation of rectifiers and the limits of signals are described too.

In IEEE (1996) new models were introduced representing the new equipment that had controllers based on digital technology; the models were presented in the continuous time domain to be used jointly with the models already proposed and programmed with available software. These models consider the flexibility that controllers based on digital technology have, particularly taking into account the use of PI and PID controllers.

Review and update of the practice recommended in 1992 was published in IEEE (2006). An extension presented is a new model for the load compensator. The most relevant change is the fact that it includes systems based on digital technology. This change is evidenced in the fact that PID or PI controllers that could be easily programmed in digital processors are included. Underexcitation and overexcitation limiters models are presented too, on real time domain to be used jointly with those already proposed and to be easily programmed in packages of power systems analysis.

The main characteristics of the described excitation system models are:

• Excitation systems are represented through mathematical models on the bases of physical laws that describe the equipment. Some models have one input and one output, and some others have two inputs and one output; generally the output variable is the generator field voltage EFD.
• These models have a reduced order and do not represent all the dynamics of the control loop. The models are in the continuous time domain, although some represent excitation systems based on digital technology. In addition, the models are described by a set of concentrated parameters, which are invariants in time.
• Some of the models include nonlinearities such as signal limits, magnetic saturation of rotating exciters, and the nonlinear effect of rectifier regulation. According to IEEE (2006), the models are valid for frequency deviations of ± 5 % from rated frequency and oscillation frequencies up to 3 Hz.

4. SYSTEM IDENTIFICATION APPLIED TO EXCITATION SYSTEMS

Generally, scientific publications about system identification applied to excitation systems cover all the stages of the identification process, additionally excitation systems exhibit unique characteristics when they are identified. Each publication on excitation system identification is focused on some of the identification stages and takes into account some of the unique characteristics of excitation systems.

To establish the state of the art of excitation system identification a bibliographic classification method has been designed to review the publications, and to detect open research issues in the topic. The method is developed in three steps. First, the characteristics in excitation system identification and consequent conditions that should be fulfilled in an identification process are defined. Then, an assessment system based on the conditions defined in the first step is designed. The third step consists of reading and assessing every article by using the assessment system to identify distinctive characteristics and condense the information obtained in a results matrix.

4.1 Characteristics of excitation system identification

Based on the prior knowledge, five characteristics of excitation system identification and four consequent conditions are defined to assess the selected articles. The criterion to select the papers to be reviewed considers paper titles or abstracts focused on system identification or parameter estimation of excitation systems. The characteristics adopted are:

1. Since the excitation system (EXS) must work in closed loop with feedback from the generator terminals, the identification experiments should be performed under this condition. When a system operates in closed loop, the dynamics of the system elements affect each other, making it difficult to estimate them, as reported in Landau and Zito (2006). The experiment to identify the EXS can be carried out in open loop with no connection to the generator, but this would mean that the system would not be identified in its most common operation state.
2. The EXSs are modeled in detail by standard models accepted by engineers to analyze the power system, and analysis software packages have most of those models, or at least those that can be implemented in their libraries. This means that detailed structures of the models to be used in the identification are available.
3. The EXS belongs to a costly process that operates continuously, so the generator availability should be maintained. This means that the experiment for identification purposes must be carried out in short periods of time and preferably with the generator connected to the power system.
4. There are several types of excitation systems and each one has specific requirements for identification. For example, brushless excitation systems do not have the generator field signals available for measurement. In this case, the terminal voltage signal is measured including the generator in the identified model. Static excitation systems generate noise due to the bridge rectifier. This noise affects directly the generator field signal, thereby increasing the difficulty in the estimation process. Filtering the noise may filter also the dynamics of the system.
5. Since the generator can operate offline or online, the identification experiments can be carried out in the two regimes. When the generator operates offline there is interaction among the dynamics of the components of the excitation control system, including the generator. However, in this regime the generator model is simple and well known. When the generator is connected to the power grid, the generator model has complex dynamics, and the excitation control system is exposed to more disturbances.

From such characteristics, the main four conditions that should be fulfilled in an identification experiment are:

1. Carrying out the experiment in closed loop, regardless the generator is online or offline. The estimation method should take into account the limitations of closed loop identification.
2. Using the detailed and standard structures of the EXS models.
3. Avoid the unavailability of the generator. Experiments in short periods of time and perturbation signals with magnitudes that do not affect the operation and security of the generator should be used.
4. Using signals sufficient to estimate all the required parameters.

4.2 Assessment system

The assessment system is shown in table 2. The system includes the four typical stages of an identification process: design and carry out the experiment, select the model structure, select the parameters estimation method, and validate the model. At each stage, there are some categories, and in each category there are the actions or elements that can be reported in an article about excitation system identification. For example in the first stage, the category was generated because the experiment can be carried out with the generator online, offline or during a disturbance, see table 2.

The actions and elements are assessed according to the conditions defined in section 4.1. Table 2 shows a number in parenthesis in front of each category, which is the maximum value that receives that category. In front of each action or element appears the value to be assigned if the paper fulfills it. Such values were defined in agreement with the categories, actions and elements contribution to the defined conditions. For example, category 1(operating conditions of the synchronous machine) has a maximum value of 2, while category 3 (signal processing) has a maximum value of 1. Such a difference is caused by the stronger influence of category 1 in the conditions defined in section 4.1 over the impact of category 3. Similarly, in the evaluation of category 1, the element increases the category value because such an operation condition is clearly required in the third condition (c) defined in section 4.1, therefore generator offline has a null value. In the same category, a null value has been assigned to the element since it is not possible to design the perturbation signal and to schedule the tests.

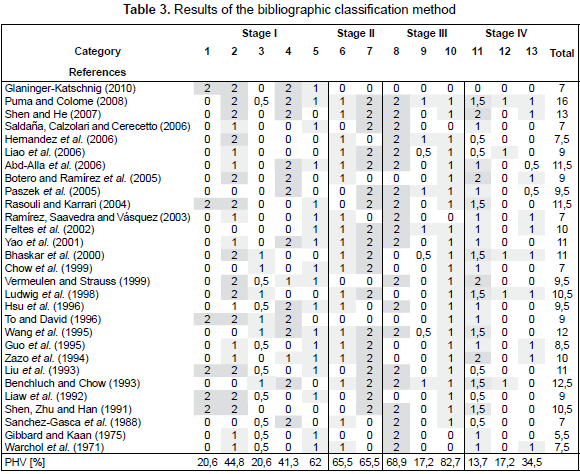
Table 3 shows the results of the bibliographic classification method condensed in a matrix, in which there are the references and the thirteen categories assessed for each paper. In the last column there is reported the total value assigned to the reference according to the four conditions previously defined. In the last row the percentage of papers with the highest value PHV [%] for each category, is presented.

There are several approaches to extract information from table 3. The table can be interpreted by categories; e.g. in category 1 only six papers, or 20,6 %, have carried out experiments with the generator operating online. In category 5, eighteen papers or 62 %, have collected data in power plants. Table 3 could also be interpreted combining categories, e.g. in categories 1 and 5 it is observed that only four papers report experiments carried out with the generator operating online into power plants. Another interpretation is to observe the total value in the last column and determine the papers that better match the conditions given in section 4.1.

Since the references are organized in a chronological form, some information can be interpreted also in this way, e.g. in category 3, authors discussed the noise and signal processing between 1971 and 2000, the broader discussion took place between 1993 and 2000, and from 2000 until now the noise issue did not discussed again.

4.3 Results of the bibliographic classification method

From the results given in table 3 several analyses can be performed, where the most important to reach the conditions defined in section 4.1 are:

In category 1, only 20,6 % of the publications have reported experiments with the generator online: Shen, Zhu and Han (1991), Liaw et al. (1992), Liu et al. (1993), To and David (1996), Rasouli and Karrari (2004), Glaninger-Katschnig (2010), and only four publications have reported experiments in power plants, and not in prototypes or models. The low percentage of publications that report experiments with the generator operating online, in contrast to the requirement to avoid the unavailability of the generation, shows that the identification experiments with the generator online must be further investigated.

In category 2, references Shen, Zhu and Han (1991), Liaw et al. (1992), Liu et al. (1993), To and David (1996), Ludwig et al. (1998), Vermeulen and Strauss (1999), Bhaskar et al. (2000), Rasouli and Karrari (2004), Botero and Ramírez (2005), Hernandez et al. (2006), Shen and He (2007), Puma and Colome (2008) and Glaninger-Katschnig (2010) report the use of signals with persistently excitation as the PRBS signal. Those signals are rich in frequencies and perturb the system dynamics in the interest frequency range. In Rasouli and Karrari (2004) the authors use square and triangular signals with maximum frequencies less than 3 Hz. The validation results support the use of those signals. In category 3, it must be highlighted the fact that among the reviewed papers it was not a noise consideration or especial processing of signals from 2001 to 2010.

In category 4, 41,3 % of the publications report the use of input/output data from the complete excitation system to estimate all the linear model parameters. Similarly, in category 7 only 65,5 % of publications report that more than four parameters were estimated using input/output data of the complete excitation system model. Therefore, taking into account that not all the elements input/output terminals are available in the excitation system, algorithms that estimate all the model parameters from input/ output data of the complete excitation system must be proposed.

In category 9, the nonlinearities estimation of excitation systems is a topic actively explored from 2002. The estimation of the nonlinearities directly from the estimation method is reported in Benchluch and Chow (1993), Feltes et al. (2002), Paszek et al. (2005), Hernandez et al. (2006), and Puma and Colome (2008), while Ramírez, Saavedra and Vásquez (2003) report the nonlinearities estimation from independent experiments, which leads to undesired offline time of the generator.

In category 10, most of the publications have reported the use of parametric estimation techniques. Only in references Warchol et al. (1971), Gibbard and Kaan (1975), Ramírez, Saavedra and Vásquez (2003), Saldaña, Calzolari and Cerecetto (2006), and Glaninger-Katschnig (2010) non-parametric techniques have been reported. Usually, non-parametric techniques require more experiment time affecting the availability of the generator, but the parameters are estimated individually increasing the accuracy of the estimated value.

Category 11 shows the percentage of publications that used more approaches to validate the excitation system models, publications that have higher scores in this topic are Zazo et al. (1994), Vermeulen and Strauss (1999), Botero and Ramírez (2005), and Shen and He (2007), therefore they are a good introduction of validation procedures. The identifiability of the parameters of the excitation system has only been discussed in Benchluch and Chow (1993), Ludwig et al. (1998), Bhaskar et al. (2000), Liao et al. (2006), and Puma and Colome (2008). No reviewed publication has presented a quantitative treatment about parameter identifiability, which is assessed in the category 12.

4.4 Review of selected publications on excitation system identification

To analyze the contributions in the characteristics defined in section 4.1, a review of the articles that closely match such conditions is presented below. In this way, the most representative papers are selected based on the total value obtained in table 3, choosing the ones with a total value higher than 70 % of the maximum value achieved, 16 by Puma and Colome (2008). Therefore, the papers discussed are: Benchluch and Chow (1993), Wang et al. (1995), Rasouli and Karrari (2004), Abd-Alla et al. (2006), Shen and He (2007), and Puma and Colome (2008).

Benchluch and Chow (1993) use a trajectory sensitivity technique to identify nonlinear excitation system models. The technique is used to identify two types of nonlinearities: limits of signals and parameters of a magnetic saturation function. An important aspect in this paper is that singular values are used to provide information about the parameters identifiability. Additionally, the effect of the noise in the parameters identifiability is also studied.

Wang et al. (1995) presents a procedure to identify excitation system models based on discrete measurements from a plant transient recorded system. The authors use data collected during a fault of the system, therefore they do not use external perturbation signals. The gradient averaging stochastic approximation method is used to estimate the nonlinearities of the excitation system model.

Rasouli and Karrari (2004) present a nonlinear identification of an excitation system operating in a power plant, where the experiments are carried out with the generator online. Grey box and black box modeling are used to estimate the excitation system parameters. In grey box approach, the parameters of a transfer function are obtained using a well known estimation algorithms like prediction error method. In black box modeling, the excitation system is identified using a discrete wavelet transform. Both approaches report good results, however, the authors highlight that transfer function model will be more useful for power engineers in power system analysis.

A nonlinear identification method for an excitation system of a power plant in China is presented by Abd-Alla et al. (2006). A genetic algorithm and prediction error method are used to estimate the model parameters. The comparison of time responses and estimated parameters shows good results from both methods, but better results were obtained from the genetic algorithm. The experiments to collect the data were carried out with the generator offline.

Shen and He (2007) present the identification of an excitation system in a simulation environment. The excitation system and a single machine models are implemented using MATLAB/Simulink. A pseudorandom binary sequence is used as perturbation signal and a genetic algorithm is adopted to estimate the model parameters. The influence of different sampling periods on parameter identification results is also analyzed. Finally, the authors provide some advices in parameter estimation of excitation systems.

A methodology to estimate linear and nonlinear parameters of excitation system models is presented by Puma and Colome (2008). Genetic algorithms are used to estimate linear and nonlinear parameters simultaneously. The identification methodology is applied in a simulation environment over two excitation system standard models DC1A and ST1A, and over an actual excitation system in a power plant. The results obtained are good enough and the model responses are close to the system responses, and the identification experiments are carried out with the generator offline. Finally, authors report that the noise in the measurements does not affect the identification results.

4.5 Open research areas in excitation system identification revealed by the bibliographic classification method

The research areas in excitation system identification that are insufficiently explored can be selected from the results in the last row of table 3, which indicates the percentage of papers that deals with a specific category. In this case, characteristics with percentage equal or smaller than 25 % are defined as insufficiently explored research areas in excitation system identification and therefore discussed below.

Only 20,6 % of the publications have reported experiments with the generator online: Shen, Zhu and Han (1991), Liaw et al. (1992), Liu et al. (1993), To and David (1996), Rasouli and Karrari (2004), and Glaninger-Katschnig (2010). Rasouli and Karrari (2004) has reported identification experiments with the synchronous machine generating different levels of active power, obtaining different parameter values of the excitation system model for each operating point. The difference in the parameter values is associated with the nonlinearities of the system. Among the reviewed papers, no one has investigated the effect of the operating conditions on the identification results, taking into account that the excitation control system operates in closed loop during the identification experiment.

The percentage of category 3 is below 25 %, however, the effect of the noise in parameter estimation was widely investigated between 1971 and 2000. Published papers from 2000 do not dedicated strong efforts to work in the noise issue. In addition, Puma and Colome (2008) show a computational algorithm to estimate the parameters without adverse effect of the noise present in the measurements.

The nonlinearity values in excitation system models usually are given by the manufacturer or are taken from databases of power system analysis handbooks. The estimation of nonlinearities on the excitation system has been addressed only by the 17,2 % of the reviewed papers. Ramírez, Saavedra and Vásquez (2003), and Saldaña, Calzolari and Cerecetto (2006) calculate analytically the nonlinearities. In contrast, in Wang et al. (1995) and Bhaskar et al. (2000) the nonlinearities are linearized and then estimated, while in references Benchluch and Chow (1993), Feltes et al. (2002), Paszek et al. (2005), Hernandez et al. (2006), and Puma and Colome (2008) the nonlinearities are estimated with the estimation method. From those developments, genetic algorithms have demonstrated to be an effective technique to estimate the linear parameters and the nonlinearities simultaneously.

Parameters identifiability is another aspect that has not been actively addressed in papers about excitation system identification. No reviewed article has focused on evaluating the identifiability of excitation system parameters, nor on the identifiability taking into account the operating conditions of the synchronous generator, which is an important aspect since the dynamics of the excitation control system changes with the generator operating condition. Benchluch and Chow (1993), Ludwig et al. (1998), Bhaskar et al. (2000), Liao et al. (2006), and Puma and Colome (2008) slightly discussed the parameters identifiability of excitation systems, but not deeper analyses based on the results have been provided.

Validation stage is the category with the lowest percentage, only 13,7 %, among the defined categories. In most cases, papers in excitation system identification report the validation of the model comparing the system output to the model output, and some of them present an error index to quantify the differences between the outputs. When papers are focused on parameters estimation, they compare the estimated parameters with a set of reference parameters. Residual analysis is another way used to validate excitation system models, where the identification experiment conditions should be taken into account; for example, data collected with or without feedback path. Zazo et al. (1994), Vermeulen and Strauss (1999), Botero and Ramírez (2005), and Shen and He (2007) use several ways to validate excitation system models, providing a good comparison scenario that helps the reader to select a validation procedure depending on its particular requirements. Finally, standard indexes or validation procedures designed for excitation system identification must be developed to allow a comparison between different identification approaches.

5. CONCLUSIONS

To establish the state of the art in excitation system identification, a bibliographic classification method was designed and implemented. The proposed method was used to review publications in excitation system identification and to detect open research issues in this topic. The bibliographic method was applied to papers published from 1971 until 2010.

Among the results obtained with the method, the next are highlighted: the topic most discussed by the authors in the reviewed publications was the estimation algorithm or method, i.e. several estimation methods were used to estimate the parameters of an excitation system model. But few authors have focused their efforts to estimate the nonlinearities of excitation system models or to investigate the effects of carrying out the identification experiments with the generator online. Similarly, few papers report identification methodologies that match completely the conditions defined in section 4.1, which are required to deal with the requirements of identify parameters of excitation systems nowadays.

ACKNOWLEDGMENTS

This work was supported by GAUNAL group of the Universidad Nacional de Colombia under the project SMART-ALEN, GICI group of the Universidad del Valle, and the Departamento Administrativo de Ciencia, Tecnología e Innovación (Colciencias) under the scholarship 095-2005.

REFERENCES

Abd-Alla, A. N.; Cheng, S. J.; Wen, J. Y. and Zhang, J. (2006). Model parameter identification of excitation system based on a genetic algorithm techniques. Proceedings of the International Conference on Power System Technology, Chongqing, China (22-26 October).         [ Links ]

Benchluch, S. M. and Chow, J. H. (1993). "A trajectory sensitivity method for the identification of nonlinear excitation system models". IEEE Transactions on Energy Conversion, vol. 8, No. 2 (June), pp. 159-164.         [ Links ]

Bhaskar, R.; Crow, M. L.; Ludwig, E.; Erickson, K. T. and Shah, K. S. (2000). "Nonlinear parameter estimation of excitation systems". IEEE Transactions on Power Systems, vol. 15, No. 4 (November), pp. 1225-1231.         [ Links ]

Botero, H. A. and Ramírez, J. M. (2005). A methodology for excitation systems identification. Proceedings of the IEEE International Conference on Industrial Electronics and Control Applications. Quito, Ecuador (29 November - 2 December).         [ Links ]

Chow, J. H.; Glinkowski, M. T.; Murphy, R. J.; Cease, T. W. and Kosaka, N. (1999). "Generator and exciter parameter estimation of Fort Patrick Henry Hydro Unit 1". IEEE Transactions on Energy Conversion, vol. 14, No. 4 (December), pp. 923-929.         [ Links ]

Eykhoff, P. System identification: Parameter and state estimation. New York: Wiley-Interscience, 1974.         [ Links ]

Feltes, J. W.; Orero, S.; Fardanesh, B.; Uzunovic, E.; Zelingher, S. and Abi-Samra, N. (2002). "Deriving model parameters from field test measurements". IEEE Computer Applications in Power, vol. 15, No. 4 (October), pp. 30-36.         [ Links ]

Gibbard, M. J. and Kaan, Q. H. (1975). "Identification of excitation system parameters". IEEE Transactions on Power Apparatus and Systems, vol. 94, No. 4 (July), pp. 1201-1207.         [ Links ]

Glaninger-Katschnig, A. (2010). "Identification of excitation system transfer functions in hydro power plants using a binarypseudo random signal". E and I Elektrotechnik und Informationstechnik, vol. 127, No. 1-2 (February), pp. 8-12.         [ Links ]

Godfrey, K. R.; Tan, A. H.; Barker, H. A. and Chong, B. (2005). "A survey of readily accessible perturbation signals for system identification in the frequency domain". Control Engineering Practice, vol. 13, No. 11 (November), pp. 1391-1402.         [ Links ]

Guo, T.-Y.; Liu, C.-S.; Chen, Y.-T.; Ko, C.-K. and Huang, C.-T. (1995). "Identification of model parameters of excitation system and power system stabilizer of Mingtan#6 via finalization field tests". IEEE Transactions on Power Systems, vol. 10, No. 2 (May), pp. 795-802.         [ Links ]

Hernandez, J. A.; Botero, H. A.; Ospina, J. D. and Perez, J. C. (2006). Excitation system parameters estimation using evolutionary algorithms. IEEE Transmission and Distribution Conference and Exposition: Latin America. Caracas (15-18 August), pp. 1-6.         [ Links ]

Hsu, Y.-Y.; Liu, C.-S.; Luor, T.-S.; Chang, C.-L.; Liu, A.-S.; Chen, Y.-T. and Huang, C.-T. (1996). "Experience with the identification and tuning of excitation system parameters at the second nuclear power plant of Taiwan Power Company". IEEE Transactions on Power Systems, vol. 11, No. 2 (May), pp. 747-753.         [ Links ]

IEEE (1968). "Computer representation of excitation systems". IEEE Transactions on Power Apparatus and Systems, vol. PAS-87, No. 6 (June), pp. 1460-1464.         [ Links ]

IEEE (1981). "Excitation system models for power system stability studies". IEEE Transactions on Power Apparatus and Systems, vol. PAS-100, No. 2 (February), pp. 494-509.         [ Links ]

IEEE (1996). "Computer models for representation of digital-based excitation systems". IEEE Transactions on Energy Conversion, vol. 11, No. 3 (September), pp. 607-615.         [ Links ]

IEEE. IEEE recommended practice for excitation system models for power system stability studies. IEEE Std 421.5-2005. New York: IEEE, 2006.         [ Links ]

Karl, D. S. and Schaefer, R. C. (2004). "NERC power industry policies". IEEE Industry Applications Magazine, vol. 10, No. 2 (March), pp. 30-38.         [ Links ]

Landau, Y. D. and Zito, G. Digital control systems: Design, identification and implementation. London: Springer, 2006.         [ Links ]

Liao, Q. F.; Liu, D. C.; Ying, L. M.; Cui, X.; Li, Y. and He, W. T. (2006). Parameter identification of excitation systems based on Hopfield neural network. Proceedings of the International Conference on Power System Technology, Chongqing, China (22-26 October), pp. 1-6.         [ Links ]

Liaw, C. M.; Liu, T. S.; Liu, A. H.; Chen, Y. T. and Lin, C. J. (1992). "Parameter estimation of excitation systems from sampled data". IEEE Transactions on Automatic Control, vol. 37, No. 5 (May), pp. 663-666.         [ Links ]

Liu, C.-S.; Hsu, Y.-Y.; Jeng, L.-H.; Lin, C.-J.; Huang, C.-T.; Liu, A. H. and Li, T.-H. (1993). "Identification of exciter constants using a coherence function based weighted least squares approach". IEEE Transactions on Energy Conversion, vol. 8, No. 3 (September), pp. 460-467.         [ Links ]

Ljung, L. System identification: Theory for the user. New Jersey: Prentice Hall, 1999.         [ Links ]

Ludwig, E.; Crow, M. L.; Erickson, L. and Shah, K. (1998). "A feasibility study of on-line excitation system parameter estimation". IEEE Transactions on Power Systems, vol. 13, No. 3 (August), pp. 910-916.         [ Links ]

Paszek, S.; Bobon, A.; Kudla, J.; Bialek, J. and Abi-Samra, N. (2005). "Parameter estimation of the mathematical model of a generator, excitation system and turbine". Przeglad Elektrotechniczny, vol. 81, No. 11 (November), pp. 7-12.         [ Links ]

Puma, J. Q. and Colome, D. G. (2008). "Parameters identification of excitation system models using genetic algorithms". IET Generation, Transmission and Distribution, vol. 2, No. 3 (May), pp. 456-467.         [ Links ]

Ramírez, J. M.; Saavedra, A. J. y Vásquez, H. Modelado de los sistemas de control de la central hidroeléctrica de Salvajina. Parte II: Control de excitación. V Congreso Nacional de la ACA. Medellín, Colombia, 2003.         [ Links ]

Rasouli, M. and Karrari, M. (2004). "Nonlinear identification of a brushless excitation system via field tests". IEEE Transactions on Energy Conversion, vol. 19, No. 4 (December), pp. 733-740.         [ Links ]

Saldaña, C.; Calzolari, G. and Cerecetto, G. (2006). "ATP modelling and field tests of the AC voltage regulator in the Palmar hydroelectric power plant". Electric Power Systems Research, vol. 76, No. 8 (May), pp. 681-687.         [ Links ]

Sanchez-Gasca, J. J.; Bridenbaugh, C. J.; Bowler, C. E. J. and Edmonds, J. S. (1988). "Trajectory sensitivity based identification of synchronous generator and excitation system parameters". IEEE Transactions on Power Systems, vol. 3, No. 4 (November), pp. 1814-1822.         [ Links ]

Shen, F. and He, R.-m. (2007). A feasibility study of excitation system parameters identification based on measured perturbation. Proceedings of the International Power Engineering Conference. Singapore (3-6 December), pp. 904-909.         [ Links ]

Shen, S.; Zhu, S. and Han, B. (1991). Identification of parameters of synchronous machine and excitation system by online test. Proceedings of the International Conference on Advances in Power System Control, Operation and Management, Hong Kong, China (5-8 November), vol. 2, pp. 716-719.         [ Links ]

Söderström, T. and Stoica, P. System identification. Hemel Hempstead, UK: Prentice Hall, 1989.         [ Links ]

To, K. W. V. and David, A. K. (1996). "On-line identification and control of an AC/DC power system". International Journal of Electrical Power and Energy Systems, vol. 18, No. 4 (May), pp. 223-227.         [ Links ]

Veloza, O. P. and Cespedes, R. H. (2006). Regulatory mechanisms to mitigate the vulnerability of power systems to blackouts. Proceedings of the IEEE Transmission and Distribution Conference and Exposition: Latin America. Caracas (15-18 August), pp. 1-6.         [ Links ]

Vermeulen, H. J. and Strauss, J. M. (1999). Off-line identification of an open-loop automatic voltage regulator using pseudo-random binary sequence perturbations. AFRICON, 1999 IEEE. Cape Town.         [ Links ]

Wang, J.-C.; Chiang, H.-D.; Huang, C.-T.; Chen, Y.-T.; Chang, C.-L. and Huang, C.-Y. (1995). "Identification of excitation system models based on on-line digital measurements". IEEE Transactions on Power Systems, vol. 10, No. 3 (August), pp. 1286-1293.         [ Links ]

Warchol, E. J.; Schleif, F. R.; Gish, W. B. and Church, J. R. (1971). "Alinement and modeling of Hanford excitation control for system damping". IEEE Transactions on Power Apparatus and Systems, vol. PAS-90, No. 2 (March), pp. 714-724.         [ Links ]

Yao, X.; Karady, G. G.; Farmer, R. G. and Agrawal, B. L. (2001). Estimation of generator excitation-system parameters by tabu search. Proceedings of the IEEE Power Engineering Society Winter Meeting. Columbus, OH (28 January - 1 February).         [ Links ]

Zazo, A.; Zamora, J. L.; Rouco, L. and Pagola, F. L. (1994). "Identification of excitation systems from time response tests". Proceedings of the International of Conference on Control, Coventry, UK (21-24 March), vol. 1, pp. 839-844.         [ Links ]