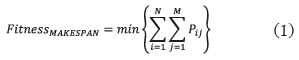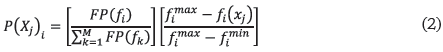Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.19 Envigado Jan./June 2013
METODOLOGÍA BASADA EN LOS ALGORITMOS VEGA Y MOGA PARA SOLUCIONAR UN PROBLEMA MULTIOBJETIVO EN UN SISTEMA DE PRODUCCIÓN JOB SHOP
METHODOLOGY BASED ON THE ALGORITHMS VEGA AND MOGA TO SOLVE A MULTIOBJECTIVE PROBLEM IN A SYSTEM OF PRODUCTION JOB SHOP
METODOLOGIA BASEADA NOS ALGORITMOS VEGA E MOGA PARA RESOLVER UM PROBLEMA MULTIOBJETIVO EM UM SISTEMA DE PRODUÇÃO JOB SHOP
Germán Augusto Coca Ortegón*, Ómar Danilo Castrillón Gómez**, Santiago Ruiz Herrera***
*Especialista en Gestión de la Calidad, Profesor Escuela de Ingeniería de Antioquia. Correo electrónico: pfgeco@eia.edu.co.
**Doctor en Bio-Ingeniería, Docente Titular Universidad Nacional de Colombia Sede Manizales. Correo electrónico: odcastrillong@unal.edu.co.
***Ingeniero Industrial Universidad Nacional de Colombia, Maestría en Investigación Operativa y Estadística, Universidad Tecnológica de Pereira. Estudiante del Doctorado en Ingeniería, Industria y Organizaciones. Universidad Nacional de Colombia. Correo electrónico: sruizhe@unal.edu.co.
Artículo recibido 12-XII-12. Aprobado 16-05-2013
Discusión abierta hasta 01-VI-2013
RESUMEN
En este artículo se presenta una metodología que pretende minimizar de forma simultánea, en un ambiente de producción tipo "job shop" correspondiente a una empresa metalmecánica, las siguientes variables: tiempo de proceso, costo de mano de obra directa y, asimismo la fracción defectuosa generada por la fatiga del operario. Con este propósito se fusionan elementos de los algoritmos genéticos Vega y Moga, desarrollando para el efecto las siguientes etapas: generar la población inicial, conformar la nueva población, realizar análisis de varianza y por último, comparar con un método híbrido entre sumas ponderadas y algoritmos genéticos.
De acuerdo con lo anterior, al evaluar el individuo de menor tiempo de proceso proveniente de la metodología basada en los algoritmos Vega y Moga, respecto al individuo de menor tiempo de desarrollo proveniente del método híbrido entre sumas ponderadas y algoritmos genéticos, se encuentra que el primero supera en desempeño al segundo así: en cuanto a la variable tiempo de proceso (en horas) en 27,86%; en cuanto a la variable tiempo de proceso (en semanas) en 1,25%; en cuanto a la variable costo de mano de obra directa (MOD) en 6,73% y, en cuanto a la variable fracción defectuosa en 25,85%.
PALABRAS CLAVE: multiobjetivo, job shop, tiempo de procesamiento, costos de mano de obra directa, Vega, Moga.
ABSTRACT
This paper presents a methodology that aims to minimize simultaneously, in a "Job Shop" production system the following variables: process time (makespan time), cost of direct labor and also the fraction defective generated by operator fatigue. For this purpose, are taken and fused elements of genetic algorithms Vega and Moga, through the following steps: generating the initial population, form the new population, obtaining the appropriate analysis of variance and finally compared with a hybrid method of weighted sums and genetic algorithms.
According to the above, when evaluating the solution faster processing time corresponding to the method based on algorithms Vega and Moga, respect to the solution faster processing time calculated from the method based on weighted sums and genetic algorithms, states that the first one exceeds the second performance as: for process time variable (in hours) at 27.86%, for variable in process time (in weeks) at 1.25%, in terms of the variable cost of direct labor in 6.73% and, as to the variable defective fraction in 25.85%.
KEY WORDS: multiobjective, job shop, makespan time, cost of direct labor, Vega, Moga.
RESUMO
Neste artigo apresentamos uma metodologia que visa minimizar ao mesmo tempo, em um ambiente de produção tipo "job shop" para uma empresa de engenharia, as seguintes variáveis: tempo de processo, custo de mão de obra direta e também a fração defeituosa gerada pela fadiga do operador. Para este efeito, os elementos de fusível e algoritmos genéticos Moga Vega, desenvolvido para efectuar os seguintes passos: geração de uma população inicial, formam a nova população, a análise de variância e, finalmente, em comparação com um método híbrido e somas ponderadas algoritmos genéticos. De acordo com o exposto, o menor tempo individual processo de avaliação da metodologia baseada em algoritmos e Moga Vega, em comparação com o tempo de processamento menor do indivíduo a partir da soma ponderada método híbrido e de algoritmos genéticos, a primeira supera a segunda maneira: como a variável de tempo do processo (em horas) 27,86%, em termos de tempo variável de processo (em semanas) a 1,25%, em termos de custo variável mão de obra direta (MOD) em 6,73% e, como a fração defeituosa variável 25,85%.
PALAVRAS-CÓDIGO: job shop multiobjetivo, tempo de processamento, custos de mão de obra direta, Vega, Moga.
1. INTRODUCCIÓN
En el presente artículo se analizarán algunas variables que influyen en el comportamiento de las prioridades competitivas de operaciones: tiempo de entrega, calidad y costos, en una compañía metalmecánica cuyo sistema de fabricación es de tipo "job shop".
Al respecto, se menciona que en este tipo de sistema de fabricación se identifican diversas variables, entre las cuales se encuentran: tiempo de proceso, tiempo de tardanza total, tiempos de carga total, tiempos de alistamiento, fracción defectuosa causada por la fatiga del operario, costo de mano de obra directa, etc. Con relación a las cuatro primeras variables, algunos autores las han caracterizado, llegando a aplicar técnicas basadas en inteligencia artificial para lograr su minimización. En cuanto a las dos últimas, no se han detectado antecedentes de análisis en la literatura especializada; por tanto se concluye la existencia de una oportunidad de desarrollo desde la perspectiva académica.
Particularmente, en los sistemas de producción que utilizan mano de obra intensiva, como es el caso de la empresa objeto de análisis, se ha establecido que la causa de fabricación de artículos no conformes se origina, la mayor parte de las veces, en la fatiga del operario. La probabilidad de obtener artículos defectuosos debido al hecho anterior, aumenta al transcurrir la jornada laboral. También debe comentarse que la producción no conforme, ocasiona entregas con retraso y pérdida potencial de mercado.
En cuanto a los componentes del costo de mano de obra directa, se establecen dos aspectos: costo de tiempo normal y costo de tiempo extendido (horas extras o turnos nocturnos). La extensión del horario normal se debe a la necesidad de atender con premura las fechas de entrega pactadas con los clientes, lo cual incrementa los costos generales y reduce la rentabilidad de una organización.
La cuantificación de las dos variables anteriores, requiere determinar de manera previa el comportamiento de la variable denominada tiempo de proceso. Específicamente, para esta variable, se busca identificar el escenario correspondiente al menor tiempo de fabricación.
Con base en lo expuesto, se decide aplicar algoritmos genéticos multiobjetivo, para minimizar el comportamiento de las variables: tiempo de proceso, fracción defectuosa causada por la fatiga del operario y costo de mano de obra directa.
Desde el punto de vista de la determinación del tiempo de proceso, debe anotarse que la programación de las operaciones en los sistemas "job shop" es compleja; en caso de existir n trabajos y m máquinas, el número de programas posibles es de (n!)m (Sipper y Bulfin, 1998).
De manera formal, el problema JSP es descrito tanto en sus aspectos cuantitativos como cualitativos en Binato et al. (2002).
El anterior problema se clasifica como NP difícil (Correa, Velásquez y Londoño, 2008), su tiempo de cómputo supera considerablemente los intervalos de tiempo en los cuales se toman decisiones a nivel empresarial, se concluye así la imposibilidad de obtener una respuesta oportuna al realizar la asignación de planta.
Cabe mencionar que la solución del problema de programación de los sistemas "job shop" se ha realizado en forma tradicional, siguiendo dos tendencias: determinación de tiempo de carga y reglas de despacho (Sipper y Bulfin, 1998).
Así mismo, el problema considerado puede resolverse por medio de la aplicación de métodos propios de la metaheurística, particularmente en este artículo se tomará como base para el análisis la técnica denominada algoritmos genéticos.
Algoritmos genéticos
El procedimiento general de los algoritmos genéticos, en nivel básico se describe en Gen y Cheng (1997).
Los algoritmos genéticos permiten resolver problemas de programación multiobjetivo, es decir, facilitan la identificación de la decisión que se va a tomar, cuando se evalúa de forma simultánea el comportamiento de varios objetivos. Respecto a lo anterior, las metodologías utilizadas para solucionar el problema multipropósito descrito en el artículo, corresponden a los algoritmos tipo Vega y Moga, de los cuales se muestra su desarrollo general enseguida.
Algoritmo tipo Vega (Toscano, 2001)
Con el propósito de aprovechar la potencialidad de los algoritmos genéticos para realizar optimización multiobjetivo, en el año de 1985 se realizó una propuesta en este sentido. Esta consistió en readaptar la aptitud del vector valorado, lo cual recibió el nombre de algoritmo genético para el vector evaluado (Vega). Se modificó por tanto, el paso correspondiente a la selección. De esta forma, en cada generación se obtuvieron cierto número de subpoblaciones, teniendo como criterio el desempeño de la función objetivo evaluada en su momento. Con base en lo expuesto, para m objetivos, m subpoblaciones con tamaño N/m serían generadas, asumiendo que la población es de tamaño N. Posteriormente, las subpoblaciones se reúnen, con el propósito de continuar con las funciones usuales de cruzamiento y mutación. El procedimiento general del algoritmo Vega es el siguiente: establecer el tamaño de la población, dividir la población en tantas subpoblaciones como objetivos tenga el problema, evaluar los individuos en la función de adaptación correspondiente a cada subpoblación, fusionar los individuos de mejor comportamiento de la anterior generación, cruzar los mejores individuos de la anterior generación y mutar.
Algoritmo tipo Moga (Toscano, 2001)
Este algoritmo fue propuesto en el año de 1993 como una variación de la jerarquización de Pareto definida por Goldberg. El procedimiento general del algoritmo hasta obtener una población mejorada es el siguiente: definir una población de inicio, evaluar las funciones objetivo, identificar los rangos de acuerdo con los frentes de Pareto, definir los nichos, determinar una función de adaptación lineal, determinar una función de adaptación de compartición, cruzar los individuos y mutar los individuos.
A su vez, con el fin de ilustrar de manera general el desarrollo y alcance de los algoritmos genéticos, se caracteriza su aplicación en el campo de análisis de los problemas correspondientes a los sistemas de operaciones, así:
- Aplicaciones en renglones económicos diferentes a la industria (López, Hincapié y Gallego, 2011; Ruiz, Toro y Gallero, 2012).
- Aplicaciones a los problemas generales de la gestión operacional (Vélez y Montoya, 2007).
- Aplicaciones a los problemas relacionados con logística externa (Daza, Montoya y Narducci, 2009).
- Desarrollos generales multiobjetivo (Raud et al., 2007; Yang et al., 2011).
- Aplicaciones a los problemas del tipo Flow Shop (Mansouri, Hendizadeh y Salmasi, 2008; Bhongade y Khodke, 2011).
- Aplicaciones a los problemas del tipo job shop.
Las aplicaciones pueden clasificarse en los siguientes tipos:
- Rediseño de operadores.
En esta categoría clasifican tres desarrollos: diseño de un algoritmo genético mejorado (Meisel y Prado, 2010), diseño de algoritmos de selección clonal (Akhshabi y Khalatbari, 2011) y desarrollo de algoritmos híbridos (Dao Er Ji y Wang, 2012). - Propuesta de diseño de algoritmos:
A esta categoría pertenecen cuatro desarrollos: diseño de un algoritmo híbrido con búsqueda tabú (Li et al., 2011), definición de un algoritmo que permite cambiar la secuencia de la programación (Thamilselvan y Balasubramanie, 2011), desarrollo de algoritmos híbridos para programar lotes de transferencia diferentes a la unidad (Zhang y Wu, 2012), desarrollo de métodos que buscan minimizar el tiempo de proceso (Bozejko, 2012). - Atención a las necesidades de los sistemas job shop
En la categoría se agrupan cuatro desarrollos: definición de un algoritmo que reduce el tiempo de proceso y el tiempo muerto (Castrillón, Sarache y Giraldo, 2011), diseño de un algoritmo que incrementa la utilización de los equipos multipropósito (Medina, Praderas y Parada, 2011), definición de un algoritmo hereditario, en el cual se modifica la operación de mutación (Anandaraman, 2011) y diseño de un algoritmo para procesar lotes en paralelo (Cheng et al., 2012). - Atención a propósitos simultáneos
A la categoría pertenecen dos desarrollos: rediseño del algoritmo Moga, considerando los principios de entropía y de inmunidad (Wang, Gao y Zhang, 2010), y definición de un algoritmo híbrido de ordenamiento (NSHA) que permite conseguir múltiples metas en los sistemas job shop (Ghiasi, Damiano y Lessard, 2011).
De manera específica, el desarrollo del artículo cubre las siguientes etapas: presentación general del problema, presentación del marco teórico, descripción de la metodología de solución utilizada, medición de las variables objeto de estudio (tiempo de proceso, fracción defectuosa causada por la fatiga del operario y costos por mano de obra directa), comparación con un método híbrido entre sumas ponderadas y algoritmos genéticos y, discusión de resultados.
Por último, se encontró que al aplicar la metodología, la solución estimada supera en desempeño a la solución obtenida con el método híbrido así: en cuanto a la variable tiempo de proceso (en horas) 27,86%; en cuanto a la misma variable (en semanas) 1,25%; en cuanto a la variable costo MOD en 6,73% y, en cuanto a la variable fracción defectuosa en 25,85%.
MÉTODOS
Metodología
Para el desarrollo del trabajo se procederá utilizando la siguiente metodología:
1. REPRESENTACIÓN GENERAL DEL PROBLEMA
Como se mencionó el problema corresponde a una compañía cuyo sistema de fabricación es de tipo job shop. De acuerdo con lo anterior, los pedidos siguen diferentes rutas de fabricación. Para este caso se toman nueve pedidos, los cuales pasan por seis centros de trabajo. En cada centro de trabajo se cuenta con una máquina. En la siguiente matriz, los pedidos se encuentran listados por fila y los centros de trabajo por columnas; a su vez, en la intersección entre filas y columnas se registra el tiempo de procesamiento en horas como se muestra en la tabla 1.
En el individuo general observado, las posiciones uno a nueve son ocupadas por cada uno de los nueve pedidos.
En cuanto al significado de las expresiones: "forma de organización por turnos" y "trabajando sin o con dominical", se encuentran definidas en la tabla 2.
2. GENERACIÓN DE POBLACIÓN INICIAL
El total de individuos es de 9! Cada individuo puede transformarse en 6 subindividuos, así:
Con base en lo anterior, se obtiene un total de 9! x 6 individuos.
Del total de individuos, se toman como población inicial 84 individuos.
La estructura general de un individuo es la siguiente:
3. GENERACIÓN Y EVALUACIÓN DE LAS SUBPOBLACIONES
La población se divide en tres subpoblaciones, una para cada objetivo. De esta forma, cada subpoblación quedará conformada por 28 individuos. Los individuos en cada subpoblación son evaluados y ordenados de menor a mayor valor, debido a que se busca su minimización. Después de realizar lo anterior, se procede a identificar en cada subpoblación el 25% de individuos que contengan los mayores valores. Posteriormente, se eliminan de las subpoblaciones el mencionado 25% de individuos, quedando cada una de ellas integrada por 21 individuos.
4. CONFORMAR LA PRIMERA NUEVA POBLACIÓN
La primera nueva población tiene tres orígenes, así:
- Las subpoblaciones son divididas en tres segmentos, cada segmento se encuentra integrado por 7 individuos. De cada segmento se extraen aleatoriamente 4 de ellos. Finalmente de cada subpoblación, se obtienen 12 individuos. En total las subpoblaciones aportan 36 individuos. La anterior cantidad equivale al 42,86% de la población.
- A los anteriores individuos se les aplica con una probabilidad de 96% la operación de cruzamiento. Esta operación permite estimar otro 30% de la nueva subpoblación. Este 30% es equivalente a 25 individuos.
- Otro 15,48% de los individuos se origina en la mutación aleatoria con una probabilidad de 4%, de aquellos individuos seleccionados de las subpoblaciones, al igual que de aquellos obtenidos por su cruzamiento. El total de individuos en este caso es de 13.
- El restante 11,9% de los individuos se obtiene aleatoriamente del total que conforman el universo de soluciones. El total de individuos en este caso es de 10.
5. ORDENAR Y EVALUAR LA NUEVA POBLACIÓN
La población constituida se ordena de forma ascendente de acuerdo con el tiempo de procesamiento; a partir de esta clasificación se generan los diversos frentes. Con este propósito, se procede comparando cada individuo con los demás de la población. Es así como se inicia el análisis con aquel individuo que presenta el menor tiempo de procesamiento. Para tal individuo se identifica el valor correspondiente al primer costo de mano de obra. Una vez identificado el valor de tal costo, se procede analizando el siguiente individuo en el respectivo orden de menor a mayor tiempo de procesamiento. De esta manera, se seleccionan aquellos individuos cuyo costo de mano de obra sea estrictamente menor al anterior. Después de obtener una primera clasificación de individuos, se aplica el procedimiento ya descrito sobre aquellos individuos seleccionados, pero utilizando esta vez como criterio base de ordenamiento, el porcentaje de producción defectuosa.
De acuerdo con lo expuesto, se obtiene el primer frente. El segundo frente se identifica aplicando el mencionado procedimiento sobre los individuos no clasificados en el frente anterior, así se continúa hasta clasificar en diversos frentes la totalidad de los individuos.
6. CONFORMAR LA SEGUNDA NUEVA SUBPOBLACIÓN
A esta población ingresarán los mejores resultados agrupados por los frentes, hasta completar 42 individuos.
Así mismo, los otros 42 individuos se obtendrán de la siguiente forma:
- Se parte de determinar el porcentaje de individuos por frente. Cada valor porcentual identificado se aplicará a 25 individuos. La cantidad de individuos obtenidos constituye la cantidad de nuevos individuos que se originan a partir del cruzamiento aleatorio con una probabilidad de 96% de los individuos que constituyen cada frente.
- Posteriormente, para los 42 individuos que presentan el mejor comportamiento de acuerdo con la clasificación por frentes, como para los 25 individuos obtenidos por cruzamiento, se realiza por selección aleatoria y con una probabilidad de 4% la operación de mutación. De esta manera, se obtienen 9 individuos.
- Por último, se obtienen del total de posibles soluciones y de forma completamente aleatoria 8 individuos, completando así el 100% de la población.
Una vez obtenida la segunda nueva subpoblación, se repite desde el paso tres (conformación de subpoblaciones) hasta completar 100 iteraciones.
Nota: El programa se elaboró en Matlab R2012a. El equipo utilizado para correr el programa cuenta con las siguientes características: Intelcore5duo de 220 Ghz y 200 GB libres en disco duro. A su vez, el tiempo de evaluación para 100 iteraciones es de 2 minutos.
7. ANALIZAR EL PRIMER FRENTE DE LA POBLACIÓN FINAL DE RESPUESTA
Con el objetivo de caracterizar el primer frente de la población final de respuesta, se procede a agrupar los datos utilizando como criterio de clasificación la variable: tiempo de proceso. De esta forma, para la cantidad de intervalos establecida al aplicar la regla de Sturges, se estiman los valores correspondientes para el rango y para el ancho del intervalo. Posteriormente, se sistematiza la información en la respectiva tabla.
8. REALIZAR ANÁLISIS DE VARIANZA
Respecto de las variables analizadas: promedio de tiempo de procesamiento, promedio de costo de mano de obra directa y promedio de porcentaje de fracción defectuosa, se efectúa previo análisis de independencia de los datos, para tres tratamientos con diez repeticiones cada una y el respectivo análisis de varianza. De esta forma, se comprueba la estabilidad estadística de los datos.
9. GENERAR UNA POBLACIÓN DE COMPARACIÓN, POR MEDIO DE LA APLICACIÓN DE UN MÉTODO HÍBRIDO ENTRE SUMAS PONDERADAS Y ALGORITMOS GENÉTICOS
Este paso se realiza a nivel general, por medio de la implementación de las siguientes actividades: generar de manera aleatoria ocho individuos. Evaluar la función lineal para cada uno de los ocho individuos, asumiendo en este caso que a cada función objetivo le corresponde el mismo nivel de importancia (los máximos y los mínimos de las funciones se toman de los ocho valores comparados). Seleccionar los cuatro individuos con mayor valor de la función lineal. Elegir dos pares de individuos para cruzar (el primer par estaría constituido por los individuos con mayor y menor valor de la función lineal. El segundo par estaría constituido por los individuos con valor intermedio). Cruzar los individuos agrupados en el punto anterior como par, utilizando en este caso una probabilidad de 95% (la operación de cruce permite obtener cuatro individuos). Mutar los individuos con una probabilidad de 4% (la operación de mutación permite obtener cuatro individuos). Evaluar la función lineal para cada uno de los cuatro individuos (los máximos y los mínimos de las funciones corresponden a los cuatro valores comparados). Guardar en 84 posiciones los mayores valores detectados de la función lineal después de 1.500 iteraciones (este número de iteraciones es equivalente al número de iteraciones utilizadas en la metodología basada en los algoritmos Vega y Moga).
10. COMPARAR LOS RESULTADOS OBTENIDOS AL APLICAR LA METODOLOGÍA BASADA EN LOS ALGORITMOS VEGA Y MOGA (MÉTODO UNO) CON LOS RESULTADOS OBTENIDOS AL APLICAR LA METODOLOGÍA BASADA EN EL MÉTODO HÍBRIDO ENTRE SUMAS PONDERADAS Y ALGORITMOS GENÉTICOS (MÉTODO DOS)
Para este efecto, se procede a realizar dos comparaciones, así:
- Se contrastan los individuos de valor mínimo correspondientes a cada función objetivo y que a su vez hayan sido el resultado de aplicar el método uno con aquellos individuos de valor mínimo en cada función objetivo y que a su vez provengan de la aplicación del método dos.
- Se contrastan los individuos de valor mínimo correspondientes a cada función objetivo y que a su vez hayan sido el resultado de aplicar el método uno con aquel individuo que logre el mayor valor ponderado al aplicar el método dos.
Experimentación
Para este efecto, se obtuvo la información en una empresa del sector metalmecánico, procediendo a evaluar el producto denominado: base torre. Con el fin de ilustrar el desarrollo experimental del problema se caracterizaron, de acuerdo con lo indicado en el punto número uno de la metodología, nueve centros de trabajo y seis pedidos:
Los datos del problema discriminados por variable a cuantificar, se muestran a continuación:
- Determinación del tiempo de procesamiento. Al respecto, se utiliza la siguiente información:
- Tiempos de operación por pedido en cada centro de trabajo. Esta información se encuentra registrada en la tabla 1. (Tiempos por pedido en cada centro de trabajo (horas)).
- Las rutas de fabricación por pedido son las que se observan en la tabla 4.
- Las cantidades que se van a procesar por pedido, las rutas de manufactura y sus tiempos de fabricación (en horas) son las que se observan en la tabla 5.
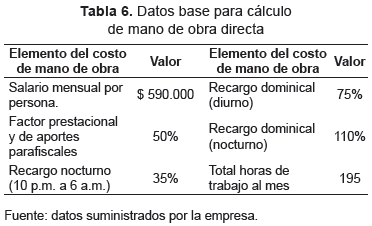
- Costos de mano de obra directa. Los datos generales utilizados para determinar los costos de mano de obra directa, se expresan en la tabla 6.
El costo total de mano de obra directa está dado por la sumatoria de los costos en tiempo normal, en jornada laboral nocturna, en jornada laboral dominical más el costo de tiempo ocioso medido en horas.
El número de personas requeridas, se obtiene identificando el máximo número de personas programadas en un turno dentro del conjunto de turnos que conforman el horizonte de planeación.
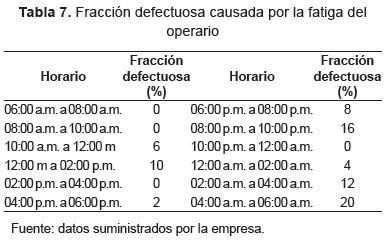
El tiempo ocioso se determina observando el tiempo libre de cada persona en un turno. Posteriormente, se realiza la sumatoria total de tiempo ocioso durante el horizonte de planeación. - Fracción defectuosa. Los datos relacionados con la fracción defectuosa generada por la fatiga del operario a lo largo de la jornada laboral, se presentan en la tabla 7.
La respuesta final de la fracción defectuosa se obtiene relacionando la sumatoria de las cantidades de salida de los diferentes pedidos con respecto a la sumatoria de las cantidades de entrada. - Factor de ponderación total por individuo (P(Xj)). El factor de ponderación se determina para el método dos. Este método se describió en el numeral 9 de la metodología. Las expresiones para utilizar con el propósito de establecer el valor del factor de ponderación por individuo, se ilustran enseguida:
Donde:
fimáx: Valor máximo encontrado para la función en el grupo de 8 individuos.
fimín: Valor mínimo encontrado para la función en el grupo de 8 individuos.
fi(xj): Valor de la función fi para el individuo Xj
FP: Factor de ponderación
FP(fi): Factor de ponderación de fi (para cada función objetivo FP(fi) = 1/3)
M: Número de funciones objetivo
P(Xj)i: Ponderación del individuo en la función objetivo
Xj: Individuo de la población
Una vez calculado P(Xj)i, se obtiene:

Donde:
M: Número de funciones objetivo
P(Xj): Ponderación del individuo
P(Xj)i: Ponderación del individuo en la función objetivo
Xj: Individuo de la población
RESULTADOS
Análisis del método uno
El análisis realizado a partir de la aplicación del método uno, incluye los siguientes aspectos:
1. TABLA RESUMEN DE RESULTADOS
Los resultados obtenidos para la población de 84 individuos se presentan de manera parcial en la siguiente tabla. De acuerdo con lo expresado, se seleccionan con fines de ilustración, solo aquellos individuos a referenciarse con posterioridad en el artículo. Ver tabla 8.
2. DEFINICIÓN DE FRENTES
Al realizar análisis de dominancia sobre aquellos individuos que conforman la población final de respuesta (tabla 8), se obtienen los frentes relacionados a continuación en la tabla 9.
3. ANÁLISIS DEL PRIMER FRENTE (INDIVIDUOS NO DOMINADOS)
De acuerdo con lo mencionado en la metodología, se procede a caracterizar el primer frente (74 individuos), tomando como criterio de clasificación la variable denominada: "tiempo de procesamiento". De esta forma, se muestran los respectivos resultados en la tabla 10.
Asimismo, se identifica a continuación la etapa del ciclo económico en la cual los individuos pertenecientes a cada intervalo, deberían ser utilizados como elemento base para elaborar el programa de ejecución de las actividades correspondientes al proceso de manufactura. La identificación de la etapa del ciclo económico se definió atendiendo el concepto pertinente de la dirección de operaciones de la organización objeto de estudio. También se muestran enseguida otros dos aspectos, el primero se relaciona con aquel individuo cuyo comportamiento es más cercano al comportamiento promedio del intervalo en las tres variables analizadas, mientras que el segundo hace referencia a los individuos que podrían seleccionarse de cada categoría, ya sea con el propósito de minimizar el tiempo de procesamiento, el costo de mano de obra o la fracción defectuosa. Ver tabla 11.
4. DIAGRAMA DE GANT PARA EL MENOR TIEMPO DE PROCESAMIENTO
Se observa en la siguiente figura, el diagrama de Gantt correspondiente al individuo con menor tiempo de procesamiento (en semanas). En el gráfico se aprecia en el eje de las ordenadas el nombre de las operaciones (centro de trabajo), mientras que en las abscisas se muestra la variable tiempo de proceso (expresada en horas). En cada cuadro se indica el número del pedido que está siendo procesado, como se puede visualizar en la figura 1.
5. ANÁLISIS DE VARIANZA
El problema se ejecutó de manera consecutiva durante 30 oportunidades, tomando cada vez los valores correspondientes al promedio de las variables de interés: tiempo de procesamiento (en semanas), costos de mano de obra directa y fracción defectuosa debida a la fatiga del operario. Los valores obtenidos se sometieron a un análisis de varianza, cuyos resultados en síntesis son los que se pueden visualizar en la tabla 12.
Del análisis de varianza presentado en la tabla 12, se observa que el valor de la distribución F establecida con el siguiente nivel alfa y grados de libertad: (0.05, 2, 27), es superior al valor de las distribuciones F calculadas sobre el mismo punto. Por tanto, se infiere que los datos definidos en los tratamientos, en cuanto al comportamiento de las diversas variables son estadísticamente iguales.
ANÁLISIS DEL MÉTODO DOS:
El análisis realizado a partir de la aplicación del método dos, incluye los siguientes aspectos:
1. TABLA RESUMEN DE RESULTADOS
A continuación se muestra el resultado parcial de los datos obtenidos por medio de la aplicación del método dos. De acuerdo con lo expresado se seleccionan, con fines de ilustración, solo aquellos individuos para referenciarse con posterioridad en el artículo. Como se puede visualizar en la tabla 13.
2. ANÁLISIS DE LOS INDIVIDUOS
Con el propósito de realizar una adecuada comparación entre los resultados de los métodos uno y dos, los datos provenientes de la aplicación del método dos se agruparán con los intervalos ya establecidos para el análisis de los individuos obtenidos como resultado de la aplicación del método uno, en lo que respecta al primer frente. Con base en lo anterior, se presenta enseguida la síntesis correspondiente a los datos observados en la tabla 13. Ver tabla 14.
Al evaluar el primer intervalo del método uno respecto al primer intervalo del método dos, se encuentra que: en cuanto a la variable tiempo de proceso (en semanas), el método uno supera al método dos en 1,23%; en cuanto a la variable costo de mano de obra, el método uno supera al método dos en 5,22% y en cuanto a la variable fracción defectuosa, el método uno supera al método dos en 24,85%.
Comparación de los métodos uno y dos
La comparación de los métodos uno y dos incluye los siguientes aspectos:
- Comparación de los individuos de mínimo valor para las variables analizadas.
A continuación se muestra la comparación entre los métodos uno y dos, considerando en cada caso, aquellos individuos que arrojan el comportamiento de mínimo valor para las variables analizadas. Como se puede observar en la tabla 15.
De acuerdo con lo apreciado en la tabla anterior, el método uno al compararlo con el método dos presenta el siguiente comportamiento, como se visualiza en la tabla 16.
- Comparación de los métodos en cuanto al comportamiento promedio de las variables analizadas.
Se muestran enseguida los valores promedio de las variables de interés para cada uno de los grupos de 84 individuos que se obtuvieron por medio de la aplicación de los métodos uno y dos, como se puede observar en la tabla 17.
Al comparar los métodos anteriores con respecto al valor tomado por el promedio de las variables analizadas se encuentra que: el método uno supera al dos en cuanto al comportamiento de la variable tiempo de proceso (en horas) en 8,38%, el método uno supera al dos en cuanto al comportamiento de la variable tiempo de proceso (en semanas) en 16,85%, el método uno es inferior al dos en cuanto al comportamiento de la variable costo MOD en 2,67% y, asimismo que el método uno supera al "dos en cuanto al comportamiento de la variable fracción defectuosa en 2,29%. - Comparación del método uno respecto al individuo con mayor ponderación obtenido a través de la aplicación del método dos.
En la tabla 18 se presenta el individuo con mayor valor de ponderación obtenido por medio del método dos. Al comparar el anterior individuo con los individuos de valor mínimo provenientes del método uno se encuentra lo que se puede observar en la tabla 19.
DISCUSIÓN DE RESULTADOS
Si bien, en la literatura revisada, los procesos de investigación de los sistemas Job shop que utilizan técnicas propias de la inteligencia artificial, se han difundido durante los últimos 10 años; se hace notar que las variables tratadas en el tipo de problema multipropósito, objeto de este artículo, no han sido analizadas previamente por ningún autor.
Particularmente, la metodología diseñada con el fin de evaluar las variables objeto de análisis, puede calificarse como precisa, los resultados establecidos, se consideran estadísticamente iguales con un nivel de confianza de 95%.
El menor tiempo de proceso establecido de 176 horas, al esquematizarse en diferentes programas de producción por turno, genera diversos resultados en cuanto al comportamiento de las variables: tiempo de proceso expresado en semanas, costo de mano de obra directa y porcentaje de fracción defectuosa debida a la fatiga del operario.
Al analizar la información obtenida por el método uno se logran identificar dos frentes, el primero de ellos agrupa el 87% de los datos, es decir, existe un 87% de individuos no dominados. En cuanto al segundo frente, corresponde a individuos que si bien generan un bajo tiempo de proceso en semanas, al esquematizarse en programas de producción de 24 horas al día, incrementan tanto el costo de mano de obra directa como la probabilidad de obtener artículos no conformes.
Con relación a la agrupación de datos realizada para los individuos de ambos métodos, debe comentarse que los individuos clasificados en el primer intervalo del método uno, dominan a los individuos clasificados en el mismo intervalo del método dos.
Al comparar el individuo de menor tiempo de proceso obtenido con el método uno con aquel individuo de mayor valor ponderado arrojado por el método dos, se encuentra que el primero supera al segundo en las variables: tiempo de proceso (en semanas), tiempo de proceso (en horas) y fracción defectuosa, mientras que el segundo presenta mejor desempeño en el costo MOD.
CONCLUSIONES
De acuerdo con los resultados encontrados y su discusión se puede concluir que: 1. El análisis de varianza permitió confirmar la estabilidad estadística de los datos calculados, para las diversas variables objeto de estudio. 2. De acuerdo con la etapa del ciclo económico (crecimiento, estabilidad o recesión), la dirección de operaciones de la compañía puede decidir la utilización de diferentes programas de producción, por medio de los cuales se logre obtener el menor tiempo de procesamiento, al mínimo costo y a la vez con la menor probabilidad de generar artículos no conformes. En cada circunstancia es conveniente que el director de operaciones interprete los resultados y valide la respuesta del modelo o establezca el curso de acción a tomar. 3. Se observa en los diferentes elementos de comparación (individuos de mejor desempeño en las diversas variables, promedio de las variables en las poblaciones de respuesta, conformación de los intervalos por datos agrupados, análisis de dominancia) que el método uno supera el desempeño del método dos. 4. El enfoque actual del proyecto puede robustecerse incorporando conceptos provenientes del análisis estocástico y la dinámica de sistemas al igual que de elementos provenientes de otros métodos propios de la misma inteligencia artificial (NSGA II, SPEA II, colonia de hormigas y minería de datos).
AGRADECIMIENTOS
Se expresan los más sinceros agradecimientos a la Universidad Nacional de Colombia -sede Manizales-, por su apoyo en la implementación del proyecto, el cual es adelantado actualmente por los autores del artículo, bajo la reglamentación del programa de maestría investigativa en ingeniería industrial. Al respecto, debe aclararse que los aspectos ilustrados en el presente artículo, corresponden a los resultados parciales del mencionado proyecto.
REFERENCIAS
Anandaraman, C. (2011). "An improved sheep flock heredity algorithm for job shop scheduling and flow shop scheduling problems". International Journal of Industrial Engineering Computations, vol. 2, pp. 749-764. [ Links ]
Akhshabi, M. and Khalatbari, J. (2011). "Solving flexible job-shop scheduling problem using clonal selection algorithm". Indian Journal of Science and Technology, vol. 4, pp. 1248-1251. [ Links ]
Bhongade, A. S. y Khodke, P. M. (2011). "Heuristics for production scheduling problem with machining and assembly operations". International Journal of Industrial Engineering Computations, vol 3, pp. 185-198. [ Links ]
Binato, S.; Hery, W.J.; Loewenstern D. M. and Resende, M. G. C. (2002). "A grasp for job scheduling". In: Ribeiro, C.C., Hansen, P. (eds.). Essays and Surveys in Metaheuristics. Kluwer Academic Publishers. [ Links ]
Bozejko, W. (2012). "On single-walk parallelization of the job shop problem solving algorithms". Computers and Operations Research, vol. 39, pp. 2258-2264. [ Links ]
Castrillón, O. D.; Sarache, W. A. y Giraldo, J. A. (2011). "Aplicación de un algoritmo evolutivo en la solución de un problema job shop - open shop". Información tecnológica, vol. 22, pp. 83-92. [ Links ]
Cheng, B.; Yang, S.; Hu, X. and Chen, B. (2012). "Minimizing makespan and total completion time for parallel batch processing machines with non-identical job sizes". Applied Mathematical Modelling, vol. 36, pp. 3161-3167. [ Links ]
Correa, A.; Velásquez, E. y Londoño, M. I. (2008). "Secuenciación de operaciones para configuraciones de planta tipo job shop flexible: Estado del arte". Avances en sistemas e informática, vol. 5, pp. 151-161. [ Links ]
Dao Er Ji, R. Q. y Wang, Y. (2012). "A new hybrid genetic algorithm for job shop scheduling problem". Computers and Operations Research, vol. 39, pp. 2291-2299. [ Links ]
Daza, J. M., Montoya, J. R. y Narducci, F. (2009). "Resolución del problema de enrutamiento de vehículos con limitaciones de capacidad utilizando un procedimiento metaheurístico de dos fases". Revista EIA, No. 12, pp. 23-38. [ Links ]
Gen, M. y Cheng, R. (1997). Genetic Algorithms and Engineering Design. Estados Unidos: Hamid R. Parsaei. [ Links ]
Ghiasi, H.; Damiano, P. y Lessard, L. (2011). "A nondominated sorting hybrid algorithm for multi-objective optimization of engineering problems". Enginnering Optimization, vol. 43, pp. 39-59. [ Links ]
Li, J.; Pan, Q.; Saganthan, P. y Chua, T. (2011). "A hybrid tabu search algorithm with an efficient neighborhood structure for the flexible job shop scheduling problem". International Journal of Advanced Manufacturing of Technology, vol. 52, pp. 683-697. [ Links ]
López, L.; Hincapié R. A. y Gallego R. A. (2011). "Planteamiento multiobjetivo de sistemas de distribución usando un algoritmo evolutivo NSGA-II". Revista EIA, No. 15, pp. 141-151. [ Links ]
Mansouri, S. A.; Hendizadeh, S. H. y Salmasi, N. (2008). "Bicriteria scheduling of a two-machine flowshop with sequence-dependent setup times". International Journal of Advanced Manufacturing Technology, vol. 40, pp. 1216-1226. [ Links ]
Medina, R.; Pradenas, L. y Parada, V. (2011). "Un algoritmo genético flexible para el problema job shop flexible". Revista Chilena de Ingeniería, vol. 19, pp. 53-61. [ Links ]
Meisel, J. D. y Prado, L. K. (2010). "Un algoritmo genético híbrido y un enfriamiento simulado para solucionar el problema de programación de pedidos job shop". Revista EIA, No. 13, pp. 31-51. [ Links ]
Raud, B.; Steyer J. P.; Lemoine, C.; Latrille, E.; Manic, G. y Printemps-Vacquier, C. (2007). "Towards global multi objective optimization of waste water treatment plant based on modeling and genetic algorithms". Water Science and Technology, vol. 56, pp. 109-116. [ Links ]
Ruiz, H. A.; Toro, E. M. y Gallego, R. A. (2012). "Identificación eficiente de errores en estimación de estado usando un algoritmo genético especializado". Revista EIA, No. 17, pp. 9-19. [ Links ]