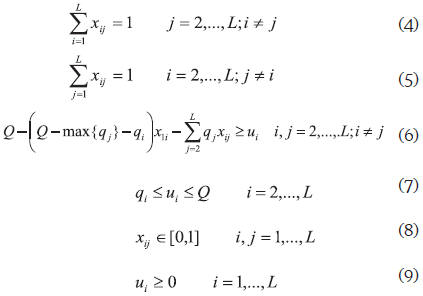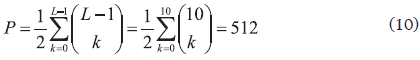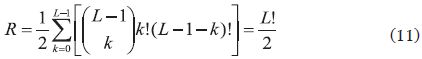Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.20 Envigado July/Dec. 2013
ALGORITMO MEMÉTICO PARA RESOLVER EL PROBLEMA DE ENRUTAMIENTO DE VEHÍCULOS CON CAPACIDAD LIMITADA
MEMETIC ALGORITHM FOR THE VEHICLE ROUTING PROBLEM
ALGORITMO MEMÉTICO PARA SOLUCIONAR O PROBLEMA DE ROTEAMENTO DOS VEÍCULOS COM CAPACIDADE LIMITADA
Juan Rodrigo Jaramillo Posada
Ph.D. Ingeniería industrial, West Virginia University. Profesor asistente de OM and SCM, College of Business Albany State University. Albany, Estados Unidos.
Autor de correspondencia: 504 College Drive Albany, GA 31705, Albany-Estados Unidos. Tel: (229) 430 4084 Correo electrónico: juan.jaramillo@asurams.edu.
Artículo recibido: 26-XI-2012 / Aprobado: 11-VII-2013
Discusión abierta hasta diciembre de 2014
RESUMEN
El diseño de rutas eficientes para vehículos que visitan un número importante de destinos es un factor crítico para la competitividad de muchas compañías. El diseño de dichas rutas se conoce como el problema de enrutamiento de vehículos. El enrutamiento de vehículos hace parte de una categoría de problemas conocida como NP-Difícil. Dado que el enrutamiento de vehículos es NP-Difícil, los diseños de rutas se hacen por medio de algoritmos de aproximación denominados metaheurísticos. El presente trabajo presenta un algoritmo memético que evoluciona utilizando un mecanismo inspirado en las mutaciones de los virus. Adicionalmente, el algoritmo utiliza la Búsqueda Tabú como mecanismo de intensificación. El algoritmo se evaluó utilizando un conjunto de reconocidas instancias de la literatura obteniendo resultados altamente favorables.
PALABRAS CLAVE: Enrutamiento de vehículos; ruteo de vehículos; algoritmos evolutivos; algoritmo memético; Búsqueda Tabú.
ABSTRACT
Solving the Capacitated Vehicle Routing Problem is critical for the success of many companies. The Capacitated Vehicle Routing Problem belongs to the family of NP-Hard problems. Consequently, the development of Meta-heuristics is critical for its solution. This work presents a Memetic Algorithm inspired on virus mutation mechanisms. In addition, the algorithm uses Tabu Search for intensification purposes. The algorithm was evaluated using a well know set of instances from the literature. The results indicate that the algorithm performed well.
KEY WORDS: Vehicle Routing Problem; Evolutionary Algorithms; Memetic Algorithm; Tabu Search.
SUMÁRIO
O desenho de rotas eficientes para veículos que visitam um número importante de destino é um fator crítico para a competitividade de muitas empresas. O desenho de estas rotas é conhecido como o problema de roteamento dos veículos. O roteamento dos veículos é parte duma categoria de problemas conhecida como NP-Difícil. Dado que o roteamento dos veículos é NP-Difícil, os desenhos de rotas fazem-se através de algoritmos de aproximação chamados meta-heurísticos. O presente trabalho apresenta um algoritmo memético que evolui utilizando um mecanismo inspirado das mutações dos vírus. Adicionalmente, o algoritmo utiliza a pesquisa tabu como mecanismo de intensificação. O algoritmo foi analisado utilizando um conjunto de reconhecidas instancias da literatura obtendo resultados altamente favorável.
PALAVRAS-CHAVE: Roteamento de veículo; Algoritmos evolutivos; Algoritmo Memético; Pesquisa Tabu.
1. INTRODUCCIÓN
El diseño de rutas eficientes para vehículos que visitan un número importante de destinos es un factor crítico para la competitividad de muchas compañías. El diseño de dichas rutas se conoce como el problema de enrutamiento de vehículos (vehicle routing problem). En efecto, el enrutamiento eficiente de vehículos es uno de los problemas más estudiados en las áreas de logística y de optimización combinatoria. El problema del enrutamiento de vehículos fue presentado en la literatura por Dantzig y Ramser (1959). Algunos de los objetivos más comunes del problema son la minimización de la distancia total recorrida por los vehículos y la minimización del tiempo utilizado por los vehículos. El enrutamiento de vehículos tiene aplicaciones en el diseño de rutas de reparto de mercancía, de recolección de basura y de rutas de servicio, entre otros.
El problema del enrutamiento de vehículos integra el problema de empaquetamiento (bin packing problem) y el problema del agente viajero (travelling salesman problem). El problema de empaquetamiento asigna destinos a cada uno de los vehículos y el problema del agente viajero diseña las rutas de cada vehículo. El enrutamiento de vehículos hace parte de una categoría de problemas conocida como NP-Difícil (NP-Hard), Garey y Johnson (1979). La principal característica de los problemas NP-Difícil es la dificultad para encontrar soluciones óptimas para instancias de tamaño mediano en adelante (en este caso, 20 destinos o más) en tiempo computacional aceptable. Esto se debe a que la única manera de encontrar la ruta óptima es evaluar todas las opciones posibles. Por ejemplo, el número de posibles rutas para un vehículo es n!, donde n es el número de destinos a visitar. Adicionalmente, la adición de un cliente más incrementa el número de posibles rutas de manera exponencial, nótese que (n+1)! - n! > n!
Existen múltiples versiones del problema del enrutamiento de vehículos de acuerdo con las características a considerar. La versión más conocida busca la minimización de la distancia total recorrida por los vehículos, cada destino se visita una sola vez y los vehículos tienen capacidad limitada. Versiones adicionales incluyen la entrega de mercancía a determinadas horas, y la recolección y entrega de mercancía de forma simultánea. Jaramillo (2010) y Jaramillo (2011) presentan variaciones del problema en las cuales el objetivo es la minimización de emisiones de CO2. Para reducir emisiones de CO2 se requiere alterar la función objetivo para minimizar el producto distancia-carga en vez de distancia. Este cambio en la función objetivo no había sido considerado en estudios previos e incrementa la dificultad del problema. Marinakis y Migdalas (2007) y Parragh, et al. (2008) partes I y II ofrecen una revisión detallada de las diferentes versiones del enrutamiento de vehículos.
Dado que el enrutamiento de vehículos es NP-Difícil, los diseños de rutas se hacen por medio de algoritmos de aproximación denominados metaheurísticos. Los algoritmos metaheurísticos permiten encontrar soluciones de calidad en tiempos de computación aceptables. Para problemas NP-Difícil, es inviable determinar si dichas soluciones son óptimas, con excepción de algunos casos en los cuales el valor la función objetivo de la solución encontrada coincide con una cota inferior/superior. Algunos de los algoritmos utilizados en la literatura para el resolver instancias del problema de enrutamiento de vehículos con capacidad limitada son: Recocido Simulado (simulated annealing); Búsqueda Tabú (tabu search) Jaramillo (2012); Colonias de Hormigas (ant colony) Bin, et al. (2009) y Algoritmos Genéticos (genetic algorithms) Baker y Ayechew (2003).
Los Algoritmos Meméticos se han utilizado exitosamente para resolver problemas caracterizados como NP-Difícil. Los Algoritmos Meméticos (Moscato, 1989) combinan algoritmos inspirados en principios de evolución, con otros métodos como: la Búsqueda Tabú y el recocido simulado; dicha integración produce algoritmos más versátiles y eficaces. Para mayor información acerca de los Algoritmos Genéticos el lector puede consultar Neri (2012).
El presente trabajo presenta la integración de un algoritmo evolutivo inspirado en la mutación viral con la Búsqueda Tabú presentada en Jaramillo (2012). La sección 2 hace una presentación formal del problema de enrutamiento de vehículos; la sección 3 discute el Algoritmo Memético en detalle; la sección 4 presenta los resultados obtenidos al aplicar el algoritmo a un grupo de instancias reconocidas en la literatura y la sección 5 resume las conclusiones obtenidas y discute áreas potenciales para futura investigación.
2. EL PROBLEMA DE ENRUTAMIENTO DE VEHÍCULOS
2.1 Definición del problema
El problema de enrutamiento de vehículos estudiado en el presente trabajo es el siguiente: dado un grupo de destinos a los cuales se les debe entregar mercancía utilizando un número determinado de vehículos con capacidad limitada; diseñar las rutas de los diferentes vehículos minimizando la distancia total recorrida, asegurando que no se exceda la capacidad de los mismos y visitando cada destino una sola vez.
2.2 Formulación matemática
La siguiente formulación matemática se basa en Kara, et al. (2004):
Índices:
i, j Destinos i, j = 1,..., L; donde i=1 representa el sitio de salida/llegada de los vehículos (base) y L representa el número total de destinos a visitar.
Parámetros:
dij Distancia entre los destinos i y j.
qi Demanda del cliente ubicado en el destino i en unidades de masa.
Q Capacidad de cada vehículo en unidades de masa.
K Número de vehículos a utilizar.
Variables:
xij 1 si un vehículo visita el destino j inmediatamente después de visitar el destino i.
0 en caso contrario.
ui Número real arbitrario.
Función objetivo:
Restricciones:
La función objetivo (1) minimiza la distancia total recorrida por todos los vehículos. El grupo de restricciones (2) asegura que cada una de las rutas se origine en la base (i=1). El conjunto de restricciones (3) asegura que cada una de las rutas termine en la base. El grupo de restricciones (4) y (5) aseguran que solamente un vehículo visite cada destino. Los grupos de restricciones (6) y (7) garantizan que la capacidad máxima de los vehículos no sea sobrepasada y que no se generen subrutas. Una subruta es una ruta que no incluye la base de los vehículos. El grupo de restricciones (6) es una extensión del grupo Miller-Tucker-Zemlin para eliminar subrutas propuesto en Kara, et al. (2004). Finalmente los grupos de restricciones presentados en (8) y (9) definen la naturaleza de las variables.
2.3 Ejemplo ilustrativo
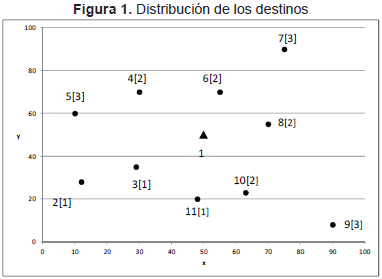
A continuación se presenta una instancia del enrutamiento de vehículos. La instancia considera 2 vehículos con una capacidad de carga de 10 toneladas y 11 destinos incluyendo la base. La Tabla 1 contiene las coordenadas (x, y) de la base y de cada uno de los sitios a visitar; la demanda en toneladas de cada destino [q] y las distancias euclidianas entre cada par de destinos. Es importante anotar que las distancias se pueden calcular utilizando sistemas de información geográfica para casos de la vida real. En este caso, las distancias se han redondeado con fines ilustrativos. Dicho redondeo no afecta la rigurosidad del análisis. Finalmente, la Figura 1 ilustra la ubicación de la base y los destinos. Los valores entre corchetes representan los pesos de los pedidos.
2.4. Complejidad del problema
El primer paso para generar una solución es repartir los destinos entre los dos vehículos (problema de empaquetamiento). El número total de posibles maneras de repartir los destinos (particiones) está dado por (10), donde k representa el número de destinos asignado al primer vehículo y L-1 es el número de destinos sin incluir la base. Nótese que no es necesario considerar el segundo vehículo dado que los destinos asignados al segundo vehículo son todos los que no se asignan al primero. Dada la simetría en las soluciones (asignar 10 destinos al primer vehículo y 0 al segundo es similar a asignar 0 destinos al primero y 10 al segundo), el valor obtenido por la sumatoria se divide por 2. El valor de P para la instancia ilustrativa es de 512 posibles particiones. Para una instancia con 20 destinos y dos vehículos, el número de particiones asciende a 524,288.
Para cada una de las 512 particiones se deben evaluar todas las rutas posibles. Por ejemplo si se asignan 10 destinos al primer vehículo existen 10! posibles rutas, o si se asignan 6 destinos al primer vehículo y 4 al segundo, existen 6! rutas para el primero y 4! rutas para el segundo. Por lo tanto, cada una de las particiones genera k!(L-1-k)! rutas posibles. El número total de soluciones posibles esta dado por la ecuación (11). El número total de soluciones a evaluar en este caso es de 2,0*107 posibles soluciones. Para una instancia con 20 destinos el número total sería de 2,6*1019. Es importante mencionar que el conjunto de todas las soluciones posibles se denomina espacio de soluciones.
3. ALGORITMO MEMÉTICO
Dada la naturaleza NP-Difícil del problema de enrutamiento de vehículos, se requieren algoritmos de aproximación (metaheurísticos) que permitan encontrar soluciones de calidad en tiempos de computación aceptables. El algoritmo metaheurístico presentado en esta sección es un Algoritmo Memético, MEMVRP, que integra un algoritmo evolutivo inspirado en la mutación viral con los principios de la Búsqueda Tabú presentada en Jaramillo (2012). Las siguientes secciones describen cada uno de los componentes de MEMVRP.
3.1 Solución inicial
El punto de partida de la mayoría de los algoritmos heurísticos es la generación de una solución inicial. Los algoritmos encargados de generar las soluciones iniciales se denominan algoritmos constructores. El algoritmo constructor utilizado en el presente trabajo, Mconst, asigna cada destino una sola vez y de forma aleatoria entre los diferentes vehículos. Por ejemplo una solución inicial posible es asignar los destinos 8, 7, 6, 4, 3 al vehículo 1 y los destinos 5, 2, 11, 10, 9 al segundo vehículo para ser visitados en dichas secuencias. Es importante recordar que cada ruta comienza y termina en la base (i=1). La distancia recorrida por el primer vehículo es 21(d1,8) + 35(d8,7) + 28(d7,6) + 25(d6,4) + 35(d4,3) + 26(d3,1) = 170 km y la distancia recorrida por el segundo vehículo es de 214 km, para un valor objetivo de 170 + 214 = 384 km. Nótese que cada vehículo transporta una carga inicial de 10 toneladas.
3.2 Representación de la solución
La solución obtenida en la sección 3.1 se puede representar utilizando la formulación matemática presentada en la sección 2.2. Esto se logra asignándole el valor de 1 a las variables x1,8, x8,7, x7,6, x6,4, x4,3, x3,1, x1,5, x5,2, x2,11, x11,10, x1,1, x10,9, x9,1 y 0 a todas las demás. Dadas las limitaciones prácticas de la formulación matemática, es importante utilizar una representación que facilite el proceso de búsqueda de soluciones de calidad utilizando algoritmos heurísticos. De hecho, cada solución se puede representar utilizando un set de vectores S0 = {[s1, si,,... sj, s1]1, [s1, sn. ,..., sm, s1]2, ..., [s1, so,,..., sp, s1]K}, donde cada vector representa una ruta que comienza y termina en la base (s1). La solución obtenida por Mconst se puede representar como S0 = {[1, 8, 7, 6, 4, 3, 1]1 [1, 5, 2, 11, 10, 9, 1 ]2}. Considerando que todas las rutas comienzan y terminan en la base, la representación se puede simplificar para obtener S0 = {[8, 7, 6, 4, 3]1 [5, 2, 11, 10, 9]2}. La Figura 2a presenta la ilustración gráfica de dicha solución.
3.3 Búsqueda local
La búsqueda local explora diferentes soluciones partiendo de una solución conocida, para obtener nuevas soluciones la búsqueda local utiliza diferentes mecanismos para alterar la solución actual. Los mecanismos aplicados en el presente trabajo se denominan Eopt y Iopt. Dichos mecanismos alteran las rutas existentes intercambiando destinos (Eopt) o eliminando e insertando destinos (Iopt). Un ejemplo del mecanismo Eopt consiste en intercambiar los destinos 5 y 3 en S0 para obtener la solución S1 = {[8, 7, 6, 4, 5]1 [3, 2, 11, 10, 9]2} con un valor objetivo de 357 km. Es importante anotar que la solución obtenida no es viable, ya que la carga inicial del vehículo 1 es de 12 toneladas. La Figura 2b ilustra S1. Con frecuencia las soluciones inviables se aceptan en la fase inicial de la búsqueda. En términos generales las soluciones inviables pueden guiar la búsqueda hacia soluciones viables de mejor calidad. Un ejemplo del mecanismo Iopt es remover el destino 8 de la primera ruta e insertarlo al final de la segunda ruta para obtener S2 = {[7, 6, 4, 5]1 [3, 2, 11, 10, 9, 8]2}. La nueva solución es viable y tiene una función objetivo de 362 km (Figura 2c). Los mecanismos Eopt e Iopt no se limitan a intercambiar destinos entre rutas diferentes, sino que también se pueden aplicar a una sola ruta. Por ejemplo el intercambio de los destinos 6 y 7 en la ruta 1 genera la solución S3 = {[6, 7, 4, 5]1 [3, 2, 11, 10, 9, 8]2} con una función objetivo de 360 km. Esta última solución es óptima para la instancia (Figura 2d). Dicha solución se confirmó de forma paralela codificando la formulación matemática presentada en la sección 2.1 utilizando OPL y resolviéndola con la versión académica de CPLEX 12.10.
En términos generales la búsqueda local se puede describir como sigue:
- Generar una solución inicial S0 utilizando Mconst.
- Aplicar los mecanismos Eopt e Iopt a S0. El conjunto de soluciones obtenidas en este proceso se denomina vecindario de soluciones (V) y cada intercambio generado por los mecanismos Eopt e Iopt se denomina una movida.
- Seleccionar la mejor solución en V (S*).
- Si S* es mejor que S0, convertir S* en S0 y repetir los pasos a, b y c. La ejecución de los pasos a, b y c se denomina iteración.
- Si S* no es mejor que S0, terminar el algoritmo. Cuando esto ocurre se dice que la búsqueda arribó a un óptimo local.
3.4 Búsqueda Tabú
La Búsqueda Tabú (Glover, 1986) es uno de los algoritmos metaheurísticos más utilizados en optimización combinatoria. La Búsqueda Tabú utiliza una serie de mecanismos para permitir que la búsqueda escape de los óptimos locales y continúe hacia mejores soluciones. La Búsqueda Tabú utiliza dos tipos de memoria: la memoria de corto plazo y la memoria de largo plazo. La memoria de corto plazo (lista tabú) permite a la búsqueda avance sin repetir soluciones exploradas previamente. La memoria de largo plazo (lista de frecuencias) se utiliza para diversificar la búsqueda. En el presente trabajo, la Búsqueda Tabú se utiliza como mecanismo de intensificación mientras que el proceso de mutaciones descrito en la sección 3.5 garantiza la diversificación de la búsqueda. Finalmente, los mecanismos de la Búsqueda Tabú utilizada por TSmem son la lista tabú, el criterio para remover soluciones tabú, la penalización de soluciones no viables y el criterio para terminar la búsqueda.
La lista tabú es el mecanismo más importante de TSmem. La lista almacena las movidas recientes y evita su repetición. La lista utilizada en TSmem es una lista tridimensional propuesta en Jaramillo (2012) y prohíbe la inserción de un destino entre otros dos. Por ejemplo, al aplicar el mecanismo Iopt (Figura 1c) la inserción del destino 8 entre los destinos 1 y 7 no se puede repetir durante cierto número de iteraciones. Cuando una movida tabú genera la solución de mejor calidad hasta el momento, la movida es removida de la lista tabú y la solución se acepta. El tercer mecanismo penaliza el valor objetivo de soluciones no viables. La penalización se incrementa en la medida que la búsqueda avanza. Este incremento en la penalización asegura que la búsqueda termine con una solución viable. La Búsqueda Tabú se puede resumir en los siguientes pasos:
- Generar una solución inicial S0 utilizando Mconst.
- Smejor = S0.
- Aplicar Eopt e Iopt a S0 de forma exhaustiva.
- Si una movida tabú mejora Smejor, remover la movida de la Lista Tabú.
- Generar V considerando solamente las movidas no tabú.
- Penalizar las soluciones no viables.
- Seleccionar la mejor solución en V (S*).
- Si S* es mejor que Smejor, Smejor = S*.
- S0 = S*. Nótese que la búsqueda no se detiene si la calidad de S* es inferior a la de S0.
- Repetir los pasos c hasta f mientras no se alcance un número predeterminado de iteraciones sin superar Smejor.
- Terminar el algoritmo.
3.5 Algoritmo Memético
La mayor fortaleza de la Búsqueda Tabú es la concentración en la exploración de áreas promisorias del espacio de soluciones (intensificación). De otro lado, la mayor debilidad es la exploración de nuevas regiones del espacio de soluciones (diversificación). Por su parte, los algoritmos inspirados en teorías evolutivas como los Algoritmos Genéticos (Holland, 1975) tienen mecanismos de diversificación eficientes. La mayor limitación de los Algoritmos Genéticos en el enrutamiento de vehículos está en el mecanismo reproductivo. Los Algoritmos Genéticos combinan dos soluciones (padres) para generar una tercera (hijo). La mayoría de las soluciones obtenidas por este método generan rutas que visitan los mismos destinos más de una vez. Estas rutas no son viables y deben ser reparadas antes de aplicarles la Búsqueda Tabú. La Figura 3 es un ejemplo de un caso típico. La primeras dos filas. P1 y P2, contienen la información de los padres. La tercera fila, RA, es un número aleatorio entre 0 y 1. La cuarta fila, P3, es la nueva solución. El mecanismo para obtener P3 consiste en seleccionar los destinos con base en RA. Si RA > 0,5 se selecciona el destino de P1, en caso contrario se selecciona el destino de P2.
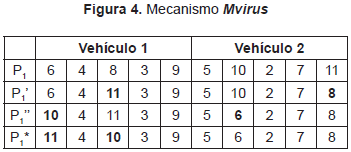
Las rutas resultantes, P3, visitan los destinos 5, 6 y 7 dos veces y no incluyen los destinos 2, 8 y 10. Soluciones como esta no hacen parte del espacio de soluciones. Por lo cual se requeriría un mecanismo adicional para corregir P3. Para obviar estas dificultades, MEMVRP utiliza un mecanismo inspirado en los procesos evolutivos de los virus, Mvirus, que genera múltiples mutaciones a una solución existente. Las mutaciones se basan en múltiples Eopt aplicados de forma secuencial y escogidas de manera aleatoria. Este mecanismo mantiene el número de destinos asociado a cada vehículo constante y asegura que cada destino sea visitado una sola vez. La Figura 4 ejemplifica el proceso para obtener P1* a partir de P1. Nótese que la solución obtenida no es viable puesto que la carga inicial del vehículo 2 es de 11 toneladas, pero hace parte del espacio de soluciones. Como se mencionó con anterioridad, el exceso de carga se controla utilizando el factor de penalización discutido en la sección 3.4.
MEMVRP se puede resumir en los siguientes pasos:
- Crear la población inicial de soluciones, MPob, utilizando Mconst.
- Aplicar TSmem a cada solución en MPob.
- Seleccionar la mejor la mejor solución y guadarla como Mbest.
- Aplicar Mvirus y TSmem a cada una de las soluciones en MPob.
- Seleccionar la solución de más baja calidad en MPob y reemplazarla con Mbest.
- Seleccionar las soluciones remanentes de más baja calidad en MPob y:
- Eliminarlas de MPob.
- Crear nuevas soluciones utilizando Mconst.
- Aplicar TSmem a cada una de las nuevas soluciones.
- Agregar las nuevas soluciones a MPob.
- Seleccionar la mejor solución en MPob y compararla con Mbest. Si es de mejor calidad, reemplazar Mbest.
- Repetir los pasos d hasta g hasta que se complete el número de generaciones deseado. Cada repetición crea una nueva generación de soluciones.
El paso f reemplaza los mecanismos de mutación utilizados en los Algoritmos Genéticos. La aplicación de la Búsqueda Tabú hace que dichos mecanismos no sean efectivos. El mecanismo utilizado en f se basa en el propuesto en Mendes, et al. 2005.
4. RESULTADOS
MEMVRP se evalu óutilizando un reconocido conjunto de instancias para el enrutamiento de vehículos denominado "Augerat set A". El conjunto de 26 instancias se puede descargar en http://www.coin-or.org/SYMPHONY/branchandcut/VRP/data/index.htm.old. Este set es uno de los más utilizados para evaluar algoritmos para el enrutamiento de vehículos y tiene la ventaja de que sus soluciones óptimas son conocidas. Es importante mencionar que la obtención de dichas soluciones requiere miles de horas de tiempo computacional en equipos avanzados. El Algoritmo Memético se codificó en Visual C++ 2010 Express Edition. En la evaluación del algoritmo se utilizó un equipo con procesador Intel Core i5 de 2.4 GHz con 8 GB de memoria y Windows 7 de 64 bits.
Los parámetros de MEMVRP se sintonizaron con base en un diseño de experimentos que consideró tres niveles para cada uno de los parámetros. Se hicieron tres repeticiones y se escogió la combinación que generó los mejores resultados. Se hicieron 3 réplicas para encontrar la mejor combinación:
- Población: se consideraron poblaciones de 5, 10 y 15 soluciones. Los mejores resultados se encontraron para el nivel de 10 soluciones. Aparentemente, considerar menos soluciones genera una convergencia alrededor de soluciones de baja calidad. Un mayor número de soluciones no generan mejoras en la calidad e incrementa el tiempo computacional de una manera apreciable.
- Generaciones: se consideraron 3 niveles, 20, 30 y 40 generaciones. Las mejores soluciones se encontraron con 40 generaciones. Un menor número de generaciones es insuficiente para que el algoritmo arribe a soluciones de calidad. Un mayor número incrementa el tiempo computacional de forma apreciable sin mejora en la calidad de la solución.
- Reemplazos. Se consideraron tres niveles 0, 2 y 4 reemplazos. Las mejores respuestas se encontraron para el nivel que reemplaza las 2 soluciones de más baja calidad en cada generación por soluciones nuevas.
- Estadía en la Lista Tabú: se consideraron cuatro niveles, 0,15*(número de destinos), 0,30*(número de destinos) y 0,45*(número de destinos). Los mejores resultados se encontraron para valores de 0,30*(número de destinos). Aparentemente, valores muy bajos permiten la generación de ciclos, mientras valores mayores afectan el proceso de intensificación.
- Penalización: se consideraron tres niveles.1,0/(número de destinos), 1,5/(número de destinos) y 2,0/(número de destinos). El incremento en el factor para penalizar soluciones ineficientes es 1,5/(número de destinos) por iteración. Menores valores generan soluciones inviables, mientras mayores valores restringen el espacio de soluciones, afectando la calidad de la solución final.
- Criterio de finalización: Se consideraron niveles de 10*(número de destinos), 15*(número de destinos) y 20*(número de destinos). Niveles superiores a 10*(número de destinos) no mejoraron las calidades de las soluciones. Valores inferiores terminan el proceso de intensificación muy pronto, generando soluciones de calidad inferior.
Los resultados obtenidos se resumen en la Tabla 2. La primera columna identifica los problemas. El valor después de la n indica en número de destinos y el valor después de la k indica el número de vehículos. Cada vehículo tiene una capacidad de 100 unidades de carga. Por ejemplo la instancia An-69-k9 considera 69 destinos para ser cubiertos por 9 vehículos. La segunda columna indica la carga total a distribuir. La tercera columna enseña la relación carga/capacidad total. La dificultad de las instancias la determina el número de destinos, el número de vehículos y CT/C. Para valores de CT/C cercanos a 1, el problema de empaquetamiento (asignar destinos a vehículos sin sobrepasar la capacidad de carga) se hace más difícil. La cuarta columna contiene las funciones objetivo óptimas. Las siguientes tres columnas contienen los resultados obtenidos por la Búsqueda Tabú presentada en Jaramillo (2012). Estas tres columnas contienen la mejor solución encontrada, el número de veces en 10 intentos en el que se encontró la solución óptima y el promedio de las funciones objetivo en los 10 intentos. Las últimas 3 columnas muestran los resultados obtenidos por MEMVRP en 10 intentos.
Al comparar MEMVRP con la Búsqueda Tabú presentada en Jaramillo (2012), TS, se puede observar que MEMVRP obtuvo un mejor desempeño. En efecto MEMVRP obtuvo la solución óptimapara todas las instancias evaluadas mientras TS fracasó en los problemas A-n60-k9 y A-n61-k9. Adicionalmente, cuando se compara el número de veces que cada algoritmo fue capaz de encontrar la solución óptima en 10 intentos, se observa que MEMVRP iguala o supera a TS en todos los casos con excepción de la instancia A-n39-k6. También se puede observar el deterioro en la calidad de las soluciones obtenidas por TS para problemas con 60 o más destinos. De otro lado, MEMVRP mantiene un desempeño mucho más estable, encontrando la solución óptima en el 99,5 % de los intentos. Finalmente, es importante mencionar que MEMVRP es robusto con respecto a los valores de los diferentes parámetros, lo que facilita su implementación.
5. CONCLUSIONES
Este trabajo presenta un Algoritmo Memético denominado MEMVRP para resolver el problema del enrutamiento de vehículos con capacidad limitada. MEMVRP utiliza un mecanismo inspirado en la mutación de los virus para crear nuevas generaciones de soluciones. Adicionalmente, MEMVRP hace uso de la Búsqueda Tabú para mejorar cada una de las soluciones de la nueva generación. El desempeño de MEMVRP es superior al de la Búsqueda Tabú presentada en Jaramillo (2012). Finalmente futuras áreas de investigación incluyen la aplicación de MEMVRP a otras versiones del enrutamiento de vehículos; la evaluación de otros esquemas de mutación y la sustitución de la Búsqueda Tabú por otros mecanismos de búsqueda como las Colonias de Hormigas o el Recocido Simulado.
AGRADECIMIENTOS
Este artículo constituye la etapa inicial para el diseño de un software propio para la empresa Enviaseo ESP. El autor agradece a Enviaseo y al grupo GPC de la Escuela de Ingeniería de Antioquia -EIA- por el apoyo al proyecto «Reducción de costos en el servicio de recolección de residuos urbanos ordinarios y hospitalarios en ENVIASEO ESP» y a Colciencias por el incentivo tributario otorgado a dicho proyecto.
REFERENCIAS
Baker, B.M. and Ayechew, M.A. (2003). A Genetic Algorithm for the Vehicle Routing Problem. Computers and Operations Research, 30(5) april, pp. 787-800. [ Links ]
Dantzig, G.B. and Ramser, J.H. (1959). The Truck Dispatching Problem. Management Science, 6(1) october, pp. 80-91. [ Links ]
Garey, M.R. and Johnson, D.S. (1979) Computers and Intractability: A Guide to the Theory of NP-Completeness. New York: W. H. Freeman and Co. [ Links ]
Glover, F. (1986). Future Paths for Inter Programming and Links to Artificial Intelligence. Computers and Operations Research, 13(5) May, pp. 533-549. [ Links ]
Holland, J.H. (1975). Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence. Ann Arbour: The University of Michigan Press. [ Links ]
Jaramillo, J.R. (2010). The Single Green Vehicle Routing Problem. Proceedings, SEInfORMS Annual Meeting, October 6-8, Myrtle Beach, South Carolina, USA. [ Links ]
Jaramillo, J.R. (2011). The Green Vehicle Routing Problem. Proceedings, SEInfORMS Annual Meeting, October 5-7, Myrtle Beach, South Carolina, USA. [ Links ]
Jaramillo, J.R. (2012). Búsqueda Tabú para el ruteo de vehículos. Revista de Ingeniería Industrial Universidad de Lima, 14(30) Enero-Diciembre, pp. 22-49. [ Links ]
Kara, I., Laporte, G. and Bektas, T. (2004). A Note on the Lifted Miller-Tucker-Zemlin Subtour Elimination Constraints for the Capacitated Vehicle Routing Problem. European Journal of Operational Research, 158(3) November, pp. 793-795. [ Links ]
Marinakis, Y. and Migdalas, A. (2007). Annotated Bibliography in Vehicle Routing. Operational Research and International Journal, 7(1) January-April, pp. 27-46. [ Links ]
Mendes, J.J.M., Gonçalves, J.F. and Resende, M.G.C. (2005). A Random Key Based Genetic Algorithm for the Resource Constrained Project Scheduling Problems. ATT Labs Technical Report TD-6DUK2C (june). [ Links ]
Moscato, P. (1989). On Evolution, Search, Optimization, Genetic Algorithms and Martial Arts: Towards Memetic Algorithms. Caltech Concurrent Computation Program (report 826). [ Links ]
Neri, F. and Cotta, C. (2012). Memetic Algorithms and Memetic Computing Optimization: A Literature Review. Swarm and Evolutionary Computation, 2(1) February, pp. 1-14. [ Links ]
Parragh, S.N., Doerner K.F. and Hartl, R.F. (2008). A Survey on Pickup and Delivery Problems Part I: Transportation between Customers and Depot. Journal für Betriebswirtschaft, 58(1) April, pp. 21-51. [ Links ]
Parragh, S.N., Doerner K.F, and Hartl, R. (2008). A Survey on Pickup and Delivery Problems. Part II: Transportation between Pickup and Delivery Locations. Journal Fur Betriebswirtschaft, 58(2) June, pp. 81-117. [ Links ]