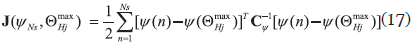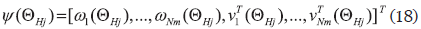Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.20 Envigado July/Dec. 2013
A COMPARATIVE STUDY OF SENSOR PLACEMENT TECHNIQUES FOR STRUCTURAL DAMAGE DETECTION
UN ESTUDIO COMPARATIVO DE TÉCNICAS DE LOCALIZACIÓN DE SENSORES PARA DETECCIÓN DE DAÑO ESTRUCTURAL
UM ESTUDO COMPARATIVO DE TÉCNICAS DE LOCALIZAÇÃO DE SENSORES PARA DETECÇÃO DE DANO ESTRUTURAL
Carlos Alberto Riveros Jerez*, Edwin Fabián García Aristizábal**, Javier Enrique Rivero Jerez***
* Ingeniero civil, Universidad Industrial de Santander; Master of Engineering, The University of Tokyo; Doctor of Engineering, Kyoto University. Profesor Asociado, Universidad de Antioquia. Medellín, Colombia.
Autor de correspondencia: (C.A. Riveros). Calle 67 53-108 Of. 20-403 Ciudad Universitaria, Universidad de Antioquia, Medellín. Tel: 219 85 80 - 219 75 70.
Correo electrónico: riveros@udea.edu.co.
** Ingeniero Civil, Universidad Nacional de Colombia; Master of Engineering, The University of Tokyo; Doctor of Engineering, Kyoto University. Profesor Asistente, Universidad de Antioquia. Medellín, Colombia.
*** Candidato a Doctor, Universidad de las Palmas de la Gran Canaria, España. Profesor ocasional Universidad de Antioquia, Medellín, Colombia.
Artículo recibido: 30-IV-2013 / Aprobado: 28-X-2013
Discusión abierta hasta diciembre de 2014
ABSTRACT
An evaluation of the capabilities and limitations of practical placement techniques used for damage detection in civil engineering structures is performed. Three previously development sensor distribution methods, Eigenvector Sensitivity, Effective Independence, Damage Measurability are compared through numerical studies. The focus of this comparative study is beam-like structures, and two representative examples are considered to evaluate the techniques. The first example considers a single span beam, which could represent a highway bridge. The second example considers a structure with intermediate supports, and could represent the entire deck of a long-span bridge. Due to its successes in previous studies, the Bayesian Probabilistic Approach is employed to identify, locate and quantify damage using the resulting sensor measurements. The impact of noise in the modal parameters is considered. The effectiveness of the resulting sensor configurations for accurately identifying damage scenarios is assessed.
KEY WORDS: Sensor Placement; Structural Damage Detection; Bayesian Probabilistic Approach.
RESUMEN
En este artículo se presenta una evaluación de las capacidades y limitaciones de técnicas de localización de sensores comúnmente usadas en la práctica para detección de daño en estructuras civiles. Tres metodologías previamente desarrolladas, sensitividad del vector propio, independencia efectiva y medida del daño son comparadas por medio de estudios numéricos. El objetivo de este estudio comparativo es estructuras tipo viga, y dos ejemplos representativos son considerados para la evaluación de las técnicas de localización de sensores. El primer ejemplo considera una viga de una sola luz, que puede representar un puente vehicular. El segundo ejemplo considera una estructura con apoyos intermedios y puede representar la zona de tránsito vehicular de un puente de gran luz. Debido a su éxito en estudios previos, el Enfoque Probabilístico Bayesiano es utilizado para identificar, localizar y cuantificar daño utilizando mediciones de las configuraciones de sensores resultantes. El efecto de ruido en la obtención de los parámetros modales es considerado. La efectividad de las configuraciones de sensores resultantes para identificación de escenarios de daño estructural es presentada.
PALABRAS CLAVE: Localización de sensores; detección de daño estructural; Enfoque Probabilístico Bayesiano.
SUMÁRIO
Neste artigo apresenta se uma evacuação das capacidades e limitações de técnicas de localização de sensores geralmente usadas na prática para detecção de dano em estruturas civis. Três metodologia previamente desenvolvidas, sensitividade do vector próprio, independência efetiva, e medida de dano são comparadas por meio de estudos numéricos. O objetivo deste estudo comparativo é estruturas tipo viga, e dois exemplos representativos são considerados para a avaliação das técnicas de localização de sensores. No primeiro exemplo considera se uma viga de uma só luz, que pode representar um ponte veicular. No segundo exemplo se considera uma estrutura com apoios intermédios, e pode representar a zona de trânsito veicular dum ponte de grande luz. Devido a seu sucesso em estudos prévios, o enfoque probabilístico Bayesiano se utiliza para identificar, localizar e quantificar dano utilizando medições das configurações de sensores resultantes. O efeito do ruído na obtenção dos parâmetros modais é considerado. A efetividade das configurações de sensores resultantes para identificação de cenários de danos estruturais é apresentada.
PALAVRAS-CHAVE: Localização de Sensores; Detecção de Dano Estrutural; Enfoque Probabilístico Bayesiano.
1. INTRODUCTION
The monitoring of engineering structures has great potential for reducing the economic impact and life-safety implications through early damage detection. The objective of continuous monitoring is to provide rapid and accurate assessment of the condition of a structure and provide useful information to decision makers regarding repair and replacement priorities. Many of the damage detection techniques currently used require a priori knowledge of the vicinity of damage and accessibility to the portion of the structure being inspected. An alternative approach is to use the dynamic characteristics of a potentially damaged structure to estimate the location and degree of damage by comparison to its baseline behavior. Since experimentally derived modal parameters such as frequencies, damping ratios, and mode shapes are functions of the physical properties of a structure, significant changes in the mechanical properties (i.e. damage) will cause measurable changes in the modal properties. The problem then is to deduce information about the damage from changes in these modal parameters.
The goals of a robust damage detection schemes are discussed by Doebling, et al. (1996) based on the classifications proposed by Rytter (1993). An effective scheme should be able to identify damage (Level I) at an early stage in its progression, locate the identified damage within the sensor resolution being used (Level II), and provide a reasonable estimate of the severity of the damage (Level III). Additionally, for prioritizing needs, it is particularly useful to predict the remaining useful life of the structure (Level IV). To the greatest extent possible, the method should not rely on the engineering judgment of the user or an analytical model of the structure. The aerospace community began to study the use of vibration-based damage detection during the late 1970s and early 1980s in conjunction with the development of the space shuttle (Farrar and Doebling 1999). The civil engineering community has studied vibration-based damage assessment of bridge structures since the early 1980's. Nevertheless, the most successful application of vibration-based damage detection technology to date has been for monitoring rotating machinery as reported by Doebling, et al. 1996.
Several challenges remain in the design of accurate and cost-effective damage monitoring systems. One challenge is in identifying the most effective placement scheme for the sensors to achieve the goals of the monitoring system. In placing the sensors, one must determine the minimum number of sensors for an economically viable implementation, and the best locations for these sensors. One should consider the ability of the sensors to measure the responses of interest for determination of the information required by the damage detection algorithm. In placing the sensors the anticipated sources of excitation should also be considered including the source, statistical characteristics and frequency content. Additionally, the approach should take into account the likelihood of damage in particular regions of the structure, if this information is available. Furthermore, the effectiveness of a placement technique will, in many cases, be linked to the requirements of the damage detection technique that is to be employed. Thus, the placement technique should be tested in conjunction with the damage detection algorithm.
Several researchers have made significant contributions to the development of methodologies for sensor placement. Sensor placement methods designed to address the issues of identification and control of dynamic structures have been developed by Udwadia and Garba (1985) and Lim (1991). An alternative approach is the Effective Independence method presented by Kammer (1991), which determines the final sensor configuration by iteratively removing sensor locations that do not contribute significantly to the linear independence of the mode shapes. Yao (1993) developed a program using genetic algorithms based on the idea of maximizing the determinant of the Fisher information matrix. The results presented by Yao (1993) showed a slight improvement over the results of the Effective Independence method. Hemez and Farhat (1994) extended the Effective Independence method by placing sensors based on the strain energy contributions of the structure. They concluded that to detect and locate damage in large flexible civil structures, it is important to stress the parts of the structure with a high load carrying capability. Udwadia (1994) proposed an algorithm to optimally locate sensors in a dynamic system, which minimizes the covariance of the error in the estimates of the structural parameters using limited sensors; the algorithm maximizes the determinant of the Fisher information matrix and is applicable to both linear and nonlinear systems. Park and Kim (1996) developed a method to iteratively remove certain DOF from the candidate sensor location set to obtain the maximum determinant of the Fisher information matrix after removing DOF. Several DOF can be deleted at each iteration, and the number of DOF that can be deleted can also be determined by the method. Schedlinski and Link (1996) developed a method using QR decomposition of the eigenvector matrix. A subset of structural DOF for sensor locations is localized by enforcing the condition that the linear independence of the mode shapes to be measured is maximized.
Heredia-Zavoni and Esteva (1998) proposed that the optimal sensor configuration is the one that minimizes the expected Bayesian loss function involving the determinant of the inverse of the Fisher information matrix. Cobb and Liebst (1997) developed the Eigenvector Sensitivity method, which uses the eigenvalue and eigenvector sensitivities for the determination of sensor locations. Based on this approach, Shi (2000) also proposed a technique in which the sensor locations are selected according to their ability to localize damage. Xia (2002) improved the method proposed by Shi, et al. (2000) by adding the effect of measurement noise in the selection of the location of sensors. Li, et al. (2007) studied the problem of sensor placement by considering that the Effective Independence method and modal kinetic energy-based methods produce similar results, and proved that the Effective Independence method is an iterated version of modal kinetic energy-based methods. They basically concluded that both methods are closely connected and provided additional support that both methods arrive at similar sensor locations. The Importance of the Effective Independence method is based on the fact that this method is already implemented in the commercial software MSC/NASTRAN (Peck and Torres 2004.) Finally, Li, et al. (2012) improved the Effective Independence method by taking into consideration actual loading conditions. Using experimental data they proved that loading conditions must be considered when placing sensors. Cruz, et al. (2009) proposed the use of genetic algorithms in order to determine the best location of sensors; the Pascual Guerrero Olympic Stadium, located in the city of Cali, Colombia, was used for validation and application of the method proposed by Cruz, et al. (2009).
Sensor placement methods which use the Fisher information matrix as a distribution of the strain energy extended the concept of the Fisher information matrix and are mainly focused on structural damage detection: Therefore, it is selected for this comparative study one method based on the Fisher information matrix, other method based on the Fisher information matrix as a distribution of the strain energy and the method proposed by Xia (2002) which includes the effect of measurement noise. Two structural models, one with relatively simple dynamics and the other exhibiting more complex behavior, are employed for the comparisons. The Bayesian Probabilistic approach (Sohn and Law 1997) is selected based on its success in previous studies, its accuracy in identifying damage with uncorrupted information, and its ability to identify damage in many cases with relatively few sensors.
2. BACKGROUND
Effective sensor placement for damage detection will depend on several factors, including: i) the damage detection algorithm employed; ii) the location of damage and relative likelihood of damage in the various locations; iii) the excitation source; iv) the objectives of the structural health monitoring system; and, v) the selected mode shapes. To focus on the placement method, and minimize the effect of the damage detection technique used in the study, we require a damage detection technique that can correctly identify damage in any element of the structure when no noise is present. Thus, herein we employ the Bayesian Probabilistic approach for identifying the existence, location and extent of damage (Sohn and Law, 1997; Sohn 1998). Experimental studies have demonstrated that this method has superior performance compared to some of the other methods (Sohn, 1998). Three previously proposed techniques are evaluated herein to place sensors on a structure, including Effective Independence, Eigenvector Sensitivity and Damage Measurability. These approaches to sensor placement are presented, followed by a description of the Bayesian Probabilistic approach for damage detection.
2.1 The Effective Independence Method
The Effective Independence (EI) method is based on the concept that sensors for conducting a modal test should be arranged such that the mode shapes obtained using the measured DOF are spatially independent of each other. To formulate this method, Kammer (1991) used the Fisher information matrix, defined by
where [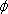 ]i = [
]i = [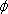 i1,
i1,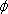 i2,...,
i2,...,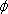 im] is a row vector of vibration mode shapes corresponding to the ith DOF, N is the number of DOF, and m is the number of mode shapes of interest that are used for the analysis. The eigensolution of this matrix is determined as
im] is a row vector of vibration mode shapes corresponding to the ith DOF, N is the number of DOF, and m is the number of mode shapes of interest that are used for the analysis. The eigensolution of this matrix is determined as
where λi and ψi are the ith eigenvalue and eigenvector of A, respectively. For this study the eigenvectors are mass-normalized. A matrix containing the eigenvectors can be formed as [ψ]i = [ψi1,ψi2,...,ψim]. Because the matrix A is symmetric and positive definite, the eigenvectors are orthogonal and can be considered as m orthogonal vectors in an m-dimensional space.
The product φψ can be viewed as a matrix of values of the projection of each of the vibration mode shape vectors in φ onto the m-dimensional space spanned by the vectors contained in the matrix ψ. Squaring each element in the matrix φψ results in a matrix in which each element represents the contribution of each DOF to each mode. If weighted by the inverse of the corresponding natural frequency of the mode, each element in this matrix has equal importance. A summation of all terms corresponding to a particular DOF yields a vector whose elements represent one DOF's contribution to all modes of interest. This vector is referred to as the effective independence distribution vector of the candidate sensor set, and is denoted Ed. The DOF corresponding to the largest element of Ed is the DOF that contributes most to the rank of A, and thus should be retained. By repeating the process of removing the DOF with the smallest contribution to the rank of A until the desired number of sensors is achieved, the sensor locations are determined.
2.2 The Eigenvector Sensitivity Method
The Eigenvector Sensitivity (ES) method for sensor placement was developed by Shi, et al. (2000). Sensor locations are optimized for the purpose of localizing structural damage sites. The mathematical derivation of the method is based on the model updating method proposed by Hemez (1993). To apply this approach we consider that the initial model corresponds to the undamaged structure, and the updated model corresponds to the damaged structure. The approach uses a truncated Taylor series expansion
where λi, 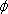 i and
i and 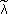 i,
i, 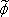 i are the ith eigenvalue and mode shape of the undamaged and damaged models, respectively, {α} and {
i are the ith eigenvalue and mode shape of the undamaged and damaged models, respectively, {α} and {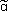 } are vectors of the elemental stiffness parameters of the undamaged and damaged models. The sensitivity matrix, Si, is defined by
} are vectors of the elemental stiffness parameters of the undamaged and damaged models. The sensitivity matrix, Si, is defined by
To compute the elemental stiffness parameter changes according to Eq. (3), the covariance matrix of the estimation errors must be minimized. Udwadia and Garba (1985) showed that maximizing the Fisher information matrix as a distribution of strain energy B in Eq. (5) for the ith mode, defined by
leads to minimization of the covariance matrix, and, the best estimate of {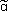 }-{α}. The Fisher information matrix as a distribution of strain energy B is defined as a summation of the contribution of the selected modes, Kammer (1991) suggested that the diagonal terms of
}-{α}. The Fisher information matrix as a distribution of strain energy B is defined as a summation of the contribution of the selected modes, Kammer (1991) suggested that the diagonal terms of
be used to rank the importance of a particular DOF to the determinant of Ei for the selected sensor locations. Thus, if a particular DOF has a small contribution to the diagonal terms of Ei, this sensor position can be eliminated from the selected sensor locations, then the remaining sensor locations maximize the contribution to the Fisher Information matrix as a distribution of the strain energy B providing the most information for damage detection.
2.3 The Damage Measurability Method
The Damage Measurability (DM) method was developed by Xia (2002), and is defined using two factors. The first factor is based on the work of Shi, et al. (2000) based on the contribution of the selected sensor locations to the Fisher Information matrix as a distribution of strain energy defined in Eq. (6) and the second factor is the sensitivity of damage to measurement noise, defined as
where {Δα} is an elemental stiffness change given by {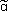 }-{α}, and Xi is a noise vector corresponding to noise contributing to the ith mode shape. Sin is the sensitivity of change in {Δα} due to a unit measurement noise and can be obtained using
}-{α}, and Xi is a noise vector corresponding to noise contributing to the ith mode shape. Sin is the sensitivity of change in {Δα} due to a unit measurement noise and can be obtained using
where ei is the modal data change vector containing the differences between the ith eigenvalues and mode shapes at the corresponding measured degrees of freedom, np, of the structure before and after updating. The first partial derivative of the eigenvalues and eigenvectors with respect to the noise vector Xi were derived by Xia (2002).
For a particular mode, Sin has dimensions ne by np. The (j, k) element of Sin for this mode is the sensitivity of the jth elemental stiffness parameter due to a unit change (due to noise) in the measurement at the kth DOF. Because damage may exist in any element of the structural model (it is assumed herein with equal likelihood), the sum of the absolute value of all terms in the kth column of this matrix yields the noise sensitivity for the kth DOF. This summation represents the influence of noise in the measurement at the kth DOF in all elemental stiffness parameters as in
and, for np modes, the noise sensitivity of all measured modes are summed
The damage measurability for a structural model is defined as the ratio of F to Sin, where the vector F is the summation of all measured modes of Ei defined in Eq. 6.
2.4 The Bayesian Probabilistic Approach
Deterministic damage detection techniques which rely only on modal parameters, may have the drawback that the damage locations and amount may not be uniquely determined from the estimated modal data (Udwadia 1978). Models with differently assumed damage locations and amount can produce identical modal parameters. These models are referred to as output equivalent models (Katafygiotis 1991). In real applications, multiple hypotheses need to be examined, because the modal testing measures the dynamic responses at limited points and estimates only a few lower modes, the number of output equivalent models can increase, and in the presence of the modeling error and the measurement noise, some erroneous models could have modal parameters closer to the estimated modal parameters than the model with the correct damage locations and amount.
Sohn (1998) proposed the Bayesian Probabilistic approach for damage detection, which is based on an output error, which is defined as the difference between the estimated vibration parameters and the theoretical ones from the analytical model. In the mathematical formulation of this method, this approach searches for the most probable damage event by comparing the relative probabilities for different damage scenarios, where the relative probability of a damage event is expressed in terms of the posterior probability of the damage event, given the estimated modal data sets from a structure. The formulation of the relative posterior probability is based on an output error, which is defined as the difference between the estimated modal parameters and the theoretical modal parameters from the analytical model. For an analytical model with Nsub substructures, the system stiffness matrix K can be expressed as an assembly of substructure stiffness matrices Ksi as shown in
where Θ = {θi; i = 1,...,Nsub>} and θi(0 ≤ θi ≤ 1) is a non-dimensional parameter which represents the contribution of the ith substructure stiffness to the system stiffness matrix. A substructure is defined as damaged when the θ value is less than a specified threshold value.
When vibration tests are repeated Ns times, the total collection of Ns, data sets is denoted in Eq. (12)
A modal data set Ψ(n) in Eq. (12) consists of both the frequencies and the modal vectors estimated from the nth vibration test as shown in
where ωin and νinT are the ith estimated frequency and modal vector in the nth data set. The modal vector νinT (νinT  RNd) has components which correspond to the instrumented DOFs. The variables Nt, Nd, and Nm represent the total number of components in a data set Ψ(n), the number of the measured DOFs, and the number of the estimated modes, respectively. Let Hj denotes a hypothesis for a damage event, which can contains any number of damaged substructures, and the initial degree of belief about the hypothesis Hj is represented with a prior probability P(Hj). Using Bayes Theorem, the posterior probability P(Hj/ψNs), after observing a set of estimated modal parameters ψNs, can be represented in Eq. (14) as
RNd) has components which correspond to the instrumented DOFs. The variables Nt, Nd, and Nm represent the total number of components in a data set Ψ(n), the number of the measured DOFs, and the number of the estimated modes, respectively. Let Hj denotes a hypothesis for a damage event, which can contains any number of damaged substructures, and the initial degree of belief about the hypothesis Hj is represented with a prior probability P(Hj). Using Bayes Theorem, the posterior probability P(Hj/ψNs), after observing a set of estimated modal parameters ψNs, can be represented in Eq. (14) as
The most likely damaged substructures are the ones included in the hypothesis Hmax, which has the largest posterior probability and can be represented using
Since the objective is to determine the most probable damage hypothesis, only the relative posterior probabilities of alternative hypotheses are of interest. The main idea is to avoid the explicit expression of a posterior probability P(Hj/ψNs), since the precise calculation of P(ψNs/Hj) is a difficult task. To overcome these difficulties, it is desirable to focus on the relative comparisons of posterior probabilities. Sohn (1998) has shown that the comparison of posterior probabilities can be conducted by examining the error function J(ψNs/ΘHjmax) and the prior probability P(Hj) as shown in Eq. (16).
Here ln denotes natural logarithm and the error function J(ψNs/ΘHjmax) is defined as
where the analytical modal set Ψ(ΘHj) for a given ΘHj set is defined as
The most probable parameter values ΘHjmax maximize the conditional probability density function f(ΘHjmax/ψNs) for given hypothesis Hj and ||CΨ|| = det|diag|σ12,...,σNt2|| = 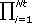 σi2. The variance σi2 can be evaluated from the observation of the estimated modal parameter sets. When a large number of experimental data sets are available, sample standard deviations (or variances) can be extracted from the data set. Now, the comparison of posterior probabilities can be conducted by examining only the error function J(ψNs/ΘHjmax) and the prior probability P(Hj).
σi2. The variance σi2 can be evaluated from the observation of the estimated modal parameter sets. When a large number of experimental data sets are available, sample standard deviations (or variances) can be extracted from the data set. Now, the comparison of posterior probabilities can be conducted by examining only the error function J(ψNs/ΘHjmax) and the prior probability P(Hj).
3. NUMERICAL SIMULATION
To evaluate the performance of the three sensor placement techniques presented, numerical simulations are performed using a limited number of structural responses to simulate the use of measurements from sensors with locations defined by these techniques. The components of the exact mode shapes at these locations, contaminated by noise, are used for the analysis. For comparative purposes, an additional sensor placement approach is used by utilizing sensor locations evenly distributed along the beam. This approach is denoted the Geometric Distribution (GD) method.
The Bayesian Probabilistic Approach is implemented for damage detection through the graphical user interface DAMTOOL developed at Stanford University (Lynch, et al., 1999). One of characteristics of the Bayesian Probabilistic Approach is that the method yields a probabilistic ranking of the most probably damage scenarios based on the error function. The results may yield several damage scenarios with the same error due to the presence of random noise in the input information, but only one of these damage scenarios is correct. Therefore it is only consider that damage is successfully identified if the correct damage scenario is located within the top five of the probabilistic ranking provided by the Bayesian Probabilistic Approach.
Two examples of two-dimensional beam-like structures are studied. The first example considers a simply supported beam with 32 elements, and the second example is a model having 30 elements with intermediate supports and boundary conditions representing a simple model of a long-span bridge. Axial deformation is not considered. Basically, changes in the mode shapes due to damage are highly sensitive in regions where there are changes in the curvature of the selected mode shapes. Therefore, the number of elements considered in the second model is kept similar to the first model due to an increment in the number of regions with changes in the curvature of the selected mode shapes for the second model. Zero mean white noise is added to the mode shapes in order to simulate the effect of deviation in the measured mode shapes. Different levels of zero mean white noise are added to the computed mode shapes for damage detection. All vertical DOF of the models are candidate sensor locations, and the first 4 vertical mode shapes are employed for the placement studies.
To successfully identify structural damage it is important to have at least one sensor located in a region where a mode shape can be identified. Therefore, two series of tests are conducted with different numbers of sensors, 7 and 11. The selection of the number of sensors is based in the number of identified mode shapes. With ambient excitation sources (e.g. traffic, wind) it is reasonable to assume that identification of only a few low frequency modes can be anticipated. Therefore, as previously mentioned, 4 mode shapes are considered in the analysis leading to a total of 8 peaks based on the fact that the first mode shares the same peak with the third mode. Structural damage is simulated in each element with a 10% reduction in the Young's Modulus of the element. Additionally, for the second example, several representative and randomly selected multiple damage scenarios are also considered.
3.1 Example 1: Single Span Model
The model of the singly span beam has 32 Euler-Bernoulli elements. Each element is 1m in length and has a cross-sectional area of 0.16m2, a mass density of 2.5x10-3 kg/m3, a Young's modulus of 2.5x1010 N/m2 and a moment of inertia of 2.5x10-3 N/m2. The nodes at each end of the structure have fixed translational DOFs and free rotational DOF.
The placement schemes resulting from the three techniques presented and the geometric distribution are shown in Figures 1 and 2 for both the eleven and seven sensor configurations. Using each of these eight configurations, damage detection is performed for each element, first without the presence of noise, to validate the abilities of the Bayesian Probabilistic Approach when exact mode shapes are available. The technique correctly identifies the damage location and extent for all cases. Subsequently, measurement errors are introduced by superimposing randomly generated vectors on the mode shape data. 7sets of mode shapes are used here and a total of 512 scenarios are studied for this example. It is assumed that only 7 sets of mode shapes are available to perform damage detection studies. For continuous monitoring implementations more sets of mode shapes will be available leading to a higher degree of probability to correctly identify structural damage. It is expected that the process of continuous collection of vibration data minimizes the error in measured mode shapes and therefore a considerable number of sets of mode shapes will be available. Noise reduction effect is also achieved by having more sets of measured mode shapes.
Table 1 provides the results of implementation of the EI method using the singly span beam model. At 1% noise level, all of damage cases are correctly identified when both the 7 and 11 sensor configurations are used. The results are more precise with 11 sensors as 30 of the cases are ranked with highest probability. When the noise level is increased to 2%, the success rate is reduced drastically to 38% with 11 sensors and 19% with 7 sensors. These results show that the sensor configurations obtained from the EI method are highly influenced by noise and the number of sensors.
Table 2 provides the results with ES method. At the low noise level, this placement scheme does not result in complete success in identifying all damage cases for either configuration. When the level of noise is increased to 2%, the success rate of the damage detection method with 7 sensors is 38% as compared to 19% in the case of the same configuration in the EI method. Thus, although the EI method showed better performance when low levels of measurement noise are used, the ES method seems to be more robust to measurement noise.
Table 3 provides the results of the DM method. Here the sensor configurations do not follow a logical trend when the noise level is reduced and the number of sensors is increased. Specifically, the success rate for damage detection decreases as the number of sensors increases. Damage in element 14 is identified with 7 sensors and 2% random noise, but with 11 sensors and the same level of noise this element is not identified. Table 4 shows the results for GD approach.
3.2 Example 2: Three Span Model
This model is used to consider sensor placement along the deck of a long-span bridge. The full model has 30 Euler-Bernoulli elements. Each element is 1m long and the main span has 16 elements and each side span has 7 elements. The material properties are identical to those in the single span beam in Example 1. Nodes 8 and 24 are pinned supports with vertical and translational constraints, and nodes 1 and 31 are only constrained in the vertical direction. Each node has three degree-of-freedom (translational, vertical and rotational).
The 4 resulting placement schemes are shown in Figs. 3 and 4 for eleven and seven sensor configurations, respectively. It was found that the results of the three span model are less sensitive to noise, it is clearly seen as the number of peaks an inflections points for the selected mode shapes increase in this model. Therefore, 4 higher levels of measurement noise are considered for each sensor configuration. In order to study the influence of noise, 15 damage scenarios are considered for each model due to the symmetry in the distribution of sensors obtained from three of the sensor placement methods. The EI method gives asymmetric distributions of sensors and therefore the first half of the model with large number of sensors is considered. The cases include 3% noise level with 8 data sets, and 4%, 5%, and 7% noise levels each with 10 measurements sets. There are 15 damage cases possible with this model, and a total of 480 simulations are performed.
Tables 5-8 provide the damage detection results for this example. Table 5 provides the damage detection results using the EI method, demonstrating that placement schemes using this method do not have high success rates when noise is present. The GD method (Table 8) also has relatively low success rates at all noise levels. The results of the ES and DM configurations, provided in Tables 6 and 7, demonstrate these two approaches to have relatively higher success rates and similar performance. The DM method has a higher success rate for low noise levels, whereas the ES method seems to be slightly more stable when the noise level is increased.
Examining these results a bit closer, it is possible to see that at higher noise levels damage detection is not always successful in the regions located near the end supports, at one-quarter of the main span and at the center of the span. Note that these locations correspond to nodes of the model. Thus, it is expected that small components of the mode shapes lead to small changes due to damage. When noise is introduced the damage can be completely masked and successful identification is challenging. However, damage is clearly identified correctly near the mid-span supports between elements 7 and 8 in nearly all of the cases. This result can be explained by the fact that the mode shapes are known to be zero at these locations and noise does not affect this point in the mode shape.
3.3 Damage Detection with Multiple Damage Locations
To properly evaluate a placement scheme it is also necessary to consider multiple damage scenarios. Here the second example is employed for this study. Damage is inflicted in two elements at the same time. Representative cases are considered in which damage is considered in element 15, and in a second element which varies. Two levels of noise are studied, including 2% and 5% with 10 measurements sets. The damage detection results for all sensor configurations are shown in Table 9. These results agree with the single damage results. Poor performance is demonstrated by the EI and the GD methods, whereas the ES and DM methods have higher success rates. Again, difficulties are observed even with these placement schemes in identifying damage in regions near the center of the main span.
4. CONCLUSIONS
The Bayesian Probabilistic Approach method is found to accurately identify damage when exact mode shapes are available, and thus reduces the dependence of the placement scheme on the damage detection technique and allowing us to focus the study on the abilities of the various sensor configurations.
The numerical results of the two beam examples demonstrate that when the level of noise was increased the accuracy of the damage detection analysis varied for the placement schemes considered. The Effective Independence and Geometric Distribution approaches for sensor placement consistently yielded low success rates, particularly as the noise level increased. The Eigenvector Sensitivity and Damage Measurability methods were found to be superior. However, the results also indicate that when damage is inflicted near the supports or nodes of the corresponding mode shapes, damage detection can be quite challenging.
ACKNOWLEDGMENTS
The authors would like to greatly acknowledge Prof. Jerome Lynch (University of Michigan) for providing DAMTOOL.
REFERENCES
Cruz, A., Vélez, W., and Thomson, P. (2009). Optimal Sensor Placement for Modal Identification of Structures Using Genetic Algorithms - A Case Study: The Olympic Stadium in Cali, Colombia. Annals of Operations Research, 181(1), pp. 769-781. [ Links ]
Cobb, R.G., and Liebst, B.S., (1997). Sensor Location and Structural Damage Localization Using Minimal Sensor Information. AIAA Journal, 35(2), February, pp. 369-374. [ Links ]
Doebling, S.W., Farrar, C.R., Prime, M.B., and Shevitz D.W. (1996). Damage Identification and Health Monitoring of Structural and Mechanical Systems from Changes in their Vibration Characteristics: A Literature Review, Technical Report LA-13070-MS, Los Alamos National Laboratory, Los Alamos, NM. [ Links ]
Farrar, C.R. and Doebling, S.W. (1999). Damage Detection II: Field Applications to Large Structures, in Modal Analysis and Testing, J.M.M. Silva and N.M.M. Maia, edts., Nato Science Series, Kluwer Academic Publishers, Dordrecht, Netherlands. [ Links ]
Hemez, F.M. (1993). Theoretical and Experimental Correlation between Finite Element Models and Modal Tests in the Context of Large Flexible Space Structures. PhD thesis, Aerospace Engineering Sciences, University of Colorado, Boulder, CO. [ Links ]
Hemez, F.M., and Farhat C. (1994). An Energy Based Optimum Sensor Placement Criterion and its Application to Structure Damage Detection. Proc. 12th International Modal Analysis Conference (Honolulu, HI: Society of Experimental Mechanics), 19, pp. 1568-75. [ Links ]
Heredia-Zavoni, E. and Esteva, L. (1998). Optimal Instrumentation of Uncertain Structural Systems Subject to Earthquake Motions. Earthquake Engineering Structural Dynamics, 27(4), april, pp. 343-362. [ Links ]
Kammer, D.C. (1991). Sensor Placement for On-Orbit Modal Identification and Correlation of Large Space Structures. Journal of Guidance, Control, and Dynamics, 14(2), pp. 251-259. [ Links ]
Katafygiotis, L.S. (1991). Treatment of Model Uncertainties in Structural Dynamics, Technical Report EERL 91-01, Earthquake Engineering Research Laboratory, California Institute of Technology, Pasadena, CA. [ Links ]
Li, D.S., Li, H.N., and Fritzen, C.P. (2007). The Connection between Effective Independence and Modal Kinetic Energy Methods for Sensor Placement. Journal of Sound and Vibration, 305, pp. 945-955. [ Links ]
Li, D.S., Li, H.N., and Fritzen, C.P. (2012). Load Dependent Sensor Placement Method: Theory and Experimental Validation. Mechanical Systems and Signal Processing, 31, pp. 217-227. [ Links ]
Lim, T.W. (1991). Sensor Placement for On-orbit Modal Identification. Proc. 32nd Conference AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials (Reston, VA: American Institute of Aeronautics and Astronautics). [ Links ]
Lynch, J.P., Sohn, H., and Law, K.H. (1999). The Development and Application of a Damage Detection Toolbox for Matlab. The 5th US National Congress on Computational Mechanics, University of Colorado at Boulder, CO, USA, August. [ Links ]
Rytter, A. (1993). Vibration Based Inspection of Civil Engineering Structures, Ph. D. Dissertation, Department of Building Technology and Structural Engineering, Aalborg University, Denmark. [ Links ]
Park, Y.S., and Kim, H.B. (1996). Sensor Placement Guide for Model Comparison and Improvement. Proceedings of the 14th International Modal Analysis Conference, pp. 404-409. [ Links ]
Peck, J., and Torres, I. (2004). A DMAP Program for the selection of accelerometer locations in MSC/ NASTRAN. Proceedings of the 45th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, pp. 19-22. [ Links ]
Schedlinski, C. and Link, M. (1996). An Approach to Optimal Pick-up and Exciter Placement. Proceedings of 14th International Modal Analysis Conference, pp. 376-382. [ Links ]
Shi, Z.Y., Law, S.S., and Zhang, L.M. (2000). Optimum Sensor Placement for Structural Damage Detection. Journal of Engineering Mechanics, 126(11), november, pp. 1173-1179. [ Links ]
Sohn, H. (1998). A Bayesian Probabilistic Approach for Damage Detection for Civil Structures. PhD Thesis, Department of Civil and Environmental Engineering, Stanford University. [ Links ]
Sohn, H., and Law, K.H. (1997). Bayesian Probabilistic Approach for Structural Damage Detection. Journal of Earthquake Engineering and Structural Dynamics, 26(12), December, pp. 1259-1281. [ Links ]
Udwadia, F.E. (1994). Methodology for Optimum Sensor Locations for Parameter Identification in Dynamic Systems. Journal of Engineering Mechanics, 102, pp. 368-390. [ Links ]
Udwadia, F.E., and Garba J.A. (1985). Optimal Sensor Locations for Structural Identification. Proc. JPL Workgroup on Identification and Control of Flexible Space Structures (San Diego, CA), pp. 247-61. [ Links ]
Udwadia, F.E., Sharma, D.K., and Shah, P.C. (1978). Uniqueness of Damping and Stiffness Distributions in the Identification of Soil and Structural Systems. Journal of Applied Mechanics, 45, pp. 180-187. [ Links ]
Xia, Y. (2002). Condition Assessment of Structures using Dynamic Data. PhD Thesis. Nanyang Technological University, Singapore. [ Links ]
Yao, L., Sethares, W.A., and Kammer, D.C. (1993). Sensor Placement for On-orbit Modal Identification via a Genetic Algorithm. AIAA Journal, 31(10), pp. 1922-1927. [ Links ]