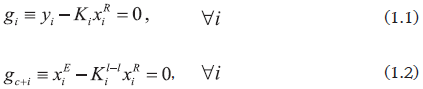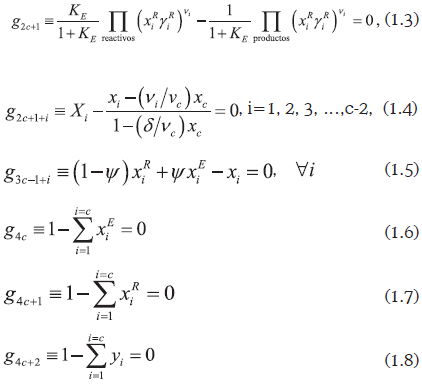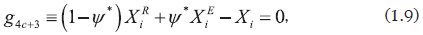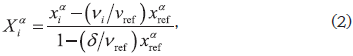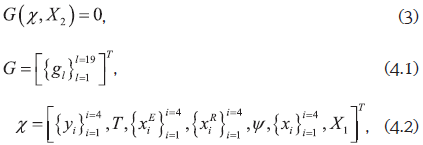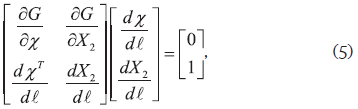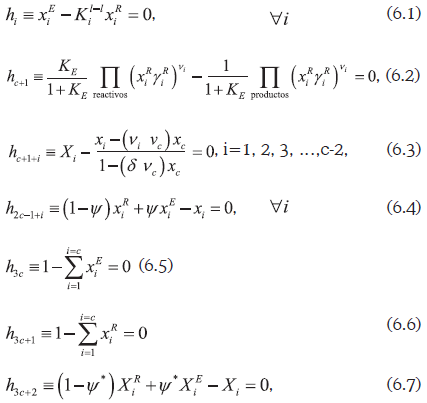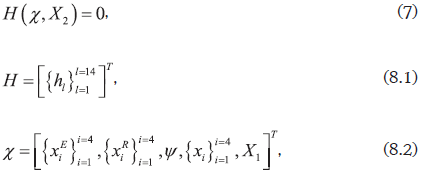Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.20 Envigado July/Dec. 2013
CARACTERIZACIÓN TERMODINÁMICA PARA SISTEMAS DE ESTERIFICACIÓN HETEROGÉNEOS EN DESTILACIÓN REACTIVA. I. ENVOLVENTES REACTIVAS
THERMODYNAMIC CHARACTERIZATION FOR HETEROGENEOUS ESTERIFICATION SYSTEMS IN REACTIVE DISTILLATION. I. REACTIVE ENVELOPES
CARACTERIZAÇÃO TERMODINÂMICA PARA SISTEMAS DE ESTERIFICAÇÃO HETEROGÊNEOS EM DESTILAÇÃO REATIVA. I. ENVOLVENTES REATIVAS
César Augusto Sánchez Correa*, Miguel Ángel Gómez García**, Gerardo Rodríguez Niño***
* Ingeniero químico Universidad Nacional de Colombia - Sede Manizales. Magíster en Ingeniería Química e Investigación, Universidad Nacional de Colombia sede Bogotá. Universidad Nacional de Colombia, sede Bogotá, Facultad de Ingeniería, Departamento de Ingeniería Química y Ambiental - Grupo de Investigación en Procesos Químicos y Bioquímicos. Bogotá, Colombia.
Autor de correspondencia: (C.A. Sánchez-Correa). Cra 45 No. 26 - 85, Ciudad Universitaria, Universidad Nacional de Colombia, Bogotá, Colombia. Teléfono: 316 53 21. Correo electrónico: casanchezc@unal.edu.co.
** Ingeniero químico Universidad Nacional de Colombia, sede Manizales. Magíster en Ingeniería Química, Universidad Nacional de Colombia, sede Bogotá. Ph. D. en Ingeniería Química, Université Louis Pasteur - Strasbourg I, Francia. Profesor Titular Universidad Nacional de Colombia sede Manizales, Departamento de Ingeniería Química - Laboratorio de Intensificación de Procesos y Sistemas Híbridos - G.I.A.N.T. (Grupo de Investigación en Aplicación de Nuevas Tecnologías). Manizales, Colombia.
*** Ingeniero químico: Universidad Nacional de Colombia, sede Bogotá. Magíster en Ingeniería Química: Universidad Nacional de Colombia, sede Bogotá. Ph. D. en Ingeniería Química, Universidad Nacional de Colombia, sede Bogotá. Profesor Asociado Universidad Nacional de Colombia, sede Bogotá, Facultad de Ingeniería, Departamento de Ingeniería Química y Ambiental, Grupo de Investigación en Procesos Químicos y Bioquímicos. Bogotá, Colombia.
Artículo recibido: 13-III-2013 / Aprobado: 24-VII-2013
Discusión abierta hasta diciembre de 2014
RESUMEN
Se presenta en este trabajo un enfoque novedoso para el cálculo de las envolventes reactivas líquido - líquido - vapor (LLV) y líquido - líquido (LL). El principal aporte consiste en indicar explícitamente las manipulaciones necesarias para transformar el cálculo de las binodales en uno de homotopía termodinámica. Así, la solución del problema se traslada a la teoría de los métodos de continuación. Esta perspectiva proporciona adicionalmente un procedimiento para localizar el punto crítico de las mezclas reactivas. Se analizaron dos casos de interés industrial: las binodales reactivas LLV a 101,325 kPa para los sistemas ácido acético + 1-pentanol + agua + n-amilacetato y ácido acético + 3-metil-1-butanol + agua + isoamilacetato. Se encontró que ellas son semejantes a las binodales del tipo I en sistemas ternarios no reactivos. Para el caso del n-amilacetato se ejemplifica la utilidad de estas envolventes en el cálculo y análisis gráfico de un rectificador con varios platos heterogéneos.
PALABRAS CLAVE: Destilación reactiva; envolventes reactivas; equilibrio líquido - líquido - vapor - reactivo; equilibrio líquido - líquido reactivo; isoamilacetato; n-amilacetato.
ABSTRACT
In this work, a novel approach for the calculation of the reactive liquid - liquid (LL) and vapor - liquid - liquid (VLL) envelopes is proposed. As the main contribution, the way of transforming the binodal lines calculation into the thermodynamic homotopy is explicitly defined. This transforms the problem solution to the theory of the continuation methods. Thus, a method for the localization of the critical point of reactive mixtures is also provided. Two cases of industrial interest are analyzed: the solution of acetic acid + 1-pentanol + water + n-amyl acetate and the solution acetic acid + 3-methyl-1-butanol + water + isoamyl acetate. At 101,325 kPa, the reactive VLL binodal lines are traced. They are similar to nonreactive type I binodal lines in ternary systems. For the n-amyl acetate case, the usefulness of those envelopes is exemplified in the calculation and graphical analysis of a distillation rectification section with multiple heterogeneous trays.
KEY WORDS: n-amyl acetate; Isoamyl Acetate; Reactive Vapor - Liquid - Liquid Equilibria; Reactive Liquid - Liquid Equilibria; Reactive Binodal Lines; Reactive Distillation.
SUMÁRIO
Apresenta-se neste trabalho um enfoque novo para o cálculo das envolventes reativas líquido - líquido - vapor (LLV) e líquido - líquido (LL). A principal contribuição consiste em indicar explicitamente as manipulações necessárias para transformar o cálculo das binodais em um cálculo de homotopia termodinâmica. Assim, a solução ao problema traslada-se à teoria dos métodos de continuação. Esta perspectiva proporciona adicionalmente um procedimento para localizar o ponto crítico das misturas reativas. Analisaram-se dois casos de interesse industrial: as binodais reativas LLV a 101,325 kPa para os sistemas ácido etanoico + 1-pentanol + água + n-amilacetato e ácido etanoico + 3-metil-1-butanol + água + isoamilacetato. Encontrou-se que elas são semelhantes ás binodais do tipo I em sistemas ternários não reativos. Para o caso do n-amilacetato exemplifica-se a utilidade destas envolventes no cálculo e análise gráfico dum retificador com vários pratos heterogêneos.
PALAVRAS-CHAVE: Destilação reativa; Envolventes reativas; Equilíbrio líquido - líquido - vapor - reativo; Equilíbrio líquido - Líquido reativo; Isoamilacetato; n-amilacetato.
1. INTRODUCCIÓN
La producción de acetatos utilizando la tecnología de la destilación reactiva (DR) constituye una alternativa atractiva para la intensificación del proceso secuencial, debido principalmente a la disminución del número de unidades de proceso y el aumento de la conversión en relación a reactores en fase homogénea (Tang, et al., 2005; Toikka, et al., 2009). En una primera aproximación al diseño de procesos de DR se usa el «modelo de equilibrio total» (denominado de esta manera porque considera el equilibrio de fases y el químico de forma simultánea) con el fin de resolver los tres problemas básicos del diseño conceptual en columnas de DR con la zona de reacción no localizada (Wasylkiewicz, 1999; Avami, et al., 2012): 1) ubicar la región de composición de productos, 2) determinar el mínimo consumo de energía y 3) calcular el número de etapas teóricas para el reflujo real de operación. La solución del modelo de equilibrio total empleando métodos geométricos es bastante popular, en especial, cuando el objetivo es el diseño conceptual de procesos de DR (Sánchez, et al., 2003; Dragomir y Jobson, 2005; Thery, et al., 2005; Pisarenko, Serafimov y Kulov, 2009; Avami, et al., 2012). La aplicación de estos métodos cortos requiere una caracterización termodinámica a priori: a) determinación de las regiones de miscibilidad parcial (cálculo de las envolventes reactivas líquido - líquido - vapor (LLV) y líquido - líquido (LL)), b) determinación de las regiones de destilación reactiva (localización de los azeótropos y fronteras termodinámicas). Para sistemas con dos grados de libertad los métodos empleados en la destilación azeotrópica de mezclas ternarias pueden ser adaptados incorporando las coordenadas transformadas de Doherty (Barbosa y Doherty, 1988; Ung y Doherty, 1995; Okasinski y Doherty, 2000; Wasylkiewicz y Ung, 2000; Taylor, Miller y Lucia, 2006). En este trabajo se utiliza este último aspecto con el fin de proponer una técnica de continuación para el trazado de las envolventes reactivas LLV y LL. La importancia de estas binodales tiene su contexto en el diseño de columnas de DR heterogénea y consiste en: a) establecer las posibles líneas de reparto para un decantador de cabeza o externo (fijando en consecuencia las posibles purezas para el destilado) y b) determinan el máximo número de etapas heterogéneas en una sección de la columna.
En la literatura conocida por los autores las binodales reactivas son «trazadas» utilizando una serie ordenada de cálculos de flash isotérmico reactivo (Wasylkiewicz y Ung, 2000; Bonilla, et al., 2008). Esta perspectiva tiene dos inconvenientes prácticos: a) no es eficiente desde el punto de vista computacional y b) no permite localizar con suficiente precisión el punto crítico. Pueden resolverse eficientemente estos dos problemas utilizando técnicas de continuación según se ha demostrado en algunos trabajos sobre sistemas sin reacción química (Ermakova y Anikeev, 2000; Yermakova, Sazhina y Anikeev, 2005; Sánchez, Estupiñán y Salazar, 2010).
Para un sistema donde se efectúa una reacción de esterificación en ausencia de inertes, a presión constante, el espacio de composiciones transformadas tiene dos dimensiones (Ung y Doherty, 1995; Wasylkiewicz y Ung, 2000; Taylor, Miller y Lucia, 2006). Esta característica se explica por la regla de las fases de Gibbs y permite tratar las envolventes reactivas (LLV y LL) del sistema de cuatro componentes (ácido + alcohol + agua + acetato) de manera semejante a las binodales no reactivas de los sistemas ternarios. Teniendo en cuenta este aspecto, en este trabajo se generalizó el método de continuación utilizado por Sánchez, Estupiñán y Salazar (2010) para trazar envolventes en sistemas no reactivos. La idea principal consiste en transformar las ecuaciones del flash isotérmico en una curva monoparamétrica para obtener la forma normalizada del problema de Davidenko (Allgower and Georg, 1990) y trasladar la solución numérica al ámbito de los métodos de continuación donde se dispone de técnicas robustas para su tratamiento (ver por ejemplo: Allgower and Georg, 1990; Wasylkiewicz, Kobylka y Castillo, 2003; Seydel, 2010; Sánchez, 2011; Sánchez, Rodríguez y Gómez, 2012).
Como casos de aplicación se presentan las binodales reactivas para la síntesis de n-amilacetato y de isoamilacetato. La utilidad de estos resultados se hace manifiesta en el papel que tienen en el cálculo y análisis gráfico de rectificadores reactivos con múltiples platos heterogéneos. En cada ejemplo se localizó la región de solubilidad limitada, la línea de vapor reactiva y el punto crítico de la envolvente. En las situaciones ilustradas el método propuesto no tiene problemas de convergencia y se sugiere como una herramienta para la caracterización termodinámica de los sistemas de esterificación en procesos de DR. Los autores subrayan que no se conocen rutinas estandarizadas en un simulador comercial para el trazado de las envolventes reactivas y el análisis de carácter geométrico que puede desprenderse de su estudio.
2. ENVOLVENTES REACTIVAS
Resulta conveniente transformar las ecuaciones del equilibrio de fases reactivo en una curva monoparamétrica sobre la cual la proporción de extractos a refinados permanece constante, ya que las trayectorias de estas curvas, de fracción de extractos constante, determinan completamente las envolventes reactivas. La misma idea fue utilizada por Sánchez, Estupiñán, y Salazar (2010) para sistemas ternarios sin reacción química. En el presente trabajo se extiende para incluir la ocurrencia de una reacción y se demuestra que al utilizar las coordenadas transformadas de Doherty (Ung y Doherty, 1995; Wasylkiewicz y Ung, 2000) las binodales reactivas pueden trazarse calculando curvas de fracción de extractos constante.
2.1. Envolvente líquido - líquido - vapor reactiva
Considérense las ecuaciones del equilibrio líquido - líquido - vapor reactivo (ELLVR) (Ung y Doherty, 1995; Wasylkiewicz y Ung, 2000):
El sistema de ecuaciones (1) puede describirse de la siguiente manera: (1.1) es la condición de ELV; (1.2) es la condición de ELL; (1.3) es la condición de equilibrio químico; (1.4) es la definición de la fracción molar transformada en el líquido global; (1.5) son los balances molares en la fase líquida; (1.6), (1.7) y (1.8) corresponden con la restricción sobre las fracciones molares. Las variables implicadas son: las fracciones molares de los componentes en el vapor (yi), el líquido global (xi), la fase de extractos (xiE) y la fase de refinados (xiR); la temperatura (T); la presión (p); la fracción molar de la fase de extractos (ψ) y las composiciones globales transformadas (Xi). Los grados de libertad son (variables menos ecuaciones): (5c+1)-(4c+2)=c-1 (donde c es el número de componentes). Un cálculo de temperatura de burbuja reactiva se define cuando los grados de libertad se eligen como la presión y las c-2 composiciones transformadas independientes (Ung y Doherty, 1995; Wasylkiewicz y Ung, 2000). De acuerdo con lo anterior, el plano de fases para un sistema de cuatro componentes (c=4) tiene dos grados de libertad. Debido a esta característica, las binodales reactivas LL y LLV resultan semejantes a las binodales no reactivas encontradas en sistemas ternarios.
Con el fin de fijar la fracción de extractos se aplica la regla de la palanca en variable transformada para obtener:
La ecuación (1.9) se escribe para cualquier componente (diferente al de referencia) y reduce los grados de libertad del conjunto de ecuaciones (1) a la unidad porque la fracción transformada de extractos (ψ*) se trata como una especificación y las fracciones molares transformadas de los refinados y los extractos (XiE y XiR) pueden obtenerse a partir de las fracciones molares de acuerdo con la siguiente relación (Ung y Doherty, 1995; Wasylkiewicz y Ung, 2000):
En la ecuación (2) el subíndice "ref" hace alusión al componente de referencia, el superíndice α se refiere a la fase (refinados o extractos), δ es el cambio en la moles ocasionado por la reacción y ν es el coeficiente estequiométrico. En la ecuación (1.4) se tomó como referencia el último componente de la serie ordenada de números enteros consecutivos 1,2,3,...,c.
Debido a que el sistema de ecuaciones (1) tiene un grado de libertad (para el caso de un sistema de cuatro componentes a una presión y una fracción transformada de extractos especificadas) es posible realizar una interpretación matemática a partir de una curva en un parámetro. La elección de este parámetro es arbitraria y la curva es independiente del mismo. Dado que las binodales se representan en el espacio de composiciones, resulta conveniente elegir la fracción molar global transformada de uno de los componentes formulando el problema en forma paramétrica:
La curva paramétrica χ(X2) es una trayectoria isobárica sobre la cual la fracción de extractos permanece constante. Para aplicar la teoría de los métodos de continuación, la ecuación (3) se transforma a la forma canónica o ecuación de Davidenko mediante una reparametrización en términos de la longitud de arco (l) (Allgower and Georg, 1990; Seydel, 2010):
Después de formular el problema a través de la ecuación diferencial (5) es posible utilizar las técnicas de continuación disponibles en la literatura para llevar a cabo la integración numérica. Para los propósitos de este trabajo, se utilizaron los métodos del tipo predictor-corrector basados en la descomposición ortogonal de Householder y tratados con detalle por Allgower and Georg (1990). Los autores subrayan que en la literatura existe una gran variedad de problemas resueltos empleando este enfoque paramétrico. Como referencia se citan los siguientes: Okasinski y Doherty (2000); Wasylkiewicz, Kobylka y Castillo (2003); Yermakova, Sazhina y Anikeev (2005); Torres y Espinosa (2009); Sánchez, Estupiñán y Salazar (2010); Sánchez (2011); Sánchez, Rodríguez y Gómez (2012).
2.2. Envolvente líquido - líquido reactiva
Las ecuaciones del ELLR pueden generarse a partir del conjunto (1) eliminando las relaciones para el ELV (ecuación (1.1)) y la sumatoria sobre las fracciones molares del vapor (ecuación (1.8)) quedando un conjunto de ecuaciones que describe un flash isotérmico líquido - líquido reactivo:
Para obtener una situación con un grado de libertad se consideran cuatro componentes y se especifica la presión, la temperatura y la fracción transformada de extractos. En este caso la curva paramétrica se obtiene al considerar el siguiente arreglo:
La curva paramétrica χ(X2) es una trayectoria isotérmica e isobárica sobre la cual la fracción de extractos permanece constante. La ecuación (7) se trata de la misma manera que el conjunto (3) para obtener el problema básico de la teoría de los métodos de continuación.
3. EJEMPLOS
Se trazaron las binodales reactivas LLV a 101,325 kPa para los sistemas ácido acético + 1-pentanol + agua + n-amilacetato y ácido acético + 3-metil-1-butanol + agua + isoamilacetato. En los dos casos, la no idealidad de la fase líquida se describió con el modelo de actividad NRTL (Renon y Prausnitz, 1968) y la no idealidad de la fase gaseosa con la teoría química (Hayden y O'Connell, 1975; Prausnitz, et al., 1980). Esta descripción termodinámica ("gamma - phi") incluye los fenómenos de asociación y solvatación en la fase gaseosa y es la más popular en la literatura para describir los sistemas de esterificación (Tang, et al., 2005; Toikka, et al., 2009; Lee y Liang, 1998; Lee y Lin, 1999; Chiang, et al., 2002; Osorio, et al., 2013).
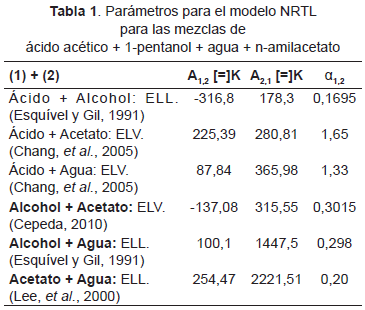
Las ecuaciones para la presión de vapor de las especies orgánicas y la densidad de los líquidos puros son las reportadas por Yaws (2003) y Yaws (2008), respectivamente. La ecuación para la presión de vapor del agua se tomó de Poling, Prausnitz, y O'Connell (2001). Las constantes básicas de las sustancias puras (temperatura crítica, presión crítica, momento dipolar y radio medio de giro) se tomaron de Yaws (2008). Los parámetros de NRTL para el caso del isoamilacetato son los ajustados por Osorio, et al. (2013) y para el n-amilacetato se presentan en la Tabla 1. Las constantes de asociación y solvatación en el método de Hayden y O'Connell (1975) se tomaron de Prausnitz, et al. (1980). Las constantes de equilibrio químico para los dos sistemas de esterificación se calcularon con las correlaciones ajustadas por Wyczesany (2009).
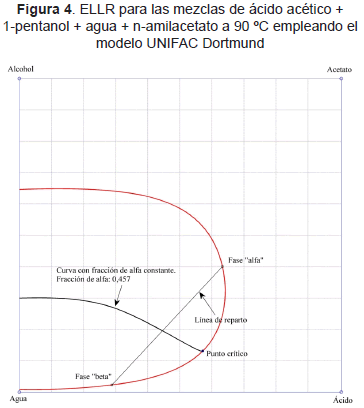
Con fines puramente demostrativos y académicos se trazó la binodal reactiva LL para las mezclas de ácido acético + 1-pentanol + agua + n-amilacetato empleando el modelo UNIFAC Dortmund (Weidlich y Gmehling, 1987; Gmehling, Li y Schiller, 1993; Jakov, et al., 2006). Debe señalarse que este modelo no distingue los isómeros 3-metil-1-butanol y 1-pentanol en solución y tampoco los isómeros isoamilacetato y n-amilacetato en solución. Como consecuencia de esto, el equilibrio líquido - líquido sin reacción química calculado utilizando el modelo UNIFAC Dortmund, es el mismo, para los sistemas de esterificación con acetato de n-amilo o de isoamilo.
La condición inicial para la ecuación (5) es la solución de un cálculo de temperatura de burbuja con reacción química (para binodales LLVR) o un cálculo de flash isotérmico reactivo (para binodales LLR). Se eligió como componente de referencia el acetato y se utilizaron las fracciones molares transformadas de ácido y alcohol como independientes. Una vez se conoce la condición inicial, la ecuación (5) se integra en las dos direcciones posibles hasta alcanzar el punto crítico o agotar uno de los componentes (en forma opcional puede localizarse la condicional inicial sobre un lado del espacio de composiciones e integrar únicamente en la dirección del punto crítico). La precisión numérica empleada fue de 10-8 (esto significa que la norma euclidiana de los vectores en las ecuaciones (3) y (7) es menor o igual a este valor sobre cada punto de la binodal).
Se consideró un último ejemplo sobre el cálculo de una sección de rectificación reactiva orientado a presentar el tipo de análisis gráfico que puede realizarse utilizando las envolventes. Se trata de resaltar uno de los contextos en el que las herramientas presentadas en este trabajo cobran importancia.
3.1. Binodal LLVR
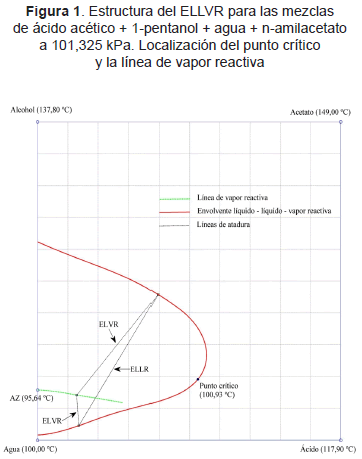
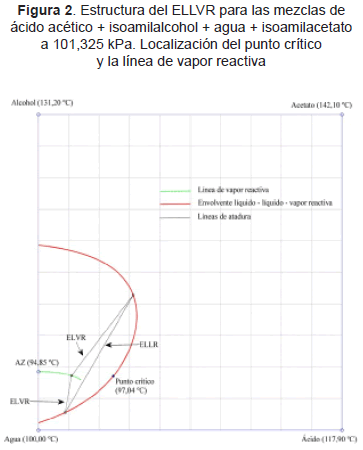
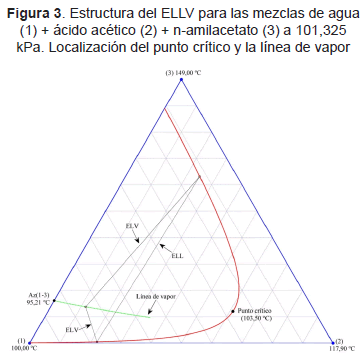
Las Figuras 1 y 2 presentan las binodales LLV reactivas a 101,325 kPa para las mezclas de ácido acético + 1-pentanol + agua + n-amilacetato y ácido acético + 3-metil-1-butanol + agua + isoamilacetato, respectivamente. Puede observarse una estructura similar a la ofrecida por las envolventes ternarias no reactivas del tipo I según la clasificación de Treybal (1968). Para demostrar con claridad esta analogía se trazó la binodal del sistema ternario agua + ácido acético + n-amilacetato a 101,325 kPa (ver Figura 3). Debe resultar claro que el origen de esta correspondencia, además del tipo de envolvente, es la dimensión del espacio de composiciones. El punto central es que los métodos de análisis, especialmente métodos gráficos, empleados en sistemas ternarios pueden aplicarse a sistemas reactivos con dos grados libertad utilizando las coordenadas transformadas. Un ejemplo práctico en este sentido se resuelve en la sección 3.3.
Aunque las mezclas no reactivas de ácido acético + 1-pentanol + agua + n-amilacetato y ácido acético + 3-metil-1butanol + agua + isoamilacetato presentan múltiples azeótropos (cinco en el primer caso y tres en el segundo ver Tabla 2) en el sistema reactivo sólo permanece el azeótropo agua - alcohol (ver Figuras 1 y 2) siendo un punto fijo no degenerado (Okasinski y Doherty, 2000) y el único nodo inestable de las líneas de residuo reactivas. Para su comparación, en la Tabla 3 se presentan la predicciones para los azeótropos marcados en las Figuras 1, 2 y 3 frente a los datos experimentales de Horsley (1973).
En un computador con un procesador AMD Athlon 64 x 2 Dual Core 4800+ y 2,0 GB RAM, empleando en la implementación, el interprete de MATLAB®, el tiempo de cómputo para las trayectorias estudiadas es como sigue: 68 segundos para el sistema con isoamilacetato (Figura 2) y 166 segundos con n-amilacetato (Figura 1). Estos tiempos son aceptables y pueden ser reducidos a unos pocos segundos utilizando un compilador.
3.2. Binodal LLR
La Figura 4 muestra el resultado de aplicar la metodología descrita en la sección 2.2 con el fin de trazar la envolvente isotérmica reactiva líquido - líquido para las mezclas de ácido acético + 1-pentanol + agua + n-amilacetato a 90 °C empleando el modelo de actividad UNIFAC Dortmund. En las mismas condiciones de las Figuras 1 y 2, el tiempo de cómputo fue de 57 segundos. Lo importante en este ejemplo es que enfatiza el motivo principal en este trabajo: una curva de fracción de extractos constante (ver por ejemplo la Figura 4) puede tratarse como una curva monoparamétrica en la fracción molar global transformada. El trazado de esta trayectoria determina completamente la envolvente y localiza el punto crítico.
Obsérvese que la especificación de la fracción de extractos (por ejemplo 0,457 en la Figura 4) define un «camino» sobre el que cambia la fracción molar transformada global manteniendo constante la fracción de extractos. Este punto de vista representa una sistematización frente al cálculo de múltiples líneas de reparto a partir de la solución del flash isotérmico reactivo cambiando la alimentación manualmente y permite el desarrollo de un algoritmo numérico que puede ser automatizado completamente.
3.3. Rectificador reactivo con varios platos heterogéneos
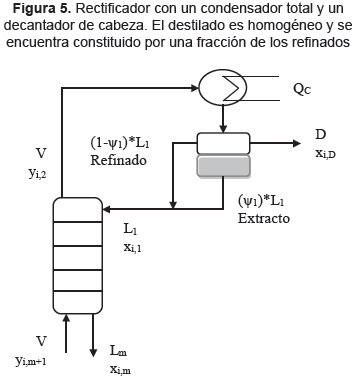
La intención en esta sección es presentar el contexto donde toman importancia las envolventes reactivas en el diseño conceptual de columnas de DR. La atención está dedicada a los rectificadores reactivos con varios platos heterogéneos (ver Figura 5). Se trata solamente de una introducción porque el objetivo del trabajo actual se orienta sobre la termodinámica de los procesos de DR y no sobre su diseño básico.
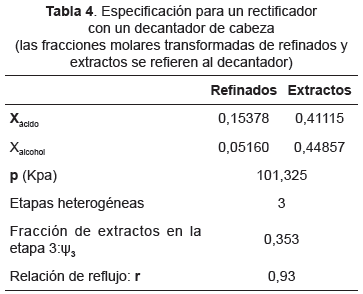
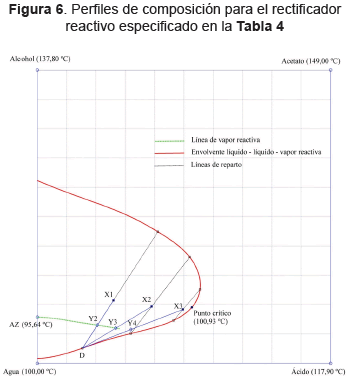
Para rectificadores de mezclas heterogéneas con un decantador de cabeza (ver Figura 5), la pureza del destilado se encuentra determinada por una de las ramas de la envolvente LLV y existe un valor máximo para el número de platos heterogéneos determinado por la posición de la línea de vapor (Urdaneta, et al., 2002; Kraemer, et al., 2011; Sánchez, Rodríguez y Gómez, 2012). Estas dos restricciones de la termodinámica pueden observarse en sistemas reactivos con dos grados de libertad en columnas con la zona de reacción no localizada. Para demostrar esto considere el rectificador especificado en la Tabla 4. Los resultados para los perfiles de composición se presentan en la Figura 6 las rectas azules que se originan en el destilado D, corresponden con los balances molares globales para la sección y expresan colinealidad de las composiciones transformadas para las corrientes m+1, m y D. Observe que los componentes en el líquido presentan solubilidad parcial solamente si el vapor en equilibrio pertenece a la línea de vapor. En consecuencia con lo anterior, una condición necesaria para que el plato m resulte heterogéneo es que la recta del balance global incluyendo los primeros m platos intercepte la línea de vapor. Las rectas de balance se calculan para que la composición del vapor resultante de mezclar el líquido del plato m (Xm, Lm) con el destilado (XD, D) pertenezca a la línea de vapor (Urdaneta, et al., 2002; Kraemer, et al., 2011; Sánchez, Rodríguez y Gómez, 2012). En la Figura 6 las líneas de balance X1-Y2-D y X2-Y3-D corresponden con esta situación. Por el contrario, la línea de balance X3-Y4-D presenta un caso donde no es posible obtener una composición sobre la línea de vapor. Resumiendo lo anterior: para el rectificador especificado en la Tabla 4 el máximo número de etapas heterogéneas es de tres. Este valor máximo es una función del reflujo y su cálculo juega un rol importante en la aplicación del método de valores en la frontera para el cálculo del mínimo consumo de energía (Urdaneta, et al., 2002; Kraemer, et al., 2011; Sánchez, Rodríguez y Gómez, 2012).
Este tipo de análisis en coordenada transformada es extensible a procesos de extracción reactiva y los métodos gráficos tradicionalmente utilizados en la extracción con solventes en sistemas ternarios (ver por ejemplo el capítulo 6 en el libro de Treybal (1968) son válidos en coordenada transformada en sistemas reactivos con una reacción de esterificación.
4. CONCLUSIONES
Se presentó una metodología para transformar las ecuaciones del equilibrio de fases reactivo (líquido - líquido y líquido - líquido - vapor) en curvas paramétricas que pueden ser trazadas utilizando los métodos de continuación tradicionales. El principio ilustrado se basa en la reducción de los grados de libertad del sistema de ecuaciones a la unidad y la elección de un parámetro de continuación entre las variables naturales del problema para definir una trayectoria donde la fracción molar de una de las fases líquidas es constante. Una consecuencia directa de esta perspectiva es que motiva un método para calcular el punto crítico de las mezclas reactivas.
La analogía existente entre las binodales ternarias de mezclas no reactivas y las binodales reactivas de los sistemas de esterificación (o en general de las binodales reactivas en planos de fases con dos grados de libertad) ofrece la posibilidad de aplicar en sistemas reactivos ideas que fueron desarrolladas para el caso no reactivo. Aunque este concepto no es completamente nuevo, sus consecuencias sobre los procedimientos de cálculo de los diagramas de fases reactivos no se encuentran completamente explotadas.
Se determinó que la estructura del equilibrio líquido - líquido - vapor reactivo de las mezclas de ácido acético + 1-pentanol + agua + n-amilacetato y ácido acético + 3-metil-1-butanol + agua + isoamilacetato está constituida por binodales reactivas del tipo I con la línea de vapor reactiva completamente contenida por la envolvente líquido - líquido. En los casos ilustrados (y en otros muchos no reportados en este trabajo) el método propuesto no presenta problemas de convergencia mostrándose como una herramienta útil en la caracterización termodinámica de los sistemas de esterificación.
El principal aporte consiste en indicar las manipulaciones necesarias para transformar el cálculo de las envolventes reactivas en homotopías termodinámicas. Al trasladar el problema al campo de los métodos de continuación, la solución resulta relativamente simple porque las trayectorias de fracción de extractos constante tienen forma semejante a la binodal.
NOMENCLATURA
c: Número de componentes.
D: Flujo de destilado, o se refiere al destilado.
g: Función de discrepancia para el equilibrio líquido - líquido - vapor reactivo.
h: Función de discrepancia para el equilibrio líquido - líquido - reactivo.
KE: Constante de equilibrio de la reacción.
K: Coeficiente de distribución.
L: Flujo del efluente líquido que abandona una etapa.
QC: Flujo de calor en el condensador.
V: Flujo del efluente vapor que abandona una etapa.
x: Fracción molar en el líquido.
X: Fracción molar transformada en el líquido.
y: Fracción molar en el vapor.
γ: Coeficiente de actividad.
δ: Cambio en las moles ocasionado por la reacción.
ν: Coeficiente estequiométrico.
ψ: Fracción molar de la fase de extractos.
ψ*: Fracción molar transformada de la fase de extractos.
χ: Vector columna que agrupa las variables dependientes en la forma paramétrica de las ecuaciones del equilibrio de fases reactivo.
l : Longitud de arco.
Subíndices
i: Se refiere al componente
m: Se refiere a la etapa.
Superíndices
E: Para los extractos
l-l: Para el equilibrio líquido - líquido.
R: Para los refinados.
REFERENCIAS
Allgower, E. L. and Georg, K. (1990). Introduction to Numerical Continuation Methods. Colorado: Springer, pp. 7-38. [ Links ]
Avami, A., Marquardt, W., Saboohi, Y. and Kraemer, K. (2012). Shortcut design of reactive distillation columns. Chemical Engineering Science, 71 March, pp. 166-177. [ Links ]
Barbosa, D. and Doherty, M. F. (1988). Design and minimum reflux calculations for single-feed multicomponent reactive distillation columns. Chemical Engineering Science, 43(7), pp. 1523-1537. [ Links ]
Bonilla, A., Acosta, A., Tapia, J. C. and Segovia, J. G. (2008). A method for flash calculations in reactive mixtures. Afinidad, 65(535), pp. 236-242. [ Links ]
Cepeda, E. A. (2010). Isobaric Vapor-Liquid Equilibrium for Binary Mixtures of 3-Methyl-1-butanol + 3-Methyl-1-butyl Ethanoate and 1-Pentanol + Pentyl Ethanoate at 101.3 kPa. Journal of Chemical and Engineering Data, 55(6), pp. 2349-2354. [ Links ]
Chang, Weixian., Guan, Guofeng., Li, Xinli. and Yao, Huqing (2005). Isobaric Vapor-Liquid Equilibria for Water + Acetic Acid + (n-Pentyl Acetate or Isopropyl Acetate). Journal of Chemical Engineering Data, 50(4) July, pp. 1129-1133. [ Links ]
Chiang, Sheng-Feng., Kuo, Chien-Lin., Yu, Cheng-Ching. and Wong, David S. H. (2002). Design Alternatives for the Amyl Acetate Process: Coupled Reactor/Column and Reactive Distillation. Industrial and Engineering Chemistry Research, 41(13) June, pp. 3233-3246. [ Links ]
Dragomir, R. M. and Jobson, M. (2005). Conceptual design of single-feed hybrid reactive distillation columns. Chemical Engineering Science, 60, pp. 4377-4395. [ Links ]
Ermakova, A. and Anikeev, V. I. (2000). Calculation of Spinodal Line and Critical Point of a Mixture. Theoretical Foundations of Chemical Engineering, 34(1) January-February, pp. 51-58. [ Links ]
Esquível, M. M. and Bernardo-Gil, M.G. (1990). Liquid - Liquid Equilibria for the Systems: Water/1-pentanol/Acetic Acid and Water/1-Hexanol/Acetic Acid. Fluid Phase Equilibria, 57(3), pp. 307-316. [ Links ]
Gmehling, J., Li, J. and Schiller, M. (1993). A Modified UNIFAC Model. 2. Present Parameter Matrix and Results for Different Thermodynamics Properties. Industrial Engineering Chemistry Research 32(1), pp. 178-193. [ Links ]
Hayden, J, G. and O'Connell, J. P. (1975). A generalized method for predicting second virial coefficients. Industrial and Engineering Chemistry Process Design and Development, 14(3), pp. 209-216. [ Links ]
Horsley, L. H. (1973). Azeotropic Data - III. Washington D. C: American Chemical Society, Advances in Chemistry Series, No. 116. [ Links ]
Jakov, A.; Grensemann, H.; Lohmann, J. and Gmehling, J. (2006). Further Development of Modified UNIFAC (Dortmund): Revision and Extension 5. Industrial Engineering Chemistry Research, 45(23), pp. 7924-7933. [ Links ]
Kraemer, K., Harwardt, A., Skiborowski, M., Mitra, S. and Marquardt, W. (2011). Shortcut-based Design of Multicomponent Heteroazeotropic Distillation. Chemical Engineering Research and Design, 89(8), pp. 1168-1189. [ Links ]
Lee, Liang-sun. and Lin, Ren-guey. (1999). Reaction and phase equilibria of esterification of isoamyl Alcohol and acetic acid at 760 mm Hg. Fluid Phase Equilibria, 165(2) November, pp. 261-278. [ Links ]
Lee, Liang-sun. and Liang, Shen-jang (1998). Phase and reaction equilibria of acetic acid - 1-pentanol - water - n-amyl acetate system at 760 mm Hg. Fluid Phase Equilibria, 149(1-2) August, pp. 57-74. [ Links ]
Lee, Ming-Jer.; Chen, Shao-Ling.; Kang, Chen-Hui. and Lin, Ho-mu. (2000). Simultaneous Chemical and Phase Equilibria for Mixtures of Acetic Acid, Amyl Alcohol, Amyl Acetate, and Water. Industrial and Engineering Chemistry Research, 39(11) September, pp. 4383-4391. [ Links ]
Okasinski, M. J. and Doherty, M. F. (2000). Prediction of heterogeneous reactive azeotropes in esterification systems. Chemical Engineering Science, 55(22) November, pp. 5263-5271. [ Links ]
Osorio-Viana, W., Duque-Bernal, M., Quintero-Arias, J.D., Dobrosz-Gómez, I., Fontalvo, J. and Gómez-García, M.A. (2013). Activity model and consistent thermodynamic features for acetic acid-isoamyl alcohol-isoamyl acetate-water reactive system. Fluid Phase Equilibria, 345 May, pp. 68-80. [online] Available DOI: http://dx.doi.org/10.1016/j.fluid.2013.02.006. [ Links ]
Pisarenko, Yu., Serafimov, L. and Kulov, N. (2009). Reactive Distillation Involving Multiple Chemical Reactions: Principles of Statics Analysis. Theoretical Foundations of Chemical Engineering, 43(5) October, pp. 591-605. [ Links ]
Poling, B. E., Prausnitz, J. M. and O'Connell, J. P. (2001). The Properties of Gases and Liquids, Fifth Edition. New York: McGraw - Hill. [ Links ]
Prausnitz, J. M.; Anderson, T. F.; Grens, E. A.; Eckert, C. A.; Hsieh, R. and O'Connell, J. P. Computer calculations for multicomponent vapor - liquid and liquid - liquid equilibria. USA: Prentice Hall, pp. 160-178, 1980. [ Links ]
Renon, H. and Prausnitz J. M. (1968). Local compositions in thermodynamic excess functions for liquid mixtures. AIChE Journal, 14(1), pp. 135-144. [ Links ]
Sánchez, C. A. (2011). Cálculo e interpretación de las trayectorias de composición constante (pinch) en columnas simples de destilación para mezclas azeotrópicas homogéneas. Revista EIA, 8(16) julio-diciembre, pp. 77-92. [ Links ]
Sánchez, C. A., Estupiñán, L. y Salazar, M. A. (2010). Herramientas para la caracterización termodinámica de sistemas ternarios en destilación, Revista EIA, 7(13), pp. 77-91. [ Links ]
Sánchez, C. A.; Rodríguez, G. y Gómez, M. A. (2012). Herramientas geométricas para el diseño básico de columnas de destilación con mezclas azeotrópicas heterogéneas ternarias. I. Cálculo del reflujo mínimo. Revista EIA, 9(18) junio-diciembre, pp. 143-157. [ Links ]
Sánchez, O., Péres, E., Bek-Pedersen, E. and Gani, R. (2003). Graphical and Stage-to-Stage Methods for Reactive Distillation Column Design. AIChE Journal, 49(11), pp. 2822-2841. [ Links ]
Seydel, R. (2010). Practical Bifurcation and Stability Analysis. New York: Springer New York Dordrecht Heidelberg London, pp. 169-261. [ Links ]
Tang, Y., Chen, Y., Huang, H., Yu, C., Hung, S. and Lee, M. J. (2005). Design of reactive distillations for acetic acid esterification. AIChE Journal, 51(6), pp. 1683-1699. [ Links ]
Taylor, R., Miller, A. and Lucia, A. (2006). Geometry of Separation Boundaries: Systems with Reaction. Industrial Engineering Chemistry Research, 45(8) April, pp. 2777-2786. [ Links ]
Thery, R.; Meyer, X.; Joulia, X. and Meyer, M. (2005). Preliminary Design of Reactive Distillations Columns. Trans IChem E, part A, Chemical Engineering Research and Design, 83(A4), pp. 379-400. [ Links ]
Toikka, A. M.; Toikka, M. A.; Pisarenko, Yu. A. and Serafimov, L. A. (2009). Vapor-Liquid Equilibria in Systems with Esterification Reaction. Theoretical Foundations of Chemical Engineering, 43(2), pp. 129-142. [ Links ]
Torres, K. A. y Espinosa, J. (2009). Incorporating Tangent Pinch Points into the Conceptual Modeling of Batch Distillations: Ternary Mixtures. Industrial and Engineering Chemistry Research, 48(2), pp. 857-869. [ Links ]
Treybal, R. E. (1968). Extracción en Fase Líquida. México: Unión Tipográfica Editorial Hispano Americana, pp. 16-51. [ Links ]
Ung, S. and Doherty, M. F. (1995). Vapor-Liquid Phase Equilibrium in Systems with Multiple Chemical Reactions. Chemical Engineering Science, 50(1) January, pp. 23-48. [ Links ]
Urdaneta, R. Y., Bausa, J., Bruggemann, S. and Marquardt, W. (2002). Analysis and Conceptual Design of Ternary Heterogeneous Azeotropic Distillation Processes. Industrial and Engineering Chemistry Research, 41(16) August, pp. 3849-3866. [ Links ]
Wasylkiewicz, S. K. (1999). Design of Heterogeneous Distillation Columns for Separation of Azeotropic Non - Reactive and Reactive Mixtures. Computers and Chemical Engineering Supplement, pp. s125-s128, 1999. [ Links ]
Wasylkiewicz, S. K.; Kobylka, L. C. and Castillo, J. L. (2003). Pressure Sensitivity Analysis of Azeotropes. Industrial and Engineering Chemistry Research, 42(1) November, pp. 207-213. [ Links ]
Wasylkiewicz, S. K. and Ung, S. (2000). Global phase stability analysis for heterogeneous reactive mixtures and calculation of reactive liquid - liquid and vapor - liquid - liquid equilibria. Fluid Phase Equilibria, 175(1-2), pp. 253-272. [ Links ]
Weidlich, U. and Gmehling, J. (1987). A Modified UNIFAC Model. 1. Prediction of VLE, hE and  , IIndustrial and Engineering Chemistry Research, 26(7) July, pp. 1372-1381. [ Links ]
, IIndustrial and Engineering Chemistry Research, 26(7) July, pp. 1372-1381. [ Links ]
Wyczesany, A. (2009). Chemical Equilibrium Constants in Esterification of Acetic Acid With C1-C5 Alcohols in the Liquid Phase. Chemical and Process Engineering, 30, pp. 243-265. [ Links ]
Yaws, C. L. (2003). Yaws' Handbook of thermodynamic and physical properties of chemical compounds: physical, thermodynamic and transport properties for 5,000 organic chemical compounds. Norwich, N. Y: Knovel. [ Links ]
Yaws, C. L. (2008). Thermophysical Properties of Chemicals and Hydrocarbons. USA: William Andrew. [ Links ]
Yermakova, A., Sazhina, O. V. and Anikeev, V. I. (2005). Calculation of binodal lines for a multicomponent mixture by the Homotopy Method. Theoretical Foundations of Chemical Engineering, 39(1), pp. 85-91. [ Links ]