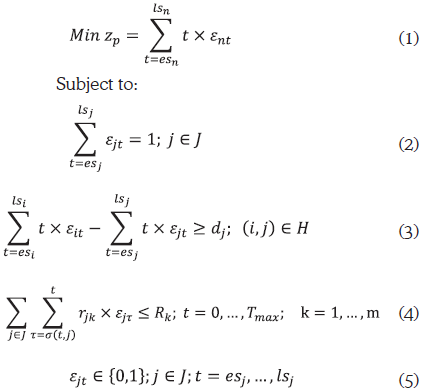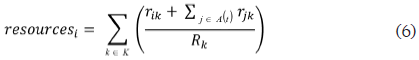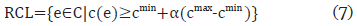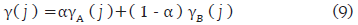Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.20 Envigado July/Dec. 2013
A HYBRID HEURISTIC ALGORITHM FOR SOLVING THE RESOURCE CONSTRAINED PROJECT SCHEDULING PROBLEM (RCPSP)
UN ALGORITMO HEURÍSTICO HÍBRIDO PARA LA SOLUCIÓN DEL PROBLEMA DE PROGRAMACIÓN DE TAREAS CON RECURSOS RESTRINGIDOS (RCPSP)
UM ALGORITMO HEURÍSTICO HÍBRIDO PARA A SOLUCAO DO PROBLEMA DE PROGRAMACAO DE TAREFAS COM RECURSOS RESTRINGIDOS (RCPSP)
Juan Carlos Rivera*, Luis Fernando Moreno V.**, Francisco Javier Díaz S.***, Gloria Elena Peña Z.****
* Ph. D. en Ingeniería. Université de Technologie de Troyes (UTT), ICD-LOSI, Francia.
Autor de correspondencia: (L.F. Moreno-V.). Carrera 49 75 Sur 50, Medellín, Colombia. Teléfono: 426 19 50. Correo electrónico: rivera_@utt.fr.
** Profesor Universidad Nacional de Colombia, sede Medellín. Facultad de Minas. Medellín, Colombia.
*** Ph. D. Profesor Asociado Universidad Nacional de Colombia - Sede Medellín. Facultad de Minas. Medellín, Colombia.
**** Doctor en Ingeniería de Organización. Profesor Universidad Nacional de Colombia - Sede Medellín. Medellín, Colombia.
Artículo recibido: 13-III-2013 / Aprobado: 24-VII-2013
Discusión abierta hasta diciembre de 2014
ABSTRACT
The Resource Constrained Project Scheduling Problem (RCPSP) is a problem of great interest for the scientific community because it belongs to the class of NP-Hard problems and no methods are known that can solve it accurately in polynomial processing times. For this reason heuristic methods are used to solve it in an efficient way though there is no guarantee that an optimal solution can be obtained. This research presents a hybrid heuristic search algorithm to solve the RCPSP efficiently, combining elements of the heuristic Greedy Randomized Adaptive Search Procedure (GRASP), Scatter Search and Justification. The efficiency obtained is measured taking into account the presence of the new elements added to the GRASP algorithm taken as base: Justification and Scatter Search. The algorithms are evaluated using three data bases of instances of the problem: 480 instances of 30 activities, 480 of 60, and 600 of 120 activities respectively, taken from the library PSPLIB available online. The solutions obtained by the developed algorithm for the instances of 30, 60 and 120 are compared with results obtained by other researchers at international level, where a prominent place is obtained, according to Chen (2011).
KEY WORDS: Project Scheduling; RCPSP; Heuristic; GRASP; Scatter Search; Justification.
RESUMEN
El Problema de Programación de Tareas con Recursos Restringidos (RCPSP) es de gran interés para la comunidad científica debido a que, por su pertenencia a la clase de problemas NP-Hard, no se conocen métodos que lo resuelvan de manera exacta en tiempos de procesamiento polinomial. Por esta razón, se utilizan métodos heurísticos para resolverlo de manera eficiente aunque no garantizan la obtención de una solución óptima. En esta investigación se presenta un algoritmo heurístico híbrido para resolver eficientemente el RCPSP, combinando elementos de las heurísticas Procedimiento de Búsqueda Adaptativa Aleatoria Agresiva (GRASP), Búsqueda Dispersa y Justificación. La eficiencia obtenida se mide por la presencia de los nuevos elementos agregados al algoritmo de base GRASP: Justificación y Búsqueda Dispersa. Los algoritmos se evalúan usando tres bases de datos de instancias del problema, así: 480 instancias de 30 actividades, 480 de 60 y 600 de 120 actividades respectivamente, tomadas de la librería PSPLIB disponible en línea. Las soluciones obtenidas por el algoritmo desarrollado para las instancias de 30, 60 y 120 actividades se comparan con los resultados obtenidos por otros investigadores a nivel internacional, donde se obtiene un lugar prominente de acuerdo con Chen (2011).
PALABRAS CLAVES: Programación de proyectos; RCPSP; heurística; GRASP; búsqueda dispersa; justificación.
SUMÁRIO
O Problema da Programação de Tarefas com Recursos Restringidos (RCPSP) é um problema de grande interesse para a comunidade científica devido a que, por a sua pertença à classe de problemas NP-Hard, não conhecem-se métodos que os solucionam de maneira exata em tempos de processamento polinomial. Por esta razão, utilizam-se métodos heurísticos para solucionar-o de maneira eficiente apesar de que não garantam a obtenção duma solução ótima. Nesta investigação apresenta-se um algoritmo heurístico híbrido para solucionar eficientemente o RCPSP, combinando elementos das heurísticas Procedimento de Busca Adatativa Aleatória Agressiva (GRASP), Busca Dispersa e Justificação. A eficiência obteida conte-se por a presenca dos novos elementos agregados ao algoritmo de base GRASP: Justificação e Busca Dispersa. Os algoritmos avaliam-se usando três bases de dados de instâncias do problema, assim: 480 instâncias de 30 atividades, 480 de 60 e 600 de 120 atividades respectivamente, tomadas da livraria PSPLIB disponível on-line. As soluções obteidas por o algoritmo desenvolvido para as instâncias de 30, 60 y 120 atividades comparam-se com os resultados obteidos por outros investigadores a nível internacional, onde obtem-se um lugar proeminente de acordo com Chen (2011).
PALAVRAS-CHAVE: Programação de projetos; RCPSP; Heurística; GRASP; Busca Dispersa; Justificação.
1. INTRODUCTION
A scheduling problem can be defined very broadly as the problem of organizing or sequencing a series of operations and locating them in time without violating any precedence and resource constraints imposed on the problem. The Resource Constrained Project Scheduling Problem (RCPSP) is a scheduling problem whose objective is to minimize the project completion time or makespan. There are two strategies for solving a scheduling problem: first, analytical algorithms, whose main characteristic is that they guarantee that an optimal solution is obtained, some of which are found in Deblaere, Demeulemeester and Herroelen (2011), Demeulemeester and Herroelen (1992; 1997), and second, heuristic algorithms that although they do not guarantee an optimal solution, they can produce solutions close to the optimal, in most cases, and in considerably less computational time.
This paper aims to present a new hybrid algorithm based on Greedy Randomized Adaptive Search Procedure (GRASP), improved with Scatter Search and Justification methods, and compare the results obtained with those of other algorithms used in solving the RCPSP.
2. DEFINITION OF THE RESOURCE CONSTRAINED PROJECT SCHEDULING PROBLEM (RCPSP)
Resource Constrained Project Scheduling Problem can be described mathematically as follows (Mingozzi, et al., 1998; Valls, Ballestín and Quintanilla, 2005; Tseng and Chen, 2006):
There is a set J={1,...,n} of activities (or jobs) which have to be processed. Every activity j J has a duration (processing time) dj. Moreover, the activities are interrelated by end-to-start precedence constraints, being Pj
J has a duration (processing time) dj. Moreover, the activities are interrelated by end-to-start precedence constraints, being Pj J\{j} the set of all the immediate predecessor activities of activity j, i.e., activities that must be completed before starting the execution of activity j. Assuming the Activity-On-Node (AON) representation, the precedence constraints can be represented by a directed acyclic graph G=(J,H), where H={(i,j)|i
J\{j} the set of all the immediate predecessor activities of activity j, i.e., activities that must be completed before starting the execution of activity j. Assuming the Activity-On-Node (AON) representation, the precedence constraints can be represented by a directed acyclic graph G=(J,H), where H={(i,j)|i Pj,j
Pj,j J}. Additionally, there is a set K={1,...,m} of types of renewable resources, where each resource type k
J}. Additionally, there is a set K={1,...,m} of types of renewable resources, where each resource type k  K has a total availability (capacity) Rk at each time interval of the scheduling period, i.e., the sum of the amount of resource type k used in the period t, Rk (t), should not exceed Rk for all t. Each activity j requires a constant amount, rjk, of units of resource type k during the entire time interval of its duration. It is assumed that rjk≤Rk for all j
K has a total availability (capacity) Rk at each time interval of the scheduling period, i.e., the sum of the amount of resource type k used in the period t, Rk (t), should not exceed Rk for all t. Each activity j requires a constant amount, rjk, of units of resource type k during the entire time interval of its duration. It is assumed that rjk≤Rk for all j J and for all k
J and for all k K, in order to ensure the existence of feasible solutions. Resources occupied by an activity will not be released until it is completed and then, they may be occupied by other activities.
K, in order to ensure the existence of feasible solutions. Resources occupied by an activity will not be released until it is completed and then, they may be occupied by other activities.
All quantities dj, rjk and Rk are non negative integers for all j and for all k; interrupting the processing of activities is not allowed and it is assumed that there are not setup times, or that they are included in the processing times.
The first and last activities, 1 and n, are fictitious activities used to represent the beginning and the end of the whole project: activity 1 must be completed before starting activities J\{1} and activity n can only start after the completion of activities J\{n}. In addition, it is assumed that d1=dn=0 and that r1k=rnk=0 for all k. It is also assumed, without loss of generality, that activities are topologically ordered, i.e., each predecessor of activity j has a smaller activity number than j.
The cost of a feasible solution is given by the project completion time (makespan). The aim is to find a schedule of activities s, for example, a series of feasible starting times (or completion times) for each activity (s1, s2, ..., sn) where s1 = 0, such that precedence and resource constraints are satisfied and the solution cost, i.e. that makespan (T(s) = sn), is minimized.
Figure 1 shows an example of a graph representing a project consisting of eleven interrelated activities and three types of resources. Each node in the graph corresponds to an activity and the arcs represent the precedence relationships between activities.
Each activity (node) has a subscript that identifies it and it is located within the node. The number above the node represents the duration of the activity, and the numbers below the node correspond to the consumption of each of the three types of ordered renewable resources. As mentioned earlier, the first and the last activity are fictitious. Rk represents the availability of type of resource k.
This example will be used later in order to clarify some concepts about the operation of the algorithm developed in this research.
3. MATHEMATICAL FORMULATION
A way to formulate the RCPSP described in the preceding section, using integer programming is presented by Mingozzi et al. (1998):
Where:
εjt: Binary decision variables are equal to 1 if and only if the activity j starts at the beginning of period t.
lsj: Late start time of activity j.
esj: Early start time of activity j.
t: Each of the periods of the planning horizon of the project.
σ(t,j)=max (0,t-dj+1).
Tmax: Upper bound on the project completion time. It can be easily computed as Tmax=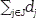 .
.
In this approach two activities are always considered artificial or fictitious (dummy jobs), which are the first one and the last one (1 and ), with zero duration and zero consumption of all resources. The purpose of these activities is to represent a single starting point and a single completion point of the project, respectively.
Equation (1) is the objective function: makespan or project completion time.
Equations (2) represent the non-preemption constraints, i.e., those that require that an activity, once initiated, must continue until its completion.
Inequalities (3) represent precedence constraints: an activity can only start after completion of all its predecessors.
Inequalities (4) represent resource constraints: In any period, the amount of resources used by all running activities must not exceed the availability of each corresponding resource.
Expressions (5) indicate that the decision variables εjt, are binary variables whose possible values are zero or one. These variables are equal to one (1) if and only if activity j begins in period t; otherwise, they are equal to zero (0).
It is easy to find a solution to the problem by means of any mixed integer linear programming (MILP) software, but there is a great deterioration of runtime when increasing the number of activities. Although the constraints (2), (3) and (4) are easy to formulate, it should be borne in mind that in each set of them there may be hundreds or even thousands of constraints for not very large instances.
The MILP approach is useful to understand what the problem is and to obtain theoretical conclusions. An additional feature of this approach is that lower bounds can be obtained using relaxation techniques (discarding some constraints).
The RCPSP treated in this research, is not the most general problem, since the it uses deterministic activity durations and renewable resources (non-renewable resources are not considered) and take into account only one way to perform the activities (as opposed to the multimodal case), among other features. In this paper, the instances analyzed are composed of 30, 60 and 120 activities and four types of resources as in Coelho and Vanhoucke (2011), Agarwal, et al. (2011), and Chen (2011). The search for efficient methods of solution is still of great interest to the scientific community due to the fact that it belongs to the class of NP-Hard problems (Blazewicz, Lenstra and Rinnooy, 1983; Ducker and Knust, 2006) and this makes it a very difficult problem to solve for which no efficient exact solution algorithms have been found. Instances with more than 60 activities show a high level of complexity because of its combinatorial nature (Valls, Ballestín and Quintanilla, 2005).
4. HEURISTIC METHODS
The model presented in the previous section can be solved through analytical techniques, such as MILP, which guarantee an optimal solution, but which are not feasible in practice because of their high processing time. Therefore, it is necessary to resort to the so-called heuristic methods that, although do not guarantee optimal solutions, provide a more intuitive understanding of the problem and make it possible to reach, in considerably less time, solutions that are usually fairly close to the optimal one.
The most general idea of the term heuristic is related to the task of solving real problems intelligently using the available knowledge. Heuristic method is the appropriate term for those procedures that, using common sense, experience or knowledge about a problem and about applicable techniques, tries to find solutions using a reasonable amount of resources (usually computation time). According to Brito, et al. (2004) heuristic methods can be used to solve optimization problems, where besides the restrictions that must be met by the feasible solutions, an objective function must be evaluated to measure the quality of the solution.
Some of the heuristic methods used for solving the RCPSP are Genetic Algorithms, Evolutionary Algorithms, GRASP, Tabu Search, Simulated Annealing, Scatter Search, Random Search and Ant Colony Systems, among others (Chen, et al., 2010; Peteghem and Vanhoucke, 2010; Montoya-Torres, et al., 2010). In this paper a hybrid algorithm which combines concepts of GRASP, Scatter Search and Justification is used. The latter is an emerging method for solving scheduling problems that has shown very good results.
5. PROPOSED ALGORITHM
The algorithm proposed in this research for solving the RCPSP is based on the GRASP method which is a heuristic method to find approximate solutions for combinatorial optimization problems, on the basis of the premise that different and good quality initial solutions play an important role in the success of local search methods (Pesek, Schaerf and Zerovnik, 2007).
A GRASP algorithm is a multi-start method, in which each iteration consists of a phase of construction of a greedy randomized solution followed by an improvement phase, using the built solution as the starting point for improvement (Anagnostopoulos and Koulinas, 2012). In the improvement phase it is very common to use a simple local search algorithm; however, in this research two algorithms are used: the first one, known as justification, is a method specifically developed for the RCPSP (Valls, Ballestín and Quintanilla, 2005; Chen, 2011), and the second one is a based-population algorithm called scatter search (Ranjbar and Kianfar, 2009; Shi, et al., 2010). The proposed algorithm is summarized by the pseudocode depicted in Figure 2.
For a more precise description of the methodology used, the following topics will be tackled: way of representing a solution, construction phase, phase 1 of improvement (heuristic justification), characterization of the population of solutions, and phase 2 of improvement (scatter search).
5.1 Ways of Representing a Solution
In order to implement the heuristic strategies chosen, two different methods of representation are used: activity list and priority values.
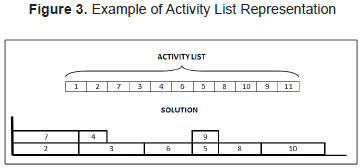
In the activity list, each solution is represented by a list where all the project activities are placed according to the scheduling order. Figure 3 shows an example of the activity list for the project of Figure 1.
The activity list in Figure 3 indicates that the first activity to be scheduled is activity 1, followed by activity 2; then, activity 7 and so on, according to the order in which they are arranged in the list. Activities 1 and 11 are not present in the solution given the fact that, being fictitious (beginning and end of the project), they have a duration of zero time units. The solution obtained from the activity list appears in the Gantt chart at the bottom of Figure 3. Each activity is scheduled in the earliest possible starting time without delaying the other activities already scheduled, taking into account both precedence and resource constraints; that is, by definition, an active schedule. Then, activity 2 is scheduled at time 0 since it does not have predecessors, then activity 7 is scheduled simultaneously since it does not have predecessors either and resources are available for both; now, activity 3 should be scheduled and, although it does not have predecessors, it can not be scheduled on time zero since the resources are not enough, then activity 3 is scheduled after the end of activities 2 or 7 when resources are available again. In this way the remaining activities are scheduled. For scheduling problems with regular objective functions, such as minimizing the makespan, the optimal solution will always be in all active schedules (Sprecher, Kolisch and Drexl, 1995, cited in Kolisch and Hartmann, 1999).
In the solution in Figure 3, activities 2 and 7 can run simultaneously at the beginning of the project. Due to resource constraints, activities 3 and 4 can be run only when resources are released after the completion of activities 2 and 7. Activity 6 can be run only after completion of activity 3 due to precedence constraints (as well as to resource constraints).
The above implies that for some activity i, its starting time could be prior to that of any other activity that is in a previous position in the activity list. For example, activity 9 is scheduled after having scheduled activities 8 and 10; however its starting time is prior to the starting time of such activities; this may be due to its consumption of fewer resources. For more information about the activity list representation, the reader is referred to Kolisch and Hartmann (1999) and Debels, et al. (2004).
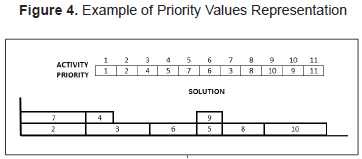
Each solution represented by the activity list can be transformed into a representation using priority values, which is a modification proposed in Debels, et al. (2004) of the form of representation known as random key. Figure 4 shows an example of activity list in Figure 3 represented by priority values.
According to the priority values in Figure 4, the first activity to be scheduled is activity 1, which has the highest priority, followed by activity 2; in third place, activity 7; in fourth place, activity 3, and so forth.
It is possible to use two representation methods in the same algorithm without causing inefficiency since it is very easy to transform the solution from a representation method to another. The transformation of the activity list representation into the priority value representation can be carried out using the algorithm represented by the pseudocode in Figure 5.
Similarly, the pseudocode in Figure 6 shows the procedure to transform the priority value representation into the activity list representation.
5.2 Constructive Phase
In the constructive phase, a greedy randomized procedure is carried out to generate multiple solutions that are different among them. This procedure involves selecting all the activities that can be scheduled in a given period t, taking into account their feasibility due to precedence and resource constraints. These activities are called eligible. Then, among all these eligible activities, the best ones are selected, defining as the best one that activity that uses the highest quantity of resources, as follows:
Being A(t) the set of activities that are already scheduled and active at period t.
The variable resourcesi is an indicator of the resource use that would cause activity i if it were scheduled in a given period, t.
The number of activities considered as candidates depends directly on the quality of each one, as follows (Glover and Kochenberger, 2003):
Let c(e) be the use of resources of the eligible activity e. A list of candidate activities is created as follows (Restricted Candidate List: RCL):
Where:
C: Set of eligible activities.
cmin: Minimum use of resources by one of the eligible activities, min{c(e)|e C}.
C}.
cmax: Maximum use of resources by one of the eligible activities, max{c(e)|e C}.
C}.
α: Parameter that controls the values c(e) accepted as candidates (α [0,1]).
[0,1]).
Then, an activity is chosen randomly from the candidate list in order to be scheduled and such list is updated. The procedure is repeated as long as the candidate activity set is not empty.
When none of the activities can be scheduled, that is the eligible activity set is empty, the scheduling time is put forward to the minimum completion time of the running activities. Then, the eligible activity list is updated.
Notice that if α=0, all eligible activities become automatically candidate activities. Therefore, the method would be equivalent to a totally random selection. If α=1, only the activities with resource use being higher than or equal to all other activities are candidates. Then, the method would be equivalent to a greedy construction.
The result of this constructive phase is a solution s, represented by an activity list, which will be then right-justified using the procedure explained below.
5.3 Improvement Phase 1: Justification Heuristic
Once an initial solution is built, an improvement is carried out using the justification procedure described below (Valls, Ballestín and Quintanilla, 2005, and Xu, et al., 2008).
In a solution or schedule S, as defined previously, the right justification of an activity j≠n involves obtaining a schedule S' so that s'i=si for i≠j, making s'j≥sj with s'j as large as possible, without increasing the makespan. In a schedule S, the right justification of activities j in decreasing order regarding its completion time (fj=sj+dj) generates an active schedule to the right, SR, called right justification. SR is not the only one, since it depends on the used tiebreaker rule(s). In this research, as a tiebreaker rule, the selection of the activity with the highest priority number in the list of activities is used.
The previous procedure guarantees that the new solution obtained has a lower or equal makespan than that of the solution before justification. There is also a procedure to carry out the left justification, but it is not considered in this research.
5.4 Characterization of the Population of Solutions
The solutions resulting from both the constructive phase and the justification are taken to a solution set (reference set or population) to carry out phase 2 of improvement: Scatter Search.
In order to obtain this population of solutions, it has to be taken into account that, as the search progresses, solutions belonging to the population must be changing to add diversification, and that there should not be repeated solutions; in order to control that, two filters are applied.
The first filter is the makespan value. If the makespan of two solutions is different, both solutions have to be different. If the makespan of two solutions is the same, the second filter must be evaluated computing the following indicator:
If there are two solutions with different IS value, it can be concluded that the two solutions are different; but if the IS value of the two solutions is the same, it does not mean necessarily that the solutions are the same, although it is very likely that this is the case. However, in this research, due to efficiency reasons, whenever two solutions have the same makespan and the same IS value, we assume that the solutions are the same and one of them is ruled out.
In order to allow for diversification in the population, after each Scatter Search iteration (described next), some solutions of the population are eliminated in order to be replaced by new solutions generated in the constructive and justification phases. The eliminated solutions correspond to the lower quality solutions (higher makespan) of the population.
5.5 Improvement Phase 2: Scatter Search
The so-called evolutionary methods are among the most known heuristic methods and the most used to solve the RCPSP. These methods are based on the generation, selection, combination and replacement of a solution set. Genetic algorithms, scatter search, path relinking and memetic algorithms are part of this group of methods.
The Scatter Search is a procedure based on formulations and strategies introduced in the sixties. The basic concepts of the method were introduced by Glover (1977) based on the strategies to combine decision rules in sequencing problems and on the combination of constraints of the surrogate constraint method.
The scatter search is based on maintaining a solution set, called reference set, and carrying out combinations with those solutions. But, unlike genetic algorithms, it is not based on randomization on a relatively large solution set, but on systematic and strategic selections from a small set.
The scatter search is based on combining the solutions appearing in the so-called reference set (equivalent to the population of a genetic algorithm). In this set are the good solutions that have been found. It is worth mentioning that the meaning of good is not restricted to the quality of the solution, but the diversity contributed by the solution to the set is also considered. One of the most important characteristics of the scatter search is that it involves integrating the combination of solutions with the local search.
The scatter search consists basically of the following elements:
Generator of diverse solutions: The method involves generating a set P of diverse solutions from which a small subset of cardinality b is selected, called reference set, in order to carry out the combinations. The selection criterion used involves obtaining quality solutions that are different from each other (quality and diversity). The solutions of the set P are ranked from best to worst, regarding their quality.
Different operations are carried out with the set P, namely:
- Creation. The reference set starts with the b* (0<b*<b) best solutions of P. The remaining b-b* are extracted from P using the maximum distance criterion (Laguna et al, 2012) with the solutions already included in the reference set. In the algorithm developed in this research, at each iteration, solutions b-b* are replaced by new solutions created with the randomized constructive method described before.
Updating. Solutions resulting from the combinations can enter to the reference set and replace some of the solutions already included if the former improve the latter.
Combination method: The scatter search is based on combining all solutions of the reference set. For this, subsets consisting of two or more elements of the reference set are considered and combined using a routine designed for this purpose. The solution or solutions obtained from this combination can be immediately introduced in the reference set (dynamic updating) or temporarily stored in a list until the process of carrying out all combinations is completed and then, to see which solutions can enter to this set (static updating).
In this research, static updating was used and solutions were combined using the following procedure:
Having each solution represented by priority values, the following formula is applied to each activity of a couple of solutions of the reference set.
Then, the γ(j) values must be fixed in order to turn them into the integer corresponding to their order and belonging to J, so that the new solution can be represented using priority values.
Improvement method: Typically, it is a local search method to improve solutions of the reference set as well as the combined ones before considering their inclusion in such set. It is worth mentioning that in those implementations where no feasible solutions are used, which is not the case in this work, this method must be able to obtain a feasible solution from one that is not feasible. If the method cannot improve the initial solution, the result is considered to be the same initial solution.
In this research, the local search was replaced by the justification method mentioned above. This means that the justification procedure is carried out in two different points of the algorithm as a way to improve the constructive phase and once the scatter search is completed.
6. RESULTS
In order to evaluate the efficiency of the algorithm, three data bases of instances of the problem were used: 480 instances of 30 activities, 480 of 60, and 600 of 120 activities respectively, taken from the PSPLIB library available online (Kolisch and Sprecher, 2004).
The solutions obtained by the developed algorithm for the instances of 30, 60 y 120 activities and four resources are compared with results obtained by other researchers at international level, where prominent places are obtained, according to Chen (2011), Tables 2, 3 and 4 for 30, 60 and 120 activities, respectively. The comparison of the results is made as follows: for problems of 30 activities, with the known optimum makespan values, available in the PSPLIB library; for problems of 60 and 120 activities, whose optimum makespan values are not known, the results are compared with the critical path lower bound as used by most of researchers.
An Intel core i3 processor of 2.53 GHz and 3 GB of RAM memory was used to run the algorithm. The methods were implemented in Visual Basic 6.0.
The algorithm efficiency is measured as the percentage of average deviation regarding the optimum makespan or lower bound as a function of the maximum number of solutions (schedules) necessary to find such deviation.
This measure has been developed in order to eliminate the disadvantage posed by the processing time, which depends on both the processor and language features. According to Kolisch and Hartmann (2005), this measure is based on the hypothesis that the computational effort to build a solution (schedule) is similar for most heuristic algorithms.
In order to evaluate the efficiency of each component of the algorithm, results with the different phases of the algorithm are presented: In table 1, first, the randomized solutions generated in the constructive phase of the algorithm (corresponding to the GRASP method) are considered individually, then, these initial randomized solutions are considered with a subsequent phase of improvement using justification (corresponding to the so-called GRASP + Just. method); finally, the whole algorithm is used, i.e., adding an improvement phase with Scatter Search, (SS), corresponding to the GRASP + Just. + SS method.
Table 1 shows the results obtained for problems of 30 activities, on the basis of the measures presented in Kolisch and Hartmann (2005).
Tables 2, 3 and 4 based on Chen (2011), show data obtained by the most advanced researchers around the world, who work with 480 problems of 30 activities, 480 of 60 and 600 of 120 activities taken from PSPLIB.
According to Table 2, for problems of 30 activities, the algorithm developed in this research is ranked in position 17th for 1.000 schedules, position 18th for 5.000 schedules and position 15th for 50.000 schedules.
It can also be noted that in Tables 2, 3 and 4, that this study is the only one that uses GRASP and one of the only two studies that uses Scatter Search.
7. CONCLUSIONS
This research confirms the good performance obtained using the Justification heuristics as a complement of any heuristic method for the RCPSP. The use of this heuristics improved around 68% the results obtained before its implementation.
Besides, it was confirmed that the use of additional elements in the algorithm improves its performance, which does not always happen.
Compared with the results obtained by other researchers, the developed algorithm finds good results. This can be confirmed because in the list presented in Chen (2011) the developed algorithm is superior to others in the list. This is so in spite of the simplicity of this algorithm due to the absence of local search procedures and of the poor presence of Scatter Search on the list of algorithms.
8. FUTURE WORK
The present research gives rise to the following lines of work for future research:
- To improve the algorithm presented here using different methods to generate and combine solutions.
- To design hybrid algorithms using other methodologies like Local Search, Simulated Annealing, Tabu Search and Path Relinking, among others.
- To design adaptive strategies that allow for the modification of parameters such as size variation of the reference set and the parameters necessary to create and combine solutions.
REFERENCES
Agarwal, A., Colak, S. and Erenguc, S. (2011). A Neurogenetic Approach for the Resource-Constrained Project Scheduling Problem. Cumputers and Operations Research, 38(1) January, pp. 44-50. [On line]. Available: http://dx.doi.org/10.1016/j.cor.2010.01.007. [ Links ]
Anagnostopoulos, K. and Koulinas, G. (2012). Resource-Constrained Critical Path Scheduling by a GRASP-Based Hyperheuristic. Journal of Computing in Civil Engineering, 26(2), pp. 204-213. [On line]. [Cited: October 10th, 2006]. Available: http://dx.doi.org/10.1061/(ASCE)CP.1943-5487.0000116. [ Links ]
Blazewicz, J.; Lenstra, J. and Rinnooy K. (1983). Scheduling Projects Subject to Resource Constraints: Classification and Complexity. Discrete Applied Mathematics, 5, pp. 11-24. [ Links ]
Brito, J., Campos, C., García, F., García, M., Melián, B., Moreno, J. and Moreno, J. (2004). Metaheurísticas: una revisión actualizada. Grupo de Computación Inteligente. Universidad de La Laguna. [ Links ]
Chen, Rue-Man. (2011). Particle Swarm Optimization with Justification and Designed Mechanisms for Resource-Constrained Project Scheduling Problem. Expert Systems with Applications, 38(6), pp. 7102-7111. [ Links ]
Chen, W.; Shi, Yan-ju., Teng, Hong-fei.; Lan, Xiao-ping.; and Hu, Lin-chen. (2010). An Efficient Hybrid Algorithm for Resource-Constrained Project Scheduling. Information Sciences, 180(6) March, pp. 1031-1039. [ Links ]
Coelho, J. and Vanhoucke, M. (2011). Multi-mode Resource-Constrained Project Scheduling Using RCPSP and SAT Solvers. European Journal of Operational Research, 213(1)August, pp. 73-82. [ Links ]
Debels, D.; De Reyck, B.; Leus, R. and Vanhoucke, M. (2004). A Hybrid Scatter Search / Electromagnetism Meta-heuristic for Project Scheduling. Working Paper. Universiteit Gent. [ Links ]
Deblaere, F., Demeulemeester, E. and Herroelen, W. (2011). Proactive policies for the stochastic resource-constrained project scheduling problem. European Journal of Operational Research, 214(2), pp. 308-316. [ Links ]
Demeulemeester, E. and Herroelen, W. (1992). A Branch and Bound Procedure for the Multiple Resource-Constrained Project Scheduling Problem. Management Science, 38(12) December, pp. 1803-1818. [ Links ]
Demeulemeester, E. and Herroelen, W. (1997). New Benchmark Results for the Resource-Constrained Project Scheduling Problem. Management Science 43(11) November, pp. 1485-1492. [ Links ]
Drucker, P. and Knust, S. (2006). Complex Scheduling. Berlin: Ed. Springer-Verlag, Berlin. [ Links ]
Glover, F. (1977). Heuristics for Integer Programming Using Surrogate Constraints. Decision Sciences, 8(1) January, pp. 156-166. [ Links ]
Glover, F. and Kochenberger, G. (2003). Handbook of Metaheuristics. Kluwer Academic Publishers. [ Links ]
Kolisch, R. and Sprecher, A. (2004). Library for Project Scheduling Problem - PSPLIB. [Cited: October 10th, 2006]. Available: http://129.187.106.231/psplib/. [ Links ]
Kolisch, R. and Hartmann, S. (1999). Heuristic algorithms for solving the resource-constrained project scheduling problem: classification and computational analysis. In: Weglarz, J. (Ed.). Project Scheduling - Recent Models, Algorithms and Applications. Boston: Kluwer Academic Publishers, pp. 147-178. [ Links ]
Kolisch, R. and Hartmann, R. (2005). Experimental Investigation of Heuristics for Resource-Constrained Project Scheduling: An Update. European Journal of Operational Research, 174(1), pp. 23-37. [ Links ]
Laguna, M., Martí, R., Gallego, M. and Duarte A. (2012). The Scatter Search Methodology. Wiley Encyclopedia of Operations Research and Management Science (Wiley EORMS). John Wiley and Sons, Inc. Available: http://dx.doi.org/10.1002/9780470400531. [ Links ]
Mingozzi, A., Maniezzo, V., Ricciardelli, S. and Bianco, L. (1998). An exact algorithm for the Resource Constrained Project Scheduling Problem Based on a New Mathematical Formulation. Management Science, 44(5) May, pp. 714-729. [ Links ]
Montoya-Torres, J., Gutiérrez-Franco, E. and Pirachicán-Mayorga, C. (2010). Project Scheduling with Limited Resources Using a Genetic Algorithm. International Journal of Project Management, 28(6) August, pp. 619-628. [ Links ]
Pesek, I., Schaerf, A. and Zerovnik, J. (2007). Hybrid Local Search Techniques for the Resource-Constrained Project Scheduling Problem. T. Bartz-Beielstein et al. (Eds.): HM, LNCS 4771. Springer-Verlag Berlin Heidelberg. pp. 57-68. [ Links ]
Peteghem, V. and Vanhoucke, M. (2010). A Genetic Algorithm for the Preemptive and Non-Preemptive Multi-Mode Resource-Constrained Project Scheduling Problem. European Journal of Operational Research, 201(2) March, pp. 409-418. [ Links ]
Ranjbar, M. and Kianfar, F. (2009). A Hybrid Scatter Search for the RCPSP. Transaction E: Industrial Engineering, 16(1), pp. 11-18. [ Links ]
Shi, Yanju., Qu., Fuzheng., Chen, W. and Li, B. (2010). A Differential Evolution with Scatter Search for Project Scheduling. Applied Mechanics and Materials, 26-28. pp. 724-727. [ Links ]
Sprecher, A., Kolisch, R. and Drexl, A. (1995). Semi-active, Active, and Non-Delay Schedules for the Resource-Constrained Project Scheduling Problem. European Journal of Operational Research, 80 January, pp. 94-102. [ Links ]
Tseng, Lin-Yu. and Chen, Shih-Chieh. (2006). A Hybrid Metaheuristic for the Resource-Constrained Project Scheduling Problem. European Journal of Operational Research, 175(2) December, pp. 707-721. [ Links ]
Valls, V.; Ballestín, F. and Quintanilla, S. (2005). Justification and RCPSP: A Technique that Pay. European Journal of Operational Research, 165(2) September, pp. 375-386. [ Links ]
Xu, N.; McKee, S.; Nozick, L. and Ufomata, R. (2008). Augmenting Priority Rule Heuristics with Justification and Rollout to Solve the Resource-Constrained Project. [ Links ]