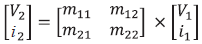UN MODELO ELÉCTRICO DE ESTRUCTURAS ALGEBRAICAS

AN ELECTRICAL MODEL OF ALGEBRAIC STRUCTURES

UM MODELO ELÉTRICO DE ESTRUTURAS ALGEBRÁICAS

Gabriel Poveda Ramos

Electrotecnia, Nacional School, California (Estados Unidos). Ingeniero eléctrico, Universidad Pontificia Bolivariana. Ingeniero químico de la Universidad Pontificia Bolivariana.Ingeniero electricista, Universidad del Valle. Magíster en Matemáticas Aplicadas de la Universidad Nacional de Bogotá. Tecnólogo textil, Instituto Textil de Lodz, Polonia. Estudios de Economía Latinoamericana en INTAL, Buenos Aires (Argentina). PhD. en ingeniería, Universidad Pontificia Bolivariana.
Autor de correspondencia: (G. Poveda-Ramos). Medellín (Colombia). Tel: 260 06 25. Correo electrónico: gapora@une.nte.co.

Artículo recibido: 28-V-2013 / Aprobado: 5-XI-2013
Discusión abierta hasta diciembre de 2014

RESUMEN

Los libros y los cursos de Álgebra Abstracta (o Álgebra Moderna) definen y estudian varios tipos de estructuras algebráicas, como los grupos, los espacios vectoriales, los anillos, los ideales y los cuerpos (o campos) de racionalidad. Estas estructuras se definen y se analizan en términos de unas operaciones que se caracterizan mediante propiedades que se presentan como salidas de la nada y que en realidad son solamente inferidas por abstracción de operaciones muy conocidas en disciplinas más elementales como la Geometría Euclidiana, la Teoría de Números y el Análisis Real. Pero nada se dice allí acerca de que hay sistemas de objetos físicos con relaciones mutuas, que son modelos (o ejemplos) rigurosamente fieles de tales estructuras algebraicas. Aquí se presenta uno de tales modelos, que está constituido por una clase de objetos eléctricos llamados cuadripolos, y que pueden conectarse mutuamente en paralelo (como ejemplo de una «suma» de tales cuadripolos) y en serie (como ejemplo de un «productos entre ellos»). En este sistema, y con estas dos operaciones eléctricas, se muestra, por consideraciones eléctricas, que se puede formar un modelo eléctrico de varias estructuras algebraicas: de un grupo conmutativo, de un espacio vectorial, de un anillo de entericidad y de un campo de racionalidad.

PALABRAS CLAVE: Álgebra abstracta; circuitos eléctricos; modelos físicos; grupos (algebraicos); anillos (algebráicos), cuerpos (campos).

ABSTRACT

Textbooks and courses in Abstract Algebra (or Modern Algebra) present and explain several kinds of algebraic structures -such as abelian groups, vector spaces, rings, ideals and fields- as if these were "free constructions of the human spirit". Usually mathematicians treat these structures as defined and analyzed in terms of operations which are characterized by properties which are presented as if comming up from a theoretical and purely platonic vacuum of ideas, in spite that they have been obtained indeed by inference and abstraction from well know, concrete operations in subjects such as Euclidean Geometry, Number Theory and Real Analysis. No considerations are done in those books about the existence and knowledge of physical objects endowed with mutual linkages, which are faithful models (or examples) of such algebraic structures with their inner operations. This paper presents one of those models, consisting of a class of electrical objects, the so-called electrical quadrupoles, which may be mutually connected in parallel (representing an "addition" between them) or in series (representing a "product" between them). Analysing these systems and these electrical operations, it is shown here how to construct a model of several of the above mentioned algebraic structures.

KEY WORDS: Abstract Algebra; Electric Circuits; Physical Models; Groups (in Algebra); Rings (in Algebra), Fields (in Algebra).

SUMÁRIO

Os livros e os cursos de Álgebra Abstrata (ou Álgebra Moderna) definem e estudam vários tipos de estruturas algebráicas, como os grupos, os espaços vetoriais, os anéis, os ideais e os corpos (ou campos) de racionalidade. Estas estruturas definem-se e analisam-se em termos de umas operações que se caracterizam mediante propriedades que se apresentam como saídas da nada e que em realidade são somente inferidas por abstração de operações muito conhecidas em disciplinas mais elementares como a Geometria Euclidiana, a Teoria de Números e a Análise Real. Mas nada se diz ali a respeito de que há sistemas de objetos físicos com relações mútuas, que são modelos (ou exemplos) rigorosamente fiéis de tais estruturas algébricas. Aqui apresenta-se um de tais modelos, que está constituído por uma classe de objetos elétricos chamados cuadripolos, e que podem ser ligado mutuamente em paralelo (como exemplo de uma "soma" de tais cuadripolos) e em série (como exemplo de um "produtos entre eles"). Em este sistema, e com estas duas operações elétricas, mostra-se, por considerações elétricas, que pode ser formado um modelo elétrico de várias estruturas algébricas: de um grupo conmutativo, de um espaço vetorial, de um anel de entericidad e de um campo de racionalidade.

PALAVRAS-CHAVE: Álgebra abstrata; circuitos elétricos; modelos físicos; grupos (algébricos); anéis (algebráicos), corpos (campos).

INTRODUCCIÓN

Los textos de Álgebra Abstracta (y también sus profesores) suele comenzar el estudio de esta materia dando algunos ejemplos de sus estructuras formales, que son tomados de la Geometría o del Análisis, y tienden a sugerir que esas estructuras solamente se encuentran en el mundo «ideal» de las Matemáticas. Ni esos libros ni esos profesores señalan que hay numerosos conjuntos de objetos físicos que están mutuamente interrelacionados por determinadas operaciones físicas que se pueden realizar entre ellos, y que con ellos pueden construirse verdaderos ejemplos objetivos y tangibles de lo que aquellos llaman grupos, anillos, espacios vectoriales, cuerpos o campos, y otros tipos de estructuras algebraicas.

Sin embargo, los físicos y los ingenieros conocedores de dicha Álgebra, y también de los objetos del mundo real y de las operaciones físicas que se pueden realizar entre ellos, pueden darse cuenta de que algunas estructuras formadas con tales objetos pueden construirse como realizaciones concretas y tangibles de las estructuras algebraicas ya mencionadas.

Pero al parecer, los ingenieros que sean buenos conocedores del Álgebra Abstracta son escasos, y los matemáticos bien relacionados con la Física son muy escasos. Porque después de leer muchísimas revistas y libros de una y otra de estas dos vastas disciplinas, el autor de estas líneas nunca ha visto publicado ningún ejemplo material y objetivo de ninguna de las estructuras mundanas que pueden ser modelos reales de las estructuras algebráicas ya mencionadas.

Este artículo pretende lograr dos resultados: uno de tipo práctico, que es el hecho de mostrar un sistema de circuitos eléctricos, que hoy no es usado -ni es conocido- como instrumento pedagógico para enseñar Álgebra Abstracta. Otro propósito es de tipo epistemológico y consiste en el intento de motivar a los matemáticos «puros» para que entiendan que su Matemática tiene su verdadero fundamento en realidades mundanas y no en presuntos axiomas gratuitos extraídos de la nada.

En su ejercicio de muchos años, como Ingeniero Electricista e Ingeniero Químico, el autor ha encontrado varios tipos de objetos reales y de fenómenos reales que, bien mirados, son verdaderas realizaciones de lo que los Algebristas llaman grupos, anillos y otras clases de estructuras, incluyendo otras más complejas que van hasta las que se llaman cuerpos o campos.

En este artículo se presenta una clase de objetos eléctricos llamados cuadripolos, que se pueden combinar entre ellos para formar así sistemas eléctricos más complejos y que, con cierto tipo de interconexiones forman conjuntos que son isomorfos con algunas estructuras abstractas de las que estudia el Álgebra Moderna.

El circuito eléctrico de dos puertos

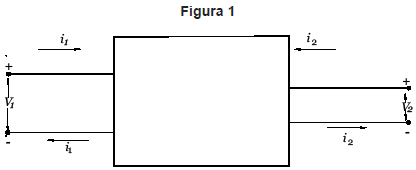
Un circuito eléctrico de dos puertos es un tipo de circuito con cuatro terminales (o cuadripolo), que consiste de una red interna, que puede ser complicada o sencilla, y dos pares de terminales exteriores que sirven para conectar dicha red con otros circuitos externos distintos de ésta. Uno de los dos pares suele llamarse «par de entrada», y al otro par se le llama «par de salida». También se les llama «terminal de entrada» y «terminal de salida», respectivamente. O bien «puerto de entrada» y «puerto de salida», en este mismo orden.

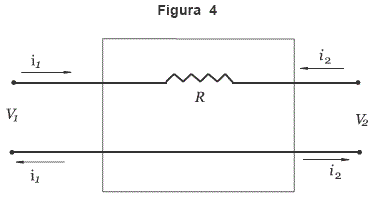
Con relación a un sistema eléctrico cualquiera (y no solamente en el que se acaba de describir), se llama «puerto» a un par de terminales tales que la corriente que entra al sistema por una de las terminales de cada puerto es igual a la que sale por la otra terminal del mismo puerto (Ver Figura 1).

Para lo que veremos, no es necesario conocer la configuración eléctrica del sistema interior de la red interna. Basta aquí establecer que, para nuestro caso, ella está constituida por elementos lineales, pasivos y bilaterales tales como resistencias óhmicas y reactancias lineales. Para simplificar el tratamiento eléctrico y para concentrar este estudio en la parte algebraica, se considerará aquí que la red interna del cuadripolo no contiene elementos activos, sino solamente elementos pasivos, bilaterales y lineales, que, de acuerdo con el teorema de Thévenin (en la Teoría General de Circuitos), se pueden reducir a una sola resistencia óhmica (o impedancia lineal, en el caso de circuitos de corrientes alternas).

Aquí se considera que se trata con corrientes directas y que aplica el teorema de Thévenin. En consecuencias, el cuadripolo más general que se tratará se representa como una «caja negra» que tiene dos terminales de entrada, otras dos de salida, y unas resistencias y otros elementos bilaterales, pasivos y lineales en su interior.

Cuadripolos elementales y sus matrices de transferencia

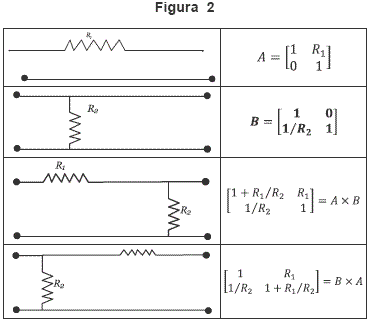
En la Teoría de Circuitos se demuestra que cada cuadripolo de los que se ha descrito, puede reducirse a uno que le es equivalente, que está constituido por una sola o por dos resistencias conectadas con los terminales y entre ellas como lo muestran las cuatro figuras vecinas. (Ver Newstead, 1959). Cada una de estas figuras queda descrita, unívocamente, por una matriz de 2 x 2 elementos, y cada uno de éstos equivale a la relación de cada una de las dos corrientes de entrada con las dos corrientes de salida. Los cuatro tipos de cuadripolos mencionados y sus cuatro respectivas matrices de transferencia se muestran en los dos dibujos vecinos. Estos cuatro cuadripolos se llaman elementales. Cada circuito interno formado por elementos lineales, pasivos y bilaterales se puede reducir a conexiones en serie y/o conexiones en paralelo de cuadripolos de uno o más de estos cuadripolos elementales.

Si los determinantes de las matrices A y B son iguales a 1 (uno), así lo son también los determinantes de las matrices A×B y B×A.

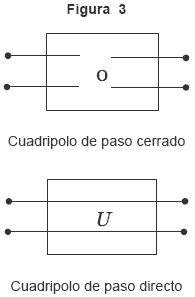
Para lo que sigue es necesario recordar que se llama cuadripolo de paso cerrado al que se muestra a la izquierda (Figura 3): toda señal de entrada no produce señal de salida. Y se llama cuadripolo de paso directo al que se muestra a la derecha (Figura 3): toda señal de entrada pasa como señal de salida, idéntica a sí misma.

Cuadripolos en paralelo

Dados dos cuadripolos Q₁ y Q₂, y sus respectivas matrices de transferencias M₁ y M₂, se demuestra sencillamente que al conectar los dos primeros como se ilustra en el dibujo del cuadro inferior de la Figura 4, la matriz de transferencia del cuadripolo resultante es la suma de las matrices M₁ y M₂ . O sea que la matriz de Q₁ Q₂ , es la matriz M₁+ M₂, en donde Q₁ Q₂ se llama la suma de los dos cuadripolos.

La matriz de transferencia M «calcula» los efectos que el voltaje y la corriente aplicados en el puerto 1 tienen sobre el voltaje y la corriente que aparecen en el puerto 2 de salida, así:

en donde la matriz {m_ij}=M es la matriz de transferencia.

Por ejemplo, en el cuadripolo vecino y usando el teorema de Thévenin (o el de Norton) es evidente que puede escribirse:

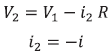
expresiones que se resumen en

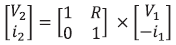
y la matriz de transferencia para este cuadripolo es la matriz cuadrada, no-singular M =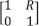

El grupo abeliano de los cuadripolos en paralelo

Dado que el conjunto M de las matrices (del tipo 2 x 2 y de las demás) es -como se sabe- un grupo abeliano respecto a la suma de matrices (Ver Gentile, 1973), se infiere de inmediato que también lo es el conjunto {Q,} de los cuadripolos eléctricos, dotados de la operación de suma eléctrica, ya descrita.

En efecto, tanto {M,+} como {Q,} cumplen las siguiente cinco propiedades, las cuales definen la estructura de grupo abeliano (o grupo conmutativo). Es decir: Tanto la operación + en M como la operación en Q, cumplen las siguientes propiedades:

Las cinco primeras propiedades definen a {M,+} como un grupo (en sentido algebraico) y la sexta le agrega el carácter de grupo conmutativo o abeliano. Y en vista del isomorfismo ya señalado, puede decirse que {Q,} es, también, un grupo abeliano: el grupo de cuadripolos dotado de la operación de composición interna que es la conexión mutua en paralelo. Así que, con una licencia menor de lenguaje, se puede decir que una clase de cuadripolos lineales, pasivos y bilaterales constituye un grupo abeliano respecto a la operación de su conexión en paralelo.

Cuadripolos en serie

Dados dos cuadripolos Q₁ y Q₂, y sus respectivas matrices de transferencia M₁ y M₂, se demuestra mediante consideraciones eléctricas que al conectar los cuadripolos como se ilustra en la figura siguiente, resulta un cuadripolo cuya matriz de transferencia es el producto de las matrices M₁ y M₂ . O sea que la matriz de Q₁ v Q₂ es M₁ × M₂, en donde el símbolo w/ significa la operación de «conexión en serie de cuadripolos», que también, por lo que se verá enseguida, se puede llamar «producto eléctrico de cuadripolos».

En efecto: tanto {M,x} como {Q,} cumplen las seis condiciones necesarias y suficientes para ser, cada uno, un grupo abeliano:

Figura 5

El espacio vectorial de los cuadripolos

Por la definición ya dada de la «suma eléctrica» Q₁ Q₂ de dos cuadripolos, se deduce que un número entero de cuadripolos eléctricos idénticos QQQ...Q=p · Q, con p N (el conjunto de los números naturales), lo cual es equivalente a lo que resulta de enlazar los p cuadripolos en paralelo.

Y que el producto de q cuadripolos idénticos es 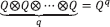, siendo q N

que es lo que resulta de conectarlos a todos ellos en serie. En consecuencia el quadripolo

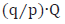
es aquel que resulta de formar q series idénticas con p paralelos cada una, interconectando así pq quadripolos idénticos.

Para las operaciones y w definidas atrás se cumplen las siguientes condiciones que se demuestran fácilmente por consideraciones eléctricas y con ayuda de los diagramas pertinentes de series de paralelos y de paralelos de series, de cuadripolos idénticos.

1. El conjunto {Q} es un grupo abeliano
   Para la ley de composición externa sobre el cuerpo conmutativo K de los números racionales (Ver nota al final del artículo), se cumple que
2. p·(Q₁Q₂ ) = p · Q₁ p · Q₂
3. (p+q)·Q = (p·Q) (q·Q)
4. p·(q·Q) = (p q)·Q
5. 1 · Q = Q

Esto significa que el conjunto {Q} es un espacio vectorial sobre el cuerpo K de los números racionales.

Los dos cuadripolos más sencillos (y no triviales) son los que se ilustran en los dos esquemas vecinos. Sus respectivas matrices de transferencia son:

Figura 6

En ambos casos, las resistencias (R₁ y R₂) pueden estar reemplazadas por impedancias, y las corrientes (i₁, i₂) pueden ser corrientes alternas, debidamente interpretadas.

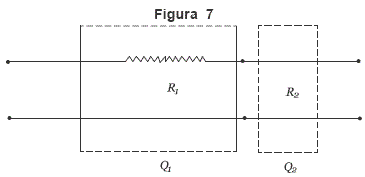
El cuadripolo anexo es equivalente al producto

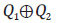
o sea, al conjunto del cuadripolo Q₁ conectado en serie con el cuadripolo Q₂.

En consecuencia, la matriz de transferencia de esta combinación es:

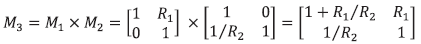
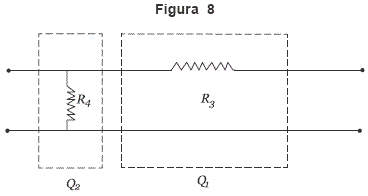
El cuadripolo de la Figura 8 equivale a

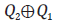
y su matriz de transferencia es

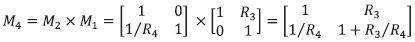
Calculando el inverso de la matriz, siguiendo las reglas usuales del álgebra de matrices, se encuentra que es

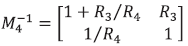
y que esta es la matriz de transferencia de Q₁×Q₂, salvo por los nombres de las resistencias. En general, se puede demostrar que

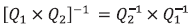
lo cual significa, en términos eléctricos, que si el puerto de entrada de un cuadripolo se convierte en puerto salida y recíprocamente, la nueva matriz de transferencia es el inverso algebraico de la matriz del cuadripolo original.

El anillo algebráico de los cuadripolos

Ya se vio que la clase de cuadripolos {Q} forma un grupo abeliano con la operación de suma () o sea, la conexión en paralelo entre ellos. Para la conexión en serie de cuadrupolos (Q₁Q₂) valen las propiedades:

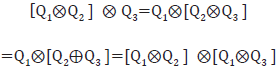
para todo Qi perteneciente a {Q,} Así queda configurado el conjunto {Q,,} con sus operaciones de suma y producto (o paralelo y serie) como un anillo no conmutativo.

De este anillo A se dice que carece de divisores de cero, lo que significa que el producto Q₁Q₂=σ se cumple si y solo si el cuadripolo Q₁ ó el Q₂, o ambos, equivalen al cuadripolo trivial σ = .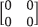

El cuerpo (o campo) de los cuadripolos

Habiendo mostrado que la clase {Q} de los cuadripolos con la conexión en paralelo () forma un grupo conmutativo y que la conexión en serie () forma un anillo sin divisores de cero (0), resulta que {Q,,} es un cuerpo (no conmutativo), que es isomorfo con el cuerpo {M,+,×} de las matrices 2×2.

El álgebra de los cuadripolos

Siendo {Q,,·} un espacio vectorial sobre el cuerpo conmutativo K de los números racionales, se puede calificar a {Q,,,·,K} como una álgebra sobre la clase de los números racionales, porque los cuadripolos y sus conexiones obedecen, evidentemente, las condiciones de que:

- Para toda terna de cuadripolos Q₁,Q₂,Q₃, se tiene que cumple la propiedad distributiva:

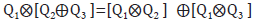
y que

- Para toda pareja Q₁,Q₂ de cuadripolos y para toda pareja p,q de números racionales, se tiene que

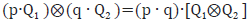
CONCLUSIÓN

Lo que se ha expuesto aquí muestra que las más conocidas estructuras algebraicas abstractas (grupos, anillos y espacios vectoriales) se pueden interpretar mediante sistemas de cuadripolos eléctricos que estén conectados en series o en paralelos que cumplen determinadas condiciones eléctricas que son bien conocidas. En otros trabajos de este mismo autor se presentarán otros ejemplos de estos modelos de estructuras algebraicas.

Nota: Se ha usado la letra K para denotar a la clase de los números racionales, en lugar de la letra Q, que es lo usual en la literatura matemática, debido a que esta última letra se ha elegido aquí para denotar la clase universal de los cuadripolos eléctricos lineales, pasivos y bilaterales, de que se habla en este mismo documento.

REFERENCIAS

Nota: Las ideas y los métodos presentados en este documento no se encuentran expuestos en el sentido ni en la forma como aquí se presentan, en los muchos libros ni en las muchas revistas sobre Circuitos Eléctricos ni sobre Álgebra Abstracta, que el autor ha conocido en muchos años de estudio de ambas materias; y aquéllas formas y métodos son aportes enteramente originales de su propia cosecha. Por lo tanto, la bibliografía que se presenta enseguida no trata de esta temática tal como aquí se expone; pero se la muestra como material didáctico que el lector puede consultar para refrescar o para ampliar sus conocimientos de cada una de las dos disciplinas.

Sobre circuitos eléctricos

Brenner, Egon, D.E.E., and Javid Mansour (1966). Análisis de circuitos eléctricos. New York: McGraw Hill Company Inc. 715 p. Trata muy didácticamente el tema de los cuadripolos en las páginas 545 a 550 y 675 a 681.         [ Links ]

Van Valkenburg, M. E. (1955). Netwok Analysis. Englewood Cliffs, N.J: Prentice Hall, Inc. 440 p. El capítulo 10, en la página 214 trata el tema de los circuitos de varios terminales y las correspondientes funciones de transferencia.         [ Links ]

Newstead, Gordon (1959). General Circuit Theory. London: Methuen and Co. Ltd. 1959. 142 p. Este pequeño y magnífico breviario sobre circuitos eléctricos trata en su capítulo II sobre teoremas generales sobre redes y en su capítulo III sobre redes lineales y pasivas de cuatro terminales, en régimen estacionario.         [ Links ]

Kron, Gabriel (1959). Tensors for Circuits. New York: Dover Publications, Inc. 250 p. El capítulo I presenta muy bien la teoría de las matrices de orden N, aplicada a circuitos eléctricos lineales.         [ Links ]

Ebert, Hermann (ed). Physicalisches taschenbuch. Braunschweig. Friedrich Vieweg & Sohn. En este diccionario manual de Física se encuentra un excelente artículo sobre la Teoría de Circuitos Eléctricos (Elektrischekreisentheorie), para quienes lean idioma alemán.         [ Links ]

Sobre Álgebra Abstracta

Los conocimientos necesarios para asimilar este artículo se pueden obtener rápida y fácilmente en uno o varios de los siguientes libros:

Queysanne, Michel et André Delachet. (1955). L'Algèbre Moderne. París: Presses Universitaires de France. 134 p. Es un pequeño y excelente tratado didáctico de la materia, como para principiantes. Expone con claridad y brevedad qué son las estructuras de «grupo» y las otras de que se trata en este artículo.         [ Links ]

Gentile, Enzo. Estructuras algebráicas I. Washington, D.C. Organización de los Estados Americanos. 1973. 128 p. Trata concisa y pedagógicamente sobre las estructura de «monoide», «grupo» y «anillo»         [ Links ].

Gentile, Enzo (1971). Estructuras algebráicas II. Washington, D.C.: Organización de los Estados Americanos. 160 p. Es continuación del anterior, pero más extenso porque trata sobre espacios vectoriales -de que se trata aquí- y de otras varias estructuras algebráicas -de que no se trata aquí         [ Links ]-.

Lentin, A. y N. Rivaud. (1965). Álgebra Moderna. Madrid: Aguilar S.A. de Ediciones. 485 p. Excelente texto didáctico para un curso completo anual de Álgebra Moderna. El capítulo IV trata sobre la estructura de grupo; el capítulo V versa sobre la estructura de anillo; y el capítulo VII, sobre la estructura de espacio vectorial, que son las estructuras algebraicas que se consideran en este artículo.         [ Links ]