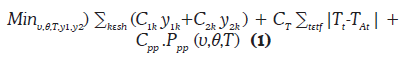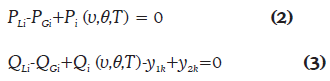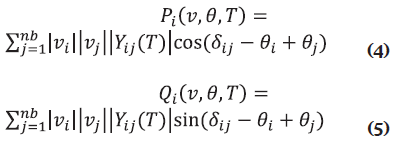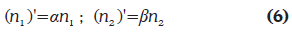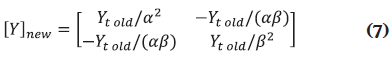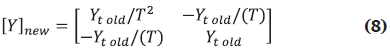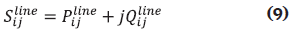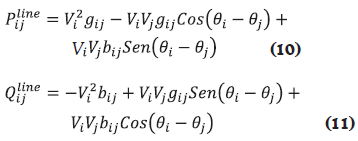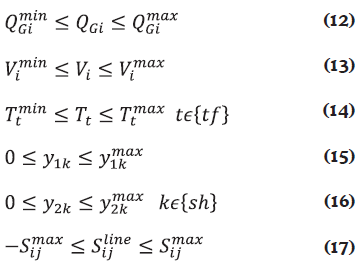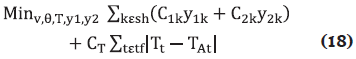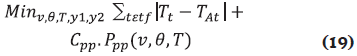Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.21 Envigado Jan./June 2014
COMBINED OPTIMAL TAP SETTING AND REACTIVE POWER INJECTION FOR LOSS REDUCTION IN DISTRIBUTION SYSTEMS
ESQUEMA COMBINADO DE MOVIMIENTO ÓPTIMO DE TAPS E INYECCIÓN DE REACTIVOS PARA REDUCCIÓN DE PÉRDIDAS EN SISTEMAS DE DISTRIBUCIÓN
Mauricio Granada Echeverri*, Ramón Alfonso Gallegego Rendón**, Jesús María López Lezama***
*Ingeniero electricista, PhD. en Ingeniería Eléctrica, profesor del programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira (Colombia).
Autor de correspondencia: Granada-Echeverri, M. (Mauricio). Universidad Tecnológica de Pereira, vereda La Julita, oficina E114, Pereira (Colombia). Teléfono: 314 812 48 15. Correo electrónico: magra@utp.edu.co.
**Ingeniero electricista, PhD. en Ingeniería Eléctrica, profesor del Programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira (Colombia).
***Ingeniero electricista, PhD. en Ingeniería Eléctrica, profesor del Departamento de Ingeniería Eléctrica, Universidad de Antioquia (Colombia).
Artículo recibido: 31-VIII-2013 / Aprobado: 28-III-2014
Disponible online: 30 de junio de 2014
Discusión abierta hasta julio de 2015
ABSTRACT
This paper presents an optimization model for a combined scheme of optimal tap setting and reactive power injection in distribution systems. The proposed model provides the reactive power injection and tap setting scheme that would minimize losses, keeping voltage magnitudes within specified limits, at minimum cost. The formulation is done as an optimal reactive power flow and is solved using commercial available software. Several tests are performed on a 33-bus distribution test system. The results obtained showed that the combined use of tap setting and reactive power injection leads to higher loss reduction than the use of any of these actions separately.
KEY WORDS: Power Loss Reduction; Optimal Reactive Power Flow; Distribution Systems.
RESUMEN
En este artículo se presenta un modelo de optimización para un esquema combinado de movimiento óptimo de taps e inyección óptima de reactivos en sistemas de distribución. El modelo propuesto indica las inyecciones de reactivos y el esquema de posicionamiento taps que minimiza las pérdidas manteniendo las tensiones en los límites permitidos, a mínimo costo. La formulación se realiza mediante un flujo de potencia óptimo reactivo y es solucionado usando un software comercial. Varias pruebas son realizadas en un sistema de distribución de 33 barras. Los resultados muestran que el uso combinado de cambio de taps e inyección de reactivos conducen a una reducción mayor de pérdidas que el uso de estas acciones por separado.
PALABRAS CLAVES: reducción de pérdidas; flujo óptimo de reactivos; sistemas de distribución.
1. INTRODUCTION
Distribution transformers are designed so that the transformation ratio to which they will operate is selected at the time of installation and remains unchanged for a long time. Any subsequent tap change requires de-energizing and opening the transformer for its reconfiguration. This configuration is known as off-circuit tap (Hindmarsh and Renfrew, 2002). Although the tap position is set at the time of the transformer installation, it can be changed later due to a long-term planning that seeks to adapt the system to new and better voltage profiles that have been degraded by load growth and changes in the system. The main objective when changing the tap position of a distribution transformer is the improvement of voltage profile. Voltage control has been identified as one of the most important strategies for efficient and reliable operation of distribution systems (Liu, Cañizares and Huang 2009), (Liang and Wang, 2003), (Spatti, et al., 2010). Recent approaches for voltage control include the modeling of uncertainty (Diwold, et al., 2012), intelligent systems (Puri and Khanna, 2011), (Golkar, 2011) and fuzzy logic (Calderaro, et al., 2011). A review of voltage control techniques in distribution networks can be consulted in Gao and Redfern, 2010. Voltage control has also been the focus of several studies involving the participation of distributed energy resources (Huijuan et al. 2010) and microgrids (Kakigano, et al., 2013). It is well known that improving voltage profile usually brings up as a side effect the reduction of power losses. In this regard, there are several methodologies, reported in the specialized literature, that aim to reduce electric power and energy losses in distribution systems. Such methodologies include feeder reconfiguration (Hsiao, and Chien, 2001), (Farahani et al. 2010) three-phase balancing (Lin et al. 2008a), (Lin et al. 2008b) and the coordination of voltage control devices (Thatte and Ilic, 2006). The strategy of tap setting for loss reduction can be implemented either along, or under a mixed control scheme. The first case is only justified when considering a combined model of loads and a three-phase modeling of the network as shown by Molina, Rodas and Gonzales (2006). On the other hand, a mixed control scheme combining tap setting and reactive power injection can lead to higher loss reduction and does not necessarily require a three-phase modeling of the network. Such scheme is known as an optimal reactive power flow. Several strategies can be used to solve this type of problem. For example, it is possible to use a two-phase strategy in which initially the reactive power injection is used to minimize power losses, and then, the tap setting is used to enforce voltage limits (Bridenbaugh, Dimascio and D'Aquila, 1992). The main disadvantage of this strategy is that the tap setting is being irrelevant from the point of view of loss reduction. Besides, given a certain injection of reactive power, proposed in the first stage, there might be some cases in which the voltage limits cannot be enforced with tap setting, and then, a new reactive power injection must be re-calculated. Another approach of the optimal reactive power flow, involving mixed tap setting and reactive power injection, is the use of metaheuristics (Leeton, Ratniyomchai and Kulworawanichpong, 2010), (Chen, Zhong and Gan, 2006). However, these techniques depend on the tuning of different parameters in order to find high quality solutions. In this paper we present a mixed tap setting and reactive power injection model for loss reduction in distribution systems. The proposed model corresponds to an optimal reactive power flow and is solved in a single stage using the commercial optimization package CONOPT (Drud, 2008) under GAMS (Brooke, et al., 2003). In addition to the minimization of power losses, the model seeks to minimize the number of tap changes and the cost of the reactive power injections. Several tests are carried out using a 33-bus distribution test system. The results show that the adjustment of both, transformer taps and reactive power injections leads to a higher reduction in power losses that each of them separately.
2. MATHEMATICAL MODEL
An optimal reactive power flow is a type of non-linear optimization problem that consists in adjusting a set of control parameters (in this case transformer taps and reactive power injections), in order to improve voltage profile (or enforce voltage limits) and reduce power losses. Considering control variables as continuous, the combined tap setting and reactive power injection model proposed in this paper can be formulated as shown below.
2.1 Objective Function
The proposed objective function shown in Equation (1) is composed of three terms. The first term corresponds to the cost of capacitive and inductive reactive power injections. Note that only a reduced set of buses (named as sh) is enabled for reactive power injection. The second term corresponds to the cost associated with changing the tap to a different position. This cost is set to CT=1. Finally, the third term corresponds to the cost of power losses. It is worth to mention that the main goal of the proposed model is not the reduction of power losses or operational costs alone. Instead, the main goal is to indicate a reactive power injection and tap setting scheme that would allow voltage magnitudes to be within specified limits at minimum cost. Also, having three terms in the objective function does not necessarily mean that the optimal solution implies the reduction of those three terms separately. In fact to minimize power losses it is necessary either to change the tap positions, inject reactive power or both.
In this case C1k and C2k are the costs of capacitive and inductive reactive power injected in bus k, respectively; y1k and y2k are the capacitive and inductive reactive power injected in bus k, respectively; v,θ are the voltage magnitude and angle, respectively; tf is the set of transformers, sh is the set of buses enabled for reactive injection, CT and Cpp are the costs of transformer tap change and peak power, respectively; Ppp represents the power losses at peak demand, TAt is the current tap position of transformer t, and Tt is the tap position of transformer t.
2.2 Equality Constraints
The equality constraints correspond to the power balance equations given by (2) and (3).
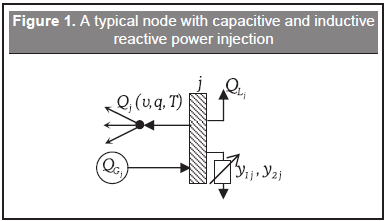
Where PGi and QGi are the active and reactive power generated in bus i, respectively. PLi and QLi are the active and reactive power demand in bus i, respectively. Pi (v,θ,T) and Qi (v,θ,T) are the active and reactive power calculated in bus i, respectively. The reactive power balance equation can be inferred from Figure 1.
Note that the active and reactive power of bus i is a function of voltage magnitude and angle, as well as the position of the transformer taps. The active and reactive power injections in bus i are given by Equations (4) and (5), respectively.
Where θi is the voltage angle at bus i; δij is the angle of bus admittance element i,j. Yij (T) is the magnitude of bus admittance element i,j; if such element is a transformer with variable tap under load, then the admittance is a function of T.
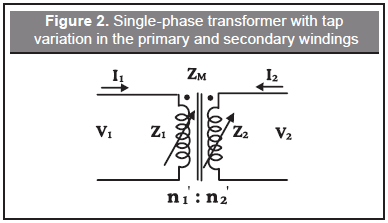
Note that in Equations (4) and (5) it is necessary to account for the impact of tap changes in the admittance matrix (Ybus). For this, the taps have been modeled and introduced in the structure of the Ybus matrix as proposed in Rodas, Restrepo and Molina (2005). Such modeling is provided below. Figure 2 shows the simplified model of transformer taps considering the variation of both, the primary and secondary windings.
The number of turns as a function of the tap position in the primary (α) and secondary (β) can be represented as shown in (6).
The new Ybus matriz can be written as a function of the tap position in the primary and secondary windings as shown in (7).
According to real applications, the transformation ratio can only be modified in the primary winding, which means β=1. Making α=T, the Ybus matrix can be expressed as shown in (8).
The interested reader can refer to (Rodas, Restrepo and Molina, 2005) for further details regarding Ybus matriz.
2.3 Inequality Constraints
For a safe operation of any distribution system, the system operator must make sure that power flows are within specified limits. Apparent power flow in line connecting nodes i,j is represented as Sijline in Equation (9). Such power flow has active and reactive components represented by Pijline and Qijline in Equations (10) and (11), respectively. In this case gij and bij are the real and imaginary components of the element Ybusij, respectively.
The inequality constraints considered in the model are shown in Equations (12)-(17). Such constraints correspond to the limits of reactive power generated, voltage magnitudes, tap settings, capacitive and inductive reactive power injections, and apparent power flow, respectively.
3. TEST AND RESULTS
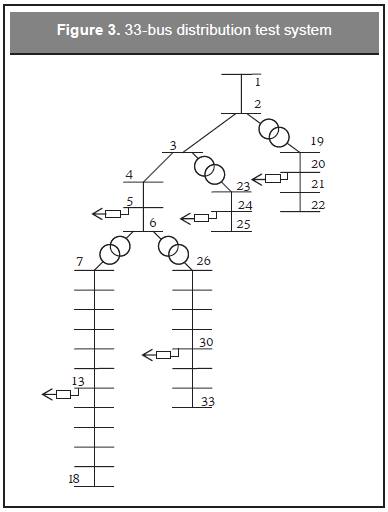
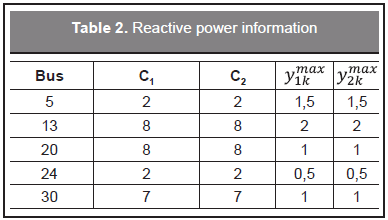
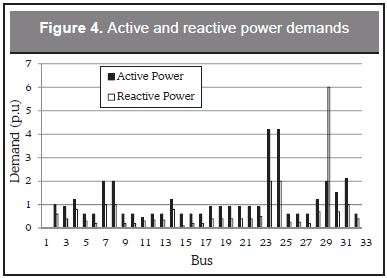
To show the effectiveness of the proposed model, several tests were carried out with the 33-bus distribution system shown in Figure 3. In this case, the slack bus is the substation (bus 1). The system data are presented in Table 1. The buses enabled for reactive injection are sh={13, 20, 24, 30}. It is worth to mention that the criteria to choose the nodes for reactive power injection are selected by the distribution system operator. Compensation can be performed, for example, in the nodes with the lowest voltage values or in those with the highest demand of reactive power. In this case it is considered that local reactive power injections are assumed and coordinated by the distribution system operator alone. Also, we have not assigned cost to the reactive power provided by the substation (reference node). The cost of the capacitive (C1) and reactive power injections (C2), given in generic currency units ($CU), and the maximum capacitive (y1kmax) and reactive (y2kmax) power injections given in p.u. with a Sbase=100 KVA are presented in Table 2. The voltage limits are considered to be between 0.95 and 1.05 p.u. Active and reactive power demand are illustrated in Figure 4. In this case, demands in every node have been considered as constant power injections that do not depend on voltage magnitudes. The total reactive power demand adds 23 p.u., while the maximum reactive power injection provided through the substation was limited to 20 p.u., then the system requires additional reactive injections.
3.1 Case 1: Base Case
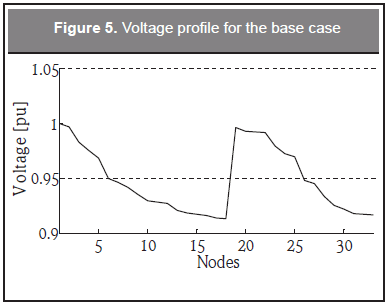
Table 3 shows the active and reactive power losses for the base case without tap setting (T=1) or reactive power injections. Also, voltage limits have not been considered. The voltage profile of the base case can be observed in Figure 5. Note that voltages in nodes located far from the substation are below the specified limits. This is a typical behavior of voltage magnitudes in radial distribution systems. Nodes 1 to 6 and 19 to 26 are within specified limits since they are closer to the substation, while the others present voltages lower than 0.95 p.u. To improve the voltage profile of the base case, and reduce power losses, some actions will be carried out and explained in cases 2 to 4.
3.2 Case 2: Tap Setting and Reactive Power Injections Neglecting Minimization of Power Losses in the Objective Function
In this case we consider the tap setting and reactive power injection with the sole purpose of enforcing voltage limits. Then, the new objective function is as shown in Equation (18). This case corresponds to an improvement of voltage profile at minimum cost.
The active and reactive power losses for this case are provided in Table 4. Note that there is an important reduction in power losses as compared with the base case. This means that the enforcement of voltage limits has as a side effect the reduction of power losses. The value of the objective function in this case is 20.486 currency units.
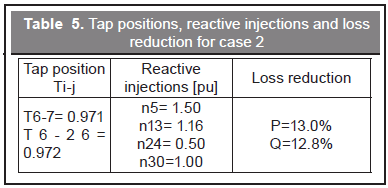
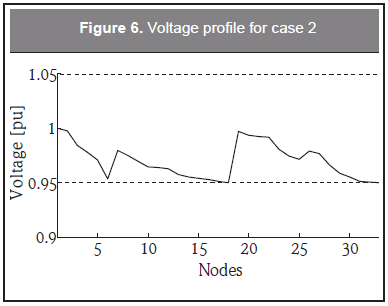
Table 5 shows the tap positions, reactive injection and loss reduction obtained in case 2. Figure 6 depicts the voltage profile for case 2. It can be observed that all voltages are within the specified limits.
3.3 Case 3: Tap Setting Without Local Reactive Power Injections
In this case we analyze the impact of tap setting for loss reduction without local reactive power injections. For the solution to be feasible, the reactive power limit at the substation has been modified to 25 p.u. The objective function considered in this case is shown in Equation (19). Note that we only consider the terms regarding tap setting and power losses.
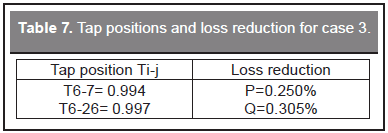
Active and reactive power losses for case 3 are presented in Table 6. The tap settings and loss reduction for this case are provided in Table 7. The value of the objective function in this case is 38.162 currency units. It was found that active and reactive power losses are quite similar to the ones obtained in the base case; in fact, there is only a small reduction of both, as shown in Table 7. Comparing these results with the ones obtained in case 2, it is possible to conclude that local reactive power injection has a greater impact in the reduction of power losses than the tap setting alone.
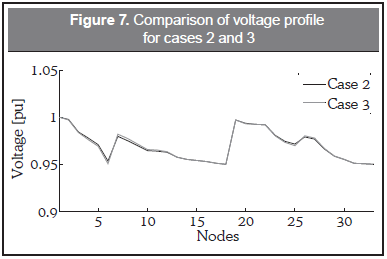
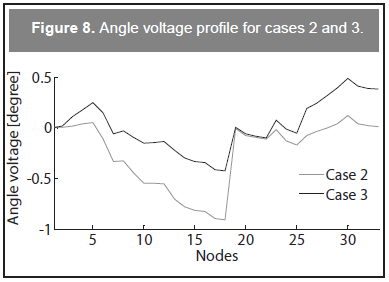
Regarding voltage profiles, Figure 7 depicts voltage magnitudes of case 2 and 3. It can be observed that both are quite similar. This fact indicates that local reactive power injection and tap setting have almost the same effect in voltage magnitudes. On the other hand, tap setting has a major impact on voltage angles, rather than in voltage magnitudes, as can be observed in Figure 8. Note that voltage angle profiles for cases 2 and 3 are quite different. The difference in voltage angles results in different power losses as was shown before.
3.4 Case 4: Mixed Tap Setting and Reactive Power Injection for Loss Reduction
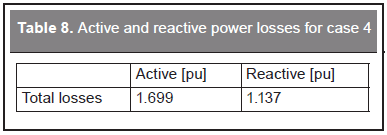
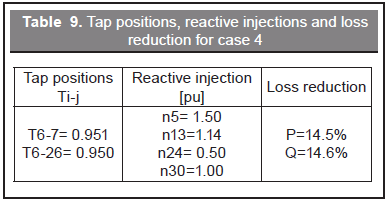
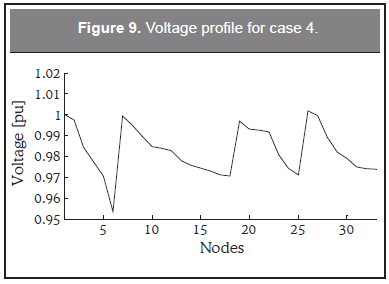
In this case we have considered the mixed operation of tap setting and reactive power injection as originally proposed in this paper. Table 8 shows the active and reactive power losses and Table 9 shows the tap positions, reactive power injections and loss reductions. It can be observed that the combined action of tap setting and reactive power injections led to a higher reduction of power losses than any of these actions performed separately. The value of the objective function in this case is 20.2980 currency units, which is slightly lower than the one obtained with the mixed strategy without considering power losses (case 2). The transformers are the same involved in case 2 but with a different tap setting. Also, the mixed strategy provided in this case results in the best voltage profile as shown in Figure 9.
4. CONCLUSIONS
This paper presented an optimization model for a combined tap setting and reactive power injection in distribution systems. The objective function consists in minimizing power losses, tap changes and the cost of reactive power injections. Several tests were performed with a 33-bus distribution system considering independent and joint strategies. It was found that the tap setting along can be used to enforce voltage limits; however, the reduction of power losses obtained with this strategy is the smallest as compared with the other cases studied.
The best results in terms of loss reduction, costs and voltage profile were obtained using the mixed tap setting and reactive power injection strategy.
Further work will include the modeling of distributed generation in the network, and its impact in voltage control and power losses.
REFERENCES
Bridenbaugh, C.J.; Dimascio, D.A and D'Aquila, R. (1992). Voltage Control Improvement through Capacitor and Transformer Tap Optimization. IEEE Transactions on Power Systems, 7(1), pp. 222-227. [ Links ]
Brooke, A.; Kendrick, D.; Meeraus, A. and Raman, R. (2003). GAMS/CPLEX: a user's guide. Whasington, DC. [ Links ]
Calderaro, V.; Galdi, V.; Piccolo, A. and Massa, G. (2011). Optimal Fuzzy Controller for Voltaje Control in Distribution Systems, 11th International Conference on Intelligent Systems Design and Applications (ISDA), Córdoba, Spain. November 2011, pp 1282-1287. [ Links ]
Chen L; Zhong J. and Gan, D. (2006). Reactive Power Flow Planning and its Cost Allocation for Distribution Systems with Distributed Generation. IEEE Power Engineering Society General Meeting, pp. 1-6. [ Links ]
Diwold K., Yan W; Garcia, A.; Mocnik, L. and Braun, M. (2012). Coordinated Voltage Control in Distribution Systems under Uncertainty, 47th International Universities Power Engineering Conference (UPEC), London, September 2012. pp- 1-6. [ Links ]
Drud, A. (2008). CONOPT user's guide. Bagsvaerd Denmark: ARKI Consulting and Development. [ Links ]
Farahani, V.; Sadeghi, S. H. H; Aslarian, H. and Mazluni K. (2010). An Improved Reconfiguration Method for Maximum Loss Reduction Using Discrete Genetic Algorithm, 4th Power Engineering and Optimization Conference. Selangor, Malaysia. June, 2010. pp. 178-183. [ Links ]
Gao, C. and Redfern, M. A. (2010). A Review of Voltage Control Techniques of Networks with Distributed Generators Using on-load Tap Changer Transformers. 45th International Universities Power Engineering Conference (UPEC). Cardiff, Wales, UK. September 2010, pp. 1-6. [ Links ]
Golkar, M. A. (2011). Reactive Power Control in Distribution Systems Using Advanced Techniques. 3th International Youth Conference on Energetics (IYCE). Budapest, Hungary. July, 2011. pp. 1-6. [ Links ]
Hindmarsh, J. and Renfrew, A. Electrical Machines and Drives. Oxford: Elsevier Science, 2002. pp. 185-222. [ Links ]
Hsiao, T. Y. and Chien, C. H. (2001). Multiobjective Optimal Feeder Reconfiguration. IEE Generation Transmission and Distribution, 148(4), August, pp. 333-336. [ Links ]
Huijuan, L.; Fangxing, L.; Yan, X.; Rizy, D. T. and Kueck, J. D. (2010). Adaptive Voltage Control with Distributed Energy Resoruses: Algorithm Theoretical Analysis, Simulation and Field Test Verification. IEEE Transactions on Power Systems, 25(3) pp. 1638-1647. [ Links ]
Kakigano, H.; Miura, Y. and Ise, T. (2013). Distribution Voltage Control for DC Microgrids Using Fuzzy Control and Gain-Scheduling Technique. IEEE Transactions on Power Systems, 28(5), pp. 2246-2258. [ Links ]
Leeton, U.; Ratniyomchai, T. and Kulworawanichpong, T. (2010). Optimal Reactive Power Flow with Distributed Generation Plants in Electric Power Distribution Systems. International Conference on Advances in Energy Engineering. Beijing, China. June 2010, pp. 166-169. [ Links ]
Liang, R. H. and Wang , Y. S. (2003). Fuzzy-Based Reactive Power and Voltage Control in a Distribution Systems. IEEE Transactions on Power Delivery, 18(2), February, pp. 610-618. [ Links ]
Lin, C. H.; Chen, C. S; Chuang, H, J.; Huang, M. Y. and Huang, C. W. (2008a). An Expert System for Three-Phase Balancing of Distribution Feeders. IEEE Transactions on Power Systems, 23(3), pp. 1488-1496. [ Links ]
Lin, C. H.; Chen, C. S; Kang M. S; Chuang, H. J. and Huang C. W. (2008b). Three-Phase Balancing of Distribution Feeders Using Immune Algorithm. IET Generation Transmission and Distribution, 2(3), pp. 383-392. [ Links ]
Liu, M. B., Cañizares C. A., and Huang, W. (2009). Reactive Power and Voltage Control in Distribution Systems with Limited Switching Operations. IEEE Transactions on Power Systems, 24(2), May, pp. 889-899. [ Links ]
Molina, A.; Rodas, J. E. and Gonzales, D. (2006). Operación de taps en transformadores de distribución para reducción de pérdidas. Scientia Et Technica, 30(1), pp. 111-116. [ Links ]
Puri, S. and Khann, R. (2011). Intelligent Control for a Radial Distribution System with Distributed Generation. International conference on Energy, Automation and Signal (ICEAS), Bhubaneswar, India. December 2011, pp. 1-6. [ Links ]
Rodas, D.; Restrepo, Y. and Molina, A. (2005). Transformador monofásico de distribución y de potencia, modelamiento con taps. Scientia Et Technica, 11(29), pp. 13-18. [ Links ]
Spatti, D. H.; Da Silva, I. N.; Usida, W. F. and Flauzino, R. A. (2010). Real-Time Voltage Regulation in Power Distribution System Using Fuzzy Control. IEEE Transactions on Power Delivery, 25(2), April, pp. 1112-1123. [ Links ]
Thatte, A. A. and Ilic, M. D. (2006). An Assessment of Reactive Power/Voltage Control Devices in Distribution Networks. IEEE Power Engineering Society General Meeting. Montreal, Quebec. June, 2006. pp. 1-6. [ Links ]