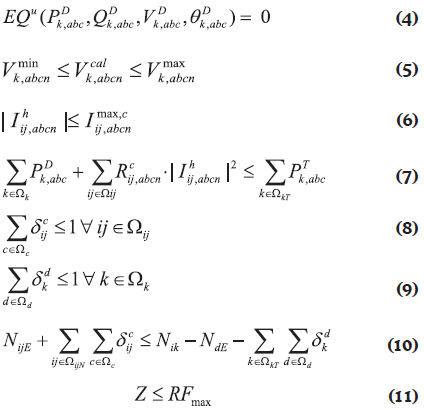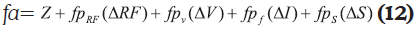Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.21 Envigado Jan./June 2014
ALGORITMO DE BÚSQUEDA TABÚ ESPECIALIZADO APLICADO AL DISEÑO DE REDES SECUNDARIAS DE ENERGÍA ELÉCTRICA
SPECIALIZED TABU SEARCH ALGORITHM APPLIED TO SECONDARY DISTRIBUTION SYSTEMS PLANNING
ALGORITMO DE PESQUISA TABU ESPECIALIZADO APLICADO NO DESENHO DE REDES SECUNDÁRIAS DE ENERGIA ELÉTRICA
Víctor Mario Vélez Marín*, Ricardo Alberto Hincapié Isaza**, Ramón Alfonso Gallego Rendón***
*Ingeniero electricista, Universidad Tecnológica de Pereira. Docente Catedrático programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Pereira (Colombia).
Autor de correspondencia: Vélez-Marín, V.M. (Víctor Mario). Universidad Tecnológica de Pereira. Carrera 27 #10-02 Barrio Álamos - Pereira (Colombia) / Tel: (576) 313 73 00. Correo electrónico: victorvelez@utp.edu.co.
**Magíster en Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Profesor Asistente programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Pereira (Colombia).
***Doctor en Ingeniería Eléctrica, Universidad de Campinas, Brasil. Profesor Titular programa de Ingeniería Eléctrica, Universidad Tecnológica de Pereira. Pereira (Colombia).
Artículo recibido: 24-IX-2013 / Aprobado: 17-III-2014
Disponible online: 30 de junio de 2014
Discusión abierta hasta julio de 2015
RESUMEN
En este artículo se presenta una metodología para solucionar el problema del planeamiento de sistemas de distribución secundarios empleando como técnica de solución el algoritmo de Búsqueda Tabú. El problema se formula como un modelo no lineal entero-mixto, en el cual se tienen en cuenta la ubicación y capacidad de nuevos elementos (transformadores de distribución y tramos de red primaria y secundaria), reubicación de transformadores de distribución existentes, aumento de capacidades de elementos existentes, reconfiguración de red secundaria y balance de fases. Adicionalmente, se consideran los costos asociados a la conexión entre red primaria y secundaria y las pérdidas de energía en transformadores. Se emplean dos casos de prueba; en el primero se realizan ensayos comparativos con el algoritmo genético de Chu-Beasley para verificar la eficiencia del método propuesto y, en el segundo, se analizan los resultados obtenidos en un sistema de distribución colombiano. En ambos casos los resultados obtenidos son de gran calidad, lo que respalda lo propuesto en este trabajo.
PALABRAS CLAVE: Búsqueda Tabú; optimización combinatorial; planeamiento de sistemas eléctricos; redes secundarias.
ABSTRACT
To solve the problem of secondary distribution systems planning, this paper proposes a methodology using a tabu search algorithm as a solution technique. The problem is formulated as a nonlinear mixed-integer model, which takes into account the location and capacity of new elements (distribution transformers and primary-secondary distribution networks), relocation of existing distribution transformers, increasing the capacity of existing elements, secondary network reconfiguration, and phase balance. It also considers the costs associated with connections between primary and secondary networks and energy losses in distribution transformers. The methodology is applied to two test cases: in the first, a comparative analysis with the Chu-Beasley genetic algorithm is made to verify the efficiency of the proposed methodology; and in the second, the results are analyzed in a Colombian distribution system. In both cases, the results are of high quality, supporting the proposed methodology.
KEY WORDS: Tabu Search; Combinatorial Optimization; Electrical Systems Planning; Secondary Networks.
RESUMO
Neste artigo apresenta-se uma metodologia para solucionar o problema do planejamento de sistemas de distribuição secundários, empregando como técnica de solução o algoritmo de pesquisa tabu. O problema formula-se como um modelo não lineal enteiro-mixto, no qual se tem em conta a localização e capacidade de novos elementos (transformadores de distribuição e tramos de rede primária e secundária), relocalização de transformadores de distribuição existentes, aumento de capacidade de elementos existentes, reconfiguração de rede secundária e balanço de fases. Ademais consideram-se os custos associados à conexão entre rede primária e secundária e as perda de energia em transformadores. Empregam-se dois casos de prova, no primeiro realizam-se ensaios comparativos com o algoritmo genético de Chi-Beasley para verificar a eficiência do método proposto, e no segundo analisam-se os resultados obtidos no sistema de distribuição colombiano. Nos ambos casos os resultados obtidos são de grande qualidade, o que apoia o que foi proposto neste trabalho.
PALAVRAS-CHAVE: Pesquisa tabu; Optimização combinatória; Planejamento de sistemas eléctricos; Redes secundárias.
1. INTRODUCCIÓN
El planeamiento de sistemas secundarios de distribución de energía eléctrica (PSSDE) considera la elaboración de planes de expansión en zonas donde se presenta crecimiento de la demanda existente y aparición de nuevas cargas. Cuando se diseñan estos planes surgen diversas alternativas dependiendo de las necesidades de cada electrificadora y las condiciones impuestas por el ente regulador. La solución más adecuada a las necesidades planteadas debe considerar un equilibrio técnico-económico que maximice los beneficios para la empresa y minimice los costos del proyecto. Encontrar dicha solución requiere de técnicas de modelado y solución que permitan optimizar el problema planteado.
En la literatura se consideran diversos métodos que incluyen el modelo matemático que describe el PSSDE, la técnica de solución y el modelo de los elementos del sistema. Algunos trabajos, para describir el problema, emplean: un modelo no lineal (Díaz-Dorado, Míguez y Cidras, 2001; Díaz-Dorado, Pidre y Míguez, 2003; Navarro y Rudnick, 2009), un modelo no lineal entero mixto (Costa y França, 2002; Cossi, Romero y Sánchez, 2005; Souza, 2006; Marroquín, 2008; González, Gallego e Hincapié, 2009; Cossi, Romero y Sánchez, 2009; Londoño, Hincapié y Gallego, 2011) y un modelo lineal entero mixto (García, et al., 2003; Tapias, Galeano e Hincapié, 2011).
Para solucionar el problema algunos trabajos han propuesto técnicas heurísticas (Da Silva, França y Da Silveira, 1996; Costa y França, 2002; Gilvanejad et al., 2007). Díaz-Dorado et al. (2001) presentan una metodología basada en programación dinámica para solucionar el problema. Díaz-Dorado, et al. (2003) y Cossi, et al. (2005) plantean un algoritmo evolutivo especializado. García, et al. (2003) resuelven el problema empleando un algoritmo Greedy Randomized Adaptive Search Procedures (GRASP). Souza (2006) usa un algoritmo de Búsqueda Tabú. Marroquín (2008) emplea un algoritmo de optimización por Colonia de Hormigas. Cossi, et al. (2009) solucionan el problema por medio de un algoritmo de Búsqueda Tabú. En el mismo año, Navarro y Rudnick (2009) emplean una metodología híbrida que considera técnicas heurísticas y un algoritmo de Búsqueda Tabú. Tapias et al. (2011) utilizan un algoritmo Branch and Bound y Londoño, et al. (2011) proponen un algoritmo genético de Chu-Beasley. Por otro lado, los elementos del sistema se han modelado por su equivalente monofásico (Costa y França, 2002; Tapias, Galeano e Hincapié, 2011), y otros han empleado modelos trifásicos (Cossi, 2003; Souza, 2006; Marroquín, 2008; González, Gallego e Hincapié, 2009; Londoño, Hincapié y Gallego, 2011).
Tradicionalmente en la solución del PSSDE se han considerado la ubicación y dimensionamiento de elementos nuevos, ampliación de existentes, balance de fases, y costos de pérdidas de energía en tramos de red. Adicional a estos aspectos, en este trabajo se considera la reubicación de transformadores de distribución que se encuentran en operación y en bodega, los costos asociados a pérdidas de energía en transformadores de distribución y los costos de conexión entre red primaria y secundaria. Para solucionar el problema se presenta en este trabajo el desarrollo e implementación de una metodología que emplea como técnica de solución el algoritmo de Búsqueda Tabú (ABT), con la cual es posible determinar en forma óptima los elementos que conforman la red de distribución de energía eléctrica cumpliendo las necesidades en demanda y criterios técnicos. Esta configuración considera el número de circuitos secundarios necesarios para suplir dicha demanda, la ubicación y capacidad adecuada de transformadores de distribución, la topología de la red secundaria y primaria, el tipo de conductores y la conexión de los usuarios a la red, cumpliendo un conjunto de restricciones técnicas, operativas y económicas. El método propuesto es aplicado en dos casos de prueba. En el primero se verifica su eficiencia realizando un análisis comparativo con los resultados obtenidos al resolver el problema con un algoritmo genético de Chu-Beasley (Chu y Beasley, 1997). En el segundo caso se ilustra su aplicación a un sistema de distribución colombiano.
El artículo es presentado de la siguiente forma: en la sección 2 se presenta la descripción y formulación del problema. En la siguiente sección se describe el método propuesto, que incluye la técnica de solución, codificación del problema, construcción de la configuración inicial, evaluación de las configuraciones, estructura de vecindad, criterio de parada y adaptación de la técnica de solución al problema. En la sección 4 se presenta la aplicación del método propuesto en dos casos de prueba. Finalmente en la sección 5 se ilustran las conclusiones derivadas de este proyecto.
2. DESCRIPCIÓN Y FORMULACIÓN DEL PROBLEMA
El PSSDEconsidera la elaboración de planes de expansión de redes secundarias para aquellas zonas donde se presenta crecimiento de la demanda existente y aparición de nuevas demandas. El objetivo principal es encontrar un diseño de la red que garantice el menor costo del proyecto, cumpliendo con exigencias técnicas, regulatorias y operativas.
Un mal planeamiento de estos sistemas puede ocasionar sobrecargas en circuitos secundarios y transformadores de distribución, problemas de regulación, desbalance de carga en las fases, incremento de pérdidas técnicas del sistema, pérdida de confiabilidad, calidad y continuidad, sobredimensionamiento de elementos y sobrecostos en los proyectos.
Para evitar estos problemas se considera un planeamiento que involucra los siguientes aspectos: ubicación y capacidad de nuevos tramos de red secundarios y transformadores de distribución, redimensionamiento de tramos de red secundarios y transformadores de distribución existentes, reubicación de transformadores de distribución que se encuentran en operación y en bodega, balance de cargas del sistema y nuevos tramos de red primaria para alimentar la red secundaria. La red se modela de forma trifásica, en la cual pueden existir cargas monofásicas, bifásicas y trifásicas (Kersting, 2007).
El problema se formula como un modelo de programación no lineal entero mixto. La función objetivo del sistema tiene en cuenta los costos fijos asociados a la inversión inicial y los costos operativos asociados a las pérdidas de energía a lo largo del horizonte de planeamiento (Ecuación 1). Los dos primeros términos representan costos de desinstalación de tramos de red existentes e instalación de nuevos tramos de red, respectivamente. El tercer término es el costo de las pérdidas de energía para todos los tramos de red. El siguiente término corresponde al costo de desinstalar un transformador existente más el costo del transporte del sitio de operación a la bodega. El quinto término es el costo de instalación de transformadores nuevos. El siguiente término garantiza que no se tenga en cuenta el costo de un transformador que ha sido previamente desinstalado y se encuentra en bodega. En el séptimo término se presenta el costo de las pérdidas de energía de los transformadores de distribución, asociados a las pérdidas en vacío y bajo carga. El siguiente término representa el costo de la operación de balance de cargas. El último término lleva en cuenta el costo de la red primaria que alimenta los transformadores. La nomenclatura empleada se presenta al final del documento.
En esta ecuación el término fact expresa en valor presente los costos operativos durante el periodo de vida útil de los elementos y está definido en la Ecuación 2. Este cálculo se realiza debido al crecimiento del costo de la energía, lo que ocasiona valores operativos diferentes en cada periodo. El término fanual lleva los costos de instalación y operación a anualidades (Ecuación 3). Los parámetros λcij, λdk y λbbk están asociados a elementos existentes como tramos de red secundarios, transformadores de distribución y cargas, respectivamente. En otras palabras, estos valores son dados por la red existente, si el elemento existe el parámetro vale 1; en caso contrario vale cero. A partir de la relación de estos parámetros con las variables binarias de decisión δcij, δdk y δbbk, se pueden considerar los diferentes costos de los términos involucrados. Por ejemplo, si en la línea ij existe un conductor tipo 1, entonces λ1ij=1; si la variable de decisión propone instalar un conductor tipo 1 (δ1ij=1), entonces en la función objetivo se anula el término correspondiente a la desinstalación de este tramo de red y al costo del tramo nuevo.
El conjunto de restricciones del modelo matemático se presenta a continuación en las Ecuaciones 4 a 11. La Ecuación 4 representa las ecuaciones de balance nodal para todo el sistema. La Ecuación 5 garantiza que los niveles de tensión permanezcan dentro de los límites permitidos. Las Ecuaciones 6 y 7 consideran los límites de operación de corriente y potencia en tramos de red y transformadores, respectivamente. Las Ecuaciones 8 y 9 garantizan que solamente se instale un calibre de conductor en cada tramo de red propuesto y un tipo de transformador en cada nodo propuesto, respectivamente. Las dos últimas ecuaciones están asociadas a la operación radial de la red y el límite máximo de inversión que se puede considerar en el proyecto, respectivamente.
3. METODOLOGÍA
3.1. TÉCNICA DE SOLUCIÓN
El problema del PSSDE se formula como un modelo de programación no lineal entero mixto, el cual posee una alta complejidad matemática del tipo NP completo, debido al elevado número de soluciones. En este trabajo se emplea el algoritmo de Búsqueda Tabú, debido a que se desempeña bien frente a problemas con las características mencionadas (Glover, 1995; Gallego, Escobar y Toro, 2008).
Este algoritmo considera una solución a la vez, por lo que requiere iniciar el proceso de búsqueda a partir de una configuración; para su determinación se emplean técnicas heurísticas, algoritmos constructivos y técnicas basadas en sensibilidad. El ABT realiza transiciones a través del espacio de búsqueda, usando estrategias de intensificación con el fin de explorar de forma eficiente el espacio alrededor de una configuración x, el cual es llamado vecindario (N(x)), y además emplea estrategias de diversificación para explorar otros vecindarios.
Con la estructura de vecindad definida, la búsqueda local permite pasar a la mejor configuración vecina. En el caso en que la configuración actual sea la mejor, se pasa a la configuración que no cumpla con el criterio de aspiración o que no sea tabú, donde se aplica nuevamente búsqueda local sobre la nueva configuración. Esta estrategia evita configuraciones ya visitadas para lograr salir de óptimos locales, lo cual se logra almacenando información del pasado reciente en memorias de corto plazo (atributos). Al pasar a una nueva configuración, el atributo aceptado en el paso anterior es prohibido durante un cierto número de iteraciones en una lista llamada tabú. Durante el proceso las mejores soluciones son almacenadas en una memoria de soluciones élite (o incumbentes).
Luego de que la etapa de búsqueda local no encuentra buenas soluciones después de un cierto número de iteraciones, se reinicia el proceso tomando una solución de alta calidad previamente almacenada. Como criterio de diversidad se usa la memoria de largo plazo para generar una nueva configuración. Una vez se parte desde otra configuración, se aplica nuevamente el proceso de búsqueda local. Si aplicando este proceso de forma cíclica no se encuentran mejores soluciones después de cierto número de iteraciones, se pueden aplicar estrategias avanzadas como oscilación estratégica o path-relinking (Glover, 1995).
3.2. CODIFICACIÓN
Se utiliza un vector de variables binarias y enteras, el cual está dividido en tres partes, como se muestra en la Figura 1. La primera contiene información de la ubicación y el calibre de los tramos de red (Figura 1a); la segunda involucra la ubicación y la capacidad de los transformadores de distribución (Figura 1b) y la última muestra la codificación para el balance de cargas (Figura 1c).
Todos los tramos de red y transformadores de distribución tienen asociados una posición en el vector, donde cada posición representa una capacidad por medio de un valor binario (Figura 1a y 1b). Por ejemplo, si se consideran tres capacidades de conductores (tipos), entonces cada tramo de red propuesto tendrá asociada tres posiciones en el vector. Si una de estas posiciones tiene un uno, entonces en dicho tramo de red se instala el conductor con la capacidad asociada a esa posición; si tiene un cero, ocurre lo contrario. En un tramo de red propuesto todas las posiciones pueden tener las tres variables en cero, lo que indica que no se instalará un conductor en dicho tramo. De manera similar sucede para los transformadores de distribución. Adicionalmente, con el cumplimiento de las Ecuaciones 8 y 9, se garantiza que no se instale más de un tipo de conductor en un tramo de red o más de un transformador en un nodo.
Las cargas nodales son representadas por números enteros, donde los números 1, 2 y 3 están asociados a las fases a, b y c, respectivamente. Como se observa en la Figura 1c, cada nodo tiene asociado el orden de conexión de sus cargas al sistema. Nótese que una configuración (topología del sistema) puede ser descrita completamente a partir de la información contenida en un vector, lo cual permite una mejor adaptación de la técnica de solución al problema tratado.
3.3. CONFIGURACIÓN INICIAL
La configuración inicial se obtiene con un algoritmo heurístico constructivo propuesto por Cossi (2008). En este algoritmo se construye una configuración radial a partir de la selección de un transformador de distribución. Cada vez que se adiciona un tramo de red se verifican límites de capacidad de carga, por lo que en cada paso se corre un flujo de carga para verificar estas condiciones. Una vez se ingresan todos los nodos de carga, se calcula la ruta de los tramos de red primaria para alimentar los transformadores de distribución. Luego se realiza una etapa de balance de las cargas, con el fin de mejorar la capacidad de carga de los elementos y costos operativos de la red.
3.4. EVALUACIÓN DE LAS CONFIGURACIONES
Con el fin de evaluar la función objetivo y verificar la factibilidad de una solución, se emplea un flujo de carga radial trifásico (Garcés, Granada y Gallego, 2004). Si una solución viola alguna de las restricciones del modelo matemático presentado en la sección 2, esta configuración es penalizada en la función objetivo. Esta estrategia permite que el proceso oscile entre la región factible y no factible, permitiendo llegar a regiones de mejor calidad (Gallego, Escobar y Toro, 2008). A continuación se presenta en la Ecuación 12 la función de adaptación empleada, la cual consiste en la suma de la función objetivo presentada en la Ecuación 1 más los factores de penalización.
Los factores fpRF, fpV, fpf y fpS están asociados a las penalizaciones por violación de la restricción financiera, límites de tensión y sobrecargas en tramos de red y transformadores, respectivamente. Estos factores multiplican el valor en el cual fue violada cada restricción (Δ). Si una restricción no es violada, los deltas son iguales a cero. Las unidades de estos factores garantizan que cada término quede expresado en unidades monetarias.
3.5. ESTRUCTURA DE VECINDAD
Para pasar de una configuración a otra (vecino), es necesario definir los criterios de vecindad que permiten este cambio. Cada criterio de vecindad está asociado a la solución de una característica del problema tratado. Como se indica en la sección 3.2, cada vector define una configuración. De acuerdo a esto, cualquier cambio realizado sobre el vector modifica la topología del sistema. Por lo tanto, para determinar un vecino, basta con realizar cambios al vector asociado a la configuración actual. Evaluar la gran cantidad de vecinos que tiene una configuración puede ocasionar tiempos excesivos de cómputo, por lo que es aconsejable trabajar con un número reducido. Para seleccionar un vecino a partir de la configuración actual, se selecciona aleatoriamente alguno de los criterios de vecindad empleados. Este proceso se repite hasta que se alcanza el número predefinido para el tamaño del vecindario reducido. En la solución de este problema fueron considerados cinco criterios, los cuales son presentados a continuación:
- Reconfiguración del sistema. Se intercambian de estado un tramo de red desconectado y uno conectado que hagan parte del mismo lazo, de tal manera que se garantice radialidad en la red.
- Reconductorización. Se selecciona el tramo de red que presente mayor sobrecarga y se cambia por un conductor de mayor calibre. Al aplicar este criterio se debe garantizar que los tramos de red aguas arriba no presenten un calibre inferior.
- Reubicación de transformadores. Se selecciona aleatoriamente un transformador y se reubica en un nodo vecino, utilizando el método de los momentos eléctricos (Ramírez, 2004).
- Balance de cargas. Se calcula el porcentaje de desequilibrio en todos los circuitos del sistema y se selecciona el de mayor valor. Posteriormente al circuito seleccionado se le aplica un algoritmo genético para balancear las cargas.
- Cambio de transformadores sobrecargados. Se identifican transformadores sobrecargados y se selecciona el de mayor índice para cambiarlo por uno que no viole su capacidad nominal.
3.6. CRITERIO DE PARADA
En la aplicación del ABT se emplean dos procesos de búsqueda: uno local y otro global. La búsqueda local se detiene después de un número de iteraciones, ya sea sin mejorar la incumbente local o si se alcanza un número máximo de iteraciones predefinido. La búsqueda global termina cuando toda la lista de soluciones élite ha sido examinada.
3.7. ADAPTACIÓN DEL ABT AL PSSDE
Inicialmente se genera una solución inicial de acuerdo al numeral 3.3, la cual está descrita por un vector con la estructura presentada en el numeral 3.2. Con esta información se ejecuta el flujo de carga para determinar las condiciones operativas del sistema propuesto. A partir de los resultados del flujo de carga se verifica el cumplimiento de las restricciones del sistema o factibilidad de la propuesta (Ecuaciones 4 a 11). Estos valores en conjunto con el vector codificación (configuración propuesta) permiten evaluar la función de adaptación descrita en la Ecuación 12. Como la solución inicial siempre es factible, evaluar esta ecuación es similar a calcular la función objetivo de la Ecuación 1; esta configuración es almacenada como la incumbente del proceso (solución con mejor función objetivo encontrada hasta el momento). En este momento se inicializa la Lista Tabú (memoria de corto plazo), la cual es cero por ser la primera iteración. Seguidamente se genera el vecindario reducido a partir de los criterios especificados en el numeral 3.5, se encuentran las condiciones operativas de cada uno de los vecinos con el flujo de carga y se evalúan aplicando la Ecuación 12 con los aspectos descritos en el numeral 3.4. De este conjunto se selecciona el mejor vecino teniendo en cuenta los atributos tabú y el criterio de aspiración, se actualiza la incumbente y la Lista Tabú. Posteriormente se regresa a la generación del vecindario reducido, se repite el proceso hasta que se cumpla un criterio de parada y se actualiza la lista élite con la mejor configuración encontrada. Estos pasos hacen parte del proceso de búsqueda local. Si se cumple el criterio de parada de la búsqueda local, se reinicia el proceso a partir de una nueva configuración, teniendo en cuenta la memoria de corto plazo con el fin de explorar otros lugares del espacio de solución. Esta secuencia hace parte de la búsqueda global. El proceso termina cuando se cumple el criterio de parada de la búsqueda global, donde la solución del problema de PSSDE es la mejor solución de la lista élite. En la Figura 2, se muestra el diagrama de flujo de la metodología propuesta.
4. RESULTADOS
La metodología propuesta en este trabajo se aplica a dos casos de prueba. En el primero se realiza un análisis comparativo entre los resultados obtenidos con el ABT y un algoritmo genético de Chu-Beasley (Chu y Beasley, 1997). En el segundo se presenta su aplicación a un sistema de distribución colombiano. El método es implementado y aplicado en Matlab. Los datos de conductores y transformadores de distribución usados para ambos sistemas se ilustran en la Tabla 1.
4.1. CASO 1
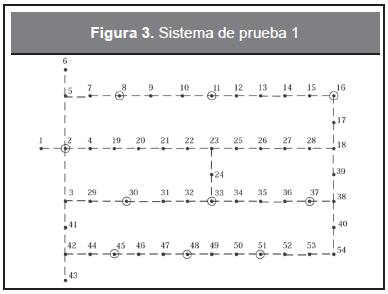
En este caso se emplea un sistema de distribución sin elementos existentes (Figura 3). La red se modela de forma trifásica. El factor de potencia de la carga es 0,9. La carga se modela como impedancia constante en un 80 % y como potencia constante en un 20 %. El periodo de vida útil de los elementos es 20 años y la tasa de descuento es 10 %. Las líneas discontinuas corresponden a nuevos tramos de red y los nodos propuestos para ubicar transformadores son 2, 8, 11, 16, 30, 33, 37, 45, 48 y 51. El voltaje nominal línea-neutro del sistema es 127 V y la regulación permitida es 5 %. El costo del kWh es US$0,16. Los datos de las cargas y los tramos de red se presentan en la Tabla 2 y la Tabla 3, respectivamente.
Para el algoritmo genético de Chu-Beasley (AGCB) se emplea una tasa de recombinación de 0,9 y de mutación de 0,05. El tamaño de la población es de 100 individuos. El número máximo de iteraciones es 100. En el ABT se emplean los siguientes factores de penalización: 1,5 en la restricción financiera, 150 y 100 para voltajes y sobrecargas en tramos de red, y 1000 para voltajes y sobrecargas en transformadores: estos valores son el resultado de realizar diversas pruebas. Se emplean dos criterios de parada para la búsqueda local: 10 iteraciones sin mejorar la incumbente y un número máximo de iteraciones igual a 40. Los valores de parametrización empleados para ambos métodos fueron los mejores obtenidos después de efectuar diferentes pruebas para su calibración.
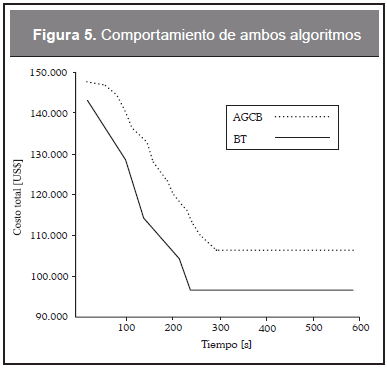
En las Figuras 4a y 4b se presentan las configuraciones encontradas por el AGCB y el ABT, respectivamente. Entre paréntesis se encuentra el tipo de conductor empleado. En la Figura 5 se observa el comportamiento de cada uno de los algoritmos, donde se puede apreciar que el criterio de parada seleccionado es el apropiado, ya que permite que cada método pueda realizar una búsqueda adecuada en el espacio de solución, encontrando respuestas de buena calidad, las cuales fueron halladas en tiempos razonables.
Con el AGCB se propone la instalación de transformadores en los siguientes nodos: 2 (45 kVA), 11 (75 kVA), 27 (45 kVA), 30 (75 kVA), 37 (112,5 kVA), 45 (75 kVA) y 51 (45 kVA). Con el ABT se propone la instalación de transformadores en los siguientes nodos: 2 (45 kVA), 8 (30 kVA), 11 (45 kVA), 16 (75 kVA), 30 (45 kVA), 33 (45 kVA), 37 (45 kVA), 45 (30 kVA), 48 (45 kVA) y 51 (45 kVA). En la Tabla 4 se observan los resultados obtenidos con ambas técnicas de solución.
El AGCB a diferencia del ABT, propone la instalación de pocos transformadores de gran capacidad y conductores de mayor calibre. Sin embargo, los costos de inversión son similares, dado que el ABT instala más transformadores de menor capacidad y conductores con menor calibre, lo que compensa este valor. La diferencia en los costos del proyecto se encuentra en la evaluación de los costos operativos. Esto se debe a que en la configuración encontrada por el ABT se tiene una mejor distribución de los flujos de potencia que circulan por el sistema. Los resultados obtenidos demuestran la validez del método planteado, dado que se tienen menores costos totales cumpliendo con los requerimientos técnicos y operativos.
4.2. CASO 2
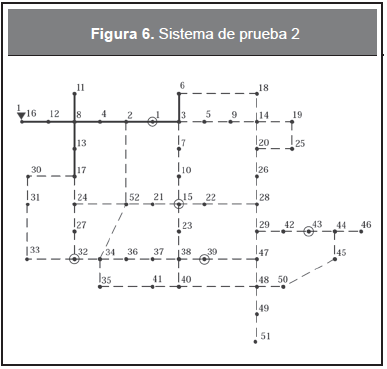
A continuación se presenta la aplicación a un sistema de distribución colombiano (Figura 6). Los datos de las cargas y los tramos de red se presentan en la Tabla 5 y la Tabla 6, respectivamente.
Este sistema de distribución tiene diez tramos de red existentes (líneas continuas), alimentados por un transformador de 30 kVA (triángulo negro en el nodo 16). Para alimentar la aparición de nuevas cargas y el crecimiento de las existentes se proponen 5 posibles ubicaciones de transformadores (nodos 1, 15, 32, 39 y 43) y 53 tramos de red secundarios (líneas discontinuas). El sistema es trifásico, el voltaje nominal es 208/120 V y el porcentaje de regulación es 5 %. El costo del kWh es US$0,16. El factor de potencia de la carga es 0,9. La carga se modela como impedancia constante en un 80 % y como potencia constante en un 20 %. El periodo de vida útil de los elementos es 20 años, la tasa de descuento es 10 % y el incremento anual del costo de la energía es 2 %. Se emplea una curva de duración de carga anual discretizada en tres niveles del 100 %, 70 % y 30 % del valor nominal de demanda, con una duración de 1000, 6760 y 1000 horas, respectivamente.
En el ABT se emplean los siguientes factores de penalización: 1,5 en la restricción financiera, 150 y 100 para voltajes y sobrecargas en tramos de red, y 1000 para voltajes y sobrecargas en transformadores: estos valores son el resultado de realizar diversas pruebas. Se usan los mismos criterios de parada del caso 1. En la Figura 7 se observa la mejor configuración encontrada por el ABT. Los transformadores seleccionados se encuentran ubicados en los nodos: 1 (75kVA), 15 (75 kVA), 32 (45 kVA) y 39 (30 kVA). En esta figura las líneas continuas representan los tramos propuestos de red secundaria y las líneas a trazos están asociadas a la red primaria diseñada para alimentar los transformadores de distribución. Entre paréntesis se observa el tipo de conductor seleccionado para cada tramo de red. Los costos de inversión y operación del proyecto son US$45 378 y US$44 256, respectivamente, por lo que el costo total del proyecto es US$89 634.
Se observa en la solución que el transformador existente de 30 kVA fue reubicado del nodo 16 al 39. En todos los circuitos secundarios se cumple el concepto de redes telescópicas. La regulación de tensión y las cargabilidades de los transformadores y conductores están dentro de los límites permitidos.
5. CONCLUSIONES Y RECOMENDACIONES
Para solucionar el problema del PSSDE se propone una metodología que emplea como técnica de solución el algoritmo de Búsqueda Tabú, la cual determina el tamaño y ubicación de circuitos secundarios, transformadores de distribución y tramos de red primaria. Adicionalmente considera la reubicación de transformadores de distribución, y costos asociados a pérdidas de energía en transformadores de distribución y conexión entre red primaria y secundaria; estas estrategias permiten modelar el problema de una forma más general acercándolo a la operación real. El método es general y flexible, ya que puede ser aplicado en redes de nivel de tensión 1.
En la solución del modelo matemático se usa un algoritmo de Búsqueda Tabú el cual presenta resultados satisfactorios al ser aplicado en dos casos de prueba. En el primero se verifica su efectividad al ser comparado con los resultados obtenidos con un algoritmo genético de Chu-Beasley, usando un sistema de prueba de dimensiones reales. En el segundo caso de prueba se emplea un sistema de distribución colombiano, el cual posee elementos existentes. En ambos casos todas las restricciones técnico-operativas son satisfechas.
La metodología tiene un gran desempeño cuando se aplica a sistemas de distribución de diferentes tamaños. Adicionalmente el modelo de red planteado incluye todos los elementos de un sistema real, el cual al ser resuelto con una metodología eficiente, permite obtener soluciones de alta calidad con respecto a los costos de inversión y operación, y los requerimientos técnicos del sistema.
Es importante que las empresas de distribución cuenten con estrategias confiables para los estudios de planeación de sistemas secundarios, de forma que se generen menores costos de inversión y operación.
REFERENCIAS
Chu, Pei y Beasley, John (1997). A Genetic Algorithm for the Generalized Assignment Problem. Computers Operations Research, 24(1), pp. 17-23. [ Links ]
Cossi, M. A.; Romero, R. y Sanches, J. (2005). Planning of Secondary Distribution Circuits through Evolutionary Algorithms. IEEE Transactions on Power Delivery, 20(1), pp. 205-213. [ Links ]
Cossi, Antonio Marcos. Planejamento de redes de distribuçao de energia elétrica de média e baixa tensao. Tesis de doctorado, Universidade Estadual Paulista, Ilha Solteira, Faculdade de Engenharia, Brasil, 2008. [ Links ]
Cossi, A.M.; Romero, R. y Sánches, J. (2009). Planning and Projects of Secondary Electric Power Distribution Systems. IEEE Transactions on power systems, 24(3), pp. 1599-1608. [ Links ]
Costa, A. y França, P. (2002). Planejamento de Redes Secundárias de Distribuição de Energia Elétrica. En: XV Congresso Brasileiro de Automática, Natal, 2002, pp. 2563-2568. [ Links ]
Díaz-Dorado, E.; Miguez, E. y Cidrás, J. (2001). Design of Large Rural low-voltage Networks using Dynamic Programming Optimization. IEEE Transactions on Power Systems, 16(4), pp. 898-993. [ Links ]
Díaz-Dorado, E.; Pidre, C. y Miguez, M. (2003). Planning of large rural low-voltage Networks Using Evolution Strategies. IEEE Transactions on Power Systems, 18(4), pp. 1594-1600. [ Links ]
Gallego, R. A.; Escobar, A. y Toro, E. (2008). Técnicas metaheurísticas de optimización. Pereira: Textos Universitarios Universidad Tecnológica de Pereira, 167 p. [ Links ]
Garces, A.; Granada, M. y Gallego, R. (2004). Flujo de carga trifásico para sistemas radiales de distribución. Revista Scientia et Technica, 10(24), pp. 19-24. [ Links ]
Garcia, V.; Morelato, P.; Vizcaino, J.; Yoshimoto, E. y Lyra, C. (2003). GRASP para o problema de planejamento de redes Secundárias de distribuição de energia elétrica. XXXV SBPO-Sociedade Brasilera de Pesquisa Operacional-A pesquisa Operacional e os Recursos Renováveis, Natal, 2003, pp. 1427-1437. [ Links ]
Gilvanejad, M.; Ghadiri, H.; Shariati, M. R.; Farzalizadeh, S. y Arefi, A. A. (2007). Novel Algorithm for Distribution Network Planning Using Loss Reduction Approach. Power Engineering Conference AUPEC Australasian Universities, Australia, 2007, pp. 1-6. [ Links ]
Glover, F. (1995). Tabu Search Fundamentals and Uses, University of Colorado, Boulder, Colorado, April 1995. [ Links ]
Gonzalez, J. D.; Gallego, R. e Hincapié, R. (2009). Modelamiento matemático del problema del planeamiento de sistemas secundarios de distribución. Revista Colombiana de Tecnologías de Avanzada, 2(14), pp. 89-95. [ Links ]
Kersting, W. H. Distribution System Modeling and Analysis. Florida. CRC Press, 2007, 145 p. [ Links ]
Londoño, J. M.; Hincapié, R. y Gallego, R. (2011). Planeamiento de redes de baja tensión considerando un modelamiento trifásico. Revista Ciencia e Ingeniería Neogranadina, 21(2), pp. 44-56. [ Links ]
Marroquín, O. Planeamiento de redes secundarias de distribución usando un algoritmo de optimización basado en colonia de hormigas. Tesis de pregrado, Universidad Tecnológica de Pereira, Facultad de Ingeniería, Pereira, 2008. [ Links ]
Navarro, A. y Rudnick, H. (2009). Large-Scale Distribution Planning-Part I: Simultaneous Network and Transformer Optimization. IEEE Transactions on Power Systems, 24(2), pp. 744-751. [ Links ]
Navarro, A. y Rudnick, H. (2009). Large-Scale distribution planning-Part II: Macro-optimization with Voronoi's Diagram and Tabu Search. IEEE Transactions on Power Systems, 24(2), pp. 752-758. [ Links ]
Ramirez, S. Libro de redes de distribución. Universidad Nacional de Colombia, Sede Manizales, Tercera edición, 2004, pp. 526-530. [ Links ]
Souza, C. H. Planejamento e projecto de circuitos secundários de distribuição de energía eléctrica utilizando algoritmo busca tabu BT. Tesis de maestría. Universidade Estadual Paulista, Ilha Solteira, Faculdade de Engenharia, Brasil, 2006. [ Links ]
Tapias, C.; Galeano, A. e Hincapié, R. (2011). Planeación de sistemas secundarios de distribución usando el algoritmo branch and bound. Revista Ingeniería y Ciencia, 7(13), pp. 47-64. [ Links ]