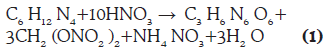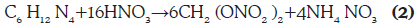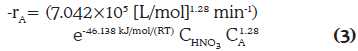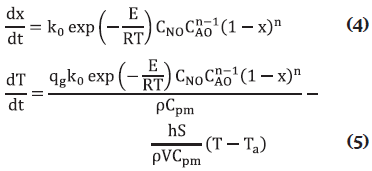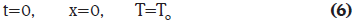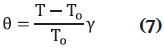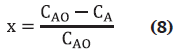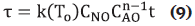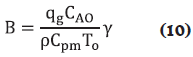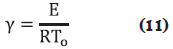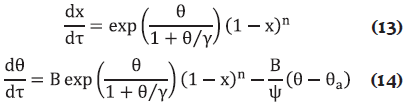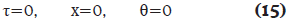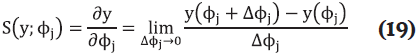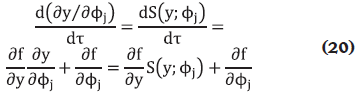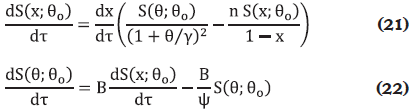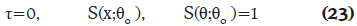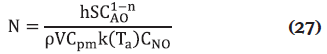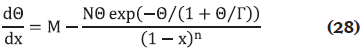Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.21 Envigado Jan./June 2014
EVALUACIÓN DE LA SENSIBILIDAD PARAMÉTRICA DEL PROCESO DE SÍNTESIS DE LA CICLONITA EN UN REACTOR POR LOTES
PARAMETRIC SENSITIVITY ASSESSMENT OF THE CYCLONITE PRODUCTION IN A BATCH REACTOR
AVALIAÇÃO DA SENSIBILIDADE PARAMÉTRICA DO PROCESSO DE SÍNTESE DA CICLONITA NUM REATOR POR LOTES
Juan Carlos Ojeda Toro*, Izabela Dobrosz Gómez**, Miguel Ángel Gómez García***
*Ingeniero químico, Universidad Nacional de Colombia, sede Manizales, MsC. en Ingeniería Química, Universidad Nacional de Colombia, sede Manizales. Grupo de Investigación en Procesos Reactivos Intensificados con Separación y Materiales Avanzados - PRISMA.
**Química, Universidad Tecnológica de Lodz (Polonia). MsC. en Ingeniería Universidad Tecnológica de Lodz (Polonia). Profesora Asociada Universidad Nacional de Colombia, sede Manizales.
***Ingeniero químico Universidad Nacional de Colombia, sede Manizales. MsC. en Ingeniería Química, Universidad Nacional de Colombia, sede Bogotá. PhD. en Ingeniería Química, Université Louis Pasteur - Strasbourg I (Francia). Profesor Titular Universidad Nacional de Colombia, sede Manizales. Grupo de Investigación en Procesos Reactivos Intensificados con Separación y Materiales Avanzados - PRISMA.
Autor de correspondencia: Gómez-García, M.A. (Miguel Ángel): Carrera 27 N. 64 - 60, Manizales, Universidad Nacional de Colombia, sede Manizales. Apartado Aéreo 127, Manizales (Colombia). Tel: (57 6) 887 93 00 Ext. 55210 / Correo electrónico: magomez@unal.edu.co.
Artículo recibido: 27-V-2013 / Aprobado: 23-III-2014
Disponible online: 12 de mayo 2014
Discusión abierta hasta mayo de 2015
RESUMEN
En este trabajo se evaluó la sensibilidad paramétrica del proceso de síntesis de la ciclonita en un reactor por lotes. Esto con el fin de definir condiciones seguras de operación para esta reacción altamente exotérmica. La ley de velocidad de la reacción se ajustó a partir de datos experimentales disponibles en la literatura. Reparametrizando los balances de materia y energía del reactor, se estableció la sensibilidad de la temperatura de reacción con respecto a la variación de la temperatura inicial del sistema reactivo y la temperatura del medio refrigerante. Para determinar las condiciones críticas de operación del reactor, se usó como criterio el cálculo de los coeficientes de sensibilidad y los perfiles de temperatura-conversión así como el lugar geométrico de los máximos de estas curvas. Se definió para el sistema reactivo un potencial crítico de generación de calor (M) igual a 34 y que las condiciones críticas de Runaway corresponden a un número de Semenov (ψ) igual a 0,684, un parámetro de calor de reacción (B) igual a 15 y un número del tipo Arrhenius (γ) con un valor de 20. Así mismo, los perfiles de temperatura-conversión precisan una relación crítica entre el potencial de enfriamiento y generación de calor de 2,5786 (N/M).
PALABRAS CLAVE: Reacción de Runaway; sensibilidad paramétrica; ciclonita; criterios de operación estable, reactor por lotes.
ABSTRACT
In the present work, the parametric sensitivity of the cyclonite production in a batch reactor was assessed. The objective was to establish safe operation conditions for this highly exothermic reaction. The reaction rate law was fitted using experimental data published in the literature. Mass and energy balances were reparametrized. Thus, reaction temperature sensitivity criteria were established as a function of initial reaction and cooling temperatures. Critical reaction conditions were defined using the temperature-sensitivity, temperature-conversion, and the locus of the temperature maxima. A critical heat generation potential (M) equal to 34 was defined together with the following runaway critical conditions: a Semenov number (ψ) equal to 0.684, a heat of reaction parameter (B) equal to 15 and an Arrhenius-type number (γ) of 20. Therefore, temperature-conversion profiles precise a critical relation between the cooling and heat potential (N/M) of 2.5786.
KEY WORDS: Runaway Reaction; Parametric Sensitivity; Cyclonite; Stable Reaction Operation Criteria, Batch Reactor.
RESUMO
Neste trabalho avaliou-se a sensibilidade paramétrica do processo de síntese da ciclonita num reator por lotes. isto para definir condições seguras de operação para esta reação altamente exotérmica. a lei de velocidade da reação ajustou-se a partir dos dados experimentais disponíveis na literatura. reconfigurando os balanços da matéria e energia do reator, estabeleceu-se a sensibilidade da temperatura de reação com respeito à variação da temperatura inicial do sistema reativo e a temperatura do meio refrigerante. para definir as condições críticas de operação do reator, usou-se como critério o cálculo dos coeficientes de sensibilidades e os perfiles de temperatura-conversão assim como o lugar geométrico dos máximos destas curvas. definiu-se para o sistema reativo um potencial crítico de geração de calor (m) igual a 34 e que as condições críticas de runaway correspondam ao número de semenov (ψ) igual a 0.684, um parâmetro de calor de reação (b) igual a 15 e um numero do tipo arrhenius (γ) com um valor de 20. assim mesmo, os perfiles de temperatura-conversão precisam uma relação crítica entre o potencial de esfriamento e geração de calor de 2.5786 (n/m).
PALAVRAS-CHAVE: Reação de runaway; Sensibilidade paramétrica; Ciclonita; Critérios de operação estável; Reator por lotes.
1. INTRODUCCIÓN
La reacción en fase líquida entre la hexamina y el ácido nítrico permite la obtención de ciclonita, un explosivo también conocido como RDX, hexógeno, ciclo-trimetileno-triamina o T4. Esta reacción es altamente exotérmica (-90938 kJ/mol de hexamina) y muy sensible a la variación de las condiciones de proceso. Así, cuando la temperatura en el reactor alcanza el punto crítico, el sistema reactivo se puede encontrar en una situación fuera de control (runaway térmico) o incluso explosión (Willey, Fogler y Cutlip, 2010). En años recientes, la operación térmica segura de reactores ha incrementado su interés con el fin de evitar los accidentes del tipo Runaway los cuales pueden generar muerte, daños a instalaciones y contaminación ambiental (http://www.csb.gov).
Son muchas las metodologías propuestas para el análisis de las condiciones de Runaway. En un primer intento, Semenov (1928) definió que las condiciones críticas dependen de la forma en que crece la curva de temperatura. Luego, Kamenetskii (1939) asumió que el enfriamiento en un reactor químico está controlado por la conducción térmica en el seno de la mezcla reactiva. Estos métodos predicen las condiciones de Runaway térmico mediante un análisis de estabilidad lineal del balance de energía. El concepto de sensibilidad paramétrica fue propuesto inicialmente por Bilous y Amundson (1956). Ellos establecieron que un reactor químico opera en la región de sensibilidad paramétrica cuando pequeños cambios en los valores de uno o más parámetros de entrada al reactor generan grandes cambios (v.g., runaway) en las variables de salida del mismo. De esta forma se desarrollaron criterios basados en las características geométricas de los perfiles de temperatura y/o conversión (Thomas y Bowes, 1961; Adler y Enig, 1964; van Walsenaere y Froment 1970; Westerterp, van Swaaij y Beenackers, 1984).
En general, se podría decir que en las últimas dos décadas, la estimación de los límites entre las regiones con condiciones de operación seguras y de runaway se ha enfrentado siguiendo tres principales metodologías: el método de sensibilidad paramétrica (Morbidelli y Varma, 1988; Varma, Morbidelli y Wu, 1999); el método de la divergencia basado en la teoría del caos (Strozzi, y Zaldivar, 1994) y el método de la extensión de trayectorias (Bosch, et al., 2004). Así, Morbidelli y Varma (1988) desarrollaron un criterio de sensibilidad paramétrica generalizado con el cual la región de sensibilidad paramétrica se identifica como aquella donde la sensibilidad objetivo normalizada del máximo de temperatura, con respecto a cualquier parámetro de entrada del modelo, alcanza un máximo. A pesar de la experiencia acumulada, se han reportado numerosos incidentes y calamidades relacionados con el proceso de producción de ciclonita (Kletz, 2009). De hecho, hasta donde conocemos, el único trabajo que se encuentra en la literatura relacionado con la evaluación de sus condiciones críticas en operación por lotes Batch fue el desarrollado por Luo, et al. (2002). Este se basó en el criterio de Kamenetskii (1939).
El objetivo de este trabajo es determinar las condiciones críticas de operación de un reactor batch para la producción de ciclonita utilizando un criterio de sensibilidad nuevo y simple. Para esto, se aplicó el modelo generalizado de Morbidelli y Varma (1988) y los perfiles de temperatura-conversión propuestos por Westerterp, van Swaaij y Beenackers (1984). Estos incluyen el análisis de los perfiles de temperatura y concentración así como de sensibilidad de la temperatura en función de las variables de operación.
2. EVALUACIÓN DE LOS PARÁMETROS CINÉTICOS
La reacción química entre la hexamina (C6H12N4) y el ácido nítrico (HNO3) para producir ciclonita (C3H6N6O6) está dada por la ecuación (1).
Existe además la posibilidad de una reacción secundaria con los mismos reactantes:
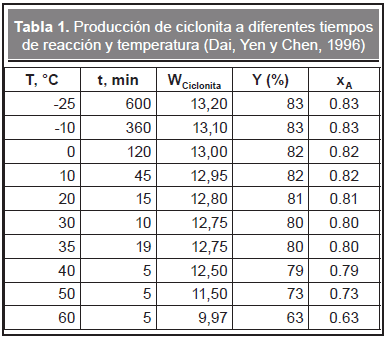
Dai, Yen y Chen (1996) realizaron experimentos en un reactor batch con masas de alimentación de ácido nítrico, WHNO3, y de hexamina, WA, iguales a 110 y 10 g, respectivamente. Para valores fijos de tiempo de reacción y temperatura, midieron la masa de producción de ciclonita, Wciclonita. De esta forma, la tasa de rendimiento de ciclonita, Y(%), y la conversión de hexamina, xA, pueden estimarse a partir de los datos experimentales reportados en la Tabla 1.
La relación másica estequiométrica entre el ácido nítrico y la hexamina, WHNO3/WA, es igual a 2,84. Sin embargo, en los experimentos, las cantidades utilizadas dan una relación másica de 11. Por esto, es posible argumentar que la concentración de ácido nítrico en los experimentos sólo sufrirá una variación menor por lo que esta se puede suponer como constante. El orden de reacción (n), el factor de frecuencia (ko) y la energía de activación (E) se pueden obtener del ajuste de los datos presentados en la Tabla 1 realizando un análisis no lineal de los mismos (utilizando la función fminsearch de MatLab®). Una vez hecho esto, la velocidad de reacción de hexamina se puede expresar de la siguiente forma:
3. COEFICIENTE DE SENSIBILIDAD
Considerando que el Reactor Batch opera bajo condiciones homogéneas e isoperibólicas (v.g., la temperatura del fluido de servicio en la chaqueta del reactor se mantiene constante) es posible demostrar que el balance molar y de energía para ese reactor tienen la siguiente forma:
donde qg es el calor de generación, ρ es la densidad de la mezcla, Cpm es la capacidad calorífica de la mezcla, h es el coeficiente de transferencia de calor, S es el área de transferencia de calor, V es el volumen del reactor y Ta es la temperatura del refrigerante. Los balances están sujetos a las siguientes condiciones iniciales:
Definiendo las siguientes variables adimensionales:
Temperatura adimensional:
Conversión de hexamina:
Tiempo adimensional:
y los parámetros adimensionales:
Incremento de la temperatura adimensional adiabática:
Energía de activación adimensional:
Número Semenov:
es posible reescribir de forma adimensional las Ecuaciones (4) y (5):
y sus condiciones iniciales:
Para determinar los coeficientes de sensibilidad, Morbidelli y Varma (1988) sugieren considerar el balance molar y el de energía mediante una ecuación diferencial general que describa el comportamiento dinámico tal como se muestra en la ecuación (16).
Con la condición inicial:
Asumiendo que la función es continua y diferenciable en todos sus argumentos, una posible solución a esta ecuación puede ser:
Si se genera una pequeña perturbación al j-ésimo parámetro de entrada, de  j a
j a  j+Δ
j+Δ j, la variable dependiente se modificará según la expresión y=y(τ,
j, la variable dependiente se modificará según la expresión y=y(τ, j+Δ
j+Δ j,). De esta manera, se define el coeficiente de sensibilidad de primer orden (S(y;
j,). De esta manera, se define el coeficiente de sensibilidad de primer orden (S(y; j )) como:
j )) como:
El valor del coeficiente de sensibilidad puede ser positivo o negativo. Cuando éste es positivo, un aumento en el valor del (los) parámetro(s) de entrada conduce a un incremento en la variable dependiente correspondiente; cuando es negativo sucede lo contrario. Existen tres métodos para evaluar los coeficientes de sensibilidad: el método diferencial directo (Rabitz, Kramer y Dacol, 1983), el método de las diferencias finitas (Kramer et al., 1984) y el método de la función de Green (Hwang et al., 1978). Para el caso bajo estudio se aplicará el método diferencial directo debido su fácil implementación computacional (v.g., en el software MatLab®). Así, diferenciando ambos lados de la Ecuación 16 con respecto a  j, se obtiene:
j, se obtiene:
La variable dependiente y incluye la conversión y la temperatura del reactante. El parámetro de entrada  j puede ser la temperatura inicial, el flujo del refrigerante, etc... Si los coeficientes de sensibilidad de la conversión y la temperatura son denotados con respecto a la temperatura inicial, entonces las ecuaciones de sensibilidad pueden ser expresadas de la siguiente forma:
j puede ser la temperatura inicial, el flujo del refrigerante, etc... Si los coeficientes de sensibilidad de la conversión y la temperatura son denotados con respecto a la temperatura inicial, entonces las ecuaciones de sensibilidad pueden ser expresadas de la siguiente forma:
Con las condiciones iniciales:
Para analizar la variación de la temperatura del reactor (variable dependiente θ) y su sensibilidad, S(θ;θo), en función del tiempo (τ), se resuelven simultáneamente los balances molar y de energía, Ecuaciones (13) y (14), y de sensibilidad paramétrica, Ecuaciones (21) y (22), junto con las condiciones iniciales, Ecuaciones (15) y (23) respectivamente.
4. PERFILES TEMPERATURA-CONVERSIÓN Y CURVA DE LOS MÁXIMOS DE TEMPERATURA
Para evaluar la sensibilidad que tiene la temperatura del sistema con respecto a la temperatura del medio refrigerante se utilizó la metodología propuesta por Velo, Bosh y Recasens (1996), basada en la propuesta de análisis de Westerterp, van Swaaij y Beenackers, (1984). Esta consiste en identificar los parámetros críticos (runaway) mediante el análisis del perfil temperatura-conversión y la curva correspondiente al lugar geométrico de los máximos de temperatura.
Combinando los balances de materia y energía del reactor batch, las Ecuaciones 4 y 5, y adimensionalizando la expresión resultante utilizando la siguiente definición de temperatura adimensional (Θ) (con respecto a la temperatura del medio refrigerante):
y los siguiente parámetros adimensionales:
Energía de activación adimensional:
Potencial de generación de calor:
Intensidad de enfriamiento:
es posible obtener:
Con la condición inicial:
El perfil temperatura-conversión se puede obtener integrando la Ecuación (28). La curva del lugar geométrico de los máximos de temperatura se determina mediante el principio de la primera derivada. Un máximo se presenta cuando la derivada de la temperatura con respecto a la conversión es igual a cero. En otras palabras, la curva de máximos de temperatura se puede obtener igualando a cero la Ecuación (28) y resolviendo para cierto conjunto de valores.
5. ANÁLISIS DEL COMPORTAMIENTO Y DE LA SENSIBILIDAD DE LA TEMPERATURA DE REACCIÓN
La Figura 1 describe el perfil de temperatura adimensional en el reactor y su sensibilidad con la temperatura inicial en función del tiempo para diferentes valores de Semenov (ψ). El número de Semenov representa la relación entre el calor generado y el calor removido por el fluido de servicio. Se puede observar que para curvas con valores del número de Semenov menor que 0.684 la temperatura aumenta lentamente con el tiempo y su correspondiente sensibilidad disminuye gradualmente. En la Figura 1 (izquierda) se puede observar que el valor crítico del número de Semenov es 0,684 (el límite de la condición de estabilidad determinado por el máximo valor de la función de sensibilidad de la temperatura que es igual a 1 (max(S(θ;θo)=1 excepto en τ=0) el cual es identificado por la línea horizontal de la Figura 1 (derecha); por encima de ese valor, la temperatura en el reactor aumenta rápidamente y el correspondiente valor de sensibilidad inicialmente disminuye levemente y luego aumenta pasando tangencialmente por el punto S(θ;θo)=1 en τ=0,15. La variación de la temperatura en el reactor y su sensibilidad en función del aumento de la temperatura adimensional adiabática (B) se compara en la Figura 2. Estas presentan un comportamiento similar al observado en función del número de Semenov. El parámetro B tiene un valor crítico de 15 como se observa en la Figura 2 izquierda. El parámetro B representa el calor generado al inicio de la reacción y el calor sensible de la mezcla reactiva. Cuando ese límite es superado, la reacción es inestable y se encuentra fuera de control, debido a la excesiva elevación de la temperatura producto del calor generado por la reacción. Este fenómeno puede ocurrir cuando la concentración del reactante es considerablemente alta o cuando la temperatura de alimento no es lo suficientemente baja. En la Figura 2 (derecha) se muestra la sensibilidad que tiene la temperatura adimensional con respecto a la temperatura inicial a diferentes valores de B. Se puede observar con más claridad que a valores mayores de B_crit, el sistema es muy sensible y tiende a que la temperatura incremente rápidamente en un corto tiempo (la energía liberada es muy superior a la removida).La energía de activación adimensional, γ, tiene un valor crítico de 20 (Figura 3 izquierda). Por encima de este valor el sistema presenta un tránsito a la región fuera de control, esto debido a la drástica elevación de temperatura producto de la energía liberada cuando se lleva a cabo la reacción. De hecho, para un γ>20 la temperatura en el reactor es muy sensible y puede incrementar fácilmente con una pequeña variación en las condiciones iniciales de operación. En el valor crítico de γ el coeficiente de sensibilidad alcanza un máximo que corresponde a τ=0,15.
Luo, et al. (2002) reportaron unas condiciones críticas de Runaway para el caso bajo estudio, a condiciones típicas de operación, aplicando el criterio de Kamenetskii. Comparando con sus resultados, se observa que se coincide con el valor crítico de γ = 20. A esa condición, el valor de la temperatura adimensional reportada por Luo, et al. (2002) es de 2.17 mientras que el predicho por el modelo utilizado en este estudio es de 1,72. La diferencia entre estos valores puede explicarse del hecho de que la simulación realizada en esta investigación involucra simultáneamente los valores críticos de los otros parámetros (v.g., B y ψ). Además, mientras el criterio usado en este trabajo se determinó numéricamente, el criterio de Kamenetskii utiliza el método de ensayo-error y la interpretación gráfica. De esta manera, se puede considerar que el nuevo criterio propuesto en este trabajo predice condiciones más conservadoras de los límites seguros de desempeño del Reactor Batch.
En la Figura 4 (izquierda) se muestra el perfil de temperatura adimensional del reactor en función de la conversión para diferentes valores del parámetro M y para una relación fija de N/M (incluye la suposición que la relación entre θ y γ es mucho menor que la unidad, evaluada del límite cuando la temperatura del medio refrigerante es considerablemente alta, lo que simplifica la Ecuación (28)). Se puede observar que para valores de M (potencial de generación de calor) iguales o superiores a 34, el sistema reactivo se encuentra térmicamente fuera de control. La línea punteada representa el lugar geométrico de los máximos de temperatura (puntos calientes). Estos se deben evitar para valores de M superiores a 34 (Mcrit), debido al incremento indefinido de la temperatura después de este valor. La relación de N/M=2 implica que el potencial de enfriamiento es dos veces mayor que el potencial de generación de calor, pero existe un valor de M crítico en el cual esta relación no es lo suficientemente grande para evitar un aumento progresivo de temperatura.
En la Figura 4 (derecha) se muestran los perfiles de las curvas máximas de temperatura a diferentes valores de N/M y a Γ=20 (valor de la energía de activación adimensional con el método de coeficientes de sensibilidad). El criterio de sensibilidad para este caso consiste en determinar la relación N/M=e en la que la curva máxima de temperatura sea tangente al eje vertical (cuando XA=0). Por lo tanto se propone la resolución de un sistema de 2 ecuaciones y dos incógnitas: la primera es la Ecuación 28 igualada a cero (primera derivada), mientras que la segunda ecuación es la derivada de la Ecuación 28 igualada a cero (segunda derivada). Resolviéndose simultáneamente se obtienen los valores críticos de la relación N/M = e = 2,5786 y el valor de Θ=1,1146 (cuando XA=0). Cuando la temperatura de alimento se encuentra por encima de estos valores, la temperatura del sistema aumenta incontroladamente. Se puede observar que por ejemplo la curva con relación N/M=3 presenta dos cortes con el eje vertical. De esta manera, si la temperatura inicial del sistema se encuentra por debajo del primer corte (Θa) la temperatura se controla fácilmente (no existe puntos calientes). Por el contrario, si la temperatura inicial se encuentra por encima del segundo corte (Θb) el reactor opera fuera de control (existen puntos calientes). Finalmente, si la temperatura inicial se encuentra en el intervalo de los dos cortes, la temperatura del reactor presentará dificultades para su control lo cual dependerá de las condiciones iniciales.
6. CONCLUSIONES
En este trabajo se evaluó numéricamente la sensibilidad paramétrica y dinámica de la temperatura de reacción mediante un criterio sencillo, para el proceso de producción de ciclonita. Los resultados demuestran que el proceso batch exhibe alta sensibilidad en el espacio paramétrico. Así, pequeñas variaciones en los parámetros de entrada generan grandes cambios en las variables de salida. Los valores críticos de los parámetros del sistema son: número de Semenov (ψ) igual a 0,684, el parámetro del calor de reacción (B) de 15 y el número de Arrhenius (γ) de 20. Así mismo, mediante el análisis del perfil temperatura-conversión se determinó el valor crítico del potencial de generación de calor, Mcrit = 34. El Mcrit corresponde a una temperatura del medio refrigerante muy similar a la temperatura del fluido reactivo (Θ⁄Γ<<1)). Finalmente, a través del perfil de la curva de los máximos de temperatura, se determinó que la relación crítica entre el potencial de enfriamiento y el de generación de calor (N/M) es de 2,5786.
AGRADECIMIENTOS
Los autores agradecen apoyo económico de Colciencias - Universidad Nacional de Colombia, sede Manizales (Programa Jóvenes Investigadores e Innovadores Convocatoria 566 de 2012 - Convenio Especial de Cooperación N. 0729 de 2012).
REFERENCIAS
Adler, J. y Enig, J.W. (1964). The Critical Conditions in Thermal Explosion Theory with Reactant Consumption, Combustion and Flame, 8, pp. 97-103. [ Links ]
Bilous, O. y Amundson, N. R. (1956). Chemical Reactor Stability. AIChE Journal, 2, pp. 117-126. [ Links ]
Bosch, J.; Strozzi, F.; Snee, T. J.; Hare, J. A. y Zaldivar, J. M. (2004). A Comparative Analysis Between Temperature and Pressure Measurements for Early Detection of Runaway Initiation. Journal of Loss Prevention in the Process Industries, 17(6), pp. 389-395. [ Links ]
Dai, R. Z.; Yen, S. E. y Chen, Y. K. The Production Technology and Design of Explosives. Weapon Industrial Pub. Co. 1996. [ Links ]
Hwang, J. T.; Dougherty, E. P.; Rabitz, S. y Rabitz, H. (1978). The Green's Function Method of Sensitivity Analysis in Chemical Kinetics. Journal of Chemical Physics, 69, pp. 5180-5191. [ Links ]
Jiang, J.; Jiang, J.; Pan, Y.; Wang, R. y Tang P. (2011). Investigation on Thermal Runaway in Batch Reactors by Parametric Sensitivity Analysis. Chemical Engineering and Technology, 34(9), pp. 1521-1528. [ Links ]
Kamenetskii, F. Diffusion and Heat Transfer in Chemical Kinetic, 2nd Ed., Plenum Press, N. Y., 1969. [ Links ]
Kletz, T. What Went Wrong?: Case Histories of Process Plant Disasters and How They Could Have Been Avoided. Butterworth-Heinemann, 2009. [ Links ]
Kramer, M. A.; Rabitz, H.; Calo, J. M. y Kee, R. J. (1984) Sensitivity Analysis in Chemical Kinetics: Recent Developments and Computational Comparisons. Internacional Journal of Chemical Kinetic, 16, pp. 559-578. [ Links ]
Luo, K. M; Lin, S. H.; Chang, J. G. y Huang T. H. (2002). Evaluations of Kinetic Parameters and Critical Runaway Conditions in the Reaction System of Hexamine-Nitric Acid to Produce RDX in a Non-Isothermal Batch Reactor. Journal of Loss Prevention in the Process Industries, vol. 15, pp. 119-127. [ Links ]
Morbidelli, M. y Varma, A. (1988). A Generalized Criterion for Parametric Sensitivity: Application to Thermal Explosion Theory. Chemical Engineering Science, 43, pp. 91-102. [ Links ]
Rabitz, H.; Kramer, M. y Dacol, D. (1983). Sensitivity analysis in chemical kinetics. Annual Review Physical Chemistry, 34, pp. 419-461. [ Links ]
Semenov N. N. (1928). Zur Theorie des Verbrennungsprozesses. Z. Physik., 48(7-8), S.571-582. [ Links ]
Strozzi, F. y Zaldivar, J. M. (1994). A General Method for Assessing the Thermal Stability of Batch Chemical Reactors by Sensitivity Calculation Based on Lyapunov Exponents, Chemical Engineering Science, 49, pp. 2681-2688. [ Links ]
Thomas, P. H.; Bowes, P. C. (1961). Some Aspects of the Ignition and Self-Heating of Solid Cellulosic Materials. Journal of Applied Physics, 12, pp. 222. [ Links ]
Varma, A.; Morbidelli, M. y Wu, H. Parametric Sensitivity in Chemical Systems, Cambridge Series in Chemical Engineering, Cambridge University Press. 1999. [ Links ]
van Welsenaere, R. J. y Froment, G. F. (1970). Parametric Sensitivity and Runaway in Fixed Bed Catalytic Reactors. Chemical Engineering Science, 25, pp. 1503-1516. [ Links ]
Velo, E.; Bosh, C. M. y Recasens, F. (1996). Thermal Safety of Batch Reactors and Storage Tanks. Development and Validation of Runaway Boundaries. Industrial and Engineering Chemistry Research, 35, pp. 1288-1299. [ Links ]
Westerterp, K. R.; van Swaaij, W. P. M.; Beenackers, A. A. C. C. Chemical Reactor Design and Operation, John Wiley and Sons, Chichester, U.K., 1984. [ Links ]
Willey, R. J.; Fogler, H. S. y Cutlip, M. B. (2010). The Integration of Process Safety into a Chemical Reaction Engineering Course: Kinetic Modeling of the T2 Incident. AIChE Journal, 30(1), pp. 39-44. [ Links ]