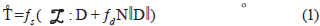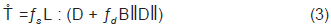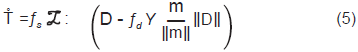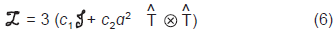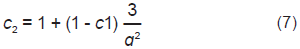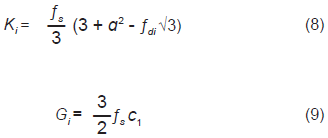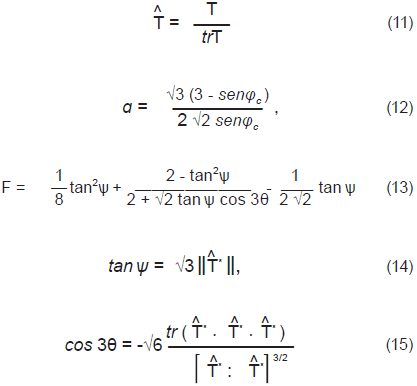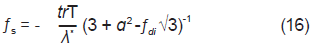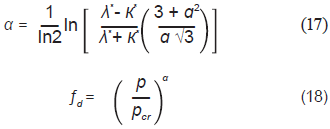Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.21 Envigado Jan./June 2014
SIMULACIÓN DE PRUEBAS DE CARGA EN PILOTES USANDO UN MODELO CONSTITUTIVO HIPOPLÁSTICO
SIMULATION OF LOAD TESTS IN PILES USING A HYPOPLASTIC CONSTITUTIVE MODEL
SIMULAÇÃO DE PROVAS EM CARGA EM PILOTES USANDO UM MODELO CONSTITUTIVO HIPOPLÁSICO
Juan Carlos Ruge Cárdenas*, Renato Pinto da Cunha**, Hugo Alexánder Rondón Quintana***
*Ingeniero civil Universidad Franciso de Paula Santander, Cúcuta (Colombia). MsC en Ingeniería Civil, Universidad de los Andes, Bogotá (Colombia). PhD en Geotecnia, Universidad de Brasilia, Brasilia (Brasil). Facultad de Ingeniería, Universidad Católica de Colombia, Bogotá (Colombia).
Autor de correspondencia: Giraldo-Tobón, E.: Diagonal 46A N. 15B-10, sede El Claustro, Bloque O, Piso 4, Bogotá, (Colombia). Teléfono: (57-1) 3277300. Correo electrónico: jcruge@ucatolica.edu.co.
**Ingeniero civil Universidad Federal de Río de Janeiro, Río de Janeiro (Brasil). MsC. Universidad Federal de Río de Janeiro, Río de Janeiro (Brasil). PhD. University of British Columbia, Canadá. Postdoctorado Universidad de Sydney, Sydney (Australia) . PhD. en Geotecnia. Departamento de Engenharia Civil e Ambiental, Universidad de Brasilia, Brasilia (Brasil).
***Ingeniero civil, Universidad Franciso de Paula Santander, Cúcuta (Colombia). MsC. en Ingeniería Civil Universidad de los Andes Bogotá (Colombia). PhD. en Ingeniería Universidad de los Andes, Bogotá (Colombia). Postdoctorado Departamento de Ingeniería Civil Universidad de los Andes. Facultad del Medio Ambiente y Recursos Naturales, Universidad Distrital Francisco José de Caldas.
Artículo recibido: 1-VIII-2013 / Aprobado: 17-V-2014
Disponible online: 12 de mayo 2014
Discusión abierta hasta mayo de 2015
RESUMEN
La presente investigación tuvo como objetivo principal, simular mediante el empleo de un programa basado en el método de elementos finitos, los resultados obtenidos de pruebas de carga en pilotes individuales fundados en arcillas porosas de Brasilia DF (Brasil), las cuales poseen características metaestables. Para las simulaciones se empleó la ecuación constitutiva hipoplástica. Los parámetros del suelo fueron obtenidos por medio de ensayos de laboratorio que permitieron estimar propiedades geotécnicas del suelo, así como parámetros de resistencia, deformabilidad e identificación estratigráfica. Como conclusión general se reporta que la predicción aportada por el modelo hipoplástico en relación a las pruebas de carga en el tramo antes de la ruptura es aceptable, sin embargo debido a la pérdida de adhesión en la interface suelo-pilote en el momento de la prueba, se nota la incapacidad del modelo para simular este efecto de manera adecuada, ya que existen condiciones de metaestabilidad y de parcial saturación presentes en el problema geotécnico.
PALABRAS CLAVE: pruebas de carga; pilotes; simulación; hipoplasticidad.
ABSTRACT
This paper presents a numerical simulation based in a FEM program related with the results of a pile load test conducted on porous clay from Brasilia DF (Brazil), which has metastable characteristics. The numerical modeling used as reference model a hypoplastic constitutive model. The analysis of the results of laboratory tests, allowed estimating soil geotechnical properties and parameters of strength, deformability and stratigraphic identification. As a general conclusion it's important to highlight that the hypoplastic prediction in the linear range, reproduce of an adequate way the tendency in the load-settlement curve, however due to the loss of adhesion in the soil-pile interfase, at the time of the test, it shows the incapability of the model to simulate this effect appropriately, since in the geotechnical problem exist unsaturated and metastability conditions.
KEY WORDS: Load Tests; piles; Simulation; Hypoplasticity.
RESUMO
Essa pesquisa tem como objetivo principal, simular mediante o emprego dum programa baseado no método de elementos finitos, os resultados obtidos de provas de carga em pilotes individuais fundados em argilas porosas de Brasília DF (Brasil), as quais possuem caraterísticas metaestáveis. Para as simulações empregou-se a equação constitutivo hipoplásica. Os parâmetros do solo foram obtidos por meio de ensaios de laboratórios que permitiram estimar propriedades geotécnicas do solo, assim como os parâmetros de resistência, deformabilidade e identificação estratigráfica. Como conclusão geral reportou-se que a predição do modelo hipoplásico em relação com as provas de carga no tramo antes da ruptura é aceitável, no entanto devido à perda de adesão na interface solo-pilote no momento da prova, percebe-se a incapacidade do modelo para simular este efeito de maneira adequada, já que existe condições de metaestabilidade e de parcial saturação presentes no problema geotécnico.
PALAVRAS-CHAVE: Provas de carga; Pilotes; Simulação; Hipoplasticidade.
1. INTRODUCCIÓN
Una de las herramientas más utilizadas en el mundo para intentar predecir el comportamiento que experimentan estructuras geotécnicas bajo diferentes condiciones de carga y de frontera, es la simulación computacional empleando Programas de Elementos Finitos (FEM por sus siglas en inglés). Estos programas utilizan ecuaciones constitutivas para el cálculo de esfuerzos y deformaciones, las cuales suponen que el material es un continuo (no se tiene en cuenta el comportamiento individual de los componentes del material, sino su comportamiento global a nivel macromecánico). Para el caso de estructuras geotécnicas, algunas de las ventajas del empleo de programas de elementos finitos radican en que pueden llegar a tener en cuenta que los suelos exhiben un comportamiento no lineal, dependiente de la condición de esfuerzos. Adicionalmente, son capaces de modelar diferentes geometrías y tipos de carga, condiciones de frontera y criterios de falla. Algunos modelos de comportamiento empleados en programas de elementos finitos para el cálculo de esfuerzos y deformaciones en suelos son: el modelo de acumulación de Bochum (p.e., Wichtmann et al., 2004, Wichtmann et al., 2004a, Wichtmann, 2005), Elastoplásticos (p.e., Hicher et al., 1999; Hau et al., 2005), Hypo-Quasi-Elastic (p.e., Tatsuoka, 1999), Hiper-elásticos (p.e., Hoff y Nordal, 1999; Taciroglu y Hjelmstad, 2002), Elásticos Lineales y no Lineales (p.e., Hicks y Monismith, 1972; Boyce, 1980; Hornych et al., 1998; Hicher y Chang, 2006), Hipoplásticos (p.e., Gudehus, 1996; Wolffersdorff, 1996; Herle y Gudehus, 1999; Mašín, 2005) y Visco-Hipoplásticos (p.e., Niemunis et al., 2009).
En la presente investigación, los resultados obtenidos de pruebas de carga a escala real, ejecutados sobre pilotes individuales fundados en arcillas porosas de Brasilia DF (Brasil), las cuales poseen características metaestables, fueron simulados utilizando un programa basado en el FEM. Se utilizó para las simulaciones computacionales, una ecuación constitutiva hipoplástica, la cual fue escogida debido a que su formulación matemática y la determinación de sus parámetros mecánicos es relativamente simple, y adicionalmente, presenta una amplia capacidad para simular el comportamiento que experimentan materiales de grano fino (Mašín, 2005).
Es importante destacar que la investigación se encuentra orientada a intentar simular numéricamente la rama lineal de la curva carga-asentamiento, pasando por el intervalo no lineal hasta la carga de ruptura, en el caso que existiera. Como se mencionó anteriormente la arcilla porosa de Brasilia presenta características metaestables, que son consecuentes con el fenómeno de colapsibilidad en condiciones saturadas, sin embargo las pruebas de carga expuestas en el documento no fueron desarrolladas bajo esta condición, por lo tanto el aumento de asentamiento mostrado en los resultados, se debe a una pérdida de adhesión entre la interfase pilote-suelo y/o al eventual rompimiento de la estructura del material.
2. MATERIALES Y MÉTODOS
2.1 Características geológicas y geotécnicas del sitio
El área donde se localiza el campo experimental de la Universidad de Brasilia, se caracteriza por poseer un perfil típico de un estrato de suelo laterítico rojo arcilloso, denominado «arcilla porosa», que presenta una baja resistencia a la penetración estándar (SPT entre 1 y 6 golpes), baja resistencia de punta (CPT variando de 0,6 a 2,3 MPa), baja capacidad de soporte, bajo nivel de saturación y alta permeabilidad (10-3 a 10-4 m/s). Debido a su alta porosidad y tipo de cementación, presenta una estructura metaestable cuando es sometida a un aumento de humedad y/o alteración de su estado de esfuerzos, mostrando en la mayoría de los casos una brusca variación de volumen conocida como colapso (Ruge y Cunha, 2011). Este material suprayace a un estrato de suelo residual proveniente de la meteorización de ardosias, denominado como limo arcilloso de comportamiento extremadamente anisotrópico (Cunha y Camapum de Carvalho, 1997).
Con el fin de conocer las propiedades del suelo, se realizaron dos perforaciones de inspección ejecutadas manualmente para toma de muestras alteradas e inalteradas. Fueron realizados ensayos de caracterización para la identificación de las propiedades físicas del suelo, ensayos para la determinación de la curva característica por la técnica del papel filtro, con medidas de succión matricial e total, ensayos de consolidación, corte directo y triaxiales K0, no drenados en condiciones de humedad natural y saturados, para la obtención del comportamiento mecánico del perfil de suelo.
Según Mota et al. (2002), el perfil de suelo del campo experimental de la Universidad de Brasilia - UnB muestra horizontes bien diferenciados:
- 0,0 m a 8,80 m - horizonte de suelo residual laterítico, que experimentó procesos de intemperismo, constituido por una arcilla arenosa roja oscura (0 m a 5 m) y una arcilla gravo-arenosa roja oscura (5 m a 8,8 m).
- 8,8 m a 10,30 m - horizonte de transición, compuesto de un suelo laterítico (8,8 m a 9,8 m) y pocas estructuras relictas (9,8 m a 10,3 m).
- 10,3 m a 15,0 m - horizonte de suelo saprolítico constituido por intercalaciones de cuarzo (10,3 m a 11,3) y un limo arcilloso rojo (11,3 m a 15,0 m).
En la Tabla 1 se pueden observar los parámetros de caracterización índice del suelo en estudio de dos muestras retiradas a 6 y 9 m de profundidad, localizadas dentro del perfil conocido como arcilla porosa, nótese que la variabilidad de los parámetros índice es relativamente baja, por tal razón para el modelo numérico se optó por usar un solo estrato en toda la longitud del pilote, ponderada usando los parámetros del modelo de referencia.
Donde w es la humedad natural, γs - peso específico de sólidos, γd - peso específico seco, γ - peso específico no saturado, Gs - gravedad específica, e - relación de vacíos, LL - límite liquido, LP - límite plástico e IP - índice de plasticidad.
Debido a que la humedad del perfil es relativamente alta, en relación al límite líquido, de primera mano se podría entender que el problema geotécnico está condicionado por un escenario no drenado, sin embargo un aspecto que se debe considerar cuando se analiza el suelo poroso y metaestable de Brasilia, es su tendencia a exhibir una respuesta drenada (similar a un suelo arenoso) ante solicitaciones de carga, de acuerdo a su alta permeabilidad y configuración de macroporos, obsérvese la relación de vacíos en la Tabla 1, (Ruge & Cunha, 2011).
Esta situación puede ser evidenciada en la Figura 1, donde se muestra un ensayo porosimétrico de mercurio que relaciona el tamaño del poro de la muestra, con el volumen de poros acumulado, dado por la cantidad de mercurio inyectado. También se presenta a la derecha, la derivada del volumen que arroja los picos correspondientes a los puntos de inflexión de la gráfica de la izquierda, estos picos revelan la presencia de macroporos dominantes en la muestra.
2.2 Pruebas de carga in situ
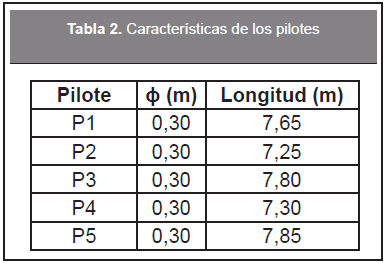
Se ejecutaron cinco pilotes preexcavados mecánicamente con diámetro (φ) de 30 cm e instrumentados a lo largo del fuste. Las características de los pilotes son presentadas en la Tabla 2.
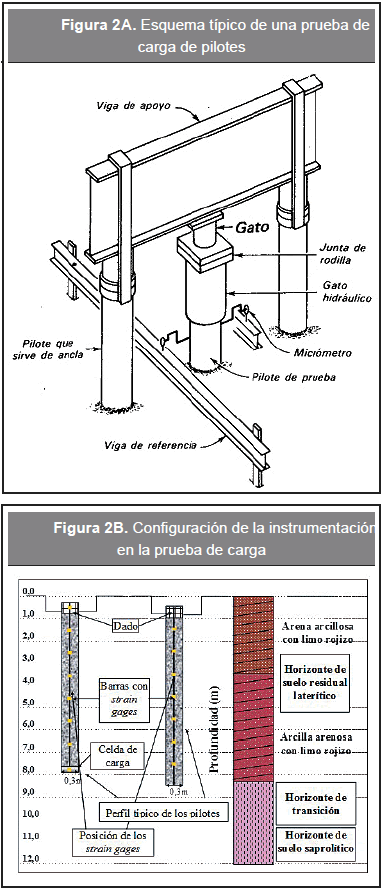
Los pilotes fueron alineados y posicionados con espaciamiento de 1,5 m. Antes de las pruebas de carga se realizó una excavación de 0,5 m de profundidad y 0,9 m de ancho en torno a los pilotes y se cubrieron superficialmente con una lechada para garantizar la nivelación para el montaje del sistema de celdas de carga y extensómetros, y la posterior realización de los ensayos de integridad del pilote (PIT). Para conformar el sistema de reacción necesario para la ejecución de las pruebas de carga, se usaron cinco pilotes de reacción excavados mecánicamente con 0,5 m de diámetro y 10 m de longitud, reforzados con cuatro barras de acero de 25 mm a lo largo del fuste. Con el fin de obtener información relevante a la transferencia de carga con la profundidad, los pilotes ensayados fueron instrumentados empleando extensómetros eléctricos de resistencia, en pares al mismo nivel, en posición diametralmente opuesta, con ligación tipo ¼ de puente. Las celdas de carga utilizadas en los pilotes P1, P2 y P4, fueron constituidas por dos placas de 29 cm de diámetro, ligadas por un tubo de aluminio de 25 cm de longitud, donde fueron colocados cuatro «strain gages» enlazados a manera de conexión puente completa como se observa en la Figura 2A.
Las pruebas de carga estáticas acogen las recomendaciones de la norma NBR-12131 (ABNT, 1991b). La carga fue realizada de forma lenta en escalones de carga progresivos. La aplicación de la carga fue realizada por un gato hidráulico con capacidad para 1000 kN accionado por una bomba manual. La lectura de carga aplicada se midió a través de una celda de carga eléctrica, con capacidad para 500 kN, instalada entre el gato y la viga metálica. En la lectura de los desplazamientos de los pilotes se utilizaron seis extensómetros de sensibilidad de 10-5 m, de los cuales cuatro se colocaron en la parte superior en posiciones diametralmente opuestas y dos laterales como se puede observar en la Figura 2B.
2.3 Modelo computacional
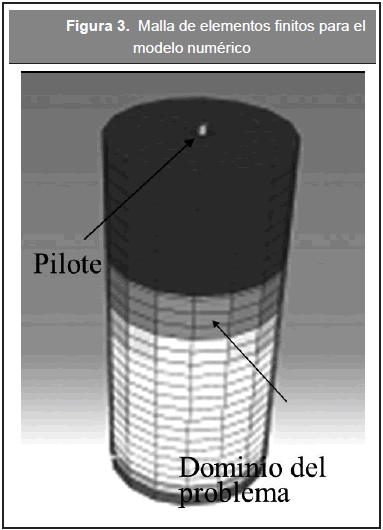
Para la fase de modelación numérica de la prueba de carga se utilizó el programa de elementos finitos ABAQUS, al cual se le insertó una subrutina (UMAT) de cálculo (detalles de la UMAT en Mendoza et al., 2011 y Gudehus et al., 2008, que permite emplear la ecuación constitutiva hipoplástica como se observa en la Tabla 3 y la Figura 3.
Es importante destacar que en este tipo de problemas geotécnicos, la selección adecuada de la interface suelo-pilote interfiere en los resultados finales de la simulación. En este caso en particular, se modeló la interacción mediante un contacto directo nodo-cara (Node-to-Face Contact) proporcionado por el programa cargade elementos finitos escogido que resuelve este tipo de contacto en cualquier análisis típico, donde se desea implementar una condición de fricción (dependiente del ángulo de fricción) entre dos materiales, por medio de una teoría elastoplástica tipo Mohr-Coulomb.
2.3.1 Modelo constitutivo de referencia (Mašín, 2005)
El modelo constitutivo de referencia escogido fue la ecuación constitutiva hipoplástica de Mašín (2005), la cual también es conocida como «hipoplasticidad para arcillas». Esta ecuación conserva la esencia de la definición básica de la Hipoplasticidad formulada por von Wolffersdorff (1996) y por otros autores (p.e., Niemunis y Herle, 1997; Niemunis et al., 2000; Herle & Kolymbas, 2004; Rondón et al., 2007, 2009; Wichtmann et al., 2010) como se puede apreciar en la Ecuación 1.
De esta ecuación se puede decir que  demarca el tensor de velocidad de esfuerzos llamado comúnmente Zaremba-Jaumann (Kolymbas & Herle, 2003), D es el tensor de elongación de Euler,
demarca el tensor de velocidad de esfuerzos llamado comúnmente Zaremba-Jaumann (Kolymbas & Herle, 2003), D es el tensor de elongación de Euler, 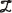 y N son tensores constitutivos de cuarto y segundo orden respectivamente, Mašín (2007) modificó los valores de barotropía fs y picnotropía fd , las cuales son definidas como cantidades escalares que simulan la dependencia del comportamiento mecánico del suelo de acuerdo a la densidad y estado de esfuerzos. Los nombres fueron propuestos por Kolymbas quien se considera el autor de la hipoplasticidad. Debido a que los tensores
y N son tensores constitutivos de cuarto y segundo orden respectivamente, Mašín (2007) modificó los valores de barotropía fs y picnotropía fd , las cuales son definidas como cantidades escalares que simulan la dependencia del comportamiento mecánico del suelo de acuerdo a la densidad y estado de esfuerzos. Los nombres fueron propuestos por Kolymbas quien se considera el autor de la hipoplasticidad. Debido a que los tensores 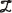 y N se encuentran interrelacionados, modificar la ecuación del modelo de von Wolffersdorff (1996), no es simple, ya que éstos actúan como una regla de flujo hipoplástica. De esta manera se incluyó la función tensorial como se puede ver en la Ecuación 2.
y N se encuentran interrelacionados, modificar la ecuación del modelo de von Wolffersdorff (1996), no es simple, ya que éstos actúan como una regla de flujo hipoplástica. De esta manera se incluyó la función tensorial como se puede ver en la Ecuación 2.
Reemplazado en la Ecuación 1, se tiene:
La condición de estado crítico se puede encontrar sustituyendo  = 0 y fd = 1 en la Ecuación 3, donde
= 0 y fd = 1 en la Ecuación 3, donde  = 0 es solucionada de manera trivial por D ≠ 0 y D = 0 por
= 0 es solucionada de manera trivial por D ≠ 0 y D = 0 por 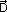 = -B, o tanto esta última ecuación impone una condición sobre el esfuerzo que puede ser hallada eliminando el tensor
= -B, o tanto esta última ecuación impone una condición sobre el esfuerzo que puede ser hallada eliminando el tensor 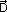 y aplicando la norma a ambos lados de la ecuación, se obtiene para el estado crítico f = ||B|| - 1 = 0. Esta función de esfuerzo puede ser vista como una contraparte del criterio de esfuerzo de estado crítico en elastoplasticidad. Usando estas operaciones, Niemunis (2002) redefinió la ecuación hipoplástica básica, la cual permite definir la regla de flujo, condición de estado crítico e independencia del tensor L. De lo anterior se puede calcular el tensor N como
y aplicando la norma a ambos lados de la ecuación, se obtiene para el estado crítico f = ||B|| - 1 = 0. Esta función de esfuerzo puede ser vista como una contraparte del criterio de esfuerzo de estado crítico en elastoplasticidad. Usando estas operaciones, Niemunis (2002) redefinió la ecuación hipoplástica básica, la cual permite definir la regla de flujo, condición de estado crítico e independencia del tensor L. De lo anterior se puede calcular el tensor N como
Donde la cantidad escalar (denominada grado de no-linealidad) permanece para la condición de estado límite, m es un tensor de segundo orden demarcado con regla de flujo hipoplástico y L es un tensor de cuarto orden hipoelástico como se observa en la Ecuación 1. Si igualamos la Ecuación 1 y 4 se llega a la llamada «hipoplasticidad generalizada».
La formulación matemática de y otros factores se presenta a continuación:
Donde c2 es calculado como:
Para el cálculo del factor c1, se define el parámetro constitutivo r como la relación del módulo volumétrico en compresión isotrópica (Ki) y el módulo de corte no drenado (Gi) para ensayos iniciando desde un estado isotrópico normalmente comprimido. Usando el modelo propuesto se llega a los valores de Ki y Gi,
De la definición del modelo se conoce que el parámetro, por lo tanto se puede encontrar:
T es el tensor de esfuerzos, 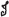 denota el tensor unitario de cuarto orden con componentes
denota el tensor unitario de cuarto orden con componentes 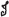 ijkl = δikδjl, φc es el ángulo de fricción crítico y los factores fs y fd tienen en cuenta la influencia que ejercen sobre el comportamiento del material, la presión media ejercida (barotropía) y la densidad del mismo (picnotropía). fs y fd se describen por medio de las siguientes ecuaciones:
ijkl = δikδjl, φc es el ángulo de fricción crítico y los factores fs y fd tienen en cuenta la influencia que ejercen sobre el comportamiento del material, la presión media ejercida (barotropía) y la densidad del mismo (picnotropía). fs y fd se describen por medio de las siguientes ecuaciones:
Donde fdi es el factor de picnotropía para los estados normalmente comprimidos y equivale a fdi = 2α, el valor de α es igual a:
El modelo está basado en el estado crítico de la mecánica de suelos y sus correspondientes parámetros (φc, N, λ*, K* y r) teniendo interpretación física similar a los parámetros del modelo Cam Clay Modificado. N y λ* localizan la posición e inclinación de la NCL (Normal Compression Line) que es la línea que simula el proceso de carga isotrópica del suelo en el espacio (e-p) de acuerdo con una modificación de la formulación de Butterfield (1979). La variable K*, controla la inclinación de la línea de descarga isotrópica y el parámetro la rigidez de corte. Así mismo, 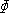 c es el ángulo de fricción del estado crítico que reproduce el tamaño del locus del estado crítico en el espacio de esfuerzos, según Matsuoka & Nakai (1974).
c es el ángulo de fricción del estado crítico que reproduce el tamaño del locus del estado crítico en el espacio de esfuerzos, según Matsuoka & Nakai (1974).
El modelo considera como variable de estado la relación de vacíos e requiriendo pocos parámetros, de igual forma éste predice el comportamiento no lineal e complejo de los suelos (Masín & Herle, 2005), incluyendo la variación de rigidez con la dirección de carga (Masín et al., 2006) y la influencia de la densidad relativa sobre la rigidez del suelo, comportamiento volumétrico y el ángulo de fricción pico (Hajek & Masín, 2006). Vale la pena destacar que el modelo hipoplástico no incluye de manera directa la SBS (State Boundary Surface), ni la BS (Boundary Surface), por tal razón (Masín & Herle, 2005) demostraron que el modelo contiene implícitamente una SBS propia para el modelo desarrollado con forma y tamaño expresados analíticamente.
3. RESULTADOS
3.1 Prueba de carga in situ
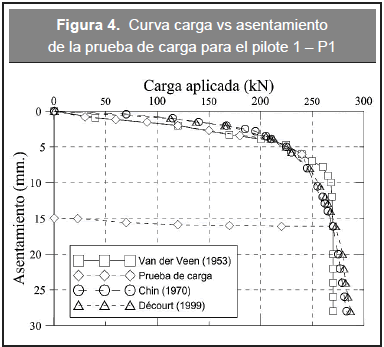
En la Figura 4 se presentan los resultados obtenidos en la prueba de carga para el pilote P1 (Mota et al, 2002) y las cargas de ruptura previstas a partir de los métodos de extrapolación de ruptura convencional, según el método de Van der Veen (1953), Chin (1970) y Décourt (1999).
De acuerdo a Décourt et al. (1996) la ruptura convencional es definida como la carga correspondiente para que el asentamiento del pilote sea el 10 % de su diámetro. Analizando las curvas carga-desplazamiento obtenidas en las pruebas de carga realizadas, como se grafica en la Figura 4, se reporta que los pilotes no alcanzaron la falla según este criterio, ya que el desplazamiento máximo que experimentó el pilote fue de 5,3 % su diámetro, por lo tanto se deduce que el rompimiento estructural del suelo no ocasionó el asentamiento después del tramo lineal en la curva; es decir asentamientos mayores al 10 % del diámetro, se consideran como rompimiento estructural debajo de la punta del pilote, en este caso al ser menor, es posible explicar el fenómeno expuesto por Meneses et al (2005), evidenciando una pérdida de adhesión en la interface suelo-pilote.
3.2 Parámetros hipoplásticos
En la Figura 5 se puede observar el proceso de calibración de parámetros del modelo basados en un ensayo edométrico realizado al suelo en estudio, sobre una muestra a 6 m de profundidad, vale la pena resaltar que debido a la uniformidad del suelo en toda la longitud de los pilotes, se decidió usar una muestra representativa a la profundidad indicada, para la obtención de los parámetros hipoplásticos del perfil completo.
Para obtener el resto de los parámetros (r y φc), fue usado un ensayo triaxial drenado a diferentes presiones de confinamiento, como se ilustra en la Figura 6.
El parámetro r puede ser definido directamente como la relación entre el modulo volumétrico bulk y el modulo de corte para ensayos que inician de u estado de esfuerzos isotrópico normalmente consolidado, sin embargo debido a que el modelo prevé una degradación gradual de la rigidez de corte, es aconsejable encontrar un valor apropiado del parámetro r mediante un análisis paramétrico, como se puede observar en la Figura 7. Este enfoque es aceptable porque no existe una interrelación con otros parámetros del modelo (Masín & Herle, 2005).
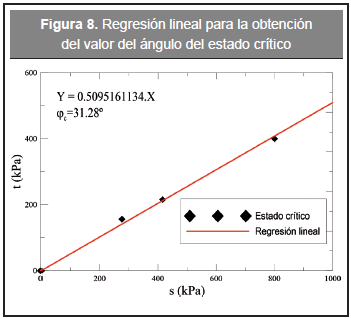
El ángulo de fricción crítico φc es un parámetro del suelo, ya que una vez alcanzado este no cambia durante el proceso de deformación o de carga. El φc es una relación de los esfuerzos principales en el estado crítico y es la base teórica de la mayoría de los modelos constitutivos modernos, puesto que define el estado crítico o último, propio de cada material, que es aquella fase en la cual el material presenta deformaciones infinitas teóricas con esfuerzo y volumen constante. Para encontrar este parámetro fue necesario realizar una regresión lineal a través de los puntos del estado critico de los ensayos triaxiales utilizados, para esfuerzo de confinamiento de 120, 200 y 400 kPa, y basados en las invariantes del MIT s= (σ1+σ3)/2 y t= (σ1-σ3)/2 como se observa en la Figura 8.
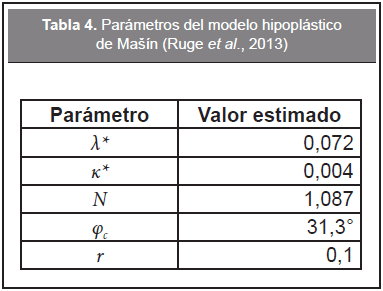
En la Tabla 4 se pueden observar los parámetros medios del modelo obtenidos de ensayos edométricos y triaxiales, y calibrado mediante simulaciones de element-test.
3.3 Simulación
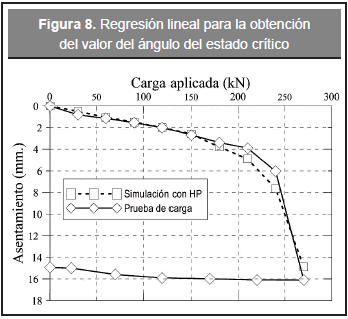
En la Figura 9 se pueden observar la modelación numérica realizada a la prueba de carga, utilizando la ecuación constitutiva de Mašín (2005). Se resalta de la simulación, la capacidad que posee el modelo hipoplástico de reproducir adecuadamente el tramo lineal (hasta 200kPa), sin embargo en el intervalo elastoplástico existe una leve separación de la medición in situ hasta el final de la curva de compresión. Es importante recalcar que aunque el comportamiento después de 200 kN de carga se puede asociar con el fenómeno de colapso por el aumento de asentamiento en un delta pequeño de carga, este se debe más a una pérdida de fricción (adhesión) lateral del pilote, ya que la prueba no fue realizada en condiciones saturadas (escenario obligatorio para inducir colapso). Adicionalmente en la Figura 9 no se presenta la rama de descarga de la simulación, ya que el modelo de referencia usado no es capaz de reproducir esta curva en la prueba.
4. CONCLUSIONES
Como se mencionó en la introducción, el objetivo de este artículo es intentar simular el comportamiento de la curva carga-asentamiento, de una prueba de carga en un pilote individual, fundado sobre una arcilla porosa con características metaestables. Uno de los factores que influye en la metaestabilidad de este tipo de suelo es la degradación del cementante, ya sea por una acción externa (carga) o una acción interna (saturación) y la parcial saturación del suelo. El modelo constitutivo usado en la modelación numérica no posee un parámetro que considere este tipo de comportamiento en el suelo, por tal razón después del tramo lineal, donde eventualmente puede existir un leve rompimiento de la estructura, el modelo no reproduce fielmente este comportamiento, ni consecuentemente en la etapa de descarga. De acuerdo a lo anterior, el modelo constitutivo usado no puede ser validado para el uso en este tipo de suelo, ya que no tiene en cuenta comportamientos tipícos de este suelo tropical, como es la degradación del cementante y la no saturación del sistema.
Como se puede observar en los resultados, la prueba de carga no alcanza la ruptura, sin embargo presenta un aumento de asentamiento que tiende a relacionarse con el fenómeno de colapso, el cual solo ocurre en condición saturada, no obstante la prueba de carga en el pilote escogido no fue realizada bajo este escenario, por lo cual el evento asociado se debe en realidad a la perdida de adherencia entre la interfase suelo-pilote que ocasionó el aumento del asentamiento.
En futuras investigaciones se pretende modelar numéricamente este tipo de pruebas de carga en suelos porosos metaestables, usando una ley constitutiva que incluya un parámetro que simule la respuesta no saturada del suelo y la degradación del cementante, acompañando de manera mas correcta de toda la curva carga-asentamiento en la prueba de carga (p.e., Mašín, 2007).
5. AGRADECIMIENTOS
Los autores agradecen a la Dra. Neusa Mota y al grupo GPFees del Posgrado en Geotecnia de la Universidad de Brasilia (UnB), por la colaboración en la ejecución e instrumentación de los ensayos de campo y pruebas de carga en el campo experimental y a la Universidad de los Andes por el apoyo en la modelación numérica.
REFERENCIAS
Boyce, H. R. (1980). A Non-linear Model for the Elastic Behaviour of Granular Materials Under Repeated Loading. In: Proceedings International Symposium on Soils under Cyclic and Transient Loading, Swansea, U.K., vol. 1, pp. 285-294. [ Links ]
Butterfield, R. (1979). A Natural Compression Law for Soils. Geotechnique, 29(4), pp. 469-480. [ Links ]
Chin, F. K. (1970). Estimation of the Ultimate Load of Piles from Tests nor Carried to Failure. In: 2nd Southeast conference on Soil Engineering, Singapore, pp. 91-92. [ Links ]
Cunha, R. P. y Camapum de Carvalho, J. (1997). Analysis of the Behavior of a Drilled Pier Foundation in a Weathered, Foliated and Folded Slate. In: XIV International Congress of Soil Mechanics and Foundation Engineering, Hamburgo, Germany, pp. 785-786. [ Links ]
Décourt, L. (1999). "Behavior of foundations under working load conditions". In: 11th Pan-American Conferenvce on Soil Mechanics and Geotechnical Engineering, Foz do Iguaçu, No. 4, pp. 453-488. [ Links ]
Gudehus G., A. Amorosi, A. Gens, I. Herle, D. Kolymbas, D. Masín, D. Muir Wood, R. Nova, A. Niemunis, M. Pastor, C. Tamagnini, and G. Viggiani (2008). The Soilmodels. Info Project. International Journal for Numerical and Analytical Methods in Geomechanics, 32(12):1571-1572. [ Links ]
Hau, K. W., McDowell, G. R., Zhang, G. P. and Brown, S. F. (2005). The Application of a Three-Surface Kinematic Hardening Model to Repeated Loading of thinly surfaced pavements. Granula Matter, 7(2-3), July, pp. 145-156. [ Links ]
Herle, I. Hypoplastizität und Granulometrie einfacher Korngerüste. Ph. D., Thesis, Schriftenreihe des Institutes für Bodenmechanik und Felsmechanik der Universität Fridericana in Karlsruhe, Issue 142, 1997. [ Links ]
Herle, I. and Gudehus, G. (1999). Determination of Parameters of a Hypoplastic Constitutive Model from Properties of Grain Assemblies. Mechanics of Cohesive-frictional Materials, 4(5), pp. 461-486. [ Links ]
Herle, I. and Kolymbas, D. (2004). Hypoplasticity for Soils with Low Friction Angles. Computer and Geotechnics, 31(5), pp. 365-373. [ Links ]
Hicher, P. and Chang, C. S. (2006). Anisotropic Nonlinear Elastic Model for particulate materials. Journal of Geotechnical and Geoenvironmental Engineering, 132, (8), pp. 1052-1061. [ Links ]
Hicher, P., Daouadji, A. and Fedghouche, D. Elastoplastic Modelling of the Cyclic Behaviour of Granular Materials. Unbound Granular Materials - Laboratory testing, In-situ testing and modelling, Gomes Correia, A. (Ed.), A.A. Balkema, Rotterdam, 1999, pp. 161-168. [ Links ]
Hicks, R. G. and Monismith, C. L. (1972). "Prediction of the resilient response of pavements containing granular layers using Non-linear Elastic Theory". In: Proceedings of the 3rd International Conference on Asphalt Pavements, Vol. 1, pp. 410-429. [ Links ]
Hoff, I. and Nordal, R. S. Constitutive model for unbound granular materials based in Hyperelasticity. Unbound Granular Materials - Laboratory Testing, In-situ Testing and Modelling, Gomes Correia editor, Balkema, Rotterdam, 1999, pp. 187-196. [ Links ]
Hornych, P., Kazai, A. and Piau, J.-M. Study of the Resilient Behaviour of Unbound Granular Materials. Proc. BCRA'98, Trondheim, Nordal and Refsdal editor's, vol. 3, 1998, pp. 1277-1287. [ Links ]
Gudehus, G. (1996). A Comprehensive Constitutive Equation for Granular Materials. Soils and Foundations, 36(1), pp. 1-12. [ Links ]
Matsuoka, H. y Nakai, T. (1977). Stress-strain Relationship of Soil Based on the SMP in Constitutive Equations of Soils. Proc. of Specialty Session 9, In: IX Int. Conf. Soil. Mech. Found. Eng., Tokyo, Japón, pp. 153-162. [ Links ]
Masín D. (2005). A Hypoplastic Constitutive Model for Clays. International Journal for Numerical and Analytical Methods in Geomechanics, 29(4), pp. 311-336. [ Links ]
Masín, D., y Herle, I. (2005). State Boundary Surface of a Hypoplastic Model for Clays. Computers and Geotechnics, 6(32), pp. 400-410. [ Links ]
Masín, D., Tamagnini, C., Viggiani, G., y Constanzo, D. (2006). Directional Response of a Reconstituted Fine Grained Soil. Part II: Performance of Different Constitutive Models. International Journal for Numerical and Analytical Methods in Geomechanics, 13 (32), pp. 1303-1336. [ Links ]
Masín, D. (2006). Hypoplastic Models for Fine-grained soils. Ph.D. Thesis, Institute of Hydrogeology, Engineering Geology and Applied Geophysics, Charles University, Prague. [ Links ]
Masín, D. (2007). A Hypoplastic Constitutive Model for Clays with Meta-Stable Structure. Canadian Geotechnical Journal, 44(3), pp. 363-375. [ Links ]
Mendoza, C.C., Ruge J.C., Cunha, R.P.; Lizcano, A.A. Comportamiento mecánico de excavaciones de pequeño diámetro para suelo estructurado pilote Alluvial Anker. In: 14th. Pan-American Conf. on soil Mech. and Geot. Engineering, 2011, Toronto. v. CD Rom. p. 1-10. [ Links ]
Menezes, S., Carvalho D., y Albuquerque PJR. (2005). Estimativa de cargas residuais obtidas na ponta de estacas cravadas em solos porosos. Semina: Ciencias exactas e Tecnologica, Londrina. v. 26. No.1. pp. 3-10. [ Links ]
Mota, N. M. B., Farias, M. P., Cunha, R. P y Parente, R. C. P. (2002). Avaliação de ensaios de CPT e DMT na obtenção do perfil estratigráfico de solos lateríticos de Brasília - DF. In: XVI Congresso Argentino de Mecânica de Suelos e Ingeniería Geotécnica (CAMSIG). Trelew-Chubut-Patagônia-Argentina, Sessão VII, CD-Rom. [ Links ]
Niemunis, A., Grandas, C. E. and Prada, L. F. (2009). Anisotropic Visco-Hypoplasticity. Acta Geotechnica, 4(4), December, pp. 293-314. [ Links ]
Niemunis, A. and Herle, I. (1997). Hypoplastic Model for Cohesionless Soils with Elastic Strain Range. Mechanics of Cohesive frictional Materials, 4(2), pp. 279-299. [ Links ]
Niemunis, A.; Nuebel, K. and Karcher, Ch. The Consistency Conditions for Density Limits of Hypoplastic Constitutive Law. In Publications of TASK, Gdansk, 2000, pp. 412-420. [ Links ]
Niemunis A. (2002). Extended Hypoplastic Model for Soils. Habilitation Thesis, Ruhr-University, Bochum. [ Links ]
Rondón, H. A., Wichtmann, T., Triantafyllidis, Th. y Lizcano, A. (2007). Hypoplastic Material Constants for a Well-Graded Granular Material (UGM) for Base and Subbase Layers of Flexible Pavements. Acta Geotechnica, 2(2), pp. 113-126. [ Links ]
Rondón, H. A., Wichtmann, T., Triantafyllidis, Th. and Lizcano, A. (2009). Comparison of Cyclic Triaxial Behavior of Unbound Granular Material Under Constant and Variable Confining Pressure. Journal of Transportation Engineering, 135(7), pp. 467-478. [ Links ]
Rondón, H. A. Comportamiento de un material granular no tratado en ensayos triaxiales cíclicos con presión de confinamiento constante (PCC) y variable (PCV). Tesis de Doctorado en Ingeniería, Universidad de Los Andes, Bogotá D.C. (Colombia), 2008. [ Links ]
Ruge, J. C. y Cunha, R. P. (2011). Determinación de parámetros geomecánicos en suelos metaestables, mediante el uso de ensayos de campo. Pre-til, 9(24) enero, pp. 59-74. [ Links ]
Ruge J. C., Cunha R. P. y Masín D. (2013). Results of Unsaturated Tests on Metastable Soils. Advances in Unsaturated Soils. Proceedings of the First Pan-American Conference on Unsaturated Soils, Cartagena, Colombia, pp. 469-474. [ Links ]
Taciroglu, E. and Hjelmstad, K. D. (2002). Simple nonLinear Model for Elastic Response of Cohesionless Granular Materials. Journal of Engineering Mechanics, 128, pp. 969-978. [ Links ]
Tatsuoka, F., Ishiara, M., Uchimura, T. and Gomes Correia, A. Non-linear Resilient Behaviour of Unbound Granular Materials Predicted by the Cross-Anisotropic Hypo-Quasi-Elasticity Model. Unbound Granular Materials - Laboratory Testing, In-situ Testing and Modelling, Gomes Correia editor, Balkema, Rotterdam, 1999, pp. 197-206. [ Links ]
Van der Veen, C. (1953). The Bearing Capacity of a Pile. In: 3rd International Conference on Soil Mechanics and Foundation Engineering, Zurich, No. 2, pp. 84-90. [ Links ]
Von Wolffersdorff, P. A. (1996). A Hypoplastic Relation for Granular Materials with a Predefined Limit State Surface. Mechanics of Cohesive-Frictional Materials, 1(3) July, pp. 251-271. [ Links ]
Wichtmann, T. Explicit Accumulation Model for Non-cohesive Soils under Cyclic Loading. Ph.D. Thesis, Des Institutes für Grundbau und Bodenmechanik der Ruhr - Universität Bochum, Germany, 2005. [ Links ]
Wichtmann, T., Niemunis, A. and Triantafyllidis, Th. (2004). Strain Accumulation in Sand Due to Drained Uniaxial Cyclic Loading. Cyclic Behaviour of Soils and Liquefaction Phenomena, Proc. of CBS04, Bochum, Germany, pp. 233-246. [ Links ]
Wichtmann, T., Niemunis, A. and Triantafyllidis, Th. (2004a ). The Effect of Volumetric and Out-of-Phase Cyclic Loading on Strain Accumulation. Cyclic Behaviour of Soils and Liquefaction Phenomena, Proc. of CBS04, Bochum, Germany, pp. 247-256. [ Links ]
Wichtmann, T., Rondón, H. A., Triantafyllidis, Th. and Lizcano, A. (2010). Prediction of Permanent Deformations in Pavements Using a High-Cycle Accumulation Model. Journal of Geotechnical and Geoenvironmental Engineering, 136(5), pp. 728-740. [ Links ]