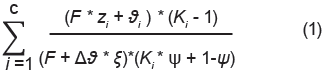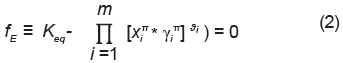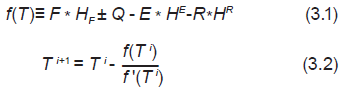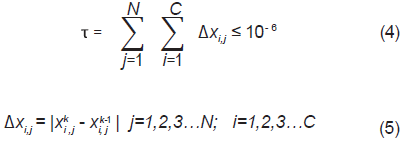CÁLCULO SECUENCIAL DE CASCADAS DE EXTRACCIÓN REACTIVA APLICANDO EL MODELO DE EQUILIBRIO

STEP-BY-STEP CALCULATION OF REACTIVE EXTRACTION CASCADES APPLYING THE EQUILIBRIUM MODEL

CÁLCULO SEQÜENCIAL DE CASCATAS DE EXTRAÇÃO REATIVA APLICANDO O MODELO DE EQUILÍBRIO

Luis Gabriel Prieto Ríos*, Jaime Eduardo Arturo Calvache**, César Augusto Sánchez Correa***

*Ingeniero químico, Fundación Universidad de América. Bogotá, D.C. - Colombia.
**Ingeniero químico, Universidad Nacional de Colombia - Sede Manizales. MsC. en Ingeniería Química, Universidad Nacional de Colombia - Sede Bogotá.
Autor de correspondencia: Arturo Calvache, J. E. (Jaime Eduardo): Fundación Universidad de América. Facultad de Ingeniería - Departamento de Ingeniería Química. Campus de los Cerros: Avda. Circunvalar No. 20 - 53. Bogotá, D.C. - Colombia. Correo electrónico: jaime.arturo@profesores.uamerica.edu.co.
***Ingeniero químico, Universidad Nacional de Colombia - Sede Manizales. MsC. en Ingeniería Química, Universidad Nacional de Colombia - Sede Bogotá.

Artículo recibido: 1-VIII-2013 / Aprobado: 17-IV-2014
Disponible online: 20 de junio 2014
Discusión abierta hasta mayo de 2015

RESUMEN

Se presenta un algoritmo de cálculo etapa por etapa para la simulación de cascadas de extracción reactiva. El fundamento teórico se encuentra en la termodinámica del equilibrio líquido - líquido reactivo. El método puede tratar arreglos en paralelo, contracorriente y cruzados, operando con las especificaciones más importantes en la práctica: división de flujos de solvente y alimento, localización de la zona de reacción, elección de los puntos de alimentación y la especificación del flujo de calor transferido. Para ilustrar la utilidad de las ideas se simularon esquemas tecnológicos de extracción reactiva para la síntesis de n-amilacetato a partir de soluciones acuosas de ácido acético. Aunque los ejemplos se encuentran orientados a demostrar las capacidades del algoritmo, también se pudo establecer que la producción de n-amilacetato por extracción reactiva presenta fuertes limitaciones a la conversión y a la separación y no representa una alternativa interesante para incrementar el valor económico de las corrientes de ácido acético y agua.

PALABRAS CLAVE: extracción reactiva; equilibrio líquido - líquido - reactivo; sistemas de esterificación; n-amilacetato; algoritmo etapa a etapa.

ABSTRACT

A step-by-step calculation algorithm for reactive extraction cascade simulation is presented. Theoretical basis is taken from reactive liquid-liquid equilibrium thermodynamics. This method can be applied to parallel, countercurrent and cross-current arranges and operate the most important practical specifications: splitting of solvent and feed streams, location of reaction zone, choice of feed points and specification of transferred heat flow. To illustrate the usefulness of this approach, reactive extraction technological schemes for synthesis of n-amyl acetate from aqueous acetic acid were simulated. Although examples are designed to prove algorithm adequacy, it was also found that the n-amyl acetate production by reactive extraction has strong limitations to conversion and separation. Besides, it is not an interesting alternative to increase the economic value of acetic acid and water streams.

KEY WORDS: Reactive Extraction; Reactive Liquid-Liquid Equilibrium; Esterification Systems; n-Amyl Acetate; Step-by-Step Calculation Algorithm.

RESUMO

Apresenta-se um algoritmo de cálculo etapa a etapa para a simulação de cascatas de extração reativa. O fundamento teórico se encontra na termodinâmica do equilíbrio líquido - líquido reativo. O método pode ser utilizado para cascatas com contato multiestágio em paralelo, cruzado e contracorrente operando nàs especificações mais importantes na prática: divisão de fluxos de solvente e alimentação, localização da zona de reação química, escolha dos pontos de alimentação e especificação do fluxo de calor transferido. Para ilustrar a utilidade das ideias, foram simulados esquemas tecnológicos de extração reativa para a síntese de n-amil acetato a partir de soluções aquosas de ácido acético. Embora os exemplos são orientados para demonstrar as capacidades do algoritmo, foi igualmente estabelecido que a produção de n-amil acetato por extração reativa tem fortes limitações pela conversão e separação e não representa uma alternativa interessante para aumentar o valor econômico das correntes de ácido acético e água.

PALAVRAS-CHAVE: Remoção de equilíbrio reativo Liquefeito - sistemas de esterificação reativa; n-amylacetate algoritmo passo a passo - líquidos.

1. INTRODUCCIÓN

La extracción reactiva (ER) es la combinación de la extracción en fase líquida y la reacción química para mejorar la capacidad de un solvente o para efectuar reacciones limitadas por el equilibrio. La principal limitación de estos procesos consiste en que deben operar a condiciones donde la separación de fases líquido - líquido y la reacción química tengan lugar simultáneamente. (Krishna, 2002; Kulprathipanja, 2002; Gutiérrez, 2008; Górak, 2011). Cuando existe «compatibilidad» entre reacción y separación es posible desplazar el equilibrio químico por la remoción in situ del producto formado. Esta posibilidad ofrece principalmente dos ventajas en relación a procesos en fase homogénea: 1) se incrementa la conversión y la selectividad, y 2) se disminuye el número de corrientes de reciclo, los costos de procesamiento y de capital (Krishna, 2002; Kulprathipanja, 2002; Gutiérrez, 2008; Górak, 2011). Las aplicaciones de la ER más conocidas en la industria se relacionan con la producción de combustibles (especialmente biodiesel), antibióticos, acetatos, y la recuperación de ácidos y alcoholes resultantes de procesos de fermentación (Krishna, 2002; Kulprathipanja, 2002; Pai et al., 2002; Bouraqadi et al., 2007; Cadavid et al., 2011).

La solución del modelo matemático controlado por el equilibrio (equilibrio químico más equilibrio de fases) constituye una herramienta para el análisis básico de procesos de ER. En este nivel se establecen los siguientes aspectos: a) formas de contacto, b) localización de la zona de reacción, c) la máxima conversión y d) el uso de diferentes esquemas tecnológicos (Gorissen, 2003; Cardona y Gutiérrez, 2007a-b; Gutiérrez, 2008). La cuantificación de estos aspectos para arreglos de extractores reactivos requiere de algoritmos robustos capaces de manejar diferentes conjuntos de especificaciones. Por esta razón resulta pertinente la investigación de técnicas numéricas para la solución del modelo de equilibrio en procesos de ER. Adicionalmente debe considerarse que los simuladores comerciales de procesos químicos (siendo el más representativo el ASPEN PLUS®) no disponen de módulos especializados para la simulación de cascadas de ER, aunque es posible obtener aproximaciones por la combinación de reactores y separadores líquido - líquido.

En este trabajo se extendió el algoritmo de cálculo para cascadas de extracción sin reacción propuesto por Sánchez et al. (2009). Se observó que esta estrategia es válida para cascadas reactivas porque se fundamenta en el cálculo de los diferentes tipos de flash. El método puede tratar especificaciones como el tipo de arreglo (paralelo, cruzado y contracorriente), la localización de la zona de reacción (número de etapas reactivas en arreglos híbridos) y la transferencia de calor (etapas isotérmicas, adiabáticas y con flujo de calor especificado). El caso con el flujo de calor especificado constituye una mejora en relación a los trabajos presentados en la literatura donde generalmente no se incluye este efecto de manera independiente (Minotti et al., 1998; Rivera, 2004; Rivera y Cardona, 2004; Gutiérrez, 2008). El fundamento del método se encuentra en los cálculos de equilibrio líquido - líquido - reactivo (ELLR), ELLR con transferencia de calor (ELLRT)y el análisis de estabilidad material desarrollado por Michelsen (Michelsen, 1982a-b; Michelsen y Mollerup, 2007).

Una cascada de ER se trata como un arreglo de etapas en equilibrio en el que cada extractor reactivo se modela como un flash con reacción química. El tipo de flash es determinado por las especificaciones. Por ejemplo en cascadas isotérmicas o adiabáticas se trata del flash isotérmico o adiabático, respectivamente. Este punto de vista permite cubrir fácilmente diferentes tipos de configuraciones y sitúa el problema de resolver el modelo de una cascada reactiva en el ámbito de la termodinámica. Por esta razón la metodología está centrada en el uso ordenado de cálculos del ELLR (o ELLRT) en un algoritmo etapa por etapa para la simulación de cascadas de ER. Las soluciones de las cascadas de ER (en particular los perfiles de composición) son representadas utilizando las fracciones molares transformadas de Ung y Doherty (1995) con el fin de disminuir la dimensión del espacio de composiciones y demostrar la posibilidad de utilizar los métodos gráficos de la extracción convencional sobre planos de fases reactivos en coordenada transformada.

El desempeño del algoritmo se ilustra mediante ejemplos relacionados con la producción de n-amilacetato por extracción reactiva. Este sistema constituye un objeto de estudio apropiado por dos razones: 1) la presencia de una región de solubilidad parcial reactiva favorable para la separación líquido - líquido y 2) los procesos de destilación se encuentran limitados por la existencia de múltiples azeótropos.

2. METODOLOGÍA

En esta sección se presentan los procedimientos empleados para el cálculo del equilibrio de fases reactivo y la forma en que estas rutinas de cálculo pueden combinarse para resolver una cascada de etapas reactivas. Para calcular el ELLR y el ELLRT se modificó la variante reactiva del algoritmo de Rachford y Rice sugerida por Henley y Rosen (1973). Para las cascadas de ER se utilizó el procedimiento secuencial sugerido por Sánchez et al., (2009) para tratar el caso no reactivo.

2.1. Flash isotérmico líquido - líquido reactivo

Considere el extractor reactivo representado en la Figura 1. Un Flash Isotérmico se define cuando se especifica la alimentación (Flujo y composición), la temperatura y la presión. El problema consiste en calcular la composición de las fases (llamadas convencionalmente fase refinados, FR y fase extractos, FE) y la relación entre sus cantidades (la fracción de extractos) (Henley y Rosen, 1973). En general la solución del sistema de ecuaciones que modela el separador reactivo en la Figura 1 puede ser tratada con cuatro alternativas: a) corrección simultánea como el Newton - Raphson y sus variaciones (Bonilla et al., 2008), b) técnicas de continuación utilizando homotopías (Jalali y Seader, 1999 y 2000), c) métodos de relajación (Wasylkiewicz y Ung, 2000) y d) procedimientos secuenciales basados en las ecuaciones de Rachford y Rice (Henley y Rosen 1973; Sánchez et al., 2011).

Figura 1

En el presente trabajo se utiliza una generalización del algoritmo de Rachford y Rice para incluir el efecto de una reacción química como lo ilustra la Figura 2. El origen de las ideas se encuentra en el trabajo de Henley y Rosen (1973). El diagrama de flujo de información como lo muestra la Figura 2 desacopla el equilibrio de fases y el equilibrio químico: los dos lazos internos guardan correspondencia con el algoritmo de Rachford y Rice de los sistemas no reactivos (Henley y Rosen, 1973; Henley y Seader, 2006; Sánchez, 2009) y se ejecutan manteniendo constante la coordenada de reacción; el lazo más externo tiene como propósito verificar el cumplimiento de la condición de equilibrio químico. El diagrama de flujo en la Figura 2 se simplifica para el caso no reactivo cuando la reacción no procede (ξ = 0) eliminando el ciclo iterativo más externo.

Figura 2

La función objetivo del ciclo interno, llamada función de Rachford y Rice, resulta de combinar los balances de materia, las relaciones de equilibrio líquido - líquido y las restricciones de las fracciones molares (Henley y Rosen, 1973):

En la ecuación anterior las variables tienen el siguiente significado: ψ es la fracción de extractos (E/F), Ki es el coeficiente de distribución del componente i (γ_i^R/γ_i^E), z_i es la fracción molar del componente i en el alimento, Δ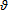 es el cambio en las moles ocasionado por la reacción (la suma de los coeficientes estequiométricos, positivo para productos y negativo para reactivos) y ξ es la coordenada de la reacción. En ausencia de reacción (ξ = 0), la ecuación (1) toma la forma de la función de Rachford - Rice para sistemas no reactivos (Henley y Rosen, 1973; Henley y Seader, 2006). La Ecuación 1 es general y aplica tanto para sistemas con o sin cambio en el número de moles. La función objetivo para el lazo externo como se observa en la Figura 2 es la condición de equilibrio químico para sistemas con una reacción en la fase líquida (Smith et al., 2007):

Figura 2

En la Ecuación 2 π se refiere a una de las fases en equilibrio (extractos o refinados) y K_eq es la constante de equilibrio químico. La convergencia del algoritmo de Rachford y Rice para sistemas reactivos se encuentra fuertemente influenciada por los estimados iniciales. Esta situación puede tratarse generando los estimados iniciales en dos pasos: 1) resolver el equilibrio químico en fase homogénea y 2) analizar la estabilidad material de la solución resultante después de alcanzar el equilibrio químico. Si la solución es materialmente estable el equilibrio es homogéneo, por el contrario, si la solución es materialmente inestable, el equilibrio es heterogéneo. Los resultados del análisis de estabilidad material resultan en excelentes estimados para el cálculo del ELL (Michelsen, 1982a-b; Firoozabadi, 1999; Michelsen y Mollerup, 2007) y el ELLR (Jalali y Seader, 1999 y 2000; Wasylkiewicz y Ung, 2000; Sánchez, 2011). Observe que este procedimiento de inicialización es equivalente a requerir que la mezcla seudoinicial en equilibrio químico resulte materialmente inestable.

Debido a que la separación de fases y la reacción química toman lugar a las condiciones del separador como se puede observar en la Figura 1, el algoritmo presentado en la Figura 2 es también válido para extractores reactivos con múltiples alimentos utilizando la composición de la solución que resultaría de mezclar en un proceso no reactivo los diferentes alimentos (Prieto, 2012). Debe observarse que una vez resuelto el flash isotérmico reactivo es posible calcular el flujo de calor transferido aplicando un balance de energía sobre el extractor reactivo. En consecuencia con lo anterior: en un cálculo de flash isotérmico el balance de energía se encuentra desacoplado de los balances de materia y las relaciones de equilibrio.

2.2. Flash líquido - líquido reactivo con transferencia de calor

En relación a la Figura 1 se define un flash líquido - líquido con transferencia de calor cuando se especifica la alimentación (flujo molar, temperatura, presión y composición), la presión de operación del extractor reactivo y el flujo de calor transferido. El problema consiste en calcular la composición de los refinados y los extractos, la fracción de extractos y la temperatura de operación. Debido al conjunto de especificaciones el balance de energía se encuentra acoplado con los balances de materia y las relaciones de equilibrio.

En este trabajo se observó que la estrategia de solución clásica presentada en los libros de texto para sistemas no reactivos (Manning y Thompson, 1995; Henley y Rosen, 1973; Henley y Seader, 2006; Sánchez, 2009) resultaba válida para el flash líquido - líquido reactivo con transferencia calor. El diagrama de flujo de información se representa en la Figura 3 y debe observarse que se reduce al algoritmo clásico si se usa el ELL en lugar del ELLR (ver bloque 3 de la Figura 3). La temperatura se varía en un ciclo externo aplicando un paso del Newton - Raphson sobre una función objetivo definida a partir del balance de energía:

Figura 3

2.3. Cascadas de extracción reactivas

La Figura 4 ilustra los tres arreglos en cascada más frecuentes (en paralelo, cruzado y contracorriente) para procesos de extracción en fase líquida (Treybal, 1968; Rydberg, 2004; Benítez, 2009). Las cascadas se diferencian en dos aspectos: 1) el sentido en el que fluyen las corrientes diferencia los arreglos en paralelo y cruzados frente al arreglo en contracorriente y 2) el empleo de uno o varios flujos de solvente diferencia el arreglo cruzado de los arreglos en paralelo y contracorriente.

Figura 4

Desde el punto de vista computacional, las cascadas en paralelo y cruzada corresponden a problemas simples porque los cálculos pueden efectuarse de manera secuencial siguiendo el orden que físicamente corresponde con el arreglo. En las Figuras 4-a y Figura 4-b se observa que cada extractor reactivo sólo es afectado por el extractor inmediatamente anterior y en consecuencia no existe recirculación de corrientes y tampoco de información. En síntesis: en los arreglos en paralelo y cruzado los extractores reactivos se encuentran desacoplados.

El modelo de equilibrio total aplicado a cascadas en paralelo lleva fácilmente a concluir que sólo es necesario un extractor reactivo porque no es posible incrementar la conversión de equilibrio sin manipular las condiciones de operación de las etapas posteriores. Si se requiere aumentar la conversión incluyendo más extractores debe «programarse» la temperatura de la etapa 2 y siguientes para desplazar el equilibrio convenientemente. Las soluciones del modelo de equilibrio total corresponden con los límites asintóticos del modelo controlado por la cinética para grandes tiempos de residencia logrados con varios extractores (Minotti et al., 1998; Gutiérrez, 2008).

En el arreglo en contracorriente como se puede observar en la Figura 4-c un extractor reactivo se encuentra acoplado con los extractores posterior y anterior dando lugar a un proceso de cálculo que requiere la consideración completa de la cascada. En principio, los métodos empleados en la destilación reactiva (DR) pueden ser adaptados para resolver el modelo matemático, no obstante, en el área específica de la simulación, no se encuentran en la literatura abierta trabajos que consideren las adaptaciones necesarias para este fin.

Para la solución de cascadas en contracorriente se generalizó el método propuesto por Sánchez et al., (2009) para tratar arreglos no reactivos. Debido a que este método se encuentra fundado en las rutinas para los diferentes tipos de flash (isotérmico, adiabático, de fracción vaporizada, etc.) puede adaptarse para sistemas con reacción química empleando las versiones reactivas de los diferentes tipos de flash. La Figura 5 muestra el diagrama de flujo de información. Este algoritmo es de fácil implementación porque sólo cuenta con un lazo iterativo y manipula las ecuaciones por subconjuntos asociados con cada extractor reactivo. El bloque 3 del algoritmo en la Figura 5, llamado «evaluación consecutiva de la cascada de extracción», consiste en calcular el arreglo iniciando en la primera etapa y procediendo consecutivamente hasta alcanzar el último extractor utilizando el tipo de flash que corresponda con las especificaciones. Los estimados iniciales se obtienen resolviendo un extractor reactivo y utilizando los resultados para especificar perfiles planos para las temperaturas, flujos y composiciones a lo largo de la cascada. El criterio de convergencia se determina cuando el cambio en las fracciones entre dos ciclos consecutivos es menor o igual a la precisión deseada:

Figura 5

El algoritmo en la Figura 5 es secuencial y su estructura tiene validez en forma independiente del método numérico utilizado para resolver el flash reactivo. Este aspecto es importante porque ofrece la versatilidad de usar las técnicas disponibles en la literatura para la solución del flash. Basados en una amplia experiencia con el uso del algoritmo, los autores observan que en arreglos con múltiples etapas se requieren típicamente alrededor de 30 iteraciones del ciclo externo en la Figura 5.

3. RESULTADOS Y DISCUSIÓN

El n-amilacetato es ampliamente utilizado como solvente en la producción de lacas y pinturas; así como en la creación de adhesivos, recubrimientos y thínneres. Puede resultar interesante su síntesis a partir de una reacción de esterificación utilizando procesos de separación reactivos (principalmente: destilación, extracción y membranas) con el fin de desplazar el equilibrio químico y evitar las limitantes a la separación existentes en el sistema no reactivo.

Primero se calculó el equilibrio de fases reactivo para el sistema ácido acético + 1-butanol + n-butilacetato + agua (caso de estudio 1), con el fin de tener un punto de comparación en un sistema recurrente en la literatura (Bonilla et al., 2008-1; Bonilla et al., 2008-2; Gutiérrez, 2008, Rivera, 2004, Minotti et al., 1998). Después se tratan ejemplos de cascadas de extracción reactiva orientados a la síntesis de n-amilacetato utilizando distintos esquemas tecnológicos. Para las disoluciones del caso de estudio 1, los coeficientes de actividad se calcularon con el modelo UNIQUAC y los parámetros de interacción reportados por Minotti et al (1998). Para las disoluciones de ácido acético + 1-pentanol + n-amilacetato + agua (caso de estudio 2), se utilizó el modelo NRTL con los parámetros reportados por Chiang et al (2002). La constante de equilibrio de las reacciones de esterificación se tomaron de Wyczesany (2009) y Minotti et al (1998) para los casos de n-amilacetato y n-butilacetato respectivamente. El caso con especificación del flujo de calor transferido fue evaluado solamente para el n-amilacetato tomando las capacidades caloríficas como líquido para los compuestos ácido acético, 1-pentanol y n-amilacetato de Yaws, (2003) y para el agua de NIST, (2012) y las entalpías de formación como líquido de NIST, (2012).

Ejemplo 3.1. ELLR para una disolución de acético + 1-butanol + n-butilacetato + agua

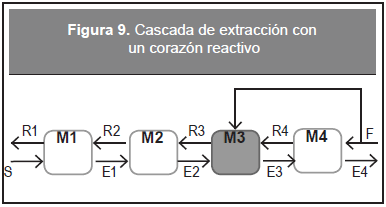
Con el propósito de validar el cálculo del equilibrio de fases reactivo se calculó un ELLR en el contexto de un ejemplo estudiado por Minotti et al, (1998) correspondiente a una cascada en paralelo para el sistema de esterificación caso de estudio 1, la información de entrada se encuentra en la Tabla 1.

En el trabajo de Minotti et al (1998) se considera un modelo controlado por la cinética y se utiliza una expresión de la ley velocidad con el fin de calcular el tiempo de residencia para una conversión conocida. En este enfoque, la representación del equilibrio químico se logra utilizando grandes tiempos de residencia (teóricamente un tiempo «infinito»). De acuerdo a Minotti et al (1998) la conversión de equilibrio es aproximadamente 91 %.

Se utilizó el diagrama de flujo de información de la Figura 2 para resolver el ELLR y se encontraron los resultados de la Tabla 2. La conversión calculada es igual a 91,4 % y concuerda razonablemente con la reportada por Minotti et al (1998). Teniendo en cuenta que el modelo de equilibrio es una solución asintótica del modelo controlado por la cinética se revisaron otros ejemplos tratados en el artículo de Minotti et al (1998) (por cuestiones de espacio no se presentan aquí) encontrando también una buena correspondencia.

Ejemplo 3.2. Producción de n-amilacetato.

3.2.1. Cascadas en contracorriente

El estudio de la producción de n-amilacetato se realiza evaluando varios esquemas de diseño que mantienen constante el arreglo a contracorriente. La selección de dicho arreglo parte de conocer que es el más usado en la industria por las siguientes razones: a) existe un enriquecimiento gradual del soluto en la fase del solvente a través de todo el proceso extractivo, b) las cantidades necesarias de solvente para llevar a cabo el proceso son reducidas considerablemente en comparación con otra clase de arreglos, por ejemplo, el arreglo cruzado, lo cual conlleva a la obtención de fases de extractos más ricas en el soluto de interés y c) la fuerza guía para efectuar la extracción es maximizada. (Rydberg, 2004). Inicialmente, se trata de una cascada de extracción reactiva de cuatro etapas operando en arreglo a contracorriente, las condiciones de operación se describen en la Tabla 3; los resultados Kse obtienen luego de 30 iteraciones y se reportan en la Figura 6.

Figura 6

Se observa en la Figura 6 que entre la tercera y cuarta etapa, los flujos de extractos (E3 y E4) y refinados (R3 y R4) no presentan cambios relativos en su concentración. Esto sugiere que la especificación de cuatro etapas se encuentra cerca del máximo para una cascada de extracción reactiva en arreglo a contracorriente. Para confirmar el número máximo de etapas reactivas fueron evaluadas diez cascadas de extracción reactivas donde cada cascada contiene un número de etapas diferente comenzando desde 1 hasta 10 etapas. Los resultados se resumen en la Figura 6a, donde se observa que la conversión del reactivo límite (ácido acético) permanece aproximadamente constante a partir de la etapa 4. Incluir más etapas reactivas no representa un beneficio debido a que el cambio relativo en las concentraciones y en la conversión del reactivo límite (ácido acético) no es significativo.

Por otro lado, la Figura 6b ilustra la utilidad que tiene expresar gráficamente los resultados obtenidos para los arreglos de cascadas de extracción reactivas en condición isotérmica empleando la transformación de coordenadas de Ung y Doherty (1995); ya que a partir de dicha gráfica se puede realizar una aproximación sobre el número máximo de etapas reactivas para un arreglo en contracorriente y esta conclusión, a nivel numérico, no resulta fácilmente deducible de forma a previa porque existe la necesidad de simular un arreglo con más de cuatro etapas para conocer la respuesta. Adicionalmente, la Figura 6b también plantea la posibilidad de realizar análisis gráficos posteriores ya que son muy similares a los análisis conocidos en la literatura para arreglos de cascadas de extracción en sistemas ternarios no reactivos. A partir de los resultados obtenidos para las cascadas de extracción reactivas en condición isotérmica, fue calculado el flujo de calor necesario para mantener esta condición. Como se puede observar en la Figura 6b existe un comportamiento endotérmico donde el flujo de calor es mayor para la etapa donde ingresa el alimento y este flujo disminuye conforme se acerca a la etapa de entrada del solvente extractivo. Esto sugiere que las necesidades caloríficas globales del proceso son determinadas por la etapa de alimento.

3.2.2. División de flujos

Otro de los esquemas de diseño analizados corresponde con la división de flujos de alimento y de solvente en cascadas de extracción reactivas a contracorriente, como se observa Figura 7.

Figura 7

Para el caso de estudio, se analizó el efecto que tiene la división de alimento y de solvente en una cascada de extracción reactiva, en contracorriente, con cuatro etapas, utilizando las mismas especificaciones descritas en la Tabla 3. Cabe resaltar que dicha división se consideró equimolar, los resultados se resumen en la Figura 7. Se observa que el algoritmo de cálculo es versátil ya que permite incluir especificaciones diferentes a los convencionales y la conversión total no se beneficia conforme se divida el flujo de alimento o de solvente; ya que, la mayor conversión total se obtiene cuando se trabaja en un arreglo convencional, como lo ilustra la Figura 6.

3.2.3. Cascadas híbridas

Para complementar el análisis, también se determinó el efecto de incluir zonas de reacción localizadas dentro de las cascadas de extracción. Este tipo de configuración solamente ha sido trabajado en la literatura en esquemas de destilación reactiva para mejorar el desempeño de la separación del soluto de la zona reactiva y disminuir costos, ya que una etapa reactiva es considerablemente más costosa en comparación con una etapa no reactiva, (Agarwal, Thotla y Mahajani, 2008).

Los resultados obtenidos de evaluar las cascadas de extracción híbridas, utilizando las mismas especificaciones descritas en la Tabla 3, se resumen en la Figura 8. En concordancia con la Figura 9: la conversión obtenida en una cascada de extracción híbrida con una sola etapa reactiva es similar a la conversión obtenida en cascadas de extracción de dos, tres y cuatro etapas reactivas. Esto sugiere que un proceso productivo puede contar con arreglos que no sean completamente reactivos, ya que aumentar la cantidad de etapas reactivas no muestra mejoras significativas respecto a la conversión y cada etapa reactiva impacta significativamente en los costos de inversión y operación. Para analizar el comportamiento de los perfiles de composiciones de los arreglos tratados en la Figura 8, se resumieron los valores de las fracciones molares de una de las fases en equilibrio en cada una de las cascadas consideradas, como lo ilustra la Tabla 4.

Figura 8

Tabla 4

En acuerdo con los resultados, se observa que el comportamiento de composiciones es similar para arreglos de cascadas con dos, tres y cuatro etapas reactivas; sin embargo, existe un cambio notorio para la cascada de extracción híbrida que trabaja con una sola etapa reactiva. La separación y recuperación de ácido acético y de amil alcohol en esta cascada híbrida es mayor, ya que estos componentes reaccionan solo en una etapa. Por otra parte, se observa una disminución clara en la separación y recuperación de n-amilacetato, ya que las fracciones molares obtenidas para este compuesto son muy bajas en comparación con los demás arreglos híbridos y el arreglo con zona de reacción no localizada.

En la Tabla 4 se muestran también los perfiles de calor para los arreglos tratados en la Figura 8. La reacción de esterificación para la producción de n-amilacetato es de tipo endotérmica, por lo cual, es necesario añadir calor en las etapas donde ocurre la reacción química. De acuerdo a los resultados encontrados, las necesidades globales de calor del proceso son muy similares entre todos los arreglos trabajados en la Figura 8 (cascadas con zona de reacción localizada y no localizada), a excepción del arreglo con una sola etapa reactiva. La razón es que el sistema distribuye las necesidades caloríficas conforme a la presencia de etapas reactivas en el proceso y en el arreglo con una sola etapa, todo el calor recae sobre la etapa de alimentación.

Con el propósito de analizar la importancia de la etapa de alimentación se evaluó una cascada de extracción híbrida con un «corazón» reactivo y se cambió la posición de este corazón utilizando las mismas condiciones descritas en la Tabla 3. Las conversiones de ácido acético alcanzadas fueron de 33,439 %, 34,526 % y 34,764 % para un ingreso del 80 % de alimento a la etapa reactiva 1, 2 y 3 respectivamente, el 20 % restante ingresa a la etapa 4. A manera de ejemplo, la Figura 9 muestra el caso en el que parte del alimento ingresa en la etapa 3.

3.2.2. Flujo de calor especificado

Para comprobar que el algoritmo de cálculo soporta también condiciones con transferencia de calor especificada, se calculó una cascada de extracción reactiva en arreglo a contracorriente para tres etapas, las condiciones de operación se resumen en la Tabla 5; los resultados se obtienen luego de 18 iteraciones y se resumen en la Tabla 6.

Tabla 5

Tabla 6

Con los resultados de las anteriores tablas se comprueba entonces que el algoritmo de cálculo permite conocer la influencia del flujo de calor transferido de forma independiente (ELLRT) o de manera dependiente (ELLR). Esto confirma sus características robustas y la posibilidad de trabajar con diferentes condiciones de proceso.

4. CONCLUSIONES

Se presentó un algoritmo de tipo secuencial para la simulación de cascadas de extracción reactiva en contracorriente operando en la condición de equilibrio total (equilibrio de fases y equilibrio químico simultáneos). El método se probó con una reacción de esterificación y diversos esquemas tecnológicos para el proceso productivo. El algoritmo puede manejar especificaciones relevantes en la práctica como: a) división de flujos de solvente y alimento; b) cascadas con la zona de reacción localizada; c) diferentes puntos de alimentación y c) la especificación del flujo de calor transferido.

El método presentado tiene una fácil implementación en un programa de computador porque incluye un único lazo iterativo. El fundamento de cada ejecución del procedimiento reside en un conocimiento bien establecido: el cálculo de los diferentes tipos de flash para los sistemas con dos fases líquidas. Este último aspecto ofrece la ventaja de utilizar en forma de subrutinas los algoritmos disponibles en la literatura para el equilibrio líquido - líquido reactivo.

La representación gráfica empleando las fracciones molares transformadas de Ung y Doherty (1995) permite simplificar el análisis de las cascadas reactivas. En este sentido uno de los ejemplos ilustra la aproximación del número máximo de etapas reactivas para el arreglo en contracorriente y sugiere la posibilidad de usar los métodos gráficos desarrollados para sistemas ternarios no reactivos en el cálculo de extracción reactiva para sistemas con dos grados libertad.

La producción de n-amilacetato por extracción reactiva a partir de soluciones acuosas de ácido acético se encuentra fuertemente limitada por restricciones termodinámicas a la reacción y a la separación. Las conversiones más altas se encuentran alrededor del 40 % en cascadas dispuestas en contracorriente. En este caso el proceso de extracción reactiva debe completarse con una secuencia de destilación para manejar la separación. Es probable que la destilación reactiva ofrezca mejores perspectivas.

NOMENCLATURA

Δ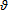: Cambio en las moles ocasionado por la reacción
γ_i: Coeficiente de actividad
K_i: Coeficiente de distribución del componente i
K_eq: Constante de equilibrio químico
X: Conversión
ξ: Coordenada de la reacción
τ: Criterio de convergencia
z_i: Fracción molar del componente i en el alimento
x_i: Fracción molar del componente i
Ψ: Fracción de extractos
F: Flujo de alimentación (mol/h)
H: Entalpía (kJ/mol)
S: Flujo de solvente (mol/h)
: Flujo de Calor (kJ/h)
T: Temperatura (K)
P: Presión (bar)

REFERENCIAS

Agarwal, V., et al. (2008). Attainable Regions of Reactive Distillation-Part I. Single Reactant Non-Azeotropic Systems. Chem. Eng. Sci., 63(11), pp. 2946-2965.         [ Links ]

Benítez, J. Principles and Modern Application of Mass Transfer Operations, 2 ed. USA: John Wiley and Sons, 2009, pp. 424-476.         [ Links ]

Bonilla, A.; et al. (2008-1). A Method for Flash Calculations in Reactive Mixtures. Afinidad, 65(535), pp. 236-242.         [ Links ]

Bonilla, A.; et al. (2008-2). Gibbs Energy Minimization Using Simulated Annealing for Two-phase Equilibrium Calculations in Reactive Systems. Chemical and Biochemical Engineering Quarterly, 22(3), pp. 285-298.         [ Links ]

Bouraqadi, A., Albet, J. y Molinier, J. (2007). Model Based on Reaction in the Aqueous Phase for Liquid - Liquid Extraction of Monocarboxylic Acids. Ind. Eng. Chem. Res., 46(15), pp. 5192-5198.         [ Links ]

Cárdenas, A. (2009). Desarrollo de un algoritmo robusto para la simulación de cascadas de extracción en fase líquida por etapas de equilibrio, sistema ácido acético - agua. Trabajo de grado. Facultad de Ingeniería. Fundación Universidad de América, Bogotá         [ Links ].

Cardona, C. y Gutiérrez, L. (2007a). Estado del arte de la extracción reactiva (I). Fundamentos. Ingeniería Química, 446, pp. 156-168.         [ Links ]

Cardona, C. y Gutiérrez, L. (2007b). Estado del arte de la extracción reactiva (y II). Aplicaciones. Ingeniería Química, No. 447, pp. 198-213.         [ Links ]

Cadavid, J., et al. (2011). Diseño y desarrollo de un proceso para la producción de biodiesel por extracción reactiva. CD-ROM: Memorias XXVI Congreso Colombiano de Ingeniería Química, Capítulo Bucaramanga, ISSN: 1692-925X.         [ Links ]

Chiang, S., et al. (2002). Design Alternatives for the Amyl Acetate Process Coupled Reactor - Column and Reactive Distillation. Ind. Eng. Chem. Res., 41(13), pp. 3233-3246.         [ Links ]

Firoozabadi, A. Thermodynamics of Hydrocarbon Reservoirs. New York: McGraw-Hill, 1999. pp. 219-233.         [ Links ]

Górak, A. y Stankiewicz. (2011). Intensified Reaction and Separation Systems. Annu. Rev. Chem. Biomol. Eng., 2, pp. 431-451.         [ Links ]

Gorissen, H. (2003). A General Approach for the Conceptual Design of Counter-Current Reactive Separations. Chem. Eng. Sci., 58, pp. 809-814.         [ Links ]

Gutiérrez, L. (2008). Estudio y diseño de procesos reacción extracción simultáneos. Tesis doctoral. Universidad Nacional de Colombia, Manizales, Colombia.         [ Links ]

Henley, E. y Rosen E. Cálculo de balances de materia y energía. España: Ed. Reverté, 1973. pp. 358-417.         [ Links ]

Henley, E. y Seader, J. Separation Process Principles. 2 ed. USA: John Wiley and Sons, 2006. pp.117-151.         [ Links ]

Jalali, F. y Seader, J. D. (2000). Use of Homotopy Method in Stability Analysis of Multiphase, Reacting Systems. Comp. and Chem. Eng., 24, pp. 1997-2008.         [ Links ]

Krishna, R. (2002). Reactive Separations: More Ways to Skin a Cat. Chem. Eng. Sci., 57(9), pp. 1491-1504.         [ Links ]

Kulprathipanja, S. Reactive Separation Processes. USA: Taylor and Francis, 2002. pp. 51-87.         [ Links ]

Manning, F. Oilfield Processing, USA: Pennwell Books, 1995. Appendix 4, pp. 418.         [ Links ]

Michelsen, M. (1982a). The Isothermal Flash Problem.Part I. Stability. Fluid Phase Equilibria, 9(1), pp. 1-19.         [ Links ]

Michelsen, M.L. (1982b). The Isothermal Flash Problem. Part II. Phase Split Calculation. Fluid Phase Equilibria, 9(1), pp. 21-40.         [ Links ]

Michelsen, M. y Mollerup, J. Thermodynamic Models: Fundamentals and Computational Aspects. Second Edition, Tie-Line Publications: Denmark, 2007. pp. 231-249.         [ Links ]

Minotti, M., Doherty, M., y Malone, M. (1998). Design for Simultaneous Reaction and Liquid - Liquid Extraction. Ind. Eng. Chem. Res., 37, 12, pp. 4748-4755.         [ Links ]

NIST (National Institute of Standards and Technology). (2012). NIST Standard Reference Database Number 69. Acetic Acid, Pentyl Ester.         [ Links ]

Pai, R., Doherty, M. y Malone, M. (2002). Design of Reactive Extraction Systems for Bioproduct Recovery. AIChE J., 48(3), pp. 514-526.         [ Links ]

Prieto, L. (2012). Simulación de esquemas tecnológicos para la producción de acetato de amilo/isoamilo a través de procesos simultáneos de extracción - reacción. Trabajo de grado. Departamento de Ingeniería Química. Fundación Universidad de América, Bogotá         [ Links ].

Rivera, A. (2004). Diseño de un Algoritmo para el Análisis de un Proceso Simultáneo Reacción - Extracción a Nivel Productivo. Trabajo de grado, Departamento de Ingeniería Química, Universidad Nacional de Colombia, Manizales.         [ Links ]

Rivera, A. y Cardona, C. (2004). Análisis de procesos simultáneos reacción-extracción a nivel productivo. Generalidades del proceso, equilibrio físico y químico simultáneos. Ingeniería y competitividad, 6(1), pp. 17-25.         [ Links ]

Rydberg, J., et al. Solvent Extraction, Principles and Practice, 2 ed. New York: Marcel Dekker, Inc., 2004. pp. 11-15.         [ Links ]

Sánchez, C., Arturo, J., y Cárdenas, A. (2009). Algoritmo etapa a etapa para la simulación de cascadas de extracción en fase líquida aplicando el modelo de equilibrio. Revista EIA, 12, pp. 39-58.         [ Links ]

Sánchez, C., Prieto, L. y Arturo, J. (2011). Solución del problema de la estabilidad material aplicando el método de sustituciones sucesivas para mezclas con equilibrios líquido - líquido y líquido - líquido reactivo. Revista de Investigación, Universidad de América, 4(2), pp. 7-17.         [ Links ]

Seader, J. (1999). Homotopy Continuation Method in Multi-Phase Multi-Reaction Equilibrium Systems. Comp. and Chem. Eng., 23(9), pp. 1319-1331.         [ Links ]

Smith, J., Van Ness, H. y Abbott, M. Introducción a la termodinámica en ingeniería química, 7 ed. México: McGraw-Hill, 2007. pp. 639-671.         [ Links ]

Treybal, R. Extracción en fase líquida. Nueva York: McGraw-Hill, 1968. pp. 224-275.         [ Links ]

Ung, S., y Doherty, M. (1995). Vapor - Liquid Equilibrium in Systems with Multiple Chemical Reactions. Chem. Eng. Sci., 50(1), pp. 23-48.         [ Links ]

Wasylkiewicz, S. y Ung S. (2000). Global Phase Stability Analysis for Heterogeneous Reactive Mixtures and Calculation of Reactive Liquid - Liquid and Vapor - Liquid - Liquid Equilibria, Fluid Phase Equilibria, 175, pp. 253-272.         [ Links ]

Wyczesany, A. (2009). Chemical Equilibrium Constants in Esterification of Acetic Acid with C1 - C5 Alcohols in the Liquid Phase. Chemical and Process Engineering, 30(2), pp. 243-265.         [ Links ]

Yaws, C. Yaws' Handbook of Thermodynamic and Physical Properties of Chemical Compounds: Physical, Thermodynamic and Transport properties for 5,000 Organic Chemical Compounds, Norwich, N.Y: Knovel, 2003.         [ Links ]