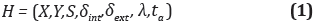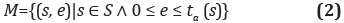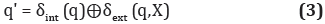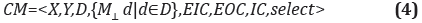Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.22 Envigado July/Dec. 2014
PRODUCTION SYSTEM MODELING AND SIMULATION USING DEVS FORMALISM
MODELADO Y SIMULACIÓN DE UN SISTEMA DE PRODUCCIÓN USANDO EL FORMALISMO DEVS
MODELAGEM E SIMULAÇÃO DE UM SISTEMA DE PRODUÇÃO USANDO O FORMALISMO DEVS
Darío Amaya Hurtado1, Ricardo Andrés Castillo Estepa2, Óscar Fernando Avilés Montaño3, Olga Lucía Ramos Sandoval4
1 Ingeniero electrónico. Especialista en Automatización Industrial. Máster en Teleinformática. PhD. en Ingeniería Mecánica. Docente Investigador, Universidad Militar Nueva Granada.
2 Ingeniero en Mecatrónica. Máster en Ingeniería Mecánica. PhD. (c) en Ingeniería Mecánica. Docente Investigador, Universidad Militar Nueva Granada.
3 Ingeniero electrónico. Especialista en Instrumentación Electrónica. Máster en Sistemas Automáticos de Producción. PhD. En Ingeniería Mecánica. Postdoctor en Ingeniería Mecánica. Docente Investigador, Universidad Militar Nueva Granada. Carrera 11 N. 101-80. Departamento Ingeniería Mecatrónica, Bogotá (Colombia). Tel.: (571) 650 00 00 Ext. 1297. Correo electrónico: oscar.aviles@unimilitar.edu.co.
4 Ingeniera electrónica. Especialista en Instrumentación Electrónica. Máster en Teleinfromática. PhD. (c) en Ingeniería Universidad Distrital Francisco José de Caldas. Docente Investigadora, Universidad Militar Nueva Granada.
Artículo recibido: 27-II-2013 / Aprobado: 1-VIII-2014
Disponible online: 30 de agosto de 2014
Discusión abierta hasta diciembre de 2015
ABSTRACT
This article presents the Discrete Event System Specification (DEVS) formalism, in their atomic and coupled configurations; it is used for discrete event systems modeling and simulation. Initially this work describes the analysis of discrete event systems concepts and its applicability. Then a comprehensive description of the DEVS formalism structure is presented, in order to model and simulate an industrial process, taking into account changes in parameters such as process service time, each station storage systems structure and process tasks coupling. For the MatLab® simulation, the Simevents Toolbox was used for theoretical developments validation.
KEY WORDS: Discrete Event Systems; DEVS; SimEvents®.
RESUMEN
En este artículo se presenta el formalismo de especificación de sistemas a eventos discretos (DEVS), en sus configuraciones atómica y acoplada. Este formalismo es utilizado en el modelamiento y simulación de sistemas que responden a eventos discretos. Inicialmente, en este trabajo se realiza una presentación de los sistemas de eventos discretos y sus aplicaciones. Luego de esto, se realiza una descripción del formalismo, en función del modelo y la simulación de procesos industriales, teniendo en cuenta el cambio en los tiempos de servicio de estaciones que trabajan de manera acoplada. Finalmente se presenta un caso de estudio, el cual es modelado y simulado utilizando la herramienta Simevent de MATLAB®.
PALABRAS CLAVES: sistema de eventos discretos; DEVS; SimEvents®.
RESUMO
Em este artigo, é apresentado o formalismo de especificação de sistemas a eventos discretos (DEVS) em suas configurações atômicas e acoplados. Este formalismo é usado em modelagem e simulação de sistemas que respondem a eventos discretos. Inicialmente, em este trabalho, é realizada uma apresentação dos sistemas de eventos discretos e suas aplicações. Depois disso, é feita uma descrição do formalismo, em funcao do modelo e da simulação e de processos industriais, tendo em conta a variação nos tempos de serviço de estações que trabalham de um modo acoplado. Finalmente, se apresenta um caso de estudo, o qual é modelado e simulado utilizando a ferramenta Simevent de MATLAB®.
PALAVRAS-CHAVE: Sistema de eventos discretos; DEVS; SimEvents®.
1. INTRODUCTION
Developments in technology, reflected mainly in computer systems, communicat ion systems and manufacturing systems, have resulted in new methodologies for modeling and analysis related to systems that respond to discrete events.
Such systems are characterized by performing tasks in real time, high efficiency, and accuracy. Thus, requiring systematic methods associated with computational tools to support the analysis and simulation of these systems (Capocchi, L., et al., 2006).
In this case, the simulation is essential, to understanding the behavior and operation of the system. Several formalisms were developed for the analysis and simulation of discrete events, the DEVS formalism being one of the most popular among them (Filippi, J.-B., and Bisgambiglia, P., 2004; Hong, K. and Kim, T., 2006).
One example is its application in industrial manufacturing systems, which are defined by Palaniappan, S., et al. (2006) and Nikolaidou, M., et al. (2006) as an activity in charge from the processing of raw materials into finished products ending with the distribution. This transformation includes product design, materials selection, process planning, purchasing, production control, product support, marketing, sales, product distribution, and customer service, among others. This type of systems consists of cells controlled by discrete events.
An event may correspond, for example, with a particular task completion in a production system, the arrival and departures of customers, a package transmission through a communications system, requests arrival and its fulfillment, machine failure, the arrival and departure of parts, signals connection and disconnection by the process operator, among others.
A discrete event system (DES) is characterized by having a dynamic evolving accordingly to the abrupt physical events occurrence. These events usually happen asynchronously in time. The events stimulate the dynamics causing a state transition system (Bergero, F., 2000). Today with the changing market demands and economic globalization, there are expectations for highly flexible production systems, able to take advantage of new information technologies and changes in demand and event-based modeling offers the possibility of representing the dynamic behavior of processes.
The acquisition of the process model is an important element in the control systems realignment. For this purpose, several formalisms were developed that allow the modeling of discrete events variables. Among the formalisms commonly used in modeling, analysis and control of discrete event systems (Van der Schaft A. and Schumacher H., 2000) are the Max-min-plus-scaling (MMPS) systems, the Automatons, Petri Nets, Discrete Event System Specification (DEVS), and Grafcet .
This article focuses in the DEVS formalism used for the discrete systems modeling and simulation applied to industrial processes using the Matlab® computational tool as simulation support. This paper is structured as follows: the first section presents an introduction to the Discrete Event Systems; the next section presents both the DEVS atomic formalism and the coupled DEVS structural descriptions. The third section describes an industrial process modeling containing discrete events variables, with the three workstations attached. The fourth section presents the manufacturing process simulation illustrated in the third section, for the event the Matlab® Simulink®, Simevents® tool was used, taking place in the fifth section are the conclusions and lastly the references and bibliographic sources.
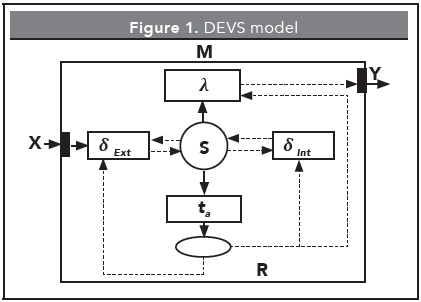
2. DESCRIPTION OF THE DEVS ATOMIC FORMALISM
For a long time, mathematical tools have been used to represent the behavior of systems governed by time or physical phenomena as differential equations. Currently, and taking into account the technological developments made by man, such as computers, transportation systems, manufacturing, communications and others. Moreover, considering that their behavior is governed by events occurring asynchronously in time (Van der Schaft A. and Schumacher H., 2000).
This system is typically called discrete event (DES), and its analysis is very complex, due to a series of requirements such as, copyrights issues, productivity requirements, limitations in response time and so on Hong, K. and Kim, T. (2006). In 1972, the mathematician Bernard Zeigler proposed a formalism to represent the DES (Villani E., et al., 2007), which was called DEVS.
Branicky M. S. (1995) describes the DEVS formalism as a conceptual environment that specifies the model, and the simulation of discrete event systems. Modeling can be done through the system decomposition into smaller models, specifying the coupling between them.
The smaller models are defined as the atomic model, the fundamental element, representing the processing "molecular" unity, and the second is the coupled model (Alur, R., et al., 2000; Kain, S., et al., 2008).
The atomic model can be defined as (1)
Where:
X: Is the input events set of values.
Y: Is the output events set of values.
S: Is the set of state values
δint, ta: It is the internal transition and the time progression functions, respectively
δext: Q × X → S : Is an external transition function, where Q is the set of states
λ: S → y: Is the output function
ta: S → R+0,∞ It is the time progression function, which determines the maximum duration that the system can stay idle. After a time ta(s) without the occurrence of external events, the system internally transitions to a new state S2, calculated by S2 = δint(s)
The transition from state S1 to S2, also produces an output event, defined by y = λ(S1).
The following equation statement (3) represents the atomic model state equation.
Meaning, that system's new state depends on one of the two transition functions, but not on both simultaneously.
Figure 1 shows the DEVS atomic model semantics (Sikun, L., et al., 2005). The model responds to external input events, according to its external transition function, in the absence of events in a specific time set by the time advance function, the model changes state according to the internal transition function and generates an output event for the other models.
3. DEVS FORMALISM FOR COUPLED SYSTEMS
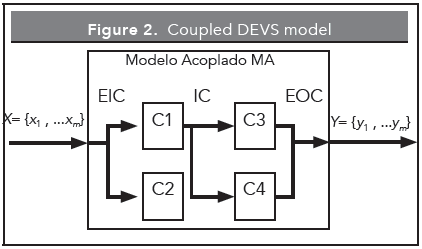
The atomic models can interact through a coupled model. This allows for to the division of a modeling issue from a complex system into small units that can be coupled and make their representation easier (Chen, C. H., and Yücesan, E., 2001; Nikolaidou, M., et al., 2006). Figure 3 shows a coupled DEVS diagram.
With its several closed loops, the coupled DEVS modules can, not only be connected in cascading form, but also allows feedback configurations between the atomic models, thus permitting an industrial production system representation.
The coupled DEVS is formed of several atomic models (D), connected through internal link and is defined by the tuple of equation (4) and present in the Figure 2.
X: Is the input set, for the reception of incoming evVents, where:
p ∈ Inport, v ∈ Xp
Y: It is the output set, for the transmission of external events.
p ∈ OutPorts, v ∈ Yp
D: It is the components package (basic model)
D: It is the DEVS model for each d ∈ D. Verifiable according to the connections. Md = < Xd, S, Y, δint, δext, λ, ta>, is the classic DEVS, with several input/output ports.
p ∈ Inportsd, v ∈ Xp
p ∈ OutPortsd, v ∈ Yp EIC: It is the input links that connects the coupled model entries to one or more of its components input areas.
EIC ⊆ {(N, ipN), (D, ipD) | ipN ∈ Inports, d ∈ D, ipd ∈ InPortsd}
Where:
(N, ipN): Represents the coupled model ipN input port.
(d, ipd): Represents the component's ipD input port.
((N, ipN),(d, ipd)): Represents the connection between the two ports.
EOC: The set of output links that connects the outputs from one or more components to the coupled model input port.
EOC ⊆ {(d,[(op)]⊥d), (N,[(op)]⊥N) | [(op)]⊥N ∈ Outports, d ∈ D, [(op)]⊥ d ∈ [(OutPorts)]⊥ d}
Where:
(d, opd): Represents the component's opd output port.
(N, opN): Represents the composite model's opN output port.
((d,[(op)]⊥d) , (N,[(op)]⊥N)): Represents the connection between the two ports.
IC: It is the internal links set connecting the components' output ports to the coupled models input ports.
IC ⊆ {(a, opa), (b, ipb) | a, b ∈ D con a ≠ b, opa ∈ OutPortsa, ipb ∈ InPortsb}
Where:
(a, opa): represents the coupled model's ipN port of entry.
(b, ipb): represents the d component's ipd input port.
((a, opa), (b, ipb)): represents the connection between the two ports.
Select: sets event priorities, even if an internal event is already scheduled for the same time.
4. EXPERIMENT
This section presents a study case to illustrate the DEVS formalism application in an industrial production process. The experiment comprises a production line consisting of three workstations, coupled sequentially. See Figure 3.
The production line model was based on each workstation's atomic model and their integration produced one coupled model. The first station is pneumatically operated, charged with supplying the raw material into a production line assembling process. The model shows this station as a black box, responsible for producing a consistent product on a support platform by completing the final product. In this manner, it can be displayed as a system with an input buffer, which serves the products to be processed by a server, which represents the delivery of the raw material to the production line.
The raw material from the previous station arrives at the next station that is in charge of the Lego type product assembling on a support platform.
With the product assembling complete, it passes to a third workstation responsible for the product labeling, similar to the previous workstations, this workstation is connected to a server able to perform the designated activity with a product-receiving buffer.
In the modeled system, each station consists of its input buffer associated with the server Px, configured in series to represent the sequential process. The raw material to serve as support for assembling is represented by the elements ax, with an arrival rate linearly independent. The red circles imply that a server is handling an event (busy) and that a product in the queue is waiting for the service.
The model is defined as follows:
The components' serial connections are accomplished as follows: output of the first process connects to the input of the second process, and lastly the output of the second process connects to the input of the third process. This represents what is called an internal coupling between components.
The corresponding coupled DEVS model composition is as follows:
CM = < X, Y, D, {M⊥ d, | d ∈ D }, EIC, EOC, IC, select>
Xin =  : Possible values that can be entered by the port A1 = {a1, a2,...}.
: Possible values that can be entered by the port A1 = {a1, a2,...}.
InPorts = {"A1"}: Composite model input port
X = {(a_x\,v) | v ∈  }: Composite model input port.
}: Composite model input port.
OutPorts = {"dx"}: Composite model output port corresponding to the process 3 output.
Yout =  : possible values that may hold the composite model {d1, d2,...}.
: possible values that may hold the composite model {d1, d2,...}.
Y = {(d, x, v) | v ∈
| v ∈ 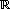 }: Composite model output port, and the probable values remaining from the output of previous process.
}: Composite model output port, and the probable values remaining from the output of previous process.
D = {p1, p2, p2}: Set of names of composite set correspondent to the atomic models of each process.
EIC = {(N, p, x), (p, 1, a, x)}: It is the input connection between the composite models in each process.
EOC = {(p3, out), (N, out)}: Output connection from the last process to the composite model output port.
IC = {((p3, out), (p2, ax)), ((p0, out), (N, ax))}
Select(D' ) = Equivalent to the internal conditions among processes.
Select: equivalent to the faster process selection.
For the model system simulation, the MATLAB ® tool and Simevents toolbox were used; these software are geared to the simulation processes involving discrete time variables, i.e., the manufacturing processes can identify bottlenecks in a production line, perform the identification of resources needed for production, execute the analysis of the performance characteristics of the system, response times and production delays, among many other behaviors that can be analyzed.
The Simevents®, "Event-Based Sequence", allows the generation of a signal of events based on data drawn by the user. With this block, a date is generated with all the Vs that arise in a server.
The "FIFO Queue" block simultaneously has N entities and provides an entity through its output port, yet it retains said entity if the output port is blocked, and other entities are still available. When keeping several entities in storage, the block will always deliver the first that was stored, i.e., the first entity to be stored is the first to exit through its output port.
The Single Server block, serves an entity for a period and then delivers an entity to its output port. In case of a blocked output port, the entity will wait in the block until the port become available. In this application, the ser vers represent each of the workstations belonging to the production line. This block input ports are represented by IN, which is the entrance way for the entities to be served, t is the service time defined in seconds, for an entity's new arrival time. The outputs are divided into two blocks; the first is "Entity Output Ports", composed of OUT, which is the exit period after the completed task. P is the port for entities displaced by the arrival of a higher priority entity. TO is port for entities with wait time; # d is the number of entities already tended by the server; # n is the number of entities that are currently on the block; w shows the entities mean waiting time, useful for showing the server usage time; # displays the number of entities that have exhausted their time.
The graph representing the industrial production model dynamics is shown in Figure 4. It can observed how each server represents the dynamics of each of the stations involved in industrial production system, activities performed in each of the three stations make up a production line, each server has a random processing time, which simulates the time it requires the station to carry out their activity. Furthermore, each station has a storage buffer containing the entities prior to being processed.
The simulation's purpose is to perform the analysis of the dynamics relating to the times of use, mean waiting time, number of units serviced at the stations.
5. RESULTS
According to the results on the behavior of each of the workstations, analysis was carried out only for workstation one. This is due to the similarity between results obtained from the other workstations.
Results were obtained for, mean waiting time, usage time, and number of units serviced at the stations.
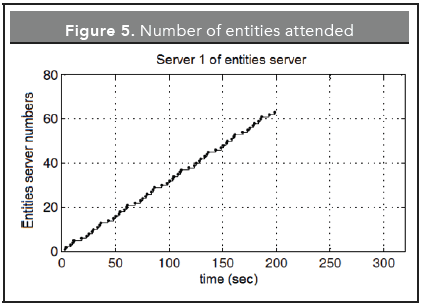
In Figure 5 displays statistics from the server one, representing the workstation with raw material input. The generator delivers the units for the workstation production line. A product provider was configured, a vector corresponding to the number of parts that the system will supply. The server's behavior, according to the serviced units is linear in function of time, ensuring a smooth transition in this workstation, including that at certain times the workstation remains idle, with no products to deliver to the next workstation.
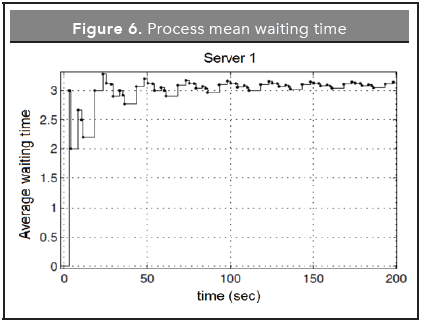
In Figure 6 s hows t he m ean w aiting t ime f or each activity at a workstation, it can be observed that at the beginning, the server has a transient response in the products waiting time, after 40 seconds it reaches a permanent regimen that ensures a continuous waiting time. The graph shows a concordance with the behavior of the number of units served by the server's unit time, and allows one to forecast the time needed for the supply of parts to arrive at the production line, thus avoiding bottlenecks at this workstation, by holding a mean waiting time of 3 sec., this is important to predict the amount of products that this workstation can produce.
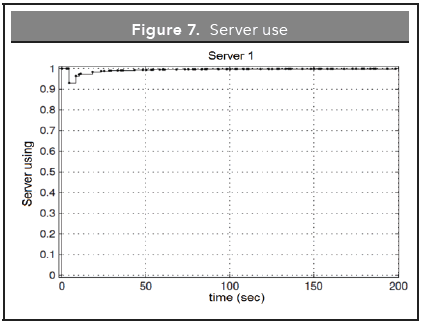
In Figure 7 shows the server's usage time, after 40 seconds the server reaches a stationary state keeping it occupied for the whole time, thus making it possible for the calculation of the system's efficiency to supply the parts to the production line.
6. CONCLUSIONS AND FUTURE PERSPECTIVES
There are several formalisms used for modeling discrete event systems, but according to the literature review, the DEVS formalism is widely used today to represent this kind of systems, it is by its uses that an equivalent representation can be performed in other formalisms.
Bu using the Simevents® simulation tool by MATLAB® it is possible to perform the system behavior analysis that respond to discrete events, and the gathering of information regarding waiting times, service times, number of units served by a workstation, among other, which is vital, when planning an industrial production system.
The simulation was performed based on three workstations, establishing the average service time, the units produced and the setting time for each server. These results allowed the analysis and planning of load distribution in an industrial production system.
By using the DVES formalism for the modeling, and employing tools such as the MatLab® Simulink®, it is possible not only to implement simulation platforms but also the control systems, applicable in industrial production systems that answer to discrete event systems.
According to market requirements, it is necessary to structure platforms that allow the implementation of production system model in embedded processors, with the purpose of creating a system that realistically mimics the physical system, thus it may deepen the analysis of industrial production systems.
REFERENCES
Alur, R.; Henzinger, T.A; Lafferriere, G.; Pappas, G.J. (2000). Discrete Abstractions of Hybrid Systems. Proceedings of the IEEE, 88(7), pp. 971-984. [ Links ]
Bergero, F., Kofman, E., Basabilbaso, C., Zúccolo, J. (2000). Desarrollo de un simulador de sistemas híbridos en tiempo real. XXI Congreso Argentino de Control Automático. [ Links ]
Branicky, M. S. (1995). Studies in Hybrid Systems: Modeling, Analysis, and Control. Submitted to the Department of Electrical Engineering and Computer Science in partial fulfillment of the requirements for the degree of Doctor of Science in Electrical Engineering and Computer Science, Massachusetts Institute of Technology. [ Links ]
Capocchi, L.; Bernardi, F.; Federici, D.; Bisgambiglia, P.-A. (2006). BFS-DEVS: A General DEVS-based Formalism for Behavioral Fault Simulation. Simulation Modelling Practice and Theory, 14(7), pp. 945-970. [ Links ]
Chen, C. H., Yücesan, E. (2001). Introduction to Discrete Event Systems: Christos G. Cassandras and Stephane Lafortune; Kluwer Academic Publishers, Dordrecht. Automatica 37(10), pp. 1682-1685. [ Links ]
Filippi, J. B. and Bisgambiglia, P. (2003). JDEVS: An Implementation of a DEVS Based Formal Framework for Environmental Modelling. Environmental Modelling and Software, 19(3), pp. 261-274. [ Links ]
Hong, K.J. and Kim, T.G. (2006). DEVSpecL: DEVS Specification Language for Modeling, Simulation and Analysis of Discrete Event Systems. Information and Software Technology, 48(4), pp. 221-234. [ Links ]
Kain, S.; Schiller, F.; Dominka, S. (2008). Reuse of Models in the Lifecycle of Production Plants Using HiL Simulation Models for Diagnosis. Industrial Electronics, ISIE 2008. IEEE International Symposium. [ Links ]
Kim, K. H.; Seong, Y.R.; Kim, T.G.; Park, K.H. (1997). Ordering of Simultaneous Events in Distributed DEVS Simulation. Simulation Practice and Theory, 5(3), pp. 253-268. [ Links ]
Nikolaidou, M.; Dalakas, V.; Mitsi, L.; Kapos, G.-D. (2008). A SysML Profile for Classical DEVS Simulators. Software Engineering Advances, ICSEA '08. The Third International Conference on, Sliema, pp. 445-450. [ Links ]
Palaniappan, S.; Sawhney, A.; Sarjoughian, H.S. (2006). Application of the DEVS Framework in Construction Simulation. Simulation Conference, 2006. WSC 06. Proceedings of the Winter. pp. 2077-2086. [ Links ]
Saadawi, H. and Wainer, G. (2007). Modeling Physical Systems Using Finite Element Cell-DEVS. Simulation Modelling Practice and Theory, 15(10), pp. 1268-1291. [ Links ]
Sikun, L.; Zhihui, X.; Tiejun, L. (2005). Distributed cooperative Design Method and Environment for Embedded System. Computer Supported Cooperative Work in Design, 2005. Proceedings of the Ninth International Conference. [ Links ]
Van der Schaft, A. and Schumacher, H. (2000). An Introduction to Hybrid Dynamical Systems. Lecture Notes in Control and Information Sciences, 251. [ Links ]
Villani, E.; Miyagi, P.; Valette, R. (2007). Modelling and Analysis of Hybrid Supervisory Systems. Advances in Industrial Control. [ Links ]
Zeigler, B. P.; Moon, Y.; Lopes, V.L; Kim, J. (1996). DEVS Approximation of Infiltration Using Genetic Algorithm Optimization of a Fuzzy System. Mathematical and Computer Modelling, 23(11-12), pp. 215-228. [ Links ]