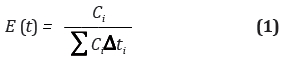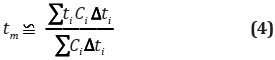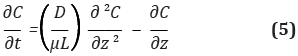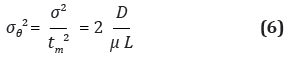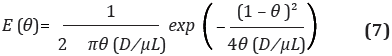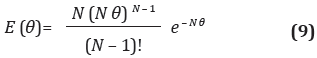Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.22 Envigado July/Dec. 2014
CARACTERIZACIÓN Y MODELACIÓN DEL COMPORTAMIENTO HIDRÁULICO DE UN REACTOR UASB
CHARACTERIZATION AND MODELING OF THE HYDRAULIC BEHAVIOR OF A UASB REACTOR
CARACTERIZAÇÃO E MODELAGEM DE DESEMPENHO HIDRÁULICO DO REATOR UASB
Germán Dimitriv Jojoa Unigarro1, Hilda Lizeth Rodríguez Zambrano2, Santiago Cardona Gallo3
1 Ingeniero químico, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín.
2 Ingeniera biológica, Facultad de Ciencias, Universidad Nacional de Colombia, sede Medellín.
3 Ingeniero sanitario, Universidad de Antioquia. MsC. en Ingeniería Ambiental y PhD. en Ingeniería Ambiental, Universidad Nacional Autónoma de México. Postdoctorado Ingeniería Ambiental, Rise University. Profesor Asociado, Escuela de Geociencias y Medio Ambiente, Facultad de Minas, Universidad Nacional de Colombia, sede Medellín. Carrera 80 N. 65-223 Oficina. M2-319., Tel: (574) 425 51 20. Correo electrónico: scardona@unal.edu.co.
Artículo recibido: 18-VI-2013 / Aprobado: 11-VII-2014
Disponible online: 30 de agosto de 2014
Discusión abierta hasta diciembre de 2015
RESUMEN
La tasa de conversión de la materia orgánica en un biorreactor depende principalmente de dos factores: la actividad biológica y la hidráulica del reactor (Peña-Varón, Mara y Avella-Rodríguez, 2006). Por lo anterior, es necesario conocer el comportamiento hidráulico de los sistemas de tratamiento usando sustancias trazadoras a fin de determinar el comportamiento del flujo: pistón, mezcla completa, dispersión; existencia de zonas muertas, corto-circuitos, flujos advectivos y el tiempo de retención hidráulico real. El objetivo de este artículo es modelar el comportamiento hidráulico de un sistema UASB-Upflow Anaerobic Sludge Blanket (en español RAFA-reactor anaerobio de flujo ascendente), por medio de una prueba de trazadores utilizando Rodamina WT a través de la técnica estímulo-respuesta, los modelos para flujo no ideal que se utilizaron son modelo de tanques en serie y modelo de dispersión. Con ello se determinó que el sistema UASB en estudio tiene un comportamiento de un reactor completamente mezclado con presencia de cortocircuitos y zonas muertas.
PALABRAS CLAVES: actividad hidráulica; reactor UASB; comportamiento de flujo; rodamina WT; modelo de tanques en serie; modelo de dispersión.
ABSTRACT
The conversion rate of organic matter in a bioreactor depends on two main factors: the reactor's biological and hydraulic activity (Peña-Varón, Mara & Avella-Rodríguez, 2006). It is therefore necessary to understand treatment systems' hydraulic behavior by using tracer substances in order to determine flow behavior: piston, complete mix, dispersion; the existence of dead zones, short circuits, advective flows, and real hydraulic retention time. The goal of this article is to model the hydraulic behavior of a UASB (Upflow Anaerobic Sludge Blanket) system through a tracer test using rhodamine WT and the stimulus-response technique. The non-ideal flow models used were the tanks in series model and the dispersion model. We thereby determined that the UASB system being studied showed the behavior of a completely mixed reactor with short circuits and dead zones.
KEY WORDS: Hydraulic Activity; UASB Reactor; Flow Behavior; Rhodamine WT; Tanks in Series Model; Dispersion Model.
RESUMO
A taxa de conversão de matéria orgânica em um biorreator depende principalmente de dois fatores: atividade biológica e a hidraulica do reator (Peña-Varón, Mara y Avella-Rodríguez, 2006). Portanto, é necessário conhecer o comportamento hidráulico dos sistemas de tratamento que utilizam substâncias marcadoras para determinar o comportamento de fluxo: pistão, mistura completa, a dispersão; existência de curto-circuitos, zonas mortas, fluxos advectivos e o tempo real de retenção hidráulica. O objetivo deste artigo é modelar o comportamento hidráulico de um sistema UASB-Upflow Anaerobic Sludge Blanket, (UASB-reator anaeróbio de fluxo ascendente em portugues) por um teste traçador usando Rodamina WT através da técnica de estímulo-resposta, os modelos para fluxo não-ideal que foram utilizadas são do modelo de Tanque serie e Modelo Dispersão. Com isto se determinou que o sistema UASB em estudo tem um comportamento de um reactor completamente misturado na presença de curto-circuitos e zonas mortas.
PALAVRAS-CHAVE: Atividade hidráulica; Reator UASB; Comportamento de fluxo; Rodamina WT; Modelo de Tanques em série; Modelo de Dispersão.
1. INTRODUCCIÓN
El diseño del sistema de tratamiento de aguas se fundamenta principalmente en los procesos biológicos que tienen lugar en el reactor, pero adicionalmente se presentan eventos hidráulicos tales como tiempos de residencia, tiempos de mezclado, régimen de flujo, geometría del reactor, los cuales pueden definir el desempeño del equipo, presentando parámetros que puedan mejorar la eficiencia de los reactores (Torres-Lozada y Pérez-Vidal 2008; Giacoman, Rejón, y Aguilar, 2006).
En los reactores, para el tratamiento de aguas residuales, se pueden encontrar los tres estados de la materia: sólido, líquido y gas. La dinámica que puede ocurrir entre estos está relacionada directamente con procesos de tratamiento que pueden optimizar el sistema de tratamiento si se opera en las condiciones hidrodinámicas adecuadas.
Los sistemas de tratamiento presentan diferentes fenómenos de transferencia de materia, tales como difusión, advección, filtración, sedimentación, etc., pero estos fueron desarrollados de manera empírica y solo en la actualidad están siendo estudiados con bases teóricas más rigurosas (Giaçoman, 1998); sin embargo, aún existe un déficit de información y conocimiento.Para que exista una mejor sustentación teórica de los fenómenos se necesitan mejores técnicas de medición. Un ejemplo es el que se menciona por Rabiger (1988), en donde para un sistema dinámico se necesita analizar el comportamiento de las burbujas de gas -para el caso de un sistema aerobio, aire y para un sistema anaerobio, metano-, en fluidos newtonianos y fluidos no newtonianos, como también los cambios de propiedades locales: densidad, viscosidad, dispersión, velocidad, etc. para el fluido, por el efecto del movimiento de las demás fases que se presentan, debido a que dichos cambios pueden afectar el tiempo de residencia (Giacoman, Rejón y Aguilar, 2006).
Con lo anterior, se fundamenta la importancia de los aspectos hidrodinámicos que se pueden desarrollar en los distintos reactores que se presentan en los sistemas de tratamiento de aguas residuales. El objetivo del presente artículo es la medición de los tiempos de residencia para un reactor anaerobio de flujo ascendente, UASB, para obtener las curvas de distribución del reactor. Se busca adicionalmente realizar el modelado del reactor a partir de los modelos de flujos no ideales como el Modelo de Tanques en Serie y el Modelo de Dispersión (Fogler, 2001).
2. METODOLOGÍA
2.1. Descripción del reactor UASB
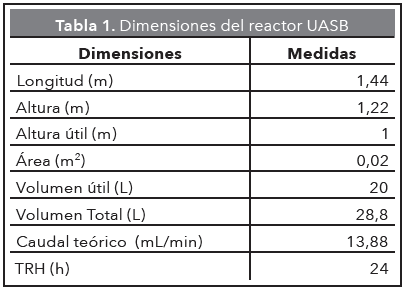
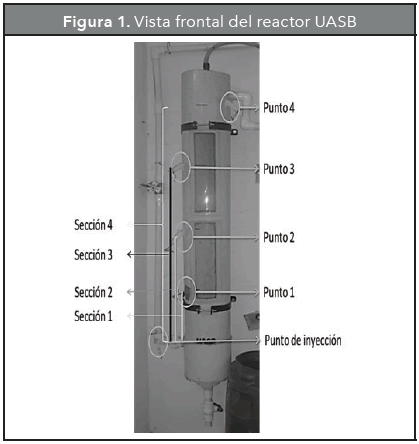
El estudio se desarrolló en el laboratorio de Hidráulica de la Facultad de Minas de la Universidad Nacional de Colombia, sede Medellín. El afluente ingresa en forma ascendente desde el tanque de alimentación ubicado a una altura de 1,3m por gravedad y se distribuye mediante un difusor. El flujo atraviesa todo el perfil longitudinal y sale por la parte superior hacia el reactor aerobio. El reactor está formado por una primera zona de manto de lodos -que tiene una altura de 0,22 m-; el resto de la altura lo constituye la zona de separación de fases, en donde se encuentra la campana extractora de gases, la cual conduce el gas liberado en el lecho fluidizado fuera de este. El sistema anaerobio cuenta con cuatro puntos de muestreo distribuidos en el perfil longitudinal del lecho, esto con el objetivo de observar cómo varía el comportamiento hidráulico a lo largo del reactor. En la Tabla 1 se presentan las dimensiones del reactor y en la Figura 1 el esquema del reactor.
2.2. Metodología experimental
Para evaluar el comportamiento hidráulico del reactor se utilizó una sustancia trazadora: Rodamina WT 20 %, por su carácter inerte, que fue aplicada en la entrada de la unidad y simultáneamente se registró la concentración de la sustancia trazadora a la salida del reactor y en los puntos de muestreo. Esta evaluación se realizó mediante la determinación experimental de las funciones de distribución de tiempos de residencia, a través de la técnica estímulo-respuesta, que consiste en estimular el sistema mediante una perturbación y observar la respuesta a este estímulo a la salida del reactor. El análisis de la respuesta proporcionará la información sobre el comportamiento del fluido dentro del sistema. En este estudio, el estímulo es una inyección de trazador en el fluido que entra a la unidad, mientras que la respuesta es una representación del trazador en diferentes puntos del reactor frente al tiempo.
Antes de realizar la prueba de trazador se estabilizó el caudal hacia un valor cercano al caudal de operación teórico, 13,88 mL/min; el caudal promedio se determinó al sumar cada uno de los caudales obtenidos en cada periodo de muestreo, dando como resultado un flujo promedio de 14,18 mL/min.
2.3. Inyección por pulso
El estudio se fundamentó en inyectar, súbitamente y en una sola ocasión, una entrada por pulso de 10 ml de una solución de Rodamina WT 20 %, con una concentración de 180.000 ppb en la corriente de alimentación que ingresa al reactor, como lo presenta la Figura 1. Luego se midió la concentración en los 4 puntos de muestreo periódicamente, durante 51 horas. La concentración de la solución trazadora fue determinada teniendo en cuenta que en la sección 1 del reactor debía tener una concentración entre 0,4 a 400 ppb, que corresponde al rango de detección lineal del equipo, marca Aquafluor modelo 8000-010.
2.4. Metodología de cálculo
Con los datos obtenidos se procedió a calcular y graficar las curvas de distribución de flujos y tiempos de residencia. Se determinaron las curvas C(t), E(t), F(t) y 1-F(t), y la función de distribución adimensional, E(θ). Estas funciones se aplicaron posteriormente para analizar el tipo de flujo del reactor en estudio; a través de dos modelos: Dispersión y Tanques en serie. Para el análisis de la tendencia de las curvas se calcularon también algunos parámetros, ti, tp, tm, tc y t10 y que al relacionarlos con el tiempo de residencia teórico t0, se tiene una descripción detallada de lo ocurrido en cada sección del reactor después de la inyección del trazador.
3. ANÁLISIS Y RESULTADOS
3.1. Curvas de distribución de flujo y de tiempo de residencia
3.1.1. Curva C (t)
Curva de concentración de trazador en el efluente contra el tiempo.
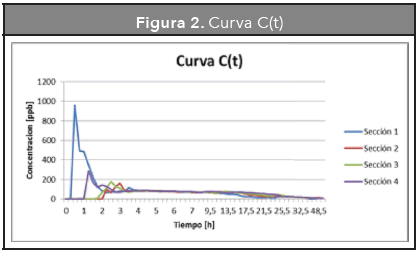
En la Figura 2 se puede observar un comportamiento similar en cada sección del reactor. Transcurrido el tiempo de residencia teórico de 24 horas, todavía por el efluente no sale la totalidad del trazador, con lo que se puede concluir que el tiempo de residencia real es mucho más grande que el teórico.
Los picos que se presentan en cada sección del análisis -siendo el de la sección 1 el más rápido en registrarse y el de la sección 2 el último- concluyen que el reactor tiene un tiempo de estabilización de aproximadamente 4 horas y en tiempos posteriores se presenta una cola decreciente en la que la concentración del trazador es similar para las cuatro secciones, lo cual permite observar una homogenización a partir de ese tiempo (Avella-Rodríguez, 2001).
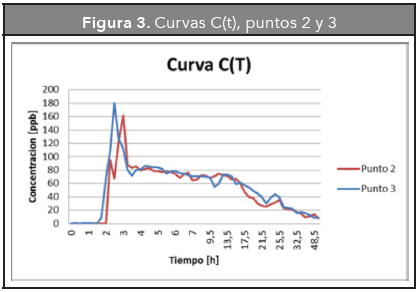
Las gráficas de los puntos de muestreo 2 y 3, presentan además del pico principal en las primeras horas, una serie de picos posteriores al periodo de estabilización, que implican posibles cortocircuitos en el sistema. Ver Figura 3.
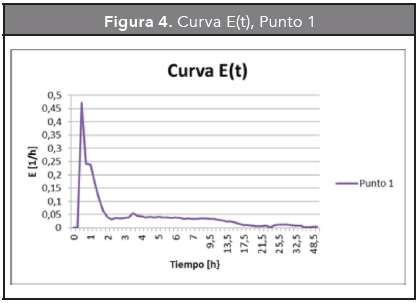
3.1.2. Curva E (t)
Físicamente, esta curva muestra la distribución de edades del fluido que sale de un recipiente (Sánchez, 2010). Lo anterior se debe a que los distintos elementos del fluido, al recorrer diferentes caminos a lo largo del reactor tardarán tiempos diferentes cuando atraviesan el reactor; la distribución de estos tiempos en la corriente de fluido que sale del reactor se denomina distribución de la edad del fluido a la salida (Levenspiel, 1981; Fogler, 2001).
Para caudales constantes E (t) se determina a partir de la siguiente ecuación:
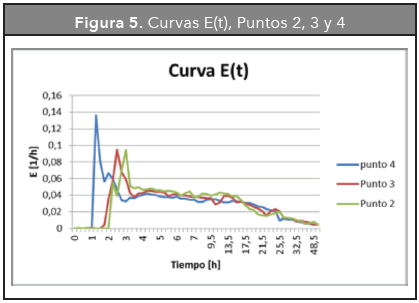
Considerando los gradientes de temperatura que modifican el comportamiento del reactor, las Figuras 4 y 5 presentan un comportamiento creciente en las dos primeras horas del estudio para los cuatro puntos, donde se pudo desarrollar la aclimatación hidrodinámica del sistema hasta alcanzar una condición temporal de equilibrio, para luego tomar la condición normal de un equilibrio hacia una tendencia decreciente del sistema, similar a lo encontrado por Sánchez-Molina (2010).
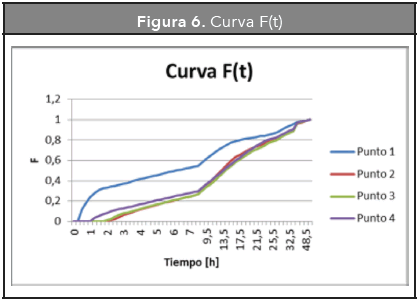
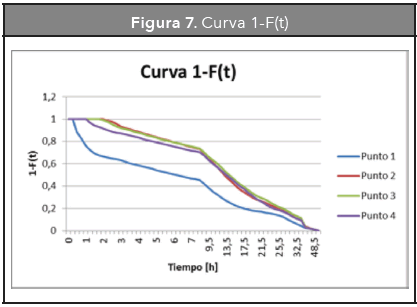
3.1.3. Curva F (t)
Se utiliza para representar la concentración acumulativa de trazador a la salida -midiendo la concentración en la salida del reactor en función de su concentración inicial (C/Co) esta función varía entre 0 y 1 (Levenspiel, 1981)-.
Para reactores con flujo no ideal y cuando las concentraciones están dadas por un número finito de datos, el caudal es constante y los intervalos de observación Δti son iguales, se tiene que:
De las Figuras 6 y 7 se puede determinar que existe un comportamiento diferente entre el punto 1 y los demás puntos. Debido a que en el punto 1, el trazador atraviesa más rápido esta sección, solo en las primeras 7 horas ha pasado aproximadamente 55 % de la masa del trazador, mientras que en los otros puntos es de aproximadamente el 30 % de la masa de trazador.
3.2. Análisis cualitativo de las curvas de concentración
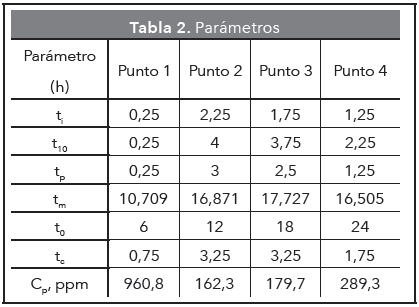
Los principales parámetros que se deben tener en cuenta para el análisis de la tendencia de la curva están registrados en la Tabla 2 (Sánchez-Molina, 2010; Arroyave-Gómez, González-Arteaga y Gallego-Suárez, 2004).
ti: Tiempo inicial desde que se aplica el trazador hasta que aparece en el efluente
tp: Tiempo modal, tiempo para la presentación de la máxima concentración
tm: Tiempo mediano, corresponde al paso del 50 % del trazador
t0: Tiempo de retención teórico
tc: Tiempo en que la concentración es mayor que Cp/2
t10: Tiempo en que la concentración es mayor que Cp/10
Cp: Concentración máxima a la salida
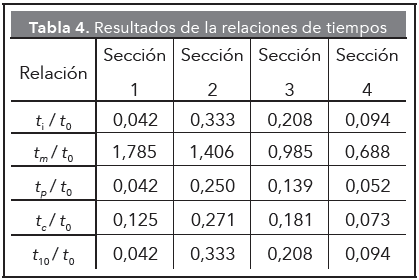
En la siguiente tabla se muestran las relaciones entre los tiempos experimentales y el tiempo teórico, con su respectiva interpretación.
En la Tabla 4 se presentan los respectivos resultados para cada sección. En esta se puede considerar que la hidráulica del reactor tiene un comportamiento de flujo completamente mezclado, además de presentar cortocircuitos y zonas muertas.
3.3. Modelos para flujos no ideales
Con los parámetros descritos anteriormente, es posible hacer una predicción sobre el comportamiento hidráulico de cada sección del reactor, a través de modelos de flujo no ideal, a) Modelo de dispersión, b) Modelo de tanques en serie.
Para aplicar los anteriores modelos se necesita normalizar el tiempo θi.
Donde tm es definida como
3.3.1. Modelo de Dispersión
Este modelo permite describir pequeñas desviaciones del flujo pistón, debidas a una dispersión axial del material que se rige por la Ley de Fick y un transporte transversal, resultado de la difusión molecular y la convección. Este modelo es descrito por la siguiente ecuación (Fogler, 2001).
En este modelo se considera que no hay zonas muertas o cortos circuitos dentro del reactor y corresponde a situaciones donde el flujo no se desvía demasiado del de flujo en pistón, donde D/L, es un parámetro adimensional denominado módulo de dispersión. Este parámetro mide el grado de dispersión axial del reactor (Levenspiel, 1981; Fogler, 2001; Cunill-García, Iborra-Urios y Tejero-Salvador, 2010).
D/(µL) → 0 Dispersión despreciable, se tiende a flujo en pistón.
D/(µL) → Dispersión apreciable, se tiende a flujo en mezcla completa.
Donde:
D: es dispersión hidrodinámica, m2/s.
L: longitud del reactor, m.
µ: velocidad del flujo en el reactor, m/s.
Una aproximación para el módulo de dispersión es a partir de la varianza normalizada (Levenspiel, 1981).
Los módulos de dispersión axial para cada sección 1, 2, 3 y 4 son 1,77, 0,70, 0,58 y 0,59 respectivamente. Como los módulos de dispersión encontrados son pequeños, el modelo puede ser descrito a partir de la siguiente expresión (Levenspiel, 1981). La obtención de los módulos de dispersión se logró con la solución numérica de la Ecuación 7, para cuando existen grandes desviaciones respecto del flujo pistón, D/µL > 0.01.
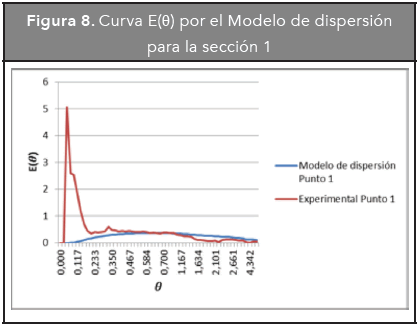
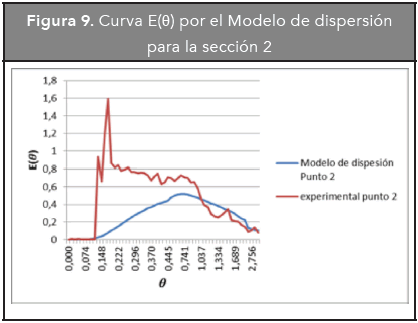
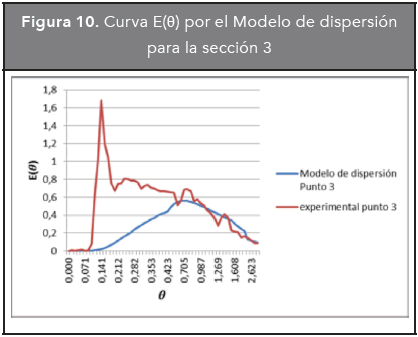
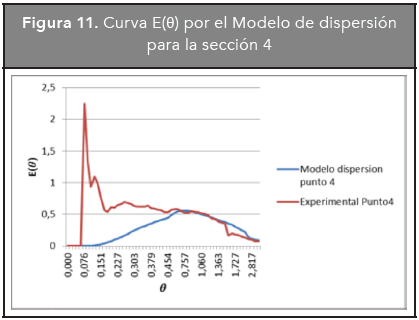
En las Figuras 8, 9, 10 y 11, se presentan las curvas experimental y correspondiente al modelo de dispersión para cada sección del reactor.
De las anteriores gráficas se puede concluir que el reactor no se ajusta al modelo de dispersión; esto puede estar determinado por el régimen de flujo laminar al que se encuentra o por otros aspectos hidrodinámicos que el modelo no tiene en cuenta como cortocircuitos y zonas muertas, debido a que es un modelo de un único parámetro.
3.3.2. Modelo de Tanques en Serie
Este modelo hace la consideración de que el reactor se puede representar por varios tanques de mezcla completa ideales, de igual tamaño, conectados en serie y el único parámetro es el número de tanques. Por lo tanto si el número de tanques es grande, el flujo tendrá un comportamiento flujo pistón. Por el contrario, si el número de tanques es pequeño, el comportamiento hidráulico del reactor tiende a ser mezcla completa.
El parámetro del número de tanques en serie N, se obtiene a partir de la varianza normalizada (Levenspiel, 1981).
A partir de la relación anterior se encontró que el número de tanque para modelar el reactor en las diferentes secciones 1, 2, 3 y 4 es de 0.883, 0.349, 0.290 y 0.295 respectivamente. Como el modelo exige un número de reactores entero, se aproxima a 1.
La curva E(θ), para el modelo de tanques en serie, se puede obtener de la siguiente ecuación (Levenspiel, 1981):
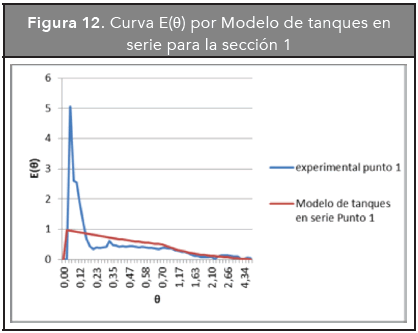
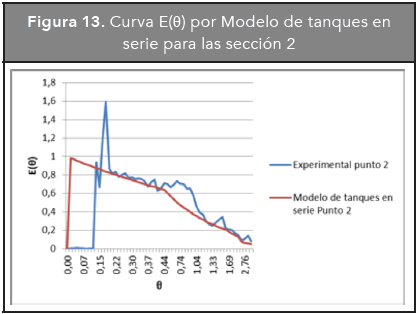
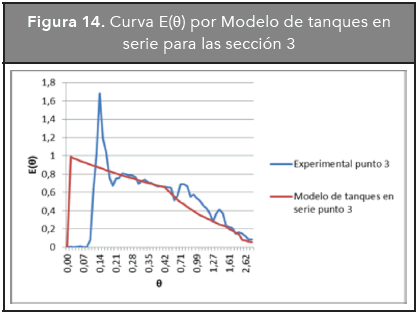
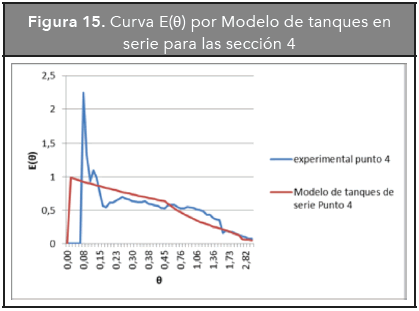
En las Figuras 12, 13, 14 y 15 se presentan las curvas experimental y correspondiente al modelo de tanques en serie para cada sección del reactor.
En las curvas anteriores se puede observar que el modelo de tanques en serie se acopla con mayor precisión a la curva experimental que el modelo de Dispersión. La representación de la curva E(θ) por el modelo de tanques en serie es más suave debido a que omite el pico que se presenta en la curva experimental.
Como el número de reactores para todas las secciones del reactor se encuentra en el rango de 0 y 1, se puede concluir que existe una situación en la que hay cortocircuito y mezcla (Cunill-García, Iborra-Urios y Tejero-Salvador, 2010).
4. CONCLUSIONES
La caracterización hidrodinámica del reactor UASB se puede clasificar como un reactor de mezcla completa, pero presenta cortocircuitos como también zonas muertas. Aun con la presencia de zonas de cortocircuitos y zonas muertas, la dinámica del reactor muestra dos periodos característicos: el periodo de estabilización que se presenta en las primeras 4 horas aproximadamente y un periodo de estado pseudo-estacionario después de las 4 horas, donde en los cuatro puntos de muestreo se obtuvieron concentraciones similares.
El modelo que mejor se aproximó a las curvas experimentales fue el Modelo de Tanque en Serie, para un número de reactores igual a 1. Pero no se logró modelar de forma adecuada las 4 primeras horas que corresponde al periodo de estabilización del sistema, debido a que modelo describe una curva suave en este periodo mientras que el comportamiento real de reactor presenta picos pronunciados que son producto tanto de los cortocircuitos como de las zonas muertas que se presentan en el mismo.
AGRADECIMIENTOS
Al laboratorio de Hidráulica de la Facultad de Minas de la Universidad Nacional de Colombia, sede Medellín. Al ingeniero Luis Fernando Ospina. A la empresa Gotta Ingeniería S.A.S. por la donación de la rodamina.
REFERENCIAS
Arroyave-Gómez, D.; González-Arteaga, M.; Gallego-Suárez, D. (2004). Evaluación del comportamiento hidráulico un reactor UASB utilizado para el tratamiento de aguas residuales. VIII congreso Peruano de ingeniería química. pp. 1-10. [ Links ]
Avella-Rodríguez, G.P. (2001). Evaluación del comportamiento hidrodinámico de un reactor UASB y su influencia en la remoción de materia. Cali: Tesis de grado (M.Sc. Ingeniería Sanitaria y Ambiental). Universidad del Valle, Facultad de Ingeniería, Postgrado en Ingeniería. [ Links ]
Cunill-García, F.; Iborra-Urios, M.; Tejero-Salvador, J. (2010). Reactores químicos, Apuntes. Barcelona: Universidad de Barcelona. [ Links ]
Fogler, H. S. (2001). Elementos de ingeniería de las reacciones químicas. Tercera Edición. México: Pearson Educación. [ Links ]
Giacoman, G.; Rejón, L. I.; Aguilar, S. R. (2006). Evaluación de las características hidráulicas de un reactor de lecho fluidificado para el tratamiento de aguas residuales. México: XV Congreso Nacional del Ingeniería Sanitaria y Ciencias Ambientales. [ Links ]
Levenspiel, O. (1981). Ingeniería de las reacciones químicas. Barcelona, editorial Reverté S. A. [ Links ]
Sánchez-Molina, J. (2010). Modelamiento de las condiciones hidráulicas de una planta compacta para el tratamiento de aguas residuales domésticas. Medellín. Universidad Nacional de Colombia. Trabajo de investigación presentado como requisito para optar al título de MsC. en Ingeniería. [ Links ]
Peña-Varón, M.R.; Mara, D. D.; Avella-Rodríguez, G.P. (2006). Dispersion and Treatment Performance Analysis of an UASB Reactor Under Different Hydraulic Loading Rates. Water Research, 40(3), pp. 445-452. [ Links ]
Torres-Lozada, P.; Pérez-Vidal, A. (2008). Evaluación del comportamiento hidrodinámico como herramienta para optimización de reactores anaerobios de crecimiento en medio fijo. Revista Facultad de Ing. Univ. Antioquia, 45, pp. 27-40. [ Links ]