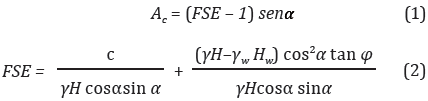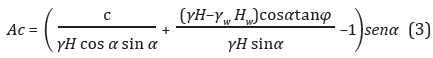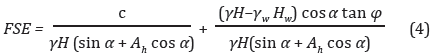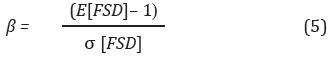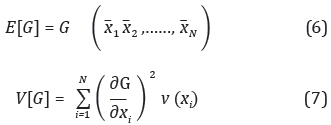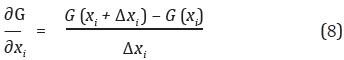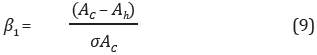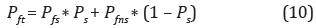Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.22 Envigado July/Dec. 2014
ESTIMACIÓN DE LA AMENAZA POR DESLIZAMIENTOS DETONADOS POR SISMOS Y LLUVIA (VALLE DE ABURRÁ-COLOMBIA)
ESTIMATION OF EARTHQUAKE AND RAINFALL TRIGGERED LANDSLIDES HAZARD (ABURRÁ VALLEY-COLOMBIA)
ESTIMAÇÃO DA AMEAÇA DE DESLIZAMENTOS CAUSADOS POR TERREMOTOS E PELA CHUVA (VALLE DE ABURRÁ COLÔMBIA)
César Augusto Hidalgo Montoya1, Johnny Alexánder Vega Gutiérrez2
1 Ingeniero civil. PhD. en Geotecnia. Profesor Facultad de Ingenierías, programa de Ingeniería Civil, Universidad de Medellín. Carrera 87 N. 30 - 65, Tel: (574) 3405555 (Antioquia, Colombia). Correo electrónico: chidalgo@udem.edu.co.
2 Ingeniero civil. MsC. en Geomática. Profesor Facultad de Ingenierías, programa de Ingeniería Civil, Universidad de Medellín.
Artículo recibido: 22-VII-2013 / Aprobado: 25-VII-2014
Disponible online: 30 de diciembre de 2014
Discusión abierta hasta diciembre de 2015
RESUMEN
En este artículo se presenta una estimación de la amenaza por deslizamientos detonados por sismos y lluvia en el Valle de Aburrá-Colombia, utilizando una plataforma de sistemas de información geográfica (SIG). Para esto se desarrolló un modelo que considera las características topográficas, geológicas, geotécnicas e hidrológicas de la zona en estudio. El modelo utilizado se basa en el modelo seudoestático de Newmark y utiliza un enfoque probabilista basado en la técnica del primer orden y segundo momento -FOSM-. El proceso calcula la probabilidad de que ocurra un deslizamiento dado que se presente un sismo que produzca una aceleración (Ah), considerando la incertidumbre de los parámetros geotécnicos y las condiciones de saturación del suelo.
PALABRAS CLAVES: amenaza; deslizamientos; Newmark; SIG; terremotos.
ABSTRACT
This article presents an estimation of the hazard by earthquake and rainfall triggered landslides in the Aburrá Valley-Colombia, using a platform for geographic information systems (GIS). For this, it was developed a model that considers the topography, geological, geotechnical and hydrological characteristics of the studied area. The model used is based on the Newmark's pseudostatic model and uses a probabilistic approach based on the technique of first order and second moment -FOSM-. The process calculates the probability of occurrence of a landslide, triggered by an earthquake that produces an acceleration (Ah), considering the uncertainty of the geotechnical parameters and conditions of soil saturation.
KEY WORDS: Earthquakes; GIS; Hazard; Landslides; Newmark.
RESUMO
Em este artigo, é apresentada uma estimativa da ameaça de deslizamentos de terra causados por terremotos e chuva no Vale do Aburrá, Colômbia, através de uma plataforma de sistemas de informação geográfica (SIG). Para isso foi desenvolvido um modelo que considera as características topográficas, geológicas, geotécnicas e hidrológicas da área de estudo. O modelo utilizado é baseado no modelo seudoestático de Newmark e usa uma técnica probabilística com base na técnica da primeira ordem e segundo momento-FOSM-. O processo calcula a probabilidade de que ocorra um deslizamento dado que se apresente um tremor de terra, que produz uma aceleração (Ah) considerando a incerteza dos parâmetros geotécnicos e as condições de saturação do solo.
PALAVRAS-CHAVE: Ameaça; Deslizamentos de terra; Newmark; SIG; Terremotos.
1. INTRODUCCIÓN
En Colombia, los movimientos en masa, al igual que las inundaciones, constituyen los fenómenos naturales que generan los riesgos más severos, lo cual se debe principalmente a sus diversas y variadas características geográficas y fisiográficas, siendo detonados por factores tanto naturales como antrópicos. Como caso particular de esto, las condiciones de la zona montañosa de la ciudad de Medellín y los municipios vecinos, en cuanto a relieve, clima, topografía, geología, entre otros, hacen a la región susceptible para la ocurrencia de procesos geomorfodinámicos, que pueden afectar tanto a la población como a su infraestructura (Vega, 2013).
En general, los movimientos en masa son originados por la conjugación de diversos factores detonantes como sismos o lluvia, y se constituyen en una causa frecuente de desastres alrededor del mundo (Hidalgo 2013). Específicamente en el Valle de Aburrá (VA), los movimientos en masa han causado considerables pérdidas económicas y humanas. Debido a la ocupación de las laderas por asentamientos humanos y por obras de infraestructura, los riesgos asociados a los movimientos en masa se han incrementado en los últimos años. Se estima que en el VA el 35 % de los daños a edificaciones y 74 % de las muertes debidas a fenómenos naturales están asociadas con movimientos en masa (Aristizábal y Gómez, 2007), mientras que a nivel mundial, a tales movimientos se les atribuye el 14 % de las pérdidas económicas (Bonachea, 2006) y el 0.53 % de las muertes debidas a desastres por fenómenos naturales (Chowdhury, et al., 2010).
Debido a los altos niveles de afectación de los movimientos en masa se ha generado una gran dinámica en el estudio de los fenómenos asociados en procura de entender los aspectos físicos (Jibson, et al., 1998; Coronado, 2006; Jaiswal y Van Westen, 2009a y 2009b; Jaiswal, et al., 2010; Delgado, et al., 2006; AMVA, 2009; y económicos Zêzere, et al., 2005; Zêzere, et al., 2008; Remondo, et al., 2008; Godt, et al., 2008; Salciarini, et al., 2008; y Vega, 2013) relacionados con los movimientos en masa.
Entre los trabajos realizados sobresalen los que se enfocan en análisis de riesgos y que requieren para su implementación que se estime la amenaza, sin embargo, estos en su mayoría están basados en mapas de susceptibilidad. En los casos en que se utilizan conceptos de amenaza. Esta, por lo general, es estimada a partir de álgebra de mapas y de datos históricos que no consideran el comportamiento de los materiales y los potenciales mecanismos de falla. Los modelos de base física y probabilista constituyen una alternativa para incluir los mecanismos de falla y la variabilidad de los parámetros en la determinación de la amenaza.
En este trabajo se presenta un abordaje que considera modelos de base física y probabilista para estimar la amenaza por deslizamiento en el VA. Se realizó la evaluación de la amenaza por deslizamientos detonados por sismos y lluvia a escala regional mediante una aplicación SIG para el VA. En este artículo se presentan la metodología, los materiales usados y los resultados obtenidos en la evaluación de la amenaza.
2. MATERIALES Y METODOLOGÍA
Se elaboró un modelo de cálculo de estabilidad de taludes considerando el modelo de talud infinito, para estimar la amenaza por deslizamiento como la probabilidad de que se presente la falla de taludes incorporando los conceptos de aceleración crítica y del factor de seguridad.
Para el caso de los deslizamientos, la probabilidad de falla P[T] se entenderá como la probabilidad de que el talud falle, dado que se produce un evento desastroso. Aunque la falla se podría dar solo por efecto de la gravedad, lo más común es que esta sea desencadenada por un agente detonante como los sismos o la lluvia. En la Figura 1 se esquematiza la metodología usada y sus pasos se describen a continuación.
Determinación de datos de entrada
La información requerida por el modelo debe ser ingresada a la aplicación en formato Raster, el cual corresponde a una cuadricula regular de celdas. Para este caso se usaron celdas cuadradas de 100m de lado. A cada tipo de material definido en el mapa de geología se le atribuyeron parámetros de resistencia y de peso unitario. El modelo asigna estos parámetros a cada celda, calcula el factor de seguridad y la aceleración crítica en la celda, para lo cual toma el ángulo de la pendiente predominante a partir del modelo digital de elevaciones (DEM). La información usada en el modelo corresponde a la usada por Vega (2013).
- DEM:
Se obtuvo el modelo que representa la distribución espacial de las alturas y la topografía de la zona de estudio, el cual originalmente tiene un tamaño de celda de 10m (AMVA, 2007) que para este trabajo es adecuado dado que para los análisis se utilizaron celdas de mayor tamaño, lo cual se muestra en la Figura 2-b.
- Unidades geológicas:
El VA se localiza hacia la parte norte de la cordillera Central de Colombia y corresponde a una depresión topográfica alargada como se muestra en la Figura 2-a. Debido a su localización, el VA se encuentra en una zona de amenaza sísmica entre media y alta (AIS, 2010) y las principales fuentes de amenaza la constituyen los sismos originados en la zona de subducción, en el sistema de falla Cauca-Romeral y otros sistemas menores (AMVA, 2007). En la Figura 2-a se muestran los principales sistemas de falla descritos en la microzonificación sísmica del VA.
Según AMVA (2007) las condiciones paisajísticas del VA están enmarcadas por un valle estrecho al sur, el cual se amplía en el municipio de Medellín alcanzando unos siete kilómetros de amplitud, y que luego se cierra nuevamente a la altura del municipio de Copacabana, altitudinalmente se presentan variaciones en las montañas que rodean el valle, las cuales pueden alcanzar hasta los 3000 metros en los altos de San Miguel, Padre Amaya y Boquerón. Además, se presentan las zonas de los altiplanos de San Vicente, Rionegro y Santa Elena al oriente, y el Llano de Ovejas al occidente.
En el VA y los altiplanos circundantes se presenta una variada geología con afloramientos de unidades litológicas que incluyen rocas de diferente edad, origen y composición. En relación con las edades, estas van desde rocas paleozoicas hasta los depósitos cuaternarios y por su origen y composición se tienen rocas metamórficas como esquistos, anfibolitas, migmatitas y gneises; rocas ígneas como granodioritas, dunitas, gabros y basaltos; rocas volcano-sedimentarias y los depósitos de origen aluvial y de vertiente, además de los llenos de origen antrópico (AMVA, 2007).
A partir del mapa geológico mostrado en la Figura 2-c se determinaron los suelos predominantes en cada sector del VA. Según la información presentada en Vega (2013), Hidalgo (2013) e Hidalgo, et al. (2012), a cada uno de estos suelos se le atribuyeron los parámetros de resistencia y peso unitario mostrados en la Tabla 1. Para cada suelo se presenta la denominación usada en el mapa geológico y los valores de la media (µ) y la desviación estándar (σ) atribuidos a cada parámetro, compilados por Vega (2013).
- Datos de lluvia:
Hidrológicamente, el VA se caracteriza por un régimen de lluvias que tradicionalmente ha sido bimodal, con dos épocas lluviosas aproximadamente en los meses de marzo-abril-mayo y septiembre-octubre-noviembre. Los mayores valores de precipitación están entre 2800 y 3200 mm/año, y se presentan en la parte norte y sur de la cuenca. Las menores precipitaciones, con valores entre los 1400 mm/año y 1800 mm/año, se dan en la zona central de la cuenca y se extienden hacia la zona occidental (AMVA, 2007).
En este trabajo se utilizaron datos de precipitación acumulada diaria de 10 estaciones pluviométricas localizadas en el VA con series de registros entre 20 y 50 años. En la Tabla 2 se presentan las estaciones usadas con su respectiva localización en coordenadas geográficas.
- Datos de sismicidad:
Para este caso se tomó un escenario dado por la distribución de aceleraciones determinada por la microzonificación sísmica del VA (AMVA, 2007) mostrada en la Figura 2-d, y otro con una aceleración uniforme de 0,2g. Para la evaluación presentada en este artículo se tomó la aceleración en el suelo dada como el producto de la aceleración en roca, por el coeficiente de importancia, y el factor de aceleración vertical (Fv) asignados para cada pixel de acuerdo con los valores determinados en la Normas Colombianas de Diseño y Construcción Sismo Resistente-NSR10 (AIS,2010).
Cálculo determinista de la estabilidad
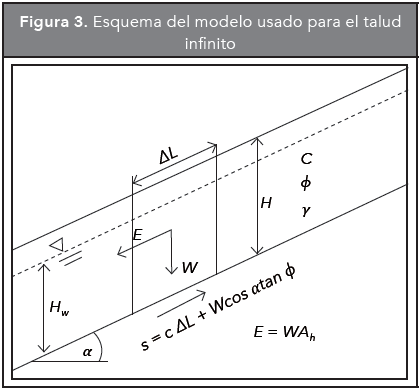
Para considerar el efecto de los sismos se usó el método de Newmark (1965) que se basa en un modelo de estabilidad de talud infinito. De acuerdo con el método de Newmark para la evaluación de estabilidad por deslizamientos detonados por sismos, se calcula la aceleración necesaria para desencadenar dicho movimiento, denominada aceleración crítica (Ac). Para esto se recurre a métodos seudoestáticos en los cuales la fuerza debida al sismo se adiciona al modelo como una fracción del peso de la masa que se desliza. A continuación se presentan las expresiones resultantes para el modelo de talud infinito que será usado en este trabajo y que se ilustra en la Figura 3.
Tanto el factor de seguridad estático calculado por el método del talud infinito (FSE), como la aceleración crítica (Ac) definida por Newmark (1965) son dadas por las siguientes ecuaciones
donde H es el espesor de la zona que falla [m], Hw es la altura del agua medida desde la superficie de falla [m], c es la cohesión del suelo [kPa], es el ángulo de fricción interna del suelo [ ], g es el peso unitario del suelo [kN/m3], gw es el peso unitario del agua [kN/m3] y es el ángulo de inclinación promedio del terreno [
], g es el peso unitario del suelo [kN/m3], gw es el peso unitario del agua [kN/m3] y es el ángulo de inclinación promedio del terreno [ ].
].
La expresión resultante para el modelo de talud infinito para la aceleración crítica se encuentra de la forma:
Por lo general, los resultados de la aceleración crítica son indicadores de la susceptibilidad del terreno, pero poco indicativos de la amenaza que existe realmente, por lo cual se debe calcular la probabilidad de falla (PF). Para esto, en primer lugar, se determinó el factor de seguridad para un valor definido de la aceleración (FSD) y a partir de este se calcula la PF. En este caso FSD se determina con la expresión:
donde Ah es la aceleración producida por el sismo dada como una fracción de la aceleración de la gravedad g.
Probabilidad de falla
La probabilidad de falla se determina como la probabilidad de que los valores considerados límites sean excedidos. En el caso del FSD, la probabilidad de falla se determina como la probabilidad de que FSD sea menor que la unidad. En cuanto a la aceleración crítica, la probabilidad de falla se determina como la probabilidad de que Ac sea superada por Ah.
Una forma de evaluar la probabilidad de falla, y a la vez cuantificar el efecto de la incertidumbre en la evaluación de amenaza por deslizamiento, es la utilización de técnicas de confiabilidad. La confiabilidad se entiende como la posibilidad que tiene un sistema para realizar las funciones para las que fue concebido. La confiabilidad se determinó por medio del índice de confiabilidad que se relaciona con una probabilidad de falla. Considerando que el valor crítico de FSD es 1.0, el índice de confiabilidad (β) de FSD, es definido por la siguiente expresión (Christian, et al., 1994; Baecher y Christian, 2003):
donde E[FSD] es el valor determinista d e FSD calculado con los valores medios de las variables independientes y s[FSD] es la desviación estándar de FSD.
El índice β está relacionado con la probabilidad de falla, lo que permite una evaluación más consistente de la estabilidad. Es de anotar que la Ecuación 5 sólo es válida si la Función de Distribución de Probabilidad (FDP) de FSD es normal. Cuando la distribución de probabilidad es diferente a la normal, por ejemplo log normal, se deben usar otras formulaciones (Christian, et al., 1994; Baecher y Christian, 2003; Rosenblueth, 1975).
La probabilidad de falla está dada por la porción del área bajo la curva FDP del FSD correspondientes a los valores de FSD inferiores a uno (1). Esta se puede determinar a partir de cualquier tabla de FDP normal con media cero (0) y desviación estándar uno (1). Es de anotar que la distribución normal arroja siempre valores de probabilidad mayores que las otras distribuciones, por lo cual su uso en evaluaciones de estabilidad presenta un abordaje conservador (Baecher y Christian, 2003).
En este tipo de evaluación, una dificultad radica en poder determinar la FDP de la función que se quiere evaluar, en este caso FSD, para lo cual resultan de utilidad los métodos probabilistas, ya que permiten la determinación de la FDP de una variable dependiente en función del conocimiento de las FDPs de las variables independientes que la generan. Según Baecher y Christian (2003), entre los métodos más utilizados en la estadística aplicada a la geotecnia están el método de Monte Carlo, el método de primer orden segundo momento (FOSM) y el método de estimativas puntuales, entre otros. En este trabajo se usó el método FOSM que de acuerdo con Baecher y Christian (2003) presenta una precisión suficiente para fines de ingeniería, a pesar de sus simplificaciones.
El método FOSM utiliza la serie de Taylor para la determinación de la distribución de probabilidad de una función con un número de variables aleatorias (Baecher y Christian, 2003). Las ventajas de este tipo de solución radican en que los cálculos matemáticos son simplificados y solo se requiere del conocimiento de los valores de los momentos de las distribuciones estadísticas de las variables que forman la función. Para N variables aleatorias no correlacionadas, G(x1, x2, ....., xN), se tiene:
donde 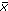 i = E[xi] corresponde al valor medio de la variable xi, V(xi) es la varianza de la variable xi, E[G] es la media o valor esperado de G y V[G] es la varianza de G.
i = E[xi] corresponde al valor medio de la variable xi, V(xi) es la varianza de la variable xi, E[G] es la media o valor esperado de G y V[G] es la varianza de G.
En las expresiones anteriores, la serie de Taylor fue truncada a partir de sus términos de segundo orden, despreciándose por tanto los efectos de los terceros y cuartos momentos probabilistas. Sin embargo, esta aproximación se considera plenamente aceptable para fines prácticos (Baecher y Christian, 2003). Los valores de las derivadas pueden ser obtenidos mediante el cálculo analítico, pero es más usual y recomendable usar la aproximación numérica sugerida por (Christian, et al., 1994), según la cual se estima la derivada con la ecuación:
De forma similar que en el índice β para el FSD, para la probabilidad de falla en términos de Ac, se determina la ocurrencia de un índice confiabilidad b1 definido como:
donde Ac es la aceleración crítica, Ah es la aceleración del sismo de diseño o del sismo más probable en la zona estudiada y σAc es la desviación estándar de la aceleración crítica. Es este caso se usaron los valores de Ah presentados para la microzonificación del VA (AMVA, 2007).
Igualmente se calculó la probabilidad de falla de los taludes frente a la acción de un sismo de magnitud probable. Para esto se consideraron las aceleraciones dadas en el mapa mostrado en la Figura 2-d para un periodo de retorno de 475 años.
Probabilidad general de falla
En la región del VA, los deslizamientos se originan con mayor frecuencia en temporadas lluviosas en las cuales se presenta un incremento de la saturación del suelo con la consecuente disminución de su cohesión y el incremento de la presión de poros. El proceso de disminución en la resistencia al cortante debido a los cambios de contenido de agua es un proceso de alta complejidad, que no fue considerado en el desarrollo de este estudio. Por lo cual, el efecto de la saturación se tuvo en cuenta solamente el incremento de la presión del agua, y para efectos de análisis en este trabajo se consideraron dos situaciones, una en la cual el nivel del agua se presenta en la condición más crítica, es decir Hw = H, y otra favorable en la cual Hw = 0.
Por simplicidad, hasta esta etapa se consideró la aceleración producida por el sismo y la presencia de agua como variables deterministas, por lo cual la probabilidad de falla del talud o ladera depende solamente de la variabilidad de los parámetros geotécnicos y de la presión de poros. La eventual condición de saturación del suelo es un fenómeno aleatorio que se debe tener en cuenta en la evaluación de la probabilidad de remoción en masa. En este caso, se hizo considerando la probabilidad de que el suelo esté saturado o no. De acuerdo con el teorema de probabilidad total, la probabilidad total de falla de un talud está dada por la ecuación:
donde Pft es la probabilidad de falla total, Pfs es la probabilidad de falla del talud debido a la acción del sismo en condición saturada, Pfns es la probabilidad de falla en condición no saturada, Ps es la probabilidad marginal de que el suelo esté saturado y (1Ps) es la probabilidad marginal de que el suelo no esté saturado.
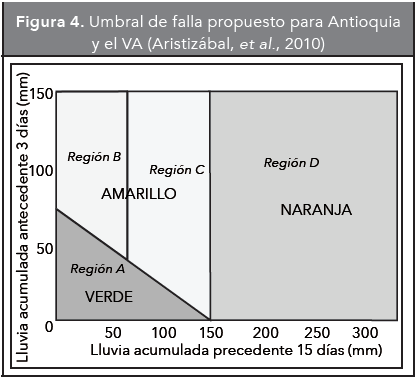
La probabilidad de falla de los taludes en condición saturada y no saturada se puede calcular independientemente, pero determinar la probabilidad de que el suelo se encuentre saturado es difícil debido a la complejidad del fenómeno de variación de las condiciones de contenido de agua del suelo. Para el caso de los suelos del VA existe poca información que permita determinar la probabilidad de que los suelos estén saturados, sin embargo, en trabajos realizados por varios autores (Echeverri y Valencia, 2004, Moreno, et al., 2006 e Hidalgo, et al., 2012) se ha podido establecer que la mayoría de los deslizamientos se producen por la saturación de los suelos debido al efecto de la lluvia acumulada, y que la ocurrencia de movimientos en masa es posible relacionarla con la cantidad de lluvia mediante los llamados umbrales de falla. En el Sistema de Alerta Temprana del Área Metropolitana (SIATA) se ha propuesto que para el VA se puede usar un umbral de falla que relaciona la lluvia acumulada de 3 días y la lluvia acumulada de 15 días (Figura 4). Este umbral había sido propuesto por (Moreno, et al., 2006) para el departamento de Antioquia como se muestra en la Figura 4. El umbral de falla está dado por la ecuación:
donde R3 corresponde a la lluvia acumulada antecedente de 3 días y R15 corresponde a la lluvia acumulada precedente de 15 días.
En este trabajo se supone que la probabilidad de saturación del suelo está relacionada con la probabilidad de que el umbral de falla sea excedido. Esta consideración parte de aceptar que la condición dada por el umbral de falla representa una situación de saturación propicia para los deslizamientos, con la ya mencionada reducción de la resistencia al cortante de los materiales debido a la disminución de la succión y la generación de presiones de poros.
En el caso tratado por Hidalgo, et al. (2012) se calculó la probabilidad de que fuera excedido el umbral dado por las lluvias acumuladas de 5 y 15 días, pero en el caso tratado en el presente trabajo se calculó la probabilidad de saturación como la probabilidad de que el par ordenado (R15, R3) esté por encima de la recta del umbral de falla, es decir, se considera que el suelo estará saturado si se cumple la relación de la ecuación:
Donde R3m es la lluvia acumulada de 3 días, calculada a partir de los registros de los pluviómetros y R3 es la lluvia acumulada de 3 días calculada con la Ecuación 12.
Siguiendo los conceptos presentados anteriormente, para cada estación pluviométrica se organizaron los registros, se calcularon las ventanas móviles de lluvia acumulada de 15 días y 3 días para cada fecha. Igualmente para cada fecha se calculó el valor de lluvia de 3 días usando el umbral definido en la Ecuación 11 y se estableció la comparación entre los valores de lluvia de 3 días como se indica en la Ecuación 12. Se determinó el número de veces que el umbral fue excedido durante el periodo de registros y este número de ocurrencias se dividió por el número total de registros de lluvia para establecer la probabilidad de que el umbral fuera excedido, lo cual para la metodología empleada en este trabajo representa que el suelo alcanzó la condición de saturación crítica.
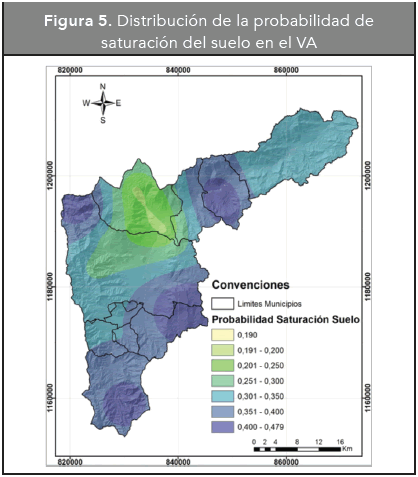
Después de determinar la probabilidad de que el suelo estuviera saturado según los datos de cada estación, se desarrolló un proceso geoestadístico para estimar por interpolación la probabilidad de saturación en cada una de las celdas. El método de interpolación usado en este trabajo corresponde al Método de Kriging, el cual es un estimador lineal insesgado que permite generar superficies continuas a partir de datos puntuales, eliminar tendencias de variación espacial puesto que asume que está presente en los datos y proporciona medidas de error. En la Figura 5 se muestra la distribución de la probabilidad de saturación determinada para el VA.
Programación del modelo
A partir de esta definición, se elaboró un modelo para la determinación de la amenaza de forma probabilísta, usando para esto técnicas de programación y modelación del software ArcGIS TM Módulo "ModelBuilder".
Los resultados del índice de confiabilidad obtenidos mediante las Ecuaciones 5 y 9, se exportan al software Microsoft Excel para calcular la PF, es decir, la probabilidad de que FSD sea menor que la unidad.
3. ANÁLISIS DE RESULTADOS
Inicialmente se realizó una serie de corridas del modelo para calcular algunas variables del análisis y luego se procedió a calcular las probabilidades de falla. Se consideraron diferentes profundidades de la superficie de falla a 2, 5, 10 y 20m. Tomando como referencia el caso de la superficie de falla a 5m de profundidad, se observó una disminución del FSD en promedio de 20 % cuando la profundidad de la superficie de falla fue 10m y de 30 % cuando esta fue de 20m.
Así mismo, se efectuaron corridas del modelo considerando diferentes alturas del nivel freático (Hw) con la superficie de falla a 5m. Se consideraron alturas de agua de 0, 3 y 5m.
Tomando como referencia los resultados obtenidos con la superficie de falla a 5m y el nivel de agua coincidiendo con la superficie de falla (Hw = 0) se observó una disminución del FSD en promedio de 20 % cuando el nivel del agua es 3m y de 33 % cuando Hw = 5m. Aunque los movimientos en masa registrados en el VA, en general son superficiales, es decir, profundidades del orden de 2m, en este trabajo se adoptó para el resto de las evaluaciones una superficie de falla localizada a 5m de profundidad, considerando que el efecto evaluado es debido no solo a la presencia del agua sino también a la acción sísmica. Por otro lado, considerando que la situación más crítica para el talud se da cuando el nivel del agua coincide con la superficie del terreno se adoptó Hw = 5m como patrón para evaluar la inestabilidad por efecto del agua.
La aceleración crítica en cada celda se determinó considerando la superficie de falla a 5m de profundidad y condiciones de agua coincidentes con la superficie de falla (Hw = 0) y del terreno (Hw = 5m) respectivamente. La aceleración crítica en condiciones húmedas varía entre 0 y 1,13g y en condiciones saturadas varía entre 0 y 0,84g. Sin embargo, hasta esta etapa aún no ha sido considerada la incertidumbre de los parámetros del suelo en la determinación de estos valores. Al considerar la incertidumbre, usando las Ecuaciones 3 y 9 se calculó el coeficiente b1 para los valores de Ah mostrados en la Figura 2-d, bajo un escenario de condición húmeda (Hw = 0) y saturada (Hw = 5m).
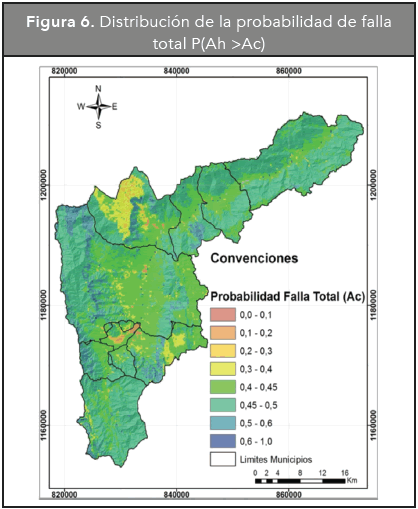
Suponiendo una distribución normal, se calculó la PF total de cada celda (Figura 6) encontrando una variación entre 0,15 y 1,0, presentándose las mayores probabilidades de falla en áreas caracterizadas por pendientes superiores al 40 % (22°) y condiciones hidrológicas desfavorables como las que se dan en el noroccidente en el corregimiento de Palmitas y en la zona sur oriental. Las áreas localizadas en la zona central del VA que tienen pendientes más suaves, menores al 40 % presentan probabilidades de falla entre 0,4 y 0,5 y representan aproximadamente el 86 % del área estudiada.
Estas probabilidades de falla están dadas para un sismo con una probabilidad de excedencia de 10 % en 50 años, lo cual significa que las probabilidades anuales de que se produzca un deslizamiento debido a un sismo varían entre 3x10-4 y 2x10-3. De acuerdo con la distribución que presentan las probabilidades de falla y considerando que la amenaza por deslizamiento puede ser clasificada como muy alta (PF anual>0,2), alta (0,02-0,2), media (0,002-0,02), baja (0,002, 0,0002), muy baja (<0.0002) (Chowdhury, et al.,2010), el VA tiene el 99 % de su territorio en condiciones de amenaza por deslizamientos originados por sismos baja a muy baja y un 1 % en condiciones medias de amenaza.
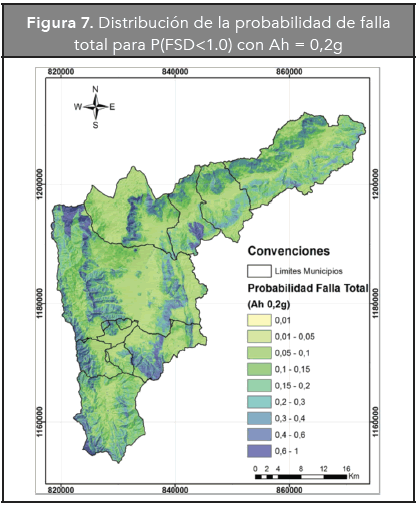
Igualmente, usando las Ecuaciones 4 y 5 se calculó el FSD y el coeficiente β para valores de Ah de 0,2g, bajo un escenario de condición húmeda (Hw = 0) y saturada (Hw = 5m). Tomando una distribución normal, se calculó la PF total de cada celda (Figura 7) encontrando una variación entre 0,1 y 1,0, presentándose una distribución similar a la observada para la Ac con las condiciones más desfavorables en el noroccidente, corregimiento de Palmitas y en la zona sur oriental del VA, y más estables en las áreas localizadas en la zona central. Los rangos de valores de las probabilidades de falla y su distribución son comparables constituyendo zonas de amenaza similares a las establecidas anteriormente en las que predominan las zonas de baja y muy baja amenaza.
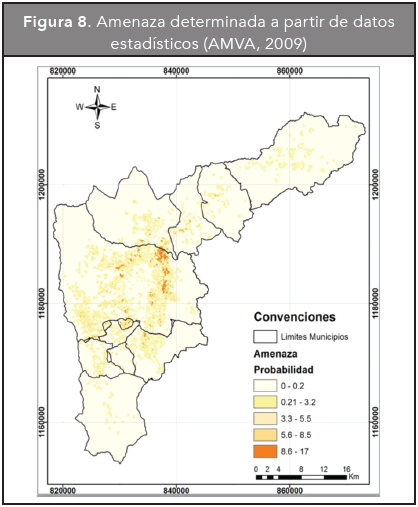
Comparando los resultados de este trabajo con resultados de la evaluación de amenaza por movimien tos de masa del estudio "Amenaza, vulnerabilidad y riesgo por movimientos en masa, avenidas torrenciales e inundaciones en el Valle de Aburrá" (AMVA, 2009) mostrados en la Figura 8, se observa cierta coincidencia entre las zonas localizadas al interior del VA, en especial en el municipio de Medellín, pero no en las zonas externas, lo cual se puede explicar porque el análisis de AMVA (2009) está basado en el uso de redes neuronales para determinar la amenaza, las cuales requieren información de eventos históricos, información que es más abundante en las zonas pobladas del VA y escasa en otras zonas, por lo cual no pueden prever eventos en las mismas. Aunque, en general, las probabilidades son moderadas, ocasionalmente se observan pequeñas áreas con probabilidades de falla muy altas que se muestran como puntos críticos en la Figura 9.
Igualmente, para verificar la capacidad del modelo para determinar zonas críticas, se identificaron los sitios que presentan las peores condiciones de estabilidad, determinados como aquellas celdas que presentaron FSD menores que 1,2 en condiciones saturadas y con aceleración de 0,2g (Figura 9-a) o con las mayores probabilidades de falla totales. Se observa que los puntos críticos identificados están localizados en zonas que frecuentemente son afectados por problemas como los descritos en trabajos como el proyecto "Amenaza, vulnerabilidad y riesgo por movimientos en masa, avenidas torrenciales e inundaciones en el Valle de Aburrá", y que se muestran en la Figura 9-b.
De igual forma, para verificar la capacidad del modelo implementado para determinar zonas críticas, se identificaron los sitios que presentan las peores condiciones de estabilidad, determinados como aquellas celdas que presentaron FSE menores que 1,2 en condiciones de contenido de agua natural, y aquellas celdas donde la Ac excede la aceleración horizontal de 0.2g estipulada para la ciudad de Medellín de acuerdo a la Norma Colombiana de Diseño Sismo resistente (AIS 2010) (Figura 9-a).
Se observa que los puntos críticos identificados están localizados en zonas que han sido afectadas por problemas como los descritos por AMVA (2009) y que se encuentran inventariados en los registros del Departamento Administrativo de Gestión del Riesgo de Desastres (antiguo SIMPAD), y en la base de datos del proyecto DESINVENTAR del Área Metropolitana del Valle de Aburrá, donde se reportan los procesos morfodinámicos, producto de movimientos en masa ocurridos en un intervalo de tiempo de aproximadamente 20 años comprendidos entre 1985-2006, los cuales se muestran en la Figura 9-b.
Resaltadas en los rectángulos de la Figura 9, se muestran las zonas obtenidas mediante un análisis espacial donde los puntos críticos calculados presentan un porcentaje de coincidencia respecto al inventario mencionado, del orden de 61 % para el caso de los puntos críticos por FSE, que representan la condición normal de las laderas. Para el caso de los puntos críticos por Ac se obtuvo un 13 % de coincidencia, lo cual representa un escenario de un sismo con una aceleración de 0.2g y que serían puntos donde el factor seguridad estaría por debajo de la unidad.
4. CONCLUSIONES
El modelo elaborado permite estimar la amenaza y la zona de influencia debido a movimientos en masa detonados por sismos, considerando la influencia de las condiciones de saturación debidas a las lluvias.
Los resultados encontrados muestran que el modelo es robusto en la identificación de zonas críticas para la estabilidad. Con esto se puede hacer una priorización de zonas que deben ser estudiadas en detalle para garantizar la seguridad de las personas e infraestructuras próximas al sitio.
Es probable que se presenten movimientos de masa en caso de que se presente un movimiento sísmico con las características previstas para el VA, y esta probabilidad se incrementa si los suelos se encuentran saturados.
En el escenario considerado, con una aceleración sísmica de 0,2g, las máximas probabilidades de ocurrencia de deslizamiento, corresponden a, 99,96 % en una condición de humedad normal del suelo y al 100 %, en una condición de saturación total del suelo. Las áreas que presentan estos valores de probabilidad de falla, corresponden a zonas de los corregimientos de Palmitas, San Cristóbal, Altavista y Santa Elena.
Este trabajo puede servir como base para la implementación de un sistema de alerta por movimientos de masa fundamentado en modelos de base física, y para la evaluación de amenaza, pudiendo establecer una zonificación en términos de la probabilidad anual de ocurrencia de deslizamientos.
En trabajos futuros se complementará el presente con nuevos análisis que permitan la evaluación de riesgos por deslizamientos y la inclusión de una mayor cantidad de datos de lluvia, y que consideren sismos con periodos de recurrencia diferentes ya que este trabajo se limitó a sismos con períodos de retorno de 475 años.
REFERENCIAS
AIS (2010). Normas Colombianas de Diseño y Construcción Sismo Resistente, NSR-10. Asociación Colombiana de Ingeniería Sísmica (AIS). Bogotá - Colombia. 2010. [ Links ]
AMVA (2007). Microzonificación y evaluación del Riesgo Sísmico del Valle de Aburrá. Área Metropolitana del Valle de Aburrá. Publicación Institucional, 29, 2007. 184 p. [ Links ]
AMVA (2009). Amenaza, vulnerabilidad y riesgo por movimientos en masa, avenidas torrenciales e inundaciones en el Valle de Aburrá. Formulación de propuestas de gestión. Proyecto en conjunto del Área Metropolitana del Valle de Aburrá con los municipios de Medellín y Envigado, Corantioquia y la Universidad Nacional de Colombia. Convenio 4800002397 DE 2007. Libro II, Julio de 2009. 225 p. [ Links ]
Aristizábal, E.; Gómez, J. (2007). Inventario de emergencias y desastres en el Valle de Aburrá. Originados por fenómenos naturales y antrópicos en el periodo 1880-2007. Gestión y Ambiente. 10(2), 2007, pp. 17-30. [ Links ]
Aristizábal, E.; Gamboa, M.; Leoz F. (2010). Sistema de alerta temprana por movimientos en masa inducidos por lluvia para el valle de Aburrá, Colombia. Revista EIA, 13, Julio. pp. 155-169. [ Links ]
Baecher, G.B.; Christian, J.T. (2003). Reliability and Statistics in Geotechnical Engineering. John Wiley and Sons. England. 620 p. [ Links ]
Bonachea, J. (2006). Desarrollo, aplicación y validación de procedimentos y modelos para evaluación de amenazas, vulnerabilidad y riesgo debidos a procesos geomorfológicos. Tesis de Doctorado. Facultad de Ciencias. Departamento de Ciencias de la Tierra y Física de la Materia Condensada. Universidad de Cantabria. Santander, España. 278 p. [ Links ]
Chowdhury, R.; Flentje, P.; Bhattacharya G. (2006). Geotechnical Slope Analysis. Taylor and Francis, London, England, 737 p. [ Links ]
Christian, J.T., Ladd, C.C.; Baecher, G.B. (1994). Reliability Applied to Slope Stability Analysis. Journal of Geotechnical Engineering, ASCE, 120(12), pp. 2180-2207. [ Links ]
Coronado, J.A. (2006). Evaluación de la susceptibilidad a deslizamientos por medio del uso de Sistemas de Información Geográfica: Aplicación en un área del Eje Cafetero Colombiano. (En portugués) Tesis de Maestría. Universidad de Brasília, Facultad de Tecnología, Departamento de Ingeniería Civil. Brasilia, DF, 92 p. [ Links ]
Delgado, J.; Peláez, J.A.; Tomás, R.; Estévez, A.; López-Casado, C.; Doménech C.; Cuenca, A. (2006). Evaluación de susceptibilidad de las laderas a sufrir inestabilidades inducidas por terremotos: aplicación en la cuenca del drenaje del río Serpis (provincia de Alicante). Revista de la Sociedad Geológica de España, 19(3-4), pp. 197-218. [ Links ]
Echeverri, O.; Valencia, Y. (2004). Análisis de los deslizamientos en la cuenca de la quebrada La Iguaná de la ciudad de Medellín a partir de la interacción lluviapendiente-formación geológica. Revista Dyna, 71(142), pp. 33-45. [ Links ]
Godt, J.W.; Sener, B.; Verdin, K.L.; Wald, D.J.; Earle, P.S.; Harp, E.L.; Jibson, R.W. (2008). Rapid assessment of earthquake-induced landsliding. Proceedings of the First World Landslide Forum, November, Tokyo, Japan, Parallel Sessions Volume, International Program on Landslides. [ Links ]
Hidalgo, C.A. (2013). Incertezas, Vulnerabilidade e Avaliação de Risco Devido a Deslizamento em Estradas. Tesis de doctorado Departamento de Engeniería Civil y Ambiental, Universidad de Brasilia, Brasilia, Brasil, 250 p. [ Links ]
Hidalgo, C.A.; Vega, J.; Assis, A. (2012). Estimación de amenaza por deslizamiento en proyectos lineales: Carreteras en suelos residuales. Memorias del IV Simposio Panamericano de deslizamientos IVSPD. Paipa, Colombia. ISBN 978-958-98770-4-3. [ Links ]
Jaiswal, P.; Van Westen, C.J. (2009a). Rainfall - based temporal probability for landslide initiation along transportation routes in Southern India. Landslide processes: from geomorphologic mapping to dynamic modelling: proceedings of the landslide processes conference, Strasbourg, France, ed. by J.P. Malet, A. Remaitre and T. Bogaard - Strasbourg: European Centre on Geomorphological Hazards (CERG), pp. 139-143. [ Links ]
Jaiswal, P.; Van Westen, C.J. (2009b). Estimating temporal probability for landslide initiation along transportation routes based on rainfall thresholds. Engineering Geology 116, 236-250pp. Geomorphology 112, pp. 96-105. [ Links ]
Jaiswal, P.; Van Westen, C.J.; Jetten, V. (2010). Quantitative landslide hazard assessment along a transportation corridor in southern India. Engineering Geology 116, pp. 236-250. [ Links ]
Jibson, R.W.; Harp, E.L.; Michael, J.A. (1998). A method for producing digital probabilistic seismic landslide hazard maps. Engineering Geology, 58, pp. 271-289. [ Links ]
Moreno, H.A.; Vélez, M.A.; Montoya, J.D.; Rhenals R.L. (2006). La lluvia y los deslizamientos de tierra en Antioquia: Análisis de su ocurrencia en las escalas interanual, intranual, y diaria. Revista EIA, 5, pp. 59-69. [ Links ]
Newmark N. (1965). Effects of earthquakes on dams and embankments. Géotechnique, 15(2), pp. 139-159. [ Links ]
Remondo, J.; Bonachea, J.; Cendrero A. (2008). Quantitative landslide risk assessment and mapping on the basis of recent occurrences. Geomorphology, 94(3-4), pp. 496-507. [ Links ]
Rosenblueth, E. (1975). Point estimates for probability moments. Proceedings, National Academy of Science 72(10), pp. 3812-3814. [ Links ]
Salciarini, D.; Godt, J.W.; Savage, W.Z.; Baum, R.L.; Conversini P. (2008). Modeling landslide recurrence in Seattle, Washington, USA. Engineering Geology 102, pp. 227-237. [ Links ]
Vega, J.A. (2013). Estimación del riesgo por deslizamientos de laderas generados por eventos sísmicos en la ciudad de Medellín usando herramientas de la Geomática. Caso aplicado a edificaciones urbanas. Tesis de Maestría de la Facultad de Ingeniería y Ciencias Astronómicas y Geofísicas de la Universidad Nacional de La Plata - Argentina. 51 p. [ Links ]
Zêrere, J.L.; Trigo, R.M.; Trigo I.F. (2005). Shallow and Deep Landslides Induced by Rainfall in the Lisbon Region (Portugal): Assessment of Relationships with the North Atlantic Oscillation. Natural hazards and Earth Systems Sciences 5, pp. 331-344. [ Links ]
Zêrere, J.L.; García, R.A.; Oliveira, S.C.; Reis, E. (2008). Probabilistic Landslide Risk Analysis Considering direct Costs in the Area North of Lisbon (Portugal). Geomorphology, 94, pp. 467-495. [ Links ]