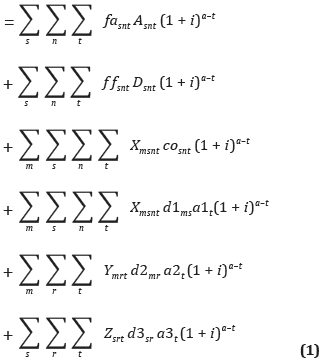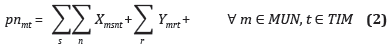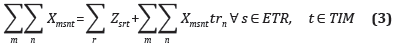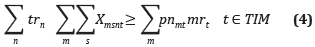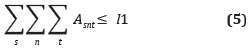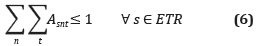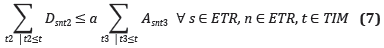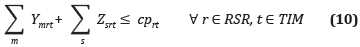Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.23 Envigado June 2015
MODELO MATEMÁTICO PARA LA UBICACIÓN DE ESTACIONES DE TRANSFERENCIA DE RESIDUOS SÓLIDOS URBANOS
MATHEMATICAL MODEL FOR TRANSFER STATION LocATION OF URBAN SOLID WASTE
MODELO MATEMÁTICO PARA LocALIZAÇÃO DE ESTAÇÕES DE TRANSFERÊNCIA DE RESÍDUOS SÓLIDOS URBANOS
Katherine Varón Valencia1, Juan Pablo Orejuela Cabrera2, Pablo César Manyoma Velásquez3
1 Ingeniera industrial Universidad del Valle.
2 Ingeniero industrial Universidad del Valle. MCs. Ingeniería Industrial Universidad del Valle. Profesor Asociado Universidad del Valle. Cll. 13 No. 100-00. Edificio 349, Cali, Colombia. Tel: (572) 23212270. Correo electrónico: juan.orejuela@correounivalle.edu.co.
3 Ingeniero industrial Universidad Autónoma de occidente. Especialista en Sistemas Generenciales en Ingeniería Pontificia Universidad Javeriana. MCs. Ingeniería Universidad del Valle. PhD. (c) Ingeniería Universidad del Valle. Profesor Asociado Universidad del Valle.
Artículo recibido: 31-I-2014 / Aprobado: 25-II-2015
Disponible online: 30 de junio de 2015
Discusión abierta hasta junio de 2016
RESUMEN
Las Estaciones de Transferencia son instalaciones que están dedicadas al manejo y traslado de Residuos Sólidos Urbanos o Municipales, desde un vehículo a otro con mayor capacidad de carga que los transporta hasta su sitio de aprovechamiento o disposición final. El objeto central de esta investigación es representar la localización de este tipo de instalaciones a través de un modelo de programación lineal entera mixta, que tiene en cuenta las principales características de las estaciones, como la capacidad total y la capacidad de recuperación de materiales. La función objetivo formulada busca reducir al mínimo los costos fijos de apertura, los costos de transporte y los costos de operación, evaluados en el momento actual a través de una función de costo presente equivalente.
PALABRAS CLAVE: Estaciones de transferencia; recuperación de materiales; problema de localización; programación lineal entera mixta.
ABSTRACT
Transfer Stations are facilities dedicated to management, and solid waste transfer of a vehicle to another with greater capacity, which transports them to their place of use or disposal. The main purpose of the research is to represent the location of these kind facilities through a model of mixed integer linear programming, which consider different characteristics of stations such as total capacity and materials recovery. Total costs minimization is the main objective. To do this, we minimize opening fixed costs, transportation costs and operating costs evaluated at the current time through a function of present cost equivalent.
KEY WORDS: Transfer Stations, Materials Recovery, Location Problem, Mixed Integer Linear Programming.
RESUMO
As estações de transferência são instalações que se dedicam ao manuseio e transporte de resíduos sólidos urbanos ou municipais de um veículo para outro com maior capacidade de transporte para o local de utilização ou eliminação. O objetivo central deste trabalho é o de representar a localização dessas instalações através de um modelo de programação linear inteira mista, que leva em conta as características principais das estações, como a capacidade total e resistência dos materiais. A função objetiva formulada visa minimizar os custos fixos de abertura, os custos de transporte e os custos operacionais, avaliados no momento através de uma função de custo presente equivalente.
PALAVRAS-CHAVE: Recuperação de estações de transferência; Problemas de localização; Programação linear inteira mista.
1. INTRODUCCIÓN
Los residuos que provienen principalmente de los hogares, oficinas, hoteles, centros comerciales, tiendas, escuelas, instituciones y servicios municipales como la limpieza de calles y el mantenimiento de áreas recreativas, son denominados Residuos Sólidos Municipales o Urbanos (RSM o RSU), representando entre el 70 % y el 80 % del total de toneladas de los residuos sólidos en el mundo (RRC.AP, 2010).
La Gestión Integral de Residuos Sólidos (GIRS) se ha convertido en uno de los grandes desafíos en las zonas urbanas de todo el mundo, especialmente en las ciudades de los países en desarrollo, siendo evaluada como un ciclo con muchas etapas estrechamente relacionadas, iniciando con la producción de bienes y continuando con la generación, almacenamiento, presentación, barrido, recolección, tratamiento y disposición final de residuos (Ekmekçioglu, Kaya, y Kahraman, 2010).
Un elemento que se ha convertido en parte importante de los sistemas modernos de gestión, son las denominadas Estaciones de Transferencia (ET), debido a que los rellenos sanitarios cada vez se encuentran más alejados de los centros urbanos (Washburn, 2012). Las ET están dedicadas al manejo, recuperación de materiales y al traslado de residuos sólidos de un vehículo recolector a otro con mayor capacidad de carga, que los transporta hasta su sitio de disposición final o sitios de aprovechamiento tales como plantas de reciclaje, centros de procesamiento, incineradores, instalaciones de compostaje, entre otras (Eshet, et al. 2007). Algunos autores (Eshet, et al. 2007; Wilson y Vincent, 2008) han identificado el crecimiento que han tenido este tipo de instalaciones en el mundo (en Estados unidos por ejemplo son más de 3.500 estaciones) dentro de los sistemas de gestión de residuos sólidos municipales, haciendo pensar en una tendencia que probablemente continuará en el futuro.
Las ventajas asociadas a las ET tales como economía de transporte, ahorros laborales, ahorros energéticos, desgaste reducido y versatilidad, entre muchas otras, generan la necesidad de estudiar estas instalaciones, desde diferentes puntos de vista para enfrentar nuevas situaciones. Entre estos desafíos, la localización surge como un problema primario a solucionar, sobre todo cuando se trata de ET regionales que afectan a diferentes áreas urbanas (Schaper y Brockway, 2001).
La localización de instalaciones es considerada como una decisión fundamental para la planeación estratégica de empresas privadas y públicas. Los beneficios de la localización son amplios y de larga duración e influyen en numerosas decisiones operativas y logísticas. Los altos costos asociados con la adquisición de la propiedad y la construcción hacen que la ubicación de instalaciones se convierta en inversiones a largo plazo. Los tomadores de decisiones deben seleccionar los sitios de tal forma que no sólo se desempeñen bien en función del estado actual del sistema, sino que sigan siendo "buenos" durante la vida de la instalación (Farahani, Steadieseifi, y Asgari, 2010).
Desde sus inicios, la teoría de localización ha sido dominada por modelos y métodos para instalaciones deseables. Esto ha venido cambiando desde los años 70's cuando se establecieron las bases para la investigación de la localización de las instalaciones no deseadas. Varias razones se pueden atribuir a la entrada tardía en el mundo académico, pero la principal de ellas es la proliferación de estas instalaciones; sitios como aeropuertos, mega-estadios, plantas nucleares y rellenos sanitarios entre otros, son derivaciones de la industrialización y los avances tecnológicos de la segunda mitad del siglo XX (Melachrinoudis, 2011).
El creciente interés en la modelación de la localización de instalaciones no deseables, se atribuye a la creciente preocupación por el medio ambiente. De hecho, cualquier tipo de centro moderno tendrá algunos efectos perjudiciales sobre la calidad de vida, esto va a depender de la percepción humana, evidenciada por los efectos físicos causados por las diferentes formas de contaminación tales como aire, agua y ruido (Saameño- Rodríguez, et al. 2006). La ubicación de estas instalaciones causa tal inconformidad en la población, que se ha convertido en una verdadera oposición de la gente hacia la instalación cercana. En los últimos tiempos, una nueva nomenclatura ha sido desarrollada para definir esta oposición (las siglas son en inglés): NIMBY (no en mi patio trasero), NIMNBY (no en el patio trasero del vecino), NIABY (no en el patio trasero de nadie), NIMTOO/NIMTOF (no en mi mandato), NOPE (no en el planeta tierra), LULU (uso de la tierra a nivel local no deseado), BANANA (construir absolutamente nada a nadie ni cerca ni lejos) (Colebrook y Sicilia, 2007). Estas definiciones reflejan el malestar que puede ocasionar este tipo de instalaciones.
En la revisión de la literatura, realizada para esta investigación, se observó cómo los modelos matemáticos son usados en diferentes situaciones, relacionadas con el problema principal, y cómo influye el lugar y las características específicas del contexto. Es el caso de Guo y Huang, (2009a, y 2009b) quienes en dos investigaciones relacionadas, desarrollaron un sistema de apoyo para la toma de decisiones a largo plazo sobre la gestión de residuos, donde se involucran las decisiones de expansión de capacidad del sistema (incluyendo las estaciones de transferencia) y la asignación de los residuos en un contexto multi-sitio y multi-período. El modelo utilizó programación entera mixta estocásticainexacta- borrosa. Con el método desarrollado, se relacionaron políticas ambientales predefinidas e implicaciones económicas asociadas. En el segundo artículo, el método desarrollado se aplicó a un caso real de planificación a largo plazo de la gestión de residuos en la ciudad de Regina, Canadá.
Un enfoque integrado de optimización y análisis multi-criterio fue presentado por Xi, et al. (2010). El documento muestra un modelo de programación lineal entera mixta inexacto y restringido, que sirve de soporte para la planeación a largo plazo de la gestión de residuos sólidos en Beijing. El modelo abordó las incertidumbres que se presentan no sólo como intervalos discretos, sino también como probabilidades y generó soluciones que representan rangos flexibles para los tomadores de decisiones en cuanto a ampliación de las instalaciones y asignación del flujo de residuos. Debido a que cada escenario tiene sus ventajas y desventajas, ellos utilizaron herramientas de MCDA como una forma de ayuda, para los decisores, en el análisis de equilibrio entre la calidad del medio ambiente y los objetivos económicos.
Entre las últimas publicaciones se tiene la de Eiselt y Marianov (2014), quienes modelaron la ubicación de los rellenos sanitarios en relación con las estaciones de transferencia y a su vez, determinaron el tamaño de los rellenos a establecer. El modelo se formuló como un problema de optimización entera mixta bi-objetivo, en el que uno de los objetivos fue el de minimización de costos tradicionales, mientras que el otro minimizó la contaminación, vista esta con una óptica de límites según la legislación. Ellos consideraron una política de zonas de saturación (exclusión), con la cual se pretendía que a una población le quedara cercano, como máximo una sola instalación no deseada. El modelo se formuló y se resolvió para la región de Bíobío en Chile.
En Colombia, el problema de la localización de instalaciones para la Gestión Integral de RSU es prácticamente nuevo. Aunque estas instalaciones han sido declaradas en las diferentes normativas de la nación, aún no presentan un claro desarrollo en la investigación de la localización. Londoño, et al. (2010) presentaron una metodología para la determinación de las áreas potenciales en el asentamiento de un parque de tratamiento y disposición final de residuos sólidos de tipo regional. Dicha propuesta se basó en un análisis matricial combinado con una herramienta de Sistemas de Información Geográfica (SIG), que permitió evaluar diferentes sitios desde su viabilidad ambiental, social, económica y física. Mientras que Mejía, et al. (2012), presentaron una guía para localizar rellenos sanitarios, combinando un SIG con una herramienta multi-criterio. Con esto se pretendía establecer prioridades en la evaluación de los criterios de selección.
El presente trabajo desarrolla un problema de localización de Estaciones de Transferencia regionales, teniendo en cuenta las relaciones que se forman entre los diferentes municipios generadores de residuos, los rellenos sanitarios que se utilizan para la disposición final y las características principales de Estaciones de Transferencia Multipropósito, tales como la capacidad total o la capacidad de recuperación de materiales, entre otras. Siendo esta última relación una dimensión que se evidencia muy poco en la literatura consultada. También cabe anotar que muchos elementos necesarios para la localización de instalaciones no deseadas, no hacen parte del alcance de esta investigación.
La meta de la situación planteada es minimizar costos fijos de apertura, costos de transporte y costos operativos de las estaciones de transferencia que se abran, con las cuales se cumplan las objetivos de recuperación de materiales durante el horizonte planeado.
2. MÉTODOS
Conociendo la ubicación de los municipios y la producción de residuos sólidos por periodo de tiempo en cada uno de ellos, al igual que la localización de los rellenos sanitarios que presten el servicio para esa región, se pretende determinar en qué momento se abre o no las estaciones de transferencia necesarias con su respectiva ubicación, tipología y los flujos de residuos entre las instalaciones.
El sistema considera tres nodos, los municipios generadores MUN = {1,... m}, cuya producción de residuos sólidos por periodo de tiempo t es igual pnmt, los posibles sitios para localizar las estaciones de transferencia ETR = {1,... s}, las cuales pueden ser de un solo tipo específico TET = {1,... n} y los rellenos sanitarios municipales RSM = {1,... r}.
Las estaciones de transferencia que se van a considerar en el modelo son estaciones multipropósito, es decir, que en ellas se pueden llevar a cabo actividades de recuperación de materiales. Estas pueden ser de diferentes tipos los cuales están determinados por la combinación de tres atributos: la capacidad de la estación casnt, el costo de apertura f1snt, y la tasa de recuperación de residuos trn.
El horizonte de planeación se constituye por un conjunto de periodos consecutivos TIM = {1,... t}, cada periodo de tiempo es equivalente a 1 año. El modelo determina en qué momento, de qué tipo y en que sitio candidato se debe abrir una estación de transferencia de manera que se minimice el costo total; compuesto de la siguiente forma:
- El costo de apertura f1snt, hace referencia a los costos de los estudios preliminares (del suelo, ambientales, económicos, etc.) y los rubros asociados a la construcción.
- Los costos de transporte a1t, a2t, a3t, son los costos por tonelada-kilómetro ($/ton.km) de trasladar los residuos desde el municipio hacia la estación de transferencia, o directamente del municipio hacía el relleno sanitario y de la estación hasta el relleno sanitario, respectivamente.
- Por último el costo de operación cosnt, incluye los costos de mano de obra y maquinaria relacionada con la operación en la estación. Están representados en unidades monetarias por tonelada de residuos ($/ton).
2.2. Nomenclatura del modelo
- Conjuntos e índices
MUN = Municipios generadores de residuos sólidos, indexado por m
ETR = Sitios candidatos para las Estaciones de Transferencia de Residuos, indexado por s
TET = Tipos de Estaciones de Transferencia de Residuos, indexado por n
RSR = Rellenos Sanitarios Regionales, indexado por r
TIM = Periodos de tiempo, indexado por t
- Parámetros del modelo
pnmt Producción de residuos del municipio en el tiempo t
l1 Número máximo de ETR que se pueden abrir en todo el horizonte de planeación
fasnt Costo de instalación de la ETR s tipo n en el tiempo t
ffsnt Costo fijo de funcionamiento de la ETR s tipo n en el tiempo t
a1t Costo por kilómetro por tonelada de residuos transportados desde el municipio hasta la ETR en el tiempo t ($/(ton-km).
a2t Costo por kilómetro por tonelada de residuos transportados desde el municipio hasta el RSR en el tiempo t ($/(ton-km).
a3t Costo por kilómetro por tonelada de resi duos transferidos desde la ETR hasta el RSM en el tiempo t ($/(ton-km).
cosnt Costo de operación de la ETR s tipo n en el tiempo t
casn Capacidad de la ETR s tipo n
cprt C apacidad del RSR r destinada para el periodo de tiempo t
d1ms Distancia entre el municipio m y la ETR s
d2mr Distancia entre el municipio m y el RSR r
d3sr Distancia entre la ETR s y el RSR r
i Índice para llevar valores al futuro
trn Tasa de recuperación de residuos de la ETR tipo n
mrt Meta de recuperación de residuos en el tiempo t
a Horizonte de planeación, número total de periodos de tiempo t
- Variables de decisión
Xmsnt Cantidad de residuos transportados desde el municipio m hasta la ETR ubicada en el sitio candidato s de tipo n en el tiempo t
Ymrt C antidad de residuos transportados directamente desde el municipio m hasta el RSM r en el tiempo t
Zsrt Cantidad de residuos transportados desde la ETR ubicada en el sitio candidato s hasta el RSM r en el tiempo t
Asnt Variable binaria igual a 1 si se abre una ETR en el sitio candidato s de tipo n en el tiempo t, de lo contrario igual a 0
Dsnt Variable binaria igual a 1 si la ETR ubicada en el sitio candidato s de tipo n está disponible en el tiempo t para recibir residuos, de lo contrario igual a 0
2.3. Estructura del modelo
- Función objetivo
Min CT
La función objetivo determina el mínimo costo total al final del horizonte de planeación y está conformada por:
- Costos fijos de apertura (primer componente).
- Costos fijos y variables operativos (segundo y tercero componente).
- Costo de transporte de RSU entre municipios m y sitios posibles para las ETR (cuarto componente).
- Costo de transporte de RSU entre municipios m y relleno sanitario r (quinto componente).
- Costo de transferencia de RSU desde los sitios posibles de las ETR hasta el relleno sanitario r (sexto componente).
- Conjunto de restricciones
a. Recolección
La producción total de RSU debe ser igual a las toneladas enviadas a las ET más las toneladas enviadas directamente al relleno sanitario.
b. Balance
La cantidad de residuos que salen de todos los municipios m hacia las estaciones de transferencia s, debe ser igual a la cantidad de residuos que van de las estaciones s hacia todos los rellenos sanitarios r, más la cantidad de residuos que se recuperan en la estación s.
c. Recuperación de residuos
La tasa de recuperación de materiales por la cantidad de toneladas enviadas a la estación, no puede ser inferior a las metas establecidas, según la producción total de RSU.
d. Apertura de instalaciones
No se pueden abrir más estaciones de transferencia que el número máximo permitido.
Una estación de transferencia solo se puede abrir, como máximo, una sola vez.
Para que una estación posible sea usada, debe ser abierta en un momento anterior o por lo menos igual al del análisis.
Cada vez que una estación posible es abierta, de inmediato puede ser usada para recibir residuos todos los periodos hasta el final del tiempo del proyecto. No se tienen en cuenta clausuras temporales.
En este caso, se garantiza que la cantidad de residuos que llegan de todos los municipios m a las ubicaciones candidatas de estaciones de transferencia s sea menor a la capacidad disponible de cada una de ellas.
Esta restricción asegura que la cantidad de residuos que llegan al relleno sanitario r de todos los municipios m y de todos los sitios candidatos de estaciones de transferencia s, sea menor que la capacidad disponible del relleno destinada para el tiempo t.
f. Restricciones de no negatividad y de dominio
3. RESULTADOS
La base de datos utilizada para conformar la instancia analizada, se basó en la información pública presentada por la empresa Proactiva Colombia (2010), dedicada a la recolección y disposición final de RSU y a la estructura presentada en la investigación de Sánchez-Gómez, Estrada-Nuñez, (1996) acerca de las estaciones de transferencia en México. Los datos fueron actualizados y puestos en contexto para los 20 años de planeación.
Teniendo en cuenta la información utilizada acerca del número de habitantes por cada municipio, la producción per cápita de residuos (ton/hab), los costos del sistema y las distancias entre las instalaciones, se elaboraron los archivos de modelo, de datos y el de comandos y se corrió el modelo de programación lineal propuesto en el lenguaje de programación AMPL bajo el solver Gurobi 5.5.0. El modelo base presentó 2.560 variables (320 binarias y 2.240 lineales) y 884 restricciones. Los resultados reflejan el buen comportamiento del modelo, el cual cumple con los requisitos de recolección y recuperación de materiales y con las demás restricciones establecidas.
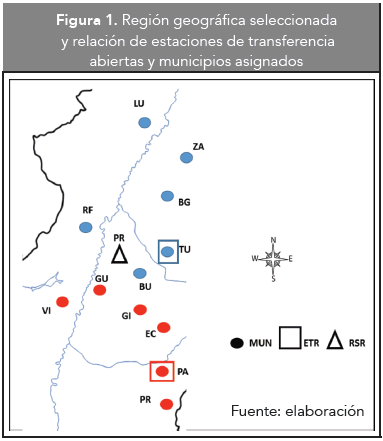
En la Figura 1 se puede observar la región seleccionada y la asignación de cada municipio a una estación de transferencia, según los resultados obtenidos. Siendo así, los municipios de PA, PR, EC, VI, GI y GU, deben enviar sus residuos a la estación de transferencia abierta en PA. La estación de transferencia localizada en el municipio de TU debe recibir los residuos de los municipios restantes. El relleno sanitario regional satisface las necesidades de los 12 municipios de la región.
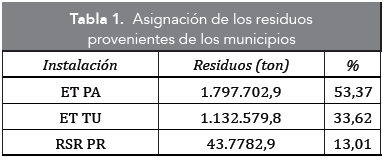
Como resultado final de la asignación de los residuos generados, más del 80 % de estos deben ser dispuestos en las ET (ver Tabla 1), mientras que una pequeña parte será enviada directamente al relleno sanitario regional. Esto se debe que el municipio BU envía sus residuos, la gran mayoría del horizonte de planeación, al relleno directamente. Solamente entre los periodos 17 a 20, hace uso de la ET correspondiente.
Se pudo observar que la instalación que recibe la mayor cantidad de residuos a lo largo del horizonte de estudio es la estación de transferencia de PA y también presenta el mayor porcentaje de utilización de su capacidad (42,80 %).
La función objetivo indica el costo óptimo total al final del horizonte de planeación (año 20), al detallarse su composición se identificó el costo de transporte es el de mayor participación con un 48 % del costo total, seguido del costo operación con 44 % y por el último el costo de apertura con apenas el 8 %.
Para valorar el impacto del modelo en comparación con la situación actual, en la que no se usan estaciones de transferencia, se obligó a que todas las variables de apertura de estaciones tomaran el valor de cero, de tal modo que los residuos se transportaran directamente al relleno sanitario. Con este análisis se identificó que la solución planteada por el modelo bajo consideración de estaciones de transferencia genera una disminución del costo futuro del 71,67%. Este ahorro en el costo se debe principalmente a dos factores, por un lado a una disminución del costo de transporte asociado a las toneladas recuperadas, ya que no se llevan al relleno, y por otro lado al beneficio obtenido por la consolidación de los envíos que se logran con la estación de trasferencia, es decir los carros recolectores llegan a la estación y en ésta se recupera y se consolida el resto de residuos de tal modo que se pueden enviar en otro tipo de transporte con más capacidad, más eficiente y a menor costo.
4. DISCUSIÓN
A partir de la variación del valor de algunos parámetros considerados importantes, se pueden observar algunos comportamientos que permiten contrastar con otras realidades:
- Variación en la producción de residuos:
En este primer escenario se realizaron dos instancias, una en donde la producción de residuos es creciente en el tiempo y en la otra decreciente, en los resultados obtenidos en ambas instancias, la configuración del sistema de recolección no cambia, se abren dos estaciones de transferencia tipo 2 en las mismas ubicaciones y en el mismo período de tiempo. El hecho de que no sea menor el número de estaciones abiertas dada la disminución en la producción de residuos se debe a que el sistema debe garantizar la recuperación de un porcentaje mínimo de residuos.
Sin embargo, los costos de transporte y de operación al tener una relación directa con la cantidad de residuos en el sistema si sufren una variación y por lo tanto al incrementar o disminuir la producción de residuos en los municipios el costo total también lo hace, pero no de manera proporcional. Por ejemplo, en la primera iteración la cantidad total de residuos crece aproximadamente 20 %, sin embargo el aumento del costo total, apenas alcanza el 0,44 %.
- Variación del número de estaciones de transferencia abiertas:
Con esta variación se obliga al modelo a abrir primero una, luego dos, y así sucesivamente hasta llegar a cuatro estaciones de transferencia que es el número de localizaciones posibles. Según los resultados obtenidos, la instalación de mayor preferencia es la ubicada en PA debido a que éste es el municipio con la producción más alta de residuos y por lo tanto localizar una estación en él puede ofrecer ahorros significativos en los costos de transporte. En la primera iteración dicha estación atiende a todos los 12 municipios en diferentes períodos de tiempo, los únicos que realizan transporte directo al relleno sanitario son BU, RF y TU y es porque se encuentran muy cercanos al relleno. En las iteraciones siguientes, algunos municipios son atendidos por varias estaciones de transferencia, la única de ellas que no es utilizada es la ubicada en Ginebra, la cual es abierta en el último período del horizonte (año 20), por tanto podríamos decir que esta instalación es la de menor preferencia.
- Variación en los costos de transporte:
Bajo este tercer escenario se realizó una variación en los costos de transporte, la cual iniciaba en 50 % e iba incrementándose de a 10 % hasta llegar al 150 %. Para los costos a1 (recolección de residuos desde el municipio hasta la estación) y a2 (transporte de residuos desde el municipio hacia el relleno sanitario) se hizo primero una variación individual y luego de manera conjunta pero inversa, es decir, que mientras el costo a1 estaba en el 50 % el costo a2 era del 150 %, la variación del costo a3 se realizó de manera individual.
Los resultados obtenidos evidencian que la variación en los costos de transporte no afectan la configuración del sistema, la cual sigue siendo igual a la presentada inicialmente, pero sí a los costos totales, los cuales se hacen mayores a medida que la variación crece. El costo total presenta una mayor razón de cambio frente a la variación del costo de transporte respecto a las demás variaciones realizadas, esto es debido a que aproximadamente el 90 % de los residuos pasa por una estación de transferencia lo que incrementa considerablemente el costo asociado con a1, además al enviarse directamente al relleno sanitario apenas el 10 % de los residuos el costo asociado con a2 no es significativo en el costo total al igual que el costo asociado con a3 por tener valores muy inferiores a los de los demás. Adicionalmente, se observa que entre mayor es la variación de los costos de transporte, el incremento en el costo total se hace cada vez menor, es decir que las curvas de costo total convergen hacia el mismo valor.
- Variación en la meta de recuperación de materiales del sistema:
En este último escenario se realizan seis iteraciones en las que varía la meta de recuperación de materiales a lo largo del horizonte de planeación, de manera que la primera iteración empieza con una meta del 0,05 % y va aumentando este mismo porcentaje en cada período, en la segunda con un 1 %, en la tercera con un 1,05 % y así sucesivamente hasta llegar al 3 %.
Los resultados obtenidos en este escenario muestran que al modificar la meta de recuperación de materiales cambia el costo total futuro y la configuración del sistema. En todas las iteraciones se siguen localizando las estaciones de transferencia en los municipios de PA y TU. En las primeras iteraciones se abren estaciones tipo 1, que son las que tienen menor capacidad de recuperación y por lo tanto presentan costos fijos de apertura y de operación inferiores. A medida que crece el porcentaje de recuperación el modelo da apertura a estaciones tipo 2 que tienen costos superiores y por lo tanto el costo total del sistema se incrementa.
5. CONCLUSIONES
El modelo de programación cumple con el objetivo de determinar la cantidad de estaciones de transferencia que se deben abrir en cada período de tiempo con su respectiva ubicación y tipología y la asignación de los flujos de residuos entre las instalaciones del sistema, garantizando el cumplimiento de las restricciones de recolección, balance, capacidad y recuperación de material.
A fin de simular el comportamiento del modelo de localización de estaciones de transferencia frente a posibles cambios en los parámetros y tomar las acciones necesarias, se realizó un análisis de sensibilidad que consideró los siguientes parámetros: producción de residuos en los municipios, número de estaciones de transferencia abiertas, costos de transporte y recuperación de materiales. Los resultados obtenidos evidenciaron que el patrón (creciente o decreciente) bajo el cual se comporta la producción de residuos en los municipios, al igual que el incremento de los costos de transporte no modifican la configuración del sistema, pero si influyen en los costos totales.
Como una forma de mejorar la modelación y lograr mejores resultados se deben tener en cuenta los ingresos que entran al sistema por la recuperación de materiales, al igual que las consecuencias derivadas de este hecho sobre la vida útil del relleno sanitario; tal como los inductores de riesgo ambiental y el impacto social que pueden ser minimizados por un mejor manejo de los RSM en las estaciones de transferencia.
Otro factor de futura investigación, es desvincular el determinismo asociado a los datos del modelo. Tal es el caso de la generación per cápita de RSM en todo el tiempo del proyecto y las tasas de crecimiento o decrecimiento de la población involucrada en la regionalización de las instalaciones. Esto sin duda, llevaría al modelo a convertirse en una mejor representación de la situación problemática expuesta en este trabajo.
REFERENCIAS
Colebrook, M.; Sicilia, J. (2007). Undesirable Facility Location Problems on Multicriteria Networks. Computers and Operations Research, 34 (5), pp. 1491-1514. [En línea]: [Consultado el 28 de febrero de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0305054805001929. [ Links ]
Eiselt, H. A.; Marianov, V. (2014). A Bi-Objective Model for the Location of Landfills for Municipal Solid Waste. European Journal of Operational Research, 235 (1), pp. 187-194. [En línea]: [Consultado el 06 de Junio de 2014]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0377221713008072. [ Links ]
Ekmekçioglu, M.; Kaya, T.; Kahraman, C. (2010) Fuzzy Multicriteria Disposal Method and Site Selection for Municipal Solid Waste. Waste Management, 30 (8-9), pp. 1729-1736, [En línea]: [Consultado el 1 de junio de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0956053X10001170. [ Links ]
Eshet, T.; Baron, M. G.; Shechter, M.; Ayalon, O. (2007) Measuring Externalities of Waste Transfer Stations in Israel Using Hedonic Pricing. Waste Management, 27 (5), pp. 614-625. [En línea]: [Consultado el 5 de Noviembre de 2012]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0956053X06001255. [ Links ]
Farahani, R. Z.; Steadieseifi, M.; Asgari, N. (2010). Multiple Criteria Facility Location Problems: A Survey. Applied Mathematical Modelling, 34 (7), pp. 1689-1709, [Online] Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0307904X09003242. [Consultado el 3 de Noviembre de 2011] [ Links ].
Guo, P.; Huang, G. H. (2009a). Inexact Fuzzy-Stochastic Mixed-Integer Programming Approach for Long-Term Planning of Waste Management-Part A: Methodology. Journal of Environmental Management, 91 (2), pp. 461-470. [En línea]: [Consultado el 13 de diciembre de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0301479709003089. [ Links ]
Guo, P.; Huang, G. H. (2009b). Inexact Fuzzy-Stochastic Mixed Integer Programming Approach for Long-Term Planning of Waste Management-Part B: Case study. Journal of Environmental Management, 91 (2), pp. 441-460. [En línea]: [Consultado el 13 de Diciembre de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0301479709003090. [ Links ]
Londoño, D. E. V., Muñoz, C. A.; Ospino, E. V. (2010). Methodology for the Location of a Treatment and Solid Waste Disposal Regional Park, from a Multidimensional Perspective. Revista Ingenierías Universidad de Medellín, 9 (17), pp. 63-74. [En línea]. [Consultado el 14 de septiembre de 2011]. Disponible en: http://www.redalyc.org/home.oa. [ Links ]
Melachrinoudis, E. (2011) The Location of Undesirable Facilities En: Eiselt, H. A. y Marianov, V. (eds.) Foundations of Location Analysis. New York. International Series in Operations Research and Management Science, Springer. [ Links ]
Mejía, C. A. Z., Castañeda, F. A. M.; Varela, P. A. M. (2012). A Methodology for Landfill Location Using Geographic Information Systems: A Colombian Regional Case. Ingeniería e Investigación, 32 (1), pp. 64-70. [En línea]. [Consultado el 20 de noviembre de 2013]. Disponible en: http://www.scopus.com.bd.univalle.edu.co/. [ Links ]
Proactiva Colombia. Proactiva Medio Ambiente. [En línea]: [Consultado el 10 de mayo de 2012]. Disponible en: http://www.proactiva.com.co/index.php?option=com_content$view=article$id=39$Itemid=274. [ Links ]
RRC.AP (2010). Municipal Waste Management Report: Status-Quo and Issues in Southeast and East Asian Countries Japan: AIT/UNEP Regional Resource Center for Asia and the Pacific (RRC.AP). [ Links ]
Saameño-Rodríguez, J. J.; Guerrero-García, C., Muñoz-Pérez, J.; Mérida-Casermeiro, E. (2006) A general model for the undesirable single facility location problem. Operations Research Letters, 34 (4), pp. 427-436. [En línea]: [Consultado el 28 de febrero de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0167637705000969. [ Links ]
Sánchez-Gómez, J.; Estrada-Nuñez, R. (1996). Estaciones de transferencia de residuos sólidos en áreas urbanas. México: Instituto Nacional de Ecología. [ Links ]
Schaper, L. T.; Brockway, R. C. Estaciones de transferencia. En: Lund, H. F. (2001). Manual McGraw-Hill de reciclaje. España: McGraw-Hill. pp. 23.1-23.37. [ Links ]
Washburn, B. E. (2012). Avian Use of Solid Waste Rransfer Stations. Landscape and Urban Planning, 104 (3-4), pp. 388-394, [En línea]: [Consultado el 27 de julio de 2012]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0169204611003367. [ Links ]
Wilson, B. G.; Vincent, J. K. (2008). Estimating Waste Transfer Station Delays Using GPS. Waste Management, 28 (10), pp. 1742-1750. [En línea]: [Consultado el 30 de junio de 2012]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0956053X07003339. [ Links ]
Xi, B. D., Su, J.; Huang, G. H.; Qin, X. S.; Jiang, Y. H.; Huo, S. L.; Ji, D. F.; Yao, B. (2010). An Integrated Optimization Approach and Multi-Criteria Decision Analysis for Supporting the Waste-Management System of the City of Beijing, China. Engineering Applications of Artificial Intelligence, 23 (4), pp. 620-631. [En línea]: [Consultado el 08 de julio de 2011]. Disponible en: http://www.sciencedirect.com.bd.univalle.edu.co/science/article/pii/S0952197610000199. [ Links ]