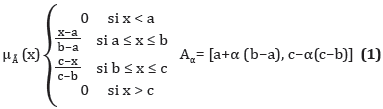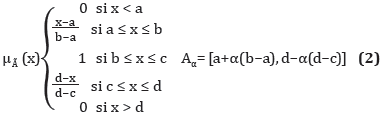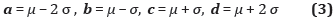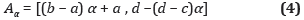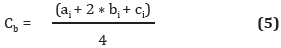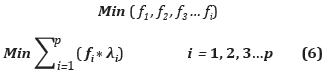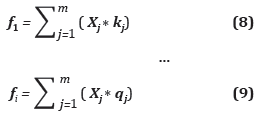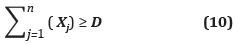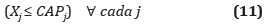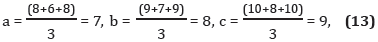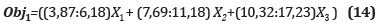Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.23 Envigado June 2015
MODELO DE PROGRAMACIÓN MULTI-OBJETIVO FUZZY PARA LA SELECCIÓN DE PROVEEDORES
MULTIOBJECTIVE FUZZY PROGRAMMING MODEL FOR SUPPLIERS SELECTION
MODELO DE PROGRAMAÇÃO MULTI-OBJETIVO FUZZY PARA A SELEÇÃO DE FORNECEDORES
Silvia Lorena Ávila Rojas1, Juan Carlos Osorio Gómez2
1 Ingeniera industrial Universidad del Valle. Ingiera Asociada de Diseño Canal Internacional Tecnoquímicas SA.
2 Ingeniero industrial Universidad del Valle. Especialista en Logística Universidad del Valle. MsC. Ingeniero Industrial Universidad del Valle. Profesor titular Escuela de Ingeniería Industrial, Universidad del Valle. Calle 13#100-00, Cali, Valle. Fax: (572) 339 84 62. Teléfono móvil: (32) 317 656 34 27. Correo electrónico: juan.osorio@correounivalle.edu.co.
Artículo recibido: 29-IV-2014 / Aprobado: 24-III-2015
Disponible online: 30 de junio de 2015
Discusión abierta hasta junio de 2016
RESUMEN
En los ambientes competitivos actuales, no sólo es necesario gestionar efectivamente las actividades internas de las organizaciones, sino garantizar los elementos de entrada del sistema. Por este motivo, la selección de proveedores se ha convertido en uno de los procesos más importantes para garantizar la calidad de los suministros de las empresas. En este sentido, se han realizado múltiples aproximaciones a los procesos de selección, utilizando modelos cuantitativos y cualitativos, cada uno de ellos con diversos aspectos a favor y en contra. En este artículo se presenta una propuesta desde la modelación matemática para la selección de proveedores, involucrando la lógica difusa en el proceso de decisión, de manera que se pueda tratar de la mejor manera posible la incertidumbre presente tanto en los juicios subjetivos de los elementos cualitativos, como en la información no siempre precisa de los elementos cuantitativos.
PALABRAS CLAVE: Selección de proveedores, modelación matemática, optimización multiobjetivo, lógica difusa.
ABSTRACT
In today's competitive environment, it is not only necessary to effectively manage the internal activities of organizations, but to ensure the input elements of the system. For this reason, the selection of suppliers has become one of the most important processes to ensure the quality of supplies companies. In this sense, there have been multiple approaches to the selection process, using quantitative and qualitative models, each with various pros and against. A proposal is presented in this article from the mathematical modeling for the selection of suppliers, involving fuzzy logic in the decision process, so it can be treated in the best possible way this uncertainty both in subjective judgments of qualitative elements, as information is not always accurate quantitative elements.
KEY WORDS: Supplier Selection; Mathematical Modeling; Multiobjective Optimization; Fuzzy Logic.
RESUMO
No ambiente competitivo de hoje, é não só necessário gerenciar efetivamente atividades internas das organizações, mas sim garantir as entradas do sistema. Portanto, a seleção de fornecedores tornou-se um dos processos mais importantes para garantir o abastecimento de qualidade empresas. Em este sentido, eles fizeram várias abordagens para o processo de seleção, utilizando modelos quantitativos e qualitativos, cada um com diferentes prós e contra. Este artigo apresenta uma proposta da modelagem matemática para a seleção de fornecedores, envolvendo lógica fuzzy no processo de decisão, para que ele possa ser tratado da melhor maneira possível esta incerteza tanto em julgamentos subjetivos de elementos qualitativos e as informações nem sempre é preciso elementos quantitativos.
PALAVRAS-CHAVE: Seleção de fornecedores; Modelagem matemática; Otimização multi-objetivo; lógica fuzzy.
1. INTRODUCCIÓN
La selección de proveedores es una de las actividades más importantes en la función del aprovisionamiento de una organización. Para tal fin existen múltiples enfoques que buscan seleccionar el proveedor que cumpla de la mejor manera con todos los requerimientos de la organización. Sin embargo, hay en juego una gran cantidad de criterios y no es fácil encontrar un proveedor que responda apropiadamente a cada uno de ellos. Por esta razón se hace necesario utilizar herramientas que involucren múltiples criterios en su desarrollo.
Existen en la literatura una gran cantidad de trabajos que utilizan técnicas multicriterio, tales como el proceso analítico jerárquico (AHP por sus siglas en inglés), el proceso analítico en red (ANP por sus siglas en inglés) y otras importantes y conocidas herramientas multicriterio. Sin embargo, todos los autores coinciden en que si bien estos trabajos constituyen importantes avances y logran buenos resultados, todavía hay muchos aspectos por mejorar en el campo.
Adicionalmente a estas herramientas, se han utilizado modelos de optimización para resolver el problema de selección de proveedores. Estos modelos resuelven el problema de manera continua, pero igual que los anteriores presentan algunos aspectos que pueden ser mejorados.
Se ha encontrado propuestas de modelación matemática que involucran la lógica difusa, buscando mejorar la incertidumbre presente en algunos datos cuantitativos y la ambigüedad presente en las calificaciones de algunos criterios cualitativos. Como dichos modelos han sido poco usados, se presenta en este artículo una aplicación del mismo, buscando ilustrar el método y las ventajas asociadas al mismo.
2. REVISIÓN DE LA LITERATURA
El ambiente competitivo en el que se ven envueltas las organizaciones de hoy día, está caracterizado principalmente por el rápido y constante cambio en las necesidades de los clientes, lo que hace que las organizaciones planteen y desarrollen estrategias innovadoras basadas no sólo en el uso eficiente de los recursos, sino también en aspectos competitivos como la calidad de los productos, la capacidad de entrega, el servicio de postventa, la capacidad de diversificación y la flexibilidad de los productos (Pérez, 2004), buscando principalmente diferenciarse de sus competidores de modo que se garantice su permanencia en el mercado.
El interés por la gestión de la calidad en la cadena de suministro ha permitido que se desarrollen diferentes enfoques para la selección de proveedores, estos enfoques han tenido en cuenta valoraciones cualitativas de los proveedores así como consideraciones de costos asociados a los procesos de contratación, entrega, entre otros. (Boer, et al., 2001 y Ho, et al., 2010), no obstante ninguno de los anteriores se ha definido como el enfoque adecuado para seleccionar proveedores, ya que dicha selección implica valoraciones ambiguas en algunos criterios que son determinados dependiendo de los intereses de las organizaciones, lo que genera que los resultados de cada enfoque sean diferentes en cada caso.
Desde el punto de vista de las organizaciones, la selección y el desarrollo de relaciones con los proveedores es un componente clave de sus estrategias corporativas (Lai, et al., 2005); el impacto que tiene la selección de estos en la calidad del producto y el servicio, ha dado paso a que en los últimos años se desarrollen diversos métodos, que permitan elegir a proveedores que cumplan una serie de requisitos o restricciones establecidas por la empresa basados en sus estructuras productivas y organizacionales.
Sin embargo a pesar de los distintos métodos de selección existentes, el establecimiento de relaciones comerciales con los proveedores, constituye una labor extenuante y acompañada en gran medida de incertidumbre (Boer, et al., 2001).
Adicionalmente, debido a que en el proceso de selección de proveedores se deben tener en cuenta los diferentes objetivos planteados por la empresa en términos de calidad, servicio, costos y otros, los métodos multi-objetivo toman una gran importancia para la solución de este problema, dado que estos permiten identificar la mejor solución considerando simultáneamente múltiples objetivos en conflicto (Pérez, 2007).
Este conflicto de criterios y objetivos que se presentan en el problema de selección son evidentes por ejemplo con criterios como la calidad que parece representar el atributo más importante al momento de la selección, pero que se debe evaluar a la vez con el impacto del servicio de entrega y los costos en dicha decisión (Verman y Pullman, 1998), así como los conflictos existentes entre ellos.
Una técnica o método multi-objetivo está diseñada para encontrar un conjunto de soluciones que son igualmente buenas entre sí. Para los problemas multiobjetivo se han desarrollado diferentes enfoques de solución que permiten obtener el conjunto de soluciones «frente de pareto», entre ellos se pueden encontrar los siguientes métodos de solución: método de las ponderaciones, método de restricciones, método de programación compromiso y el método de programación por metas. Entre todos estos el método de las ponderaciones es el más utilizado (Chen y Shieh. 2000).
La incertidumbre que rodea el proceso de selección en términos de definición y calificación de criterios, es una realidad con la que se deben enfrentar los decisores al momento de la selección de una alternativa de proveedor, debido a que generalmente la información por medio de la cual se definen los criterios no es exacta y maneja rangos, para el caso de los criterios cuantitativos, o calificativos ambiguos en el caso de los cualitativos.
El desarrollo de teorías como la lógica difusa y a su vez, de los conjuntos difusos, que permiten representar la experiencia del ser humano y los conjunto de normas establecidos, mediante el uso de variables lingüísticas y/o, por medio de un modelo matemático, ha dado paso a que gran parte de los enfoques desarrollados integren sus criterios y se desarrollen herramientas más precisas como por ejemplo el AHP difuso, análisis de clusters difuso, S.M.A.R.T difuso, entro otros (Ho, et al., 2010).
La lógica difusa es una teoría que se ha implementado en los campos científico y técnico, y que resulta útil cuando se quiere que una máquina, programa ó aplicación "piense" como lo haría la mente humana. Esta lógica se basa fundamentalmente en la creación de una relación matemática entre un elemento y un determinado conjunto difuso con el fin de que se realice una valoración similar a la que haría el decisor (Briceño, 2004).
La lógica difusa permite representar el conocimiento común, que es principalmente del tipo lingüístico cualitativo y no necesariamente cuantitativo, aunque su aplicación también permite trabajar la imprecisión de estos, en un lenguaje matemático a través de la teoría de conjuntos difusos y funciones características asociadas a ellos. Permite trabajar a la vez con datos numéricos y términos lingüísticos; los términos lingüísticos son inherentemente menos precisos que los datos numéricos pero en muchas ocasiones aportan una información más útil para el razonamiento humano.
Los métodos de Programación Multi-objetivos Difusos, surgen como una forma para manejar la incertidumbre en la definición de criterios en el proceso de selección de proveedores, adicionalmente permiten considerar aspectos de negociación claves como los son: la capacidad de los proveedores en consideración, y calcular las cantidades a ordenar a cada uno de estos (Amid, et al., 2006).
Chen y Shieh (2000) presentan una tipología de la optimización multi-objetivo, a partir de la cual se pueden determinar consideraciones importantes para la formulación de este tipo de programación. La metodología descrita en su artículo, permite modelar las funciones objetivo y restricciones del modelo, relacionando los conceptos más importantes para la formulación de modelos de programación difusos y brinda un marco conceptual para el entendimiento de los mismos.
Otra forma de plantear y resolver problemas multi-objetivos difusos, fue presentada por Wu, et al. (2010), quienes sostienen que normalmente la información histórica que manejan los proveedores, para definir algunos criterios tales como la calidad, los costos, el cumplimiento en las entregas entre otros, no siempre se encuentra asociada a algún tipo de distribución probabilística y por ende constituye una fuente de incertidumbre.
Por medio de estos dos autores se logran identificar dos posibles caminos de modelación para los problemas multi-objetivo difusos; uno basado en la ma nipulación del modelo matemático con el fin de modelar la incertidumbre desde ese punto, y el otro apoyado en el manejo de la incertidumbre desde la información de entrada del modelo.
Otro punto importante de mencionar es el relacionado con la valoración de los criterios, más cuando en este tipo de procesos se cuenta con criterios tanto cualitativos como cuantitativos. Para aquellos de naturaleza cualitativa, es decir, los que su definición se encuentra caracterizada por una gran subjetividad o aquellos cuantitativos que manejan alto valor de incertidumbre, pueden ser trabajados a partir del uso de números difusos propios de la lógica difusa, con ellos se modela la incertidumbre presente en la información determinada por cada criterio, sobre los cuales no se cuenta con información exacta, lo que da paso a que en ocasiones estos deban ser definidos a partir de las valoraciones subjetivas o por medio de promedios acumulados, desviaciones estándar o calificaciones subjetivas emitidas por el decisor.
Dentro de algunas aplicaciones locales de la lógica difusa en modelos de optimización pueden también revisarse los siguientes trabajos, que si bien no son aplicaciones en la selección de proveedores, muestran como integrar la lógica difusa en los modelos de optimización. Dichos trabajos son: Tovar, et al. (2007), Galeano y Montoya (2008), Jaramillo y Vinasco (2005).
A continuación se presentan tanto la metodología, como el modelo matemático propuesto para la selección de los proveedores; y en el siguiente apartado, se validará la aplicación de dicha metodología y modelo mediante un caso de estudio adaptado de la literatura.
3. METODOLOGÍA PROPUESTA
La metodología propuesta tiene en consideración las principales etapas del proceso de selección de proveedores; por medio de esta, se logrará realizar la caracterización, evaluación y posterior elección de los proveedores considerados por la empresa como las posibles alternativas en todo el proceso.
Las etapas contenidas en la metodología, incluyen: la clasificación de criterios; en esta etapa los criterios de evaluación serán seleccionados y clasificados, dependiendo de la naturaleza de los mismos, de modo que con esta información se pueda determinar el método por medio del cual serán procesados; también se considera el uso del modelo matemático que se presentará más adelante; etapa fundamental en la que se realizará la selección del proveedor por medio de la herramienta, y la interpretación de la información resultante, consiste en la traducción a términos explícitos y concretos de los resultados arrojados por la herramienta utilizada.
Es importante antes de continuar, realizar algunas definiciones:
Número difuso: Es una función normalizada de los número Reales cuya función de pertenencia es un valor continuo entre 0 y 1 (Sakawa, et al., 2011)
Número difuso triangular (Carrasco, 2003): Se denomina así al número borroso real, continuo, tal que la forma de su función de pertenencia determina con el eje horizontal un triángulo. Su función de pertenencia es lineal, a izquierda y derecha, y el α-corte para α = 1 tiene un solo elemento, es decir, la función de pertenencia alcanza el valor uno para un único número real.
Un número triangular está determinado de manera única por tres números reales a, b y c, tales que a ≤ b ≤ c, entonces es usual representarlo como à = (a, b, c). La función de pertenencia y sus α-cortes respectivamente son:
Número difuso trapezoidal (Carrasco, 2003): Se denomina así al número real continuo, tal que la forma de su función de pertenencia determina con el eje horizontal un trapecio. Su función de pertenencia es lineal a izquierda y derecha, y el α-corte para α = 1 es un intervalo de números reales.
Un número trapezoidal está determinado de manera única por cuatro números reales a, b, c y d, tales que a ≤ b ≤ c ≤ d, entonces es usual representarlo à = (a, b, c, d). De igual forma, la función de pertenencia y los α-cortes por los cuales se puede representar este número difuso son:
3.1. Clasificación de criterios de selección
Para llevar a cabo la modelación de los distintos criterios seleccionados para la evaluación de los proveedores, será necesario determinar la naturaleza de los mismos, teniendo en cuenta que, se definen como criterios cualitativos, a aquellos criterios que son valorados por medio de calificaciones lingüísticas, y criterios cuantitativos, a aquellos para los cuales su definición se realiza en términos numéricos. La importancia de realizar esta clasificación radica en que a partir de ella, se determina el método de modelación por medio de la lógica difusa que se deberá implementar.
Una vez realizada la clasificación de los criterios en términos de su naturaleza, se realizará la modelación como se presenta a continuación.
Criterios cuantitativos: para aquellos criterios que se han clasificados como criterios cuantitativos, será necesario contar con información referente a la media-promedio, definido a partir de información histórica manejada por el proveedor y la desviación estándar de los datos.
Por medio de estos dos parámetros se realizará la construcción de números difusos trapezoidales teniendo en cuenta que las componentes de dicha clase de números a, b, c, y d, se determinará como se presenta en las siguientes expresiones, donde "µ" hace referencia al promedio y "σ" a la desviación estándar de los datos:
Posterior a la construcción del número difuso correspondiente al criterio, se debe aplicar la técnica de α-cortes, la cual para números trapezoidales se definen como:
Con el intervalo discreto correspondiente al número difuso trapezoidal conformado, los valores pertenecientes serán los considerados como datos de entrada para el desarrollo del modelo propuesto. Con el fin de usar los múltiples valores existentes dentro del intervalo definido, se hará uso de la función aleatorio. entre(), de Microsoft Office Excel®, la cual permite tomar valores aleatorios entre un intervalo definido.
Criterios cualitativos: para los criterios que se han clasificado como cualitativos, la transformación a números discretos se realizará a partir de las evaluaciones subjetivas emitidas por el grupo decisor, de modo que por medio de estas, se represente la importancia relativa de cada una de estos criterios en el proceso de selección.
La transformación de las valoraciones cualitativas en valores discretos se realizará con el uso de números difusos triangulares, una escala de valoración determinada y la técnica de defusificación propuesta por Facchinetti (2002), que permite calcular el valor más probable del número difuso.
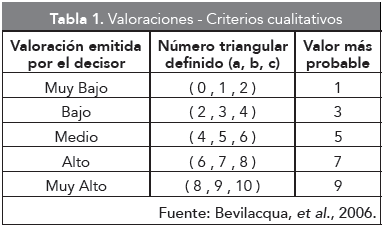
Los valores tomados por estas componentes se asignarán teniendo en cuenta los juicios emitidos por el decisor sobre un criterio en particular, según se presenta en la Tabla 1, en ella además, se encuentra el valor más probable frente a cada una de las valoraciones.
Posterior a la definición del número triangular difuso, se transformará en un número discreto por medio de la ecuación propuesta por Facchinetti (2002), para realizar la defusificación de la información. Este nuevo valor, corresponderá un nuevo dato de entrada para el desarrollo del modelo.
3.2. Modelo matemático
El modelo planteado corresponde a un modelo de programación multiobjetivo difuso, sustentando en los trabajos desarrollados por Chen y Shieh (2000) y Wu, et al. (2010), y para la construcción de este modelo se tuvo en consideración las siguientes características y supuestos.
- El resultado o solución del modelo, viene representado por las cantidades que se deseen ordenar a cada uno de los proveedores evaluados, de modo que la no asignación de cantidades a ordenar a un proveedor en particular, significará la no selección del mismo.
- El modelo de selección desarrollado tiene en consideración la evaluación de diferentes proveedores frente a un solo cliente.
- La caracterización por medio de parámetros de proveedores y cliente, dependen del caso particular que se esté evaluando, dado que las prioridades pueden cambiar dependiendo de las situaciones y los parámetros, dependiendo de las características que se tengan en consideración.
- La información por medio de la cual se caracteriza al cliente, en términos de demanda y otras necesidades, hacen referencia a las información agregada de la empresa.
- Los datos de entrada del modelo son el resultado del manejo de información de cada proveedor por medio de la lógica difusa, como se explicará en la metodología propuesta.
- El modelo desarrollado tiene en consideración la importancia relativa que tienen los decisores frente a cada uno de los objetivos establecidos, esta importancia es determinada por medio de los juicios emitidos por los decisores.
- Para la definición de criterios cualitativos y cuantitativos se usarán números difusos trapezoidales y triangulares, técnicas de defusificación y de alfa cortes.
4. OBJETIVOS
Minimizar los objetivos considerados en el problema de selección de proveedores teniendo en cuenta la importancia que tiene cada uno de ellos para el decisor, representada por λ.
Donde fi, representa el i-ésimo objetivo en consideración para el desarrollo del proceso de selección y λi, es la ponderación asignada a cada uno de los objetivos y se debe cumplir que:
Es de anotar que los valores de λi, son obtenidos por medio del proceso de ponderación de juicios, el cual se presentará más adelante, mediante el cual se busca representar la importancia relativa de cada uno de los objetivos considerados, para la selección del proveedor.
A su vez, cada objetivo tiene en consideración las cantidades a ordenar y el criterio al que haga referencia, a partir de esto:
Donde Xj, son las cantidades que se piden al proveedor j y kj, ...qj, hace referencia a los criterios por medio de los cuales se esté caracterizando el proveedor j. Entre otros criterios, estos pueden hacer referencia a costo, calidad, tiempo de entrega, reputación. Es necesario aclarar que todos los proveedores que se consideren en el proceso de selección deben estar caracterizados por medio de los mismos criterios, al menos en la evaluación de un artículo en particular, dado que se busca evaluar las diferentes alternativas de proveedores teniendo en cuenta los criterios definidos con anterioridad para dicha evaluación.
5. RESTRICCIONES
Las principales restricciones tenidas en consideración se refieren a la demanda registrada por parte del cliente, las restricciones lógicas que indican la no negatividad de los valores asignados a Xj y que se asigne únicamente valores enteros a esta variable.
Donde D, es la demanda presentada por el cliente; esta restricción garantiza que, la sumatoria de las cantidades que se pidan a cada uno de los proveedores j, sean mayores o iguales a la demanda del cliente, es decir que esta sea satisfecha.
Casos particulares para el proceso de selección se podrían formular teniendo en consideración la capacidad de atención, en términos de cantidades, de cada uno de los proveedores; este tipo de situaciones se podrían presentar en los casos en los que las empresas establezcan acuerdos de desarrollo de proveedores y otros similares, en los que sus pedidos se supeditan a la capacidad del proveedor.
Teniendo en cuenta lo anterior, una alternativa adicional para restringir el problema de selección se puede construir a partir de la consideración de las capacidades de los proveedores que se están evaluando. Esta alternativa se podría representar como:
Donde CAP, se refiere a la capacidad del proveedor; de esta forma se respetan las capacidades de cada uno de los proveedores, es decir que, las cantidades que se pidan al proveedor j deben ser iguales o menores a la CAPj para cada uno de los proveedores en consideración. Las restricciones lógicas se presentan como:
Con esta expresión se garantiza que las unidades asignadas no sean inferiores a cero. Se tiene entonces que el modelo entregará las cantidades discretas a ordenar a cada uno de los proveedores de acuerdo con los criterios considerados y las ponderaciones dadas a ellos.
5.1. Uso del Modelo desarrollado
Una vez caracterizados los parámetros de entrada del modelo de programación desarrollados en el paso anterior y de definir la importancia relativa de cada uno de los objetivos tenidos en consideración, será necesario el uso de un software de optimización que permitan determinar las cantidades que se deben pedir a un proveedor, es decir, permita conocer el resultado de la selección, teniendo en cuenta los distintos parámetros determinados anteriormente.
Para iniciar es necesario desarrollar el modelo matemático teniendo en consideración los objetivos que se deseen evaluar y los parámetros usados para la caracterización de los proveedores. Una vez se cuente con esta información se realizará la respectiva preparación del modelo para ser optimizado por medio de la herramienta - software, que se seleccione para tal fin.
Posterior a la ejecución del modelo matemático, la solución presentada por este estará expresada por el número de unidades definidas como las cantidades óptimas para pedir o con las cuales negociar con cada uno de los proveedores tenidos en cuenta, durante el proceso de selección.
El modelo desarrollado, opera identificando la mejor alternativa de proveedor entre el conjunto en consideración y realiza la asignación de cantidades a esta alternativa, limitándose por la capacidad máxima de la misma en el caso en que se considerara la capacidad de cada uno de los proveedores, una vez esta capacidad fuese alcanzada, el modelo asignaría las cantidades restantes a la segunda mejor alternativa y así sucesivamente, hasta que la demanda del cliente sea satisfecha.
6. CASO DE ESTUDIO Y VALIDACIÓN DEL MODELO
El caso de estudio que se desarrollará en el presente capítulo, se basa en un caso de selección de proveedores encontrado en la literatura (Toskano, 2005). En él, se analiza la situación de una empresa dedicada principalmente a la impresión de envolturas flexibles la cual se encuentra ante la decisión de seleccionar un proveedor para una de sus materias primas.
El ambiente que rodea la decisión acerca de seleccionar el proveedor para el proceso, adquiere mayor complejidad, al considerar que son varios los criterios de evaluación que se deben tener en consideración, existiendo entre ellos cualitativos y cuantitativos; y además, que se puede presentar que estos se encuentren en conflicto entre sí.
6.1. Definición de criterios
Tiempo de entrega: criterio cuantitativo relacionado al plazo de entrega del material ofrecido por los proveedores.
Calidad del material: criterio definido cualitativamente relacionado con las características técnicas y estado del material.
Facilidad del uso del material: criterio relacionado con la preparación y tratamiento que requiere adicionalmente para el uso del material de impresión, es cualitativo.
Precios: criterio cuantitativo relacionado con el precio de las bobinas de 150 kg y 80 cm de ancho, de BOPP transparente.
Ventas: criterio cuantitativo relacionado con la proporción de ventas del material.
Facilidades de pago: criterio cualitativo relacionado con las facilidades de pago y relaciones mantenidas con el proveedor para el manejo de las transacciones financieras.
Confiabilidad del proveedor: este criterio se relaciona con la capacidad que tienen los proveedores para responder a los pedidos de la empresa, se calcula cuantitativamente.
Posterior a la definición de los criterios, se contó con la opinión de un grupo conformado por siete personas. Los juicios realizados por este grupo permitieron determinar la valoración de los criterios cualitativos por medio de la escala difusa definida. En el caso de los criterios cuantitativos, se tuvo en consideración la información histórica a la que pudo acceder la empresa sobre los proveedores a evaluar. A continuación un ejemplo para un criterio cuantitativo y uno cualitativo, donde se busca ilustrar la metodología. Este procedimiento fue desarrollado para cada uno de los criterios seleccionados en el estudio.
De la información obtenida, se pudo contar con elementos puntuales para caracterizar cuantitativamente a cada uno de los proveedores, uno de estos elementos corresponde a los tiempos de entrega. A partir de la información de dos años, se determinó el tiempo promedio y la desviación en los tiempos de entrega de cada proveedor, de modo que a este criterio se le dio el manejo propuesto para los criterios cuantitativos.
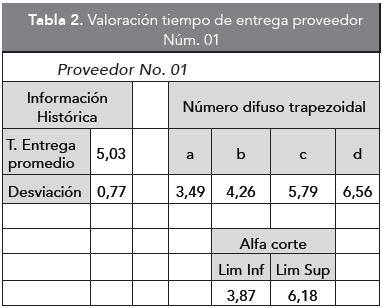
Con la información referente a promedio y desviación de los tiempos de entrega históricos manejados por cada proveedor, se dará paso a la transformación de estos datos en números difusos trapezoidales con componentes a, b, c y d, posteriormente se aplicará la técnica alfa corte con el fin de determinar un intervalo de valores para los tiempos de entrega de cada proveedor como se muestra en la Tabla 2.
Para el criterio cualitativo, por ejemplo en el caso del Proveedor No. 01, el criterio calidad del material obtuvo las valoraciones Muy Alto, Alto y Muy Alto por parte de los expertos. Para determinar la valoración general del criterio se promedian los tres números triangulares asociados de acuerdo con la Tabla 1 y se tiene que:
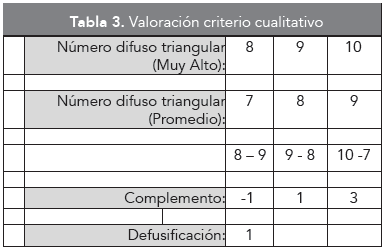
Por otra parte para determinar el complemento, a la mayor valoración «Muy Alto», con componentes (8, 9, 10), se resta el número difuso triangular promedio resultante (en cruz, tal como se establece en las propiedades entre números difusos), como se muestra en la Tabla 3.
7. MODELO MATEMÁTICO
7.1. Determinación de parámetros del modelo
Acorde con el modelo matemático y la metodología propuesta, se formula cada uno de los criterios tenidos en consideración, como una función objetivo que será incluida en el modelo, posterior a ello se determinará la importancia o prioridad de cada uno de estos objetivos sobre la decisión de qué proveedor elegir y por último se plantearán las restricciones del caso.
Para la formulación del modelo se tendrá en cuenta que X, hace referencia a las cantidades a ordenar a cada uno de los proveedores, los cuales estarán representados por 1 para el Proveedor N. 01, 2 para el Proveedor N. 02 y 3 para el Proveedor N. 03.
7.2. Determinación de objetivos
Los objetivos serán formulados teniendo en cuenta los resultados de las valoraciones de cada uno de los criterios con los dos métodos descritos en la sección anterior y teniendo en cuenta al factor que corresponden, según las directrices de la empresa caso de estudio.
7.3. Factores de producción
Tiempo de entrega: de acuerdo a este criterio la función objetivo corresponde a:
Donde, los valores (3,87:6,18), (7,69:11,18) y (10,32:17,23) indican los intervalos entre los cuales se mueve la calificación dada a los proveedores 1, 2 y 3 respectivamente. Así mismo se expresa la función para los otros objetivos.
7.4. Determinación de prioridades
Para la asignación de prioridades a cada uno de los objetivos formulados, se consideró la clasificación de criterios definida por la empresa agrupada en tres factores principales (factores de producción, factores contables y confiabilidad del proveedor), a partir de ella se indagó a las personas del grupo de expertos de la empresa sobre la preferencia de cada uno de los factores anteriores; los resultados de estas opiniones (presentadas en la escala difusa propuesta) se convierten en valores que para el caso son: factor producción 33 %, factores contables 29% y la confiabilidad del proveedor 38 %.
7.5. Planteamiento de restricciones
Las restricciones que limitan el presente caso de estudio, están determinadas por la demanda, las restricciones lógicas referentes a la asignación de pedidos de cantidad únicamente positivas, y a que estas sean en términos de unidades enteras.
Una vez establecidos los objetivos, sus prioridades, así como las restricciones de demanda y las restricciones lógicas, se da paso a la solución del modelo de programación multi-objetivo difuso. Para esta situación se consideraron dos software: Lingo1 y Risk Simulator 2.
Teniendo en cuenta las características de las herramientas y además, que dentro de los criterios establecidos para realizar la caracterización de los proveedores, se encuentran la confiabilidad y el tiempo de entrega, criterios definidos por medio de un intervalo de datos, se tomó la decisión de encontrar la solución al problema multi-objetivo difuso propuesto en dos situaciones específicas: Tomando un solo valor dentro del intervalo usando el software Lingo y tomando distintos valores dentro de él, usando Risk Simulator para crear una simulación. El uso de la herramienta para cada situación se determinó buscando la eficiencia de la solución y la consistencia de las soluciones planteadas por cada software.
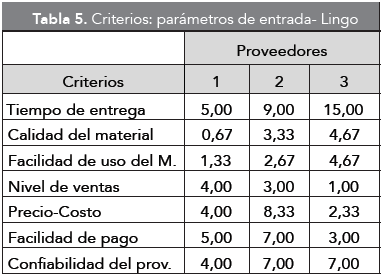
En la Tabla 4 se presentan los valores de la solución global obtenida por medio de esta asignación con el software Lingo, donde se aprecia que el proveedor seleccionado es el número 1; adicionalmente en la Tabla 5 se presentan los valores asignados a los criterios-parámetros del modelo, para la realización de la optimización.
Como se mencionó, para esta optimización solo se tuvo en cuenta un valor dentro de los intervalos determinados para la valoración de los criterios cuantitativos.
7.6. Solución del modelo matemático con RISK SIMULATOR
Para realizar la optimización del modelo de programación con el software Risk Simulator, fue necesario determinar las características de los parámetros introducidos en el modelo, con el fin de determinar las restricciones existentes, la clase de las variables de decisión, la cantidad de simulaciones y optimizaciones a realizar, así como también, el tipo de optimización.
En la Optimización Estocástica que corresponde al tipo de optimización usada en el presente caso de estudio, el software realiza una simulación con N pruebas a partir de las cuales, ejecuta una optimización con M iteraciones para obtener el resultado óptimo final. Los resultados obtenidos en cada una de estas optimizaciones, permiten que al final del proceso de optimización, las variables de decisión finales tengan un análisis individual, indicando el alcance de las variables de decisión óptimas y un rango de valores óptimos para cada variable de decisión.
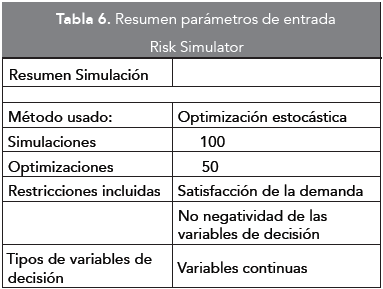
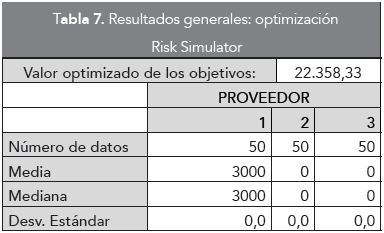
Para determinar el número de simulaciones y optimizaciones a ejecutar, se realizaron diferentes arreglos de optimización donde se evaluaron distintas cantidades de simulaciones y optimizaciones y su impacto en el resultado, concluyendo que la estabilidad del sistema o de la optimización se alcanza con gran rapidez, por lo anterior, se estableció un arreglo de 100 simulaciones para la evaluación del proveedor, con 50 optimizaciones. Adicionalmente, para esta optimización se tuvieron en cuenta los intervalos por medio de los cuales fueron valorados los criterios cuantitativos -tiempo de entrega y confiabilidad, a fin de conocer el impacto que tiene sobre la decisión final la variación de estos criterios. El resumen de estos elementos se presenta en la Tabla 6. Y en la Tabla 7 se presentan los resultados de la aplicación del modelo, donde se observa que en todas las simulaciones realizadas, el proveedor No 1 fue el seleccionado.
Como se observó, los resultados obtenidos por medio de la optimización en Lingo y Risk Simulator coinciden en la selección del proveedor N. 01, como la mejor alternativa para las negociaciones de la empresa.
8. ANÁLISIS DE RESULTADOS
El proceso de selección, está compuesto de diferentes etapas de las cuales las más críticas en la decisión final corresponden a: la definición de criterios por medio de los cuales se realizará la evaluación de los proveedores, la calificación de proveedores evaluando los diferentes criterios que permiten identificarlo, y por último, la selección final de estos, esto explica la importancia que ha tenido el desarrollo de métodos de solución que permitan modelar estas etapas. Pero a pesar de que se han desarrollado diferentes métodos de selección de proveedores, algunos incluso creados para etapas específicas del proceso, ninguno se ha declarado como el mejor; sin embargo se reconoce que los métodos de programación matemáticos representan una gran herramienta en todo el proceso de selección, debido a la forma en la que permiten modelar simultáneamente los criterios y objetivos contemplados en ellos.
Como se mencionó, una de las etapas críticas en el proceso de selección es la valoración de los proveedores por medio de diferentes criterios. En parte, su criticidad radica en la gran cantidad de criterios existentes, así como en la naturaleza de los mismos, dado que dependiendo de esta se puede determinar con mayor precisión la valoración de cada uno. Es por esto que el proceso de valoración de criterios es un punto crítico en el problema de selección de proveedores, así como en el uso de métodos de solución. La determinación de valoraciones por medio de los juicios emitidos por expertos tiene asociada una gran incertidumbre por lo cual, se reconoce la importancia de técnicas como la lógica difusa, por medio de la cual se puede manejar la vaguedad de la información. Tal como se apreció en el modelo desarrollado, la lógica difusa permite involucrar los elementos vagos asociados a los juicios y darle un manejo matemático que permita tranquilidad para los analistas.
Referente a la etapa de evaluación y selección del proveedor, el desarrollo de un modelo matemático multi-objetivo representa una gran alternativa para soportar la decisión, debido a que permite considerar una gran cantidad de criterios simultáneamente y obtener resultados con gran rapidez, esto en comparación de métodos como el AHP y el QFD, en los cuales gran cantidad del tiempo es usado en la comparación de criterios y las operaciones matriciales.
El uso de la herramienta multi-objetivo difusa desarrollada es un medio eficiente para seleccionar proveedores entre un conjunto de alternativas, dado que permite: identificar al proveedor que contribuye en mayor proporción al cumplimiento de los objetivos determinados por la organización y determinar las cantidades sobre las cuales realizar la negociación, sin embargo es importante destacar la necesidad de información histórica para desarrollar las calificaciones de los criterios cuantitativos y la necesidad de tener conocimiento por parte de los expertos involucrados para los criterios cualitativos.
En la medida que la organización posea esta información, la efectividad de la herramienta mostrada será mayor y la confiabilidad de los resultados garantizará la tranquilidad en el proceso de toma de decisión.
Un último elemento a considerar asociado al caso de estudio presentado, es que en la medida que los proveedores no tengan la capacidad de abastecer totalmente los materiales solicitados, el modelo permite seleccionar el que mejor cumple los criterios definidos y completar las cantidades restantes con el siguiente mejor.
9. CONCLUSIONES
Se ha desarrollado una herramienta matemática que soporta la decisión sobre a qué proveedor seleccionar, teniendo en cuenta una serie de criterios (cualitativos y cuantitativos) determinados por la organización y la valoración de los mismos. Para la validación de esta herramienta se realizó su aplicación a un caso de estudio formulado para tal fin.
A pesar de la gran utilidad que representan los métodos matemáticos para la selección de proveedores en términos de velocidad de procesamiento y automatización en el manejo de los datos, existen dudas frente al uso de estos, debido a que se considera que por su naturaleza matemática dejan de lado factores como la experiencia y la intuición en la definición de criterios y toma de decisiones; por lo anterior el uso de modelos matemáticos integrados con técnicas como la lógica difusa, representan herramientas de apoyo con mayor credibilidad dado que permiten modelar con mayor eficiencia la vaguedad de la información.
El modelo planteado recoge aspectos presentes en la bibliografía actual, pero los ha integrado y presentado de manera que sea de fácil implantación en las organizaciones, claro está, que es necesario tener información de los proveedores para que el modelo opere apropiadamente.
_____________________________
NOTAS
1 Optimization Modeling Software for Linear, Nonlinear, and Integer Programming. http://www.lindo.com/index.php?option=com_content$view=article$id=2$Itemid=10.
2 http://www.realoptionsvaluation.com/Spanish-ROV/risksimulator-software.php.
REFERENCIAS
Amid, A.; Ghodsypour, S.H.; Brien, C.O. (2006). Fuzzy Multiobjective Linear Model for Supplier Selection in a Supply Chain. International Journal of Production Economics. 104, pp. 394-407. [ Links ]
Bevilacqua, M.; Ciarapica, F.E.; Giacchetta, G. (2006). A Fuzzy-QFD Approach to Supplier Selection. Journal of Purchasing and Supply Management, 12. pp. 14-27. [ Links ]
Boer, L.; Labro, E.; Morlacchi, P. (2001). A Review of Methods Supporting Supplier Selection. European Journal of Purchasing and Supply Management, 7. pp. 75-89. [ Links ]
Briceño (2004). Serie procesos industriales N. 02: Modelamiento de procesos mecánicos y químicos: diseño y control. Cali: Cenicaña. [ Links ]
Carrasco, R.A. (2003). Lenguajes e interfaces de alto nivel para Data Mining con aplicación práctica a entornos financieros. Tesis Doctoral. Universidad de Granada. [ Links ]
Chen, T.Y; Shieh, C.C. (2000). Fuzzy Multiobjective Topology Optimization. Computers and Structures, 78. pp. 459-466. [ Links ]
Facchinetti, G. (2002). Ranking Functions Induced by Weighted Average of Fuzzy Numbers. Fuzzy Sets and Systems. [ Links ]
Galeano, E.; Montoya, V. (2008) Optimización multiobjetivo de la operación en sistemas automatizados de distribución de energía eléctrica. Trabajo de grado. Universidad Tecnológica de Pereira. [ Links ]
Ho, W.; Xu, X.; Dey, P. (2010). Multi-criteria decision making approaches for supplier evaluation and selection: A literature review. European Journal of Operational Research. 202. pp. 16-24. [ Links ]
Jaramillo, P.; Vinasco, L. (2005). Análisis multiobjetivo difuso espacial: Una herramienta para localizar proyectos lineales con un enfoque de gestión ambiental. Gestión y Ambiente, 8 (1). pp. 19-34. [ Links ]
Lai, K.; Cheng, T.C.E.; Yeung, A.C.L. (2005). Relationship Stability and Supplier Commitment to Quality. International Journal of Production Economics, 96. pp. 397-410. [ Links ]
Pérez, B. J. (2004). Competitividad empresarial: una visión sobre la estrategia de operaciones para la competitividad empresarial. 1 ed. Cali. Artes Gráficas del Valle Ltda. 59 p. [ Links ]
Pérez, F.; Molina, J.; Cabellero, R.; Coello, C.; Hernández-Díaz, A. (2007). Hibridación de métodos exactos y heurísticos para el problema multiobjetivo. XV Jornadas de ASEPUMA y III Encuentro Internacional (09: 2007, Palma). Memorias de la XV Jornadas de ASEPUMA y III Encuentro Internacional. Palma, España, pp. 13. [ Links ]
Sakawa, M.; Ichiro, N.; Hideki, K. (2011). Fuzzy Stochastic Multiobjective Programming. Springer. [ Links ]
Toskano, G. (2005). El Proceso de análisis jerárquico (AHP) como herramienta para la toma decisiones en la selección de proveedores. Tesis digitales. [ Links ]
Tovar, L.; Coronell, M.; Donoso, Y. (2007). Optimización multiobjetivo en redes ópticas con transmisión Multicast, utilizando algoritmos evolutivos y lógica difusa. Revista Ingeniería y Desarrollo, 21. pp. 39-55. [ Links ]
Verma, R.; Pullman, M. (1998). An Analysis of the Supplier Selection Process. Omega. 26. pp. 739-750. [ Links ]
Wu, D.; Zhang, Y.; Wu, D.; Olson, D. (2010). Fuzzy Multi-Objective Programming for Supplier Selection and Risk Modeling: A Possibility Approach. European Journal of Operational Research. 200. pp. 774-787. [ Links ]