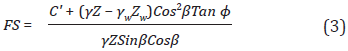Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.26 Envigado July/Dec. 2016
INFLUENCES OF ANTECEDENT RAINFALL AND HYDRAULIC CONDUCTIVITY ON LANDSLIDES TRIGGERED BY RAINFALL OCCURRENCE USING THE MODEL SHIA_LANDSLIDE
INFLUENCIA DE LA LLUVIA ANTECEDENTE Y LA CONDUCTIVIDAD HIDRÁULICA EN LA OCURRENCIA DE DESLIZAMIENTOS DETONADOS POR LLUVIAS UTILIZANDO EL MODELO SHIA_LANDSLIDE
INFLUÊNCIAS DA CHUVA ANTECEDENTE E A CONDUTIVIDADE HIDRÁULICA NA OCORRÊNCIA DE DESLIZAMENTOS TETONADOS PELAS CHUVAS UTILIZANDO O MODELO SHIA_LANDSLIDE
Edier Vicente Aristizábal Giraldo1, Jaime Ignacio Vélez Upegui2, Hernán Eduardo Martínez Carvajal1,2
1 PhD, Departamento de Geociencias y Medioambiente, Universidad Nacional de Colombia, Medellín, Colombia. Carrera 80 No 65-223. Teléfono: 425 51 97. Correo electrónico: evaristizabalg@unal.edu.co.
2 PhD, Departamento de Ingeniería Civil y Ambiental, Facultad de Tecnología, Universidad de Brasilia, Brasilia, Brasil.
Paper received: 13-IV-2016 / Approved: 16-XI-2016
Available online: February 30, 2017
Open discussion until April 2018
ABSTRACT
Human and economic losses generated by landslides occur every year in all countries; however, the impact of landslides varies considerably according to local geological conditions and socio-economic vulnerability. Although the occurrence of landslides has impacted the Colombian Andes for a long time, few studies considering rainfall as a triggering factor have been carried out in our country. SHIA_Landslide (Open and Distributed Hydrological Simulation & Landslides) is a conceptual and physically based model to analyze shallow landslide processes by incorporating a comprehensive distributed hydrological tank model that includes water storage in the soil coupled with a classical analysis of infinite-slope stability under saturated conditions. This paper evaluates the influence of antecedent rainfall and hydraulic conductivity on landslides triggered by rainfall using the SHIA_Landslide model. The results obtained in this study are similar to those presented by different authors in the literature. Soils of highconductivity values only need short and intense rainstorms for failure, and the antecedent rainfall conditions donot play an important role for these kinds of soils.
KEY WORDS: Physical models; Landslide triggered by rainfall; SHIA_Landslide.
RESUMEN
Las pérdidas económicas y humanas por movimientos en masa ocurren cada año en todo el mundo; sin embargo el impacto varía considerablemente debido a las condiciones geológicas locales y vulnerabilidad socioeconómica. Aunque la ocurrencia de movimientos en masa ha golpeado Los Andes colombianos, pocos estudios que consideren la lluvia como factor detonante se han realizado. SHIA_Landslide (Simulación Hidrológica Abierta para deslizamientos detonados por lluvia) es un modelo conceptual y de base física para analizar los procesos de deslizamientos superficiales mediante la incorporación de un modelo hidrológico de tanques y distribuido que incluye el almacenamiento de agua en el suelo, acoplado con un análisis clásico de estabilidad de talud infinito en condiciones saturadas. En este trabajo se evalúa la influencia de la lluvia antecedente y conductividad hidráulica de los deslizamientos detonados por lluvias utilizando el modelo SHIA_Landslide. Los resultados obtenidos en este estudio son similares a los obtenidos por diferentes autores en la literatura. Los suelos con altos valores de conductividad solo necesitan lluvias cortas e intensas para fallar, y las condiciones de lluvia antecedentes no juegan un papel importante para este tipo de suelos.
PALABRAS CLAVE: Modelos físicos; deslizamientos detonados por lluvias; SHIA_Landslide.
RESUMO
As perdas humanas e econômicas geradas por deslizamentos de terra ocorrem todos os anos em todos os países; no entanto, o impacto de deslizamentos de terra varia consideravelmente devido ás condições geológicas locais e a vulnerabilidade sócio-econômica. Embora a ocorrência de deslizamentos de terra têm impactado os Andes colombianos, poucos estudos que considerem a chuva como fator detonante tem- se realizado. SHIA_Landslide (Simulação Hidrológica aberta para deslizamentos detonados pela chuva) é um modelo conceitual e de base física para analisar os processos de deslizamentos superficiais pela incorporação de um modelo hidrológico de tanques e distribuidos que inclui o armazenamento de água no solo, acoplado com uma análise clássica da estabilidade talude infinito em condições saturadas. Em este artigo avalia-se a influência da precipitação antecedente e condutividade hidráulica dos deslizamentos detonados por chuvas utilizando o modelo SHIA_Landslide. Os resultados obtidos neste estudo são semelhantes aos obtidos por diferentes autores na literatura. Os solos com altos valores de condutividade só precisam de chuvas curtas e intensas para falhar, e as condições de chuva antecedentes não desempenham um papel importante para estes tipos de solos.
PALAVRAS-CHAVE: Modelos físicos; Deslizamentos detonados pelas chuvas; SHIA_Landslide.
1. INTRODUCTION
Even though mass movements make part of the continuous and natural geomorphological cycle that models the earth's surface, they are also one of the leading causes of human and financial loss around the world. This is especially true in tropical environments and mountainous regions because of expansion and human settlement in susceptible areas (Schuster, 1996; Sidle and Ochiai, 2006). It is for this reason that threat evaluation and prediction capacity of this phenomena have been topics of interest for the scientific community for the implementation of earlyalert systems (Caine, 1980; Montgomery and Dietrich, 1994; Finlay et al., 1997; Crosta, 1998; Terlien, 1998; Crozier, 1999; Polemio & Petrucci, 2000; Iverson, 2000; NOAA-USGS, 2005; Restrepo et al, 2008; Larsen, 2008).
Landslides are caused by a great variety of factors that demand the adoption of an interdisciplinary focus, integrating concepts from geomorphology, hydrology and soil mechanics (Crosta and Frattini, 2008). Notwithstanding, only one solitary external factor becomes the factor which triggers mass movement. In tropical environments and mountainous regions such as the Colombian Andes, a high percentage of these mass movements are caused by intense rains or long lasting events (Aristizábal and Gómez, 2007). They are characterized by their slight thickness (0,3 - 2 m), flat surface parallels to the faulty surface of the ground, and with small area escarpment (Anderson & Sitar 1995). These movements are generated as a consequence of rainfall events for the rapid increase in the pressure of positive pores or for the loss of apparent component of cohesion (Wang y Sassa, 2003; Terlien, 1998; Crosta, 1998; Crosta y Frattini, 2003).
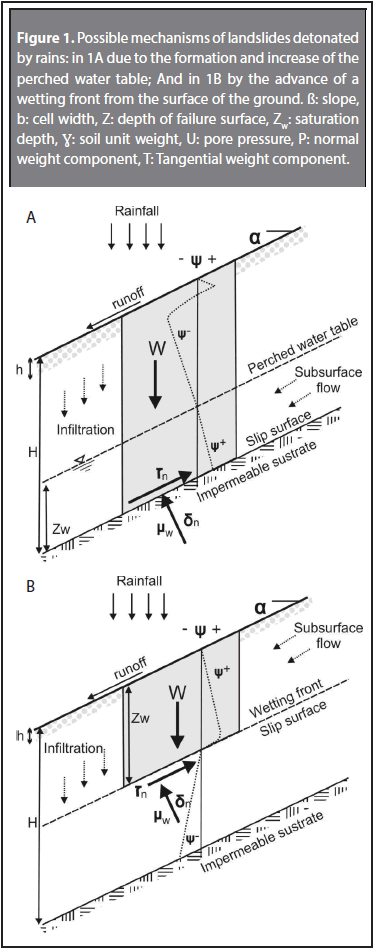
Collins & Znidarcic (2004) propose two failure mechanisms different from landslides triggered by rainfall. In the first mechanism, the failure is produced due to positive pore pressure, where subsequently to the terrain's failure, the displaced material, throughstatic liquefaction and rapid reduction of shear strength in nondrained conditions, is converted into a flow which spreads down the slope. This, in turn, increases the initial volume of the material POR ARRANQUE Y TRANSPORTE along the surface of displacement (Wang and Sassa, 2003; Wieczorek and Guzzetti, 2000). Some authors point to the initiation of movement and its mobilization as simultaneous and non-differentiable (Eckersley, 1990; Anderson y Sitar, 1995). The second failure mechanism is produced under negative pore pressure where the material is still in a non-saturated state. The failure occurs due to the decrease of the suction and the fault mass behaves as a rigid body. (See Figure 1).
Recently, Aristizábal et al. (2016), coupled a conceptual hydrological model with a geotechnical fixed base, which they named SHIA_Landslide (Open and Distributed Hydrological Simulation & Landslides). SHIA_Landslide is an original and meaningful contribution which offers a new analysis perspective of the superficial landslide at a basin scale. This is carried out by incorporating a complete and distributed hydrological tank model withstorage of water in the soil, along with a geotechnical and classic analysis of infiniteincline under conditions of saturation. SHIA_Landslide is accessible through a graphic user interface (GUI), which enables the user to interact with the model.
One of the scopes of the SHIA_Landslide model is to improve the comprehension of the associated mechanism with the instability of the slopes and the infiltration of rainfall in mountainous regions located in tropical environments, where demographic pressure is leading to the expansion of development in landslide prone areas.
This paper evaluates the influence of hydraulic conductivity and antecedent rain in the occurrence of mass movements triggered by rain, using modeling with a physical base through the SHIA_Landslide model. For this, we used the September 21, 1990 event at La Arenosa ravine, where an intense rain event triggered 823 superficial landslides.
2. MECHANISMS FOR LANDSLIDES TRIGGERED BY RAINFALL IN TROPICAL ENVIRONMENTS
Mountainous terrain in tropical environments are characterized by high rainfall values and deep weathering profiles in saturated or humid field conditions. This is why superficial landslides triggered by rainfall in tropical environments are controlled by the weathering profile and storage capacity of the water in the soil.
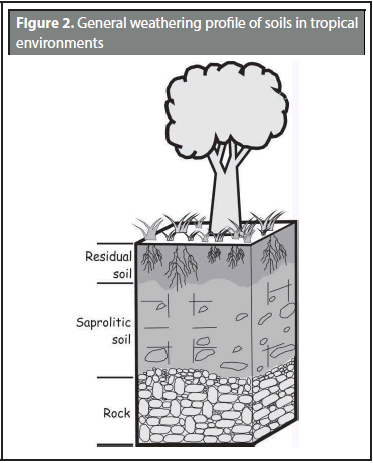
According to studies conducted by Little (1969), Deere and Patton (1971) and Anon (1981), residual tropical soil profiles can be simplified in three basic horizons with specific and particular engineering characteristics. Initially, a horizon was named residual soil, where the material completely corresponds to soil and there are no identified parent rock structures. Along this horizon, there are meaningful changes that affect the soil volume and increase the hydrological permeability and conductivity. This top floor horizon is influenced by areas of vegetation roots and processes of animal origin that generate structures of macro pores and ducts. These structures develop a system of secondary porosity, substantially increasing hydraulic conductivity of the soil, which act as preferential flow trajectories, originating a rapid increase of the saturation grade and pore pressure during rainfall events. There are saprolitic horizons below residual soil, which also correspond to soil material but original structures from the parent rock remain. The mineral and volume changes, as well as the influence of earth surface, are not important in these horizons, resulting in a decrease of the hydraulic conductivity in several matters of magnitude and a marked contrast with respect to residual soil. Lastly, there are horizons with behavior and characteristics similar to the stone and with very low conductivity. (See Figure 2).
In terms of water content along the weathering profile, it is important to note that the storage capacity is function of the available pores in the soil and the grade of saturation. A significant portion of the water that is precipitated on the land surface an important share infiltrates the ground, thereby filling empty pores among soil particles. In non-saturated conditions, the soil has the capacity to maintain water inside its smallest pores due to tension force (Fredlund and Rahardjo 1993). This water content is known as pore water. If gravity exerts enough force to surpass the surface tension, the water percolates to lower horizons of the weather profile. This water content is known as gravitational water and this threshold is named field capacity (Wfc) in terms of water content. Field capacity is achieved when soil suction is approximately 30 kPa in clay or 10 kPa in sandy soil (Richards and Weaver 1944; Saxton and Rawls 2006). Water excess above the Cano capacity is freely drained, according to the hydraulic conductivity of the soil, until reaching new field capacity. Water content below the point of field capacity is eliminated by evapotranspiration until it reaches the point of permanent wilting (Wpwp). At this point, the water volume content is too low for the plant to be able to extract water from the soil, which corresponds to approximately 1.500 kPa suction (Veihmeyer and Hendrickson 1928; Saxton and Rawls, 2006).
Under said weathering profile scheme and water behavior, the existing contrast between residual soil and saprolitic soil, in terms of hydraulic conductivity gives way to the fact that a great amount of gravitational water that percolates along residual soil cannot drain to deeper levels, such as saprolitic soil and a phreatic level is formed. This saturation of weathering profile from the bottom up generated a parallel superficial flow of the land. In terms of the stability of slopes, this means that the potential failure surface is found along the contact between relatively permeable residual soil and saprolitic soil that is relatively water resistant. When a critical altitude of phreatic level is reached, and consequently the increase of positive pore pressure, mass combined type movements are produced, according to the classification of Cruden and Varnes (1996). These initially correspond to planar landslides which rapidly convert to flows by static liquefaction phenomena due to the rapid reduction of resistance to the sharp in not drained conditions (Anderson and Sitar, 1995).
This means that non saturated soil conditions dominate at the start of rainfall events or when the antecedent rainfall has been very low. It is only during these times can landslides occur because of suction reduction. However, after a short period of rainfall, saturated conditions prevail and control the occurrence of surface landslides.
3. SHIA_LANDSLIDE MODEL
SHIA_Landslide is a program on FORTRAN for the evaluation of the stability of slopes in a basin under conditions of rainfall, coupling a conceptual hydrological model and distributed with a geotechnical model of limit balance using the Mohr- Coulomb failure criteria.
The model requires an event or series of rainfall as input, which causes an increase in the phreatic level and, in consequence, an increase in positive pore pressure which leads to the decrease in conditions of stability of slopes. A more detailed description of the SHIA_Landslide can be found in Aristizábal (2014) and Aristizábal et al. (2015).
To model hydrological processes at basin and slope levels, the SHIA_Landslide uses the Open and Distributed Hydrological Simulation & Landslides developed by Vélez (2001), which considers different linear or non-linear focuses to estimate water flows in vertical and horizontal directions.
The model depicts a basin as a set of interconnected cells following the topographical configuration, taken from a Model of Digital Elevation. Each cell in the grid corresponds to an interconnected system of five tanks that communicate with their respective tank in the lower water cell via the river network. This way, the variables of state of the model are the content of water in each tank during each passage of time of the simulation. Also, the flows between tanks represent the physical processes of the exchange of water that are a function of the adopted conceptual scheme, the tank type and the morphological and hydrological characteristics of the soil present in each cell.
The first storage tank, called capillary or static, represents the interception and detention of the puddled water and the storage of capillary water in the soil. The fundamental parameter of soil in this tank is the maximum water storage capacity of the soil, "useful water" in the soil, which is an input for the function of the field capacity model and depth of roots. The only output of this storage is real evapotranspiration.
The second tank is named surface storage and represents water that has not infiltrated and makes up the surface run-off. Since some quantity of water has already been previously derived for the static soil storage, we consider that the infiltration capacity can be associated with the saturated hydraulic conductivity of the soil, which is an input parameter for the model. For surface run-off, we estimate flow speed function of the flow magnitude through the Manning equation:
where A is the section of flow, β the slope, n Manning coefficient, and ξ and e1 parameters associated with the surface type. For flows over natural flows, Parsons et al. (1994) recommend values of 0.038 and 0.315, respectively.
The third tank represents gravitational water storage in the residual soil between field capacity and saturation, which corresponds to the conditions of stability of the soil and at phreatic level responsible for the reduction of stability conditions of the slope and that can be moved to the inferior tank by percolating or making part of the sub-surface's flow. Both flows are related to the saturated hydraulic conductivity of the rocky substrate, entrance parameter to/of the model.
The fourth tank corresponds to underground storage where the vertical water flow represents the output of the system and the horizontal water flow represents the base flow. Lastly, the fifth tank represents the basins of the drainage network.
For the translation of flow along the length of the drainage network, a method proposed by Vélez (2001) is used. This method is named drainsis used in the method proposed by Vélez (2001), named Geomorphological Kinematic Wave (OCG). OCG is a simplification of SainVenant's equations, in which the terms of inertia and pressure are depreciated. The GKW using roughness calculation correlate equations proposed by Leopold and Maddock (1953), relate the geometry of the flow section and the speed in the section with the basin, using potential equations with the Manning equation, which relates flow velocity and the transversal flow section. These correlations enable us to obtain an equation for flow velocity en the canal as a function of the canal of geometry and the geomorphology of the terrain:
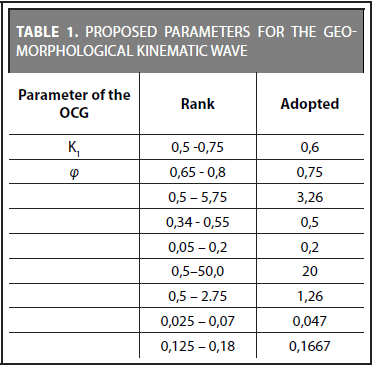
The OCG requires new independent exponents and coefficients that can be obtained from a regional geomorphological study in zones that are hydrological homogeneous. For this, empirical studies have been conducted by various authors who propose different values according to local conditions (Frances et al. 2012). Table 1 shows the values for the regional constant parameters proposed by Vélez (2001) and Frances et al. (2007).
In order to evaluate the stability of banks after the hydrological simulation of the basin and hillside, SHIA_Landslide uses a stability analysis based on the physics of the model known as "infinite slope." According to Graham (1984), for slopes with a constant sub-surface flow and parallel to said slopes, with a water level of Zw above the failure surface, the safety factor is:
where C' is the effective cohesion, γ is the unitary weight of the soil, Z is the thickness of the soil measured vertically, γw is the unitary weight of water, β is the slant of the slope, and φ is the angle of friction.
For the calibration process, SHIA_Landslide includes the model proposed by Frances et al. (2007). The parameters in each cell are divided into two components, one hydrological or geotechnical characteristic and a common correction factor to all cell errors in modeling. The correction factors represent the effects of scales of space and time, along with the errors of the model and input parameters, leaving hydrological or geotechnical characteristics free of those problems maintaining the physical meaning of the parameter (Frances et al., 2012).
To evaluate the development model and in the case, there are observed data of flow at any point of the basin. SHIA_Landslide generates as an output value the mean quadratic error (RMSE) and the efficiency coefficient of Nash-Sutcliffe (NS). On the other hand, the model uses total precipitation of the catchment water zone and output of the basin to create a balance of water, considering water storage in the basin.
In terms of results, the model generates four output products for each simulation. The hydrograph and variation of the phreatic level for any point in the basin, the landslide susceptibility map of the basin and a map of landslide threats which corresponds to the distribution of space of landslides caused by the simulated rainfall event.
Figure 3 presents the flowchart structure of the coupled model, SHIA_Landslide.
4. IMPLEMENTATION OF THE SHIA_ LANDSLIDE MODEL
In order to evaluate the influence of antecedent rainfall and the hydraulic conductivity of the soil in surface landslides detonated by rainfall, the SHIA_ Landslide model was implemented in La Arenosa ravine basin, which is typical of mountain regions and tropical zones. The basin of La Arenosa river has an area of 9,91 km2 and is located southeast of the Central Mountain Range in the department of Antioquia. The region has a humid tropical climate with an average precipitation of 4.300 mm and an average annual temperature of 23° (IGAC 2007). The geology is made up of residual soil of granodioritic rock covered in soft slope areas with fluvio torrential deposits (Mejía and Velásquez, 1991).
On September 21, 1990, a high intensity rainfall event affected La Arenosa basin. In less than 3 hours, 208 mm of precipitation fell on the basin. This provoked 823 mass movements. During this event, the population was strongly affected. Twenty persons died and 260 were evacuated. Twenty-seven houses were destroyed and 30 others were damaged. Several bridges and more than 100m of roads were ruined. The Calderas Hydro-Electric Power Plant, owned by ISAGENS.A E.S.P. was flooded and severely damaged by large blocks traveling through La Arenosa ravine. Total losses were estimated to be more than US$ 6 million (Hermelin et al., 1992).
A later analysis of the event with real photos and field research enabled a partial reconstruction of the pattern and characteristics of the landslides in La Arenosa ravine Integral (1990) and Mejía and Velásquez (1991) conducted a detailed inventory of the landslides caused during the event, as well as a complete description. Mejía and Velásquez (1991) reported 669 movements in La Arenosa basin.
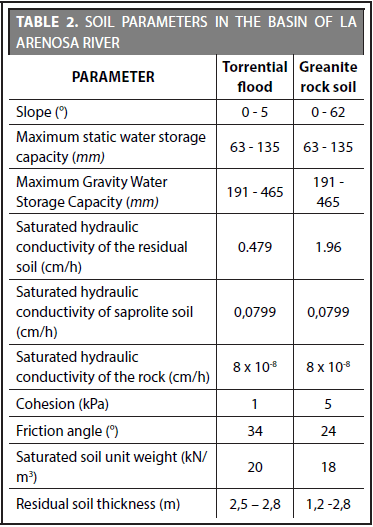
Three morphometric maps are required as input parameters for the implementation of the SHIA_Landslide model: accumulated area, flow direction and slope. Also, nine maps of the hydrological and geo-mechanic properties of the soil: thickness, cohesion, saturated weight, friction angle, saturated hydraulic conductivity of the rock, maximum static storage capacity of the water and maximum storage capacity of gravitational water. The morphometric parameters were calculated using ArcGIS 10.1, hydrological tools and a DTM supplied by the Instituto Geográfico Agustín Codazzi (IGAC) with a length of 10 m. The soil parameters were calculated from the soil map devised by IGAC (2007), and the floor descriptions, field tests and lab analysis of the soil were conducted by Mejía and Velásquez (1991) and Integral (1990) (Table 2). A series of hourly rainfalls at La Arenosa basin between 2007 and 2012 were used to calibrate and validate the hydrologic component of the model. For the geotechnical component, the September 21, 1990 event was used, since there was a detailed inventory of landslides. The calibration and validation process of the model can be consulted in detail in Aristizábal (2014) and Aristizábal et al. (2015).
5. RESULTS AND DISCUSSION
Although literature regarding antecedent rainfall as a condition for the occurrence of landslides widely exists, its influence is difficult to quantify since it depends on several factors, among which are hydraulic conductivity and soil humidity. Hydraulic conductivity is a basic soil property and no doubt plays an essential role from the point of view of the balance that should exist between the generation of pore pressure and its dissipation, which is fundamental to initiate movement (Wang & Shibata, 2007).
In order to evaluate the effect of antecedent rain in La Arenosa basin, the basin's response for the September 21, 1990 was evaluated, modifying rainfall conditions for the preceding three months and 24 hours. Subsequently, the changes in the phreatic levels from some selected cells inside the basin.
According to the results, the increase in preceding rain in the three months prior to the September 21, 1990 event did not generate any significant change in the peak of the phreatic level for the cells evaluated. Likewise, the increase in antecedent rain during the previous 24 hours to the event didn't represent any changes in the phreatic level.
In the same manner, both the influence of volume of rainfall and the possible influence of HIETOGRAMA of different storms were studied. Four representative patterns of storms at an hourly scale were used for a period of 1,000 hours and a maximum rainfall intensity of 50 mm/h. The pattern, named uniform keeps the intensity of rain equal to (50 mm/h) during the entire simulation. The advanced pattern begins with the maximum intensity and progressively decreases to an intensity of (50 mm/h). The pattern known as reversal begins with a rain intensity of 0 mm/h, progressively increasing up to 50 mm/h. Lastly, the central pattern begins with a rain intensity of 0 mm/h, reaching a maximum intensity at the half-point of the simulation period, and progressively decreases until reaching a rain intensity equal to the initial value of 0 mm/h. The four rain patterns produced the same number of unstable cells. No difference of maximum peaks in La Arenosa basin were observed if storm intensity is at the beginning, the middle or the end. The difference is at the moment in which the landslides occur, due to the fact that most of the landslides occur during the peak of the storm.
In order to evaluate the hydraulic conductivity model in saturated conditions, a series of hourly rainfalls during three months was used and the change in the phreatic level upon variation of the conductivity values in the basin was tested (See Figure 4). These variations are hypothetical as a numerical experiment through sensibility analysis and do not represent real conditions since possible changes in the characteristics of the soil that can be related are not considered.
When hydraulic conductivity decreases by two orders of magnitude, the phreatic level peaks disappear, with a constant increase that reaches a maximum peak slightly above 50% of the thickness of the soil. The phreatic level maintains its high levels even after the end of the rainfall, which indicates a lesser capacity to dissipate positive pore pressure in the soil due to its low conductivity.
If conductivity is reduced in order of magnitude, in general terms, maximum peaks are reduced. Initially, there is a constant increase of phreatic level with small peaks that correspond to short rainfall events. When it reaches an altitude of close to 50% of total soil thickness for this cell, there is a rough descent in the depth of the phreatic level and behavior changes completely, adjusting to the conductivity behavior in the soil, from this point showing small peaks and valleys which represent rainfall events on the basin. For conductivity in one and two orders of magnitude greater than the hydraulic conductivity of the soil, small increases in the phreatic level occur, all below 30% of the soil thickness and with a pattern similar to the measured conductivity.
These results imply that in the sandy soils that make up La Arenosa ravine basin, characterized by its high conductivity, the positive pore pressure is rapidly reduced after the rain event, which is why short, intense rainfall events are required for its failure, such as the September 21, 1990 event. In addition, its capacity to dissipate pore pressure because of its high conductivity values limit preceding rain from having a considerable influence in its behavior.
These results are coherent with different authors' finding for residual soils with high permeability, characteristic of residual sandy soils of granite rock. Preceding rain and humidity conditions do not always play a determining role in soils (Rahardjo et al., 2008; Brand, 1985; Corominas and Moya, 1999). In fact, some authors such as Tsaparas et al. (2002) and Rahardjo et al. (2007) register differences in failure mechanisms associated to the permeability of of the soils. Hillsides with high permeability usually fail due to a suction reduction. On the other hand, Terlien (1998) finds that the difference in the number of days of preceding rain depends on the surface depth of the failure, where detonated movements because of daily high precipitations are superficial, with depths of less than 2 m, and detonated movements due to antecedent rainfall have failure surface depths above 6 m.
As part of the hydraulic conductivity sensitivity analysis and preceding rain, it is possible to use the SHIA_Landslide model to establish rainfall thresholds in order to predict when landslides will occur. For this case, series of rainfalls were created with maximum rain peaks of different magnitudes and the number of cells which failed were evaluated.
For a storm with 20 mm/h peaks, 13% of potentially unstable areas fail. For 40 mm/h peaks, 32% of potentially unstable areas fail. And for 80 mm/h peaks, 48% of potentially unstable areas fail (see Figure 5).
Figure 6 depicts a percentage of basin cells which fail due to rain, with a maximum percentage obtained under different rain peaks.
The maximum value obtained is close to 50% of peaks close to 100 mm/h. For greater peaks, there is no significant increase of landslides. This behavior points to an asymptotic relationship between rain peaks and the occurrence of landslides. There is a tendency to linearly increase for small rain peaks and decrease until reaching an asymptotic value close to 50%.
These results point to a non existence of a minimum threshold of rain from which there is a marked greater percentage of landslides. On the contrary, there is a maximum threshold close to 100 mm/h above which there are no more landslides independent of the intensity or duration of rain. The 50% value of cells that fail means a maximum occurrence of landslides due to rain, which apparently emerge as a maximum natural threshold for La Arenosa ravine basin, associated to its hydrological and geotechnical conditions, However, it is necessary to evaluate this behavior for other basins, since said threshold could also point to a limitation of the model imposed by the calibration process.
In this sense, the stability conditions of each one of the cells that make up the basin were evaluated under the height increase of the phreatic level. The different simulation scenarios represented the altitude of the phreatic level (Zw) as a percentage of soil depth that fails (Zs). The scenario where Zw = Zs, corresponds to the most critical scenario in which the phreatic level for all cells that make up the basin coincide with the surface of the terrain. Under such a scenario, all cells identified by the susceptibility map as potentially unstable fail. For Zw = 0.5Zs, only 13.6% of the potentially unstable cells fail. When the phreatic level approaches conditions of saturation, the number of unstable cells increases considerably, when Zw = 0.8Zs, 65.6% of the cells fail.
Figure 7 depicts the percentage of unstable basin cells in function of the increase of phreatic level for La Arenosa ravine basin. When the phreatic level increases above 40% of soil depth, potentially unstable areas begin to fail. Below said value there are no landslides. However, it is important to note that said threshold does not make physical sense at basin level since it is not possible that all cells simultaneously present a relationship or percentage Zw/Zs equal. The relationship is a function of the quantity of infiltrated water, the hydraulic and geomechanic properties of the soil, position of the cell in the hillside and soil thickness.
6. CONCLUSIONS
Tropical environments such as the Colombian Andes are characterized by deep weathering profiles and the presence of rainfall during great part of the year. Most landslides that occur in these regions are induced by rainfall. In Colombia, however, there are few events which include landslide inventories that have been characterized in detail. For La Arenosa event on September 21, 1990, Mejía and Velásquez (1991) and Integral (1990) conducted a detailed evaluation and a partial landslide evaluation. This enables the implementation and evaluation of a model for the prognosis of landslides triggered by rainfall.
According to the results obtained in the implementation of the SHIA_Landslide model, we can establish that the model is highly sensitive to soil thickness, the decrease in contact depth between the residual and saprolitic soil that produces a greater occurrence of landslides. With respect to geo-mechanic properties, there is an expected inverse relationship, an increase in the angle of friction or cohesion generate a decrease of the cells that fail. And, similarly to results from numerous models, the safety factor is more sensitive to changes in cohesion, thickness and slope, moderately sensitive to changes in the angle of friction and slightly sensitive to changes in the unitary weight of soil.
Results found in the present study, in general terms, point to the fact that hillsides made up of high conductivity soils require only short and intense rainfall events for their failure, and that antecedent rain conditions do not play and important role.
ACKNOWLEDGEMENTS
The authors thank the Wildsdorf Hans Foundation and the Colombian Association of Oil Geologists and Geophysicists (ACGGP) for their financial support for the realization of this research.
REFERENCES
Anderson, M.G.; Lloyd, D.M. (1991). Using a combined slope hydrology-stability model to develop cut slope design charts. Proc. Inst. Civ. Engineers, 91, 705-718. [ Links ]
Anderson, S.A.; Sitar N. (1995). Analysis of rainfall-induced debris flows. Journal of Geotechnical Engineering, pp. 544-552. [ Links ]
Aristizábal, E.; Vélez, J.I.; Martínez, H. (2016). SHIA_Landslide: a distributed conceptual and physically based model to forecast the temporal and spatial occurrence of shallow landslides triggered by rainfall in tropical and mountainous basins. Landslides,13, pp. 497-517. [ Links ]
Aristizábal, E. (2014). SHIA_Landslide: Developing a physically based model to predict shallow landslides triggered by rainfall in tropical environments. Ph Thesis, Universidad Nacional de Colombia, pp. 217. [ Links ]
Aristizábal, E.; Gómez, J. (2007). Inventario de emergencias y desastres en el Valle de Aburrá: originados por fenómenos naturales y antrópicos en el periodo 1880-2007. Revista Gestión y Ambiente, 10(2), pp. 17-30. [ Links ]
Brand, E.W. (1985). Predicting the performance of residual soil slopes. Proceedings 11th Int. Conf. Soil Mech. & Found. Engineering. San Francisco, 5, pp. 2541-2578 [ Links ]
Caine, N. (1980). The rainfall intensity - duration control of shallow landslides and debris flows. Geografiska Annaler, 62A(1-2), pp. 23-27. [ Links ]
Collins, B.D.; Znidarcic D. (2004). Stability analyses of rainfall induced landslides. Journal of Geotechnical and Geoenvironmental Engineering. 130(4), pp. 362-371. [ Links ]
Corominas, J.; Moya, J. (1999). Reconstructing recent landslide activity in relation to rainfall in the Llobregat river basin, Eastern Pyrenees, Spain. Geomorphology, 30, 79-93. [ Links ]
Crosta, G. (1998). Regionalization of rainfall threshold: an aid for landslide susceptibility zonation. Enviromental Geology, 35(2-3), 131-145. [ Links ]
Crosta, G.; Frattini, P. (2003). Distributed modeling of shallow landslides triggered by intense rainfall. Natural Hazard and Earth System Sciences, 3, pp. 81-93. [ Links ]
Crosta, G.; Frattini, P. (2008). Rainfall-induced landslides and debris flows. Hydrological Processes, 22, pp. 473-477. [ Links ]
Cruden, D. M.; Varnes D.J. (1996). Landslide types and processes. En: A. K. Turner y R.L. Schuster (Editores): Landslides. Investigation and mitigation. Transportation Research Board Special Report 247. National Academy Press. Washington D.C. pp. 36-75. [ Links ]
Deere, D.U.; Patton F.D. (1971). Slope stability in residual soils. Proc., Fourth Pan American Conference on Soil Mechanics and Foundation Engineering, Puerto Rico. 1, pp. 87-170. [ Links ]
Eckersley, J.D. (1990). Instrumented laboratory flowslides. Geotechnique. London, England, 40(3), pp. 489-502. [ Links ]
Finlay, P.J.; Fell, R.; Maguire, P.K. (1997). The relationship between the probability of landslide occurrence and rainfall. Can. Geotech. Journal, 34. pp. 811-824. [ Links ]
Frances, F.; Vélez, J.I.; Vélez, J.J. (2007). Split-parameter structure for the automatic calibration of distributed hydrological models. Journal of Hydrology, 332, pp. 226-240. [ Links ]
Frances, F.; Vélez, J.J.; Munera, J.C.; Medici, C.; Busii, G. (2012). Descripción del modelo conceptual distribuido de simulación hidrológica TETIS v.8. Universidad Politécnica de Valencia. 86 pp. [ Links ]
Fredlund, D.G.; Rahardjo, H. (1993). Soil mechanics for unsaturated soils, Wiley-Interscience, New York. [ Links ]
Graham, J. (1984). Methods of Stability Analysis, Department of Civil Engineering, University of Manitoba, Slope Instability: In D. Brunsden and D.B. Prior (Eds), John Wiley & Sons Ltd., pp. 171-215. [ Links ]
Hermelin, M.; Mejía, O., Velásquez, E. (1992). Erosional and depositional features produced by a convulsive event, San Carlos, Colombia, September 21, 1990. Bulletin of the International Association of Engineering Geology, 45, pp. 89-95. [ Links ]
IGAC - Instituto Geográfico Agustín Codazzi (2007). Estudio general de suelos y zonificación de tierras del departamento de Antioquia. Bogotá. 207 p. [ Links ]
INTEGRAL S.A. (1990). Informe sobre daños en la central de calderas por la avalancha ocurrida en l quebrada LA Arenosa el 21 de septiembre de 1990 y su reparación. Internal Report Interconexión Eléctrica S.A. ISA.45 p. [ Links ]
Iverson, R. (2000). Landslide triggering by rain infiltration. Water Resources Research, 36(7), pp. 1897-1910. [ Links ]
Larsen, M.C. (2008). Rainfall-triggered landslides, anthropogenic hazards, and mitigation strategies. Advances in Geosciences, 14, pp. 147-153. [ Links ]
Leopold, L.B.; Maddock, T.J. (1953). Hydraulic geometry of stream channels and some physiographic implications. U. S. Geological Survey Professional Paper, 252, 55 p. [ Links ]
Little, A.L. (1969). The engineering classification of residual tropical soils. Proceedings of 7th International Conference of Soil Mechanics and Foundation Engineering, 1, pp. 1-10. [ Links ]
Matula, M. (1981). Rock and soil description and classification for engineering geological mapping. Bulletin of International Association of Engineering Geology, 24, pp. 253-274. [ Links ]
Mejía, R.; Velásquez, M.E. (1991). Procesos y depósitos asociados al aguacero de septiembre 21 de 1990 en el Área de San Carlos (Antioquia). Tesis de grado, Universidad Nacional de Colombia, Medellín. 160 p. [ Links ]
Montgomery, D. R.; Dietrich, W. E. (1994). A physically based model for the topographic control on shallow landsliding. Water Resources Research, pp. 1153-1171. [ Links ]
Montgomery, D. R.; Sullivan, K.; Greenberg, M. (1998). Regional test of a model for shallow landsliding. Hydrol. Process.,12, pp. 943-955. [ Links ]
National Oceanic & Atmospheric Administration NOAA, United Status Geological Survey USGS (2005). NOAA-USGS Debris flow warning system-final report, circular 1283. [Online] Disponible en: http.//pubs.usgs.gov/circ/2005/1283/. [ Links ]
Parsons, A.J.; Abrahams, A.D.; Wainwright, J. (1994). On determining resistance to interrill overland flow. Water Resources Research, 30(12), pp. 3515-3521. [ Links ]
Rahardjo, H.; Ong, T.H.; Rezaur, R.B.; Leong, E.C. (2007). Factors controlling instability of homogeneous soil slopes under rainfall. Journal of Geotechnical and Geoenvironmental Engineering, 133(12), pp. 1532-1543. [ Links ]
Rahardjo, H.; Leong, E.C.; Rezaur, R.B. (2008). Effect of antecedent rainfall on pore-water pressure distribution characteristics in residual soil slopes under tropical rainfall. Hydrological Processes, 22. pp. 506-523. [ Links ]
Restrepo, P.; Jorgensen, D.P.; Cannon, S.H.; Costa, J.E.; Laber, J.; Major, J.A.; Marter, B.; Purpura, J.; Werner, K. (2008). Prototype debris flow warning system for recently burned areas in Southern California. Bulletin of the Meteorological Society, Insights and Innovation, American Meteorological Society, pp. 1845-1851. [ Links ]
Richards, L.A.; Weaver, L.R. (1944). Moisture retention by some irrigated soils as related to soil moisture tension. Journal of Agricultural Research, 69, pp. 215-235. [ Links ]
Saxton, K.E.; Rawls, W.J. (2006). Soil Water Characteristic Estimates by Texture and Organic Matter for Hydrologic Solutions. Soil Science Society of America Journal, 70, pp. 1569-1578. [ Links ]
Schuster, R.L. (1996). Socioeconomic significance of landslides. In: A.K. Turner & R.L. Schuster (Eds) Landslides Investigation and Mitigation. Transportation Research Board, National Research Council, Special Report 247, National Academy Press, Washington, DC, ISA. pp. 129-177. [ Links ]
Sidle, R.C.; Ochiai, H. (2006). Landslides: processes, prediction, and land use. Water Resources Monograph 18. American Geophysical Union, Washington D.C. [ Links ]
Tsaparas, I.; Rahardjo, H.; Toll, D.G.; Leong, E.C. (2002). Controlling parameters for rainfall-induced landslides. Computers and Geotechnics, 29, pp. 1-27. [ Links ]
Terlien, M.T.J. (1998). The determination of statistical and deterministic hydrological landslide-triggering thresholds. Environmental Geology, 35(2-3), pp. 124-130. [ Links ]
Veihmeyer, F.J.; Hendrickson, A.H. (1928). Soil moisture at permanent wilting of plants. Plant Physiol. 3(3), pp. 355-357. [ Links ]
Vélez, J.I. (2001). Desarrollo de un modelo hidrológico conceptual distribuido orientado a la simulación de crecidas. Valencia. Tesis Doctoral. Universidad Politécnica de Valencia. [ Links ]
Wang, G.; Sassa, K. (2003). Pore pressure generation and movement of rainfall-induced landslides: effects of grain size and fine particle content. Engineering Geology, 69, pp. 109-125. [ Links ]
Wang, F.; Shibata, H. (2007). Influence of sol permeability on rainfall-induced flowslides in laboratory flume tests. Can. Geotech. Journal, 44, pp. 1128-1136. [ Links ]
Wieczorek, G.F.; Guzzetti, F. (2000). A review of rainfall thresholds for triggering landslides, Mediterranean Storms, Proceeding of the EGS Plinius Conference, Maratea, Italia. [ Links ]











 text in
text in