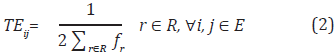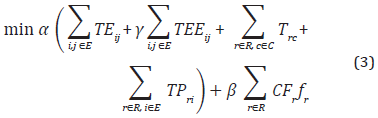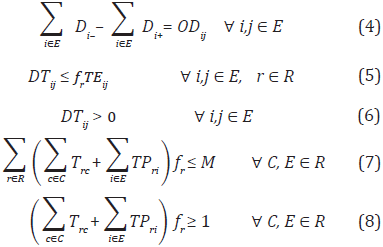APPROPRIATE FREQUENCY ALLOCATION FOR A BRT SYSTEM THROUGH A MULTIOBJECTIVE MODEL

ASIGNACIÓN DE FRECUENCIAS APROPIADAS A TRAVÉS DE UN MODELO MULTIOBJETIVO PARA UN SISTEMA BRT

ATRIBUIÇÃO DE FREQUÊNCIAS APROPRIADAS ATRAVÉS DE UM MODELO MULTIOBJETIVO PARA UM SISTEMA BRT

Diego Armando Galindres Guancha¹, Jose Adalberto Soto Mejía², Sandra Estrada Mejía³

1 Ingeniero Industrial, Estudiante de Maestría en Investigación Operativa y Estadística. Universidad Tecnológica de Pereira. Carrera 27 #10-02 Barrio Alamos. Universidad Tecnológica de Pereira. Blq 5. piso 4, oficina de Proyectos especiales y Maestrias. / Tel.: 3218567297. Correo electrónico: diegogal@utp.edu.co.
2 Ph.D. en Ingeniería Eléctrica, área Ingeniería de Computación. Universidad Tecnológica de Pereira.
3 Ph.D. en Ciencias Pedagógicas. Universidad Tecnológica de Pereira.

Paper received: 18-I-2016/ Approved: 29-XI-2016
Available online: February 30, 2017
Open discussion until April 2018

ABSTRACT

This article addresses the search for adequate frequencies of bus dispatching in an Integrated Public Transportation Systems (IPTS). An optimization model is proposed to find these frequencies for bus dispatching travelling in different exclusive lane routes. The model was applied to a reduction of the Integrated Public Transportation Systems (IPTS) in the city of Pereira (Risaralda, Colombia), which is of the Bus Rapid Transit (BRT) type. Nevertheless, the model can be applied to a larger BRT system. The frequencies are determined according to an estimated travel demand in a given bus station, the capacity of the buses, and the size of the available fleet. There is resolution of a multi-objective function that minimizes downtimes at the stations, the economic costs of the business operators and takes into account a penalty that occurs when users must wait for a second bus. Finally, a methodology to choose the weights of the multi-objective function is shown. The model was solved using a genetic algorithm (GA). Dispatch frequencies are bounded, achieving a reduction of the solution space and obtaining operable intervals.

KEY WORDS: Bus Rapid Transit (BRT); Dispatch frequency; Integrated Public Transportation Systems (IPTS); Optimization Model; Waiting time; Travel time.

RESUMEN

En este artículo se aborda el problema de la búsqueda de frecuencias apropiadas de despacho de buses en un Sistema Integrado de Transporte Público (SITP). Se propone un modelo de optimización multiobjetivo para encontrar estas frecuencias de despacho de buses que transitan por un carril exclusivo en diferentes rutas. El modelo se aplicó a una reducción del SITP en la ciudad de Pereira (Risaralda, Colombia), el cual es del tipo Bus Rapid Transit (BRT), no obstante puede ser empleado en otro sistema BRT de mayor tamaño. Las frecuencias se determinan de acuerdo a la demanda de viajes estimada en una estación de buses dada, la capacidad de los buses, y el tamaño de la flota disponible. Se resuelve una función multiobjetivo que minimiza el tiempo de parada en las estaciones, los costos económicos de las empresas operadoras, y considera una penalización cuando un usuario debe esperar por un segundo bus, por falta de cupo. Finalmente, se propone una metodología para escoger los ponderadores de la función objetivo. El modelo fue resuelto con un Algoritmo Genético (AG). Las frecuencias de despacho fueron acotadas, para lograr una disminución del espacio de soluciones, obteniéndose de la solución intervalos de despacho operables. El modelo fue probado en diferentes escenarios con demanda baja, media y alta, lo que permitió evidenciar el impacto de estos en los tiempos de espera, tiempo de viaje promedio, y en general evidenciar los cambios en la calidad del servicio.

PALABRAS CLAVE: Bus Rapid Transit (BRT); frecuencias de despacho; modelo de optimización; Sistema Integrado de Transporte Público (SITP); tiempo de espera; tiempo de viaje.

RESUMO

Neste artigo aborda-se o problema da procura de frequências apropriadas de envio de ônibus num Sistema Integrado de Transporte Público (SITP). Propõe-se um modelo de optimização multi - objetivo para encontrar estas frequências de envio de ônibus que transitam por um carril exclusivo em diferentes rotas. O modelo aplicou-se a uma redução do SITP na cidade de Pereira (Risaralda, Colômbia), o qual é do tipo ônibusRapid Transit (BRT), não obstante pode ser empregue em outro sistema BRT de maior tamanho. As frequências determinam-se de acordo à demanda de viagens estimada numa estação de ônibus devido, a capacidade dos ônibus, e o tamanho da empresa disponível. Resolve-se uma função multi- objetivo que minimiza o tempo de parada nas estações, os custos económicos das empresas operadoras e considera uma penalização quando um usuário deve esperar por um segundo ônibus, por falta de vaga. Finalmente, propõe-se uma metodologia para escolher os ponderadores da função objetivo. O modelo foi resolvido com um Algoritmo Genético (AG). As frequências de envio foram disminuidas, para conseguir uma diminuição do espaço de soluções, obtendo da solução intervalos de envio operáveis. O modelo foi provado em diferentes cenários com demanda baixa, média e alta, o que permitiu evidenciar o impacto destes nos tempos de espera, tempo de viagem média, e em general evidenciar as mudanças na qualidade do serviço.

PALAVRAS-CHAVE: ÔnibusRapid Transit (BRT); Frequências de envio; Modelo de optimização; Sistema Integrado de Transporte Público (SITP); Tempo de espera; Tempo de viagem.

1. INTRODUCTION

The operative planning of an Integrated Public Transportation System (IPTS) is very important for a city, since an improvement translates to a reduction of expected time travel, impacts service quality and cost and increases trust in users, as well as, decreasesthe possibility for preference of another transport means. This is why the development of a public transportation system is one of the priorities of public management. It is also one of the most efficient ways to solve mobility problems (Luhua, Yin, & Xinkai, 2011).

The fact that it is common for travelers to experience stressful situations due to unfavorable travel conditions, such as excessive wait times and system saturation, because of the accumulated demand at stations, makes one think of planning mechanisms that will enable the improvement of conditions. These mechanisms must take into account the need for reasonable costs of operation, as well as, new demands from users (fast and reliable service, wide coverage, cheaper service and friendly drivers) (Rohani, Wijeyesekera, & Karim, 2013).

In accordance to the above, (Martínez, Mauttone, & Urquhart, 2012) establish that an appropriate decision of frequencies improves users' conditions (wait time, travel time), as well as operators' conditions (determined operational cost, mainly, for the size of the required fleet of vehicles).

In the present research paper, we determine the exit frequencies of the bus fleet for routes in a reduction of the Megabus IPTS in the city of Pereira. This system is a Bus Rapid Transit one (BRT), (Cervero, 2013). Also, the sequence of the bus stations is considered, as well as, transportation times between them, trip demands at each station, given by an Origin-Destination matrix and the size of the fleet. The applied methodology can be extended to another BRT system of greater size.

The model looks to improve the quality of the service, decrease in average travel time of passengers, average wait time at a station, financial costs of operators considering a penalty when a user has to wait for a second bus due to lack of bus seats. Lastly, a methodology is proposed for choosing the weighted averages of the multi-objective function.

This article is organized as follows. First, there is a review of the state of the art. Then, the mathematical model is formulated, after which the resolution algorithm is described. Following, results are analyzed and, finally, conclusions are provided and future work is proposed.

2. THEORETICAL FRAMEWORK

The definition of frequencies in an ITPS is a problem that has been widely addresses by different researchers. In (Ceder, 2015), it is established that the design and planning process of an ITPS should be considered in five stages. The second stage should be the definition of appropriate frequencies, after having defined the appropriate routes, sincethese depend on the demand variation(Martínez et al., 2012). The problem with optimization of routes and frequencies in public transportation systems, known as Transit Network Design Problem (TNDP), solves both the planning stages mentioned above. In this problem, the routes must be defined according to the infrastructures of streets and stops, satisfying a determined demand.

The problem of frequency configuration on a transportation network (Transit Network Frequency Setting Problem - TNFSP) is dealt with in the present research, where the total number of necessary buses for the operation of the ITPS, mainly depends on the time intervals of the departures (inversely to the frequencies). The public transportation operators try to offer maximum departure intervals in order to reduce operation costs. Passengers, on the contrary, demand minimal departure intervals in order to reduce wait times, as well as, travel times.

(Cepeda, Cominetti, & Florian, 2006), (Kov, Fukuda & Yai, 2011) address the previous problem modeling different contexts. For example, they take into account traffic congestion on the streets and look to improve the performance of each route exposed to variables of transportation time due to vehicular congestion. This also affects wait times of users and therefore, their behavior within the system. In the context of the present research, the congestion of routes is not taken into account, since is has its own runner, making it possible for wait times in the stations to be assumed as constants due to the bus' transit.

Moreover, (Qian, Luo, & Zeng, 2005)apply models which are reduced in mathematical complexity and consider a maximum of cargo allowed on buses. This conditions dispatch frequencies. The intention is to reduce, in the objective function, only the saturation of passengers but it does not take into account stop times at stations or size of thefleet, conditioning only the maximum and minimum frequencies allowed.

In (Luhua et al., 2011), a simplified mathematical model is proposed where the net social and financial benefits are maximized. Shared routs are considered for the calculation of wait time. A factor to determine the amount of persons who gets off at a determined station is used and, through an average time per person, the amount of time the bus stays at a station is calculated.

A mathematical reason is introduced which determines the percentage of passengers that have to transfer in a determined origin-destination. Also, maximum stop times at the stations are defined, as well as maximum cargo factors in the routes. The leading difficulty of this focus is related to the parameterization of the information used as input for the model.

(Huang, Ren, & Liu, 2013) consider the demand and its uncertainty as an additional factor influencing the variation of transportation times, directly affecting the time a bus takes at a station. This is why they include, in the objective function, the reduction of the variability of expected travel times for the purpose of improving system reliability. Notwithstanding, these efforts to reduce the time variability are subject to the characterization level of the potential demand of trips, in a very detailed and current manner, which implied having and information system that constantly updates the information of the operation. In (Ibeas, Alonso, dell'Olio, y Moura, 2014), congestion on the public transportation system is considered, as well as, elastic demand. They propose a model of fleet frequency optimization with different capacities (buses of different sizes). The objective is to minimize the costs of operations and the users, enabling the analysis of the impact of the dispatch configuration on changes in users' transportation means.

In (Y. Li & Si, 2014), a multi-objective optimization model is presented which includes the travel cost and benefit of the transit company, where acceptable wait time is limited to a fixed value. Dissatisfaction is generated on this factor. It also contemplates dissatisfaction of passengers who stand. Time costs are converted to monetary units, which implies estimating the parameter associated to the cost of the time unit.

In (Herbon & Hadas, 2015), a focus is presented which combines, both for passengers and operator within, a general model. The model intends to find the combination of frequencies that maximize benefits, taking into account wait and overcrowding costs, as well as, operator costs related to the size of the vehicle, empty seats and lost sales. A stochastic demand is assumed. The saturation of passengers is modeled under the concept of aggregate demand, that is, that this one considers not only the station of origin but also the other stations that are intermediary to reach a destination. However, in the formulation, a factor penalizing the unsatisfied demand that doesn't actually get on the buses and must wait for another one is not considered.

The previous formulations implicitly carrying an assignation sub-model for the purpose of adequately representing the way in which passengers use to available supply (in terms of infrastructure, line frequencies ad other predefined functioning regulations) to travel through the transit network (Cortés, Jara-Moroni, Moreno, & Pineda, 2013). These types of models are complex in their solution because they present decision variables that, not only have to do with frequency, but also with user behaviors within the system. (S. Li, Ye, y Wang, 2016) use the law of gravitation to analyze the relationship between the volume of passengers and the different frequencies of the service. The model is parameterized for the information gathered in a survey which asks about the factors that most greatly influence the choice of transportation means (bus, metro): ticket cost, travel time, comfort, convenience and distance from home to bus or metro station.

For the present research, the allocation of passengers is proportional to the service level (frequency) of each route, assuming these passengers lack a priority strategy to choose a bus, as is considered in (Spiess & Florian, 1989), (Leurent, Chandakas, & Poulhès, 2012), (Verbas, S. Mahmassani, & F. Hyland, 2016). This is mainly due to the size of the IPTS considered, since choosing one or another feasible route to his destination does not represent a significant difference for the passenger regarding travel time. When not considering the effect on congestion of routes, stop time at stations is the factor that most greatly impacts travel time, as Wirasinghe y Szplett (1984) ); Lam, Cheung y Poon (1998) describe. All of the above enables simplifying the formulation of the models, and thus the complexity of the solution.

This way, the proposed multi-objective model minimizes operation costs and travel times, penalizing, in the objective function, the amount of passengers that have to wait for a second bus, focusing on balancing factors, such as stop time at stations (according to the amount of passengers that get on and off at each station) and the cost of operation, considering as restrictions the size of the available fleet, given an origin-destination matrix.

3. MATERIALS AND METHODS

The ITPS structure has 3 routes (see Figure 1). Route 1 shares the same transportation stations (origin and destination). On route 2, both transportation routes share some stations (first and last station of each route). Route 3 is circular but divided in half (node 13), to define a route of origin and a destination route.

Figure 1

Following the mathematical model proposed by (Luhua et al., 2011) and including the amount of passengers that have to wait for a second bus, a topological structure is defined through the graphs R = (E, C), which represent each one of the three routes of the system considered, divided in two ways, destination and return, for a total of six graphs. Graphs 1 (route 1 - destination) and 4 (route 1 - return), graphs 2 (route 2 - destination) and 5 (route 2 - return), 3 (route 3 - destination) and 6 (route 3 - return) make up each one of the complete cycle.

The IPTS system is represented by frequencies that will be assigned to graphs R. The demand is given by users (passengers) that need to take trips between different stations of the system. Table 1 shows the parameters and variables used.

Table 1

The demand distribution within the system is not conditioned by a strategy of allocation, that is, it is assumed that passengers board the first feasible bus that serves them in order to get to their destination. As such, the demand at a station is distributed throughout the route proportionately to the value of the frequency assigned, according to the following expression:

The previous expression shows that if a station is shared by more than one route R in the same direction, then the demand shall be proportionately distributed at the level of service offered, 0 < P_ri < 1, and in another case, P_ri = 1, when there is only one route to choose from. Thus, it is assumed that the user does not consider information about travel times on board, the frequencies of each route, and wait times in order to make a priority choice of the route he should use.

In the present case, the demand of each station is taken as a known factor. The previous information implies that the model calculates the appropriate frequencies for a given time, without taking into account the variability of the demand on time. As such, different scenarios are considered (low, medium and high demand) and the appropriate frequencies are calculated for each one.

When considering a simplified user routes allocation model, the problem for calculating appropriate frequencies for the entire system is reduced to minimize wait time at each station.

The average wait time (TE_ij), at each station is obtained from the distribution of times between bus arrivals, given by the following expression:

The expression above assumes that, once the appropriate frequencies are found, bus arrival times remain constant as proposed by (Spiess & Florian, 1989), where average wait time of a passenger is calculated taking into account the different feasible routes the user may board.

For any passenger, wait time will be between .

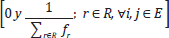It is important to note the this time strictly depends on the service level offered (f_r). This way, wait time for a second bus (TEE_ij) results from the sum of average wait time (TE_ij) and maximum wait time, .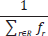

The time invested by passengers once they've boarded the bus, reached their destination (stopping at intermediate stations) and getting off at the station of their destination, will be called travel time. The run time between stations will be noted as T_rc. Stop times at stations (TP_ri), will vary according to the assigned frequencies.

The frequency is defined by the set of values f_r = {φ₁, φ₂,... φ_m}, where each element φ_i, is not negative and represents a possible frequency to be assigned to a route R composed by graphs 1 & 4, 2 & 5 and 3 & 6.

3.1. Optimization Model

The following formula minimizes a combination of objectives corresponding to users and operators, weighted by coefficients of importance that, additionally, should convert common units.

The users' objective is represented as a minimization of average travel times, (wait at one station TE_ij, wait time for a second bus TEE_ij, run time between stations T_rc, stop time at stations TP_ri) for all pair of feasible stations on routes R. The weighted averages α, β, associated to each one of the objectives depend on the priority given to the user's and operator's interests, respectively. The weighted average γ will depend on the degree of importance with which the operator wishes to reduce the amount of persons waiting for a second trip. The objective of the operators are represented by the cost of the frequencies (or level of service they represent) CF_r.

α, β affect the model in any demand scenario, while γ is only useful from a determined demand. The formula is as follows:

Subject to:

In the Equation (4), D_i− is the amount of passengers (served) that reach a station i, which is given by the origin-destination matrix D_i+, is the amount of passengers that board a bus and it is calculated as D_i+ = P_riOD_ij. In Equation (5), a level of service in accordance with the system demand is offered. In Equation (7), the service level is restricted according to size of the available fleet (M). In Equation (8), the presence of at least one bus per route is assured.

3.2. Application of Genetic Algorithm

The solution to the system of equations 3 to 8 defines a frequency for each one of the six graphs of the trajectories/trips 1 and 4, 2 and 5, 3 and 6. When we discretize the feasible values of the frequencies, we get a combinatorial optimization problem whose search space has an exponential value of |f_c|^r (Martínez et al., 2012).

Given the nonlinear complexity of the problem and its multi-objective structure, algorithm focuses, as those based on decomposition of the problem or other gradient methods, are not usually the most appropriate, (Huang et al., 2013). In the present project we searched for solutions by means of metaheuristics based on Genetic Algorithms (GA) (Holland, 1992), which enables finding solutions for non-linear problems using the Pyevolve de Python (Perone, C. S., 2009) library. Following, some generalities of the GA used are shown.

Coding. Each route R must have an assigned frequency f_r. As such, an individual (chromosome) of the population will be composed of three possible frequency values (the value of the outgoing frequency is equal to the return for each one of the routes).

Initial population. By default, a list of 500 chromosomes is created whose size coincides with the amount of routes, that is, 3. The assigned value of each gene varies between 3.5 and 15.5 minutes (converted to frequencies). These are the limits the current operation has. The values to be assigned have an interval of discretization of 0.5 minutes. Therefore, 25 possible values are obtained which could take f_r in each gene. Consistent with the above, each chromosome is initiated with random values equally distributed, for which the random number generator, Pyevolve's IntegerRangeMutator, was used.

Adaptation function. The given object function is calculated by Equation 3, according to the assigned frequencies and the object function of individuals of the population who exceed any of the restriction Equations 5, 7, and 8 are penalized.

Selection. The selection enables solutions with the best object functions to have more survival and reproduction possibilities. By default, the 20 best individuals were chosen by the PyevolveGRankSelector.

Crossings. The production of new solutions were generated combining the best existing solutions with fixed point crossing.

Convergence criterion. The Pyevolve evolve method was used. The method analyzes statistics from the last 5 generations and if they were unchanged for 20 generations, the process is detained. The average computation time was 30,405 seconds and the end uncertainty found was obtained after 2016 iterations.

4. EXPERIMENTATION, RESULTS AND DISCUSSION

Three scenarios were run under high, medium and low demands. Frequencies found were compared in each scenario against the current system operation. We were able, then, to compare operation configurations (combinations of frequencies) in terms of fleet size, average travel times (travel time it takes to complete a full cycle in each route is taken as reference) and passengers waiting for a second bus. The base system for the model is shown in Section III, Figure 1.

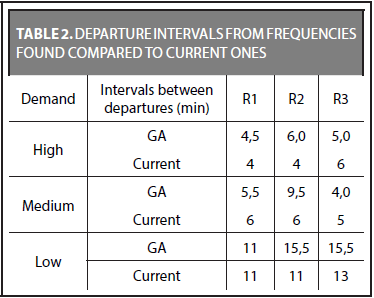
Time intervals between departures, for each one of the scenarios were obtained calculated the inverse of frequencies found, upon solving the model given in Equations 3 to 8.

Results are shown in Table 2. For comparison, intervals of departures that are currently applied in the Megabus system are also shown.

Table 3 shows how all the solutions obtained through the optimization model (resolved via GA) have a lesser objective function (with respect to average time and the required fleet size) compared to the current strategy of operation.

Table 3

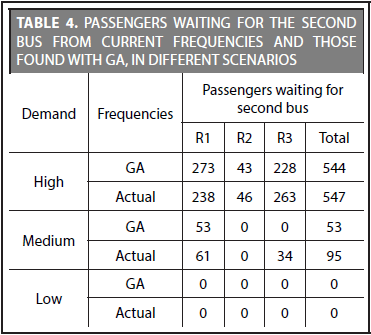
Currently, in the high demand scenario (see Table 3), the real dispatch frequency plus buses (32) would be used in the reduced system. This results in lesser travel times, if both configurations are compared. However, as is shown on Table 4, we can see the difference between the number of persons that have to wait for a second bus, under both fleet sizes, is only three passengers in the total of the three routes. This indicates that the current system is overestimating the number of buses under the high demand scenario.

In the medium demand scenario, the contrary occurs. The configuration with the three frequencies and the GA (see last column of Table 3), uses 3 buses above the current configuration, which reduces average travel times on all three routes. Notwithstanding, there is a significant difference in this case between the medium demand scenario and the GA frequency and the current one, reducing the number of passengers that need to wait for a bus from 95 to 53 (see Table 4, last column).

The low demand scenario shows little difference in both configurations (objective function, average travel time, fleet size and number of passengers waiting for a second bus). This is due to the fact that under this scenario, there are no critical points (saturation of passengers) which elevate users' costs for having to wait for a second bus or for the operators for having to offer smaller departure intervals.

We can observe that by solving the model by means of GA, we get a strategic operation overview which can improve the use of available resources. It is not necessarily true that the maximum available fleet should be used with a high demand. Other departure configurations exist with lesser fleet in use, for example, by reaching the same average number of passengers that need to wait for a second bus.

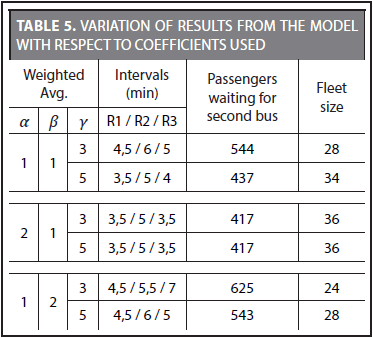
On Table 5, for the high demand scenario, the impact of different values in the coefficients α, β, γ, is shown, as well as, the objective functions (see Equation 3) on the number of passengers waiting for a second bus and the fleet size.

If α = β =1, user and operator objectives, respectively, have the same priority. The weight factorγ determines the service level in the high demand scenario, increasing the size of the fleet and reducing the average amount of passengers that have to wait for a second bus, similarly, when varying α y β, contrasts are produced in both variables analyzed. It is important to note that, in Equation 3, α, affects all scenarios, whether low, medium or high demand. While parameter γ, only affects wait time of the second bus, TEE_ij which occurs in high demand scenarios.

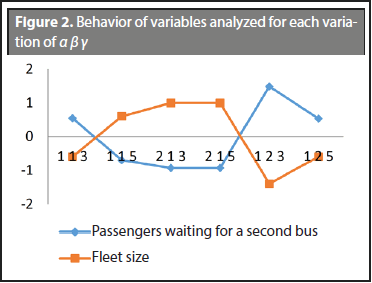
This article proposes, as a possible methodological strategy to choose the weight factors α, β, γ appropriately, graphing the behavior of the variable analyzed (passengers waiting for the second bus and fleet size), as shown in Figure 2.

To avoid the impact of the magnitude of the values and the measurement units, the values "passengers waiting for a second bus" and "fleet size" given in Table 5 were standardized (the average value was subtracted from the original value of the variable and was divided by the standard deviation).

The average of "passengers waiting for a second bus" and its standard deviation was calculated, this way standardizing the value for each combination of values assigned to the weight factors α, β, γ. So, in Graph 1, the abscissa 113, corresponds to α = 1, β = 1, γ = 3. In the ordinate, we find the value of the standardized value.

Figure 2 shows the relationship between two variables analyzed and the nature of the conflict (upon the reduction of number of passengers waiting for the second bus, the size of the fleet increases and vice versa). The graph also shows crossings in which a combination of weighted averages is found, α, β, γ, which tend to balance the interests of the user and the operator. This way, under a high demand, the weighted averages of commitment between the parties are obtained by averaging, one by one, each pair of weighted averages among which there is a crossing, obtaining, for the first crossing α = 1, β = 1, γ = 4 or for the second crossing α = 1.5, β = 1.5, γ = 4. In both cases, the result is 526 passengers waiting for the second bus and a fleet size of 29 required buses.

5. CONCLUSIONS AND FUTURE WORK

The departure time intervals defined through the appropriate frequencies are key for the improvement of the quality of public transportation. The definition of frequencies must be in accordance with what both implicated parties expect, users and operators. For the former, a reduction of average travel time and amount of users that have to wait for a second bus was taken into account. For the latter, operators, the reduction of costs of operation measured by the size of the fleet was considered.

Results obtained through GA show that with the configuration of GA (see Table 3), one does not always obtain the least average travel time (see high demand scenario), since this configuration uses less buses than the current configuration. However, one can observe that the medium demand scenario with similar fleet sizes, 22 and 19 buses, respectively, for the GA and current configurations (see Table 3), does have a marked reduction in the number of passengers expected on a second bus, from 53 passengers found according to the frequencies obtained for GA, to 95 passengers who wait for a second bus with current frequencies (see Table 4). The previous result shows that there was a better distribution of the fleet in a routes, until the number of passengers waiting for a second bus came down to zero in routes R2 and R3, in the medium demand scenario.

As future work, the proposed model in the expanded MEGABUS system will be evaluated. Research associated with the estimated demand of passengers and their behavior within the system must be addressed, given their importance in the estimation of frequencies.

ACKNOWLEDGEMENTS

The Masters in Operations and Statistics Research of the Pereira Technological University for offering all the necessary conditions to develop this paper in the most favorable environment. COLCIENCIAS for being the financing institution for the research. MEGABUS S.A. for its cooperation and disposition when offering requested information.

REFERENCES