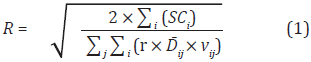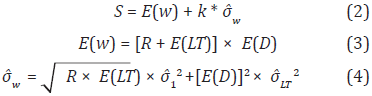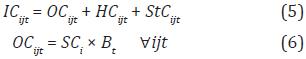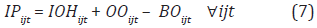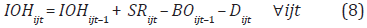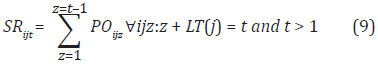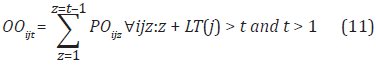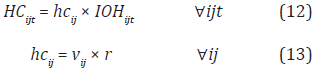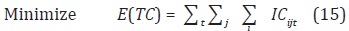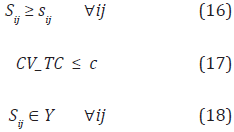Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Revista EIA
versão impressa ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.27 Envigado jan./jun. 2017
A PRACTICAL APPROACH TO DEVELOP CENTRALIZED INVENTORY POLICIES FOR 1-WAREHOUSE/N-RETAILERS SYSTEMS THROUGH SIMULATION/OPTIMIZATION
ENFOQUE PRÁCTICO PARA LA DETERMINACIÓN DE POLÍTICAS DE INVENTARIO CENTRALIZADAS EN UN SISTEMA 1-BODEGA/N-MINORISTAS A TRAVÉS DE SIMULACIÓN/OPTIMIZACIÓN
ENFOQUE PRÁTICO PARA A DETERMINAÇÃO DE POLÍTICAS DE INVENTÁRIO CENTRALIZADAS NUM SISTEMA 1-ADEGA/N-VAREJISTAS ATRAVÉS DE SIMULAÇÃO/OTIMIZAÇÃO
Liliana Delgado1, Héctor Hernán Toro2, Juan José Bravo3
1 Maestría en Ingeniería con Énfasis en Ingeniería Industrial. Profesora, Escuela de Ingeniería Industrial, Universidad del Valle, Colombia. Escuela de Ingeniería Industrial. Calle 13 No. 100 - 00. Edificio 357 - Ciudadela Universitaria Meléndez. Universidad del Valle, Cali, Colombia Tel.: (572) 3212100. Ext. 7006. Correo electrónico: liliana.delgado@correounivalle.edu.co.
2 Ingeniero industrial, Especialista en Logística y M.Sc., en Ingeniería, Universidad del Valle, Colombia.
3 Doctorado en Ingeniería. Magíster en Ingeniería de Sistemas. Universidad del Valle, Colombia.
Artículo recibido: 14-II-2014 / Aprobado: 12-VI-2017
Disponible online: 30 de agosto de 2017
Discusión abierta hasta octubre de 2018
ABSTRACT
Collaboration in supply chain management has become a key success factor. Operational strategies in which each node operates under optimum operating conditions have proven to be inadequate, and it has been determined that a strategy of coordination of the chain as a whole is best perceived. The One-warehouse N-retailer chain typically operates with each retailer placing orders to the warehouse according to its own inventory policies. In this article we study the case where the warehouse makes centralized decisions, defining retail inventory replenishment policies using the (R, s, S) periodic review policy. The optimal policy is determined using a heuristic that combines Monte Carlo simulation with Optimization, based on an implementation in a spreadsheet scheme. The approach is tested in one case, showing reductions in the relevant inventory costs when centralized versus decentralized approaches are compared.
KEY WORDS: One-warehouse/N-retailers, Simulation/Optimization, Periodic Review, Joint Inventory Policy.
RESUMEN
En la administración de la cadena de suministro la colaboración se ha convertido en factor clave de éxito. Estrategias de operación en las cuales cada nodo opera en condiciones óptimas han probado ser inadecuadas, y se ha determinado que es mejor una estrategia de coordinación de la cadena como un todo. Una cadena de 1-Bodega/N-Minoristas típicamente opera con cada minorista haciendo sus pedidos a la bodega de acuerdo con sus propias políticas de inventario. En este artículo se estudia el caso en el que la bodega toma decisiones centralizadas, definiendo las políticas de reabastecimiento del inventario de los minoristas usando la política de revisión periódica (R, s, S). La política óptima se determina usando una heurística que combina simulación Montecarlo con Optimización, basada en una implementación en hoja electrónica. El enfoque se prueba en un caso, observándose reducciones en los costos relevantes del inventario cuando se comparan los enfoques centralizado versus el descentralizado.
PALABRAS CLAVE: 1-Bodega/N-, Simulación/Optimización, Revisión Periódica, Política de Inventario Conjunta.
RESUMO
Na administração da corrente de fornecimento a colaboração converteu-se em fator chave de sucesso. Estratégias de operação nas quais a cada nó que opera em condições óptimas de operação têm provado ser inadequadas, e se determinou que é melhor uma estratégia de coordenação da corrente como um tudo. Uma corrente de 1-adega/NVarejistas tipicamente opera com a cada varejista fazendo seus pedidos à adega de acordo a suas próprias políticas de inventário.Neste artigo estuda-se o caso no que a adega toma decisões centralizadas, definindo as políticas de reabastecimento do inventário dos varejistas usando a política de revisão periódica (R, s, S).A política óptima determinase usando uma heurística que combina simulação Montecarlo com Otimização, baseado numa implementação em folha eletrônica.O enfoque prova-se num caso, observando-se reduções nos custos relevantes do inventário quando se comparam os enfoques centralizado versus o descentralizado.
PALAVRAS-CHAVE: Uma adega N pontos de venda, simulação - otimização, revisão periódica, política de inventário conjunta.
1. INTRODUCTION
One of the problems in which the literature has developed great interest is the so-called One warehouse - N retailers problem (OWNR). This system is clearly stated in the article written by Pukcarnon et al (2014) in which they explain that the OWNR system is a two-step system that seeks to determine the optimal inventory replenishment policies of the retailers and the central warehouse so that the total relevant inventory cost be minimal. They also mentioned that the randomness of the demand is an increasingly important factor to consider.
The most known methodology to address this kind of problem is the Schwarz Heuristic (1973), from which new heuristics have been developed. For instance, Abdul-Jalbar et al (2010) and Pukcarnon et al (2014) have proposed heuristics that offer results with a broader control of variables. Some articles have dealt with deterministic demand. Abdul-Jalbar et al. (2010) considers that customer demand arrives at each retailer location at a constant rate. Senyigit & Akkan, (2012), presented a new heuristic with deterministic demand where they compared the replenishment cost with the inventory holding cost. They also compared its heuristic with the one by Abdul-Jalbar et al. (2010), and the computational results showed that the new heuristic exhibits a better performance. On the other hand, Gayon et al (2016) analyzed the problem with deterministic variable demand where shortages were allowed.
The use of stochastic demand was considered by Pukcarnon et al., (2014) who used a continuous review inventory policy with a combined simulation optimization algorithm. It is not common to find articles with both stochastic demand and lead time as the present article is going to show.
Regarding the consideration of (R, s, S) periodic review inventory policies, that will be used in next sections, Monthatipkula & Yenradee (2008) tested the (R, s, S) inventory policy and contrasted it against the Inventory Distribution Planning they proposed. They selected this periodic review policy because of the good performance it exhibits in terms of the total inventory cost. This control policy is well described in Whybark & Yang (1996) while Schneider et al. (1995) showed a good approximation for parameter setting for this control policy using simulation procedures.
The present article is going to face the OWNR problem with both stochastic demand and lead times under an (R, s, S) periodic review inventory policy, using simulation-optimization strategies supported by an easy-to-implement algorithm. To the best of our knowledge the used solution strategy has not been considered in the literature yet for the problem under study.
In addition, the general approach is going to focus on the centralized approach where the warehouse controls de information about inventory position and demand of all retailers and products. Cheng and Zheng (1997) analyzed the OWNR problem with a centralized continuous review policy under stochastic demand dealing with a poisson process. They exposed that many companies, in light of the current modern technology can share and deliver information in a more precise way. The cooperation and well established information systems need to be present in this kind of systems. The present article considers that the central warehouse has enough information, and all the cooperation considerations needed to control the inventory replenishment policies of its retailers.
The section 2 will present the problem statement, while sections 3, 4 and 5 will show the heuristic strategy used. Section 6 will state the results that were obtained and finally some conclusion will be presented in section 7.
2. PROBLEM STATEMENT
This article faces the problem of one warehouse which controls the inventory policies of retailers (customers), which exhibit both a stochastic demand and a random lead time between the warehouse and retailers. We implement the Joint Replenishment Policy (JRP) with periodic review inventory system, where the review period (that is called R) is the length of time at the end of which the warehouse checks the inventory position of all retailers and products. Therefore, the system is also a multiperiod, multiproduct problem and the inventory control policy that we have selected to apply is the (R, s, S), where s is the reorder point and S is the maximum inventory allowed of a product at the retailer location. The policy works with the following dynamics: once the end of the period R has arrived then the inventory position of the products in each retailer is revised and a decision is taken: if the inventory of any product is below the reorder point (s) then the warehouse sets an order for the product that is equal to the difference between the maximum inventory (S) and the current inventory position at the review moment.
This system can exist when the warehouse and retailers share information about two kinds of data sets: demand and inventory levels. In this case the retailers rely on the control capacity of warehouse related to the inventory system. Thus, the core issue is the centralized strategy to manage the inventory decisions.
For the warehouse, the optimal inventory policies for all products and all retailers can lead to a minimum Total Inventory Cost.
If we set "i" as the subindex referred to products and "j" the subindex of retailers, then the optimal policy must obtain the optimal values of R, sij for all i,j, and Sij also for all i,j, assuming that R is a common parameter. However, to determine the optimal values for these three type of parameters is a very complex task (Silver et al, 1998) and this difficulty can be stated at a greater extent if we consider the stochastic nature of the problem under study.
In the next section we define the heuristic procedure used which is a combination of simulation and optimization strategies.
3. GENERAL HEURISTIC PROCEDURE
Due to the complexity of the problem, we propose a heuristic that starts from the generation of fixed values for R and sij, while using an only decision variable called Sij.
In order to find the optimal value of Sij, considering the stochastic nature of the problem, it was firstly designed a montecarlo simulation procedure supported by a spreadsheet. Basically, the spreadsheet is capable with a given values of R, sij and Sij to calculate the total Inventory cost of the retailers inventory system, which includes the inventory holding cost, stockout cost, and the ordering cost.
The Figure 1 illustrates the procedure that considers the montecarlo dynamics where the demand and lead time scenarios are being generated.
According to Figure 1, the procedure begins with the values of R and s, which are initially given. In next section we show how to appropriately determine these values that can be even defined as a subjective management decision. It is worth mentioning that the solution framework is general enough so that different values for R and s can be tested as alternatives.
Observe that n is the number of times that the random variables have to be generated for each set Sij, while m is the number of times that the set Sij have to be generated. Note also that one of the information that is to be collected is the Coefficient of Variation of the Total Cost, because this data will be important in the optimization process as it will be seen.
With the montecarlo simulation implemented in Excel, the optimization of Sij was conducted by using of CrystalBall software with the optimizer OptQuest that goes with it. The general optimization procedure is depicted in Figure 2.
4. ABOUT THE INITIALIZATION OF R, s AND S
The value of R is usually related to administrative requirements, and it implies not only when to review the inventory but also how often the warehouse would potentially have to make deliveries. However, if the company has not a clear administrative rule to define it, it can be used the formulation taken from Silver et al. (1998) and Ballou (2004), as follows:
Where:
SCi: Setup cost for ordering product i [$/order].
r: inventory holding cost [%/time period].
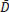 ij : average demand of product i for each customer j during the planning horizon [units/time period].
ij : average demand of product i for each customer j during the planning horizon [units/time period].
vij: cost of product i for the customer location j [$/unit].
Note that Equation (1) takes into account all products used by all customers thank to the control that the central warehouse has over the whole inventory. This is only possible in case of a centralized scheme. However, there could have other review strategies, possible to implement under inventory centralized decisions.
On the other hand, the value of the reorder point s can be viewed as a proxy of the safety stock, which is in turn a function of the required service level and the variability that the system has to face. Again, it is possible to define s considering administrative requirements (service level).
On the other hand, in order to analytically define the initial value of S, based on the assumptions of both stochastic demand and lead times, it can be used the following Equations (2), (3) and (4), the last one proposed by Ross (1993) for composite stochastic processes:
Where:
E(w): Expected value of demand between two consecutive review moment (units)
k: Safety factor for the desired service level (see Silver, 1998)
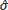 w: Standard deviation of demand between two consecutive review moment (units)
w: Standard deviation of demand between two consecutive review moment (units)
R: Inventory review period (time units)
E(LT): Expected value of lead time (time units)
E(D): Expected demand rate value (units per time unit)
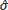 1: Standard deviation of demand forecast errors (units)
1: Standard deviation of demand forecast errors (units)
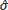 LT: Standard deviation of lead time (time units)
LT: Standard deviation of lead time (time units)
5. ANALYTICAL BACKGROUND
In this section, the equations that support the spreadsheet simulation-optimization process are shown. First, the stochastic parameters are defined:
Dijt: demand of product i for the customer j in period t [units].
LTijt: lead time of product i for the customer j for orders generated in period t [days].
The Inventory Cost (ICijt) is comprised of several components, as follows:
Where,
OCijt = ordering cost for product i and customer j in period t [$]
HCijt = inventory holding cost for product i and customer j in period t [$]
StCijt = stockout cost for product i and customer j in period t [$]
SCi = Setup cost for ordering product i [$/ order]
Bt = a binary variable that takes the value 1 when products are ordered in period t, and 0 otherwise.
The decision about ordering each product depends on the inventory control policy. For the case of an (R, s, S) system, if the inventory position is checked at a period t and if it is at or below the reorder point s, an order would be placed. The order size corresponds to the difference between S and the inventory position. The inventory position was calculated with the following expression:
Where,
IPijt = inventory position for product i at customer j and period t [units]
IOHijt = inventory on hand of product i at customer j and period t [units]
OOijt = On-order inventory of product i pending to arrive at customer j in period t [units]
BOijt = backorder of product i at retailer j in period t [units]
Where,
SRijt = scheduled receipts of the product i arriving at customer j at the beginning of period t [units]
Where:
POijz = order of product i placed for customer j at period z [units]
Figure 3 is used to illustrate the meaning of POijz and SRijt just introduced. The line numbered as 1 in Figure 3 shows a planned order that was placed in period 1 to certain customer. In this moment the order is called PO, but four days later the order arrives at the customer location becoming an SR. Other possible orders are illustrated as well to better explain the calculation of orders arriving at certain period of time.
Following the inventory policy, if an order needs to be placed, then the order size is:
The pending orders at t, are defined as:
Note that in Equation (9) we had z:z+LT(j) = t. Instead, in Equation (11) we have z:z+LT(j) > t, because OOijt means that the order has not arrived yet at the time period t.
The inventory holding cost is expressed as:
Where,
hcij = holding cost in the customer site j for each unit of product i [$/unit].
vij = cost of product i for the customer j [$/unit].
r = inventory cost rate [%/day].
Finally, the stockout cost is defined by the following expression:
Where,
stci = cost for each unit that has not been delivered yet [$/unit].
Regarding the optimization procedure, the only variable that was defined to be optimized was:
Sij = maximum inventory level of product i for customer j [units].
Objective function
Subject to:
Where,
E(TC) = Expected total cost [$]
ICijt = inventory cost for product i and customer j in period t [$]
sij = reorder point for product i for customer j [units]
CV_TC = coefficient of variation of the total cost
c = maximum coefficient of variation allowed
Y = represents a region defined by the other constraints of the inventory system under study
Expressions (16) and (17) were considered in Figure 2. Constraint (17) imposes a maximum value for the coefficient of variation of the total cost, guaranteeing that the mean minimum value of the objective function it is also a stable value. Recall that some parameters are random (demand and lead times) and hence the objective function is a random variable, and it is optimized its mean value by defining multiple scenarios for the random parameters. For a given inventory policy, if we generate demands and lead times following their corresponding probability distributions it is possible to generate an empirical probability distribution for the total cost.
6. COMPUTATIONAL EXPERIMENTS
The model was implemented for a case study with 15 customers, one central warehouse, 9 types of products and a planning horizon of 7 days. The value of R obtained by using Equation (15) was 1 day. Without loss of generality, some probability distributions were selected. The normal distribution was used to simulate demand values while the lead times were modeled by empirical discrete distributions. The simulation model has 1.830 stochastic input variables and one output variable, as well as 135 decisions variables (resulting from the order-up-to level of 9 products for each of the 15 customers, so 9×15=135 variables), 136 constraints (the upper limit of each decision variable plus the upper limit on the coefficient of variation of the objective function) and 1 objective function (the total cost).
Six scenarios were considered as shown in Table 1.
In Table 1, the first scenario is the base one, and the rest are used to make a contrast and give some relevant conclusions. Observe that another inventory policy is to be tested: the traditional (R,S) where the inventory is revised every R units of time and an order is always placed and its size corresponds to the difference between the maximum inventory (S) and the current inventory position. Scenarios (d), (e) and (f) are considered as a proxy of a decentralized approach, where each customer defines its own moment to review the inventory position.
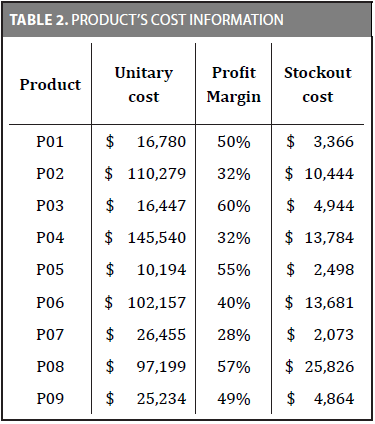
A hypothetical data set was used to test the procedure and the currency was established as Colombian Pesos. The interest rate was fixed at 24% annual. The lead times were generated by using a discrete uniform distribution with lower and upper bounds equal to 2 and 5 days respectively. The ordering cost equals $31.285. Table 2 gives cost information associated to the products been analyzed. Table 3 shows the mean daily demand and coefficient of variation (in parenthesis) for each pair customer/product.
Using Crystal Ball and its OptQuest add-in, the optimization procedure was conducted for 1.000 iterations, each of them with a sample size of 100 scenarios of the stochastic parameters. Results are presented in the Tables 4 and 5.
Table 4 presents the total cost for each scenario, before and after running the optimization procedure. Observe that the minimum total cost was obtained for the base scenario as expected. Table 3 also illustrates the savings that are attainable by running the optimization process.
Table 5 shows the results when changing from a decentralized to a centralized approach. For the scenario in which each customer is allowed to define their inventory policies the value of R ranges from 3 to 8 days.
Tables 4 and 5 shows that under a periodic review strategy of inventories, the centralized approach exhibits a better performance, and that the (R, s, S) policy is the most relevant in terms of costs with the same service level. Moreover, the use of simulationoptimization strategies as a combined methodology leads with better solutions with large savings when compared with montecarlo simulation strategies.
7. CONCLUSIONS
This paper analyses the definition of inventory replenishment policies in the One-warehouse/Nretailer problem, dealing with the (R, s, S) periodic review policy under a centralized approach, where the warehouse controls the inventory policy strategies of retailers. The results show that the centralized approach exhibits a better performance than the decentralized one, and also that the (R, s, S) periodic review strategy performs better than the (R, S) policy traditionally implemented. Regarding the simulation-optimization method used in this paper, the results have shown that the solutions can imply important savings ranging from 20% to 75% with respect to the case when Montecarlo Simulation is only used. Future research can be done by exploring new problem instances, in order to clarify the benefits that simulation-optimization strategies can obtain. In addition, this research framework can serve to other kinds of research maybe focused on different types of inventory policies, like continuous review policies.
REFERENCES
Abdul-Jalbar, B., Segerstedt, A., Sicilia, J., & Nilsson, A. (2010). A new heuristic to solve the one-warehouse N-retailer problem. Computers & Operations Research, 37(2), 265-272. [ Links ]
Ballou, R.H. (2004). Logistica: administración de la cadena de suministro, Pearson Education. [ Links ]
Chen, F, and Zheng, Y, (1997). One-warehouse multiretailer systems with centralized stock information. Operations Research, 45 (2), 275-287. [ Links ]
Gayon, J., Massonnet, G., Rapine, C., & Stauffer, G. (2016). Constant approximation algorithms for the one warehouse multiple retailers problem with backlog or lost-sales. European Journal of Operational Research, 250(1), 155-163. [ Links ]
Monthatipkula, C., and Yenradee, P (2008). Inventory/distribution control system in a one-warehouse/multi-retailer supply chain. Int. J. Production Economics 114 (2008) 119-133. [ Links ]
Pukcarnon, V., Chaovalitwongse, P., & Phumchusri, N. (2014). The Can-Order Policy for One-Warehouse N-Retailer Inventory System: A Heuristic Approach. Engineering Journal, 18(4), 53-72. [ Links ]
Schneider, H., Rinks, D.B., Kelle, P., 1995. Power approximations for a two-echelon inventory system using service levels. Production and Operations Management 4, 381-400. [ Links ]
Schwarzt, L. B. (1973). A simple continuous review deterministic One Warehouse N retailer Inventory Problem. Management Science, 19, 555-566. [ Links ]
Senyigit, E., & Akkan, H. (2012). A New Heuristic for one Warehouse and N Retailers Problem. Procedia - Social and Behavioral Sciences, 62, 656-660. [ Links ]
Silver, E. A., D. F. Pyke, et al. (1998). Inventory management and production planning and scheduling, Wiley New York. [ Links ]
Whybark, D.C., Yang, S., 1996. Positioning inventory in distribution systems. International Journal of Production Economics 45, 271-278. [ Links ]