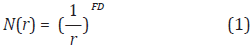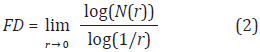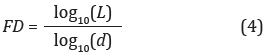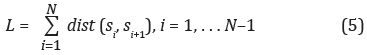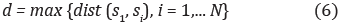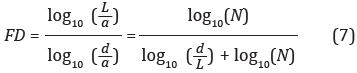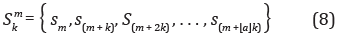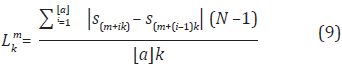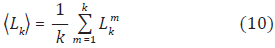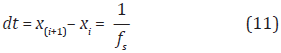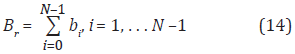Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Revista EIA
Print version ISSN 1794-1237
Rev.EIA.Esc.Ing.Antioq no.27 Envigado Jan./June 2017
COMPARATIVO DE LOS ALGORITMOS DE DIMENSIÓN FRACTAL HIGUCHI, KATZ Y MULTIRESOLUCIÓN DE CONTEO DE CAJAS EN SEÑALES EEG BASADAS EN POTENCIALES RELACIONADOS POR EVENTOS
COMPARISON OF HIGUCHI, KATZ AND MULTIRESOLUTION BOX-COUNTING FRACTAL DIMENSION ALGORITHMS FOR EEG WAVEFORM SIGNALS BASED ON EVENT-RELATED POTENTIALS
COMPARATIVO DOS ALGORITMOS DE DIMENSÃO FRACTAL HIGUCHI, KATZ E MULTI-RESOLUÇÃO DE CONTAR AS CAIXAS EM SINAIS EEG BASEADAS EM POTENCIAIS RELACIONADOS POR EVENTOS
Santiago Fernández Fraga1, Jaime Rangel Mondragón2
1 Estudiante Doctorado en Ciencias de la Computación. Instituto Tecnológico de Querétaro. Querétaro, México. Av. Tecnológico s/n esquina Mariano Escobedo. Colonia Centro. C.P. 76000. Querétaro, México / Tel.: +52 (442) 2274424. Correo electrónico: sfernandez@mail.itq.edu.mx.
2 Doctorado en Matemáticas Aplicadas. Universidad Autonoma de Querétaro. Querétaro, México.
Artículo recibido: 08-VII-2016/ Aprobado: 15-V-2017
Disponible online: 30 de agosto de 2017
Discusión abierta hasta octubre de 2018
RESUMEN
La obtención de información por medio de la medición de señales registradas durante diferentes procesos o condiciones fisiológicas del cerebro es importante para poder desarrollar interfaces computacionales que traduzcan las señales eléctricas cerebrales a comandos computacionales de control. Un electroencefalograma (EEG) registra la actividad eléctrica del cerebro en respuesta al recibir diferentes estímulos externos (potenciales por eventos). El análisis de estas señales permite identificar y distinguir estados específicos de la función fisiológica del cerebro. La Dimensión Fractal se ha utilizado como una herramienta para el análisis de formas de ondas biomédicas, en particular se ha utilizado para determinar la medida de la complejidad en series de tiempo generadas por EEG. El presente documento pretende analizar la base de datos HeadIT de series de tiempo biomédicas obtenidas por EEG a las cuales se obtendrán la FD por medio de los métodos Higuchi, Katz y Multi-resolución de Conteo de Cajas, que muestre la relación entre el método para la obtención de la Dimensión Fractal y la condición fisiológica de la señal basada en Potenciales Cerebrales Relacionados por Eventos.
PALABRAS CLAVE: Dimensión Fractal, Higuchi, Katz, Multiresolución de Conteo de Cajas, señales EEG.
ABSTRACT
Obtaining information through the measurement of brain signals recorded during different processes or physiological conditions is important for developing computer interfaces that translate electrical brain signals to computer control commands. Electroencephalography (EEG) records the electrical activity of the brain in response to its receipt of different external stimuli (potential events). Analysis of these signals makes it possible to identify and distinguish specific states of physiological brain function. The Fractal Dimension has been used as a tool for biomedical waveform analysis, in particular to measure the complexity of time series generated by EEG. This paper aims to analyze a database (HeadIT) of biomedical time series obtained by EEG for which the fractal dimension will be obtained by the Higuchi, Katz and multiresolution box-counting methods, showing the relationship between the method for obtaining the fractal dimension and the physiological condition of the brain event-related potentials.
KEY WORDS: Fractal Dimension, Higuchi, Katz, multiresolution box-counting, EEG waveforms.
RESUMO
A obtenção de informação por médio da medida de sinais registados durante diferentes processos ou condições fisiológicas do cérebro é importante para poder desenvolver interfaces computacionais que traduzam os sinais elétricos cerebrais a comandos computacionais de controle. Um eletroencefalograma (EEG) regista a atividade elétrica do cérebro em resposta ao receber diferentes estímulos externos (potenciais por eventos). A análise destes sinais permite identificar e distinguir estados específicos da função fisiológica do cérebro. A Dimensão Fractal utilizou-se como uma ferramenta para a análise de formas de ondas biomédicas, em particular utilizou-se para determinar a medida da complexidade em séries de tempo geradas por EEG. O presente documento pretende analisar séries de tempo biomédicas obtidas por EEG às quais obter-se-ão a FD por médio dos métodos Higuchi, Katz e Multi-resolução de Conteo de Caixas, que mostre a relação entre o método para a obtenção da Dimensão Fractal e a condição fisiológica do sinal baseado em Potenciais cerebrais relacionados por eventos.
PALAVRAS-CHAVE: Dimensão Fractal, Higuchi, Katz, Multi resolução da conta de Caixas, sinais EEG.
1. INTRODUCCIÓN
Las interfaz cerebro computadora (Brain Computer Interface, BCI) monitorean la actividad cerebral del usuario y traducen sus "intenciones" en órdenes sin activar ningún músculo o nervio periférico (Millán et al, 2014). Para el desarrollo de los sistemas BCI es necesario encontrar herramientas que permiten homogenizar la condición fisiológica de los usuarios para poder llevar dichos sistemas a un control basado en la "intención" del usuario. Las señales eléctricas obtenidas por medio de electroencefalograma (EEG) se utilizan para evaluar clínicamente la actividad cerebral. Los sistemas BCI interpretan el comportamiento fisiológico del cerebro (intensión) a través de potenciales eléctricos relacionados con eventos (Related Evoked Potentials, ERP), para crear comandos computacionales que permitan el desarrollo de aplicaciones de control de dispositivos electrónicos. En el presente documento se analizaran señales de EEG biomédicas obtenidas en respuesta a estímulos externos visuales (Visual Evoked Potencial, VEP), las cuales son representadas como secuencias temporales (series temporales) de potenciales eléctricos que se obtienen por medio de electrodos colocados en el cuero cabelludo.
Unas de las herramientas utilizadas para el análisis de las señales EEG es la Dimensión Fractal (Fractal Dimention, FD). Término propuesto por Mandelbrot (1983) el cual se aplica a objetos en el espacio o a fluctuaciones en el tiempo que poseen una forma de auto-similitud y no pueden ser descritas en una sola escala de medida absoluta. La FD se refiere a un número no entero o dimensión fraccional de cualquier objeto.
Definimos a (X, d) como un espacio métrico donde el espacio X es un conjunto de objetos llamados puntos y d una métrica como una función d : X × X 
 , la cual mide la distancia entre un par de puntos (x, y) en el espacio X. Consideremos el número N(r) como la cantidad de círculos de radio fijo máximo r necesarios para cubrir completamente a X, X
, la cual mide la distancia entre un par de puntos (x, y) en el espacio X. Consideremos el número N(r) como la cantidad de círculos de radio fijo máximo r necesarios para cubrir completamente a X, X 
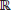 2. N(r) es inversamente proporcional a r. Podemos decir que
2. N(r) es inversamente proporcional a r. Podemos decir que
cuando el valor de r 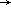 0 podemos encontrar el número más pequeño de áreas cerradas de radio r necesarias para cubrir al espacio X, entonces la FD está definida por
0 podemos encontrar el número más pequeño de áreas cerradas de radio r necesarias para cubrir al espacio X, entonces la FD está definida por
Análisis FD se utiliza con frecuencia en el procesamiento de señales biomédicas, incluyendo el análisis de EEG, lo cual ha permitido estudiar la dinámica caótica del cerebro (Lutzenberger et al, 1995) e identificar y distinguir estados específicos de sus funciones fisiológicas (D. Easwaramoorthy y R. Uthayakumar, 2010), en particular se ha utilizado para determinar la medida de la complejidad en las señales de EEG (B. S. Raghavendra y D. N. Dutt, 2009).
El análisis de FD se utilizado con frecuencia en el procesamiento de señales biomédicas, incluyendo el análisis de EEG (Bachmann et al, 2013), (Baljekar y Patil, 2012), (Bojié et al, 2010), (Jevtic, y Paskas, 2011), (Esteller et al, 2001), (Georgiev et al, 2009), (Harne, 2014), (Katz, 1988), (Khoa y Toi, 2012), (Loo et al, 2011), (Paramanathan y Uthayakumar, 2008), (Polychronaki et al, 2010), (Raghavendra y Dutt, 2009) y (Spasicmet al, 2011) así como en una variedad de sistemas de ingeniería (Cervantes-De la Torre et al, 2013), (Gálvez et al, 2013), (Martins et al, 2012), (Millán et al, 2014), (Perlingeiro et al, 2005). El presente documento se centra en señales experimentales derivados de EEG y los algoritmos propuestos son los algoritmos de Higuchi, Katz, y el método de Multi-resolución de Conteo de Cajas (MRCC); sus resultados son ampliamente aplicables a cualquier tipo de señal.
La implementación de los algoritmos de dimensión FD se han implementado en diferentes estudios con señales de EEG; Polychronaki et al (2010) para la detección del inicio de crisis epilépticas; Easwaramoorthy and Uthayakumar (2010) utilizó señales EEG para analizar la actividad cerebral durante procesos cognitivos (lectura, atención, memoria, etc.); Loo et al (2011) utilizó señales EEG basadas en imágenes motoras para sistemas BCI; Bashashati et al (2003) se basó en métodos de FD para identificar los componentes de control de las señales de EEG en sistemas BCI; Esteller et al (2001) y Raghavendra y Dutt (2010, 2009) utilizaron señales sintéticas como series de datos para el cálculo de FD basándose en el comportamiento fractal similar al de las señales de EEG.
La relación de la condición fisiológica de la señales biomédicas de EEG, basadas en ERPs, y el método para medir la complejidad de la señal, permitirá mostrar en forma general como los métodos de FD para el análisis de señales pueden ser implementados en los sistemas BCI, donde parte de los retos es que la condición generalizada de los usuarios sea interpretada de forma específica por algún dispositivo de control. En el presente documento se analizará la complejidad de señales biomédicas de EEG en periodos cortos de tiempo (fractogramas) por medio del cálculo de la FD utilizando los algoritmos de Higuchi, Katz y Multi-resolución de Conteo de Cajas (MRCC).
2. METODOLOGÍA
2.1. Experimentación
Las señales analizadas en éste trabajo se registraron durante la prueba denominada prueba de las 5 cajas, donde las señales obtenidas se basaron en VEP descritos por S. Makeig (1999). El estudio se realizó con 15 personas voluntarias diestras, 12 hombres y 3 mujeres entre 19 y 53 años con una media de 30 años; 12 con visión normal y 3 con visión corregida.
En la prueba de las cinco cajas, los usuarios fijaban su vista en una cruz, por encima de la cual se exhibieron constantemente cinco cajas (cuadros) Figura 1. En cada bloque de prueba de 76 s, una de las cajas (caja gris) fue de diferente color. La ubicación de éste cuadro fue de manera aleatoria durante los periodos de pruebas. Una serie de círculos se presentaron brevemente en cualquiera de las cinco cajas en un orden aleatorio. Se le pidió al usuario responder presionando un botón lo más rápidamente posible cada vez que un disco apareciera en uno de los cuadros.
Los datos de EEG se obtuvieron de 29 electrodos en el cuero cabelludo montados en una maya de electrodos estándar (ElectroCap, Inc.) con base al sistema Internacional 10-20 modificado como se muestra en la Figura 2, y de dos electrodos perioculares colocados debajo del ojo derecho y en el canto externo izquierdo. Los datos fueron muestreados a 256Hz con un filtro pasa banda analógico de 0.01-50 Hz. Posteriormente, las respuestas fueron digitalmente filtradas con un filtro paso bajo por debajo de los 40 Hz antes del análisis (S. Makeig et al., 2004).
2.2. Selección de datos
Los datos (obtenidos de The Human Electrophysiology, Anatomic Data, and Integrated Tools, HeadIT; perteneciente al Swartz Center for Computational Neuroscience, SCCN de la Universidad de California en San Diego, Estados Unidos de América; desarrollado y fundado por U.S. National Institutes of Health grants R01-MH084819, Makeig Grethe PIs y R01-NS047293, Makeig PI) están organizados en sesiones, cada sesión representa la implementación de la prueba de las cinco cajas con un número aleatorio de eventos, cada sujeto de estudio realizó una o varias sesiones. La información obtenida durante el experimento genera un EEG de 32 canales los cuales fueron obtenidos por medio del software EEGLABv7.1.3.13b, software de libre distribución bajo la licencia de software libre GNU GPL, desarrollado por Delorme y Makeig (2004).
1. Señales de onda y series de tiempo
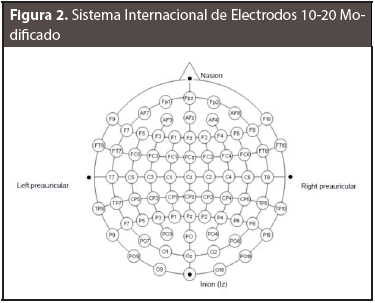
Las señales EEG obtenidas de un conjunto de electrodos fijos en la corteza cerebral son series de tiempo irregulares representadas en forma de onda. Consideremos a la forma de onda como una serie de tiempo discreta de la forma
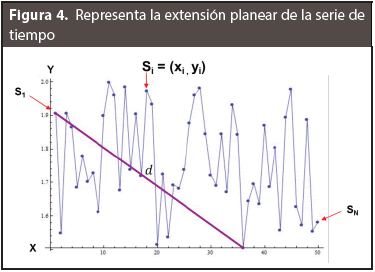
donde N representa el total de puntos de la serie y s los valores sucesivos del EEG. La gráfica de la serie es representada como si = (xi, yi), i = 1,2, ... N, donde xi son los valores de las abscisas y yi los valores de las ordenadas, Figura 3. En las formas de onda de las series de tiempo si = ti, aumentan monotónicamente en el instante de tiempo en la que se muestrea la onda (Dubravka et al, 2011).
Los algoritmos de FD permiten interpretar el comportamiento caótico en las series de tiempo irregulares representadas en forma de señales de onda y discriminar los patrones en función de la similitud (P. Paramanathan y R. Uthayakumar, 2007).
2. Algoritmo de Katz
El cálculo de la FD propuesto por Katz (1988) se describe como la proporción de la longitud de la curva L, calculado como la suma de las distancias Euclidena entre dos puntos sucesivos, dividida por la distancia máxima d de cualquier punto en la trama en cuestión desde el primer punto (M. Katz, 1988). Podemos interpretarlo como la relación de la longitud total de la curva en comparación con la línea recta correspondiente a la distancia Euclidiana máxima desde el primer punto. El Algoritmo define a la FD como
donde L es la longitud total de la curva o la suma de las distancias euclidianas entre puntos sucesivos
y d es el diámetro (o extensión planar) de la curva, es decir, la distancia entre el primer punto de la secuencia y el punto más lejano de la secuencia (Figura 4), d puede ser expresada como
Katz propuso normalizar d y L por la longitud de la etapa media o la distancia promedio entre puntos sucesivos, 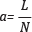 , donde N es el número de pasos en la curva. De esta manera (4) se convierte en
, donde N es el número de pasos en la curva. De esta manera (4) se convierte en
3. Algoritmo de Higuchi
Para el algoritmo de Higuchi se considera a S como la serie de tiempo a analizar. El algoritmo consiste en formar nuevas formas de onda, subsecuencias de S, por muestras de la selección iterativa que difieren en su punto de origen m y su factor de retardo o intervalo de tiempo discreto entre puntos k (delay). Primero seleccionamos el factor de retardo máximo, kmax así, por cada factor de retardo k, donde k varía de 1 a kmax. Formamos k's series de tiempo nuevas, Skm definidas como
donde 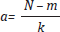 , m = 1,2,..., k; k = 1,..., kmax, m y k son enteros positivos.
, m = 1,2,..., k; k = 1,..., kmax, m y k son enteros positivos.
Por ejemplo, si k = 3 y N = 100, las series de tiempo construidas están definidas como
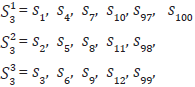
para cada serie de tiempo Skm construida, su longitud promedio Lkm está definida por N
donde N es la longitud total de la secuencia de datos S y (N -1)/(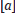 k) es el factor de normalización para la longitud de la subsecuencia.
k) es el factor de normalización para la longitud de la subsecuencia.
Posteriormente calculamos la longitud media de la curva para cada k, 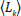 como el valor medio de las Lkm de las k subsecuencias y está definido por
como el valor medio de las Lkm de las k subsecuencias y está definido por
La longitud media 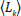 de las serie S se obtiene por el promedio de todas las longitudes Lkm de las k subsecuencias. Éste procedimiento se repite para cada rango de k desde 1 hasta kmax (G. E. Polychronaki et al, 2010).
de las serie S se obtiene por el promedio de todas las longitudes Lkm de las k subsecuencias. Éste procedimiento se repite para cada rango de k desde 1 hasta kmax (G. E. Polychronaki et al, 2010).
Si 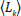
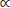 k-FD, entonces la curva es un fractal con dimensión FD, en ese caso la gráfica log10(
k-FD, entonces la curva es un fractal con dimensión FD, en ese caso la gráfica log10(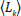 ) vs log10(k) debe aproximarse a una recta con pendiente igual a -FD, por lo que la FD se puede calcular por una aproximación lineal de mínimos cuadrados (G. E. Polychronaki et al, 2010).
) vs log10(k) debe aproximarse a una recta con pendiente igual a -FD, por lo que la FD se puede calcular por una aproximación lineal de mínimos cuadrados (G. E. Polychronaki et al, 2010).
4. Algoritmo de Multi-Resolución de Conteo de Cajas
El Algoritmo de Multi-Resolución de Conteo de Cajas (MRCC) está basado en las propiedades de llenado del espacio de una curva. La curva se cubre con un conjunto de objetos de la misma área o cajas (en éste caso cajas cuadradas), se determina un tamaño para el área del objeto y se cuenta el número de cajas mínimo necesarias para cubrir a la curva completamente. A medida que el tamaño de las cajas se aproxima a cero, el área total cubierta por las cajas convergerá a la medida deseada de la curva.
El algoritmo de MRCC propone obtener la FD para varios tamaños de cajas y hacer un ajuste lineal a una gráfica log10(N(r)) sobre log10(r). La pendiente de la recta de mínimos cuadrados se toma como una estimación de la FD de la curva (B. S. Raghavendra, y D. N. Dutt, 2010).
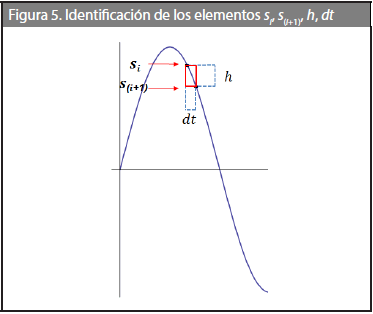
Consideremos a S, con una frecuencia fs. Cada punto si en la secuencia está representado como (xi, yi), i = 1, ... N. Así mismo la señal está representada por un periodo (resolución) 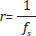 .
.
Para iniciar el MRCC se toman dos puntos en la curva que representa la señal si, s(i+1). El intervalo de tiempo entre los puntos está dado por
la altura entre los puntos es
(Figura 5) el tamaño de la caja considerada para cubrir los dos puntos es dt y el número de cajas requeridas para cubrir los puntos es
el total de cajas de resolución r requeridas para cubrir la curva se calcula por
el procedimiento se repite para todos los puntos en la curva.
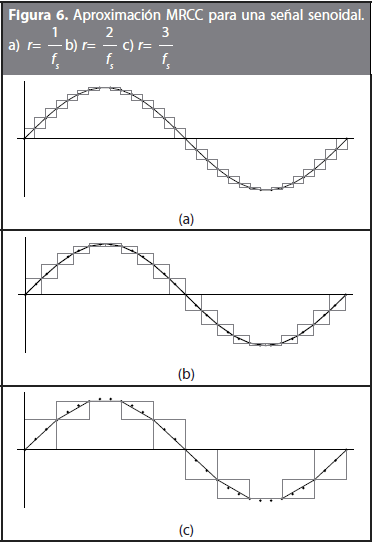
Como siguiente paso del MRCC, se considera la repetición del procedimiento anterior para múltiples resoluciones 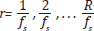 , donde
, donde 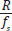 es la resolución máxima que se pueda observar en la curva, Figura 6 (B. S. Raghavendra, y D. N. Dutt, 2010).
es la resolución máxima que se pueda observar en la curva, Figura 6 (B. S. Raghavendra, y D. N. Dutt, 2010).
3. RESULTADOS
Para el presente trabajo se tomó una muestra de 10 sesiones del trabajo de Makeig; las cuales fueron seleccionadas de manera aleatoria. Las señales fueron convertidas a formato de texto y se generaron fractogramas de 10 seg. en el rango 500-510 seg. para su análisis (Figura 7).
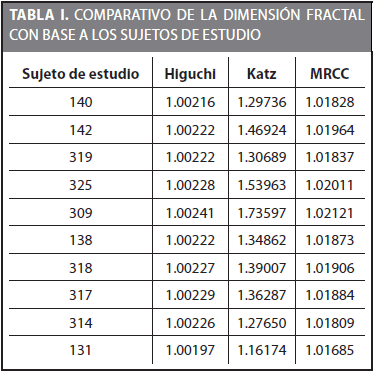
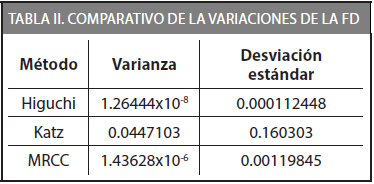
La implementación de los algoritmos se realizó en lenguaje Mathematica V9.0.1.0. Se consideró N = 2561 como el número total de puntos de la serie para todos los algoritmos implementados. Para el algoritmo de Higuchi se consideraron m= 2, k = 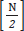 , y para el método MRCC se consideró a R = 1000. La Tabla 1 muestra los resultados obtenidos de la FD, la Tabla 2 muestra las variaciones estadísticas obtenidas en cada algoritmo.
, y para el método MRCC se consideró a R = 1000. La Tabla 1 muestra los resultados obtenidos de la FD, la Tabla 2 muestra las variaciones estadísticas obtenidas en cada algoritmo.
4. CONCLUSIONES
El cálculo de la FD nos permitió determinar la complejidad de las señales de EEG obtenidas, en los resultados obtenidos en la Tabla 2 podemos observar que la FD en el algoritmo de Higuchi se mantuvo en el rango de 1.000 < FD < 1.0003 en el algoritmo de Katz se mantuvo en 1.0 < FD < 2.0 y en el MRCC 1.00 < FD < 1.03. La variación de la FD en el algoritmo de Higuchi y MRCC es lo suficientemente pequeña para poder considerar que la FD como una sola; el algoritmo de Higuchi, principalmente es una buena opción para su implementación en sistemas BCI.
5. DISCUSIÓN
En el experimento utilizado en el presente documento, los ERP fueron aleatorios para cada usuario, para poder tener una mejor visión del comportamiento de los algoritmos de FD en señales de EEG se debe disminuir la aleatoriedad de los eventos, así como el tamaño de los fractogramas, a más pequeños, ya que los eventos tienen una duración menor a 1s. Existen otros algoritmos para el cálculo de la FD: Bouligand-Minkowski, Grassberger-Proccacia, el exponente de Hurst, entre otros; los cuales es necesario implementar y comparar para una visión más completa. Los trabajos siguientes se centrarán en la implementación de los algoritmos presentados en éste documento bajo condiciones experimentales más controladas con referente a los VEP y a fractogramas en el rango de 1s. Así mismo se implementarán los algoritmos de Bouligand-Minkowski, Grassberger-Proccacia, el exponente de Hurst para su comparación.
REFERENCIAS
M. Bachmann, J. Lass, A. Suhhova and H. Hinrikus, (2013). Spectral asymmetry and Higuchi's Fractal Dimension Measures of Depression Electrencephalogram, Computational and Mathematical Methods in Medicine, Hindawi Publishing Corporation, vol. 2013, 8 pages. [ Links ]
P. N. Baljekar and H. A. Patil, (2012). A comparison of waveform fractal dimension techniques for voice pathology classification, IEEE ICASPP ISSN 978-1-4673-0046-9, pp. 4461-4464. [ Links ]
T. Bojic, A. Vuckovic, A. Kalauzi, (2010). Modeling EEG fractal dimension changes in wake and drowsy states in humans-a preliminary study, Journal of Theoretical Biology, 262, pp. 214-222. [ Links ]
A. Bashashati, R.K. Ward, G.E. Birch, M.R. Hashemi, MA. Khalilzadeh, (2003). Fractal Dimension-Based EEG Biofeedback System, Proceedings of the 25th Annual International Conference of the IEEE EMBS, pp. 2220-2223, 2003. [ Links ]
F. Cervantes-De la Torre, J.I. González-Trejo, C.A. Real-Ramirez and L.F. Hoyos-Reyes, (2013). Fractal dimension algorithms and their application to time series associated with natural phenomena, 4th National Meeting in Chaos, Comlex Sustem and Time Series, Journal o Physics: Conference Series, 475, 10 pages. [ Links ]
A. Delorme and S. Makeig, (2004). EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics. Journal of Neuroscience Methods, 134:9-21. [ Links ]
Dubravka R. Jevtic, and Milorad P. Paskas, (2011). Application of Katz Algorithm for Fractal Dimension in Analysis of Room Impulse Response, 19th Telecommunications forum TELFOR 2011, pp. 1063-1066. [ Links ]
D. Easwaramoorthy and R. Uthayakumar, (2010). Analysis of EEG Signals using Advanced Generalized Fractal Dimensions, Second International conference on Computing, Communication and Networking Technologies, 978-1-4244-6589-7, 6 pages. [ Links ]
R. Esteller, G. Vachtsevanos, J. Echauz, and B. Litt, (2001). A Comparison of Waveform Fractal Dimension Algorithms, IEEE Transactions on Circuits and Systems-I: fundamental theory and applications, vol. 48, no. 2, pp. 177-183, 2001. [ Links ]
G. Gálvez Coyt, A. Muñoz Diosdado, J. A. Balderas López, J. L. del Rio Correa, and F. Angulo Brown, (2013). Higuchi's Method applied to the detection of periodic components in time series and its application to seismograms, COMPLEX SYSTEMS Revista Méxicana de Física, S 59 (1), pp. 1-6. [ Links ]
S. Georgiev, Z. Minchev, C. Christova, D. Philipova, (2009). EEG Fractal Dimension Measurement before and after Human Auditory Stimulation, Bioautomaton, pp. 70-81. [ Links ]
B. P. Harne, (2014). Higuchi Fractal Dimension Analysis of EEG Signal before and after OM Chanting to Observe Overall Effect on Brain, International Journal of Electrical and Computer Engineering (IJECE), vol. 4 pp. 585-592. [ Links ]
HeadIT, Swartz Center for Computational Neuroscience (SCCN) of the University of California, San Diego. Its development has been funded by U.S. National Institutes of Health grants R01-MH084819 (Makeig, Grethe PIs) and R01-NS047293 (Makeig PI). [ Links ]
M. Katz, (1988). Fractals and the analysis of waveforms, Computers in Biology and Medicine, vol. 18, pp. 145-156. [ Links ]
T. Q. D. Khoa, V. Q. Ha and V. V. Toi, (2012). Higuchi Fractal Properties of Onset Epilepsy Electroencephalogram, Computational and Mathematical Methods in Medicine, Hindawi Publishing Corporation, vol. 2012, 6 pages. [ Links ]
C. K. Loo, A. Samraj and G. C. Lee, (2011). Evaluation of Methods for Estimating Fractal Dimension in Motor Imagery-Based Brain Computer Interface, Hindawi Publishing Corporation, Discrete Dynamics in Nature and Society Vol. 2011, Article ID 724697, 8 pages. [ Links ]
W. Lutzenberger, H. Preissl, F. Pulvermüller, (1995). Fractal dimension of electroencephalographic time series and underlying brain processes, Biological Cybernetics Springer-Verlag, vol. 73, pp. 477-482. [ Links ]
S. Makeig, A. Delorme, M. Westerfield, T-P. Jung, J. Townsend, E. Courchesne and T. J. Sejnowski, (2004). Electroencephalographic brain dynamics following visual targets requiring manual responses, Public Library of Science Biology, 29 pages. [ Links ]
S. Makeig, M. Westerfield, T-P Jung, J. Covington, J. Townsend, T. J. Sejnowski, and E. Courchesne, (1999). Functionally Independent Components of the Late Positive Event-Related Potential during Visual Spatial Attention, The Journal of Neuroscience, 19 (7), pp. 2665-2680. [ Links ]
A. S. Martins, L. A. Neves, M. Z. Nascimento, M. F. Godoy, E. L. Flores and G. A. Carrijo, (2012). Multiscale Fractal Descriptors and Polynomial Classifier for Partial Pixels Identification in Regions of Interest of Mammographic Images, IEEE Latin America Transactions, Vol. 10, No. 4, pp. 1999-2005. [ Links ]
G. Millán, E. S. Juan and M. Jamett, (2014). Simple Estimator of the Hurst Exponent for Self-Similar Traffic Flows, IEEE Latin America Transactions, Vol. 12, No. 8, pp. 1341-1346. [ Links ]
Müller K.R., and Mattia D. (2010). Combining Brain-Computer Interfaces and Assistive Technologies: State-ofthe-Art and Challenges. Frontiers in Neuroscience, Vol 4, pp. 161. [ Links ]
H. H. Mueller, (2010) "QEEG Brain Mapping, Evaluating the rhythms of the Brain", Edmonton Neurotherapy, 2010, On line http://www.edmontonneurotherapy.com/Edmonton_Neurotherapy_QEEG_brain_mapping.html. [ Links ]
P. Paramanathan, R. Uthayakumar, (2008), Application of fractal theory in analysis of human electroencephalographic signals, Computers in Biology and Medicine, no. 38, pp. 372-378. [ Links ]
P. Paramanathan and R. Uthayakumar, (2007). Detecting Patterns in Irregular Time Series with Fractal Dimension, International Conference on Computational Intelligence and Multimedia Applications, pp. 323-327. [ Links ]
F. R. Perlingeiro, L. L. Ling, (2005). Uma Nova Abordagem para Estimação da Banda Efetiva em Processos Fractais. IEEE Latin America Transactions, Vol. 3, No. 5, pp. 436-446. [ Links ]
G. E. Polychronaki, P. Y. Ktonas, S. Gatzonis, A Siatouni, P. A. Asvestas, H. Tsekou, D. Sakas and K. S. Nikita, (2010). Comparison of fractal dimension estimation algorithms for epileptic seizure onset detection, Journal of Neural Engineering, 046007, 18 pages. [ Links ]
B. S. Raghavendra, and D. N. Dutt, (2010). Computing Fractal Dimension of Signals using Multiresolution Boxcounting Method, International Journal of Information and Mathematical Sciences, 6:1, pp. 50-65. [ Links ]
B. S. Raghavendra and D. N. Dutt, (2009). A note on fractal dimensions of biomedical waveforms, Computers in Biology and Medicine, 39, pp. 1006-1012. [ Links ]
S. Spasic, Lj. Nikolic, D. Mutavdzic, J. Saponjic, (2011). Independent complexity patterns in single neuron activity induced by static magnetic field, Computer Methods and Programs in Biomedicine, vol. 104, pp. 212-218. [ Links ]
Sabogal S., Arenas G. (2011). Una Introducción a la geometría Fractal, Escuela de Matemáticas, Universidad Industrial de Santander. Bucaramanga, Cap I, pp. 2-15. [ Links ]