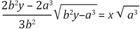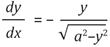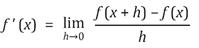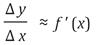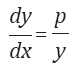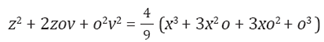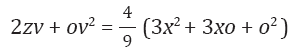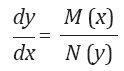1. INTRODUCCIÓN

El análisis histórico permite identificar la importancia de incorporar procesos heurísticos y algunos razonamientos específicos en la enseñanza y aprendizaje de las ecuaciones diferenciales ordinarias. El objetivo de este artículo es identificar algunos obstáculos epistemológicos que surgieron en el proceso de constitución de las ecuaciones diferenciales ordinarias (EDO). Estos obstáculos se pueden determinar en el movimiento teórico que va de la modelación de fenómenos físicos a la instauración de un formalismo conceptual al interior del análisis matemático.

La modelación matemática de algunos problemas físicos se hizo con base en el naciente cálculo en términos de ecuaciones diferenciales ordinarias. A finales del siglo XVII se publicaron algunos trabajos en los cuales se exponían métodos para resolver ecuaciones diferenciales ordinarias, entre ellos separación de variables, solución de ecuaciones homogéneas por sustitución, solución por series y resolución de ecuaciones exactas. Aunque muchos de éstos no fueron generalizados sino hasta Euler, es posible encontrar casos particulares de estos métodos antes del siglo XVIII. Si bien a partir de estos problemas se encontraron diversas técnicas de solución, hubo un estancamiento en esta disciplina, pues, en su conjunto, todas estas técnicas resolvían casos particulares, pero no dieron lugar a algoritmos generales de resolución de las EDO. Como consecuencia de ello, en el siglo XVIII no se produjeron resultados teóricos, como el Teorema de Existencia y Unicidad.

Durante los siglos XVII y XVIII fueron diversos los avances que se dieron en el campo de las matemáticas. Uno de ellos se vincula con el desarrollo del cálculo de Newton y Leibniz. El nacimiento de este cálculo permitió que se perfilaran diversas disciplinas de las matemáticas, entre ellas las ecuaciones diferenciales, y otros conceptos fundamentales como el de función. Un catalizador importante en el desarrollo de las ecuaciones diferenciales ordinarias fueron las investigaciones, elaboradas por los científicos europeos, entorno al movimiento; la necesidad de cambiar de paradigma cualitativo a uno cuantitativo en el que se lograra estudiar desde lo matemático los fenómenos físicos posibilitó que emergieran las primeras ecuaciones diferenciales ordinarias. La física se relacionó tan directamente con las matemáticas que llegó un momento en el que los avances de esta ciencia provenían de los requerimientos de la física.

De esta manera se puede sustentar que las ecuaciones diferenciales ordinarias, surgen como producto de dos eventos; el primero vinculado con los diversos problemas de la física que fueron modelados mediante ecuaciones diferenciales ordinarias, y el segundo relacionado con los diversos métodos de resolución de ecuaciones producto de los avances en el cálculo. Estos dos aspectos se presentan de manera general en el presente documento¹.

El análisis histórico realizado nos ha llevado a identificar algunos obstáculos epistemológicos que se describen en el presente documento. Esto nos permite argumentar que en los cursos de ecuaciones diferenciales ordinarias se debería de incluir la reflexión y discusión epistemológica de los conceptos involucrados en las ecuaciones diferenciales; en particular el concepto de diferencial. En la mayoría de cursos de ecuaciones diferenciales y aún de cálculo, no se estudia este aspecto. Obviar esta reflexión ha causado que los estudiantes aprendan procesos algorítmicos para encontrar derivadas, integrales y resolver ecuaciones, pero con poca posibilidad de utilizar esos conocimientos para modelar situaciones que involucren ecuaciones diferenciales en sus respectivas carreras.

2. LOS PROBLEMAS DE LA FÍSICA Y LAS ECUACIONES DIFERENCIALES

Algunos de los problemas que permitieron la constitución de las ecuaciones diferenciales ordinarias se pueden ubicar a finales del siglo XVII y comienzos del siglo XVIII. Los matemáticos de estos siglos intentaron dar respuestas a problemas de la física vinculados con el campo de la mecánica, la elasticidad y la astronomía, entre otros. Uno de los primeros problemas que históricamente se conoce y que dio lugar al planteamiento de una ecuación diferencial ordinaria fue el problema de la curva isócrona, el cual fue abordado por Huygens utilizando métodos geométricos y propiedades de la física. Posteriormente fue solucionado por Leibniz y Jacques Bernoulli, quienes utilizaron el cálculo infinitesimal. Otros problemas fundamentales en la constitución de las ecuaciones diferenciales ordinarias fueron: el problema de la tractriz, el problema de la catenaria y el problema de la braquistócrona, todos estos problemas fueron solucionados por Leibniz, los hermanos Bernoulli y Newton mediante el uso del cálculo infinitesimal. Algunos de los métodos y técnicas que surgieron de la solución de estos problemas fueron la separación de variables y el uso de series.

El problema del péndulo isócrono consistía en construir un péndulo cuyo periodo de oscilación fuera el mismo independientemente de la altura de donde iniciara a oscilar la lenteja. Christiaan ^{Huygens, en 1673}, en la Horologium Oscillatorium sive motu pendulorum ad horologia aptato demostrationes geometricae describe con detalle la construcción de un reloj isócrono.

La ecuación diferencial que modela el problema de la curva isócrona, en términos de Bernoulli, es 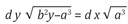, donde a y b son constantes. La solución de esta ecuación fue presentada en las Acta Eruditorum de 1690. Bernoulli concluyó que las integrales de esta igualdad de diferenciales tenían que ser las misma, por lo tanto, la curva buscada era la cicloide, es decir:

Es importante destacar que en la solución de Jacques Bernoulli se identifica una ecuación diferencial de primer orden, la cual se resolvió aplicando la separación de variables y encontrando la solución de las integrales por cuadraturas.

El problema de la tractriz fue estudiado en 1674 por Leibniz. Este problema también se conoce como la curva del hueso del perro, ya que se puede considerar el caso en que el amo se sitúa inicialmente en el origen de las coordenadas y el perro a una distancia d sobre el eje positivo y. El amo caminaría en el sentido positivo del eje de la x, mientras el perro, que sería arrastrado por la correa del amo, haría resistencia para volver al punto de partida, que sería donde estaría situado el hueso. Esta curva es formada mediante dos movimientos uno que se da de izquierda a derecha, es decir desde el origen hacia el eje positivo de la x, y otro que se origina al descender el perro por la acción de la fuerza ejercida por el amo. Una de las propiedades que cumple esta curva y que fue utilizada por Leibniz para demostrar su resultado es que la distancia entre el punto de tangencia de la curva que se busca y el eje en donde se mueve el otro extremo de la cuerda es siempre constante e igual a la longitud de la cuerda.

Leibniz utilizó el cálculo con diferenciales para solucionar el problema. Consideró una cuerda de longitud a, la cual en el instante inicial se encuentra ubicada en el eje vertical, es decir las coordenadas de sus extremos son (0,0) y (0, a). El extremo que está ubicado en el origen se mueve sobre el eje horizontal positivo de las x y el otro recorre la tractriz. Bajo estas condiciones Leibniz notó que debía encontrar una curva tal que la parte de su tangente entre la curva y el eje horizontal fuera siempre igual a una constante dada. No fue difícil para Leibniz concluir que el trazado de esta curva también se podría reducir a la cuadratura de una hipérbola. Teniendo presente las condiciones del problema, Leibniz utiliza las propiedades de la semejanza de triángulos para establecer relaciones entre un triángulo de dimensiones finitas y un triángulo infinitesimal. De esta manera, concluye que la relación entre las diferenciales de la ordenada y la abscisa es:

Separando las variables la ecuación queda transformada en 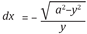. Para resolver esta ecuación Leibniz utilizó la solución por cuadraturas, que consiste en encontrar la primitiva de la función. Jacques ^{Bernoulli en el año 1690}, en su artículo sobre la isócrona, planteó a los matemáticos el problema de encontrar la curva que modelaba el comportamiento de una cuerda flexible e inextensible colgada libremente de dos puntos fijos. Dicha curva fue denominada por Leibniz como catenaria.

El problema de la catenaria fue abordado, primeramente, por Galileo, el cual planteó que la curva era una parábola, sin embargo Huygens en 1646 argumentó que esto no era correcto mediante razonamientos físicos, concluyendo que la curva era la catenaria, puesto que permitía que el peso por unidad fuera uniforme a lo largo del cable.

De igual manera, otros matemáticos como Leibniz y Jean Bernoulli, publicaron diversos métodos de resolución al problema planteado por Jacques Bernoulli en el año anterior (el cable colgante). Ambos encontraron en el cálculo infinitesimal la respuesta, de hecho la solución de Johann Bernoulli se encuentra en los textos de mecánica y cálculo infinitesimal (^{Kline, Las ecuaciones diferenciales ordinarias en el siglo XVIII, 1992}), la cual se basa en la ecuación 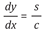, en donde s y c son constantes que dependen del material utilizado. La solución de esta ecuación diferencial lleva a lo que hoy en día escribimos como .

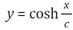El problema de la braquistócrona fue planteado en junio de 1696 por Johann Bernoulli en las Acta Eruditorum. El problema consistía en hallar la trayectoria que debería seguir una partícula móvil, descendiendo por su propio peso, empleando el menor tiempo posible. Bernoulli llega a la conclusión que la ecuación diferencial que rige este tipo de movimiento es 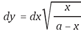, y que la curva braquistócrona era la cicloide.

En conjunto los anteriores problemas muestran que la teoría de ecuaciones diferenciales empieza a emerger en el siglo XVII con la modelación y solución de problemas de la mecánica. En este sentido, uno de los aspectos de causalidad que motivó el surgimiento de las ecuaciones diferenciales ordinarias se deriva del tratamiento de los problemas físicos. Entre las primeras técnicas que se aplicaron para solucionar ecuaciones diferenciales se encuentra la separación de variables. Las integrales a las cuales conducía esta técnica eran resueltas por cuadraturas o aplicando métodos geométricos. Es importante señalar que paralelamente a la emergencia de las ecuaciones diferenciales se ponía a prueba el nuevo cálculo y se desarrollaba el concepto función, esto último sustentado en el hecho de que se empezaron a trabajar curvas transcendentes.

3. EL DESARROLLO DEL CÁLCULO Y LAS ECUACIONES DIFERENCIALES

En su expresión genérica, la noción de ecuación diferencial va íntimamente ligada a la noción de diferencial; una noción empleada constantemente en el cálculo, pero cuyo uso conlleva dificultades conceptuales. ¿Formalmente hablando, qué es un diferencial? En la actualidad se usa como una herramienta para calcular valores aproximados de algunas funciones trascendentes. De esta manera, si la función ƒ es diferenciable en el punto x, con derivada ƒ ' (x), se tiene que:

Geométricamente, ƒ '(x) corresponde a la pendiente de la recta tangente a la gráfica de ƒ en el punto (x, ƒ (x)). Si realizamos sobre x, un pequeño cambio, denotado por Δ x, se produce un pequeño cambio en y, denotado por Δ y, tal que Δ y = ƒ (x + Δ x) - ƒ (x), de tal forma que el cociente 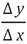es aproximadamente ƒ ' (x):

Se suele denotar a Δ x como d x, diferencial de x, y a Δ y como d y, diferencial de y. De tal suerte que: dy ≈ ƒ ' (x)dx . En este contexto los diferenciales corresponden a números reales diferentes de cero; sin embargo en los inicios del cálculo y de las ecuaciones diferenciales, el concepto de diferencial, el cual emerge en la nomenclatura de Leibniz, designaba una cantidad infinitamente pequeña.

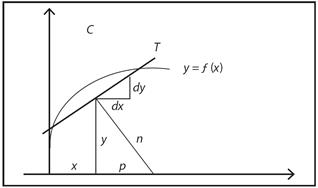
Para Leibniz, el concepto de diferencial se identificaba con una variación (o incremento) infinitesimal. De esta forma, dada la curva y = ƒ (x), tal que la recta T es tangente a la curva en el punto C = (x, y). Trazando paralelas al eje x y al eje y, Leibniz consideraba el triángulo rectángulo de catetos dx y dy, infinitesimalmente pequeños. Sea la recta n, la normal correspondiente; esto es, n es perpendicular a T.

Lo interesante para Leibniz era considerar el cociente 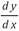que daba lugar a la proporción:

Observemos que la anterior igualdad enmarca una ecuación diferencial elemental, dado que p es una variable x, y además dx y dy se puede considerar cantidades que operan con las otras cantidades, de tal forma que y dy = p(x)dx:

En Newton, el concepto equivalente a los diferenciales de Leibniz corresponde a los infinitesimales. En el cálculo de “anti cuadraturas”, Newton incorpora el símbolo “o” para representar una cantidad infinitamente pequeña. Ello significa que puede actuar como denominador, pero cuando aparece sumando se desvanece, por ser tan pequeña que no adiciona nada: “o” simboliza un incremento infinitesimal.

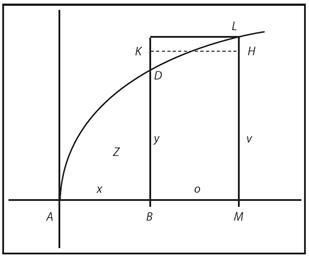
Consideremos el siguiente ejemplo, dado por el mismo Newton: sea la figura siguiente, en la cual, área ABD = z, AB = x, BD = y. Tomamos, BM = o, BK=ML = v, tales que, área BDLM = área BKHM = ov.

Newton toma específicamente la curva, 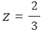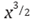de donde,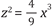

Una variación de o en la abscisa, produce una variación ov en el área total, de tal suerte que,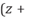

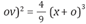
Desarrollando los dos binomios quedará:

Empleando la sustitución 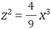simplificando y dividiendo los dos miembros de la expresión resultante por o, dado que es diferente de cero, se obtiene,

Entonces Newton toma BM infinitamente pequeño, de tal manera que v se hace igual a y, y además o se hace igual a cero, quedando: 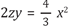, de tal forma que al sustituir z por su valor inicial se obtiene, .

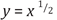Dadas las críticas que en torno al uso de las cantidades infinitamente pequeñas, Newton reformula sus desarrollos en términos de “fluentes” y “fluxiones”. Las cantidades “fluyentes” son aquellas cantidades que varían respecto al tiempo. La rapidez de cambio de estas cantidades las llamó “fluxiones”. De esta manera, si tomamos de referencia la figura anterior, Newton concebía la curva ADL generada a partir del movimiento del punto genérico D, lo cual ocasionaría que las coordenadas x y y, así como la cuadratura z “fluyeran” o cambiaran con el tiempo. En términos modernos, Newton estaba describiendo la curva de acuerdo a una ecuación paramétrica (x (t), y (t)). En primera instancia, uso letras diferentes para diferenciar las fluxiones de sus fluentes; pero luego adoptó la notación que se conoce, en la cual las fluxiones se representan con un punto superior de las fluentes; si x, y representan las cantidades fluentes, ẋ, ẏ representan las fluxiones respectivas. Al igual que a Leibinz, a Newton no tanto le interesa las fluxiones individualmente, sino la razón .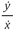

Newton pensaba que a través de incorporar al tratamiento de curvas una visión cinemática quedaría resuelto el problema de los incrementos infinitamente pequeños, los cuales cumplían la “extraña ley” de poder dividir, por ser diferentes de cero, y desaparecer a conveniencia por no incidir en el resultado. “Cantidades evanescentes” que aparecen y desaparecen a conveniencia.

De esta manera nos encontramos frente a un problema histórico muy significativo a nivel de la enseñanza del cálculo. Para obtener los resultados se hace necesario involucrar cantidades cuya naturaleza ontológica se desconoce, pero que funcionan operativamente. Muy similar a los procesos que generalmente se dan en una clase cuando los estudiantes se aprenden la mecánica de los procedimientos sin ninguna relación conceptual.

El uso de las cantidades infinitamente pequeñas se convirtó en un serio problema para los matemáticos de los siglos XVII y XVIII. Fue el francés Agustín-Louis Cauchy (1789-1857) quien proporcionó una salida rigurosa a través de concepto de límite en el Curso de análisis de 1821 y las Lecciones sobre cálculo Infinitesimal de 1823. En estos dos textos, basados en sus cursos dictados en la École Polytechnique de Paris, Cauchy perfila un cuerpo teórico que contiene los conceptos soporte del análisis matemático moderno: número real, función, límite, números complejos, derivada e integral. A través del concepto de límite, Cauchy introduce las funciones continuas, la convergencia de series, las nociones de derivada e integral, con base a la noción de límite y demuestra, de manera rigurosa, el teorema fundamental del cálculo. Estamos en un momento de fundamentación en el cual los elementos de una ecuación diferencial están claramente establecidos. Cuando nos referimos a la solución de una ecuación diferencial estamos buscando una función derivable, que cumpla las especificidades requeridas.

4. REFLEXIONES EPISTEMOLÓGICAS SOBRE LA CONSTITUCIÓN DE LAS ECUACIONES DIFERENCIALES ORDINARIAS COMO DISCIPLINA DE LAS MATEMÁTICAS

Del siglo XV al siglo XVIII se realizó la conformación de diversas disciplinas. Antes del siglo XV la ciencia se desarrolla en función de la solución de problemas. Históricamente la noción de ciencia, tal como la concebimos hoy, es relativamente reciente, data de los inicios del capitalismo europeo de los siglos XVI y XVII. Este hecho hace que, en muchas ocasiones, la ciencia se encuentre íntimamente ligada a los procesos de producción. En la segunda mitad del siglo XV comenzó a gestarse la primera revolución científica que dio lugar a una ciencia desligada de la escolástica, dando inicio a las ciencias naturales modernas. Con respecto a la matemática y la física, es un periodo en el que es casi imposible establecer si un determinado problema es propio de las matemáticas o si es un problema de aplicación, que buscaba solucionar alguna necesidad práctica humana. Por su parte, ^{Cantoral y Farfán (2004)} señalan que, la matemática en el siglo XVIII incluía el cálculo, el análisis, la aritmética, el álgebra, la geometría, la astronomía, la óptica, la mecánica e hidrodinámica y hasta la construcción de artillería y barcos. Justamente estos aspectos (los problemas de interés durante los siglos XVII y XVIII y las maneras de abordarlas desde la matemática) se constituyen en elementos de causalidad para entender la conformación de disciplinas matemáticas, en este caso las ecuaciones diferenciales. En este sentido y entendiendo que si bien no podemos hablar de un divorcio con las necesidades, nos interesa analizar la manera en que a partir de ciertos problemas prácticos surgía la necesidad de constituir una disciplina particular con una epistemología propia, como las ecuaciones diferenciales.

Como lo detallamos antes, algunos problemas que interesaban a los científicos en el siglo XVII conllevaron al surgimiento de las ecuaciones diferenciales como disciplina matemática. En principio, esta disciplina respondía a algunas problemáticas presentes en el campo de la física especialmente en la mecánica. En ese momento histórico, desde la física, la solución de una ecuación diferencial correspondía a una curva que cumplía determinadas propiedades vinculadas con el fenómeno físico que se modelaba. Paralelamente, desde la matemática, el proceso de solucionar ecuaciones diferenciales estaba ligado al problema de las cuadraturas. A mediados del siglo XVIII las ecuaciones diferenciales se habían convertido en un campo independiente de los problemas de la mecánica y de las cuadraturas, perfilando un capítulo del análisis, cuyo objetivo era encontrar métodos que permitieran la solución de diferentes tipos de ecuaciones diferenciales.

La naturaleza de lo que se asumía y se encontraba como solución de una ecuación diferencial ordinaria fue cambiando en la historia. En el siglo XVII las soluciones estaban determinadas por curvas. Por ejemplo, en el caso de los problemas de la tractriz y la braquistócrona se buscaban curvas que cumplieran determinadas propiedades que se establecían mediante una ecuación diferencial ordinaria. En el caso de la tractriz era necesario hallar la expresión analítica de la curva cuya longitud entre el punto de tangencia y un eje de coordenadas fuera constante.

Para la braquistócrona se buscaba la expresión analítica de la curva de descenso más rápido.

Matemáticamente hablando, el trabajo con las ecuaciones diferenciales ordinarias guardaba relación directa con la búsqueda de cuadraturas. Las diversas técnicas que empezaron a utilizarse como la separación de variables, la sustitución y el factor integrante, condujeron a que la solución de una ecuación diferencial ordinaria se identificara con el hallazgo de una cuadratura. En otras palabras, solucionar ecuaciones diferenciales implicaba descubrir una expresión analítica que diera cuenta de una determinada curva, pero dicha expresión era posible encontrarla siempre que se resolviera un problema de cuadratura.

Ecuaciones diferenciales muy sencillas, en el sentido de que su solución se reduce a un problema de integración y separación de variables, conducía, en ocasiones, a integrales difíciles o incluso imposible de efectuar explícitamente (analíticamente). Esta dificultad se vincula con el hecho de que la teoría de funciones estaba en desarrollo, y apenas se iniciaba el estudio de algunas curvas transcendentes. Las ecuaciones diferenciales que involucraban curvas trascendentes o cuadraturas de esta naturaleza no eran posible solucionarlas analíticamente. Los problemas que comprendían este tipo de ecuaciones en las que no se podía encontrar ni una curva ni su cuadratura obligaron a los matemáticos a buscar nuevos métodos. Surge de este modo el uso de series para solucionar ecuaciones diferenciales, el cual fue ampliamente utilizado por diversos matemáticos.

5. OBSTÁCULOS EPISTEMOLÓGICAS EN LA CONSTITUCIÓN DE LAS ECUACIONES DIFERENCIALES ORDINARIAS COMO DISCIPLINA DE LAS MATEMÁTICAS

En este artículo se toma como referencia la noción de obstáculo epistemológico expuesta por Guy ^{Brousseau en (Brousseau, 1998)}. Brousseau retoma la noción de obstáculo epistemológico, que Bachelard había definido para las ciencias empíricas en 1938 en su libro Formación del espíritu científico, una contribución a un psicoanálisis del conocimiento objetivo.²

Para Brousseau los obstáculos constituyen un conocimiento que tiene validez en un contexto determinado, pero que en otros contextos genera respuestas falsas. Desde esta perspectiva, un obstáculo no es un conocimiento falso, sino un conocimiento que está obstaculizando la adquisición de uno nuevo. Una característica principal de los obstáculos epistemológicos es que son constitutivos del saber, por esta razón, es posible identificarlos en la historia del propio concepto. Bachelard definió cinco obstáculos principales, a saber: la experiencia básica o conocimientos previos, el obstáculo verbal, el peligro de la explicación por la utilidad, el conocimiento general y el obstáculo animista. Desde la perspectiva de Brousseau y la clasificación de Bachelard es posible analizar algunos obstáculos epistemológicos presentes en la constitución de las ecuaciones diferenciales ordinarias.

El primer obstáculo se vincula con el hecho de pensar que desde la perspectiva de la modelación es posible estudiar en profundidad todos los elementos vinculados en las ecuaciones diferenciales ordinarias. Durante el siglo XVIII las ecuaciones diferenciales surgieron en la dinámica de la resolución de problemas del campo de física. Si bien a partir de estos problemas se encontraron diversas técnicas de solución, también ocasionó un estancamiento en esta disciplina, pues en su conjunto todas estas técnicas resolvían casos particulares de ecuaciones, pero no hubo la creación de principios amplios y generales para resolver ecuaciones diferenciales ordinarias. En esta misma vía, es posible señalar que la modelación de problemas en el siglo XVIII no permitió estudiar aspectos teóricos como el teorema de existencia y unicidad. Este teorema solo se abordó 100 años después del surgimiento de las ecuaciones diferenciales ordinarias y sus técnicas, ya que por las condiciones de los problemas (modelado de un problema físico) era evidente que existiera una solución. Este hecho se presentó a pesar de que las ecuaciones que resolvían los científicos del siglo XVIII eran de valores iniciales, pero la pregunta de existencia y unicidad de la solución a una determinada ecuación no tenía sentido si estaba estudiando un problema de modelado.

En la actualidad existen posturas que señalan que desde una perspectiva de modelación es posible acercarse al aprendizaje de las ecuaciones diferenciales ordinarias, sin tener presente que es necesario ampliar esta perspectiva con el estudio de factores teóricos involucrados en las ecuaciones diferenciales ordinarias, tales como: la reflexión sobre el concepto de diferencial y la relación con las técnicas. Este obstáculo lo podemos ubicar dentro de los que Bachelard denomina el peligro de la explicación por utilidad, pues se crea un conocimiento alrededor del concepto de ecuación diferencial ordinaria en base a la utilidad y aplicación del mismo. En consecuencia, parece conveniente que, en el proceso de enseñanza de las ecuaciones diferenciales ordinarias, se debe partir de la modelación de problemas, sin dejar de lado los aspectos teóricos y relaciones matemáticas involucradas en su solución.

Otro obstáculo epistemológico que se evidencia en la historia de las ecuaciones diferenciales es la dualidad que presenta el uso del 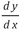. Para Leibniz, Newton y Euler 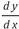es el cociente entre dos variaciones infinitamente pequeñas. Sin embargo, con Cauchy 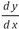se convierte en el límite de un cociente de incrementos. Estas dos perspectivas permiten identificar dos formas de comprender d y; una vinculada con la aplicación en la solución de problemas físicos, perspectiva de Leibniz, Newton y Euler, y otra vinculada con la aplicación en el campo matemático. Al respecto Artigue, Menigaux y Viennot (1990) señalan que ambas formas de entender este concepto circulan en los estudiantes, sin embargo, no existe una comprensión sobre estos, ya que aplican algoritmos sin asociarle algún significado. Este hecho refleja el viejo conflicto entre las dos formas de entender el 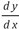desde la matemática y la física. Conflicto que continua hasta la actualidad pues no existe una claridad frente a este concepto.

En los cursos de cálculo se plantea d y desde la 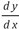perspectiva de Cauchy. Pero en los cursos de física se utiliza la perspectiva de Leibniz, Newton y Euler. En consecuencia, es necesario que los estudiantes entiendan ambas perspectivas y establezcan relaciones entre ellas. De acuerdo a las categorías de Bachelard este tipo de obstáculo estaría ubicado en el de conocimiento general, puesto que las definiciones para entender el d y son demasiado amplias, y dejan de lado aspectos esenciales y detalles que son los que permiten definir con claridad cada perspectiva. Este obstáculo se hace evidente con Leibniz y Newton al momento de definir las cantidades infinitamente pequeñas, ya que la caracterización que realizan es general y no profundizan en detalles, tales como: la operatividad y naturaleza de las mismas. En consecuencia, es evidente, que las definiciones que circulen en los estudiantes, sobre el concepto de 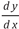, sean generales y poco profundas en relación a la naturaleza de las diferenciales.

6. UNA REFLEXIÓN DIDÁCTICA

El proceso histórico de constitución de las Ecuaciones Diferenciales Ordinarias muestra que el razonamiento empírico-inductivo fue usado con frecuencia por los matemáticos del siglo XVII y XVIII para establecer resultados. De hecho, en muchas ocasiones se favoreció más este tipo de razonamiento que el deductivo, pues conducía a mejores desempeños en la construcción de técnicas para solucionar ecuaciones diferenciales. Esta situación puede vincularse con el hecho de que el campo de las ecuaciones diferenciales surge y se aplica en los femémonos físicos y en consecuencia la verificación experimental valida los resultados. Por ejemplo, los procesos usados para solucionar los problemas del péndulo isócrono, de la tractriz, la catenaria y la braquistócrona permitieron la aparición de una de las primeras técnicas para solucionar ecuaciones diferenciales, la separación de variables. Además la manera de modelar y solucionar estos problemas muestra que la intuición ocupa un papel fundamental. A modo de ejemplo, se puede recordar la solución del problema de la braquistócrona, elaborada por Johann Bernoulli, el cual supuso que el compartimento del objeto que cae por la curva braquistócrona es igual al realizado por un rayo de luz en un medio plano con un índice de refracción adecuadamente elegido, y logra llegar mediante esta hipótesis a la solución del problema. Este hecho revela que la intuición ocupa un papel importante en la construcción de conocimiento.

En esta misma dirección, la historia de las ecuaciones diferenciales ordinarias pone en evidencia que el razonamiento inductivo fue protagonista en la construcción de conocimiento. En parte, porque la sistematización de técnicas para solucionar ecuaciones diferenciales ordinarias se dio en la dinámica de ejemplos que luego eran generalizados mediante un proceso de abstracción. Por ejemplo, el trabajo elaborado por Leibniz en 1691 (carta realizada a Huygens) ilustra casos particulares de la técnica de separación de variables, la cual fue generalizada por Jean ^{Bernoulli en las Actas Eruditorum de 1694}. Este evento muestra que el desarrollo de las ecuaciones diferenciales se dio mediante un razonamiento inductivo.

Una vía para abordar la enseñanza de las ecuaciones diferenciales es mediante el trabajo con el razonamiento empírico-inductivo así lo muestra la historia de este campo. El planteamiento de problemas de la física y su posterior modelación y solución exige que los estudiantes hagan uso de la intuición y de estrategias heurísticas en las que se privilegia el razonamiento inductivo. Esta afirmación se sustenta en la idea de que el surgimiento de las técnicas de solución de ecuaciones diferenciales se dio en la modelación de problemas. De aquí, la necesidad de diseñar actividades que involucren la modelación de situaciones que lleven al planteamiento de ecuaciones diferenciales y posteriormente a la creación de técnicas. Sin embargo, las actividades no deben quedarse en el plano empírico en el que se validan resultados, puesto que se caería en el error de centrarse en procesos algorítmicos en los cuales no existe una reflexión profunda sobre los objetos y procesos matemáticos involucrados en los problemas. Es por ello, que se debe pasar de los ejemplos y solución de problemas particulares a la reflexión y abstracción de las nociones, propiedades y relaciones matemáticas que se pueden establecer.

La modelación de problemas se constituyó en un obstáculo para el avance en las ecuaciones diferenciales. Este hecho produjo un estancamiento en el estudio de las ecuaciones, ya que las técnicas se habían elaborado para dar respuesta a problemas de aplicación física. Además, aspectos teóricos importantes, como el teorema de existencia y unicidad, solo se abordó años después del surgimiento de las ecuaciones diferenciales, pues debido a las condiciones del problema era evidente la existencia de soluciones. En consecuencia, parece conveniente que, en el proceso de enseñanza de las ecuaciones diferenciales ordinarias, se debe partir de la modelación de problemas típicos, sin dejar de lado los aspectos teóricos y relaciones matemáticas involucradas en su solución.

De otra parte, la enseñanza de las ecuaciones diferenciales debería incluir la reflexión y discusión del concepto de diferencial. En la mayoría de cursos de ecuaciones diferenciales y aún de cálculo, no se estudia este aspecto. Obviar esta reflexión ha causado que los estudiantes aprendan procesos algorítmicos para encontrar derivadas, integrales y resolver ecuaciones, pero sin adquirir una comprensión profunda de este concepto. Esta misma situación se presentó al inicio de la creación del cálculo con Newton y Leibniz, los cuales desarrollaban satisfactoriamente sus procesos algorítmicos, pero tenían problemas para explicar la naturaleza de los objetos con los que trabajaban, como en el caso de la diferencial; por ello en ocasiones llegaban a resultados válidos sin preguntarse sobre el formalismo matemático que soportaba estos conceptos. Es importante que tanto el alumno como el docente entiendan el papel de diversa representaciones de los objetos. En este sentido, es común que los docentes manejen ideas erroneas de los diferenciales, señalandolos como cantidades infinitamente pequeñas. Eso ocurre porque en los libro de texto hay un manejo libre de los símbolos dx y dy. Así pocas veces se entiende que el rol del símbolo dx en la integral definida 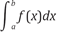es meramente convencional y no corresponde a cantidades infinitamente pequeñas. Igual cuando se plantea una ecuación diferencial de la forma

la cual se expresa como N(y)dy = M(x)dx. Aquí se maneja operativamente dx y dy, sin mediar una explicación conceptual sobre su naturaleza. El manejo operatorio de los diferenciales se hace, entonces de manera arbitraria al persisitir la carga conceptual proveniente de los trabajos de Leibniz en los primeros estadios del cálculo.