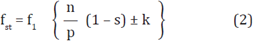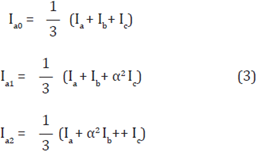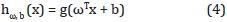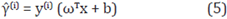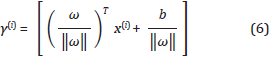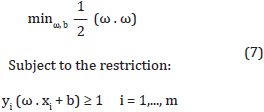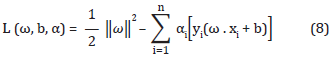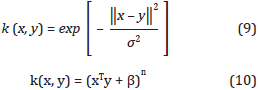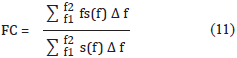1.1. Rotor's Broken Bars

(Thompson, 1994) describes the rotor's broken bar fault mechanism as consequence of high starting currents, which produce mechanical and thermal fatigue in the cage bars. In addition, heavy-duty cycles and long starting times increase the incidence of breakages in the bar-ring junction region. The model for this type of fault (See Equation 1) represents the fault related sidebands that appear once there is a broken bar fault:

Where f_b is the sideband frequency, k = 1, 2, 3, ... and f₀ is the motor supply current frequency.

1.2. Stator's Shorted Winding

This type of fault usually starts as a non-detected isolation loss between two winding turns and progressively, because of high temperatures, evolves into a short circuit, isolating a major number of winding turns (^{Awadallah and Morcos, 2004}). Equation (2) corresponds to shorted winding fault model (^{Poncelas et al., 2008}):

Where f_st are the frequency values associated with shorted winding fault, f₁ is the supply current frequency, p is the number of pole pairs, n = 1, 2, 3 ... k = 1, 3, 5 ... and s is the motor's slip.

4.1. Fault emulation and data acquisition

To emulate shorted winding fault, the stator windings of the induction motor were reconstructed. The windings in one motor phase were equipped with several accessible taps so that a stator winding short type fault with varying severity could be introduced, emulating 2%, 5% and 10% shorted turns, corresponding to incipient, moderate and severe faults, respectively. Finally, the data were analyzed in time and frequency domain according to the motor current signature analysis technique.

To emulate broken bars condition, the rotor's bars were drilled progressively until the bar material was completely worn out but the discontinuity of the bar is guaranteed. The severity level is determined by the number of drilled bars. Thus, three severity levels are induced, corresponding to 1, 2, and 3 broken bars. The same induced levels are labeled incipient, moderate and severe broken bar fault, respectively.

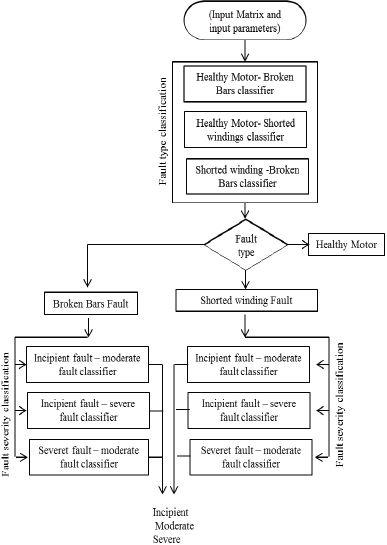
Finally, since the determination of the fault severity is based on the isolation of a given fault, the architecture proposed in this work to determine the type and severity of the fault is shown in Figure 2. It is important to mention that the features used in the severity estimation for shorted winding fault were different from those used in broken bars severity estimation. The blocks observed in Figure 2 correspond to bi-class classifiers; the classification method used was one versus one because a certain set of features allowed correct classifying of the data with acceptable error margin for each case.

Figure 2 Fault severity determination and diagnosis architecture. 

4.2. Current signature analysis

The tests carried on using the test bed with shorted winding fault demonstrated that the frequency domain components that were selected as indicators are independent from any other fault related frequency components. Additionally, the experiments showed the frequency components are only suitable indicators under low load condition. Thus, the MCSA technique is degraded by the increment of the load in the motor affecting the amplitude of the selected frequency domain fault indicator. Moreover, the frequencies associated with this type of fault depend on the motor particular operation conditions.

The NSC (negative sequence current) monitoring technique was also studied in dept. This method showed a reliable sensitivity when increasing the shorted winding severity, under several load conditions. Previous tests allowed concluding that there is a consistent increase in the NSC indicator when the load is coupled to the motor (^{Oviedo et al., 2014}), i.e. the baseline for healthy condition depends on the load regime. Further details about the use of the NSC as a motor fault indicator using the same test bed can be found in (^{Oviedo et al., 2011}).

In order to overcome the dependency of NSC magnitude with load regime, the use of the PSC/ NSC ratio is proposed as a fault indicator. As it was stated, the negative sequence current is widely known as unbalance indicator which is sensitive to the addition of load. In the same manner, the value of the positive sequence current (PSC) magnitude increases proportionally with the addition of load. Therefore, the load effect can be attenuated with the use of PSC/NCS ratio. Additionally, in order to guarantee a reliable and robust fault detection, power quality must be guaranteed in the motor supply network since the negative sequence current indicator is produced by unbalances, not all caused by stator shorted windings.

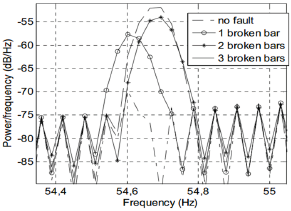
On the other hand, tests carried out with broken bar fault lead to the conclusion that it is possible to perform reliable monitoring of rotor bars condition using MCSA. As stated by Equation (1), there will exist frequency components with increasing power surrounding the supply frequency due to the fault condition. Moreover, when load is added the motor slip s increases and thus, the faulty frequency component (sidebands) move away from the supply frequency, facilitating the identification of the fault and its severity. Figure 3 presents the PSD magnitude change in the 54,7 Hz sideband when increasing fault severity at a 85% load.

Figure 3 PSD for several broken bar scenarios and 85% load. 

However, the increase of mechanical load when there is a broken bar condition leads to the development of sidebands around certain frequencies related to other motor faults like air gap eccentricity. Due to the previous fact, only the sidebands in the 56-66 Hz range were considered as a reliable range for broken bar fault detection in frequency domain. Further details about current signature analysis for broken bars detection using the same test bed can be seen in (^{Oviedo et al., 2011}).

4.3. Feature extraction and feature selection

With the aim of classifying motor faults, a set of representative features must be chosen and those features should appropriately represent the current signature (^{Ghate and Dudul, 2009}). As it was previously established, the MCSA (Motor Current Signature Analysis) technique allows identifying the frequency components with increasing energy as a fault consequence. Most common faults in previous studies include shorted winding, bearing defects, air gap eccentricity, broken bars, with outstanding results regarding broken bars detection using the power spectral density (^{Penrose, 2004}).

On the other hand, time domain features are mostly statistical features that can be interpreted in terms of the data histogram (^{Theodoridis and Koutroumbas, 2009}). For instance, skewness is a histogram symmetry indicator while kurtosis is a measurement of how sharp is the histogram

distribution; entropy is a measure of the histogram uniformity, therefore, the closer the histogram values are to each other, the higher the entropy value is. The crest factor is the signal peak amplitude divided by rms value. The purpose of using crest factor as a feature is to give an indication of how much certain abnormal condition is affecting the machine signals with spikes. Those impacts are associated with faults in motors and rotating machinery (^{Ghate and Dudul, 2011}). Other time domain features are mean and variance, which depending upon the type of fault, can be successful features for discriminating abnormal conditions. Furthermore, among the frequency features useful to describe changes in the spectrum of a given signal. The frequency center is calculated as the mass center of the spectrum s(f) regarding the fundamental frequency between frequency f₁ and frequency f₂, using sum intervals Δf. A variation in the center frequency is usually related to mechanical or electrical faults in the rotating machine and is commonly used in vibration analysis. The frequency center is calculated according Equation (11) (^{Deraemaeker, 2006}).

In general, previous works in the same field allow establishing the initial set of features for the classification performed in this work (using machine learning methods). In (^{Ghate and Dudul, 2009}), for example, the statistical features used include rms value, kurtosis and skewness maximum and minimum values. In (^{Gordi and Roshanferk, 2010}) the area under the curve of power spectral density of fault related sidebands and harmonics and the amplitude of the PSD using FFT were proposed as the most important features. Finally, in (^{Widodo et al., 2007}) a SVM based fault classification system was elaborated using vibration and current signals. For that end, the selected features were crest factor, entropy, rms value, central frequency, skewness and arithmetic mean, among others. The initial set of parameter for this work were established based on previous works, but also on the results of motor current signature analysis studies carried on.

Feature selection consists on reducing the initial feature set dimension with the aim of reducing complexity and to avoid overfitting. To this end, it is common to check individual features using statistical tools like t-test of fisher discriminant ratio. In this work, the features discrimination capability was assessed using t-test (p=0.05). This test provides an indication of which features should be kept and which ones should be discarded, especially if the classification is made up using several bi-class classifiers, as in this case.

For the broken bars severity, the selected features in time domain were:

On the other hand, the frequency domain features where:

For shorted winding fault severity classifier the selected features were PSC/NSC ratio and rms value of Power Spectral Density using the t-test method for all possible fault severity bi-class scenarios (e.g. 2% shorted winding fault vs. 5% shorted winding fault and so on). The features with the majority of success outputs were chosen.

5.1. Fault classification

This section describes the fault classification method and the results of using John Platt's SMO (Sequential Minimal Optimization) function, adapted by Michael Mavroforakis for bi-class classification problems (^{Theodoridis, 2010}). Some of the inputs were Matrix X, containing the input data set; vector Y that contains the class labels (1 and -1); Tol is a scalar that controls the algorithm's precision. Once this number is reached, the algorithm stops if it has not surpassed the step condition yet. Meanwhile, the output parameters are: 1) The vector with the estimated Lagrange multipliers, Alpha 2) The intercept term, b 3) The separating hyperplane normal vector, w (only makes sense when using a linear separator) 4) The number of times the norm is evaluated in the algorithm, evals 5) The number of steps until convergence, stp.

In addition, the training error is calculated as the ratio between the number of data outside the correct side of the classifier during the training (including those on the correct side, but inside the margin) and the total samples. Likewise, the validation error is the ratio between the number of samples outside the correct side of the classifier during the validation (including those on the correct side, but inside the margin) and the total samples ratio. The penalty constant C and kernel parameters were modified systematically and observing the training success percentage. As previously stated, error counting is based on the samples outside the correct class (including those points in the correct class, but inside the margin). When a non-linear classifier was required in the proposed classifying architecture the best results (in terms of convergence and error) were obtained using the Radial Basis Function Kernel, also known as Gaussian Kernel, expressed for vectors x and y by Equation (9).

In order to exploit the original data set in the training and validation procedures a random set of 50% of the data set was used in the training algorithm and the rest in the validation algorithm. Then, the data were crossed and the algorithm performance is assessed averaging the two results of the algorithms, in terms of error and support vectors. Two folds were used in order to establish a tradeoff between the generalization capability of each classifier and the limited training data. It is important to mention that in this work, the induced levels of shorted windings were labeled according to a specific severity level. Thus, 2% of shorted winding corresponds to an incipient fault; 5% shorted winding correspond to a moderate fault. Finally, 10% shorted winding corresponds to a severe fault. The same labeling scheme was used for broken bar fault severity classification; 1 broken bar corresponds to incipient fault, 2 broken bars corresponds to moderate fault and 3 broken bars corresponds to severe fault.

5.2. Fault type Classification

This type of classifier determines the class to which a given datum belongs. The classifier consists in three learning machines that classify data into one of three possible classes: 1) Healthy motor 2) Shorted winding motor or 3) Broken bars motor.

Healthy motor- broken bars motor classification

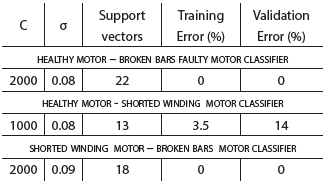
This bi-class machine works using Mean, PSC/NSC, Central Frequency and the RMS of Power Spectral Density as features. The SVM training exercises showed the performance stated in Table 1 . As stated before, the results are measured using training error, test error (or validation error) and the support vector count.

TABLE 1 PARAMETERS AND RESPONSE OF FAULT TYPE CLASSIFIERS 

Healthy motor - shorted winding motor classification

This bi-class machine works using Entropy and PSC/NSC as features. The training and validation results are displayed in Table 1. As stated before, the results are measured using training error, test error (or validation error) and the support vector count. The machine training and validation can be observed in a two dimensional graphic which depending upon features observed, can give a performance indication. Figure 4, shows the machine response with Entropy (abscissa) and PSC/NSC (ordinate) as features.

Figure 4 Healthy motor - shorted winding motor classifier response 

Shorted winding motor - broken bar classification

This bi-class machine works using mean, PSC/ NSC, central frequency and power spectral density RMS value as features. The training and validation performance results are showed in Table 1.

5.3. Fault severity classification

According to the fault classifier architecture proposed in this work, once the fault type is identified, it must be determined whether the fault is incipient, moderate or severe, depending on the established severity levels for the induced faults. The addition of load makes it difficult to identify the severity level because data form separated clusters depending upon the load regime. Sometimes these clusters are closer to other data corresponding to another severity level, so the learning machine must be flexible enough to classify well.

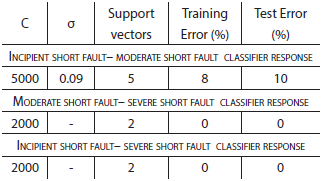
Shorted winding severity classifier

This classification task was achieved using three support vector machines that classify data into one of three possibilities: 1) incipient short circuit fault 2) moderate short circuit fault, 3) severe short circuit fault. This classifier uses PSC/NSC ratio and Power Spectral Density RMS value in all machines.

Incipient short fault- moderate short fault machine

Table 2 shows the training constants used in this machine and the performance parameters SV (support vectors), training error and validation error.

TABLE 2 PARAMETERS AND RESPONSE FOR SHORTED WINDINGS FAULT SEVERITY CLASSIFIERS 

Moderate short fault- severe short fault machine and Incipient short fault- severe short fault machine

Table 2 shows the training constants used in both bi-class machines and the performance parameters SV (support vectors), training error and validation error. Both are linear machines, and the scalar product did not require a kernel function.

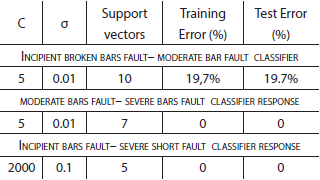
Broken bars severity classifier

This classifier uses three support vector machines that classify data into one of three possibilities: 1) incipient broken bars fault, 2) moderate broken bars fault, 3) severe broken bars fault. This classifier uses Crest factor, Mean, Entropy and PSC/NSC ratio as features.

Incipient broken bars- moderate broken bars machine

This bi-class machine works using Arithmetic mean, and Crest Factor as features. The experiments using those features when training a SVM showed the performance enounced in Table 3.

TABLE 3 PARAMETERS AND RESPONSE FOR BROKEN BARS FAULT SEVERITY CLASSIFIERS 

Moderate broken bars- Severe broken bars machine

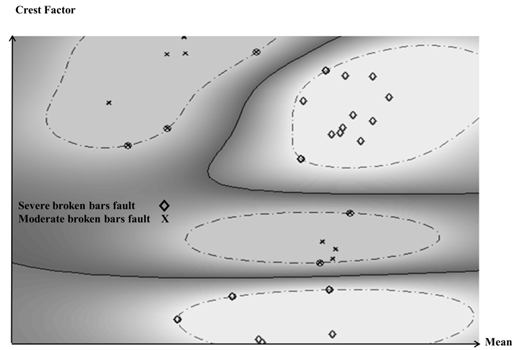
This machine also uses Mean, and Crest factor as features (see Table 3). The machine response in a two dimensional graphic is showed in Figure 5 with Mean (abscissa) and Crest factor (ordinate) as features.

Figure 5 Moderate broken bars fault- severe broken bars fault machine response 

Incipient broken bars- severe broken bars machine

This bi-class machine works using Arithmetic Mean, PSC/NSC, Crest Factor and Entropy as features. The experiments using those features when training a SVM showed the performance enounced in Table 3. These results show that even though broken bars are mechanical faults, it is feasible to use the proposed feature (PSC/NSC ratio) to determine the severity of this type of fault in several load scenarios, since this feature reflects in a very reliable way the asymmetries in the stator current when bar breakage is present.

The above results demonstrate that, combining MCSA technique and time domain features is a reliable way to detect and identify faults in induction motors. Whereas MCSA allows predicting faulty components in the current power spectral density, time domain features like Crest factor allow measuring unbalances directly from the waveform, which is useful for fault isolation purposes.

Finally, it can be stated that the PSC/NSC ratio performed well for both identification of the type of fault and severity estimation. This ratio allows normalizing the current signal in the presence of load and therefore makes it possible to adapt classifiers.