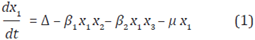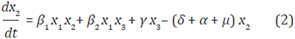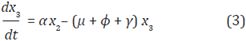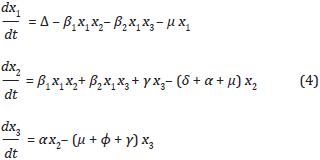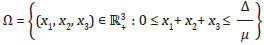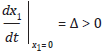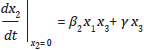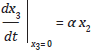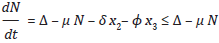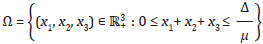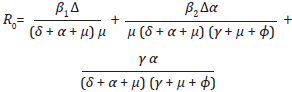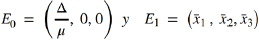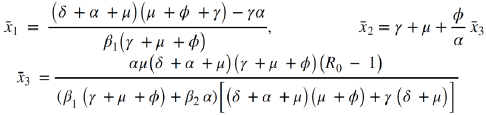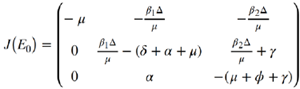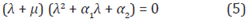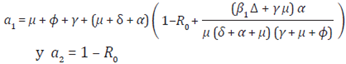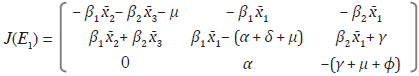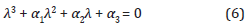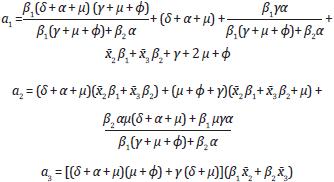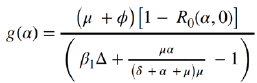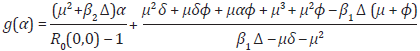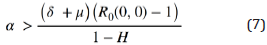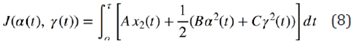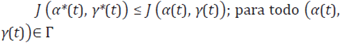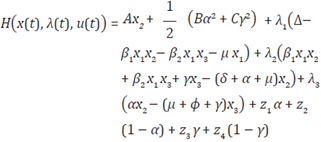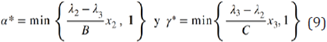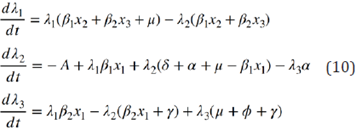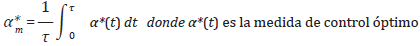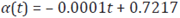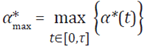Español (pdf)
Articulo en XML
Referencias del artículo
Traducción automática
Enviar articulo por email
Citado por SciELO 
Citado por Google 
Similares en
SciELO 
Similares en Google 
Permalink
1. Introducción
La infección por el Virus de Inmunodeficiencia Humana (VIH) y el Síndrome de Inmunodeficiencia Adquirida (SIDA) son un problema de salud a escala mundial, que tiene impactos negativos a nivel psicológico, biológico, sociocultural y económico, tanto en la persona infectada como en sus familiares (Organización Mundial de la Salud, 2015). Las principales vías de transmisión del virus del VIH son: el contagio por relaciones sexuales con una persona portadora del virus, por transfusión de sangre contaminada, por compartir agujas, jeringas o diferentes objetos punzocortantes o de la madre al feto (Grupo Trabajo sobre Tratamientos del VIH, 2011) El virus logra desgastar el sistema inmune hasta que produce una deficiencia que incrementa el riesgo de sufrir infecciones oportunistas. Una vez la persona es diagnosticada como portadora del VIH, deberá iniciar tratamiento antirretroviral (TAR), que generalmente consiste en un politerapia constituida por tres o más antirretrovirales, los cuales actúan inhibiendo la replicación del virus, bloqueando las enzimas del VIH o creando nuevas barreras para la enfermedad.
El concepto de acceso efectivo al TAR hace referencia a la proporción de personas que pueden iniciar el uso de antirretrovirales. Generalmente, dado el alto costo de los tratamientos frente al VIH, el acceso es limitado y depende mucho de su inclusión en los sistemas de salud de los países. Se debe tener en cuenta que el concepto de los altos costos afecta directamente a la calidad de medicamentos utilizados, dado que aunque los medicamentos de primera línea generan mejores resultados disminuyendo los efectos secundarios y la resistencia del virus a los medicamentos, producen mayores costos, y es por esto que generalmente en los países del sur global se utilizan medicamentos de segunda línea que brindan resultados aceptables (Zaidi, 2011).
En Colombia, se rige por la resolución número 5592 del 24 de diciembre de 2015 del Ministerio de Salud y Protección Social, en la cual se establece todo lo relacionado con el Plan de Beneficios en Salud con cargo a la Unidad de Pago por Capitación (UPS) del Sistema General de Seguridad Social en Salud (SGSSS) (Ministerio de Salud y Protección Socia, 2015).
Es fundamental la capacidad del paciente para seguir las indicaciones del médico de manera adecuada, concepto que se denomina adherencia y se refiere a todo lo relacionado con el correcto cumplimiento del tratamiento antirretroviral (Tarinas, et al., 2000), la adherencia presenta dos tipos de barreras, adherencia farmacológica y adherencia no farmacológica, relacionadas con factores como: olvido, múltiples ocupaciones, el estar enfermo o deprimido, experimentar efectos secundarios a causa del uso de los antirretrovirales, el tipo de alimentación, la actividad física, el consumo de bebidas alcohólicas y sustancias psicoactivas, e interacciones medicamentosas (infosida, 2005), (infosida, 2017), (Santillán, 2014), (Varela & Hoyos, 2015).
En el ámbito del modelado del VIH y SIDA, se encuentran diversas publicaciones donde proponen modelos matemáticos en los que se contempla la dinámica del virus a nivel inmunológico o la dinámica poblacional de la enfermedad. Algunos modelos planteados en la literatura se han enfocado en el modelado de la infección y el tratamiento (Adams, et al., 2005), (Campos & Palacios, 2005), (Cleary, et al., 2010), (Culshaw, et al., 2004), (Del Valle, et al., 2004), (Ding & Wu, 1999), (Hsu, 2000), (Nelson, et al., 2000), (Revilla & García, 2003), (Shim, et al., 2003), (Stengel, 2008), (Wandeler, et al., 2011), (Zaric, et al., 2008); en el modelado de costos (Haacker, 2002), (Oliva, et al., 2010) , (Trujillo & Toro, 2015), (Zaric, et al., 2008) el modelado de la dinámica del VIH (Dalal, et al., 2008), (Tan & Byers, 1993), (Taylor, et al., 1994) o han hecho uso de los procesos estocásticos para modelar la dinámica (Chao, et al., 2004), (Dalal, et al., 2008), (Gray, et al., 2003) (Hsu, 2000), (Jiang, et al., 2017), (Kouyos, et al., 2006), (Ribeiro & Bonhoeffer, 1999).
En particular, en lo que respecta al número básico de reproducción, Rivera B., et al. (2011), estudian la dinámica de VIH-SIDA en la ciudad de Cali por medio de un modelo SIR, toman como supuesto que la transmisión sexual es el único medio de contagio, estiman el número básico de reproducción y encuentran dos puntos de equilibrio (Sepulveda, et al., 2011).
Nelson P., et al. (2000), investigan las mediciones experimentales sobre el VIH, especialmente utilizando datos de experimentos en la administración de potentes fármacos antirretrovirales y considerando que tras la infección de una célula, esta comienza inmediatamente a producir el virus (Nelson, et al., 2000). Por otro lado, Marco A. (2012), observa una relación entre el cumplimiento del tratamiento antirretroviral con el fracaso virológico, llegando a una implicación directa del concepto de adherencia en las personas que tienen tratamiento antirretroviral (Marco, 2012).
En correspondencia con lo anterior, en la sección 2 se propone un modelo matemático basado en ecuaciones diferenciales ordinarias, que interprete la dinámica de infección por el virus del VIH en una población humana considerando individuos en un intervalo de edad de 15 a 25 años (sin consideraciones de género u orientación sexual), con el fin de estudiar el efecto que, el acceso efectivo y el fracaso terapéutico al TAR tienen sobre la dinámica de la enfermedad; en la sección 3 se plantea un problema de control óptimo, considerando un funcional de costos que acumule los costos directos e indirectos del acceso efectivo y el abandono al TAR, determinando un problema de contorno el cual es solucionado por medio de un software matemático, y por último en la sección 4 se establecen algunas conclusiones relacionadas con los umbrales propuestos en la sección 2.
2. Planteamiento del modelo
En la formulación del modelo, se asume que la población humana se encuentra dividida en tres categorías o subpoblaciones, que corresponden a (i) personas susceptibles de adquirir el virus; es decir, personas que son sexualmente activas en un rango de edad de 15 a 25 años y que podrían, eventualmente, entrar en contacto con personas infectadas; (ii) personas infectadas con el virus pero que no están en TAR, bien sea porque no han sido diagnosticados, porque no han iniciado el tratamiento, o porque han decidido abandonarlo. Finalmente, (iii) personas infectadas que se encuentran en TAR.
Sea la variable de estado x 1 = x 1 (t) que denota el número promedio de personas susceptibles a adquirir el virus del VIH en un determinado tiempo t, la variable de estado x 2 = x2(t) que representa el número promedio de personas portadoras del virus sin TAR y x3 = x3(t) el número promedio de personas infectadas que acceden efectivamente al tratamiento. Se asume que la población x 1 crece a una tasa constante Δ y que disminuye proporcionalmente a su tamaño según una tasa de muerte natural x, de manera que ¡x x 1 denota el número promedio de personas susceptibles que mueren por causas naturales. Se considera que ß1 x1 x2 representa el número promedio de contactos efectivos entre infectados sin tratamiento y susceptibles, y ß2 x1 x3 es el número promedio de contactos efectivos entre infectados con tratamiento y susceptibles; lo que implica asumir que la tasa de infección puede ser descrita por la ley de acción de masas, formulada por Hamer en 1906 y la cual describe que el número de contactos infecciosos, por unidad de tiempo es proporcional al número total de contactos entre individuos infectados y sanos (Cuddington & Beisner, 2005). Según lo anterior, la variación de la población susceptible con respecto al tiempo se describe por la ecuación:
Sea αx 2 el término que representa al número promedio de personas infectadas que "acceden efectivamente" al tratamiento antirretroviral, por lo tanto α denota la proporción de acceso efectivo a tratamiento; es decir, α = 0 implica que ninguna persona infectada puede acceder al tratamiento, mientras que α = 1 implica que el 100% de la población infectada accede efectivamente al tratamiento, es decir, cobertura completa. Considere ahora que las personas infectadas sin tratamiento, tienen una tasa de muerte asociada con la enfermedad 8, así que 8x 2 denota el número promedio de personas que mueren como consecuencia de la infección, en general, estas muertes están asociadas con la aparición de enfermedades oportunistas. Nuevamente, con xx 2 se denota el número promedio de personas infectadas sin tratamiento que mueren por causas naturales. La ecuación que describe la variación de x2 con respecto al tiempo, queda de la forma:
Finalmente, se asume que la variación de la población infectada con tratamiento x3 está dada por:
donde µx 3 denota el número promedio de personas infectadas y con TAR que mueren por causas naturales. También considera que las personas infectadas con tratamiento, tienen una tasa de muerte asociada con la enfermedad ϕ así ϕx3 denota el número promedio de personas infectadas sin tratamiento que mueren como consecuencia de la infección, yx 3 denota la proporción de personas que presenta fracaso terapéutico, por lo cual se está asumiendo que 1 - γ es la proporción de personas que se "adhieren" al tratamiento, y γ es la proporción de personas infectadas que lo abandonan, es decir, tuvieron fracaso terapéutico.
El sistema de ecuaciones diferenciales ordinarias y no lineales que interpreta la dinámica del proceso es:
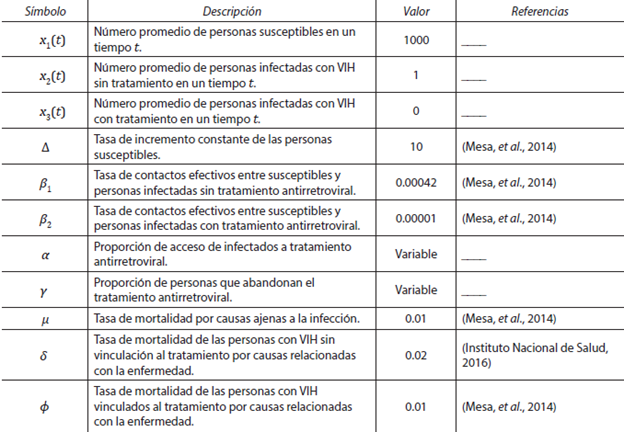
Donde Δ, μ, δ, ϕ > 0, 0 ≤ β1 ≤ 1, 0 ≤ β2 ≤ 1, 0 ≤ α ≤ 1, 0 ≤ γ ≤ 1 y las condiciones iniciales son x1(0) = x10, x2(0) = x20 y x3(0) = x30 las cuales se asumen no negativas. La descripción de variables y parámetros pueden verse en el Cuadro 1.
Proposición 1:
Las soluciones del sistema (4),
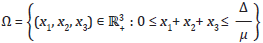es un conjunto positivamente invariante:
Prueba: Para que las soluciones sean no negativas; note que,
Por lo tanto x1(t) es creciente, luego la función x1(t) será no negativa. De manera semejante,
Como γ ε [0,1] se obtiene β2 x1 x3+ γ x3 ≥ 0, en cuyo caso se concluye que x2(t) es creciente y no negativa. Por último,
De donde se concluye que α x2 ≥ 0 debido a que α > 0, por lo tanto x3(t) es creciente y no negativa. Para probar que las soluciones están acotadas superiormente, sea N = x1+ x2+ x3, por lo tanto su variación respecto a t está dada por:
Por lo tanto
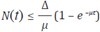de donde
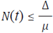cuando t → ∞, por lo anterior se concluye
que la región de
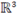definida por:
es un conjunto positivamente invariante para sistema (4).
2.1. Análisis del modelo
Para el modelo formulado anteriormente se hace un análisis que consiste en determinar el número básico de reproducción R0, se encuentran los puntos de equilibrios que presenta el modelo y la estabilidad local de los mismos, se finaliza determinado dos umbrales de control con base en el nivel de acceso efectivo y del fracaso terapéutico, finalmente se muestran las simulaciones del sistema de ecuaciones diferenciales.
2.1.1. Número básico de reproducción R0
El número básico de reproducción R0, está definido como el número esperado de casos secundarios producidos por un individuo infectado típico durante todo su período de infecciosidad en una población susceptible demográficamente estable, matemáticamente se puede definir como el radio espectral de la matriz de la siguiente generación (Heesterbeek, 2002). Para el sistema (4) el R0 está dado por:
TABLA 1 DESCRIPCIÓN DE LAS VARIABLES Y PARÁMETROS USADOS EN EL MODELO (4), LOS VALORES ASIGNADOS PARA SIMULACIÓN Y LA FUENTE BIBLIOGRÁFICA DE DONDE SON OBTENIDOS
Para una mejor comprensión del significado del número básico de reproducción R0 se debe tener en cuenta que se presentan efectos aditivos y multiplicativos, el término
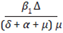representa los nuevos casos que produce una persona infectada sin tratamiento antirretroviral los cuales se encuentran en la categoría x2, mientras que los términos
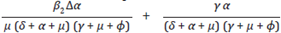representan los nuevos casos que producen las personas infectadas con tratamiento antirretroviral, los cuales se encuentran en la categoría x3.
Del primer término
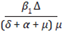se tiene que
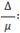población susceptible en ausencia de infección, β
1 representa la tasa de contactos efectivos entre susceptibles e infectados sin tratamiento y
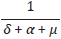indica el periodo infeccioso de una persona infectada sin tratamiento antirretroviral.
El segundo término
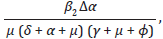se tiene que β
2 es la tasa de contactos efectivos entre susceptibles e infectados con tratamiento,
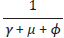es el periodo infeccioso de una persona infectada con tratamiento antirretroviral y α es la tasa de personas infectadas que acceden al tratamiento antirretroviral. El tercer término
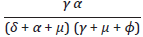tiene elementos ya interpretados, por lo cual solo se dará la interpretación del restante, este es γ, el cual indica proporción de personas que abandonan el tratamiento antirretroviral.
2.1.2. Puntos de equilibrios
Los puntos de equilibrio indican soluciones constantes que satisfacen el sistema no lineal, es por esto que se considera
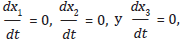resultando así un sistema algebraico no lineal, que al resolverlo permite determinar los puntos de equilibrio. El sistema presenta dos puntos de equilibrios:
Donde
El punto de equilibrio E 0 indica que el Virus de Inmunodeficiencia humana no se encuentra en la población; es decir, no se encuentran personas infectadas, este punto de equilibrio puede llamarse en ausencia de infección o en ausencia de enfermedad. Por otro lado el punto de equilibrio E1 representa que en la población se encuentran personas susceptibles e infectadas con VIH; en particular, el grupo de las personas infectadas con VIH se divide en dos subgrupos, las personas infectadas con VIH sin tratamiento y los infectados con tratamiento.
La estabilidad del punto de equilibrio E 0 y del punto de equilibrio E 1 se encuentran descritas en las siguientes proposiciones:
Proposición 2: El equilibrio libre de infección E 0 es local y asintóticamente estable si y solo si R 0 < 1.
Prueba: Se evalúa la matriz jacobiana en el punto de equilibrio
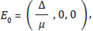con lo que se obtiene:
La ecuación característica de la matriz J(E0) está dada por:
Donde
Por lo tanto un valor propio es λ1 = - µ el cual es siempre negativo, para establecer los signos de la parte real de los otros dos valores propios se acude al criterio de Routh-Hurwitz (Perko, 2013) que permite establecer que cuando a1 > 0 y a2 > 0 entonces la ecuación cuadrática tiene solución con parte real negativa, y esto se cumple cuando R0 < 1.
Así R0 < 1 es condición suficiente y necesaria para que el punto de equilibrio E 0 sea local y asintó-ticamente estable.
Proposición 3: El equilibrio en presencia de infección E1 es local y asintóticamente estable si y solo si R0 > 1.
Prueba: Se evalúa la matriz jacobiana en el punto de equilibrio
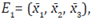con lo que se obtiene:
ßi X2+ ß2 X3 ßi Xi- (a + 8 + x) ß2 Xi+ y 0 a -(y + x + 0) J
La ecuación característica de la matriz J(E 1 ) está dada por:
Donde:
Se hace evidente que a1 > 0, a2 > 0 y a3 > 0, y teniendo en cuenta la regla de los signos de descartes se puede afirmar que todas las raíces de la ecuación característica tiene parte real negativa y así R0 > 1 (si R0 > i entonces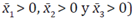 
es condición suficiente y necesaria para que el punto de equilibrio Ei sea local y asintóticamente estable.
2.1.3. Umbral de adherencia en función del acceso al tratamiento
Teniendo en cuenta la Proposición 2, y considerando R0 como una función de los parametros α y y, se tiene que la enfermedad es controlada si R 0 (α, y) < i. Con el fin de determinar un valor umbral de y en función de a tal que R0(α, y) < i, se tiene que y < g(α) donde:
o explícitamente
En la Figura 1 se muestra la recta y = g(α), además se ilustra la región y < g(α), dicha región representa un conjunto de valores (α, y) donde propician R0(α, y) < 1, al igual en la figura se ilustra la región y > g(α), en esta región los valores (α, y) establecen R0(α, y) > 1 . De esta manera, en la Figura 2 figuestablecen los distintos valores de α y y en los cuales se propicia un escenario para que R0(α, y) < 1, R0(α, y) > 1 y R0(α, y) = 1.
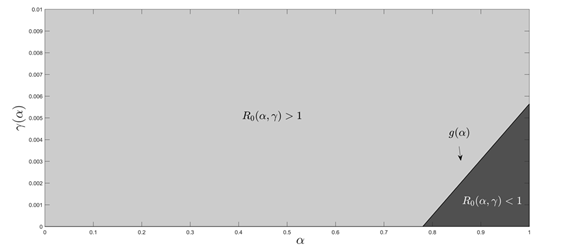
Figura 1 La gráfica y=g(α), divide el plano, (α,y) en dos regiones, donde se representa de color gris oscuro R0 (α,y)<1 y en la región de color gris claro se muestra R0 (α,y)>1, utilizando los valores de los parámetros de la Tabla 1
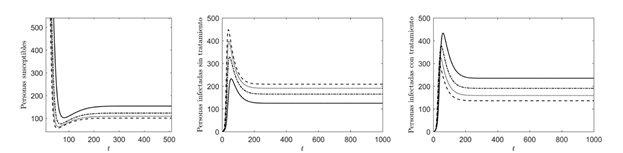
Figura 2 Dinámica de las poblaciones con R 0(α, γ) > 1 y para valores de γ = (0.3, 0.5, 0.7, 0.9) que corresponden a las curvas (-, - ∙ -, ∙ ∙ ∙, - -), con los correspondientes valores de R 0(α, γ) = (1.58, 1.6, 1.605, 1.608)
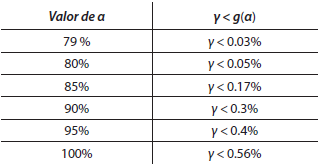
En la Tabla 2 se muestran valores de a, los cuales representan el acceso efectivo que se debe garantizar a las personas infectadas con VIH, y a partir de ellos se obtuvo el porcentaje máximo de fracaso terapéutico que se puede presentar en la población infectada, buscando así un R0(α, y) < 1, lo que sugiere teóricamente y bajo los supuestos de este modelo condiciones de evitabilidad para evitar manifestaciones de la infección.
TABLA 2 VALORES DE ACCESO EFECTIVO Y FRACASO TERAPÉUTICO AL TRATAMIENTO ANTIRRETROVIRAL QUE EVITAN TEÓRICAMENTE MANIFESTACIONES DE LA INFECCIÓN.
2.1.4. Umbral de acceso a tratamiento
Se considera que el abandono a la terapia antirretroviral es nulo, es decir, y = 0 con el fin de establecer un nivel mínimo de acceso a la terapia antirretroviral, tal que R0(α, 0) < 1, es así que se tiene:
Donde
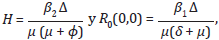para que el umbral de acceso tome sentido se debe establecer que H < 1 y R0(0, 0) > 1; en efecto R0(0, 0) > 1 garantiza que la infección se ha establecido en la población, ya que en caso contrario y según la proposición 3 no tiene sentido controlarla.
Por otro lado si R0(0, 0) > 1 entonces se requiere H < 1 para que el lado derecho de (5) sea no negativo.
2.2. Simulaciones
Se realizaron simulaciones del sistema de ecuaciones diferenciales; en las Figuras 2-5 se observa el comportamiento de las personas susceptibles, infectadas sin tratamiento e infectadas con tratamiento teniendo en cuenta los valores para los parámetros que se encuentran en el Tabla 1.
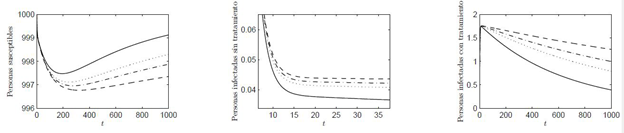
Figura 3: Dinámica de las poblaciones con R0 (a,Y) <1 y para valores de Y = (0.000002, 0.0009, 0.0012, 0.0015) que corresponden a las curvas (- , ∙ ∙ ∙ , - ∙ -, - -) con los correspondientes valores de R0 (a,Y) = (0.96, 0.98, 0.98, 0.99)
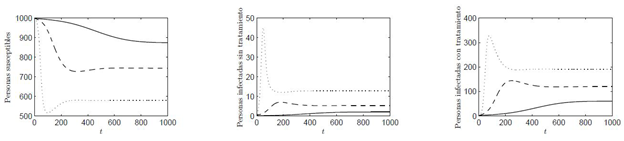
Figura 4 Dinámica de las poblaciones con R0 (a,0) >1 y para valores de α = (0.3, 0.45, 0.6) que corresponden a las curvas (∙ ∙ ∙ , - -, -) con los correspondientes valores de R0 (α,0) = (1.72, 1.34, 1.14)
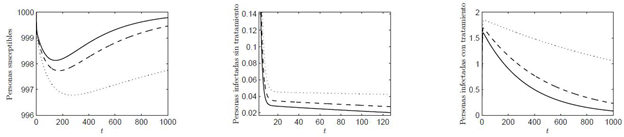
Figura 5 Dinámica de las poblaciones con R0 (α,0) <1 y para valores de α = (0.8, 0.88, 0.95) que corresponden a las curvas (∙ ∙ ∙ , - -, -), con los correspondientes valores de R0 (α,0) = (0.98, 0.94, 0.91)
En la Figura 2 se considera una variación en los valores de γ en un intervalo de [0,1], en donde la línea (-) representa el valor de γ = 0.3, la línea (- -) representa el valor de γ = 0.9, la línea (- ∙ -) representa el valor de γ = 0.5 y la línea (∙ ∙ ∙) representa el valor de γ = 0.7, y con un valor fijo de α = 0.6, el cual se considera a partir de la Figura 1 garantizando un R 0(α, 0) > 1.
En la Figura 2 estableciendo una variación en los valores de γ en un intervalo de [0,1], en donde la línea (-) representa el valor de γ = 0.000002, la línea (- -) representa el valor de γ = 0.0015, la línea (- ∙ -) representa el valor de γ = 0.0012 y la línea (∙ ∙ ∙) representa el valor de γ = 0.0009, y con un valor fijo de α = 0.85, el cual se considera a partir de la Figura 1 garantizando un R 0(α, 0) < 1.
Se realiza una variación en las simulaciones en donde se considera el valor de γ = 0 y variando el valor de a, con lo que se obtiene.
En la Figura 4 se realiza una variación en los valores de a en un intervalo de [0,1], en donde la línea (-) representa el valor de α = 0.6, la línea (- -) representa el valor de α = 0.45, y la línea (∙ ∙ ∙) representa el valor de α = 0.3, los valores de a implementados ilustran un escenario donde R0(α, 0) > 1.
En la Figura 5 considerando una variación en los valores de a en un intervalo de [0,1], en donde la línea (-) representa el valor de α = 0.95, la línea (- -) representa el valor de α = 0.88, y la línea (∙ ∙ ∙) representa el valor de α = 0.8, los valores de a implementados ilustran un escenario donde R0(α, 0) < 1.
3. Problema de control óptimo
Considere un funcional de costos que acumula los costos directos e indirectos del acceso efectivo y el fracaso terapéutico al TAR.
Donde α(t) es la función de acceso efectivo al TAR en función del tiempo t y γ(t) es la función de fracaso terapéutico en función del tiempo t, ambas funciones definidas en el intervalo [0,T], y A, B y C son ponderadores usados para equilibrar las unidades de los términos que se suman en (8).
Considere
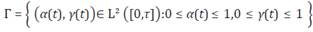el conjunto de controles admisibles. El objetivo es minimizar /(α(t), y(t)) es decir encontrar un par de funciones óptimas (α*(t), y*(t)) tal que
Se aplica el Principio del Máximo de Pontrya-gin para estudiar el problema de control óptimo, para esto se tiene en cuenta u(t) = (α(t), y(t)) y se determina el siguiente Halmitoniano
donde
son funciones continuas que denotan variables de coestado y los z
i
con i = 1, 2, 3 son cantidades de penalización positivas usadas para garantizar que 0 ≤ α(t) ≤ 1 y 0 ≤ γ(t) ≤ 1.
Según la función Hamiltoniana tenemos:
Aplicando la condición de primer orden
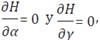se obtiene:
El sistema adjunto se describe a través de las variables λ
1
, λ
2
, y λ
3
, las cuales están determinadas por medio de la siguiente expresión
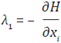para i = 1, 2, 3. Explícitamente
con las condiciones terminales λ1(τ) = 0, λ2(τ) = 0, Y λ3(τ) = 0. El problema de contorno está dado por el sistema de variables de estado (4) los controles óptimos (9) y el sistema adjunto (10).
3.1. Resultados numéricos
Se simula el problema de contorno utilizando el software Matlab, con los valores de los parámetros dados en la Tabla 1, con un valor fijo del ponderador A = 1 y C = 10 y variando el ponderador B con valores de 10, 50, 110, y 160.
Se observa a partir de las simulaciones, que, al variar los valores del ponderador B, esto es al considerar costos mayores generados por brindar acceso efectivo, se produce una curva óptima que refleja niveles bajos de acceso a los antirretrovirales, caso contrario si se establece un bajo costo de acceso efectivo, la curva óptima generada muestra que se debería garantizar un mayor porcentaje de acceso. Por lo anterior, se podría considerar que la relación entre el costo de acceder de forma efectiva al tratamiento y el porcentaje óptimo que se debe garantizar para brindar control en la población infectada son inversamente proporcionales. También se observa que en los diferentes escenarios propuestos se debe asegurar que el nivel óptimo de adherencia a los antirretrovirales sea del 100%, para obtener así un escenario donde el VIH tenga un nivel de control adecuado.
3.2. Controles subóptimos
Por medio de la medida de control de acceso efectivo al tratamiento antirretroviral, se pretende disminuir el número de infecciones generadas a causa del VIH, aunque la implementación de esta medida de control se ve afectada por diferentes factores; es por esto que se buscan, estrategias de forma constante y más simples que la función óptima, logrando así que los protocolos de tratamiento dado que no cambian diariamente, se ajusten de manera adecuada o mucho más fácil a la curva de control, estas estrategias las denominaremos estrategias subóptimas.
Control óptimo promedio: una de las estrategias subóptimas consideradas, como medida de control, es el control óptimo promedio, este control se considera con el fin de tener una estrategia no muy lejana a la óptima ya considerada (ver Figura 6) pero con el cual se tiene una medida constante, la cual podría facilitar la utilización del tratamiento antirretroviral; para determinar esta medida de control, se hizo uso del valor promedio de una función y consiste en determinar:
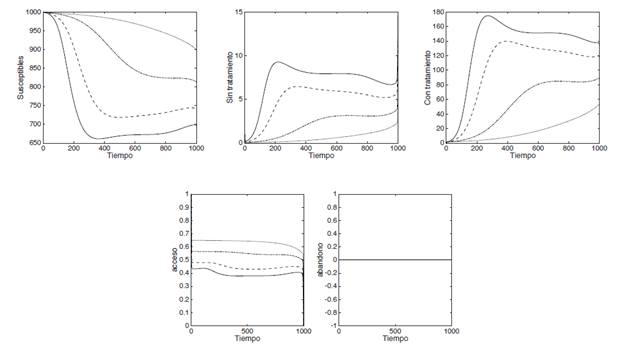
Figura 6 Simulación del problema de contorno formado por (4), (9) y (10), utilizando los valores de los parámetros de la Tabla 1 y con los valores de los ponderados A=1, C=10 y B=(10,50,110,160) que corresponden a las curvas (∙ ∙ ∙, - ∙ -, - -, -)
Utilizando los valores de los parámetros de la Tabla 1, el control óptimo promedio es de
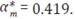
Regresión lineal: se considera otra medida subóptima, por medio de una regresión lineal, generada a partir de los valores tomados en el control óptimo, con la cual se pretende considerar una medida de control de forma variable que propicie valores similares o muy cercanos a los valores de la curva óptima, con el fin de que sea una curva más simple que la función óptima. Para determinar la regresión lineal se utiliza el comando polyfit de Mat-lab, y esta regresión tiene como ecuación:
en donde se observa que la pendiente de la recta de regresión es negativa con lo que indica que a medida que el tiempo aumente, la tasa de acceso efectivo disminuirá.
Valor máximo: la última estrategia subóptima aquí considerada, se hace por medio del valor máximo del control óptimo, la cual está dada por:
utilizando los valores de los parámetros de la Tabla 1,
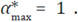
La Figura 7 ilustra la curva óptima, considerando los valores de los parámetros dados en el Tabla 1 y con un valor de B = 10, al igual se muestra el valor máximo de la curva óptima, el valor promedio de ella y la regresión lineal.
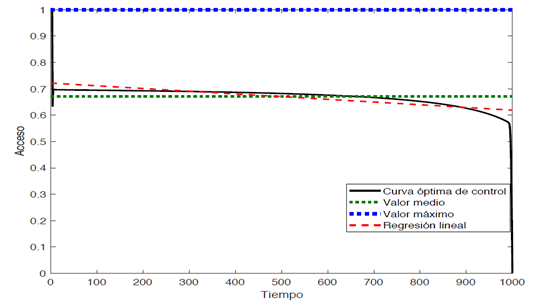
Figura 7 Curva óptima de acceso efectivo al tratamiento antirretroviral, considerada con el valor del ponderador B=10 y los valores de los parámetros del Tabla 1., donde la función de la curva de regresión es α(t) = -0.0001t + 0.7217,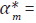 
0.419, y 
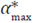= 1
En la Figura 7 se observa que la dinámica de la línea promedio y de la regresión lineal, varían de forma cercana a la curva óptima, haciendo que ellas se encuentren por encima y por debajo de la misma; es por esto que se podría considerar alguna de estas curvas como sustituta aceptable del control óptimo, al momento de no poder considerar la curva óptima como medida de control.
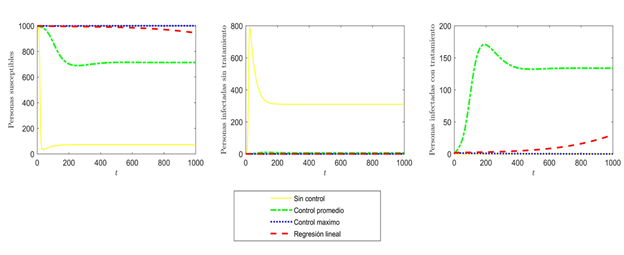
La Figura 8 ilustra el efecto que tiene las distintas estrategias subóptimas, consideras en la dinámica generada por el VIH en la población humana.
La incidencia que tiene la medida del máximo del control óptimo, sobre la dinámica de las poblaciones, como es de esperarse, genera que solo exista población susceptible y que los niveles de infectados ya sea con tratamiento o sin tratamiento antirretroviral sean nulos, al compararse esta estrategia de control con las curvas óptimas mostradas en la Figura 6, se puede observar que sería de gran ayuda para las diferentes poblaciones, pero al momento de observar qué sucede en la relación con el acceso efectivo al tratamiento antirretroviral, mostrado en la Figura 7 se observa que si muchas veces la implementación de medidas óptimas son difíciles, lo sería mucho más la del máximo de la misma.
El efecto generado por el control óptimo promedio, evidencia que esta medida de control genera un aumento en la población de susceptibles al igual que la población infectada con tratamiento antirretroviral, y disminuye la población infectada sin acceso efectivo al tratamiento, generando así que la enfermedad sea controlada teóricamente de una manera efectiva evitando que se genere manifestaciones de la infección en la población.
Por último se observa que el control por medio de la regresión lineal, al igual que las otras estrategias subóptimas refleja que la cantidad de infectados sin acceso efectivo al tratamiento antirretroviral tiende a niveles muy bajos, generando así que la enfermedad sin importar la estrategia subóptima utilizada tenga buenos beneficios para la población infectada; si se observa la Figura 6, la cual muestra curvas óptimas, y la Figura 8 se podría afirmar que existe gran similitud en la dinámica de las diferentes poblaciones, por lo cual las medidas subóptimas constituyen una medida de control eficiente.
Conclusiones
Bajo el modelo planteado, se puede establecer que si el acceso de forma eficaz es limitado (valores bajos de o), se debe evitar que las personas tengan un fracaso terapéutico (garantizar valores bajos de y) con el fin de que no se presente manifestaciones de la infección. En contraste, si la adherencia al tratamiento es del 100%, es decir y = 0, se debe considerar un valor alto de o, superior al 70% con los valores de los parámetros considerados para este caso y los supuestos respectivos, para así garantizar el control de la enfermedad.
En la Tabla 2 se muestran algunos casos especiales en que se determina el valor umbral de y en porcentaje (porcentaje de fracaso terapéutico del tratamiento) que se debe satisfacer, dado el valor de acceso efectivo a en porcentaje. Como puede verse, aún para los niveles más grandes de acceso efectivo, es necesario contar con niveles de fracaso al tratamiento muy bajos. En particular, en el caso hipotético en que se garantiza acceso efectivo al tratamiento antirretroviral al 100% de la población infectada, se requiere que la tasa de fracaso terapéutico no supere el 0.56%, este escenario se cumple solo se si satisface todos los supuestos del modelo.
En el planteamiento del problema de control óptimo donde se consideran como medidas de control el acceso efectivo y el fracaso terapéutico a la terapia antirretroviral en función del tiempo, para este caso se considera una escala temporal de 1000 días, en el cual se mostró que siempre el nivel de fracaso terapéutico debe ser de cero, mientras que el acceso óptimo que se debe brindar varía de forma significativa dependiendo de los valores considerados para los ponderadores, entre más alto se considere el valor del ponderador B, más bajos serán los niveles de acceso efectivo al tratamiento antirretroviral, a pesar de estas variaciones en los pondera-dores se observó que los niveles de acceso efectivo al tratamiento se encuentran entre el 40% y el 60% aproximadamente, todo esto si se cumplen todos los supuestos del modelo.
Según los parámetros usados y el tiempo de simulación considerado, la curva óptima promedio contribuye a que solo se genere población susceptible y población infectada con tratamiento antirretroviral, contribuyendo con un control de manera adecuada. En la medida de control subóptima relacionada con la regresión lineal se ve reflejado que garantiza mejores medidas de control que la curva promedio, dado que disminuye la cantidad de personas infectadas con acceso efectivo al tratamiento, y genera una mayor cantidad de personas susceptibles; a pesar de esto, como es de esperarse, al considerar el valor máximo en la medida de control, la dinámica de las poblaciones no presenta infección, y aunque las simulaciones reflejan que esta sería la mejor manera de controlar la infección se deben considerar factores como el alto costo que esta medida podría demandar, debido a que no corresponde a una solución óptima del problema.
