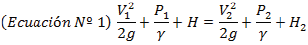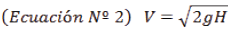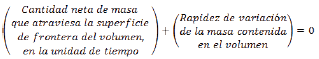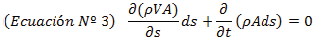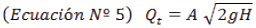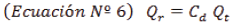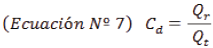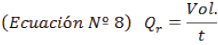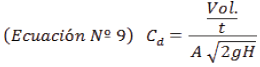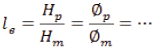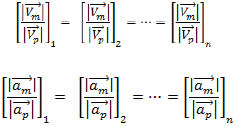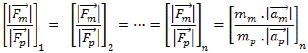Introducción
Los orificios son parte de las obras de la ingeniería hidráulica, estos se consideran como estructuras de control (Barragán M, 1993), sin embargo, se ha encontrado escasa información bibliográfica, específicamente de los coeficientes de descarga para orificios circulares de pared delgada, situación que ha motivado esta investigación. La importancia de las estructuras de control se debe al uso que se la da para la medición y regulación de caudales (Barragán M, 1993), (Silva, 2011). La medición de caudales se realiza a través de la cantidad de masa que circula en un determinado tiempo por un sistema de control (Garcia Gutierrez, y otros, 1999), se lo determina de dos formas: directamente, mediante dispositivos de desplazamiento, e indirectamente por medio de dispositivos que controlan la presión diferencial, área variable, velocidad, conformación del orificio, aceleración de la gravedad (Garcia Gutierrez, y otros, 1999).
Entre las estructuras de control más utilizadas para regular y medir caudales se encuentran los orificios y vertederos (Barragán M, 1993), (Silva, 2011), (Instituto Mexicano de Tecnología del Agua, 1992). Desde el punto de vista hidráulico, los orificios se consideran como perforaciones en una superficie, poseen forma regular y perímetro cerrado, y se pueden realizar en reservorios, canales, tanques, tuberías, captaciones (Silva, 2011), (Rodríguez Díaz, 2000), (Azevedo Netto, 1998), (Sotelo Ávila, 2002).
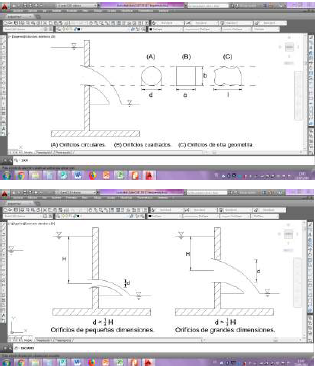
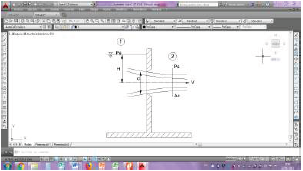
En la figura N° 1, según las condiciones de trabajo, un orificio descarga libremente cuando el nivel del fluido (aguas abajo) se encuentra por debajo de la perforación (Silva, 2011), (Rodríguez Díaz, 2000), (Azevedo Netto, 1998), (Sotelo Ávila, 2002); cuando el nivel del fluido se localiza por encima del orificio se considera que la descarga es sumergida o ahogada (Silva, 2011), (Rodríguez Díaz, 2000), (Azevedo Netto, 1998), (Sotelo Ávila, 2002). Además, se pueden clasificar según su forma o geometría: circulares, cuadrados, rectángulos, y según su tamaño: orificios de pequeñas dimensiones y de grandes dimensiones (Rodríguez Díaz, 2000), (Azevedo Netto, 1998). Cuando el diámetro de la perforación es menor a un tercio de la profundidad del fluido hasta su baricentro, se lo denomina orificio de pequeñas dimensiones, caso contrario es un orificio de grandes dimensiones (Rodríguez Díaz, 2000), (Azevedo Netto, 1998).
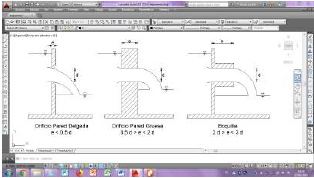
Considerando el espesor de la pared en la que se encuentra el orificio, se clasifica en: pared delgada, pared gruesa y pared ancha (Silva, 2011), (Rodríguez Díaz, 2000), (Sotelo Ávila, 2002) como se muestra en la figura N° 2.
Fuente: Elaboración de los autores.
Figura N° 2 Clasificación de los orificios según el espesor de pared.
Se estima que el orificio es de pared delgada cuando el espesor de esta es menor a 0,50 veces el diámetro de la perforación, de pared gruesa cuando el espesor de la pared está comprendido entre 0,50 y 2 veces el diámetro del orificio (Sotelo Ávila, 2002), (Camatón, Encalada, & Pavón, 2018). Cuando el espesor de la pared se encuentra entre 2 y 3 veces el diámetro de la perforación, se tiene el caso de una boquilla (pared ancha) (Azevedo Netto, 1998), estas están constituidas por piezas adaptadas a los orificios, su función es dirigir el chorro del fluido. El chorro que se descarga libremente a través de un orificio se lo denomina vena líquida y su trayectoria es parabólica (Rodríguez Díaz, 2000).
Modelo Matemático
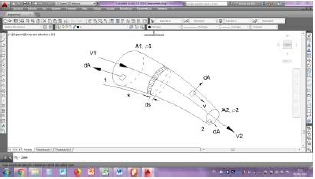
En un orificio tal como se muestra en la figura N° 3, las partículas del fluido que se acercan a la abertura se mueven en dirección al baricentro (Rodríguez Díaz, 2000), (Sotelo Ávila, 2002), por lo que, la deflexión produce una contracción del chorro a la que se le denomina sección contraída "A c "" A c", la cual posee un área menor al área del orificio "A""A", en la sección contraída se considera que las partículas son uniformes y poseen un valor medio de velocidad "V""V", bajo la misma carga "H""H" (Azevedo Netto, 1998), (Sotelo Ávila, 2002).
Se asume que la carga del fluido "H""H", permanece constante, bajo esta condición el orificio descarga un caudal teórico "Q t ""Q t ", cuya ecuación se determina a partir del trinomio de Bernoulli, entre la superficie libre del fluido "Punto 1" y la sección contraída del chorro "Punto 2" (Rodríguez Díaz, 2000), (Azevedo Netto, 1998), (Sotelo Ávila, 2002), trinomio de Bernoulli expresado así:
Para la ecuación N° 1 se considera que el plano referencial pasa por el baricentro del orificio, al no existir velocidad del fluido en el punto 1 (Rodríguez Díaz, 2000), y al ser la presión atmosférica la misma en los puntos 1 y 2 del fluido, esta se anula (Azevedo Netto, 1998), de aplicar estas condiciones en la ecuación N° 1 se obtiene la velocidad teórica del fluido a la salida del orificio (ecuación de Torricelli) (Azevedo Netto, 1998), (Sotelo Ávila, 2002).
Según el principio de conservación de materia, la masa de un fluido en una unidad de tiempo entra a un volumen especificado dentro del flujo, una parte de esta queda almacenado en el interior y el resto sale del volumen (Sotelo Ávila, 2002), (Ven Te Chow, 1994), suponiendo que el volumen estudiado es de forma y magnitud constante, llamado volumen de control, el almacenaje no puede ser indefinido (Sotelo Ávila, 2002). La cantidad de masa que entra y sale, sumadas algebraicamente, según el principio de conservación de la materia, se expresa como:
Este principio aplicado a un volumen de control de tamaño diferencial que a uno finito (figura N° 4), deriva la llamada ecuación de continuidad (Ven Te Chow, 1994).
En una vena líquida, en un punto donde la velocidad en una misma sección se la considera como media "V""V", el volumen elemental de la vena líquida se encuentra separada por una distancia "d s ""d s ", la cual representa la coordenada que sigue el eje de la vena líquida, y tomando en cuenta la rapidez con la que varía la masa, se establece según el principio de conservación de masa que (Sotelo Ávila, 2002):
De resolver la ecuación anterior se obtiene la ecuación de Continuidad (Sotelo Ávila, 2002):
De aplicar en la ecuación de Continuidad la velocidad teórica del fluido (Sotelo Ávila, 2002), se obtiene que el caudal teórico "Q t ""Q t ", siendo esta ecuación conocida como la Ecuación General para descarga en un Orificio de pared delgada, no sumergido, expresándose así (Rodríguez Díaz, 2000), (Azevedo Netto, 1998), (Sotelo Ávila, 2002):
El modelo teórico matemático de descarga no se ajusta a la realidad, razón por la cual este debe ser corregido por un coeficiente de descarga "c d "" c d ", para estimar el caudal real "Q r " "Q r ".
Para obtener el coeficiente de descarga "c d ""c d " de forma experimental, es necesario partir del caudal teórico "Q t ""Q t " y el caudal real "Q r ""Q r ", tomando de base la ecuación 6, y se expresa como (Rodríguez Díaz, 2000):
De forma experimental el caudal real "Q r ""Q r " se consigue a través de la evacuación de cierto volumen "Vol.""Vol." en un intervalo de tiempo determinado "t""t" a través del orificio (Rodríguez Díaz, 2000).
Reemplazando las ecuaciones N° 5 y N° 8 en la ecuación N° 7, se obtiene el coeficiente de descarga "c d ""c d " de forma experimental, siendo este adimensional (Rodríguez Díaz, 2000).
Similitud Hidráulica
La Hidráulica al ser una ciencia empírica, no maneja teorías generales, debido a lo difícil de establecer procedimientos totalmente analíticos, ya que no siempre generan soluciones óptimas, la modelación hidráulica plantea soluciones óptimas y sus resultados guardan relación directa con el comportamiento del fenómeno real, razón por la cual es necesario recurrir a la experimentación en modelos físicos reducidos de los prototipos (Silva, 2011), (Sotelo Ávila, 2002), (Simon, 1982).
La similitud indica las condiciones de funcionamiento del prototipo a partir de ensayos realizados en modelos físicos, siendo el fundamento de la modelación hidráulica (Rodríguez, Valero, & Mendoza, 2015). Para que un modelo sea válido, se necesita mantener tres similitudes básicas: similitud geométrica, similitud cinemática y similitud dinámica (Silva, 2011), (Sotelo Ávila, 2002), (Simon, 1982), (Rodríguez, Valero, & Mendoza, 2015). La figura N° 5 muestra el modelo y el prototipo, siendo el modelo el que se produce en laboratorio y tiene dimensiones menores; el prototipo es la estructura a construir (Sotelo Ávila, 2002).
La similitud geométrica indica que todas las longitudes del prototipo y modelo deben tener la misma razón (Silva, 2011), (Simon, 1982), es decir que las relaciones entre magnitudes homologas se deben mantener, siendo "l e ""l e " la escala de líneas que cuantifica el tamaño relativo de los dos sistemas (Sotelo Ávila, 2002), (Rodríguez, Valero, & Mendoza, 2015).
La similitud geométrica exacta refleja que las relaciones de áreas y volúmenes se pueden expresar en términos del cuadrado y cubo de "l e ""l e " (Sotelo Ávila, 2002), (Simon, 1982), (Rodríguez, Valero, & Mendoza, 2015).
Se debe considerar que la escala vertical puede ser distinta a la escala horizontal en casos donde la profundidad del agua sea pequeña, a estos modelos se los conoce como modelos distorsionados (Sotelo Ávila, 2002), (Rodríguez, Valero, & Mendoza, 2015). La semejanza cinemática implica que tanto las velocidades y aceleraciones en puntos homólogos entre el modelo y el prototipo son las mismas (Silva, 2011), (Sotelo Ávila, 2002), (Rodríguez, Valero, & Mendoza, 2015). Esto quiere decir que las líneas de corriente de ambos flujos son semejantes de forma geométrica (Silva, 2011).
La similitud dinámica indica que en un mismo punto del prototipo y el modelo las fuerzas que actúan en el deben ser coincidentes, tanto en dirección y sentido de los vectores fuerza (Silva, 2011), (Simon, 1982).
Es imposible tener físicamente similitud en todas las fuerzas, por lo que se da prioridad a las fuerzas más importantes del sistema, es decir aquellas que condicionan al fenómeno (Silva, 2011), (Rodríguez, Valero, & Mendoza, 2015), por medio de parámetros como los números de Euler, Froude, Reynolds y Cauchy (Sotelo Ávila, 2002), (Rodríguez, Valero, & Mendoza, 2015). Si existe similitud geométrica y similitud dinámica se considera que existe similitud cinemática (Silva, 2011), (Simon, 1982) y el modelo se encuentra diseñado de forma correcta para representar los fenómenos que ocurren en el prototipo de forma experimental en el modelo hidráulico (Sotelo Ávila, 2002).
Materiales y Métodos
En el Laboratorio Piloto de Hidráulica de la Facultad de Ciencias Matemáticas y Físicas de la Universidad de Guayaquil - Ecuador, ubicado a 4,00 m.s.n.m., se construyó el modelo donde se realizaron los ensayos experimentales para la determinación de coeficientes de descarga en orificios circulares, no sumergidos de pared delgada, con una temperatura ambiente, promedio de 26 ° C.
El modelo consiste en una estructura rectangular de acero, de 3,80 m de alto, la cual sirve de soporte a una tubería de PVC de 160 mm de diámetro nominal, en la parte inferior de la tubería posee un accesorio "tipo Tee"- 160 mm de diámetro, conectado a un tubo Venturi, 160 mm en su diámetro mayor y 50 mm en su diámetro menor, en cada uno de los diámetros se instaló un piezómetro para determinar las cargas de presión, por medio de las cuales fue factible calibrar el caudal de descarga de los orificios, generado por mediciones volumétricas. A través de un sistema de bombeo se alimentó la tubería de 160 mm de diámetro, la cual da la carga hidrostática a los orificios estudiados. Los diferentes orificios, construidos en placas acrílicas, fueron instalados en una posición posterior al tubo Venturi.
Se construyeron un total de 8 placas acrílicas, cuadradas de 100 mm de lado, de las cuales, 7 tienen un espesor de 4 mm, en donde se encuentran los orificios de 12, 18, 24, 30, 36, 42 y 48 mm de diámetro.
La placa restante (6 mm de diámetro), cuenta con espesor de 3 mm, para cumplir la condición de pared delgada. El caudal real se determinó volumétricamente de acuerdo a la ecuación N° 8.
Resultados
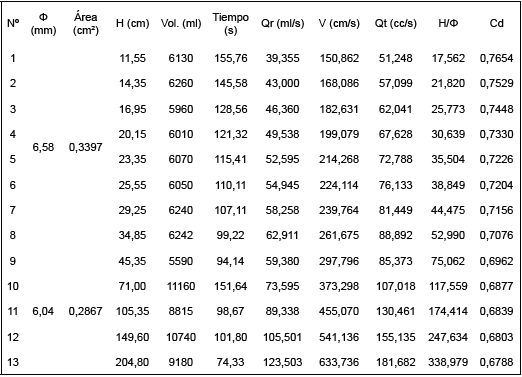
La Tabla N° 1, presenta datos para el orificio de 6 mm de diámetro, este orificio se ha escogido como cálculo tipo de los 8 orificios.
La tabla de resultados de los orificios consideran los siguientes parámetros:
"H""H", altura hidrostática o carga de presión promedio en base a las lecturas "h 1 ""h 1 " y "h 2 ""h 2 " tomadas de los piezómetros.
"Q r ""Q r ", caudal real obtenido por mediciones volumétricas.
"Q t ""Q t ", caudal teórico encontrado a partir del área real del orificio "A""A" y la altura promedio "H""H" El área real del orificio se lo obtuvo a través de 6 valores de diámetros obtenidos con un escalímetro digital.
"C d ""C d ", coeficiente de descarga, resulta de dividir el caudal real para el caudal teórico.
"H/ Ø ""H/ Ø " Relación entre altura promedio para el diámetro real del orificio.
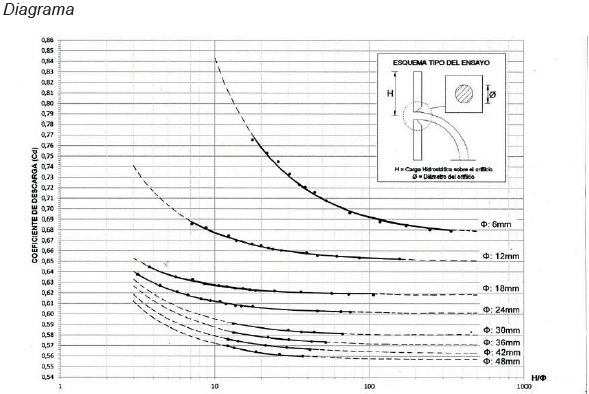
La figura N° 6 representa los coeficientes de descarga que se encontraron para cada uno de los orificios circulares estudiados bajo la relación carga hidrostática/ diámetro del orificio, los coeficientes de descarga para orificios con diámetros comprendidos entre 6 y 48 mm oscilan entre 0,765 - 0,560.
Discusión
La escasa información existente para la determinación de los coeficientes de descarga en orificios de pared delgada no sumergidos, presentados en ábacos y tablas, proporcionan rangos de valores sin ningún sustento de cómo aplicarlos adecuadamente a este tipo de estructuras. Con el pasar de los años, no ha habido la actualización suficiente para la determinación de los coeficientes de descarga en orificios, es decir, existe tablas y gráficos que proveen diferentes autores sobre cómo encontrar estos coeficientes, pero siempre con limitantes. Gilberto Sotelo en su libro Hidráulica General menciona que, mediante un estudio adimensional, se demostró que los coeficientes de descarga dependen exclusivamente del número de Reynolds "Re""Re" para orificios circulares en donde "Re""Re" es mayor a 105 los coeficientes de descarga son independientes de dicho número y toma un valor constante de 0,60 (Sotelo Ávila, 2002).
A su vez, Handbook of Hydraulics de H. King, presenta estudios realizados por Smith and Walker, Judd and King, Medaugh and Johnson y Strickland, para orificios de 2,50 cm de diámetro con coeficientes de descarga superiores a 0,594. Contrastando las fuentes anteriores, la presente investigación genera el diagrama "C d ""C d " vs "H/ Ø ""H/ Ø "; en donde se observa que mientras el diámetro de los orificios " Ø "" Ø " aumenta su tamaño, los coeficientes de descarga "C d ""C d " disminuyen significativamente su valor, esto se da para todos los orificios que se estudiaron en esta investigación.
Los libros de H. King (King, Brater, Lindell, & Wei, 1996), Azevedo Netto (Azevedo Netto, 1998) y Fernández Diez (Fernández Díez, 2000), muestran en sus tablas que el coeficiente de descarga "C d ""C d " también disminuye según va aumentando el diámetro del orificio, guardando una relación con el diagrama generado en esta investigación. Cabe señalar que los textos antes citados, para orificios con diámetros entre 5 y 30 cm, y cargas menores a 1 m, los coeficientes de descarga "C d ""C d " aumentan su valor, diámetros que no fueron considerados en el presente estudio.
Los valores de coeficientes de descarga "C d ""C d " para orificios con diámetros entre 0,60 y 4,80 cm, encontrados en esta investigación, oscilan entre 0,765 y 0,560, para cargas máximas de hasta 2,30 m. Siendo similares a los valores determinados por Arreaga Paredes en su estudio (Arreaga Paredes & Mantilla Villalta, 2016). Los coeficientes de descarga "C d ""C d " mostrados en los textos de H. King (King, Brater, Lindell, & Wei, 1996) y Fernández Diez (Fernández Díez, 2000) para orificios de diámetros entre 0,50 y 5 cm con cargas de hasta 2,30 m, oscilan entre 0,657 y 0,599. Estos valores difieren de los encontrados en esta investigación debido a las condiciones del fluido, ya que utilizaron mezclas de fluidos, glicerina y algunos aceites (King, Brater, Lindell, & Wei, 1996). Azevedo Netto muestra coeficientes de descarga "C d ""C d " para orificios de diámetros entre 2 y 5 cm con cargas de hasta 2,30 m, oscilan entre 0,653 y 0,607, mostrando una diferencia significativa con los coeficientes de descarga encontrados en esta investigación y los mostrados por H. King (King, Brater, Lindell, & Wei, 1996) y Fernández Díez (Fernández Díez, 2000).
Conclusión
Se realizó la experimentación en laboratorio a través de las placas acrílicas diseñadas para cada diámetro de orificio circular mediante las cuales se obtuvo los datos experimentales que sirvieron para el cálculo de los coeficientes de descarga, los cuales se encuentran en un rango de 0,76 a 0,56, valores que generaron el ábaco FCMF-UG-Cd-OCPD-2018 que sirve de gran aporte a estructuras donde se emplea orificios tales como desarenadores, captaciones y sumideros, por lo tanto se concluye que estos coeficientes de descarga son considerados válidos mediante comparaciones realizadas con otras fuentes bibliográficas, según las condiciones de flujo.
Se determinó que el coeficiente de descarga disminuye, conforme se incrementa el diámetro del orificio.
Recomendación
Determinar el modelo matemático para la determinación de coeficientes de descarga, presentados en el ábaco FCMF-UG-Cd-OCPD-2018, modelo matemático que se aplicaría a cualquier diámetro de orificio.
El modelo físico construido permitirá investigar experimentalmente los coeficientes de descarga en orificios de pared gruesa, pared ancha y chimeneas de equilibrio. Además se podría investigar la distancia y fuerza de impacto del chorro para el diseño de obras de protección para evitar socavación.