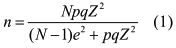INTRODUCCIÓN
Este trabajo de investigación centra su atención en la ciudad de Guayaquil; en este sector se busca caracterizar la enseñanza de la asignatura de Física en el nivel de bachillerato de las instituciones educativas de nivel medio.
Guayaquil es la capital de la provincia de Guayas; esta provincia es el mayor centro industrial de este país, además la más poblada del Ecuador con alrededor 3,8 millones de habitantes, esto representa el 24,5% de la población de la República. La provincia toma el nombre del río más grande e importante de su territorio, el río Guayas. La ciudad de Guayaquil no es sólo la mayor ciudad de la provincia, con sus 2,5 millones de habitantes (más del 68% de la población provincial), sino también la ciudad más poblada de Ecuador (EcuRed, 2018).
La población objeto de investigación la constituyen todos los estudiantes de BGU de la ciudad de Guayaquil, aquellos que cursan los tres niveles de bachillerato, por lo que se tomará en cuenta únicamente las instituciones educativas que ofertan BGU. En la Tabla 1 del trabajo de Barros, V Martínez, M. (2018), (Gallegos, Barros, & Pavon, 2018) se resume de la estructura del sistema educativo ecuatoriano.
Por las características de la población, la cual está dividida en estratos o conjuntos homogéneos (distritos), respecto a la variable objetivo (instituciones con BGU) y el tamaño de esta, la selección de los elementos de la población se la realizo utilizando el muestreo estratificado.
Se ha considerado cada distrito educativo como una categoría (estrato) conformado por instituciones educativas de características similares, tales como currículo, régimen, modalidad, jornada, ente otras.
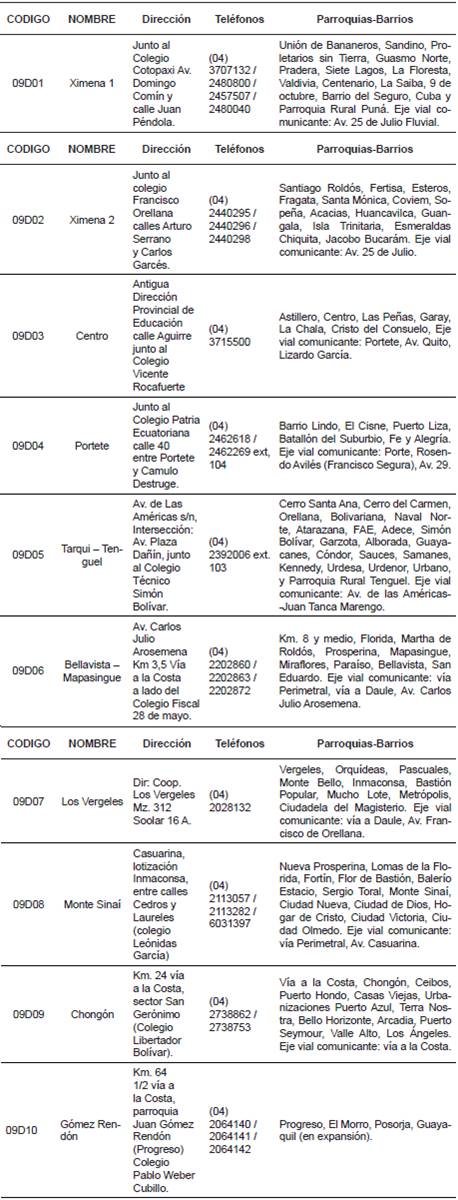
En la Tabla 1. Se describen las instancias administrativas desconcentradas (distritos) pertenecientes al Ministerio de Educación de la Zona 8, ciudad de Guayaquil, distribuida por Distritos. Cada distrito educativo tiene instituciones fiscales, particulares, municipales y fiscomisionales, y otras.
MATERIALES Y MÉTODOS
El muestreo estratificado es adecuado puesto que la población de estudio, en este caso el cantón Guayaquil ya está dividido en distritos educativos (estratos) cada uno de diferente tamaño. La ventaja de las muestras estratificadas es que cuando se diseñan bien, reflejan más exactamente las características de la población de donde se extrajeron, que otras clases de muestreo (UNEG, 2016).
Para aplicar el muestreo estratificado, se divide la población de interés en grupos homogéneos (estratos), los grupos constituyen los diez distritos educativos descritos en la Tabla 1, los cuales son heterogéneos entre sí, (Galmes, 2011), la variable de interés es el número de instituciones con BGU en cada distrito, así se puede observar en la Tabla 2.
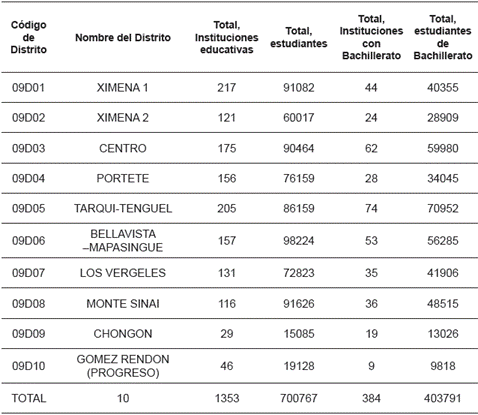
Tabla 2 Distribución de Instituciones Educativas y estudiantes por distrito.
Fuente: Elaborado por los autores.
Se clasificó la información en función del número de instituciones con BGU en cada distrito, luego se calculó el tamaño de la muestra usando la fórmula para determinar la muestra en estudios descriptivos donde la variable es de tipo cualitativa en una población finita, ecuación 1 (Aguilar-Barojas, 2005), para después ser ponderado respecto del total de unidades y se establece el tamaño porcentual de los estratos.
Donde:
n = tamaño de la muestra
N = tamaño de la población
p = proporción aproximada del fenómeno en estudio en la población de referencia
q = proporción de la población de referencia que no presenta el fenómeno en estudio (1 -p).
Z = valor de Z crítico, calculado en las tablas del área de la curva normal. Llamado también nivel de confianza.
e = nivel de precisión absoluta. Referido a la amplitud del intervalo de confianza deseado en la determinación del valor promedio de la variable en estudio.
Una vez calculado el tamaño muestral adecuado, este se reparte de manera proporcional entre los distintos estratos (distritos) definidos en la población usando una simple regla de tres, (Otzen & Manterola, 2017) de manera que se obtenga las 192 instituciones. Luego se utilizó el muestreo aleatorio simple; para finalmente definir cuantas instituciones de la muestra se han de seleccionar de cada uno de los distritos (Tabla 3).
Tabla 3 Muestreo estratificado en relación con los 10 distritos educativos.
| CÓDIGO | NOMBRE | CANTIDAD IE(POBLACIÓN) | PORCENTAJE | PROPORCION(MUESTRA ni) |
|---|---|---|---|---|
| 09D01 | XIMENA 1 | 44 | 11% | 22 |
| 09D02 | XIMENA 2 | 24 | 6% | 12 |
| 09D03 | CENTRO | 62 | 16% | 31 |
| 09D04 | PORTETE | 28 | 7% | 14 |
| 09D05 | TARQUI-TENGUEL | 74 | 19% | 37 |
| 09D06 | BELLAVISTA- MAPASINGUE | 53 | 14% | 27 |
| 09D07 | LOS VERGELES | 35 | 9% | 18 |
| 09D08 | MONTE SINAI | 36 | 9% | 18 |
| 09D09 | CHONGON | 19 | 5% | 10 |
| 09D10 | GOMEZ RENDON (PROGRESO) | 9 | 2% | 5 |
| TOTAL | 384 | 100% | 192 |
Fuente: Elaborado por los autores.
RESULTADOS
En la Tabla 2 se describe la población objeto de investigación, se observa los 10 estratos constituidos por los distritos educativos, los nombres y códigos de cada uno, la totalidad de instituciones educativas que abarca, la totalidad de la población estudiantil, las instituciones que tienen bachillerato y el total de estudiantes del nivel bachillerato.
Con la información de esta última tabla se puede evidenciar que la población objetivo constituyen las instituciones educativas que ofertan los tres niveles de bachillerato son 384 establecimientos con un total de 403791 estudiantes. Para calcular el tamaño de la muestra para datos cuantitativos, se utilizó la ecuación (1). Aplicando la ecuación (1) a los datos descritos, se obtiene el tamaño de la muestra:
La Tabla 3, describe las características del muestreo estratificado.
DISCUSIÓN
Basados en los resultados, se debe realizar la encuesta en 192 instituciones educativas de nivel bachillerato como muestra representativa de las 384 que conforman la población. Con esta información se calculó la proporción de instituciones por cada distrito. La columna proporción, de la Tabla 3, detalla la cantidad de instituciones por distrito que serán investigadas, luego con el muestreo aleatorio simple se definió cuales instituciones de la muestra se han de seleccionar de cada uno de los distritos.
CONCLUSIONES
La planificación del tamaño de la muestra a menudo es importante y casi siempre difícil. Requiere cuidado en la obtención de objetivos científicos y en la obtención de un método adecuado antes del estudio. Los problemas de tamaño de muestra dependen del contexto (Habib, Johargy, Mahmood, & Humma, 2014).
Sin embargo, no es raro que los investigadores tengan diferentes opiniones sobre cómo se debe calcular el tamaño de la muestra (Bartlett, Kotrlik, & Higgins, 2001), siempre se deben informar los procedimientos utilizados en este proceso, lo que permite al lector emitir su propio juicio sobre si aceptan las suposiciones del grupo de investigación y procedimientos.