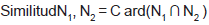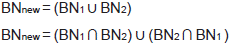INTRODUCCIÓN
La educación se puede ver como un proceso intencional, continuo y sistemático de perfeccionamiento de las personas en cualquiera de sus dimensiones (intelectual, física, estética, profesional, ética, etc.). En su modalidad de proceso, la educación está sujeta a la supervisión constante de todos los procesos de enseñanza y aprendizaje que la componen. La monitorización del proceso educacional, es por tanto un método que analiza constantemente cómo marchan las actividades de enseñanza y aprendizaje en correspondencia con los objetivos propuestos; esto permite garantizar la dirección del proceso hacia una situación deseada, introducir acciones educativas adicionales y obtener la información necesaria y útil para tomar las decisiones que correspondan. Se debe recordar que monitorizar no es sinónimo de evaluar, aunque sin dudas son procesos que tienen muchos puntos en común.
En la actualidad la deserción y pérdida estudiantil en el sistema de enseñanza superior tiene un índice alto de suspensión o abandono de estudios, ya que por diferentes motivos y circunstancias los estudiantes no logran conseguir la culminación de su carrera estudiantil. Esto es más importante en los cursos a distancia mediante ordenador en los que la interacción y la capacidad de adaptación son muy limitadas en la actualidad. Conocer las razones de la deserción y tratar de construir sistemas de aprendizaje que se adapten mejor a las características de cada alumno son objetivos de indudable interés y que mejorarían el proceso educativo.
En este sentido han sido utilizados distintos métodos de Inteligencia Artificial para el aprendizaje automatizado, con el objetivo de encontrar relaciones entre variables y cuantificar la importancia de estas para la toma de decisiones. El objetivo de los algoritmos de aprendizaje consiste en determinar un modelo gráfico a partir de un conjunto de datos en bruto u observaciones realizadas sobre el comportamiento del sistema, referencias importantes son (Cooper, 1992) y (Heckerman, 1995).
Existe en la actualidad una gran diversidad de enfoques y métodos de resolución. Dentro del modelo de aprendizaje automatizado más utilizados en el área de la educación se encuentran las redes bayesianas, junto con los árboles de decisión y las redes neuronales artificiales.
En los últimos años los sistemas expertos probabilistas o redes bayesianas han alcanzado un alto grado de desarrollo. Hasta los 80 se había dado por supuesto que la probabilidad requería mucha información y unos cálculos demasiado complejos para poder resolver problemas reales en los que interviniesen un gran número de variables. Sin embargo, esto cambió a partir de una serie de trabajos entre los que destacan los de (Pearl, 1988).
La idea esencial fue la de aprovechar las relaciones de dependencia (y por tanto también las de independencia) existentes entre las variables de un problema antes de especificar y calcular con los valores numéricos de las probabilidades. Estas relaciones se representan a través de modelos gráficos, habitualmente grafos a cíclicos dirigidos (Nielsen, 2009).
La determinación de las relaciones existentes entre las variables se manifestó desde el principio como una cuestión fundamental. En muchas ocasiones el problema está bien estructurado y el experto sabe determinar directamente un modelo gráfico. Sin embargo, es más habitual que no se conozcan, al menos en forma total, las relaciones de influencia entre los elementos que intervienen. Las Redes Bayesianas tienen numerosas aplicaciones en distintos ámbitos: bioinformática (redes de regulación genética, estructura de proteínas, expresión genética) (Friedman, 2000), etc.
En este trabajo nos centraremos en aplicaciones de los modelos gráficos probabilistas en educación, enseñanza, y aprendizaje. Uno de los problemas básicos que ha recibido más interés es investigar las razones por las que un estudiante abandona sus estudios. (Lykourentzou, 2009) en su publicación usa un método de predicción de deserción en los cursos de e-learning, basado en tres técnicas populares de aprendizaje automático: redes neuronales feedforward, máquinas de soporte vectorial y métodos de ARTMAP difuso simplificado. Puesto que una sola técnica puede fallar para clasificar con precisión a algunos estudiantes de e-learning, mientras que otro puede tener éxito, tres sistemas de toma de decisiones, que se combinan de diferentes maneras los resultados de las tres técnicas de aprendizaje automático fueron probadas.
(Dekker, 2009) comparan distintos modelos para predecir las tasas de abandono durante el primer semestre de los estudios de grado en la Universidad de Eindoven. Utilizan árboles de clasificación, Naive bayes, regresión logística, bosques de árboles, obteniendo unas tasas de acierto entre el 75% y el 80%.
En la misma línea podemos citar el trabajo de (Porcel, 2010) en el que se analiza la relación del rendimiento académico de los alumnos ingresantes a la Facultad de Ciencias Exactas y Naturales y Agrimensura de la Universidad Nacional del Nordeste (FACENA-UNNE) en Corrientes, Argentina, durante el primer año de carrera con las características socioeducativas de los mismos. Se ajustó un modelo de regresión logística binaria, el cual clasificó adecuadamente el 75% de los datos. Entre las variables más relevantes para explicar el rendimiento académico se encuentran el título secundario obtenido, la carrera elegida y el nivel educacional alcanzado por la madre.
Dentro de los problemas de diagnóstico (García, 2009) propone un modelo basado en redes bayesianas para determinar el estilo de aprendizaje de cada estudiante. La red se construye a partir de la información proporcionada por expertos (docentes). Dicho modelo es validado con alumnos obteniendo un alto grado de precisión.
Algunas aplicaciones van enfocadas al estudio de medidas de rendimiento colectivo, en lugar de centrarse en un estudiante. En esta línea podemos citar el trabajo de (Oviedo Bayas, 2016) en el que se propone el uso de modelos gráficos probabilísticos en el campo de la enseñanza para la realización del diagnóstico de los estudiantes y poder predecir su comportamiento. En los últimos años ha cobrado gran importancia el uso de indicadores para describir el perfil de las Universidades españolas en términos tanto académicos como investigadores y económicos. Estos indicadores son utilizados para tomar decisiones de gran importancia, llegando a afectar incluso a aspectos de financiación. Sin embargo, el número de indicadores a veces es excesivo, lo que aumenta el riesgo de redundancia y disfuncionalidad. Los modelos gráficos permiten obtener, a primera vista, las principales relaciones entre las variables a considerar. La metodología propuesta se aplica a un caso práctico, mostrando que es una herramienta útil para ayudar en la toma de decisiones en la elaboración de políticas basadas en indicadores de rendimiento. Esta tarea requiere el manejo de un alto número de variables de distintas naturalezas (cualitativas y cuantitativas), que pueden tener una compleja estructura de dependencias.
MATERIALES Y MÉTODOS
El aprendizaje estructural se puede definir como el proceso que a partir de un conjunto de datos D, compuesto por una serie de valores de un conjunto de variables X para n casos diferentes, encuentra una topología de red Bayesiana B que consigue un mejor ajuste al conjunto de datos D (Friedman N. a., 1999). El proceso de aprendizaje estructural consiste en la selección de una red sobre un conjunto de dimensión exponencial de estructuras de redes. Por tanto, este proceso lleva asociada una gran dificultad en términos del número de casos requeridos para el muestreo de las posibles redes y el tiempo requerido para la optimización. El proceso de aprendizaje estructural se fundamenta en la utilización de una estrategia de búsqueda para explorar todas las posibles topologías de redes Bayesianas. Como el número de posibles grafos crece de forma exponencial con el número de nodos, no se puede realizar una búsqueda exhaustiva sobre todos los posibles grafos, sino que se utilizan diferentes algoritmos de aprendizaje estructural. Los algoritmos de aprendizaje estructural se pueden clasificar en dos grupos de aproximaciones (Heckerman, 1995).
Nuestro estudio se llevará a cabo para para definir otra forma de aprendizaje estructural basado en la búsqueda de estructuras a través de modelos meta-heurísticas evolutivas. Una de las primeras ideas de en este sentido fue la propuesta de un algoritmo genético con codificación binaria presentado en (Kuijpers, 1996). En este modelo un cromosoma codifica una matriz de adyacencia G que representa la estructura de una red bayesiana y cada hijo es corregido por un operador que elimina ciclos si llegan a existir.
Existe también el algoritmo de Optimización basada en Colonias de hormigas (De Campos, 2002) propuesto por L.M. de Campo donde cada camino de una hormiga k es representado como un grafo, de tal forma que cada arista añadida en el camino, representa la unión de dos nodos cualquiera (xi, xj), y la probabilidad con la cual una hormiga k añade una arista en su camino, depende de una función heurística que mide la deseabilidad de dicho estado.
Una meta-heurística recientemente introducida en la comunidad científica es la Optimización basada en Malla Variables (Variable Mesh Optimization, VMO). VMO (Puris, 2012) es una meta-heurística poblacional con características evolutivas donde un conjunto de nodos que representan soluciones potenciales a un problema de optimización, forman una malla (población) que dinámicamente crece y se desplaza por el espacio de búsqueda (evoluciona). Para ello, se realiza un proceso de expansión en cada ciclo, donde se generan nuevos nodos en dirección a los extremos locales (nodos de la malla con mejor calidad en distintas vecindades) y el extremo global (nodo obtenido de mejor calidad en todo el proceso desarrollado); así como a partir de los nodos fronteras de la malla. Luego se realiza un proceso de contracción de la malla, donde los mejores nodos resultantes en cada iteración son seleccionados como malla inicial para la iteración siguiente. La formulación general de la meta-heurística abarca tanto los problemas de optimización continuos como los discretos.
Este modelo ha sido probado en dominios reales con muy buenos resultados. De aquí el interés por probar su desempeño en el problema del aprendizaje estructural de redes bayesianas. Para ello debemos de proponer una estructura del algoritmo para ambientes discretos, como es el caso del problema en cuestión.
Variable Mesh Optimization (VMO) (Oviedo, 2016) es una población metaheurística donde las soluciones se distribuyen como una malla en el espacio M-dimencional. Esta malla contiene P soluciones candidatos (n1; n2;...; np), en este contexto llamadas nodos, y con una representación según el problema de dos operaciones: los procesos de expansión y contracción son ejecutados por VMO para explorar el espacio de búsqueda. Estos procesos son utilizados para introducir un equilibrio adecuado entre la explotación y exploración en algoritmo VMO. Ambos elementos, expansión de malla y contracción, usan una distancia mínima % recomendada entre los individuos (Oviedo, 2016). Esta distancia, se reduce durante la búsqueda y es responsable de mantener la diversidad en la malla. En las subsecciones siguientes, cada fase del algoritmo es descrito y los parámetros están identificados.
1. Operación de expansión de malla: la operación de expansión se ejecuta para mover la población por el espacio de búsqueda utilizando diferentes estrategias para crear nuevas soluciones. Cada nodo creado en el proceso de expansión se introduce en una malla temporal Mtemp que se inicializa al comienzo de cada iteración. El algoritmo comienza con una fase inicial, donde la malla inicial M se crea con P (parámetro que identifica el número de nodos de la malla para comenzar cada iteración) soluciones generado al azar con la distribución uniforme. A continuación, se describe cada paso de esta operación:
Fase 1. (Exploración local): en este paso, el vecindario de cada nodo (ni) de M es explorado. Primero, el k (parámetro que identifica el tamaño del vecindario) nodos más cercanos (usando la función de distancia o simulitud) para (ni) son identificados y el mejor nodo (fitness) en el vecindario se selecciona como el extremo local (n*). En esta fase, solo cuando ni * es óptimo local (mejor fitness que ni) se genera un nuevo nodo usando ni y ni * a través de una función que permite combinar funciones.
Fase 2. (Exploración global): Este paso tiene como objetivo explorar en dirección de un óptimo global (nodo de la malla actual con mejor fitness, ng). P-1 nuevas soluciones son generadas combinando cada nodo ni de la malla con ng.
Fase 3. (Exploración selectiva) En este paso, la frontera interior (más similar a los otros nodos de la malla, nu) y la frontera exterior (la menos similar a los otros nodos de la malla, ns) son identificadas usando una matriz de similitud. Entonces, tanto nu como ns son transformadas para crear dos nuevos nodos.
2. Proceso de contracción de malla: la operación de contracción es utilizada para seleccionar los nodos más representativos entre las mallas M y los nuevos nodos M temp, eso se mantendrá en la malla M para la próxima iteración. La idea es mantener los nodos que no están demasiado cerca de los mejores nodos, manteniendo un mínimo distancia entre los nodos seleccionados. En lo siguiente, un operador de compensación adaptativa se describe con el fin de obtener el nodo más representativo:
Fase 4. Todos los nodos (Mυ M temp) se ordenan dependiendo de su fitness (primero del mejor fitness).
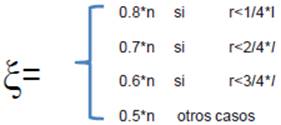
Fase 5. Se calcula la similitud entre cada par de nodos. Si este valor es más que un valor ξ, entonces el peor nodo es borrado. El valor de ξ se calcula en función del problema y cambia dependiendo de la iteración. Este paso reduce el número de nodos a B nodos.
Fase 6. Los nodos con mejor fitness son seleccionados como M para la próxima iteración. Si el tamaño M alcanza su valor mínimo la malla se completa con nuevos nodos de manera aleatoria.
En este proceso, los nodos con mejor fitness y más diferentes tienen una mayor probabilidad de ser seleccionados para la próxima iteración.
El algoritmo VMO se puede aplicar al aprendizaje estructural de una red bayesiana (BayesVMO), pero algunos elementos deben adaptarse a las condiciones del problema:
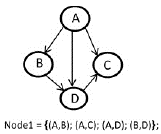
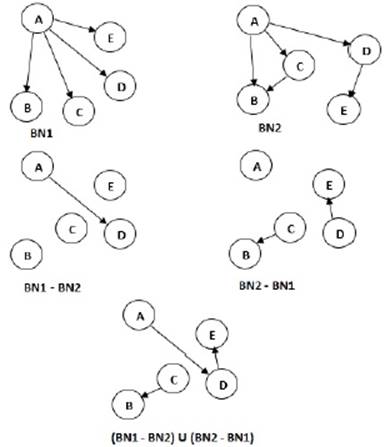
Representación, representamos el nodo de la malla como un conjunto de arcos dirigidos (a, b), donde a, b son variables de la BN y el orden define la dirección del arco (ver Figura 1).
Medida de similitud, para calcular la similitud entre dos BN, aplicamos la operación de intersección entre los conjuntos de arco (N1 ∩ N2) y la cardinalidad del conjunto de intersección representa la similitud:
Esta similitud se usa en la fase 3 del algoritmo para crear una matriz de similitud y encontrar los BNs más (la suma de las similitudes con otras redes es la más alta) y menos (la suma de las similitudes con otras redes es la más baja) nodos similares representativos.
Generación de BN, cada vez que se crea una BN, debemos verificar que no haya ciclos. En caso de que exista un ciclo, uno de sus arcos se selecciona aleatoriamente y su dirección cambia o se elimina (aparece el arco en ambas direcciones). Este proceso se repite hasta que se eliminen todos los ciclos. Para generar un nuevo BN, se usan dos operaciones:
Generación aleatoria: cada arco se genera aleatoriamente y se agrega al BN si las dos restricciones siguientes son verdaderas: el arco no incorpora un ciclo en el BN y no está dirigido a la variable clase. El proceso se repite hasta que se genera un ciclo, en cuyo caso el arco no se agrega y el proceso se detiene.
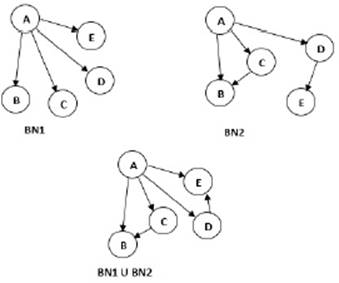
Generación a partir de dos BNs: para generar un nuevo BN a partir de dos BNs, se usan dos operaciones en nuestros experimentos. La operación unión y la operación unión de diferencias.
La operación Unión obtiene una nueva BN con todos los arcos de las dos BN operadas. Por otro lado, la unión de las diferencias genera una nueva BN con los arcos presentes en una de las BN pero no en la otra. Las dos operaciones se presentan en la figura
La cota de distancia o valor de separabilidad entre soluciones, es otro elemento que se redefine. Donde n representa el número de variables o características del problema, la iteración actual del algoritmo VMO e I el número máximo de iteraciones, se incorporan la variabilidad de ξ. En este caso es el siguiente:
La Figura 4 muestra el esquema BayesVMO. Para obtener el valor de fitness, se utiliza la precisión de clasificación con una validación cruzada de 10 veces. No utilizamos las métricas locales como, K2, BIC, MLD u otros tipos de métricas de puntaje.
RESULTADOS
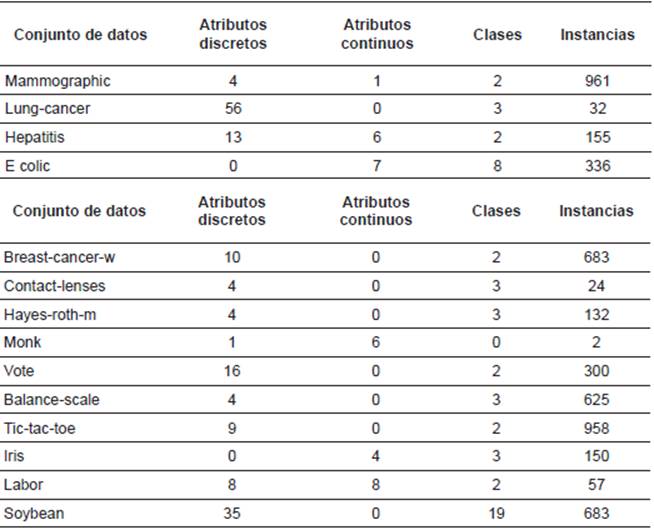
El punto de referencia utilizado para este estudio experimental está compuesto por 14 conjuntos de datos del repositorio UCI ML [Uci (2013). La descripción de estos conjuntos de datos se presenta en la Tabla 1.
Los valores para los parámetros der VMO son: tamaño de la red inicial P = 12, tamaño de vecindad k = 3, número de iteraciones del algoritmo I = 10000.
DISCUSIÓN
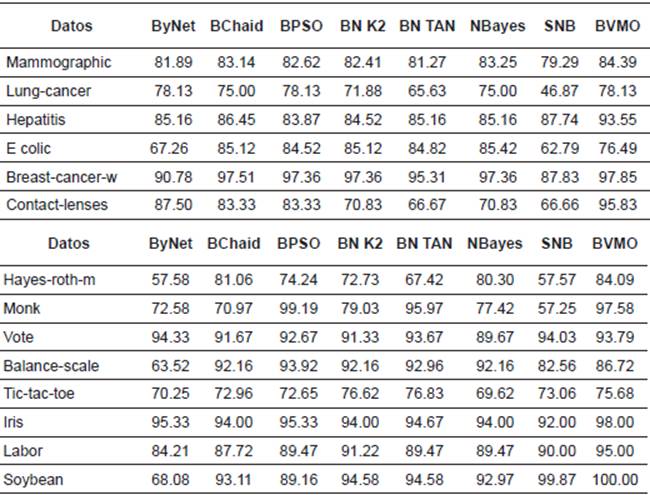
Se realiza un estudio comparativo con otros algoritmos. Los clasificadores bayesianos con los que se compara son: K2, TAN, NBayes, SNB y otros descritos por María del Carmen Chávez M. en su tesis doctoral (Chávez, 2008).
Los experimentos se han llevado a cabo siguiendo la especificación del punto de referencia. La Tabla 2 muestra los valores medios de 25 ejecuciones independientes de cada algoritmo.
La prueba de Iman-Davenport es similar a la prueba de Friedman y se usa para identifique las diferencias significativas en un grupo de algoritmos (más de dos). Si las diferencias existentes son significativas, luego se aplica la prueba de Holm para comparar el algoritmo de control (el mejor ranking) con los restantes.
La Tabla 3 muestra los resultados de la prueba de Iman-Davenport donde la hipótesis de igualdad ha sido rechazada (valor de prueba estadística, 3.929, es mayor que el valor crítico, 2.032) detectando diferencias significativas en el grupo.
Tabla 3 Resultados de la prueba de Iman-Davenport.
| Valor de la prueba | Valor Crítico | Hipótesis |
|---|---|---|
| 3.929 | 2.032 | Rechazada |
Fuente: (Oviedo Bayas, 2016).
A continuación, se realiza la prueba de Holm utilizando BayesVMO como algoritmo de control. La Tabla 4 muestra los resultados de esta prueba donde se puede visualizar que los resultados obtenidos por BVMO son significativamente superiores en relación a los otros clasificadores. Se concluye esto en virtud de que los p-valores son menores a los valores correspondientes de α/i.
Tabla 4 Resultados de la prueba de Holm teniendo BVMO como algoritmo de control.
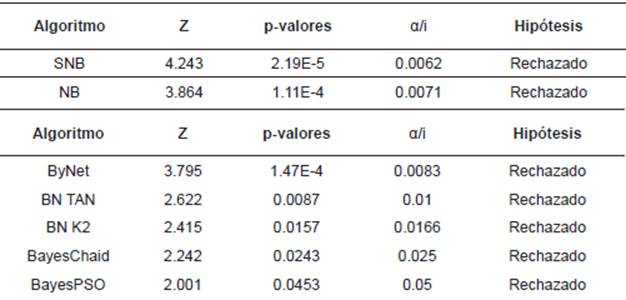
Fuente: (Oviedo Bayas, 2016).
CONCLUSIONES
En este trabajo, hemos adaptado la optimización de malla variable (VMO) metaheurístico al aprendizaje estructural de los clasificadores de redes bayesianas (BVMO). Hemos utilizado como puntaje métrico la precisión de clasificación y las operaciones de la VMO se han adaptado a este problema Entonces, hemos llevado a cabo experimentos utilizando 14 conjuntos de datos del repositorio UCI como punto de referencia. Los resultados de BVMO se han comparado con 8 clasificadores del estado del arte y los análisis estadísticos mostraron que el BVMO alcanza lo mejor resultados.
Para el futuro, planeamos aplicar la metaheurística VMO al aprendizaje genérico de las redes bayesianas, cuando el objetivo es estimar una probabilidad conjunta distribución para las variables problema, en lugar de construir un clasificador.