Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Avances en Psicología Latinoamericana
Print version ISSN 1794-4724
Av. Psicol. Latinoam. vol.30 no.1 Bogotá Jan./June 2012
La naturaleza no lineal de los funcionamientos inferenciales: un estudio empírico con base en el humor gráfico*
The nonlinear nature of inferential functioning: an empirical study based on graphic humor
A natureza na lineal dos funcionamentos inferenciais: um estudo empírico com base no humor gráfico
REBECA PUCHE-NAVARRO**
ERNESTO COMBARIZA***
JULIO CÉSAR OSSA****
* La información contenida en este texto forma parte del proyecto de investigación "El desarrollo cognitivo desde los sistemas dinámicos no lineales: un intento empírico", proyecto identificado con el consecutivo 139 y financiado en la convocatoria interna de la Vicerrectoría de Investigaciones de la Universidad del Valle (Cali, Colombia) de 2006
** Universidad del Valle, Colombia. La correspondencia relacionada con este artículo puede dirigirse a Rebeca Puche-Navarro, Grupo Cognición y Desarrollo Representacional. A.A. 25360. Correo electrónico: rebecapuche2010@gmail.com
*** Profesor del Departamento de Física de la Universidad del Valle, Cali, Colombia. Correo electrónico: combadiaz@yahoo.es
**** Profesor Facultad de Psicología, Universidad de San Buenaventura, Cali, Colombia. Correo electrónico: jcossa@usbcali.edu.co
Para citar este artículo: Puche-Navarro, R., Combariza, E., Ossa, J.C. (2012). La naturaleza no lineal de los funcionamientos inferenciales: un estudio empírico con base en el humor gráfico. Avances en Psicología Latinoamericana, 30 (1), 27-38.
Fecha de recepción: 11 de mayo de 2011
Fecha de aceptación: 9 de febrero de 2012
Resumen
Se analiza si los funcionamientos inferenciales tienen una estructura propia de los sistemas dinámicos no lineales, estudiados a partir de cuatro gráficas humorísticas. Los primeros resultados con el tratamiento estadístico lineal de K-medias arrojan la presencia de perfiles de diferentes funcionamientos inferenciales en función de los diferentes chistes. Los resultados con la técnica de la wavelet, proveniente de los sistemas dinámicos no lineales, muestran patrones de los funcionamientos inferenciales que dan cuenta de su naturaleza multifractal, sin una secuencialidad fija y sin un orden aparente. Esto implica que es necesario revisar la concepción de estadios secuenciales fijos como los que dominan los estudios del desarrollo cognitivo.
Palabras clave: funcionamientos inferenciales, wavelet, multifractalidad
Abstract
This paper is meant to open the question of whether inferential functioning has a dynamic non lineal system structure. Inferential functioning has been studied from four graphic jokes. The first outcomes on the statistical linear k-means, show different profiles according to different inferential functioning in terms of different jokes. And when these results are been analyze by wavelet technique, it has been found that inferential functioning have a multifractal nature. These results show patterns of inferential operations that account for multifractal nature, without a fixed sequential and no apparent order. This implies a need to reconsider the design of fixed and sequential stages that dominate the study of cognitive development.
Keywords: inferential functioning, wavelet, multifractality
Resumo
Analisa-se se os funcionamentos inferenciais têm uma estrutura própria dos sistemas dinâmicos não lineais, estudados a partir de quatro gráficas humorísticas. Os primeiros resultados com o tratamento estadístico lineal de K-medias projetam a presencia de perfis de diferentes funcionamentos inferenciais em função das diferentes piadas. Os resultados com a técnica da wavelet, proveniente dos sistemas dinâmicos não lineais, mostram patrões dos funcionamentos inferenciais que dão conta de sua natureza multifractal, sem uma sequencialidade fixa e sem uma organização aparente. Isto implica que é necessário revisar a concepção de estádios sequenciais fixos como os que dominam os estudos de desenvolvimento cognitivo.
Palavras chave: funcionamentos inferenciais, wavelet, multifractalidade.
Desde los sistemas dinámicos y la psicología del desarrollo
Cronológicamente hablando, las primeras incursiones en los sistemas dinámicos no lineales (en adelante SDNL) en el campo de la psicología datan, aproximadamente, de hace 20 años (Thelen, Kelso & Fogel, 1987). Para algunos investigadores, los SDNL constituyen el proyecto teórico más novedoso e integrador de la psicología del desarrollo en las últimas décadas (Cortés, Combariza & Puche-Navarro, 2009; Fischer & Bidell, 2006; Lewis, Lamey & Douglas, 1999; van Geert & Steenbeek, 2005). La posibilidad de estudiar fenómenos del campo del desarrollo cognitivo bajo esta perspectiva, ha sido objeto de un creciente número de estudios (Lewis, 2000, Smith & Thelen, 2003; van Geert, 1998, 2003).
Este estudio tiene como objetivo trabajar las relaciones entre distintos funcionamientos inferenciales ante distintos tipos de chistes gráficos. En este escenario, la propuesta es identificar si los funcionamientos inferenciales tienen una dinámica no lineal y avanzar en la identificación de los patrones que subyacen a dichos procesos.
Smith y Thelen (2003) proponen una forma de repensar fenómenos del desarrollo a partir de la autoorganización y la no linealidad, conceptos que se ilustran en el paso de la conducta de gatear a la conducta de caminar. Aunque el gatear funciona de manera estable por algunas semanas, luego, diversos componentes tales como "la postura del infante, la fuerza de los músculos y el impulso del ambiente actúan conjunta y coherentemente en un momento en el tiempo para crear o inhibir el movimiento de las piernas" (Smith & Thelen, 2003, p. 344). Su abordaje consiste, entonces, en postular las conquistas del desarrollo, a partir de la misma interacción entre múltiples componentes y sus respectivas contravariaciones en procesos autorregulatorios, para entender la emergencia de soluciones mejores y más adaptadas en el desarrollo.
El vigor conceptual del análisis de Smith y Thelen contrasta con su abstinencia respecto al uso o tratamientos metodológicos propios de los SDNL: cuando estudian el control motor, por ejemplo, su preocupación para determinar la dirección del movimiento, es rigurosa y precisa, pero sin acudir a técnicas que busquen la modelación dinámica (González, Benavides & Riascos, 2009).
Otra referencia obligada en la adopción de los SDNL por parte de la psicología es Kurt Fischer, quien integra la dinámica no lineal con los conceptos propios del desarrollo. Por ejemplo, Fischer y Bidell (2006) proponen, a partir de los SDNL, una reconceptualización original del desarrollo. En esta posición resulta privilegiado el concepto del desarrollo como red, concepto que remplaza los vínculos únicos y simples por un escenario de intercomunicación y de interrelaciones. En la misma dirección, Yan y Fischer (2007) hablan de habilidades dinámicas y complejas que se integran en una concepción interactiva y autorreguladora. En ese panorama la autoorganización se considera como la fuente de cambio y el motor que da lugar a la emergencia de nuevas habilidades.
Los funcionamientos inferenciales
Cuando se quiere estudiar la manera como el sujeto conoce, pocos procesos tienen el estatus y la importancia de la inferencia. Ella constituye un componente crucial del razonamiento humano; prueba de ello es el estudio de la construcción del razonamiento científico de Piaget (1973). Dentro de esas operaciones, las distintas clases de inferencia han marcado derroteros sobre la pregunta crucial de cómo es que la mente accede al conocimiento.
En nuestros estudios hemos trabajado sobre tres tipos de inferencia, lo que no quiere decir que sean las únicas (Puche-Navarro, 2004, 2009): la inferencia inductiva, que resume el paso de una información conocida a otra información nueva o ausente previamente (Hume 1739/1984). La inferencia relacional, que parte de un juicio universal y un juicio particular referidos a los mismos términos (de Gortari, 1969, p. 163). Y la inferencia transductiva, que implica transferir (de las premisas a la conclusión) la relación entre los términos en el mismo grado de generalidad o particularidad (de Gortari, 1969, p. 183).
Una de las inferencias emblemáticas es la abductiva (Peirce, 1955). Este tipo de inferencia da lugar al descubrimiento y es el escenario propicio para jugar con las hipótesis que permiten emprender un camino innovador, como lo plantean Eco y Sebeok (1983). Pese a la importancia de la inferencia abductiva, o precisamente porque ella sola exigiría un estudio aparte, se invita a los lectores a consultar el trabajo que le ha dedicado de la Rosa(2010).
En la historia de la psicología del desarrollo, los estudios sobre la inferencia están presentes desde muy temprano (Spearman, 1923; Binet & Simon, 1916/1973). Cronológicamente, son muy conocidos los estudios en el primer semestre de vida del bebé sobre las inferencias perceptivas (Baillargeon, 1991; Spelke, 1991; Spelke, Breinlinger, Macomber & Jacobson, 1992), así como en el primer año los estudios sobre las capacidades inferenciales (Frye, Zelazo, Brooks & Samuels, 1996; Kobayashi, 1997; McDonough & Mandler, 1998). La inferencia se estudia desde diversas áreas psicológicas: en el área del razonamiento científico del niño (Klahr, 2000; Kuhn & Dean, 2004), de las relaciones causales (Gopnik & Schultz, 2004), y también en los trabajos sobre teoría de la mente (Astington, 2001; Leslie, Friedman & German, 2004).
Este primer balance permite comprender la razón de no hablar de la inferencia en singular, sino de funcionamientos inferenciales en su pluralidad y diversidad. El caso particular de este estudio se trabaja sobre inferencias: inductivas, relacionales y transductivas.
Funcionamientos inferenciales y chistes gráficos
Existe una larga tradición de estudios que muestran cómo las escenas fundadas en incongruencias que subvierten las reglas, producen un efecto divertido en niños y niñas desde los cuatro y cinco años (Bariaud, 1988; Jalongo, 1988; Loizou, 2005; McGhee, 1988; 1989). El chiste gráfico está construido sobre una transgresión o incongruencia que muestra un desfase entre la representación subvertida y la representación subyacente que es la convencional (Puche-Navarro & Lozano, 2002). Plantear que un ratón grande asusta a un gato pequeño subvierte el sentido original. La relación que se subvierte, por ejemplo, cambiar el tamaño de un ratón -a muy grande- que asusta al gato, altera su sentido, es subyacente. Establecer las relaciones entre los sentidos subvertidos y los convencionales exige e involucra funcionamientos inferenciales. La comprensión de distintos tipos de humor, basados en diferentes incongruencias, exige distintos funcionamientos inferenciales:
El chiste hiperbólico, con la exageración de tamaño que antes mencionábamos, ofrece indicios directos y empíricamente observables de la incongruencia característica. Esa incongruencia hace posible que el lector (en este caso el niño) cree una relación inducida por el tamaño. A partir del elemento referencial -tamaño- se subvierte la relación convencional entre los elementos. El disfrute del chiste se produce cuando el niño infiere la incongruencia, implícita, a partir de un proceso inductivo.
El chiste mentalista se basa en lo que Dennet (1998) llamó un sistema de segundo orden, que funciona a partir de relaciones intencionales, como la proyección de estados mentales. En la proyección de un estado mental, es el caso del gato que se mira en el espejo y ve un león, esa relación gato-león exige inferencias de tipo relacional facilitadas por la empatía con el estado mental. Se considera una inferencia relacional porque el niño debe establecer un vínculo entre dos elementos del chiste a partir de un tercer elemento y dicho elemento se presenta en el "espacio mental" de uno de los personajes del chiste.
El chiste de substitución se caracteriza porque hay varias clases de relaciones subvertidas y la incongruencia se plantea a partir del remplazo del elemento central. Es este tipo de chiste de substitución que se juega en la transposición de un elemento estructural del objeto humorístico, como en el caso de una vaca con cabeza de orquídea. La comprensión del sentido de esta transposición supone la capacidad de hacer "bucles mentales", como los llama Perinat (1995), donde el sujeto pueda disfrutar la incongruencia en el sentido de lo pedestre de la vaca con la exquisitez de la orquídea.
Es claro que estos tres tipos de chistes requieren operaciones inferenciales distintas y en ese contexto no resulta arriesgado plantear lo privilegiado que resulta el escenario del chiste gráfico para diferenciar distintos funcionamientos inferenciales (Puche-Navarro, 2004, 2009).
Con base en esas relaciones entre distintos funcionamientos inferenciales ante distintos tipos de chistes gráficos, la pregunta es identificar si esas inferencias aparecen en forma gradual y en secuencias fijas de acuerdo con un nivel de complejidad diferenciado, o si ellas tienen otras formas no lineales de aparición y funcionamiento. Finalmente, se quiere observar si el funcionamiento y las interrelaciones entre los diferentes tipos de inferencias arrojan patrones identificables utilizando el análisis wavelet (propio de los SDNL).
Método
Participantes
Fueron seleccionados 22 niños (12 niños y 10 niñas, Medad = 3.8 años, rango de edad: tres años-seis meses y cuatro años) de cuatro jardines infantiles privados de la ciudad de Cali, Colombia. Los jardines pertenecen a un estrato socioeconómico alto (estratos 5 y 6), de acuerdo con la clasificación del Departamento Administrativo Nacional de Estadística (DANE). Se tomó un número similar de niños y niñas de cada jardín para no introducir sesgos en la distribución de los participantes en función del género ni del lugar de procedencia. La participación de los niños en el estudio se hizo siguiendo los protocolos de consentimiento informado y escrito de sus padres y de la aprobación correspondiente de la dirección de la institución educativa.
Materiales
La situación experimental se diseñó en un formato virtual y se aplicó utilizando un computador portátil. El objetivo de la tarea es construir una historia con cuatro objetos humorísticos, pero siempre el primer objeto fue predeterminado por el software. Una vez se despliega el primer estímulo, el niño debe seleccionar entre cuatro alternativas (hiperbólica, mentalista, de substitución y congruente) para ir construyendo, en cada paso, la historia con el objeto humorístico "más gracioso". El contenido de los objetos humorísticos cambió en función de la elección inmediatamente anterior, pero las alternativas, antes mencionadas, siempre fueron constantes.
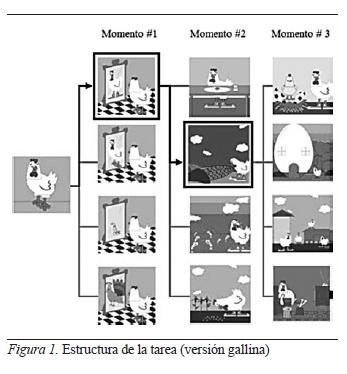
La estructura de la tarea supone tres momentos de elección diferenciados. El niño puede configurar la historia eligiendo una de las alternativas: hiperbólica, mentalista, de substitución o neutra. En la figura 1 se ilustra una secuencia de elección que se encuentra en el tercer momento; el niño tiene en este momento cuatro alternativas para terminar la historia de la gallina. En la alternativa hiperbólica la incongruencia se plantea a partir de una exageración de tamaño (se observa en este caso la casa de la gallina como un huevo gigante). En la alternativa mentalista la incongruencia se plantea en el espacio de las representaciones mentales de uno de los personajes; en este caso la gallina "imagina" que de un balón de fútbol "nace" un pollito. En la alternativa de substitución la incongruencia se presenta al subvertir el orden cambiando el elemento central del chiste, en este caso una gallina que ocupa el espacio de un televidente humano. La alternativa neutra no implica ninguna incongruencia; en este caso se muestran las gallinas en un espacio habitual.
Procedimiento
La aplicación de la tarea se realizó de forma individual. La investigadora presentaba al niño la primera pantalla y le planteaba: "esta es la historia de este gato (se señala el gato), que se está mirando en el espejo". Luego se preguntó: "y aquí ¿qué está viendo el gato? (se señalaron cada una de las cuatro imágenes y el niño debe describirlas)". Después que el niño identificó lo que el gato estaba haciendo se formuló la siguiente consigna: "y de lo que está viendo el gato en el espejo, dime, ¿cuál es la imagen que te parece más graciosa?" Una vez el niño señalaba la imagen elegida, la investigadora la seleccionaba sobre la pantalla del computador. Una vez seleccionada, el programa presentaba automáticamente la segunda pantalla, en donde de nuevo se le dice al niño lo que el personaje está haciendo: "aquí el gato está de visita, ¿cuál es la imagen que te parece más graciosa?". Ante la tercera pantalla: "aquí vive el gato, ¿cuál es la imagen que te parece más graciosa?".
Diseño
Se trata de un estudio de mediciones repetidas: intra e interaplicación, a lo largo de tres meses, con nueve sesiones, a lo largo de 13 semanas, con intervalos de 10 días. En cada aplicación se utilizaron dos versiones diferentes de la tarea y cada versión se repitió una vez, para un total de cuatro aplicaciones de los mismos contenidos. En las aplicaciones impares las versiones "gato" y "mico". En las aplicaciones pares las versiones "gallina" y "perro". En la misma aplicación cada versión se presentó dos veces de manera alternativa (gato, mico, gato, mico), configurando cuatro experimentos por aplicación. Finalmente, se debe recordar que en cada experimento el niño realizó tres elecciones.
Medición
Se asignaron puntajes diferentes a cada una de las cuatro posibles elecciones del niño, de acuerdo con el tipo de inferencia que cada gráfica humorística suponía. De esta manera, si el niño o niña seleccionaba la imagen congruente, se asignaba el puntaje 1; si seleccionaban la imagen hiperbólica, se asignaba el puntaje 2; a la mentalista se asignaba el puntaje 3; y si elegía la substitución, se asignaba el puntaje 4. Esto en función del grado de complejidad creciente de estos tipos de funcionamientos inferenciales. Cada elección de los niños y la secuencia en conjunto se da cuenta de diferentes tipos de funcionamientos inferenciales.
Abordaje metodológico desde la wavelet
La historia de la wavelet es insólita, pues ha sido redescubierta un sinnúmero de veces y de manera independiente (Mackenzie, 2001). El término wavelet se encuentra por primera vez en un artículo de Goupillaud, Grossman y Morlet (1984). Algunas veces se traduce como "ondícula", haciendo referencia a la síntesis entre onda y partícula. Esta técnica se utiliza en el estudio de las señales: su virtud es identificar en un conglomerado de datos un código que permite la representación visual -cualitativa- y con ello identificar los patrones que subyacen. Por otra parte, es capaz de revelar rupturas y discontinuidades y, por consiguiente, su estructura fractal. El análisis de datos -señales en series de tiempo individuales- permite utilizar la transformada de wavelet para estudiar fenómenos tales como los movimientos de las bolsas del mercado y la dinámica de las relaciones entre grupos, entre otros fenómenos caóticos (Wheelan & Williams, 2003).
Resultados
En primera instancia se presentan los resultados obtenidos a partir de la técnica K-medias, la que puede catalogarse como un tratamiento lineal de los datos. Ella permite obtener el promedio de todo un conjunto, en este caso el de las elecciones de los niños, y comparar los promedios de cada niño con el promedio general obtenido. En un segundo momento se presentan los resultados obtenidos a partir del análisis wavelet. Con este procedimiento se trata de establecer si los funcionamientos inferenciales arrojan una estructura irregular con patrones claramente diferenciables.
Resultados K-medias
Las elecciones de los 22 niños (2376 en total) se clasificaron con la técnica K-medias, utilizando como unidad de análisis dos versiones de la misma tarea que fueron aplicadas en la misma sesión.
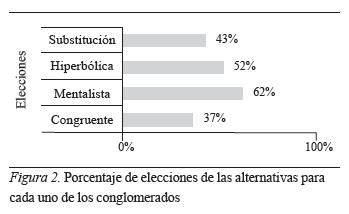
En la figura 2 se observan los porcentajes de elecciones de las alternativas para cada uno de los conglomerados: congruente, mentalista, hiperbólica, de substitución. En el conglomerado congruente se observan 37% de elecciones de tipo neutral. En el conglomerado mentalista se observan 62% de elecciones que comprometen inferencias relacionales. En el conglomerado hiperbólico se observan 52% de elecciones que comprometen inferencias inductivas. Y en el conglomerado de substitución se observan 43% de elecciones que involucran inferencias transductivas.
En la figura 3 el eje Y representa la frecuencia de elección de las alternativas en la misma versión de los chistes, para cada uno de los experimentos, y en el eje X se representan los pares ordenados que corresponden a cada versión con el mismo contenido. Las matrices de los perfiles constituyen modelos generales de todos los sujetos tomados en conjunto, con evidencia de que casos elegidos al azar responden consistentemente con uno de los perfiles.
Los datos dan cuenta de una diferenciación entre los diferentes funcionamientos inferenciales inductivo, relacional y transductivo; los traslapes entre ellos son menos claros. No obstante la claridad para dar cuenta de esas diferenciaciones, no ocurre lo mismo con las zonas que dan cuenta de interacción entre los tres funcionamientos inferenciales. Este tratamiento de las K = medias privilegia la identificación de las inferencias en tanto que variables, mas no su interacción en el tiempo. El siguiente paso será entonces utilizar un tratamiento no lineal que permita establecer si las variables están acopladas en el sistema y el paso del tiempo propios a un sistema dinámico.
En resumen, el conjunto de diferentes elecciones realizadas por los niños y niñas de tres años y ocho meses de edad dan cuenta de que ellos son sensibles a los distintos chistes hiperbólicos, mentalistas y de substitución e involucran para su comprensión las inferencias inductivas, relacionales y transductivas, respectivamente. La pregunta siguiente es: ¿cómo funcionan esas diferenciaciones?
Resultados wavelet
Estos resultados tienen como propósito dar cuenta de las zonas en que se traslapan las elecciones de los niños y pretende explorar en qué medida el conjunto de elecciones son el resultado de interacciones no lineales entre los múltiples componentes del sistema, así como la interdependencia entre ellos en las diversas escalas de tiempo. En esta segunda parte se aplica la técnica wavelet al conjunto de elecciones que los niños y niñas realizaron sobre las diferentes gráficas humorísticas.
Veamos las wavelets discretas de los desempeños de seis de los niños, tomados al azar entre los 22 de la muestra total.
Las wavelets discretas de las trayectorias que trazan las secuencias de las elecciones entre las distintas gráficas humorísticas describen la combinación que de manera consistente (es decir matemáticamente), tienen esos datos. La figura 4 muestra la captura de la secuencia de elecciones de las cuatro gráficas humorísticas, a lo largo de las 108 observaciones en las 13 semanas. En dicha figura el eje vertical Y es la escala temporal. En ese eje se ven representados unos arcos difusos y autocontenidos que expresan la articulación en las diferentes escalas de tiempo. Estos arcos congelan la información e introducen orden en el conjunto. En este, el eje X es la secuencia de los datos de cada sujeto en formas sucesivas simples, en escalas de dos, o cuatro u ocho, etc., de los datos. Esas regularidades o patrones en dichos arcos autocontenidos dan cuenta de una periodicidad sui generis1. No obstante, esos patrones no logran diferenciar a simple vista entre los distintos tipos de inferencias. Lo que sí se puede afirmar es que los funcionamientos inferenciales involucrados en la comprensión de las gráficas humorísticas, poseen una estructura no periódica. Esas wavelets arrojan regularidades que son la expresión de la invarianza de escala. Los segmentos del conjunto de secuencias repiten la forma de toda la secuencia. Ello es un indicador de lo que permanece (en el proceso de cambio) y del rango (o el ancho de posibilidades del eje X) y da cuenta de la riqueza de las posibilidades del sistema.
En otras palabras, lo que la técnica wavelet arroja es que los desempeños de los niños son oscilantes, aunque con algunas ondas perdurables que pueden ser localizadas en diferentes momentos (tiempo). Dichas amplitudes no son estacionarias (es decir, que tienen la misma regularidad), sino que se pasa por diferentes "ritmos" o momentos de tensión variable. Los desempeños de los niños presentan patrones de frecuencia que son variables en el tiempo. Dicha variabilidad o cambios de amplitud depende sustantivamente del tipo de funcionamiento inferencial que el niño despliega en cada momento de elección. Esto significa que los niños no privilegian un solo tipo particular de funcionamiento inferencial, sino que utilizan diferentes tipos de inferencias. La técnica wavelet permite observar la configuración de los diferentes modos inferenciales utilizados por los niños. Se debe observar que dichos modos de inferencia no constituyen patrones regulares de desempeño: los trayectos de los niños (vistos en la representación grafica wavelet) permiten evidenciar diferentes patrones de orden y desorden. El orden se observa al interior de los arcos que se cierran en forma de  y la ruptura de dicho orden se evidencia cuando la señal no puede ser contenida en un mismo arco.
y la ruptura de dicho orden se evidencia cuando la señal no puede ser contenida en un mismo arco.
Análisis y discusión Análisis K-medias
A partir de la técnica K-medias se confirma la diferenciación pero también la coherencia entre las distintas gráficas humorísticas que involucran distintos funcionamientos inferenciales de tipo inductivo, relacional y transductivo. Dicha técnica arroja información de las elecciones que aparecen dentro de una enorme zona de fluctuación. Al focalizar las fluctuaciones y traslapes de las distintas elecciones, aparece el cruce de las variables, donde se puede reconocer la simultaneidad de la presencia de funcionamientos inferenciales de naturaleza inductiva, relacional y transductiva. Las regiones diferenciadas de los funcionamientos inferenciales muestran espacios específicos a cada funcionamiento inferencial y también espacios que muestran que las variables están relacionadas.
La técnica K-medias no parece estar en capacidad de dar cuenta de la zona amplia de interrelación que aparece en la gráfica sobre las elecciones de los sujetos, ni de la ausencia de una jerarquía entre los conglomerados. La necesidad de identificar formalmente esta zona de interrelaciones se hace evidente, de ahí que se afirme que el uso de técnicas no lineales lo permita.
El paso siguiente en el estudio, por consiguiente, es buscar en los datos la amplificación de la zona de traslapes y de correlación entre las variables y, a partir de allí, reconocer que esa diferenciación es más una situación particular asociada a un proceso de medición que permite monitorear las variables de forma más controlada.
Análisis wavelet
¿Qué es lo que los resultados informan sobre los funcionamientos inferenciales, relacional, inductivo y transductivo, involucrados en la comprensión de las gráficas humorísticas: mentalistas, hiperbólicas y de substitución?
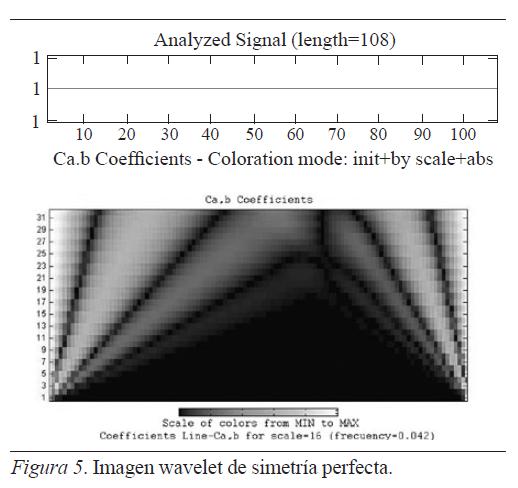
Los patrones que arroja la wavelet permiten confirmar que los funcionamientos inferenciales inductivo, relacional y transductivo corresponden matemáticamente a una estructura multifractal y, en consecuencia, que les subyace un atractor extraño; es decir, se trata de una zona de fuerzas encontradas donde los diversos funcionamientos inferenciales se interrelacionan entre sí. Si no fuera un espacio multifractal, la forma de la wavelet sería como aparece en la figura 5, con una simetría perfecta.
En contraste, los arcos que se pueden observar en cada una de las wavelet graficadas son indicio de que los diferentes tipos de funcionamientos inferenciales se comportan como una región de atractores. En los arcos autocontenidos de la figura 4 se puede observar una región recurrente no cíclica; es decir, que cada uno de los funcionamientos inferenciales (la variable) no abandona la región de posibles valores. Las oscilaciones corresponden a un sistema de variables acopladas que se controlan unas a otras y que al actuar de manera simultánea, interactuando entre sí, lo que formalmente significan es no linealidad. Este equilibrio y regulación son sinónimos de no linealidad.
Otro dato importante es que esa mutifractalidad señala que los funcionamientos inferenciales evolucionan con el tiempo, pero no necesariamente a partir a relaciones pasado-futuro como única y exclusiva opción, sino en escenarios cada vez más bifurcados.
Los tres tipos de funcionamientos inferenciales registrados: inductivo, relacional y transductivo, a pesar de mostrar especificidades respecto a la frecuencia de aparición, por ejemplo, también arrojan características semejantes. Los tres tipos de inferencias tienen en común que no evolucionan en estadios con secuencias fijas entre sí, donde cada uno aparecería en un estadio diferente según su orden de complejidad. Los datos permiten afirmar que esos niveles de complejidad a los que los funcionamientos inferenciales corresponden, no aparecen escalonados.
Lo que quizá es más importante es que estos datos no permiten establecer relaciones de filiación entre sí. Los funcionamientos inferenciales inductivos (chiste hiperbólico) no preceden necesariamente a los funcionamientos inferenciales relacionales (comprometidos en la elección del objeto visual mentalista o la inversa). Los datos obtenidos no permiten afirmar que la evolución de los tres tipos de funcionamientos inferenciales siga secuencias en las que el paso de un funcionamiento inferencial siga a otro en función de su complejidad creciente.
Con la multifractalidad sabemos ahora que los funcionamientos inferenciales presentan una diversidad y una simultaneidad de vías entre ellos, dadas las bifurcaciones y las formas de interactuar entre sí. Se confirma un funcionamiento de elecciones abierto y flexible entre los tres tipos de inferencias. El espacio de elecciones se abre y se da paso a una riqueza de alternativas como múltiples espacios simultáneos con las mismas posibilidades de futuro para todos esos funcionamientos. Precisamente allí radica su diferencia con comportamientos lineales que guardan un orden en la secuencialidad entre un estado anterior y el posterior, sin bifurcaciones.
Esto quiere decir que hablar de la aparición de funcionamientos inferenciales en función de la edad o en función de su nivel de complejidad debe ser objeto de revisiones. En esta misma línea y dado que, como se sabe, el humor involucra diversos funcionamientos inferenciales, ello querría decir que concebir el desarrollo del humor en etapas, debería igualmente estar sujeto a revisiones. Los resultados obtenidos con el K-medias apuntan, precisamente, a una dirección, toda vez que ellos muestran una presencia marcada de la comprensión de chistes mentalistas, que comprometen inferencias relacionales y que en principio implicarían una mayor complejidad que los chistes hiperbólicos que involucran inferencias inductivas.
De cara a esos resultados y frente a esa lectura de los resultados, los tratamientos con la wavelet, podrían tener otra lectura diferente a la de leer los funcionamientos de los tres funcionamientos inferenciales detectados, no ya como en relaciones secuenciales como se decía antes, sino de verlos como evidencia de una zona de atracadores. Efectivamente ésta técnica de las wavelet, permite plantear con algún fundamento, dada la evidencia empírica y los patrones encontrados, que se trata de una zona de atractores. La co-habitación o simultaneidad de los tres funcionamientos inferenciales puede paradójicamente leerse entonces en dirección de mostrarlos como evidencia de cambios cualitativos entre los funcionamientos. Con la wavelet se identifican momentos de inestabilidad y otros de estabilidad, como los que corresponden a los cambios cualitativos y a los procesos de bifurcación.
Metodológicamente, se podría plantear una complementaridad entre los tratamientos lineales y no lineales para dar cuenta de los funcionamientos inferenciales. Por una parte, técnicas como la K-medias permiten diferenciar, dados los desempeños ante los chistes hiperbólicos, metalistas y de substitución, y poner en evidencia los diferentes funcionamientos inferenciales inductivo, relacional y transductivo. Por su parte, la wavelet discreta hace explícita la fractalidad subyacente a esos funcionamientos inferenciales y a postular hipótesis de cara a identificar los cambios entre ellos. Mandelbrot (2006) afirma que donde hay fractales hay discontinuidades y esta vía permite la aproximación a los momentos de cambio de una inferencia a otra. Ese nuevo sendero para las investigaciones en desarrollo queda para el horizonte futuro.
1 Distintas a las de Fourier, que son periodicidades estrictas con repeticiones exactas.
Agradecimientos
Los autores quieren expresar sus agradecimientos al profesor Alberto Bohórquez por su colaboración en el proceso de los cálculos de la wavelet.
Referencias
Astington, J. W. (2001). The paradox of intention: Assessing children's metarepresentational understanding. En B. F. Malle, L. J. Moses & D. A Baldwin (Eds.), Intentions and intentionality: Foundations of social cognition (pp. 85-103). Cambridge, MA, Estados Unidos: MIT Press. [ Links ]
Baillargeon, R. (1991). Reasoning about the height and location of a hidden object in 4.5- and 6.5-month-old infants. Cognition, 38, 13-42. [ Links ]
Bariaud, F. (1988). Age differences in children's humor. Journal of Children in Contemporary Society, 21 (1-2), 15-45. [ Links ]
Binet. A. & Simon, T. (1916). The development of intelligence in children. Baltimore, Estados Unidos: Williams y Wilkins (reimpreso en 1973, NY: Arno Press; 1983, Salem, NH: Ayer Company). [ Links ]
Cortés, M., Combariza, E. & Puche-Navarro, R. (2009). Entre nubes y relojes. En R. Puche-Navarro (Comp.), ¿Es la mente no lineal? (pp. 45-72). Cali: Fondo Editorial Universidad del Valle. [ Links ]
Dennet, D. (1998). La actitud intencional. Madrid: Gedisa. [ Links ]
de Gortari, E. (1969). Iniciación a la lógica. México: Grijalbo. [ Links ]
de la Rosa, Adriana (2010). Emergencia de la comprensión de la metáfora visual en niños pequeños. Tesis doctoral, Universidad del Valle, Cali. [ Links ]
Eco, U. & Sebeok, J. U. (1983). El signo de los tres. Barcelona: Lumen. [ Links ]
Fischer, K. W. & Bidell, T. (2006). Dynamic development of action and thought. En W. Damon & R. Lerner (eds.), Handbook of child psychology: theoretical models of human development (6a ed., vol. 1, pp. 313-399). NY, Estados Unidos: Wiley. [ Links ]
Frye, D., Zelazo, P. D., Brooks, P. J. & Samuels, M. C. (1996). Inference and action in early causal reasoning. Developmental Psychology, 32 (1), 120-131. [ Links ]
González, J., Benavides, J. & Riascos, Y. (2009). De Bloomigton a Groningen. En R. Puche-Navarro (Comp.), ¿Es la mente no lineal? (pp. 73-109). Cali: Fondo Editorial Universidad del Valle. [ Links ]
Gopnik, A. & Schulz, L. (2004). Mechanism of theory formation in young children. Trends in Cognitive Sciences, 8, 371-377. [ Links ]
Goupillaud, P., Grossman, A. & Morlet, J. (1984). Cycle-octave and related transforms in seismic signal analysis. Geoexploration, 23 (1), 85-102. [ Links ]
Hume, D. (1937/1984). Del conocimiento. Madrid: Sarpe. [ Links ]
Jalongo, M. R. (1988). Young children and pictures books: Literature from infancy to six. Washington D.C.: National Association for the Education of Young Children. [ Links ]
Klahr, D. (2000). Exploring Science: The cognition and development of discovery processes. Cambridge. MA, Estados Unidos: MIT Press. [ Links ]
Kobayashi, N. (1997). The role of actions in making inferences about the shape and material of solid objects among Japanese 2 year-old children. Cognition, 63, 251-269. [ Links ]
Kuhn, D. & Dean, D. (2004). Connecting scientific reasoning and casual inference. Journal of Cognition and Development, 5 (2), 261-288. [ Links ]
Leslie, A., Friedmand, O. & German, T. P. (2004). Core mechanisms in "theory of mind". Trends in Cognitive Sciences, 8, 528-533. [ Links ]
Lewis, M. (2000). The promise of dynamic systems approach for an integrated account of human development. Child Development, 71, 36-43. [ Links ]
Lewis, M., Lamey, A. V. & Douglas, L. (1999). A new dynamic systems method for the analysis of early socioemotional development. Developmental Science, 2, 458-475. [ Links ]
Loizou, E. (2005). Infant humor: The theory of the absurd and the empowerment theory. International Journal of Early Years Education, 13 (1), 43-53. [ Links ]
Mackenzie, D. (2001). Wavelets: Seeing the forest and the trees. Beyond discovery: the path from research to human benefit. Recuperado de http://www.beyonddiscovery.org/content/view.txt.asp?a=1952 [ Links ]
Mandelbrot, B. (2006). Los objetos fractales. Barcelona: Tusquets Editores. [ Links ]
McDonough, L. & Mandler, J. M. (1998) Inductive generalization in 9- and 11-month-olds. Developmental Science, 1, 227-232. [ Links ]
McGhee, P. E. (1988). The contribution of humor to children's social development. Journal of Children in Contemporary Society, 20 (1-2), 119-134. [ Links ]
McGhee, P. E. (1989). Introduction: Recent developments in humor research. Journal of Children in Contemporary Society, 20 (1-2), 1-12. [ Links ]
Peirce, C. S. (1955). Abduction and induction. En J. Buchler (Ed.), Philosophical writings of Peirce (pp. 150-156). NY, Estados Unidos: Dover. [ Links ]
Perinat, A. (1995). Prolegómenos para una teoría del juego y del símbolo. Cognitiva, (7), 185-204. [ Links ]
Piaget, J. (1973). Introduction a l'epistemologiegenetique: La pensée mathématique. París: PUF. [ Links ]
Puche-Navarro, R. (2004). Graphic jokes and children's mind: An unusual way to approach children's representational activity. Scandinavian Journal of Psychology, 45, 343-355. [ Links ]
Puche-Navarro, R. (2009). From implicit to explicit representation in children's response to pictural humor. International Journal of Behavioral Development, 33, 543-555. [ Links ]
Puche-Navarro, R. & Lozano, H. (2002). El sentido y el humor en el niño pequeño: Estudio empírico. Bogotá: Siglo del Hombre. [ Links ]
Smith, L. & Thelen, E. (2003). Development as a dynamic system. Trends in Cognitive Sciences, 7, 343-348. [ Links ]
Spearman, C. (1923). The nature of intelligence and the principles of cognition. London: Macmillan. [ Links ]
Spelke, E. S. (1991). Physical knowledge in infancy: Reflections on Piaget's theory. En S. Carey & R. Gelman (Eds.), Epigenesis of mind: Studies in biology and cognition (pp. 133-169). Hillsdale, NJ, Estados Unidos: Erlbaum. [ Links ]
Spelke, E. S., Breinlinger, K., Macomber, J. & Jacobson, K. (1992). Origins of knowledge. Psychological Review, 99, 605-632. [ Links ]
Thelen, E., Kelso, J. A. S. & Fogel, A. (1987). Self-organizing systems and infant motor development. Developmental Review, 7, 39-65. [ Links ]
Thelen, E. & Smith, L. (1994). A dynamic systems approach to the development of cognition and action. Cambridge MA, Estados Unidos: MIT Press. [ Links ]
van Geert, P. (1998). We almost had a great future behind us: The contribution of nonlinear dynamics to developmental science in the making. Developmental Science, 1, 143-159. [ Links ]
van Geert, P. (2003). Dynamic systems approaches and modeling of developmental processes. En J. Valsiner & K. J. Conolly (Eds.), Handbook of Developmental Psychology (pp. 640-672). London: Sage. [ Links ]
van Geert, P. & Steenbeek, H. (2005). Explaining after by before: Basic aspects of a dynamic systems approach to the study of development. Developmental Review, 25, 408-442. [ Links ]
Wheelan, S. & Williams, T. (2003). Mapping dynamic interaction patterns in work groups. Small Group Research, 34, 443- 467. [ Links ]
Yan, Z. & Fischer, K. (2007). Pattern emergence and pattern transition in microdevelopmental variation: Evidence of complex dynamics of developmental processes. Journal of Developmental Processes, 2 (2), 39-62. [ Links ]