Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Earth Sciences Research Journal
Print version ISSN 1794-6190
Earth Sci. Res. J. vol.14 no.1 Bogotá Jan./June 2010
DETERMINATION OF EFFECTIVE ELASTIC THICKNESS OF THE COLOMBIAN ANDES USING SATELLITE-DERIVED GRAVITY DATA
Remy A. Galán1, Iván F. Casallas1
1Universidad Distrital Francisco José de Caldas, Facultad de Ingeniería. Kr 7 40-53. Bogotá. Colombia geophysicalthings@gmail.com
Manuscript received: 04/01/2010 Accepted for publication: 18/03/2010
ABSTRACT
Gravity anomaly values derived from Global Geopotential Models (calculated from the CHAMP and GRACE satellite missions), are compared with free air ground gravity data to find the best representation of surface data. Using these values and topographical heights extracted from digital topography models, we applied the isostatic response function (admittance) to a collection of profiles, to find an average of elastic thickness for the Colombian Andes.
Key words: isostasy, elastic thickness, satellite, admittance, flexure, gravity, topography.
RESUMEN
Se extraen valores de anomalía de gravedad de aire libre derivadas de Modelos Geopotenciales Globales, (calculados de las misiones satelitales CHAMP y GRACE) los cuales son comparados con datos de gravedad terrestre para encontrar entre estos modelos la mejor representación de los datos de superficie. Usando estos valores de anomalía y valores de alturas topográficas extraídos de un modelo de topografía digital, se aplica la función de respuesta isostática (admitancia) a un conjunto de perfiles, para hallar un promedio del espesor elástico de los Andes colombianos.
Palabras clave: isostasia, espesor elástico, satélite, admitancia, flexura, gravedad, topografía.
Introduction
This paper essentially makes use of gravity anomalies and topographical heights to obtain an average of the effective elastic thickness (Te) for the Colombian Andes. The gravity anomalies are derived from data obtained from satellite missions, which are a recent technology that is revolutionizing the world of the geosciences. To get this purpose, geophysical and geodetics concepts are used. In this way, obtaining the value of elastic thickness becomes a technical task, under the principle of a methodological application (Admittance analysis), but in the scientific world the debate about the selection of the method to find the Te even continuous open; under this context, two schools of thought can be find: The school that accepts Admittance analysis developed by Dormán and Lewis (Dormán and Lewis, 1970) as the function that shows the better fit between Topography and Gravity functions and argues that Coherence analysis function overestimates the values of Te, and in the same way, the Coherence's school (Forsyth, 1985) argues that Admittance analysis does not take into account of subsurface loads in computes of Te, and for this reason this latest subestimates Te value. The authors with this work do not pretend to take sides in this debate, because this work seeks to be a further contribution to the knowledge of the Colombian Andes, as well as to contribute to the understanding of the new technologies such as satellital geophysics.
Isostatic model
Isostatic models can be classified into two categories: Local and Regional models. In the isostatic local model, compensation occurs directly beneath the load, which is supported by materials which have a behavior similar to liquids and do not have rigidity. In the isostatic compensation regional model, the load is supported by a material that presents a certain degree of rigidity and hence their behavior is similar to an elastic plate that bends to support the load. Among the isostatic local models can found the hypothesis proposed by Airy and Pratt, whereas the most representative isostatic regional model is proposed by Vening Meinesz.
The concept of lithospheric elastic behavior is developed inside the context of Regional isostatic model, in this way the present work takes the theoretical frame of Vening Meinesz model.
Gravity data
The analytical representation of the ground gravity field is one of the main aims of Geodesy; this is work carried out through analysis of different measurements on the Earth's surface (values of gravity, topographical heights, etc.). This analysis leads to the formulation of the equation AV=0 known also as Boundary value problem which is treated in the branch of Physical Geodesy under the topic of Potential Theory.
The representation of this phenomenon is more understandable when a reference figure that represents the Earth is taken. Geodesy takes several reference surfaces ofrepresen-tation of the Earth's shape, a physical shape known as geoid and a geometrical-mathematical shape known as ellipsoid; the geoid is the equipotential surface most similar to the sea level mean at rest and it is represented by W = W0. This potential W0 is called real gravity potential, and with the normal gravity potential U0 generated by ellipsoidal surface, make up the theoretical basis of mathematical Boundary Value Problem.
The difference between these two potentials is known as perturbation potential or just as potential difference T:

When atmospheric attraction disregards, T is harmonic outside Earth and satisfies Laplace's equation:

These parameters allow obtaining several functions of the gravity field (gravity anomalies, geoid undulations, vertical deflections, etc.) through its relationship with the anomalous potential T, whose series development is according to (Heiskanen and Moritz 1967, Torge 2001):
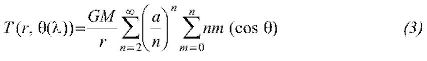
Analysis of perturbations of artificial satellite orbits has made the largest contribution to global determination of the long-wavelength components of the Earth's gravitational field. The resulting global geopotential models (GGM), are usually provided as truncated series of spherical harmonics. Due to several limiting factors these satellite-only GGMs are of a limited spherical harmonics degree (typically 20-30), hence spatial resolution.(Featherstone W. E., 2003).
Among the largest list of available global geopotential models (GGM), three models with several properties have been selected to achieve the purpose of obtaining a surface of gravity anomaly that represents the gravity function in admittance analysis.
Obtaining gravity surface for Colombian Andes
The global geopotential models offer a uniform coverage of the study area, so it is possible to obtain the required term in the gravity field for a particular study. Data from ground gravity do not have a uniform distribution, although the generation of maps of gravity anomaly is possible thanks to the applications of several interpolation methods. The selection of the final model that best represents the field of ground gravity, takes place through the analysis of the correlation parameters between the map of ground gravity anomaly and each of the different maps resulting from the models.
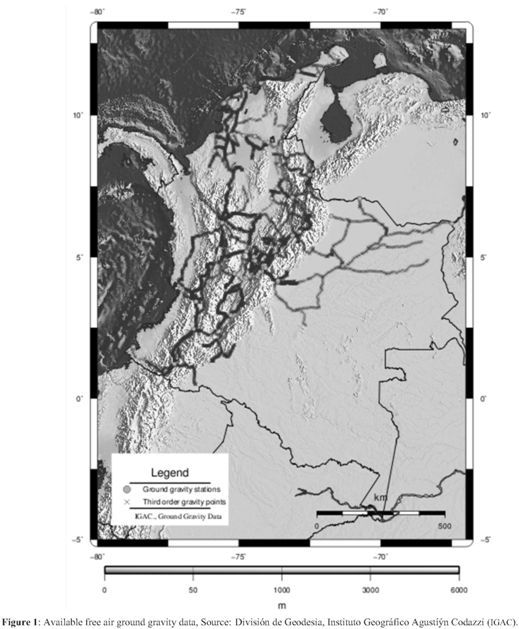
To achieve the purpose of obtaining a gravity field representation for Colombian Andes that best fits with ground gravity data, it is necessary to obtain data from sampling grids of free air gravity anomalies from global geopotential models (GGM), with a spacing resolution of approximately 0.5 degrees or 30 arcmin, and subsequently to obtain the anomaly maps through interpolation method. The available data of ground gravity anomaly are the third order gravity network of IGAC showed in the figure 1. The GGM derived gravity anomalies can be computed from spherical harmonics coefficients to degree nmax using:
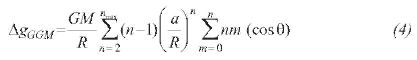
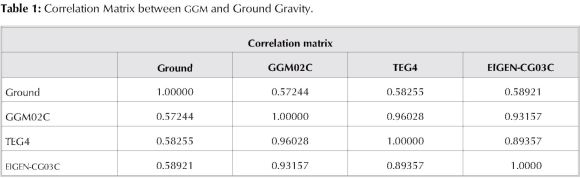
The selection of the final model that best represents the Earth gravity field is done by analyzing the parameters ofcorrelationbetween the groundgravitymap andeachof the maps resulting from different models. Table 1 shows the obtained correlations. According to data in the Table 1, there is a high level of correlation existing between TEG4 and GGM02 models, while the correlation between these models and EIGEN-CG03C model is the lowest. On the other hand, the same table shows the correlation between GGM models and ground gravity data maps and suggests that the average of correlation which only is up to 55 percent. This is the result from low and non uniform ground gravity data coverage over Colombia's continental territory (i.e. Colombian Amazonia). Finally, this suggests that the model that best represent the terrestrial gravity field in Colombian continental crust is EIGEN-CG03C (Figure 2) with a correlation coefficient of 0.58921.
Effective elastic thickness determination
On large time scales the Earth's lithosphere exhibit a regional behavior, thus it tends to experiment flexure, due to the loads. It can be assumed that the lithosphere presents the behavior of a filter which removes large amplitudes, i.e., short wavelengths associated with local isostasy models allow the pass of small amplitudes, or long wavelengths are associated with flexural models (Watts, 2001). In this filter, load h1(x) produces a deflection y1(x) and load h2(x) produces a deflection y2(x) then load h1(x) + h2(x) produce a flexure y1(x) + y2(x). The filters that have this kind of behavior are called Linear Space Invariant (LSI) and are characterized because when they are subjected to periodic loads its output is also periodic (Watts, 2001).
In the Earth's internal structure the part which supports the deflection is called Effective elastic thickness (Te). "This is defined as the thickness of the crust that behaves elastically and that supports some or all topographical load". (Burov and Diament, 1995). It lies on a fluid asthenosphere; therefore the largest value of elastic thickness increments the capacity of the lithosphere to support topographical loads without having deflection. Airy's model represents a special case in which the value of Te is null. To calculate the effective elastic thickness, there are several methods that are most based on spectral and spatial relationships between topography and gravity, which are obtained through the use of maps or profiles. The approach to be adopted in this work is to use a technique within the framework of spectral methods, using information from profiles.
Admittance analysis
Admittance analysis or also known as isostatic response function was developed by LeRoy M. Dorman and Brian T. R. Lewis in the year 1970. The Gravitational admittance "is the wave number parameter that modifies the topography so as to produce gravity anomaly. (Watts, 2001). This allows "expresses the dependence of the gravity anomaly on topography as a function ofseveral physical parameters (plate thickness, plate rigidity, density distribution) and wavelength". (Billen, 2001).
Admittance function Z(k) is defined as:

Where k is wavenumber, G(k) and H(k) are Fourier transforms of gravity and topography respectively. Cross spectrum C(k) is given by:
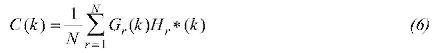
Here * denotes conjugate complex and N is the total number of profiles employed.
The power spectrum of topography E(k) is given as:
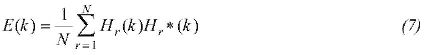
Finally, Observed Admittance average Zobs(k) is computed from:

The observed admittance curve is compared with a set of theoretical admittance curves for several values of effective elastic thickness. The final value of Te is obtained through the selection of the lowest mean square error between the observed admittance curve and each one of the theoretical curves.
Theoretical Admittance is defined as:
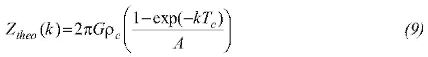
With:

And D (flexural rigidity):

Where:


The mean square error is calculated using:

Here:

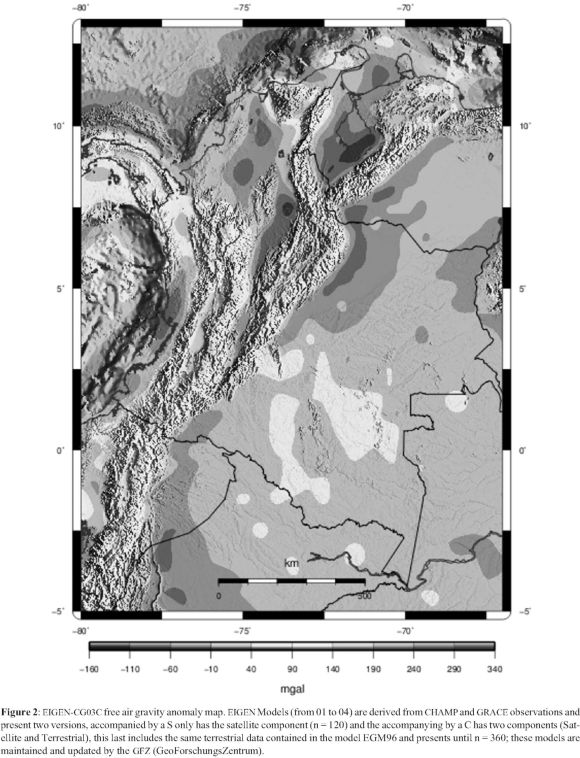
To obtain the observed admittance curve, data were used from the free air gravity anomaly map produced from the model EIGEN-CG03C (Figure 2) and the digital terrain model constructed with data from SRTM (Shuttle Radar Topography Mission) show in Figure 3.
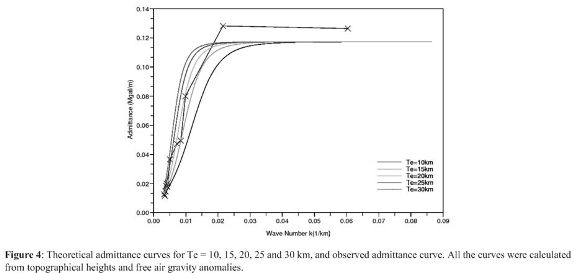
A set of seven (7) profiles was drawn, both in the map of free air anomaly, as in the digital terrain model, crossing the Andes on a perpendicular path and covers it homogeneously, Figure 3. Profiles were sampled each 1800 m taking the ratio of DTM spatial resolution and free air gravity anomaly map resolution. To employ the Fourier analysis this profiles should complete a number of 2n data, where n = 8 because the total distance of the profiles have a range between 400 and 700 km approximately. Theoretical admittance curves were computed for Te values of 10, 15, 20, 25 and 30 km, in the same way observed admittance curve and its square medium errors were computed too. The results are showed in Figure 4 and Table 2.
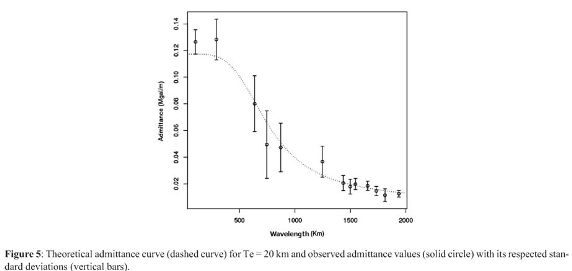
In conclusion according to Table 2, the average of effective elastic thickness for Colombian Andes is 20 km. Taking into account this value, theoretical admittance curve and observed admittance values with its standard deviations are represented in Figure 5.
Discussion
Effective elastic thickness computes studies made in Andes mountain belt inside Colombia, have employed several techniques and also have obtained several values. Some of this works were made for South American continental surface and some others specifically in Colombian Andes employing different methods.
Kellogg et al. (1995) used flexural models 2D employing a fractured plate, obtaining a value of effective elastic thickness between 20 and 25 km below volcanic arc and 60 km for mountain belt placed at north of volcanic arc. Quintero (1998) used admittance method with profiles employing Bouguer anomaly and topographical heights, in the same way used flexural modeling using a continuous plate; in West and Central mountain belt found an elastic thickness value of 10 km, while Eastern mountain belt does not have elastic support, this means that it has a null value of elastic thickness.
Londoño (2004) also employed flexural modeling with continuous plate finding for Putumayo Basin, an Elastic Thickness value between 20 and 40 km. Recently Cerón et al (2007) found for Plato Basin an elastic thickness value of 27 km, this value was computed from Flexural Analysis with continuous plate. Finally, Stewart and Watts (1997) through continuous plate modeling obtained a value of Te for Colombian Andes of 45 km with 40 km bias.
In South America have been conducted several studies, with the main aim of obtaining elastic thickness variations maps, although there are works that provide specific values. Ojeda (2000) made his research for Andes north region; this region includes Colombian East Cordillera and Sierra del Mérida in Venezuela. To find the value of Elastic Thickness was used Coherence technique employing Hanning and Multitaper spectral estimators, obtaining an average value of 30 km. Montavani et al (2001) get a spatial variations map using empirical correlations between tidal gravity anomalies and elastic thickness values, finding for Colombian Andes a value between 69 and 79 km. Into recent studies and that have employed satellite-derived data too, there are two works Tassara et al (2007) and Perez-Gusinye et al (2007). Tassara et al (2007) has used topographical heights and EIGEN-CG03C model data to derive Bouguer anomalies, which were applied Coherence method using continuous Wavelets transform's Morlet family, getting an Elastic Thickness structure map for all South America, in Colombian Andes found a 40 km value with 15 km bias. Perez-Gusinye et al (2007) has used topographical heights and EIGEN-CG03C model data and also ground gravity data, which were applied Coherence technique employing multitaper spectral estimators, obtaining the elastic thickness value between 25 and 30 km.
In the field of studies that employ spectral methods to find elastic thickness value, all ofthese make use ofCoher-ence technique with Bouguer anomalies and several estimators like Hanning, Multitaper o more recently like Wavelet Morlet family. Starting with this approach, the obtained value of 20 km, in comparison with Ojeda (2000) and Perez-Gusinye (2007) works, is low; although with Tassara's research, there is more agreement, because ifthe lowest limit value of this study is taken, it will be 25 km of Te. Finally making a comparison with Montavani et al (2001) study, it is noticeable that the value that it gets is markedly high, but is important to highlight that Perez-Gusinye et al (2007) argue that this values cannot be compared with studies that make use of gravity anomalies and topographical height, because while the tidal loads have a short duration, the elastic thickness responses to a deformation process that only can be measured in geological time.
The average value of Elastic Thickness for the Colombian Andes obtained in this work, it means, 20 km comparing it with other studies, suggests that this one is similar to the values obtained for the Putumayo Basin and the Volcanic Arc. Now, comparing this work with Quintero's (1998) study, a value of 20 km is equivalent to twice the obtained value for this author, but, the 10 km value is the lowest inside the totally of known studies. If the same confrontation is made with the obtained value from Plato Basin study, 20 km value is low too, in the same way that occurs with Steward and Watts (1997) in which this value is only a half.
Conclusions
The Te value obtained in this work is relatively low with the most studies, like it could be expected. The main cause is the kind ofmethod that was used, because other techniques like Coherence suggest that Admittance gets an underestimation or lower limit of the elastic thickness true value, argument that can be debated, because researchers that have employed Admittance argue that processes as erosion and sedimentation tends to thin the topographical surface, and in this way the response of Crust is reduced in presence of subsurface loads.
Although 20 km value is low in relation to other works, it is totally congruent with the results that have to be expected in Admittance studies, that make use of free air anomalies, because in studies like McKenzie and Fairhead (1997), it has been found that for continental lithosphere the elastic thickness value, with some exceptions, do not exceed 25 km, since, it is usually close to the seismogenic thickness value, this argument is still in discussion.
Acknowledgments
We thank Laura Sánchez (DGF - München), Miguel Ávila (Universidad Distrital) and very especially to Andrés Tassara (Universidad de Concepción) for their suggestions, collaboration, and encouragement in the elaboration of this project.
References
Billen, M. I. (2001). I. Seafloor morphology ofthe Osbourn Trough and Karmadec Trench and II. Multiscale dynamics subductions zones, Ph.D. Thesis, California Institute ofTechnology, Pasadena, U.S.A.. [ Links ]
Burov, E. B., and Diament, M. (1995). The effective elastic thickness (Te) of the continental lithosphere: What does it really mean?, Journal of Geophysical Research. 100, No. B3, 3895 - 3904. [ Links ]
Cerón J. F., Kellogg, J. N. and Ojeda, G. Y. (2007). Basement configuration ofthe Northwestern South American-Caribbean margin from recent geophysical data, CT & F -Ciencia, Tecnología y Futuro, 3, No. 3, 25 - 49. [ Links ]
Dorman, L. T. and Lewis, B. T. R. (1970). Experimental Isostasy: 1. Theory of the Determination of the Earth's Isostatic Response to a Concentrated Load, Journal of Geophysical Research, 75, No. 17, 3357 - 3365. [ Links ]
Featherstone, W. E. (2003). Improvement to long-wavelength Australian gravity anomalies expected from CHAMP, GRACE and GOCE dedicated satellite gravimetry missions, Exploration Geophysics, No. 34, 69 - 79. [ Links ]
Forsyth, D. (1985). Subsurface loading and estimates of the flexural rigidities of continental lithosphere, Journal of Geophysical Research, 90, No. B14, 12,623 - 12,632. [ Links ]
Heiskanen, W. A., and Moritz, H. (1967). Physical Geodesy, W. H. Freeman and Company, San Francisco, 392 pp. [ Links ]
Kellogg J., Salvador, M. and Ojeda, G. (1995). Lithospheric structure of the Colombian Andes: Flexure and Crustal Shortening, EOS Transactions, 76, 374. [ Links ]
Londoño, J. (2004). Foreland basins: Lithospheric Flexure, Plate strength and regional stratigraphy, Ph.D. Thesis, Louisiana State University, Baton Rouge, U.S.A. [ Links ]
Mantovani, M. S. M., De Freitas, S. R. C. and Shukowsky, W. (2001). Tidal gravity anomalies as a tool to measure rheological properties of the continental lithosphere: Application to the South American Plate, Journal of South American Earth Sciences, 14, 1 - 14. [ Links ]
McKenzie, D. and Fairhead, D. (1997). Estimates of the effective elastic thickness of the continental lithosphere from Bouguer and Free Air gravity anomalies, Journal of Geophysical Research, 102, No. B12, 27,523 - 27,552. [ Links ]
Ojeda, G. Y. (2000). Analysis of flexural isostasy of the Northern Andes, Ph.D. Thesis, Florida International University, Miami, U.S.A.. [ Links ]
Pérez, Gusinyé M., Lowry, A. R. and Watts, A. B. (2007). Effective elastic thickness of South America and its implications for intracontinental deformation, Geochemistry Geophysics Geosystems, 8, No. 5, 1 - 22. [ Links ]
Quintero, Camacho W. (1998). Interpretación de la estructura cortical de los Andes Colombianos a partir de las redes magnética y gravimétrica del IGAC, Tesis de Maestría, Universidad Nacional Autónoma de México, México D.F., México. [ Links ]
Smith, W. H. F., and Wessel, P. (1990). Gridding with continuous curvature splines in tension, Geophysics, 55(3), 293 - 305. [ Links ]
Stewart, J. and Watts, A. B. (1997). Gravity anomalies and spatial variations of flexural rigidity at mountain ranges, Journal of Geophysical Research, 102, No. B3, 5327 - 5352. [ Links ]
Tassara, A., Swain, C., Hackney, R. and Kirby, J. (2007). Elastic thickness structure of South America estimated using wavelets and satellite-derived gravity data, Earth and Planetary Science Letters, 253, 17 - 36. [ Links ]
Torge, W. (2001). Geodesy, Third Edition, Walter de Gruyter, Berlin, 416 pp. [ Links ]
Watts, A. B. (2001). Isostasy and Flexure of the Litho-sphere, First Edition, Cambridge University Press, Cambridge, 458 pp. [ Links ]
Wessel, P. and Smith, W. H. F. (1998). New improve version of Generic Mapping Tools Released, EOS Transb AGU, 79(47),579. [ Links ]