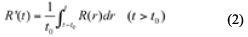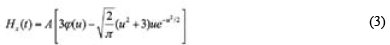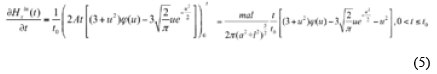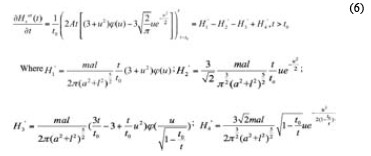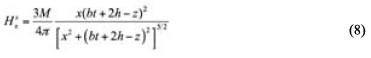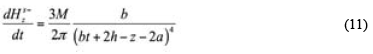1. Introduction

With the continuous improvement of precision requirements for borehole geophysical exploration, the application of TEM in a borehole has become a hot spot (^{Strack, 2014}; ^{Gan et al., 2016}; Khoshbakht et al., 2014; Karinskiy et al., 2014; Gorbatenko et al., 2014). In the study of TEM in borehole and well drilling, ^{Stolz (2003}) examined the borehole electromagnetic method of the gold-bearing tectonic zone, and the borehole electromagnetic method can detect significant anomalies in the shear zone. ^{Wilkinson et al., (2005}) studied the underground distribution of saline-alkali materials using the aeronautical electromagnetic method, ground electromagnetic methods, and borehole TEM, combined with soil, subsurface materials, and groundwater data. ^{School and Edwards et al. (2007)} studied the resolution of the electromagnetic method and high-resistance targets in submarine borehole dipole-dipole devices. ^{Ren et al., (2011)} studied the response characteristics of the transient electromagnetic signal in production wells by mean of numerical simulations. ^{Wang (2012)} supplemented the forward and inverse models of cased well logging and introduced the overall design scheme of the cased well logging system. ^{Zhang (2012)} studied the design and implementation of high-power electromagnetic pulse source, and detailed description of the proper logging instrument structure and the particular circuit implementation method. ^{Guo and Song (2012)} designed the parameters of the TEM receiving loops of the production well by studying the signal response characteristics of the receiving loops. ^{Zang et al. (2014)} used the open-hole model to study the propagation characteristics of electromagnetic waves in the well and gave a two-dimensional spectrum and its dispersion curve describing the propagation of electromagnetic waves in the well. ^{Shen et al. (2016)} proposed an induction logging method based on transient electromagnetic excitation.

Borehole TEM reduces the size of the excitation source and receiving loops and places them in the borehole for excitation and reception, achieving better coupling between the device and the underground medium and more evident abnormal response. For ^{Roslee et al. (2017)}, the burial depth of the anomaly can be more accurately distinguished by increasing measure points. However, the conventional borehole TEM can only determine the longitudinal burial depth of the geological anomaly, the radial azimuth and depth cannot be resolved (^{Liu et al., 2014}). To solve this problem, in this paper the response equations of the transmitting-receiving mode of double-transmitting and sextuple-receiving borehole TEM will be deduced. A negative transformation algorithm will be proposed, and the borehole TEM instrument will be created, and two kinds of physical simulation experiment study of the radial azimuth and radial depth detection of the anomaly will be carried out.

2. Principle

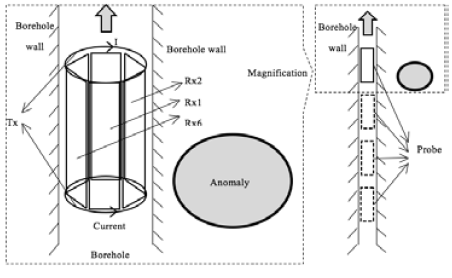
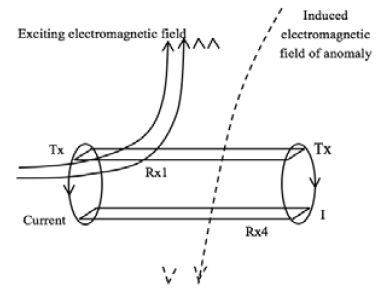
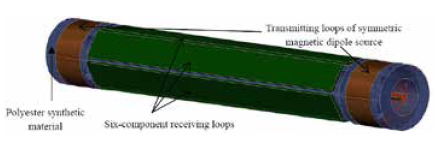
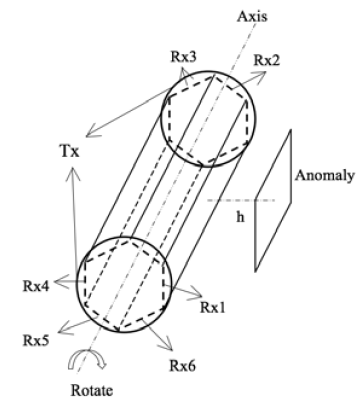
As shown in Figure 1, the probe detects signals with measuring points in the borehole, and it can be seen from the enlarged view that the entire probe consists of two transmitting loops and six receiving loops. The transmitting circuit conveys electromagnetic field with the same value and opposite direction so that the electromagnetic field diffuses to the radial azimuth from the middle of the probe. ^{Lindang et al. (2017)}, as shown in Figure 2, the six receiving loops produce a positive primary field response to the magnetic field excited by the transmitting loops. ^{Kamsani et al., (2017)} the response to the electromagnetic signals generated from the outside anomaly of the borehole is different: for the loops directly facing anomaly, the signal of reply value is positive; for the loops reversely facing anomaly, the induced voltage is negative.

Figure 1 

Figure 2 Schematic diagram of borehole TEM signal response. 

When excitation source is ramp function turn-off source (^{Mcneil et al., 1984}; ^{Fitterman and Anderson, 1987}), the expression of the ramp function turn-off transient electromagnetic field response can be obtained according to the Duhamel integral (Zhong and Zheng, 1986). Induction segment:

Attenuation segment:

Where t₀ is the turn-off time; R (r) is the transient response excited by the ramp function turn-off source; r = t -s is a replacement function.

Under the excitation of ramp function turn-off source, the horizontal magnetic component of the single magnetic dipole in the whole space is (^{Yang, 2009}):

Where is the vacuum permeability, , m is the magnetic moment of the single transmitting loop; a is the distance from the center of receiving loop to transmitting loop axis; 2l is the distance between the centers of the two transmitting loops; r0 is the absolute distance from the midpoint of the receiving loop to that of the transmitting loop,

It can be seen from Figure 2 that the two transmitting circuits produce an electromagnetic field with the same value and opposite direction.

^{Lai et al., (2017)} according to the symmetry of the electromagnetic field, the vertical components cancel each other, and the horizontal components are doubled, so the magnetic field response at the midpoint of the receiving loop of the transmitting-receiving device is:

Take Equation (4) into Equations (1) and (2). Induction segment:

Attenuation segment:

The induced voltage curve of the receiving loop can be obtained by

The layered medium is a standard medium for studying the propagation of transient fields. The particular case is that there is a small plate in the layered strata with high conductivity, and the response equation of the magnetic field of receiving point at any position in the thin plate:

Where b = 2/ μS, is the height of the dipole source above the horizontal plate S, x is the horizontal projection distance between the field source and the receiving point, Z is the vertical projection distance between the point of receipt and the field source, M is the magnetic moment of the double magnetic dipole source, M=2m.

When a receiving loop is directly facing the thin plate, the receiving point

receives only the signal of vertical component, and the loop of receipt is coaxial

with the dual transmitting source , and x =0 , substitute in equation (7):

Obtain the time derivative:

As shown in Figure 2, the transient response of the dual transmitting system shows that the primary response to the six receiving loops is the same, and the secondary response is different. The secondary field response of the loop directly confronting the thin plate is positive, while the secondary field response of the channel reversely facing the thin plate is negative. ^{Lai et al. (2017)}, considering the 2a space between the two faceto-face receiving loops in the device, the secondary field response values are different when the distance between the plates is close, and the value of reply of the reversely facing the plate is:

3. Negative Transformation Algorithm

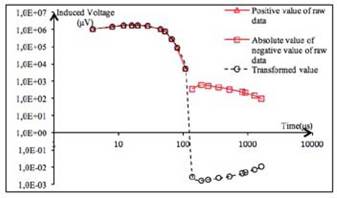
As mentioned above, the response signal value received by some receiving loops is negative when the probe detects a low-resistance anomaly, and the negative value usually cannot be expressed in the double logarithmic coordinate system. ^{Lai et al., (2017)} it is necessary to use an algorithm to express negative values in the correct geometric form in the double logarithmic coordinate system.

The transformed value is obtained through the following transformations of the original data:

Where n is a symmetric coefficient. (12)

Taking the induced voltage data of the receiving loop Rx4 as an example, the symmetry coefficient n=0. The horizontal axis is chosen as the axis of symmetry before and after transformation. As shown in Figure 3, the curve with positive values did not change before, and after the Rx4 data transformation, the absolute value of the negative value data is symmetrical to the transformed value along horizontal axis V=1, and the curve attenuation is normal.

Figure 3 Comparison of Rx4 measuring data before and after data transformation. 

4. Physical Simulation of Abnormal Azimuth Recognition

The transmitting-receiving unit is placed in an open space, and the plate low-resistance anomaly situated on one side of the probe. ^{Roslee et al., (2017)} the borehole TEM instrument is independently created by our research group, and the instrument and the probe structure are shown in Figures 4-5 respectively. The physical simulation experiment is shown in Figure 6, and the first measuring point is the anomaly directly facing 1# receiving loop. For the following measuring points, the distance between the anomaly and the probe remains the same, and every time the probe is rotated by 5° when each measuring point is set for detection.

Figure 4 Borehole TEM instrument. 

Figure 5 Schematic diagram of probe structure 

Figure 6 Schematic diagram of physical simulation. 

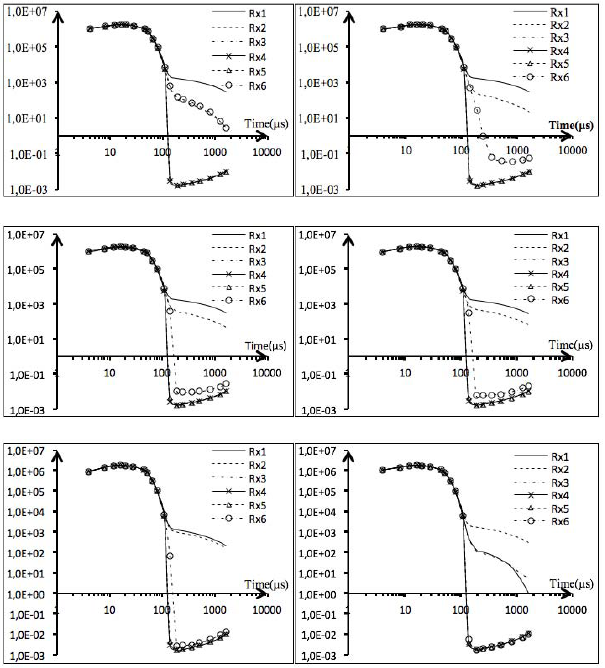
From the probe structure in Figure 5, it is known that the receiving loops are combined to form a regular hexagonal prism structure. Since the structure is centrosymmetric and the minimum symmetry angle is 30°, the rotation angle selects: 0°, 5°, 10°, 15°, 30° and 60°, and the measuring data are shown in Figure 7.

Figure 7 Response attenuation curves of the receiving loops at different rotation angles. 

The induced electromotive force of receiving loops Rx3, Rx4 and Rx5 are negative values, and the data is calculated by Equation (11) with symmetric coefficient n=0, and transformed and drawn in the double logarithmic coordinate system. As can be seen from the figure 7-a, the secondary field response value of the receiving loop Rx1 directly facing anomaly is positive and maximum, and the raw values of the secondary field response of receiving loops Rx3, Rx4, and Rx5 reversely facing the anomaly are negative. ^{Kamsani et al., (2017)} according to the law of attenuation, the attenuation curves of each receiving loop eventually converge to zero. Since the data is transformed, its value should converge to the symmetry axis V=10n, and the curves converge to one in the graph, and the curve configuration of negative values conform to abnormal response characteristics.

It can be seen from Figure 7 that the response value is the highest when the anomaly directly faces Rx1 receiving loop, the response signals of Rx2 and Rx6 loops are the same and are positive; while the response values of Rx3, Rx4, and Rx5 loops reversely face Rx1 loop are negative, and it is shown as the characteristics of the six curves in Figure 7-a. When the anomaly is within the normal angle between two adjacent receiving loops, the abnormal response value of the two loops is positive, and the response value of the loop is higher when the anomaly is closer to a certain loop; as shown in Figure 7-b and Figure 7-c, the anomaly is closer to Rx1 loop.

When the defect is located on the angular bisector of the two adjacent loops, the responses of the two loops are positive, and the values are the same, as shown in Figure 7-e. By comparing Figure 7-a and Figure 7-f, when the anomaly directly faces a certain loop, the response of the loop is the highest, and the value of the loops on both sides are positive and approximately same, and the remaining three loops have a negative response. From the above phenomenon, the following four laws can be summarized: (1) When there is a low-resistance anomaly, there exist at least two measuring curves with the positive secondary field. (2) The normal direction of the several receiving loops with the positive secondary field of measuring curves must be the azimuth of the anomaly. (3) If there is only one highest curve among the measuring curves with the positive secondary field, then the anomaly is near the normal direction of the receiving loop. (4) If there are two higher curves among the measuring curves with positive secondary field and coincide, the anomaly is near angular bisector of the two receiving loops.

Therefore, the measuring curves obtained by the borehole transient electromagnetic system can identify the azimuth of the radial anomaly, and the resolution is 30°. It can be seen from Figure 7-b, 7-c and 7-d that when the anomaly is at different angles within the range of 30°, the curves are also different, but cannot be directly distinguished from the significant difference among the curves.

5. Physical Simulation of Anomalies with Different Radial Depth

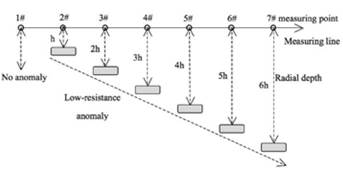
From the above theoretical derivation, it is known that the borehole TEM has different response signals for different anomalies, and the physical simulation experiments were carried out for low-resistance anomaly with different radial depths of the same azimuth (^{Roslee et al., 2017}; ^{Lindang et al., 2017}; ^{Kamsani et al., 2017}; ^{Lai et al., 2017}). As shown in Figure 8, the probe moves along a measuring line, the direction of the probe remains the same, and the low-resistance anomalies of different radial depths are placed in the same direction directly facing Rx1 receiving loop. There are seven measuring points in the measuring line, and the 1# measuring point is no anomaly detection, and the radial depths of 2#-7# measuring points are from h to 6 h.

Figure 8 Schematic diagram of physical simulation experiment of different radial depths. 

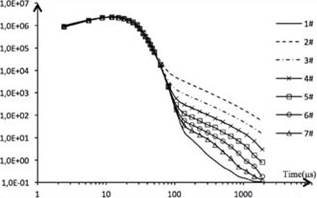
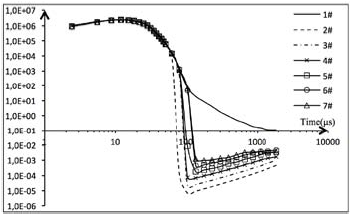
In the experiment, the anomaly directly faces Rx1 receiving loop, so Rx1 gets a positive response signal, Rx4 gets a negative response signal. The experimental data of the two receiving loops were extracted to obtain the response curves shown in Figures 9-¹⁰, and the symmetry coefficient n=-1 in negative value transformation algorithm.

Figure 9 Contrast curve for each measuring point of Rx1 

Figure 10 Contrast curve for each measuring point of Rx4 

It can be seen from Figure 9 that when the anomaly directly faces a receiving loop, the secondary field response signal of the anomaly decreases with the increase of the radial depth of the transmitting-receiving device and the low-resistance defect. The secondary field segments of curves are parallel to each other, which is in line with the correct attenuation law. At the same time, the transient time (^{Zhong and Zheng, 1986}; ^{Jiang, 1988}) of each curve increases with distance, which accords with the time law of abnormal response.

It can be seen from Figure 10 that when the anomaly faces the Rx4 receiving loop reversely, the anomaly response is negative. The amplitude of the secondary field response signal decreases with the increase of radial depth between the transmitting-receiving device and the abnormality, and the subsequent field segments of curves are parallel to each other, which accords with the correct attenuation law.

Figures 9-¹⁰ show that there is a same law between the receiving loop directly facing the anomaly and reversely facing anomaly. The change of the anomaly depths can be determined by the induced voltage difference of fixed time window. Through data analysis, the best resolution window ranges from 138us to 975us. The geometric distance between the two curves under the double logarithmic coordinate system can be solved by the following equation:

The equation shows the geometric induced voltage difference of the curve distance in the double logarithmic coordinate system, V1 is the transformed value in a fixed time window when receiving loop faces the anomaly directly, and V2 is the transformed value in a fixed time window when receiving loop reversely faces the anomaly.

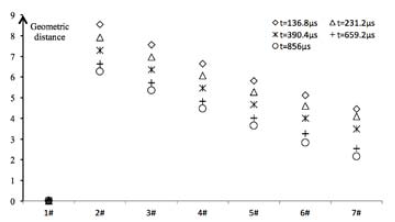
The response values of t=136.8μs, 231.2 μs, 390.4μs, 659.2μs and 856μs in the response signals of Rx1 and Rx4 receiving loops are calculated in equation (8) to obtain the curve graph for the geometric difference of different fixed time windows shown in Figure 11, where the length of a standard grid in the vertical axis represents the length of the 10 times of data difference in the double logarithmic coordinate system.

Figure 11 Curve graph for the geometric difference of different measuring points 

It can be seen from Figure 11 that the geometric distance between the positive and negative signals decreases as the anomaly depth increases, so the geometric difference between the response signals of different measuring points can be used to evaluate the radial depth of the anomaly qualitatively. Two curves of Rx1 and Rx4 are coincident with zero geometric distance when there is no anomaly. In the fixed time window, the geometric difference is the lower when the time is larger. From the curve comparison, the curves of several different windows are parallel, and the radial depth does not affect the attenuation speed of its secondary field response signal when the same low-resistance anomaly is detected.

5. Conclusion

Borehole TEM is a kind of fine geophysical method which effectively utilizes the drilling space. In this paper, through theoretical derivation and physical simulation experiment, the response of borehole TEM double transmitting loops is analyzed and studied. Through the negative transformation algorithm, the negative values obtained by double-transmitting and sextuple-receiving borehole TEM can be plotted correctly in the double logarithmic coordinate system, which provides an effective method for the radial direction and depth experimental data analysis. From the analysis of the electromagnetic principle, it can be seen that the borehole TEM has efficient resolution ability for the radial azimuth of low-resistance anomaly. By physical simulation experiment, the effective resolve of the double-transmitting and sextuple-receiving borehole TEM is 30°. At the same time, the borehole TEM can qualitatively analyze the radial depth between the low-resistance anomaly and borehole TEM probe by the geometric difference, so the double-transmitting and sextuple-receiving borehole TEM is an efficient way to identify the radial azimuth and depth of low-resistance anomaly.

Since each measuring point of the double-transmitting and sextuple-receiving borehole TEM can obtain different pattern signals of six receiving loops, which has the advantages of less time consuming and a large amount of data. Therefore, the next step in research should take advantage of the multi-parameter advantage of double-transmitting and sextuple-receiving borehole TEM to achieve high-resolution quantitative interpretation.