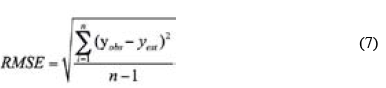1. Introduction
Meteorological observations are important for identifying and understanding variations and changes in regional and global climate (Feng et al., 2004). These observations are also essential to a wide range of meteorological applications, such as climate monitoring, weather forecasting and the evaluation of numerical weather prediction (NWP) models (He et al., 2016; Ingleby and Lorenc, 1993). Therefore, it is of particular importance to improve the accuracy of meteorological observations, especially surface observations (Barnes, 1964; Gandin, 1988). On the one hand, surface meteorological observations have a longterm history in China. On the contrary, surface meteorological observations can more accurately represent the atmospheric characteristics of the nearsurface compared to other meteorological observations (Xu et al., 2013; Hu et al., 2002; Mi et al., 2014). However, surface observation stations are easily affected by the gross error and random error during the data acquisition process. Thus, the primary task and purpose of quality control (QC) are to identify the gross error and large random error associated with large numbers of observations (Shi-wei et al., 2009).
In surface meteorological observations, air temperature is one of the most important elements because it has a considerable impact on human activity (Cheng et al., 2016). Hence, a variety of QC methods has been recently proposed for surface air temperature observations. The QC methods include the extreme range check (Reek et al., 1992; Kubecka, 2001; Allen et al., 1998; Forsythe et al., 1995), internal consistency check (Baker, 1992), time consistency check (Shafer et al., 2000; Lanzante, 1996), and spatial consistency check methodologies. QC research has focused on spatial consistency check, which is used for multi-station QC. The spatial QC method predicts the value at the target station based on the values at neighboring stations, and it can evaluate the reliability of observations. The inverse distance weighting (Wade, 1987) method (IDW) uses the proportions of the inverse distances between multiple neighboring stations and the target stations as weights, and it requires the terrain features and distribution of neighboring stations. The Bayesian QC method (Lorenc and Hammon, 1988) uses the probability of observations as a gross error. In 2007, Hubbard et al. (2007) proposed the spatial regression test method (SRT). SRT calculates weights based on the standard error between the target station and neighboring stations, and it is less influenced by terrain and the distribution of neighboring stations compared to the IDW method. Based on the SRT method, Xu et al. (2014) proposed the probabilistic spatial-temporal method (SRT-PS). This method considers the uncertainty in temperature observations and eliminates the associated effect on temperature fluctuations.
The most widely used traditional methods discussed above are the IDW method and SRT method, and the SRT method is considered superior to the IDW method (Hubbard and You, 2005). Thus, the SRT method is for comparison with the Random Forest quality control algorithm based on the principal component analysis (PCA-RF) method proposed in this paper. The PCA-RF method is used to reconstruct the training samples by extracting high correlation factors from meteorological elements using PCA. Therefore, the efficiency and accuracy of RF model are improved. The specific objectives of this paper are as follows: (1) to compare the evaluation indexes of the RF and SRT methods using training samples over different periods (Ridzuan et al., 2017). (2) To set different correlation factor thresholds and compare the evaluation indexes and run times of the PCA-RF QC model based on these different thresholds. And (3) to compare the detection rates of the SRT and PCA-RF methods and evaluate the predictive performances of the QC models.
2. Data
China is a large country with an area of approximately 9.6 million km2. About 98% of the land area stretches between the latitudes of 20° N and 50° N. Thus; the country extends from the subtropical zones in the south to the temperate zones (including warm temperate and cool temperate) in the north (Yang et al., 2013; Jiang et al., 2016). With recent global climate warming, the national annual average temperature increased by approximately 1.1 degrees Celsius, with high temperatures in north and low temperatures in the south. Additionally, the magnitude of the temperature increase in winter was larger than that in summer (Asis et al., 2017)
Moreover, other climate factors exhibited fluctuations in different regions (Zheng et al., 2010, CHENG et al., 2009). Therefore, it is more meaningful in spatial QC to consider different climates and geomorphological regionalization.
In this paper, data were collected from January 1, 2005, to December 31, 2014, four times daily (02:00, 08:00, 14:00 and 20:00 Beijing time (CST)) in different climate regions in China. The data include six types of meteorological elements: ground surface temperature (GST), pressure (PRE), relative humidity (RH), temperature (TEM), wind direction (WD) and wind speed (WS). These data were obtained from the China National Meteorological Center and had undergone basic QC; thus, the accuracy of the data is acceptable. Missing data, changes in station locations and changes in precipitation measurement instruments during the observation period can influence the homogeneity of datasets (Irannezhad et al., 2016). Small percentages of missing data at some stations can influence an analysis, but PCA can reduce the effect of missing data to a certain degree. Zheng et al. (2010) suggested dividing China into 12 temperature zones, including a humid region, a semi-humid region, a semi-arid region and an arid region. Li et al. (2013) discussed the specific steps and methods associated with dividing China into six major categories. In this paper, 15 stations with different climates and topographies are selected; however, stations 59948, 59985 and 59287 (in the mid-tropic, equatorial tropic and south subtropical areas) are not selected because they do not have sufficient numbers of neighboring stations (Rahim et al., 2017)
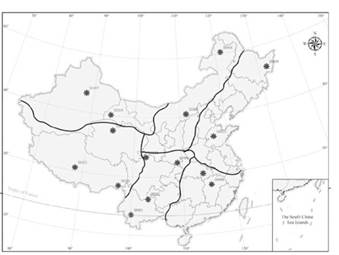
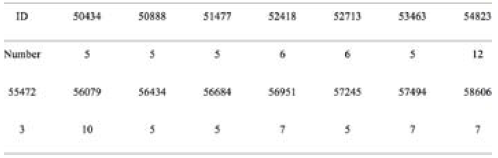
The target stations are shown in Figure 1, and the selection of target stations accounted for the distribution of climate zones and geomorphologic regionalization. Neighboring stations are selected based on the distance between the target station and neighboring stations, where the radius of the neighboring stations is not more than 100 km. The number of neighboring stations is 5-10, as shown in Table 1. However, stations 55472 and 54823 have a limited number of neighboring stations or significant gaps in data.
To test the feasibility of the PCA-RF method, artificial error is added randomly to the observations at the target station. A comparative analysis is performed using observations with artificial random error and the predicted values of the PRF method. Hubbard et al. (2005) presented a method of adding false error to data. A random number q with a mean of zero and a range of ± 3,5 was selected and added to the observations (Hubbard et al., 2007):
Where E and s denote the error magnitude and standard deviation, respectively, of temperature observations at the target station. Additionally, x is the location of mistake value insertion.
3. Method
3.1. Random Forest algorithm
Random Forest (RF) is an ensemble learning method for classification and regression that constructs some randomized decision trees during the training phase and make predictions by averaging the results (Scornet et al., 2015). In ensemble learning, each decision tree is a weak classifier, and some weak classifiers are combined into a strong classifier. This approach is much easier than looking for a strong classifier directly. RF generates many regression trees to improve the prediction performance of the model, and each split in the tree is determined using a randomized subset of variables/factors at each node (Rahmati et al., 2016). The outcome is the average of the results of all the trees (Cutler et al., 2007).
3.2. Principal Component Analysis algorithm
Principal Component Analysis (PCA) is a method for analyzing a positive semi-definite Hermitian matrix. The goal of PCA is to identify the most urgent basis by using a new base to filter out the noise and reveal hidden structures (Shlens, 2014). Notably, PCA is used to analyze the covariance matrix of sampled random vectors (Lloyd et al., 2014). High-dimensional data are mapped into a new coordinate system and transformed to low-dimensional data that can partly represent the original data. In this manner, PCA can significantly reduce the run time of algorithms, especially in big data processing.
3.3. PCA-RF algorithm
Combined with the above concepts, the PCA-RF algorithm is proposed in this paper. The concrete steps in the algorithm are divided as follows (Asis et al., 2017)
Step 1: The PCA method is used to analyze the multiple element observations in space. Assuming that n represents the number of samples, m represents the number of features, and X
n,m represents the feature set, the average value of the ith feature  is calculated using (2).
is calculated using (2).
The standard error Si of the ith feature is calculated using (3).
Then, through standardization, (4) is obtained
Finally, the correlation matrix of feature sample Rm,m is obtained, as shown in (5).
An optimal feature sample is established by extracting the matrix with high correlation factors.
Step 2: The RF algorithm is used to train and test the optimal feature samples, and the PCA-RF model produces a predictive value y est .
Step 3: The predicted values y est and observed values y obs are tested for a given threshold, as shown in (6):
Where f is the QC parameter and ∂ is the standard error between observed values and predicted values at the target station. If the conditions of (6) cannot be met, the data are considered incorrect (or associated with error). If the conditions of (6) are met, the data are considered correct values (Ridzuan et al., 2017).
3.3. Evaluation of model performance
To analyze different forecasting models with different conditions, the root means square error (RMSE) and mean absolute error (MAE) were selected as evaluation metrics. RMSE is the square root of the ratio of the square of the predicted value and the real value, and MAE can accurately reflect the size of the prediction error. Their formulas are as follows.
4. Results and Discussion
The estimates using PCA-RF were evaluated against the measurements at 15 target stations, and selected observations are shown in Figure 1 and Table 1 (You et al., 2017). In the analysis of sample dependence, observations over different periods were selected to predict observations of daily mean temperature, and the training samples were the six meteorological elements observed four times daily in the 1, 3, 5, 7 and 9 years before 2014. The testing samples were the six meteorological factors founded four times daily in 2014. In the analysis of the correlation factor, the same observations were used as the training samples and testing samples at different correlation factor thresholds (>0, >0.5, >0.8, >0.9, >0.95). In the analysis of the detection rates of the PCA-RF and SRT methods, the evaluation indexes (MAE and RMSE) and two types of error (type I and type II) were used to compare the performances of PCA-RF and SRT, and observation selection was the same as that utilized in the correlation factor analysis.
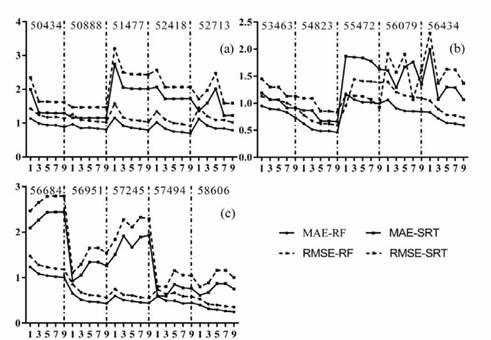
Observations over different periods were selected to analyze the sample dependence based on RF and SRT, and the results are shown in Figure 2. In general, as the number of training samples increased, the error in the testing samples decreased. As shown in Figure 2, the error trends at 15 target stations exhibited this pattern. Regardless of the observation period (one year, three years, five years, seven years or nine years), the MAE and RMSE values of the RF method are smaller than those of the SRT method, and the fluctuations in training samples are smaller. Hence, the RF method performed better than SRT method based on the sample dependence. Although the error associated with the training samples for seven years of observations is less than that associated with the training samples for nine years of observations at target station 57494, the training samples based on nine years of observations exhibited less error in general. Therefore, the training sample based on nine years of observations was used in the following analysis.
Moreover, Figure 2 shows that stations 54823, 56951, 57245 and 58606 have relatively small evaluation index values because the neighboring stations around these target stations are relatively dense (You et al., 2017).
- Additionally, the main reason for the performance difference between the SRT method and RF method is the sparse distribution of neighboring stations or low spatial correlation between values. The RF method has relatively less error at the target stations compared to the large error of the SRT method, such as at stations 51477, 56684 and 57245. This result suggests that the RF method is superior to the SRT method.
To investigate the performance of the PCA-RF method under different thresholds of the correlation factor, the evaluation index values and run time of the model obtained for seven cases (no, >0, >0.5, >0.8, 0.9, 0.95, alone) are shown in Figure 3, where "no" means that the RF model does not perform PCA and "alone" means that modeling is only based on temperature observations at neighboring stations. Additionally, the unit of "Time" (run time of the model) is 100 seconds. Figure 3 shows that the evaluation index (MAE and RMSE) values increased slightly as the correlation factor threshold increased. Moreover, the run time of the model decreased as the correlation factor threshold increased. The results show that the choice of correlation factor determines the run time of model and affects the size of the type error. A correlation factor threshold of 0.5 was chosen as the optimal value to construct the QC model. Compared to the other correlation factor thresholds, the correlation factor threshold of 0.5 produced the shortest run time of the model, and the model error is relatively small. On the one hand, although the model error is reduced without PCA, the run time of the model increases considerably, as PCA effectively reduces the run time of the model. On the other hand, although the run time of the quality control model with only temperature elements is short, the error is larger than the error when six elements are considered in the spatial QC model. In summary, the accuracy and run time of the QC model can be improved by choosing a correlation factor threshold of 0.5. Thus, the RF model performed better than the SRT approach based on the evaluation indexes and error detection rate analysis.
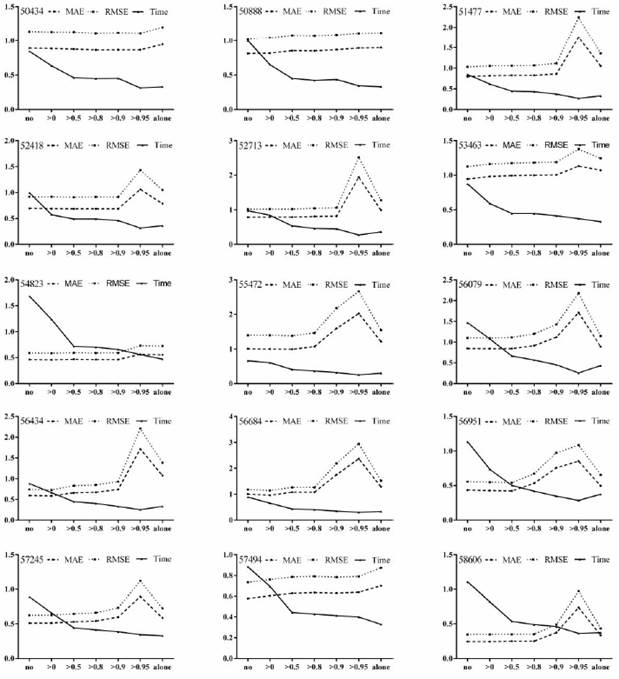
Figure 3 Evaluation indexes and run time of the model for the 15 target stations under different thresholds of the correlation factor.
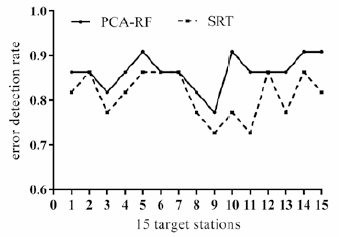
The error detection rate is the ultimate criteria for a QC model. The error detection rate is related to the size of the QC parameter, and the choice of QC parameter is related to the two types of error. In type I error, the real value is treated as an incorrect value. In type II error, an incorrect value is treated as the true value. In the realm of QC, the intersection of the two types of error is chosen as the optimal QC parameter. The optimal QC parameters for the PCA-RF and SRT methods obtained based on the intersection of the two types of error are listed in Table 2, in which the 15 target stations are numbered 1 to 15 according to the order of their previous names. The corresponding error detection rate is shown in Figure 4. Table 2 and Figure 4 illustrate that the error detection rate of the PCA-RF method is superior to the error detection rate of the SRT method. Thus, the PCA-RF method is more stable and efficient based on the target stations with different terrain and climate characteristics.
5. Conclusions
This paper studies a spatial QC model of six meteorological elements and temperature observations using the PCA-RF model, and the results are compared to those of the SRT method. The performance of QC has a considerable effect on the selection of the correlation factor threshold and the density of neighboring stations around the target station. The simulation results show that the PCA-RF method is less dependent on training samples than is the SRT method, and it performed better at target stations with sparse neighboring stations or low spatial correlation. The run time of the model can be reduced effectively by choosing the appropriate correlation factor at the expense of a small increase in the error. The PCA-RF method is more stable and has a higher error detection rate compared to the stability and detection rate of the SRT method.
In the next study, time series will be combined with the PCA-RF method, and the error detection rate of the PCA-RF QC model may be improved by eliminating the influence of noisy time series. The physical connection between multiple elements at neighboring stations must be taken into account to improve the performance of the model through the establishment of a new sample set based on physical connections.