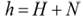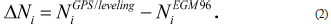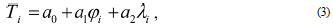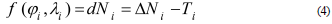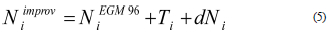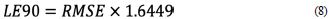1. Introduction
Digital elevation models (DEMs) are necessary for the solution of many practical problems in the areas of the earth and environmental sciences (such as tectonics, the study of landslides, mineral exploration, water and land resources management, disaster prevention, and others) in Uzbekistan (Sayyidkosimov & Kazakov, 2018; Sabitova et al., 2020; Sharipov et al., 2020; Khasanov & Ahmedov, 2021). Topographic maps, Global Navigation Satellite System (GNSS) measurements, photogrammetry techniques, and airborne laser scanning are the main data sources for DEMs production used in Uzbekistan for small areas (Takhirov et al., 2020; Shukina et al., 2022). Despite the accuracy, the traditional DEM generation methods are tedious and time-consuming for using over large areas. Modern satellite remote sensing technologies have made it possible to map large areas with minimal labor and technological costs (Smith &Clark, 2005). The widespread use of publicly available satellite-based DEMs such as SRTM, ASTER, and ALOS is an example of these benefits. However, available open-source these and many others have coarser resolutions. Their accuracy is affected by measurement error, data acquisition method, the instrument's capability, resolution, terrain type and relief, slope, roughness, land cover, and others (Mukherjee et al., 2011; Hu et al. 2017; Shetty et al., 2022). The vertical accuracy assessment of space-borne elevation data sets has been one of the major concerns for worldwide researchers (Mukherjee et al., 2013; Elkhrachy, 2018; González-Moradas & Viveen, 2020; Preety et al., 2022). For the practical application of the DEM, it is necessary to identify the influence of error sources on the vertical accuracy of the DEM and refine the models using terrestrial measurements for each area separately (Dragut & Eisank, 2011). Global DEMs have got an upsurge in their usage in Uzbekistan. But so far there are few works on assessing their accuracy and developing methods for improving it. In earlier studies, the accuracy of DEMs, such as SRTM, ASTER GDEM, and ALOS PALSAR, was assessed using various data (DEMs of higher resolution, the utilization of Differential Global Positioning System (DGPS), terrestrial measurements (Bakiev & Khasanov, 2021). It was revealed that for the territories located near the reservoirs, ASTER DEM gives a more realistic representation of steep slopes and mountain ridges compared to SRTM or ALOS (Fazilova et al., 2021). The goal of this study is to quantify and compare the vertical accuracy of open access DEMs obtained using the Shuttle Radar Topography Mission (SRTM30), Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER GDEM2), and Advanced Land Observing Satellite (ALOS AW3D30) for the territory of the Fergana Valley in the Republic of Uzbekistan.
2. Data and method
The area taken for the study is the territory of the Fergana Valley in Uzbekistan, which is an east-west-trending intra-orogenic intermountain depression, the most seismically active and densely populated region of the country. It is located in the eastern part of the Republic of Uzbekistan and borders the Republic of Tajikistan and Kyrgyzstan. The width of the research area is 370 km by 19 km. It is bounded by the Alai and Turkestan systems mountain uplifts in the south, by the Fergana Mountain in the northeast, and by the Chatkal-Kurama Mountain in the north and northwest (Umurzakov & Rabbimkulov, 2022). The maximum topographic relief between the Fergana Valley floor, with an altitude of roughly 330 m, and the surrounding mountain peaks is about 1000 m. The main problem for the territory of the republic, which has a complex relief, is the need for better knowledge of the geoid by gravimetric methods. The geoid of the Fergana Valley is the only area that has been sufficiently well studied by classic leveling. As a result, the influence of the Tien Shan and Pamir Mountain ranges on gravitational anomalies was revealed (Ustyantsev, 2011) (Fig.1). In the work, the entire territory of the Fergana Valley is considered from the point of view of the fact that for many geodetic engineering applications, the assessment of the accuracy of DEMs has not yet been made.
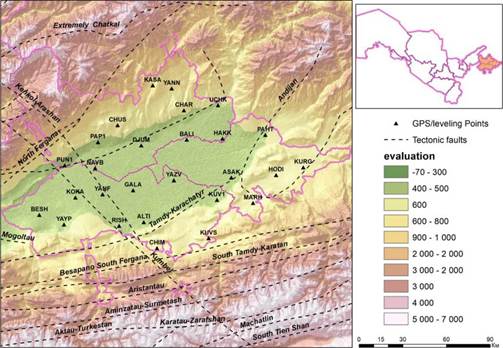
Figure 1 Topography of the study area generated by SRTM30 and distribution of GPS points over Fergana Valley
The study utilized three sources of DEMs generated from various data acquisition techniques, namely Shuttle Radar Topography Mission (SRTM) DEM of 30 m, Advanced Space Borne Thermal Emission and Reflection Radiometer (ASTER)-Global DEM of 30 m, and ALOS World-3D of 30 m. The important technical details of DEMS are explained in Table 1.
Table 1 Description of digital elevation models (DEM)
| Data | SRTM30 v. 2.0 | ASTER GDEM v.2 | ALOS World 3D |
|---|---|---|---|
| Source | Space Shuttle Radar | ASTER | DAICHI/ALOS |
| Generator/Distributor | NASA/USGS | METI/NASA | JAXA |
| Period of observation | from February 11th, 2000 to February 22nd, 2000 | March 1, 2000 - November 30, 2013 | from 2006 to 2011 |
| Spatial resolution (m) | 30 | 30 | 30 |
| Vertical datum | EGM96 | EGM96 | EGM96 |
| Horizontal datum | WGS84 | WGS84 | WGS84 |
| Data type | Interferometry synthetic aperture radar | Optical stereoscopy | Optical stereoscopy |
| Vertical accuracy (LE90) | < 10 m | <15-20 m | <7m |
SRTM30 v. 2.0. It can be considered to be either an SRTM30 data set enhanced with GTOPO30 or an upgrade to GTOPO30. 1-arcsecond (about 30 meters) resolution DEM, delivered in 1°x1° tiles. Systematic interferometric data were collected for each terrain segment at least twice from different angles (on ascending, north-going, and descending orbit pass) to fill in areas shadowed from the radar beam by terrain. The finished product contains 'no-data' termed as voids where water or heavy shadow prevented the quantification of elevation. At a 90% confidence level, the vertical accuracy is expected to be 10 m (Rodríguez et al., 2006). Eight tiles of the SRTM30 elevation data for the study area were downloaded from https://www.usgs.gov/centers/eros website.
ASTER GDEM v.2 (ASTER GDEM2). The 1-arc-second (30 m) stereoscopic product ASTER GDEM2 was created by stacking all individual cloud-masked scene DEMs and non-cloud-masked scene DEMs, then applying various algorithms to remove abnormal data. The reason for considering this model is that ASTER GDEM2 has some advantage over SRTM30 because its stereo pair has more nadir view when collecting data in very steep and rugged terrain (Abrams et al., 2010). ASTER GDEM2 data has a vertical accuracy of ±15-20 m, depending on the region's environmental situation (Thomas et al.2014). For this study, 7 ASTER GDEM2 elevation data tiles were downloaded from https://asterweb.jpl.nasa.gov/gdem.asp website.
ALOS World 3D (AW3D30). The global digital surface model dataset with a horizontal resolution of approximately 30-meter mesh (1 arcsec. latitude and longitude) generated from 5 m resolution. The worldwide digital elevation model DEM and ortho-rectified image (ORI) were created using the archived information about the Panchromatic Remote Sensing Instrument for Stereo Mapping (PRISM). PRISM comprised three panchromatic radiometers that were procured along with track stereo images. It had a spatial resolution of 2.5 m in the nadir-looking radiometer and accomplished worldwide coverage, making it an appropriate potential candidate for exact worldwide DEM and ORI generation (Tadono et al., 2014). This is a non-standard version of the ALOS AW3D30 dataset provided in a WGS84 ellipsoidal vertical datum. For this study, 9 tiles of data were downloaded from https://www.eorc.jaxa.jp/ALOS/en/aw3d30/index.htm website.
The raster values (heights) of these DEMs were extracted from the coordinates of the GPS points. These heights are referred to as heights obtained from each of the DEMs.
The vertical accuracy of DEM at the scale of the study area is verified using 27 reference stations of the State Satellite Geodetic Network (SSGN) in the region, which is developing quite rapidly, considering the developed infrastructure of the country (Fazilova, 2022). To date, only these points of SSGN have been installed in the region (Fig. 1). These points are the so-called "common points," with the values of normal heights in the Baltic system of 1977 available in the database of the International Gravimetric Bureau in Toulouse (Drewes et al., 2016). Measurements of other global navigation satellite systems (GNSS) such as GLONASS, Galileo, and Beidou are currently not available at the stations. The GAMIT/GLOBK software package version 10.71 was used to calculate the coordinates of points (Herring et al., 2018). According to Dong et al. (1998), processing was carried out according to the recommendations and standards of the International Earth Rotation Service IERS2010 (IERS, 2010). The ITRF2014 coordinate system (Altamimi et al., 2016) was chosen as the reference coordinate system for the regional solution. The coordinate component residuals' weighted RMS (WRMS) value was 1.03.2 mm and 3.2-6.5 mm for horizontal and vertical components, respectively.
The quality of the DEM is a primary requirement from the various processing steps, the interpolation used for resampling, and the local properties (land cover and slope). Typically, the quality assessment includes two approaches, namely with (external) or without (internal) reference data set. The DEM is compared with a reference data set (external validation). In contrast, in the second case, inconsistencies are sought within the DEM itself with no reference data (internal validation) (Polidorit & Hage, 2020). The vertical accuracy can be directly estimated by comparing the heights extracted from a DEM and their values interpolated to the location of the GPS points. In order to make a consistent comparison of GPS surveys with SRTM, ASTER, and ALOS DEMs, all measurements must refer to the same horizontal coordinate system and vertical datum. The datum of the GPS's height is the ellipsoidal surface based on the World Geodetic System 1984 (WGS84) reference ellipsoid. For SRTM, ASTER, and ALOS DEMs, each grid cell's horizontal and vertical coordinates referenced to WGS84 and EGM96 (Lemoine et al., 1997) were output as a text file. Then elevations were transformed to ellipsoid heights (h) relative to WGS84 using EGM96 derived geoid undulations (N) by algebraic summation:
The geoid undulations according to the EGM96 global geopotential model can be determined using the service of the International Center for Global Earth Models (ICGEM) (Barthelmes & Kó'hler, 2016). The practical application of equation (1) to determine the required normal heights is complicated by a number of factors, including random errors (noise) in determining the heights, the difference in relevance for different types of heights, and insufficient knowledge of the relationship between them, geodynamic phenomena (soil subsidence, deformation of tectonic plates near subduction zones, etc.).
By the extensive use of GPS technique with geodetic aims, great interest has been collimated to the precise determination of local/regional geoid with an aim to replace levelling measurements with GPS surveys. Geoid models derived from the global geopotential models (such as EGM2008, EIGEN-6C4, EGM96) are the one alternative solution, but their accuracy needs to be estimated first for tectonic territories like Fergana Valley. There are two approaches for the transformation: gravimetrically determined geoid model, and interpolation between geometrically derived geoid heights where GPS measurements have been collocated with benchmarks. The gravimetric method offers benefits for areas with a homogeneous coverage of terrestrial data, but it is involving mathematical and computational procedures (Featherstone et al., 1998). The geometric approach has been widely used for a relatively small area, which interpolates geoid heights based on the GPS-derived heights and leveled heights at some points (Zhong, 1997; Erol & Çelik, 2004; Rabah & Kaloop, 2013; Ligas & Kulczycki, 2018; Dawod & Abdel-Aziz, 2020). The global geoid models like EGM96 can achieve the accuracy of regional or local geoid models by this method. It is used to determine the shortwave and ultra-shortwave components of the geoid, to improve of accurate geopotential models (Erol & Celik, 2004; Soycan, 2014). Early studies used the method due to its efficiency for local areas with poor knowledge of the geoid. The high accuracy of the estimation, especially for engineering surveys, is shown (Mishra & Ghosh, 2017; Jassim & Yousef, 2021). To improve its accuracy parametric models (or a corrective surface) introduced when refining heights (Fotopoulos et al., 2003). Such models include high-order polynomials with interpolation with different basis functions (Zhao et al., 2022), least squares collocation (Lyszkowicz et al., 2014), finite element method (Zaletnyik et al., 2007), Fourier series (Grigoriadis et.al., 2021), and artificial neural networks (Konakoglu & Akar, 2021). Interpolation methods (such as inverse distance weighting, bilinear interpolation, polynomial regression, triangulation, radial basis functions and nearest-neighbor interpolation) were considering according the application area, surface features, distribution of data and their accuracy. Early studies are devoted to assessing the accuracy of the employed calculation method of the geoid as well as the accuracy, density, and distribution of the used data. Polynomial, least squares collocation, multiquadric (MQ) methods had the best results for geoid undulation calculation. The results confirmed that the radial basis functions (RBF) method is the popular approach to interpolate irregularly spaced data. Especially RBF with multiquadric (MQ) function gives the lowest standard deviation and noise level for the prediction of gravity anomalies, distortion modeling (Soycan, 2014; Doganalp & Selvi, 2015). We use RBF with MQ function interpolator for construction of the surfaces in the work.
The improvement of EGM96 model is based on the corrector surface fitting (CSF) algorithm and consists of several steps. The first step calculates the difference between the GPS/leveling geoid heights N GPS /leveling and the geoid height according to EGM96 N EGM 96 at each control "common point" (i=1...27) (Soycan, 2014):
The second step is to define the trend T based on the calculated differences, which is approximated by a polynomial or harmonic series. In our case, we chose a 3-parametric trend solution for a first-order polynomial:
where α 0 represent a bias, α 1, α 2 represent tilt of the geoid plane with respect to WGS84 ellipsoid, while j i , and l are the are the northings and eastings in some plane coordinate system. CSF dN i values was defined by removing the polynomial trend from the value of DN i :
The refined values of EGM96 geoid height anomalies are determined by the expression:
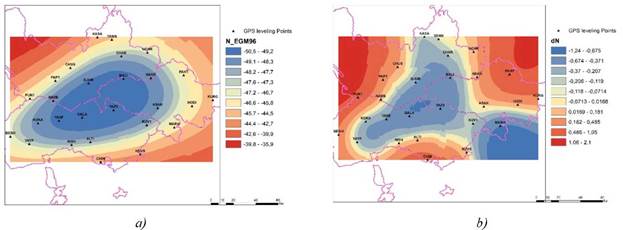
Vertical accuracy of DEMs was assessed statistically using GPS data based on point-wisely analysis. The surface continuity is a crucial issue in local geoid modeling. In this regard, the results of this study make a significant contribution to the practical use of local geoids. Therefore, we performed the construction of the surface grid using RBF with MQ function interpolation method. Using the 1'x1' EGM96 global geoid height (Fig. 2a) and 1'x1' the geoid corrector grid surfaces (Fig. 2b) were constructed for the study area. The geoid height corrections range ranged from -0.66 m to 0.88 m.
3. Results and discussion
The ellipsoidal heights had been calculated using the corrected EGM96 geoid undulations for all three DEMs at 27 points. The descriptive statistics of ellipsoidal heights from each data source range (min, max), the measures of central tendency (mean), and the dispersion (standard deviation, SD) are shown in Table 2.
Table 2 Summary statistics of DEMs for the study area
| Min, m | Max, m | Mean, m | SD, m | Equation of correlation GPS and DEM | Coefficient of correlation R2 | |
|---|---|---|---|---|---|---|
| GPS | 330.080 | 836.060 | 485.922 | 150.833 | - | - |
| SRTM30 | 324.284 | 823.250 | 476.552 | 147.652 | y = 0.989x - 4.182 | 0.9996 |
| ASTER | 326.362 | 808.831 | 470.957 | 147.131 | y = 0.985x -7.736 | 0.9981 |
| ALOS AW3D30 | 324.771 | 830.344 | 479.847 | 149.187 | y = 0.999x -5.914 | 0.9997 |
For all models, the average elevation was found to be varying between 471 m and 480 m and is also comparable to the reference GPS value of 486 m. At the same time, the linear correlation coefficient between the reference surface and all three DEMs is at the level of 99% and confirms at first glance that the models do not have significant discrepancies from the reference data. Next, we analyzed the differences between the DEM surfaces and the reference surface from GPS measurements. For this, the differences of the grids (GPS-SRTM30), (GPS-ASTER GDEM2) and (GPS-ALOS AW3D30) were determined (Fig. 3 (a-c)). We can observe that compared with the reference model, all the global DEMs in mountainous areas generally overestimated elevation. But the range of elevations the ALOS AW3D30 versus GPS elevations are from 1.5 m to 10.64 m, that compared to the SRTM30 and ASTER GDEM2 elevations is two times less.
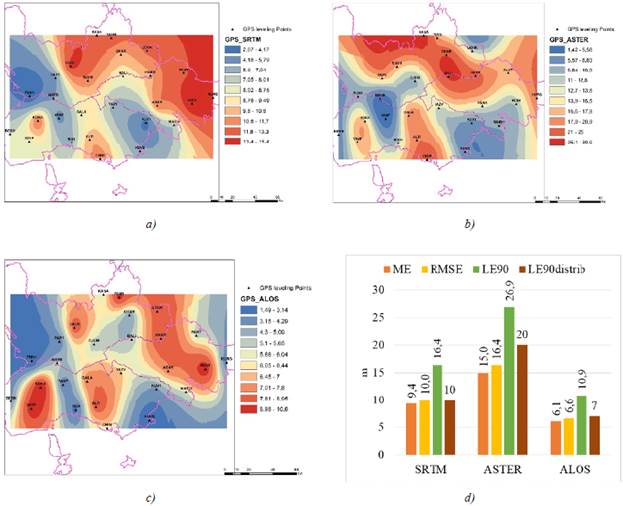
Figure 3 Surfaces of residuals of ellipsoidal heights according to DEM and GPS: (a) SRTM30, (b) ASTER GDEM2, (c) ALOS AW3D30, and (d) comparative statistics of DEMs
The vertical errors of the DEMs were quantified by comparing individual test DEM elevations and reference GPS elevations at sample points by using the following metrics. The first, root mean square error (RMSE), characterizes the difference between the DEM values Z MODEL and the reference ones (Z GPS in our case). The Mean Error (ME) will estimate of the offset from the reference model. In fact, the absolute vertical accuracy of LE90 at a 90% confidence level (LE90) can be estimated based on the obtained RMSE (Mukherjee et al., 2013):
The performance of the DEM over the study region is shown in Fig3d. SRTM30 and ALOS AW3D30 DEM have the least error with ME and RMSE of 9.4 m and 10.0 m for SRTM30 and 6.1 m and 6.6 m for ALOS AW3D30, respectively. ASTER GDEM2 has the highest RMSE of 16.4 m. Comparison of GPS measurements at Fergana Valley with DEMs indicated that LE90 were about 16.4 m, 26.9 m, and 10.9 m for SRTM30, ASTER GDEM2, and ALOS AW3D30, respectively. From Fig. 3d, it can be visualized that, for the Fergana Valley the absolute vertical accuracy error (LE90) of all three DEMs is close to that declared by the manufacturers (LE90distrib), but slightly worse. These variation in the accuracy defines the role of tectonic and terrain features in measurement of elevation irrespective of their spatial resolution. The values implied that ALOS AW3D30 elevations approximated Earth's surface elevations better than SRTM30 and ASTER GDEM2 at the region.
4. Conclusions
In this work, for the first time for the territory of the Fergana Valley in Uzbekistan, the vertical accuracy of three publicly available DEMs, SRTM30, ASTER GDEM2, and ALOS AW3D30 was statistically assessed using high accuracy GPS survey data. The geometric approach using GPS/leveling data and EGM96 global geopotential model-based geoid undulations was applied for local geoid modeling. The geoid height corrections range ranged from -0.66 m to 0.87 m. Root-Mean-Square errors of ~10.0 m, ~16.4 m, and ~6.6 m was obtained for SRTM30, ASTER GDEM2, and ALOS AW3D30, respectively. It was found that compared with the reference model, all the global DEMs in mountainous areas generally overestimated elevation and the value of vertical accuracy at a 90% confidence level by 3-6 meters exceeded the declared by distributors. But the range of elevations the ALOS AW3D30 versus GPS elevations are from 1.5 m to 10.64 m, that compared to the SRTM30 and ASTER GDEM2 elevations is two times less. ALOS AW3D30 proved to be the most accurate DEM that best represents the topography of the earth's surface and could be used for some engineering applications in Fergana Valley. In future works, we intend to perform a more detailed morphometric analysis (slope and aspect) for applications of tectonics, hydrology and other applications.