Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Ingeniería y Ciencia
versión impresa ISSN 1794-9165
ing.cienc. v.6 n.11 Medellín ene./jun. 2010
Sobre el parámetro de no extensividad para algunos sistemas super-aditivos
Soube o parâmetro de não extensividade para alguns superaditivos
Over the non-extensivity parameter for some superadditives systems
R. Borja–Tamayo1, C. Cartagena–Marín2, G. Loaiza–Ossa3, G. Molina–Vélez4 y M. Puerta–Yepes5
1 Magíster en Matemáticas aplicadas, rborjata@eafit.edu.co, profesor, Universidad EAFIT, Medellín–Colombia.
2 Físico, ccartage@eafit.edu.co, profesor, Universidad EAFIT, Medellín–Colombia.
3 Doctor en Matemáticas, gloaiza@eafit.edu.co, profesor, Universidad EAFIT, Medellín– Colombia.
4 Magíster en Matemáticas aplicadas, jmolinav@eafit.edu.co, profesor, Universidad EAFIT, Medellín–Colombia.
5 Doctora en Matemáticas, mpuerta@eafit.edu.co, profesora, Universidad EAFIT, Medellín–Colombia.
(Recepción: 08-jun-2009. Modificación: 15-dic-2009. Aceptación: 27-ene-2010)
Resumen
Este artículo propone una relación biunívoca entre el parámetro de no extensividad q y la función de densidad de probabilidad estacionaria f correspondientes a un observable u para algunos sistemas super–aditivos en los que la Entropía de Tsallis sea aplicable. Dicha relación se da en términos de comparación entre funciones de enlace que caracterizan la falta de memoria de ciertas variables aleatorias asociadas al parámetro q y a la densidad estacionaria f. Finalmente, a partir de los resultados anteriores, se propone un método que permite aproximar el parámetro q, mediante una estimación de f, cuando la energía efectiva asociada a u sea la energía cinética efectiva.
Palabras claves: entropía, termoestadística no extensiva, sistemas super–aditivos.
Resumo
Este artigo propõe uma relação biunívoca entre o parâmetro de não extensivdade q e a função de densidade de probabilidade estacionaria f correspondente a um observável u para alguns sistemas superaditivos nos que a entropia de Tsallis seja aplicável. Esta relação dei-se em termos de comparação entre funções de enlace que caracterizam a falta de memória de certas variáveis aleatórias associadas ao parâmetro q e à densidade estacionaria f. Finalmente a partir dos resultados anteriores, se propõe um método que permite aproxmar o parâmetro q, mediante uma estimação de f, quando a energia efetiva associada a u seja a energia cinética efetiva.
Palavras chaves: entropia, termoestadistica não extensiva, sistemas superaditivos.
Abstract
In this paper one introduces a bijective relation between the non–extensivity parameter q and the stationary probability density function f corresponding to an observable u for some super–additive systems for which the notion of Tsallis entropy applies. This relation is given as a comparison of linking functions characterizing memoryless of certain random variables associated to parameter q and the stationary density f. Then these results are used to formulate a method for approximating the parameter q based on an estimation of f, provided that the effective energy associated to u equals the effective kinetic energy.
Key words: entropy, thermostatistics non expansive, super–additives systems.
1 Introducción
En el desarrollo conceptual de la termoestadística se han propuesto diferentes maneras para describir las propiedades macroscópicas de los sistemas físicos bajo estudio en términos de sus propiedades microscópicas. La formulación dada por Boltzmann–Gibbs constituye un paso fundamental en la búsqueda del cumplimiento de este propósito. Sólo recientemente se ha visto la necesidad de generalizar el concepto de Entropía (y por consiguiente de las funciones de distribución de probabilidad que la maximizan) para describir sistemas con un alto grado de complejidad que se han manifestado en muchos campos de la física no lineal, como el estudio de los fenómenos de turbulencia, percolación, multifractales, radiación cósmica de fondo, etcétera. En 1988, Constantino Tsallis [1] introdujo un nuevo concepto de Entropía y conjuntamente nuevas restricciones para el correspondiente funcional, el cual se utiliza para describir sistemas que poseen propiedades no extensivas. Esta formulación generalizada de Entropía depende de un parámetro real llamado parámetro de no extensvidad, q, el cual ha sido propuesto de acuerdo a las condiciones específicas que describen el sistema. Para que el formalismo de Tsallis constituya una teoría física completa cerrada es necesario determinar, en el marco de la mecánica no extensiva, el valor particular (o valores particulares) de q para un sistema físico dado.
En la literatura se encuentran varios cálculos para determinar q en sistemas físicos particulares [2]. En algunos casos, los procedimientos parten de principios primeros o leyes derivadas para determinar el valor o valores de q correspondientes a distribuciones de probabilidad que se ajusten a los datos observados en un sistema. Otros procedimientos consisten en partir de datos experimentales para encontrar una función de ajuste (asumiendo características no extensivas) y plantear un valor o valores de q óptimos.
En el marco de la mecánica no extensiva interesa conocer, para algún sistema físico dado, nuevas formas de calcular el parámetro q: el presente artículo aporta precisamente en dicho conocimiento. Concretamente, el objeto de este artículo es introducir una nueva forma de relacionar el parámetro q para un observable u, con su función de densidad de probabilidad estacionaria f, siempre que ésta tenga media cero en un sistema superaditivo y la energía efectiva asociada a u cumpla ciertas condiciones. La relación se plantea mediante la comparación de funciones de enlace que permitan describir la pérdida de memoria (según una caracterización de Ghitany [3]) para ciertas variables aleatorias. La comparación entre las funciones de enlace se usa como criterio para obtener el parámetro q a partir de una estimación de la función de densidad de probabilidad estacionaria. Dicho criterio es constructivo en cuanto no requiere suponer un valor específico para q.
El artículo está dividido en dos secciones: en la 2, se presenta una breve revisión de temas necesarios relacionados con termoestadística generalizada y funciones de enlace; en la 3 se expone el objeto central del artículo, donde se establece una relación entre el parámetro q y la función de densidad para el observable u del sistema físico con las características descritas previamente, además, se establece un criterio de aproximación para q a partir de una estimación de la función de densidad.
2 Preliminares
2.1 Entropía Sq de Tsallis
Considérese un sistema con n estados posibles, cada uno con probabilidad pi, (1 ≤ i ≤ n) tales que 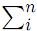 =1 pi = 1. La Entropía de Boltzman–Gibbs–Schannon (BGS) es el fundamento de la mecánica estadística clásica y se define para p = (p1, . . . , pn) mediante
=1 pi = 1. La Entropía de Boltzman–Gibbs–Schannon (BGS) es el fundamento de la mecánica estadística clásica y se define para p = (p1, . . . , pn) mediante
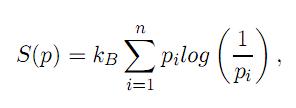
donde kB es la constante de Boltzman (que para efectos de este artículo será tomada como uno) y log es el logaritmo natural.
Si bien la propuesta de Boltzmann–Gibbs ha mostrado efectividad, su uso se restringe a los sistemas conocidos como aditivos o extensivos; tales sistemas son aquellos que cumplen la propiedad de aditividad S(A + B) = S(A)+S(B), donde A y B son dos sistemas independientes en el sentido probabilístico. Para sistemas no extensivos es necesario generalizar la Entropía de forma tal que se cubran los casos subaditivos o superaditivos. En este sentido, la estadística no extensiva de Tsallis es considerada como un nuevo paradigma en mecánica estadística.
La Entropía Sq, definida por Tsallis [1], para cada real q, con q ≠ = 1, está dada por
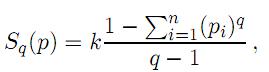
y toma el valor S(p) si q = 1.
La entropía Sq de Tsallis verifica las siguientes propiedades [4]:
1. Sq es extensión de S en el siguiente sentido: si q → 1 se tiene Sq → S.
2. Sq(P) = 0 sólo en el caso de que alguna pi= 1.
3. El máximo para Sq bajo la única restricción, Σipi =1, se obtiene para pi = 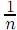 para 1 ≤ i ≤ n.
para 1 ≤ i ≤ n.
4. Propiedad de no extensividad. Supóngase que se tienen dos sistemas independientes A y B, en sentido probabilístico, esto es 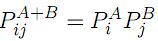 . Entonces se tiene
. Entonces se tiene
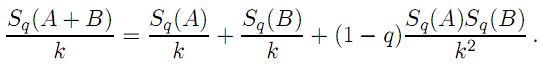
O de forma equivalente
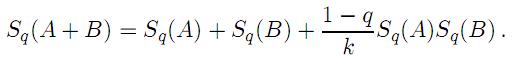
Del último numeral se concluye que: para q > 1 se tienen sistemas superextensivos, para q = 1 se tienen sistemas extensivos y para q < 1 sistemas subextensivos. El caso de Boltzmann–Gibbs se reduce así a los sistemas extensivos.
En las últimas tres décadas se ha encontrado evidencia experimental que presenta casos de sistemas termodinámicos (con suficiente complejidad) que son no extensivos, hecho que en gran medida ha servido como muestra de la importancia de la teoría de Tsallis en la termoestadística. Una situación entre estos casos anómalos se ofrece en consideraciones hidrodinámicas de los fenómenos de turbulencia en tres dimensiones. Particularmente en el estudio presentado por Cristian Beck [5], de la diferencia de la velocidad radial u entre dos puntos en un líquido separados por una distancia r descrita mediante su relación con la energía cinética 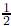 u2. Las propiedades dinámicas de estos sistemas, como la difusión anómala, la simetría y la ley de potencia para el decaimiento de correlaciones, están en buena coincidencia con las predicciones de los modelos no extensivos en un amplio rango de parámetros.
u2. Las propiedades dinámicas de estos sistemas, como la difusión anómala, la simetría y la ley de potencia para el decaimiento de correlaciones, están en buena coincidencia con las predicciones de los modelos no extensivos en un amplio rango de parámetros.
La manifestación de las propiedades no extensivas de la Entropía de Tsallis ha conducido a la representación de Sq en términos de generalizaciones de las funciones logaritmo y exponencial, llamadas q–logaritmo y q–exponencial, que son inversas una de la otra y se definen respectivamente para q ≠1 por
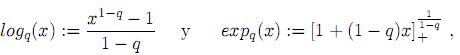
donde [u]+ = máx{0, u}. Cuando q → 1, las expresiones anteriores se reducen a las funciones logaritmo natural y exponencial respectivamente. La función q–logaritmo permite representar la Entropía Sq mediante
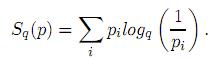
La distribución de probabilidades de equilibrio p = {pi} se obtiene maximizando Sq con respecto a los pi sujeto a la restricción Σipi = 1 Para el. conjunto microcanónico (sistema aislado), ésta será la restricción; en tal caso el resultado de la optimización es pi = 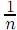 . Si se considera un sistema en contacto con un baño térmico, en el conjunto canónico, además de la anterior restricción, es necesaria una de las tres siguientes:
. Si se considera un sistema en contacto con un baño térmico, en el conjunto canónico, además de la anterior restricción, es necesaria una de las tres siguientes:
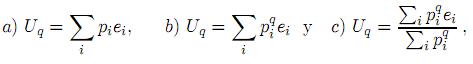
donde Uq es el valor esperado de energía E asociada al sistema y los ei son los autovalores del Hamiltoniano cuántico del sistema. Cada restricción fue introducida en diferentes trabajos de Tsallis [1, 2, 6].
El uso de cualquiera de las anteriores restricciones conduce a distintas termoestadísticas, donde a cada una de ellas le corresponde una distinta distribución de probabilidades p = {pi}, que expresa la distribución de probabilidades de ocupación de los microestados. Ferri, Martínez y Plastino [7] muestran que cada una de ellas se deriva de una sola expresión, que depende de un parámetro (multiplicador de Lagrange) β y está dada por p = {pi}, donde
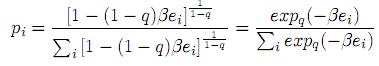 válido para 0 < q ≤ 2;
válido para 0 < q ≤ 2;
y las expresiones para β corresponden al β∗ que aparece en [7] para cada una de las correspondientes restricciones.
En el caso continuo, el funcional de Entropía se define por
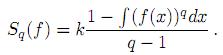
A continuación se presentan resultados sobre optimización de Sq con notación tomada de [6] y [8], pero el proceso como tal se puede consultar en [6].
Considérese el problema de maximizar Sq, sujeto a las restricciones
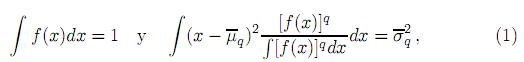
donde 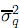 y
y 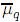 son la varianza y la media generalizadas de x respectivamente. El resultado de la optimización, válido para q < 3, es
son la varianza y la media generalizadas de x respectivamente. El resultado de la optimización, válido para q < 3, es
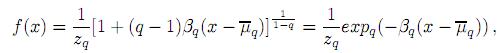
donde la constante βq > 0 se puede determinar usando la segunda restricción de (1) y zq corresponde a zq := ∫ expq(−βq(x−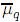 ))dx.
))dx.
Para modelos estacionarios es necesario considerar una tercera restricción de (1) dada por
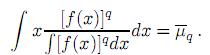
En este caso, la función de densidad de probabilidad estacionaria que resulta β de la optimización (escribiendo respectivamente 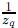 y
y 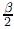 en lugar de la notación Αq y βq de [8]) es
en lugar de la notación Αq y βq de [8]) es
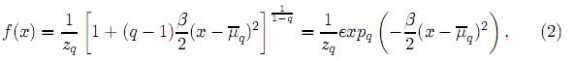
válido para q <3, donde zq:= ∫ expq(−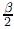 (x−
(x−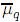 ))dx, el parámetro β puede ser determinado por β =
))dx, el parámetro β puede ser determinado por β = 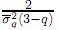 y las varianzas usual y generalizada están relacionadas por
y las varianzas usual y generalizada están relacionadas por 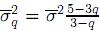 . Además β =
. Además β = 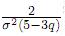 y zq se puede calcular por
y zq se puede calcular por
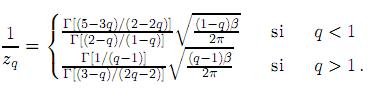
2.2 Propiedad de pérdida de memoria y funciones de enlace
Si se considera una función de distribución exponencial, la función de distrbución acumulada asociada está dada por F(t) = 1 − 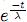 con t > 0, donde el parámetro λ > 0 representa la media de la variable aleatoria que tiene asociada dicha distribución. En tal caso, la función de supervivencia asociada es
con t > 0, donde el parámetro λ > 0 representa la media de la variable aleatoria que tiene asociada dicha distribución. En tal caso, la función de supervivencia asociada es  (t) = 1 − F(t) =
(t) = 1 − F(t) = 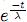 . Por otro lado, es conocida la propiedad de pérdida de memoria dada por P (X > t + a) = P (X > t)P (X > a) que cumple una variable aleatoria con distribución exponencial.
. Por otro lado, es conocida la propiedad de pérdida de memoria dada por P (X > t + a) = P (X > t)P (X > a) que cumple una variable aleatoria con distribución exponencial.
Observación 1. Considérese una variable aleatoria X con función de distrbución de probabilidad F , continua y estrictamente creciente en un intervalo. Dado que en tal caso F y  distribuyen uniformemente en (0, 1), se tiene que g(X) := log(
distribuyen uniformemente en (0, 1), se tiene que g(X) := log(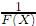 )y h(X) =: log(
)y h(X) =: log(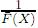 ) están exponencialmente distribuidas con media uno.
) están exponencialmente distribuidas con media uno.
Así, la propiedad de pérdida de memoria para F y  respectivamente (o bien, para X mediante g y h respectivamente) es caracterizada por Ghitany [3] por medio de las funciones de enlace g y h de la forma:
respectivamente (o bien, para X mediante g y h respectivamente) es caracterizada por Ghitany [3] por medio de las funciones de enlace g y h de la forma:
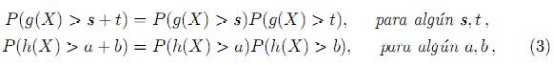
o igualmente
P (X > h−1(a + b)) = P(X > h−1(a))P (X > h−1(b)), para algún a, b.
De tal forma, existen λ1 > 0 y λ2 > 0 tales que
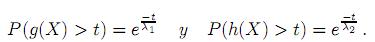
3 Funciones de enlace y el parámetro de no extensividad
Es claro que la propiedad de pérdida de memoria, en la forma (3), para una variable aleatoria X que distribuya siguiendo una función de densidad de probabilidad continua definida mediante una función exponencial, permite caracterizar a X mediante la relación  Y(t) =
Y(t) = 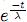 = λfY(t) (t > 0). En la subsección 3.1 se mostrará que en el caso en que la variable aleatoria X tenga función de densidad q–exponencial, se obtiene una caracterización smilar, para lo cual es necesario establecer una biyección que identifique a una restrición de la función de supervivencia asociada a la variable aleatoria, con otra función de supervivencia definida mediante una función de enlace. En la subsección 3.2 se propone una nueva forma de de relacionar (mediante comparación de funciones de enlace) la función de densidad estacionaria estimada con una función que permite decidir el parámetro de no extensividad correspondiente para ciertos sistemas super–aditivos.
= λfY(t) (t > 0). En la subsección 3.1 se mostrará que en el caso en que la variable aleatoria X tenga función de densidad q–exponencial, se obtiene una caracterización smilar, para lo cual es necesario establecer una biyección que identifique a una restrición de la función de supervivencia asociada a la variable aleatoria, con otra función de supervivencia definida mediante una función de enlace. En la subsección 3.2 se propone una nueva forma de de relacionar (mediante comparación de funciones de enlace) la función de densidad estacionaria estimada con una función que permite decidir el parámetro de no extensividad correspondiente para ciertos sistemas super–aditivos.
3.1 Parámetro de no extensividad y propiedad de pérdida de memoria
Para modelos canónicos no extensivos se han propuesto funciones de densidad estacionarias f asociadas a un observable u, maximizando el funcional de Entropía con las restricciones adecuadas, descritas por
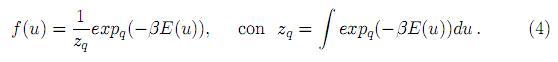
En adelante, se supondrá que f es una función de densidad de probabilidad continua y simétrica para un observable u asociado a un sistema no extensivo con parámetro de no extensividad q > 1.
Se define una probabilidad en [0, ∞), para alguna variable aleatoria Y, mediante
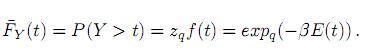
Para cada r > 1, en el intervalo [0,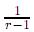 ), se define la probabilidad para una variable aleatoria Xr por medio de
), se define la probabilidad para una variable aleatoria Xr por medio de
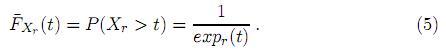
Sea  la restricción de
la restricción de  Y al intervalo [0,
Y al intervalo [0,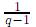 ), claramente
), claramente  no es una función de supervivencia. Nótese que la asignación
no es una función de supervivencia. Nótese que la asignación 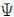 dada por
dada por 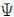 (
( (t)) =
(t)) =  Xr(t) es una biyección en [0,
Xr(t) es una biyección en [0, 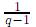 ).
).
Proposición 2. La única biyección en [0, 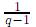 ) definida por
) definida por 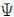 (
(  (t)) =
(t)) =  Xr(t) ocurre cuando r = q.
Xr(t) ocurre cuando r = q.
Demostración. Nótese que para q < r no es posible tener una biyección dada por 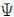 (
( (t)) =
(t)) =  Xr(t) porque el dominio de la primera incluye propiamente al dominio de la segunda (aún si se redefiniera
Xr(t) porque el dominio de la primera incluye propiamente al dominio de la segunda (aún si se redefiniera  Xr(t) = 0 para
Xr(t) = 0 para 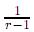 ≤ t <
≤ t < 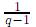 , la asignación no sería inyectiva). Análogamente, cuando q > r no es posible una biyección como la planteada anteriormente, ya que [0,
, la asignación no sería inyectiva). Análogamente, cuando q > r no es posible una biyección como la planteada anteriormente, ya que [0, 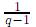 ] se incluye propiamente en [0,
] se incluye propiamente en [0,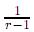 ). Gracias al decrecimiento estricto, tanto de
). Gracias al decrecimiento estricto, tanto de  Xq como de
Xq como de  , la única biyección (como las sugeridas) que puede plantearse es
, la única biyección (como las sugeridas) que puede plantearse es 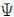 (
( (t)) =
(t)) =  Xq(t) para todo t ∈ [0,
Xq(t) para todo t ∈ [0, 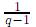 ).
).

A continuación se muestra que la biyección 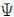 permite caracterizar la pérdda de memoria de Xq en términos de
permite caracterizar la pérdda de memoria de Xq en términos de  (t) y, por tanto, de Y. En efecto, siendo
(t) y, por tanto, de Y. En efecto, siendo  Xq y
Xq y  Y las funciones de supervivencia para Xq e Y respectivamente, las funciones de enlace mediante las cuales se expresa la pérdida de memoria para Xq e Y están definidas respectivamente por
Y las funciones de supervivencia para Xq e Y respectivamente, las funciones de enlace mediante las cuales se expresa la pérdida de memoria para Xq e Y están definidas respectivamente por
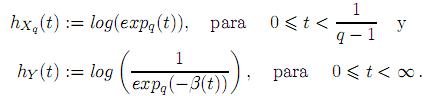
En consecuencia, existen λ1, λ2 > 0 tales que
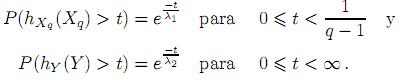
En particular, si t ∈ [0,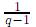 ), se satisfacen las dos igualdades anteriores y si se toma k =
), se satisfacen las dos igualdades anteriores y si se toma k = 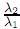 , entonces se tiene
, entonces se tiene
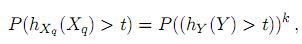
o igualmente, P (Xq > 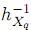 (t)) = P (Y >
(t)) = P (Y > 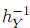 (t))k; que se puede escribir como
(t))k; que se puede escribir como  Xq (
Xq (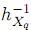 (t)) =
(t)) =  Y (
Y (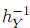 (t))k, o bien
(t))k, o bien
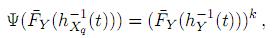
con lo cual, la pérdida de memoria de Y se puede expresar mediante las funciones de enlace y la biyección.
3.2 Estimación del parámetro de no extensividad
Considérese una función de densidad de probabilidad continua y simétrica f para un observable u asociado a un sistema no extensivo con parámetro de no extensividad q > 1. Para plantear una relación entre f con una función que permite decidir el parámetro de no extensividad, se planteará una relación entre dicho parámetro y la familia de funciones  xr (con 1 < r < 3 construidas como en la subsección anterior). Dicha relación será establecida mediante un criterio que determine: cuándo una de las gráficas correspondiente a las funciones de la familia corta a la gráfica de
xr (con 1 < r < 3 construidas como en la subsección anterior). Dicha relación será establecida mediante un criterio que determine: cuándo una de las gráficas correspondiente a las funciones de la familia corta a la gráfica de  u en un único punto (a, b) tal que a > 0. Lo anterior equivale a comparar la familia de funciones de enlace hr(t) = log(expr(t)) con hY(t) = log[1/expq(−βE(t))], o más directamente, la familia de funciones expr(t) con la función ef(t) :=
u en un único punto (a, b) tal que a > 0. Lo anterior equivale a comparar la familia de funciones de enlace hr(t) = log(expr(t)) con hY(t) = log[1/expq(−βE(t))], o más directamente, la familia de funciones expr(t) con la función ef(t) := 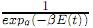 .
.
El siguiente resultado plantea que efcumple condiciones para ser consderada como exponencial k–deformado en el sentido de Naudts [9].
Proposición 3. Considérese una función de densidad de probabilidad estacionaria, continua y simétrica correspondiente a un observable u de un sistema no extensivo con parámetro de no extensividad q > 1, y sea E(u) la energía asociada a u según (4). Si además, para todo t > 0 se cumplen E(t) > 0 y
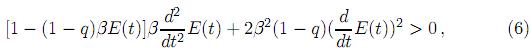
entonces se tiene: ef(0) = 1, ef(t) → ∞ cuando t → ∞, y ef es función continua, estrictamente creciente y cóncava en el intervalo [0, ∞). Además, ef tiene derivada cero a derecha de cero.
Demostración. Sólo se justificará las propiedades decrecimiento concavidad de ef, ya que las demás afirmaciones son fáciles de probar a partir de las propiedades de expq.
Para considerar las dos primeras derivadas de ef respecto a t, resultan
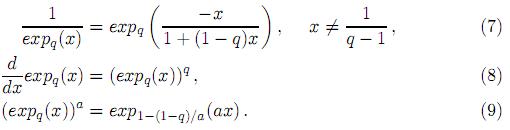
Aplicando (7) para reescribir a ef(t), derivando en ambos lados y simplficando, se obtiene
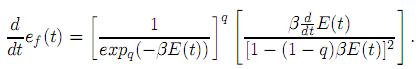
Ahora, empleando (7), (8) y (9), mediante cálculos laboriosos, la segunda derivada es dada por
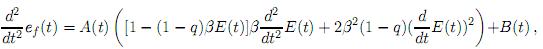
donde
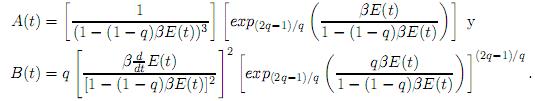
Ahora bien, si se cuenta con un sistema para el cual E(t) > 0 para t > 0, entonces 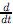 ef(t) es positiva para todo t > 0 y por tanto ef es estrictamente creciente en los reales positivos,
ef(t) es positiva para todo t > 0 y por tanto ef es estrictamente creciente en los reales positivos, 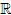 +.
+.
Además, las funciones A(t) y B(t) son estrictamente positivas en 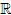 +, por lo que
+, por lo que 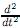 ef(t) es estrictamente positiva y ef(t) es función cóncava en
ef(t) es estrictamente positiva y ef(t) es función cóncava en 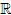 +, siempre y cuando se cumpla (6).
+, siempre y cuando se cumpla (6).

Observación 4. Es de importancia resaltar que la familia de funciones expr para 1 < r < 3 presenta el siguiente comportamiento:
• Cada expr es una función: continua en [0,
), estrictamente creciente, cóncava, que pasa por (0, 1) y tiene asíntota vertical en
. Además, expr tiene derivada uno a derecha de cero.
• Es familia ordenada en el siguiente sentido: Si r1 < r2 entonces, para todo t ∈ [0,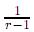 ), expr1(t) < expr2(t).
), expr1(t) < expr2(t).
Ahora, por las características dadas en la observación 4 para la familia de funciones er(t) y por las características de ef según la proposición 3, existe un único r0 para el cual la gráfica de er0 corta a la gráfica de ef en un condiciones para que r0 sea precisamente el parámetro de no extensividad q.
Si se considera q como el parámetro de no extensividad, según la proposición 3 y expq(t0) = ef(t0) para algún t0 > 0, se tiene que expq(t0) =[expq (−βE (t0))]−1. Aplicando (7) se llega a expq(t0) = expq(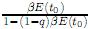 ) de donde se obtiene t0=
) de donde se obtiene t0= 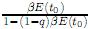 . Ahora, la función
. Ahora, la función
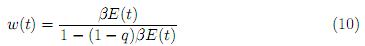
es acotada por 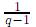 siempre que E(t) → ∞ cuando t → ∞. Además, si t0 es el w(t), entonces la gráfica de eq corta a la de ef
siempre que E(t) → ∞ cuando t → ∞. Además, si t0 es el w(t), entonces la gráfica de eq corta a la de ef













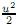 , entonces se satisfacen las condiciones de la proposición 3. Si además se considera β =
, entonces se satisfacen las condiciones de la proposición 3. Si además se considera β = 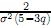 entonces w(t) se transforma en
entonces w(t) se transforma en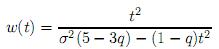
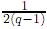 siempre y cuando sea cero su discriminante
siempre y cuando sea cero su discriminante 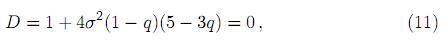
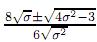 y σ2 ≥
y σ2 ≥ 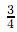 . Con las anteriores condiciones, y teniendo presente que β =
. Con las anteriores condiciones, y teniendo presente que β = 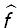 la función de densidad estacionaria estimada y tal que
la función de densidad estacionaria estimada y tal que 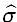 ≥
≥ 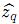 el inverso multiplicativo de la máxima altura de
el inverso multiplicativo de la máxima altura de 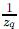 es la máxima altura de f o bien, la imagen bajo f de la media µ = 0). El método para determinar el valor de q consiste en comparar las gráficas de expr(para 1 < r < 3) con la gráfica de
es la máxima altura de f o bien, la imagen bajo f de la media µ = 0). El método para determinar el valor de q consiste en comparar las gráficas de expr(para 1 < r < 3) con la gráfica de 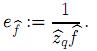
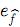 en un único punto que sea de coordenadas positivas.
en un único punto que sea de coordenadas positivas.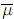 =0. Considérese: la energía cinética efectiva E(u) =
=0. Considérese: la energía cinética efectiva E(u) = 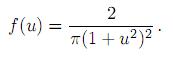
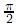 y por consiguiente
y por consiguiente 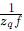 .
. 
