Atractividad local en la bifurcación de zip

Atração local na bifurcação da zip

Local atractivity in zip bifurcation

Carlos Mario Escobar-Callejas¹, José Rodrigo González-Granada² y Abel Enrique Posso-Agudelo³

¹ Magíster en Matemáticas, ccescobar@utp.edu.co, profesor, Universidad Tecnológica de Pereira, Pereira-Colombia.

² Doctor en Matemáticas, jorodryy@utp.edu.co, profesor, Universidad Tecnológica de Pereira, Pereira-Colombia.

³ Doctor en Matemáticas, posssoa@utp.edu.co, profesor, Universidad Tecnológica de Pereira, Pereira-Colombia.

(Recepción: 17-mar-2009. Modificación: 26-ago-2009. Aceptación: 28-ago-2009)

---

Resumen

En el presente trabajo se estudia la atractividad local del segmento de equilibrios que se forma en el fenómeno de la bifurcación de zip para un sistema tridimensional de ecuaciones diferenciales no lineales. Este trabajo puede ser considerado como una generalización de un resultado de Farkas en bifurcación de zip de modelos en competición.

Palabras claves: bifurcación zip, k-estratega, r-estratega, respuesta funcional, dinámica población, principio de exclusión competitiva.

---

Resumo

Este trabalho estuda o segmento local de atracção contrapesos que faz sobre o fenômeno da bifurcação da zip de três sistema bidimensional de equações diferenciais não-linear. Este trabalho pode ser considerado como uma generalização de um resultado na bifurcação Farkas zip modelos competención.

Palavras chaves: bifurcação zip, k-estrategista, r-estrategista, a resposta funcional, dinâmica populacional, princípio de exclusão competitiva.

---

Abstract

In this paper the local segment attractiveness equilibrium that forms on the phenomenon of zip bifurcation for a three-dimensional system of differential equations nonlinear is studied. This work may be regarded as a generalization as a result on Farkas's zip bifurcation in competition models.

Key words: zip bifurcation, k-strategist, r-strategist, functional response, dinamical population, competitive exclusion principle.

---

1 Introducción

En el estudio del problema concerniente a la validez del principio de la exclusión competitiva, para el caso de dos especies predadoras, compitiendo por una presa que se regenera, el modelo (1) ha sido ampliamente considerado por varios autores [1].

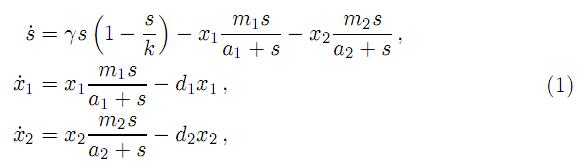
donde x₁, x₂ y s son los tamaños de la población de los dos predadores y el de la presa que se regenera; y se supone que en ausencia del predador existe un crecimiento logístico de la presa. La respuesta funcional es saturada de acuerdo con la cinética de Michaelis-Menten, donde γ > 0 es la rata de crecimiento intrínseca de la presa, k > 0 es la capacidad de carga del medio con respecto a la presa, m_i> 0, d_i> 0 y a_i> 0 son la rata de nacimiento maximal, la rata de muerte y la constante de saturación media, respectivamente, del predador (i = 1, 2).

Considerando [1], las constantes en este modelo son

que se introducen teniendo el siguiente significado: x_i se incrementa si y sólo si s > λ_i, según sea x_i positivo, llegando a ser cero en s = λ_i. Los autores de [2] han mostrado que las soluciones del sistema (1), correspondiente a valores iniciales positivos, son acotadas y permanecen en el octante positivo y que la especie predadora i-ésima puede sobrevivir únicamente si 0 < λ_i < k, lo cual implica que m_i > d_i. También han estudiado el caso genérico con λ₁ ≠ λ₂, en [2] y [3] se demuestra que, para algunos valores de los parámetros, algunas soluciones periódicas pueden obtenerse en el octante positivo significando que la coexistencia es posible. En [4] se ha probado (usando teoría de bifurcación) que, en el caso 0 < λ₁< λ₂, existen soluciones periódicas en el octante positivo para valores suficientemente pequeños de | λ₁ λ₂ | y k (a₁ + 2λ₁). En [5] se ha tratado el caso λ₁ = λ₂ = λ. Se ha establecido, en el caso a₁ = a₂ = a, que si k a + 2λ entonces hay un segmento de línea de equilibrio estable, mientras que, si k > a + 2λ entonces "todas las tres especies sobreviven en un ciclo límite permanentemente". También ha probado que, en el caso a₁> a₂, si k > a₁+ 2λ entonces x₂ va a cero, s y x₁ permanecen en un ciclo límite, si k = a₁ + 2λ entonces x₂ va a cero, s y x₁ tienden al equilibrio, si k < a₁ + 2λ entonces las tres especies sobreviven y la solución tiende a un punto de equilibrio del segmento de la línea de equilibrio.

En [6] se ha mostrado que la mayoría de resultados concernientes al modelo de Hsu y otros pueden ser investigados para toda clase de modelos del tipo dos predadores y una presa, modelo cuya característica común es que la tasa de desarrollo de la presa y la respuesta funcional del depredador son funciones arbitrarias que satisfacen ciertas condiciones naturales.

En [7] se ha estudiado el modelo de Hsu y otros bajo la hipótesis especial de que: cierto valor de un parámetro umbral es igual en las dos especies predadoras; este parámetro puede inteR^pretarse como la cantidad de presa necesaria para alcanzar una tasa de crecimiento intrínseca igual a la tasa de muerte natural del predador. Esta hipótesis, en el caso de los modelos naturales, hace posible la identificación de uno de los predadores como un r-estratega y el otro como un k-estratega. Los términos r-estratega y k-estratega tienen un significado semejante al asignado en la teoría de la dinámica de poblaciones, es decir, un r-estratega es un predador cuya rata maximal de nacimiento y muerte es alta, por lo cual necesita una gran cantidad de alimento para incrementar su rata de nacimiento, mientras un k-estratega significa un predador con una rata de nacimiento y muerte relativamente baja, pero con la habilidad de mantener la tasa de nacimiento relativamente alta aún cuando pequeñas cantidades de alimentos le sean posibles lograr.

En [8] se ha introducido el concepto de bifurcación zip para denotar el siguiente fenómeno: "a bajos valores de la capacidad de carga k del ecosistema con respecto a la presa, una línea de equilibrio es un atractor del sistema, ella representa coexistencia estable de las tres especies. Si k es incrementado, los equilibrios son continuamente desestabilizados, empezando por aquellos que representan la dominancia del k-estratega sobre el r-estratega. Arriba de cierto valor de k, el sistema no tiene más equilibrios estables que representen coexistencia, sin embargo, un ciclo límite permanece representando la oscilación de coexistencia del k-estratega y la presa". Recientemente, en [9] se ha generalizado el fenómeno de zip a un sistema ODE cuatro dimensional con respuesta funcional generalizada tipo Holling III. En [10] se ha tratado la ocurrencia de la bifurcación zip en un sistema predador-presa (n+1)-dimensional con respuesta funcional tipo Holling II.

En este artículo se generalizan resultados sobre la atractividad local desestabilizados en el fenómeno de la bifurcación de zip [7] y global del conjunto de equilibrios los cuales son continuamente para el sistema (1). Por último, se ha simulado por computador, mediante los programas Phaser y Mathematica, algunos casos particulares [11] que muestran la actractividad del segmento de equilibrios.

2 Atractividad local en la bifurcación de zip

2.1 Preliminares

En el presente trabajo de investigación se estudia la atractividad local y global del conjunto de equilibrios L_k en la bifurcación de zip, en la clase de sistemas EDOs que modela la competición entre dos especies predadoras por una presa singular, y se generalizan los resultados sobre atractividad local de recubrimiento tubular [7] para el sistema (2). éste es modelado por el siguiente sistema de ecuaciones diferenciales, en el cual se nota el punto encima de la letra como diferenciación con respecto al tiempo

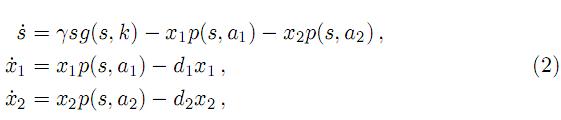
donde s(t) representa la población de especie de la presa y x₁(t), x₂(t) describen las poblaciones de las especies predadoras que compiten por la presa s(t); p(s, a_i) representa la tasa de nacimiento o respuesta funcional del predador i, y g(s, k) significa la resistencia ambiental del medio al crecimiento de la presa. Las constantes γ, d_i > 0 son, respectivamente, la tasa de crecimiento maximal de la presa y la tasa de muerte de la especie predadora i. Por último, a_i > 0, (i = 1, 2) representan los parámetros de escala en la respuesta funcional del predador i. Se asume, además, que el modelo (2) satisface las condiciones [6] y [12] siguientes:

La función g satisface las condiciones:

A la función se le imponen condiciones de uniformidad en [δ, S₀] para cualquier δ, 0 < δ < S₀ y la integral, posiblemente impropia, (s, k)dS debe ser uniformemente convergente en [k₀, ∞), para cualquier valor k₀ > 0. Por último se impone la condición sobre g

La función que representa la respuesta funcional del predador i, p(s, a_i) con a_i constante, (i = 1, 2) satisface las condiciones:

Las condiciones (3) a (8) son condiciones apropiadas. éstas coinciden aproximadamente con las hechas por [6]. La condición (3) significa que la rata de crecimiento específica máxima de la presa es alcanzada en s = 0, x₁ = 0, x₂ = 0 y es γ > 0; la rata de crecimiento decrece si la cantidad de presa se incrementa, y la rata de crecimiento de (s, k) se incrementa con la capacidad de carga k. La relación (4) establece que para altos valores de k, el cambio en la cantidad de presa tiene un efecto despreciable en la rata de crecimiento. La desigualdad (5) significa que (en ausencia del predador) la rata de crecimiento de la presa es positiva si s está abajo de la capacidad de carga k, y es negativa si s está arriba de ésta. Es claro que las condiciones (3) y (4) implican

La condición (6) significa que la rata de nacimiento per capita p de los predadores (también llamada la rata de predación o respuesta funcional) es cero en ausencia de la presa y es una función que se incrementa con la cantidad de presa. La condición (7) es una condición de concavidad débil, algunas veces llamada condición Krasonselskij. Si p es una función estrictamente cóncava de s (para cualquier a > 0), (7) implica que ésta se tiene, salvo puntos aislados donde se tiene un signo de igualdad. La desigualdad (8) establece que la rata de depredación decrece con el parámetro a (entre más alto sea el parámetro a, más alimento es necesario para mantener la misma tasa de nacimiento de la especie predadora). En el modelo original de Hsu y otros, a es la constante media de saturación. En el caso en que p es una función acotada para un valor a dado, se tiene que

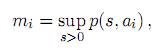
es la rata maximal de nacimiento del predador i. Claramente

Para el caso en que los parámetros a₁, a₂ son distintos, sin pérdida de generalidad se supone:

En correspondencia con esta última condición, a un nivel de presa dado, la rata de nacimiento del predador dos es mas alta que la del predador uno, en otras palabras, el predador uno necesita más alimento para llegar a la misma tasa de nacimiento que el predador dos.

Ahora bien, si d₁ es más grande que d₂, la condición (11) implica que

es decir, la rata de crecimiento del predador dos es más alta que la del predador uno. Se puede mostrar en este caso que el predador dos saca de competencia al predador uno. Se supone por lo tanto que

Tal como consecuencia de (11), ahora esta condición no implica necesariamente que la tasa de crecimiento neta del predador dos excede la del predador uno. Si en la respuesta funcional del predador i, para un valor del parámetro de escala a_i, se satisface la desigualdad m_i > d_i, por la continuidad de p, existirá un nivel de presa s = λ_i, en la cual se tiene la relación

A λ_i se le llamará parámetro umbral del predador i; éste puede inteR^pretarse como la cantidad de presa necesaria para alcanzar una tasa de nacimiento intrínseca, igual a la tasa de muerte natural del depredador i. En general no se tiene que λ₁ = λ₂, pero para una clase importante de modelos se puede suponer que λ₁ = λ₂. Dados d₁ y d₂, existen λ, a₁, a₂, tales que p(λ, a_i) = d_i para los modelos que satisfacen la condición

Para el modelo hallado, la condición (14) se reduce a la desigualdad

m₂ ≥ d₂ ,

ya que bajo el supuesto inicial de d₁< d₂ y la forma específica de la función p se satisface la condición 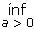p(s, a) = 0 para todo s ≥ 0.

Los parámetros a_i, i = 1, 2, son parámetros de escala del modelo y el parámetro λ actúa como ajustador o seleccionador del tipo de modelo, por esta razón la condición λ₁= λ₂= λ no es tan restrictiva como parece a primera vista.

En lo que sigue se supone que las dos especies poseen igual parámetro umbral de la presa, es decir, m₂ ≥ d₂, por lo tanto existe un λ > 0 tal que se tiene (13).

La clase de modelos bajo consideración serán divididos en tres subclases de acuerdo con la siguiente definición.

Definición 2.1. Se dice que el modelo (2), bajo las condiciones (3) a (8) y (11) a (13), es natural, artificial, o degenerado si

respectivamente.

La primera desigualdad de (15) significa, por continuidad, que el cociente de las ratas de nacimiento (la cual es, por (11), más grande que la unidad) decrece en un entorno de s = λ, es decir, la ventaja de la especie dos sobre la uno expresada por (11), decrece a medida que la presa se incrementa; que es lo que usualmente se espera que suceda. La segunda desigualdad de (15) significa que la ventaja de la especie dos sobre la uno expresada por (11) se incrementa a medida que la presa se incrementa.

Especial caracterización puede hacerse en el caso en que el modelo es del tipo natural ya que, teniendo en cuenta las relaciones (11)-(13) se tiene que:

Por lo tanto, para s > λ, aplicando la primera condición de (15), se tiene que:

La última condición muestra que, en este caso, el predador uno tiene mayores tasas de crecimiento relativo que el predador dos. En [7] se ha caracterizado a la especie uno como un r-estratega, ya que su estrategia de supervivencia se basa en el mantenimiento, a lo largo del tiempo, de altas tasas de crecimiento relativo. Mientras en la especie dos, de las condiciones(6)-(8), se deduce fácilmente que hace un uso más eficiente e inteligente de la energía, pues requiere menos cantidad de presa para mantener iguales tasas de nacimiento que la especie uno, por esto Farkas ha llamado a este predador un k-estratega.

2.2 Puntos de equilibrio del sistema

El sistema (2) tiene los puntos de equilibrio: Q₁ = (0, 0, 0), Q₂(k, 0, 0) y los puntos del segmento de línea recta L_k,

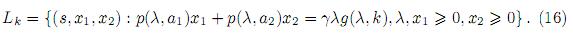
Mediante la linealización del sistema (2), se determina que Q₁ es inestable y Q₂ es asintóticamente estable para k < λ, e inestable para k > λ; pero la condición 0 < λ = λ₁ = λ₂ < k es necesaria para la supervivencia de cada predador. Por lo tanto, se asumirá en lo que sigue: si k < λ, por la condición (5), entonces L_k es vacío, y si k = λ, el único punto de equilibrio es el origen Q₁. A continuación se verifica la estabilidad de los puntos Q₁ y Q₂ por linealización del sistema.

Sea J (s, x₁, x₂) la matriz Jacobiana que representa la linealización del sistema (2) en el origen e I₃ la matriz identidad de orden tres, las cuales están dadas tal como sigue

donde F₁, F₂, F₃ son funciones dadas por las expresiones:

Teniendo en cuenta las condiciones para las funciones p y g en el origen:

se obtiene

El polinomio característico de J(0, 0, 0) está dado por D(µ) = Det[J µI₃]

cuyos valores propios están dados por µ = d₁, µ = d₂ y µ = γ, por lo tanto, el origen es inestable. En forma semejante se considera la linealización J (s, x₁, x₂) del sistema (2) en el punto Q₂, por lo tanto, se obtienen las condiciones para la función g:

Entonces la matriz J = J (k, 0, 0) adopta la forma

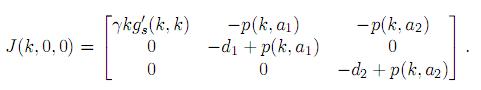
El polinomio característico de J = J (k, 0, 0) es

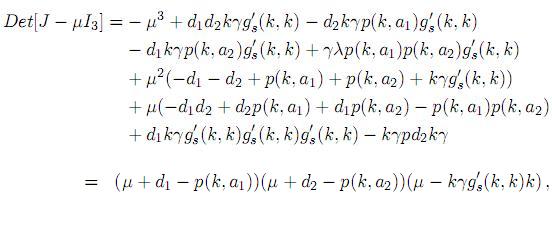
cuyos valores propios son dados por:

De la expresión anterior y las condiciones (6) y (13), claramente se tiene que el punto Q₂ es inestable para k > λ, y asintóticamente estable para k < λ.

2.3 Coexistencia y extinción por bifurcación zip

En esta sección se trata la estabilidad del conjunto L_k. Los elementos del conjunto L_k son denotados con (λ, ξ₁, ξ₂). Sea J = J (s, x₁, x₂) la matriz Jacobiana que representa la linealización del sistema (2) en un punto arbitrario (λ, ξ₁, ξ₂ ) de L_k. Aplicando las condiciones p(λ, a₁ ) = d₁ , p(λ, a₂) = d₂ y s = λ para la función p, se tiene

El polinomio característico de J = J (λ, ξ₁, ξ₂), está dado por

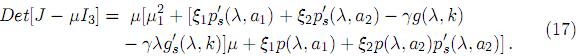
Así que µ = 0 es siempre un valor propio. El polinomio cuadrático entre corchetes es estable, es decir, los dos valores propios tienen parte real negativa, si y únicamente si

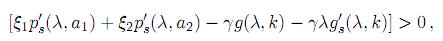
ya que el término lineal es siempre positivo por la condición (6). Se escribe la desigualdad anterior así

Multiplicando por λ, y adicionando al lado derecho de la desigualdad el término

se puede re-escribir la desigualdad de la forma

Tomando en cuenta el hecho de que (ξ₁, ξ₂) satisface (16), se obtiene la desigualdad

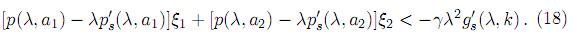
En vista de la condición (7), el lado izquierdo es positivo para todo (λ, ξ₁, ξ₂ ) 2 L_k. Teniendo en cuenta las condiciones (4) y (5), el lado derecho es positivo, decreciente y tiende a cero para k → ∞. Al considerar el segmento de línea recta B_k, tomando el signo de igualdad en la desigualdad dada por (18):

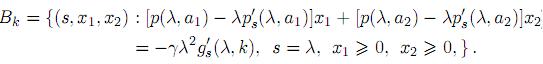
Fijando k, se puede determinar un punto de intersección entre las dos rectas L_k y B_k. Se denota dicho punto de intersección por (x₁(k), x₂(k)). Resolviendo el sistema de dos ecuaciones lineales determinado por rectas L_k y B_kse tiene, para (x₁(k), x₂(k)),

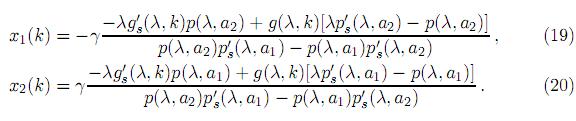
Como una preparación al teorema siguiente, se mostrará que el denominador de x₁(k) y x₂(k) es positivo, negativo o cero si el modelo es natural, artificial o degenerado, respectivamente. Desarrollando la expresión (15) se tiene que

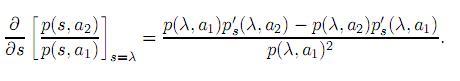
De la expresión anterior claramente se concluye lo deseado. Igualmente se puede mostrar que las funciones x₁(k), x₂(k) son estrictamente creciente y estrictamente decreciente, respectivamente, si consideramos que el modelo es natural; y estrictamente decreciente y estrictamente creciente, respectivamente, si consideramos que el modelo es artificial. Por la simetría entre x₁(k) y x₂(k) basta demostrar que x₁(k) es estrictamente monótona. Derivando x₁(k) con respecto a k, se tiene

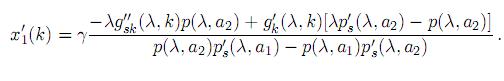
El numerador de x´(k) es positivo por (3), (7) y

El denominador será positivo o negativo si el modelo es natural o artificial, respectivamente. Por lo tanto, x₁(k) es estrictamente creciente si el modelo es natural y estrictamente decreciente si el modelo es artificial; igualmente se tiene que x₂(k) es estrictamente decreciente si el modelo es natural y estrictamente creciente si el modelo es artificial.

Teorema 2.1. Si el sistema (2) es natural y satisface las condiciones (3) a (8) y (10) a (13), existen k₁, k₂ únicos, tal que si λ < k₁< k₂< 1, entonces para todo k 2 (λ, k₁) todos los puntos del segmento L_k son estables en el sentido de Liapunov y L_k es un atractor del sistema. Para k ∈ (k₁, k₂ ) el punto (λ, x₁(k), x₂(k)) divide L_k en dos partes (una de las cuales puede ser vacía). Los puntos de L_k a la izquierda de este punto son inestables, los puntos a la derecha son estables, en el sentido de Liapunov y la parte del lado derecho de este punto es un atractor del sistema. Para k ∈ (k₂, 1), el sistema no tiene puntos de equilibrios estables en el octante positivo del espacio cerrado s, x₁, x₂ .

Prueba: Por hipótesis, este modelo es natural. Evaluando x₁(λ) y x₂(λ), se observa que:

Claramente las expresiones x₁(λ) y x₂(λ) son negativa y positiva, respectivamente, bajo las condiciones impuestas a las funciones p y g. Igualmente se tiene que x₁(k) > 0 y x₂(k) < 0 teniendo en cuenta que:

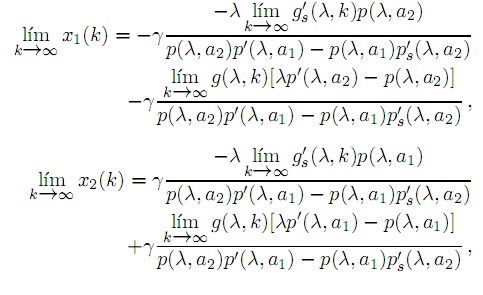
y las condiciones (4) a (8) y (9). Así, por continuidad, por ser la función x₁(k) estrictamente creciente y, además, por presentar variación de signo en el intervalo (λ, 1), existe un único k₁ > λ, en el cual x₁(k₁) = 0. Sin embargo, dado que la línea L_k intercepta el eje x₂ en un punto de coordenada positiva con k = k₁> λ, se tiene que x₂(k₁) es mayor que cero. Similarmente, existe un k₂ > k₁ en el cual x₂(k₂) = 0. En conclusión, para k ∈ (λ, k₁), las líneas L_k y B_k se interceptan en el segundo cuadrante y el conjunto L_k se encuentra debajo del segmento de línea B_k, es decir, la condición (18) se tiene en cada punto de L_k. Sin embargo, (18) implica que estos puntos del sistema linealizado tienen dos valores propios con parte real negativa, y en cada punto de L_k se tiene una variedad estable bidimensional por el teorema de Harman sobre la existencia de variedades estables e inestables. Para k ∈ (k₂, ∞) el conjunto L_k está arriba del segmento de línea B_k, es decir, la condición (18) con signo opuesto en la desigualdad se tiene para cada punto de L_k. Esto significa que los puntos son inestables. Si k ∈ (k₁, k₂), L_k se divide en dos partes: en la parte izquierda la condición (18) se tiene con signo invertido en la desigualdad, por lo tanto se tiene que la parte izquierda del segmento de línea L_k queda arriba de la parte izquierda del segmento de línea B_k, esto significa que los puntos son inestables, eso mismo implica que en la parte derecha (18) es válida la desigualdad (18), es decir, en cada punto de L_k se tiene una variedad estable bidimensional. Se resalta en esta parte como g(λ,^.) es una función no decreciente y x₂(^.) es una función monótona decreciente; como una consecuencia de ello, si k es incrementado de k₁ a k₂, los puntos (λ, x₁(k), x₂(k)) se mueven constantemente a lo largo de L_k del extremo del lado izquierdo al extremo del lado derecho, mientras el segmento L_ksufre un desplazamiento paralelo hacia arriba. En este proceso los puntos detrás del lado izquierdo con (λ, x₁(k), x₂(k)) llegan a ser desestabilizados; Farkas llama a este fenómeno una bifurcación de zip y se concluye la prueba.

A continuación se presentan, sin prueba, algunos resultados que se utilizan en la prueba de la atractividad del segmento derecho de L_k, si k ∈ (k₁, k₂). Definición 2.2. La variedad diferenciable M es orientable si puede encontrarse un atlas tal que para dos entornos arbitrarios V_i = V y V_j = , si V_i ∩ V_j ≠ ∅ ;, entonces para todo punto de la intersección se tiene que

A continuación se define el conjunto invariante del flujo. Un sistema dinámico puede ser considerado a lo largo de una vecindad de un punto de equilibrio bajo un sistema de ecuaciones diferenciales autónomo. Se supone, sin pérdida de generalidad, que el equilibrio está en el origen y que el sistema es de la forma

donde A es una matriz constante de orden n X n, g ∈ C¹(Rⁿ), g(0) = 0, = 0, (0) es la matriz derivada de g en x = 0. El flujo generado por el sistema se denota por φ_t, es decir, φ_t(x) = φ_t(t, x) es solución de (22) que satisface las condiciones iniciales φ(0, x) = x. Se supone que la solución está definida para t ∈ R.

Definición 2.3. La variedad diferenciable M, pasando a través del origen x = 0, es llamada variedad invariante local del sistema (22), o del flujo φ_t, si existe un ε > 0 tal que para x ∈ M , | φ(t, x) < ε implica φ(t, x) ∈ M.

El sistema variacional del sistema (22), con respecto a la solución φ(t, x), es

Se denota la matriz fundamental del sistema como Φ(t, x); se supone que Φ(0, x) = I. Además,

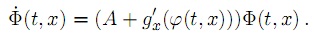
Se muestra que Φ(t, x) = (t, x). En particular, si x = 0 entonces φ(t, 0) ≡ 0. También (φ(t, 0)) = (0) = 0 y (23) toma la forma

por lo tanto, Φ(t, 0) = (t, 0) = exp(At). Esto significa que el flujo φ_t es

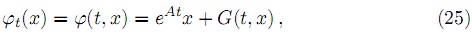
donde

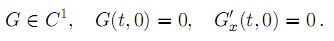
De (25) se puede asumir, sin pérdida de generalidad, que la matriz de coeficiente A tiene s ≥ 0, valores propios con parte real negativa, 0 ≤ c valores propios con parte real cero y 0 ≤ u, valores propios con parte real positiva contando la multiplicidad en el polinomio característico de A, se tiene por lo tanto que s + c + u = n.

Se denota con R^s, R^c y R^u los subespacios propios s-dimensional, c-dimensional y u-dimensional, correspondientes a los valores propios positivos, cero y negativos, respectivamente. Entonces Rⁿ es la suma directa de estos subespacios propios

los cuales son invariantes con respecto al sistema lineal (24). Las restricciones de las proyecciones de (24) en estos subespacios propios generan tres sistemas lineales independientes. Uno de ellos, R^s, es asintóticamente estable. Todas las soluciones tienden a cero exponencialmente cuando t tiende a infinito; R^c puede tener algunas soluciones acotadas y también puede tener soluciones que tienden a infinito cuando t tiende a infinito, y R^u es completamente inestable, es decir, todas las soluciones no triviales tienden exponencialmente a infinito cuando t tiende a infinito.

En otras palabras, existe una transformación de coordenadas lineal regular que lleva (24) a la forma

siendo à = diag[S, C, U], donde S es una matriz estable de orden s X s, C una matriz cuyos valores propios tienen parte real cero de orden c X c, y U una matriz inestable de orden u X u.

Considérese el vectorc η ∈ Rⁿ como suma directa de vectores η^s ∈ R^s, η^c ∈ R^c y η^u ∈ R^u

El sistema (26) puede ser llevado a la forma

Una pregunta importante que surge es si (22) permite una estructura similar. La respuesta es positiva. Para una prueba véase [13], página 243.

Teorema 2.2. Se supone que la matriz A tiene la forma del sistema (22), que existe un entorno V_x del origen x = 0 de Rⁿ y una transformación de coordenadas regular de orden C¹, r : V_x → V_x de esta vecindad, en la vecindad V_x del origen z = 0 de tal manera que r(0) = 0. El flujo (25) es transformado en el flujo ψ_t(z) := (r ο φ_t ο r^-1)(z) de la forma

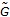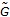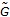donde, para un T > 0 arbitrario, la matriz exp(ST) es de orden s X s con todos sus valores propios en módulo menores que uno, exp(CT), es de orden c X c con sus valores propios en módulo iguales que uno, exp(UT), es de orden u X u con sus valores propios en módulo mayores que uno, la función vectorial es la suma directa de la función vectorial ^s, ^c, y 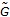^u de dimensión s, c y u respectivamente, es decir, 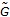= 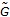^s ⊕ ^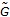c ⊕ 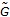^u, es decir,

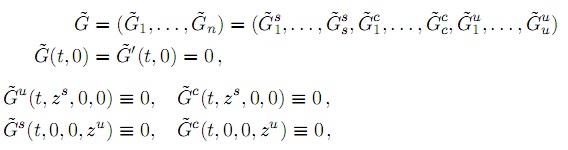
donde z = z^s ⊕ z^c ⊕ z^u ∈ R^s, z^c ∈ R^c, z^u ∈ R^u; la misma transformación de coordenada tranforma (22) en:

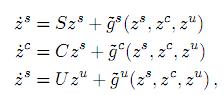
donde S es una matriz estable, C una matriz con la parte real de sus valores propios iguales a cero, y la matriz U de orden u X u con sus valores propios con parte real positiva:

Se necesitan algunas generalizaciones a los teoremas propuestos por [13] (Capítulo IX, lema 5.1, corolario 5.2).

Lema 2.1. Para s ∈ [0, s₀], s₀ > 0, sea P(s) una matriz estable p X p y Q(s) una matriz cuyos valores propios tienen parte real no negativa para todo s ∈ [0, s₀]; se supone que P, Q ∈ C⁰[0, s₀], y el mapeo T¹: R^p x R^q x [0, s₀] → R^p x R^q definido por:

para (y, z, s) ∈ R^p x R^q x [0, s₀] donde Y, Z, , , ,, 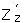∈ C⁰, Y (0, 0, s) ≡ Z(0, 0, s) ≡ 0 y para las matrices Jacobianas ∂_(y,z)Y(0, 0, s) ≡ 0, ∂_(y,z)Z(0, 0, s) ≡ 0. Entonces existe una vecindad del origen W_p ⊂ R^p y una función g : W_p x [0, s₀] → W_q(un recubrimiento en el origen de R^q) tal que g, g´ ∈ C⁰, g(0, s) ≡ 0, g´ (0, s) ≡ 0, y la transformación de coordenadas

transformando (30) a la forma

donde

Se observa que las últimas identidades significan que si (u, v) = (u, 0), entonces su imagen, con el mapeo (32), es tal que (u₁, v₁) = (u₁, 0). Esto significa que en el origen de coordenadas z = g(y, s), por (30), también se tiene que z₁= g(y₁, s), es decir, el conjunto {(y, z) ∈ R^p x R^q: z = g(y, s)} es una variedad invariante de T¹ para cada s ∈ [0, s].

Prueba: La prueba coincide paso a paso con la prueba de [13] (capítulo IX, lemma 5.1).

Lema 2.2. Para s ∈ [0, s₀], s₀ > 0 sean las matrices P(s) y Q(s) como en el lema anterior, sea la familia de sistemas dinámicos T: [0, ∞] x R^p x R^q [0, s₀] → R^p x R^q dependiente de un parámetro s definido por:

para t ∈ [0,∞], y₀ ∈ R^p, z₀∈ R^q, s ∈ [0, s₀] donde

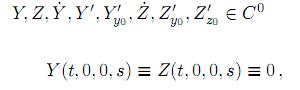
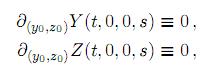
y con

si g es la función construida por el lema anterior para T¹, entonces (31) transforma (34) a la forma

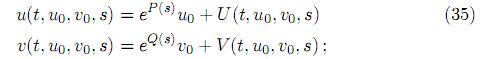
donde

Si y ≠ 0, z, |y₀| es suficientemente pequeño y z₀ = g(y₀, s), entonces se tiene que, z(t, y₀, z₀, s) = g(y(t, y₀, z₀, s), s) para todo t ∈ [0, ∞],

Éste es consecuencia del lema anterior.

Se considera ahora la atractividad del segmento derecho de L_k, si k ∈ (k₁, k₂). Sea el segmento de línea L_s el conjunto

y la relación

Se considera el subconjunto propio cerrado de Lsdado por

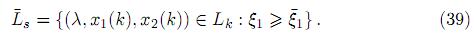
Sea M una superficie suave interceptando L_k transversalmente en (λ, ₁, ₂) ∈ L_k. Se denota como T_m y se denomina recubrimiento tubular de al conjunto compacto y acotado con la parte de M dentro de la superficie que define el conjunto

con ρ > 0 y d la distancia Euclidiana y la parte de la superficie de (40) entre M y el plano s, x₁ y la parte del plano s, x₁ dentro de la superficie (40). Claramente, si ρ > 0 es suficientemente pequeño, la intersección de M y la superficie (40) es una curva de Jordan simple, L_s ⊂ T_m y el interior del segmento de línea L_s está en el interior de T_m. Teniendo en cuenta la notación introducida se tiene el teorema

Teorema 2.3. Para cualquier k tal que k₁ < k < k₂, y k₁, k₂ solución de las ecuaciones x₁(k) = 0 y x₂(k) = 0, respectivamente, con x₁(k) y x₂(k) dados por las expresiones (19) y (20), y para cualquier ₁ que satisface (38), el segmento de recta dado por (39) es un atractor del sistema (2) en el siguiente sentido: tiene un recubrimiento tubular T_m tal que las trayectorias con condiciones iniciales en T_m tienden a cuando t tiende a infinito.

Prueba: Parametrizando L_s de la forma:

si s = 0, se obtiene el punto extremo en L_k en el plano s, x₁; si s = 1, se consigue el punto (λ, ξ_1s(k), ξ_2s(k)) = (λ, x₁(k), x₂(k)) con x₁(k), x₂ (k) dados por (19) y (20). Sea ξ₁correspondiente a un valor de 0 < s₀< 1, es decir,

Así, L_s, dado por (37), corresponde al intervalo [0, s₀]. Para cada s ∈ [0, s₀], un sistema de referencia puede ser introducido de la siguiente manera: el origen está en (λ, ξ_1s(k), ξ_2s(k)), dos vectores de la base pueden ser fijados en el subespacio generado por los vectores propios correspondientes a los dos valores propios con parte real negativa del sistema (2), linealizado en (λ, ξ_1s(k), ξ_2s(k)) y el tercer vector puede ser fijado en la dirección del vector de la línea L_k dado por (41), el cual es el valor correspondiente al valor propio cero. En el sistema (41), ξ_1s, ξ_2s dependen continuamente de s, como una consecuencia de ello las raíces del polinomio característico (17) dependen continuamente también de s. Claramente, los dos vectores en el subespacio bidimensional de vectores propios correspondiente a las raíces con parte real negativa pueden ser escogidos como funciones continuas de s en el intervalo [0, s₀], dado que la dirección del plano varía continuamente. Se concluye que la familia uniparamétrica de transformación de coordenadas dependiente de s ∈ [0, s₀] descrita arriba puede ser representada por

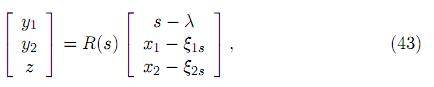
donde y = (y₁, y₂) denota las coordenadas en el subespacio bidimensional de vectores propios, z es la coordenada en L_k, y R(s) es una matriz tres por tres regular, R ∈ C⁰[0, s₀]. Bajo la transformación de coordenadas, el sistema (2) toma la forma:

donde P es una matriz estable de orden dos por dos, F un vector de dimensión dos y G un escalar, P, F; 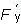, , , ∈ C⁰ en un recubrimiento del origen (y₁, y₂, z) = (0, 0, 0) y para todos los s ∈ [0, s₀], F (0, 0, s) = G(0, 0, s) = 0, ∂_(y,z)F(0, 0, s) = 0, ∂_(y,z)G(0, 0, s) = 0. El sistema dinámico generado por (44) es de la forma (35) con Q(s) = 0, y satisface todas las condiciones del lema 2.2. Así la función g : W [0, s₀ ] → R del lema 2.1 existe donde W es un recubrimiento de (y₁, y₂) = (0, 0), g ∈ C⁰ y para cada s ∈ [0, s₀] la superficie

es localmente una variedad invariante de (44). Realizando la transformación inversa de (43) al sustituir la función g por z se tiene

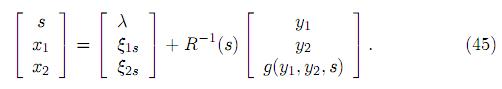
Para s fijo, s ∈ [0, s₀], (45) es la ecuación paramétrica de la variedad invariante estable del sistema (2) pasando a través del punto de equilibrio en el espacio(λ, ξ_1s, ξ_2s) ∈ . El mapeo (y₁, y₂, s) → (S, x₁, x₂) del cilindro W [0, s₀] s, x₁, x₂, definido por (45), es continuo y uno a uno (por la unicidad de la solución y la regularidad de la matriz R^-1(s)). Por lo tanto, este mapeo es un homeomorfismo y esto prueba que para cada ξ₁ que satisface (38), sus variedades invariantes correspondientes a los puntos de sen (39) llenan un recubrimiento tubular de . Por el teorema 2.1 se tiene que, a través de cada punto de , pasa una variedad local bidimensional invariante tal que todas las trayectorias en esta variedad tienden a (λ, ξ₁, ξ₂) exponencialmente cuando t tiende a infinito. Claramente, (λ, ξ₁, ξ₂) es asintóticamente estable con respecto a la restricción del sistema (2) a la variedad invariante bidimensional; por la argumentación anterior se tiene que estas variedades llenan un recubrimiento de y por lo tanto se concluye la prueba del corolario.

Un resultado análogo al teorema 2.3 se tiene para el caso de los modelos artificiales.

Un modelo artificial se comporta de forma similar a un modelo natural, excepto que la dirección del zip es diferente. La prueba del siguiente teorema es análoga a la del teorema 2.1, por lo tanto sólo se presenta su enunciado.

Teorema 2.4. Si el sistema (2) es artificial y satisface las condiciones (3) (8) y (10) a (13), existen k₂, k₁ únicos, tal que si λ < k₂ < k₁ < ∞, entonces para todo k ∈ (λ, k₂) todos los puntos del segmento L_k son estables en el sentido de Liapunov; y L_k es un atractor del sistema. Para k ∈ (k₂, k₁), el punto (λ, x₁(k), x₂(k)) divide L_ken dos partes, una de la cual puede ser vacía. Los puntos de L_k a la izquierda de este punto son estables, los puntos a la derecha son inestables en el sentido de Liapunov, y la parte del lado izquierdo de este punto es un atractor del sistema. Para k ∈ (k₁, 1), el sistema no tiene puntos de equilibrio estables en el octante positivo del espacio cerrado s, x₁, x₂.

3 Modelos numéricos del tipo exponencial algebraico

3.1 Generalidades

En este sección se exponen los resultados numéricos de un modelo de tipo natural. Para este modelo se presenta los retratos de fase para el caso de competición interespecífica λ₁ = λ₂ = λ, a₁ > a₂.

En la selección del modelo se definen los parámetros de manera natural, es decir, eligiendo las propiedades intrínsecas que lo definen desde el punto de vista de la dinámica de poblaciones. Es así como se eligieron las tasas de mortalidad dide los predadores, i = 1, 2, la tasa de nacimiento maximal de la presa γ, y el parámetro umbral λ de los predadores. Respecto al parámetro λ, aunque no resulta evidente que la cantidad de presa λ necesaria para que la especie i alcance tasa de natalidad igual a la tasa de mortalidad d_i, i = 1, 2; es claro que λ es una característica intrínseca del predador. En el modelo se supone la mismas característica del medio respecto al crecimiento de la presa definidas por la resistencia ambiental g(s, k). Una vez elegidos los parámetros básicos de las especies en el sistema, éstos definen la escala de respuesta funcional de los predadores a₁, a₂, mediante la siguiente ecuación

La ecuación (46) define en el modelo hallado la expresión

Para la presentación de los cambios cualitativos de los retratos de fase de los diferentes modelos, conforme avanza el parámetro de bifurcación k en el caso a₁ > a₂ (bifurcación de zip), se evalúa el valor de k para valores menores de k₁, entre k₁ y k₂, y mayores de k₂.

3.2 Modelo natural

Los siguientes son los parámetros del modelo natural:

la resistencia ambiental g de la presa y la respuesta funcional p de los predadores adoptan la forma:

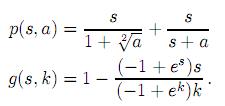
Se define la función f, la cual simplifica la presentación de la fórmula de Bautin para el cálculo de la constante de Poincaré-Liapunov, como sigue

La ecuación (47) para a₁ es de la forma

La ecuación (47) para a₂ es de la forma

3.3 Caracterización del sistema tridimensional, caso a₁> a₂

En esta parte se hallan los valores del parámetro de bifurcación donde se presenta la bifurcación zip. Además, se muestran las ecuaciones paramétricas de la línea de equilibrio L_k y la línea de intersección definida por la condición de estabilidad (18). Se representan los retratos de fase del sistema para los distintos valores del parámetro de bifurcación seleccionados a propósito, para mostrar los cambios cualitativos que ocurren. El parámetro k₁ está definido por la condición

Resolviendo la ecuación anterior para k se tiene que k₁= 14,0964, el cual coincide con el caso a₁= a₂= a con a = a₂. Igualmente el parámetro k₂ está definido por la condición

Resolviendo la ecuación anterior para k se tiene que el valor de k₂ = 15,1131 que coincide con el obtenido en el caso a₁= a₂= a con a = a₁. La intersección de las líneas de equilibrios L_k y la línea B_k está definida en forma paramétrica por (x₁(k), x₂(k)).

Condición para k = 14. Las ecuaciones paramétricas de los segmentos de línea L_k y B_k están dadas por

El segmento B_k está por encima del segmento de línea L_k en el plano coordenado x₁, x₂, por lo tanto, por la condición (18), el conjunto de equilibrios es asintóticamente estable para k = 14, como se observa en el retrato de fase correspondiente a un valor del parámetro de bifurcación de k = 14, figura 1.

Las trayectorias del sistema con condiciones iniciales en el octante positivo permanecen en éste y son acotadas y tienden asintóticamente hacia la línea de equilibrios L_k, por lo tanto, el segmento L_k es un atractor del sistema y su cuenca de atractividad es el octante positivo. Los equilibrios en este caso representan coexistencia estable entre el k-estratega, el r-estratega y la presa.

Condición para k = 14,5. Las ecuaciones paramétricas de los segmentos de línea L_k y B_k están dadas por

El segmento B_k y el segmento de línea L_k se interceptan en el cuadrante positivo, por lo tanto el punto de intersección divide el segmento L_k de tal manera que los puntos a su izquierda están por encima de los del segmento B_k, significando inestabilidad de dichos equilibrios; y los puntos a su derecha están por debajo del segmento B_k, representando estabilidad asintótica para k = 14,5. A medida que se incrementa el parámetro k, entre k₁ y k₂, se va presentando desestabilización del sistema de izquierda a derecha, iniciando por los puntos que representan dominio del k-estratega sobre el r-estratega. Como se aprecia en el retrato de fase para una valor del parámetro k = 14,5, figura 2, existe una zona localizada a la izquierda del punto (x₁(k), x₂ (k)) tal que los puntos situados en ellas son equilibrios inestables y los puntos situados a la derecha son equilibrios estables existiendo un segmento de recta dado por (39) que es un atractor del sistema (2) en el siguiente sentido: tiene un recubrimiento tubular Tmtal que las trayectorias con condiciones iniciales en T_m tienden a cuando t tiende a infinito. La coexistencia entre las tres especies es aún posible, a pesar de que existen zonas del segmento de la recta de equilibrios del sistema que ahora no son estable desde el punto de vista de Liapunov.

A medida que se aumenta el parámetro k, crece la inestabilidad del segmento L_k, significando la pérdida de terreno del k-estratega con respecto al r-estratega hasta su extinción a valores mayores del parámetro k₂.

Condición para k = 15,2. Las ecuaciones paramétricas de los segmentos de línea L_k y B_k están dadas por

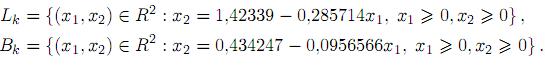
El segmento de línea B_k se encuentra por debajo del segmento de línea L_k en el cuadrante positivo, significando inestabilidad del conjunto de equilibrios L_k, como se observa en el retrato de fase correspondiente al valor del parámetro k = 15,2, figura 3.

Diagrama de bifurcación. En la figura 4 se presenta el diagrama de la bifurcación zip con respecto al plano de los predadores x₁, x₂conforme el parámetro k es variado, el área más fina corresponde a los puntos de equilibrios en el octante positivo estables y los del área menos fina a los inestables.

Claramente se observa el fenómeno descubierto por [8]. "A bajos valores de la capacidad de carga k del ecosistema con respecto a la presa, una línea de equilibrio es un atractor del sistema, ella representa coexistencia estable de las tres especies. Si k es incrementado los equilibrios son continuamente desestabilizados, empezando por aquellos que representan la dominancia del k-estratega sobre el r-estratega. Arriba de cierto valor de k, el sistema no tiene más equilibrios estables que representen coexistencia; sin embargo, un ciclo límite permanece representando la oscilación de coexistencia del k-estratega y la presa ".

4 Conclusión

En el presente trabajo de investigación se estudia la atractividad local de una clase de modelos: del tipo dos predadores una presa los cuales exhiben la bifurcación zip, cuya característica común es que la tasa de desarrollo de la presa y la respuesta funcional del depredador son funciones que satisfacen ciertas condiciones naturales que coinciden con las planteadas por [6] y [7]. Se generalizan los resultados sobre atractividad local de recubrimiento tubular [7] para el sistema (2).

Agradecimientos

Al Profesor Miklós Farkas por su amable y acertada orientación en esta investigación.

Referencias

1. GJ. Butler, P. Waltman. Bifurcation from a limit cycle in a two predator- one prey ecosystem modeled on a chemostat. Journal of Mathematical Biology, ISSN 0303-6812, 12(3), 295-310 (1981). Referenciado en 12        [ Links ]

2. SB. Hsu, SP. Hubbel, P. Waltman. Competing predators. SIAM Journal on Applied Mathematics, ISSN 0036-1399, 35(4), 617-625 (1978). Referenciado en 13        [ Links ]

3. A. Koch. Coexistence resulting from an alteration of dendity dependent and density independent growth. Journal of Theoretical Biology, ISSN 0022-5193, 44, 373-386 (1974). Referenciado en 13        [ Links ]

4. HL. Smith. The interaction of steady state and Hopf bifurcations in a two- predator-one-prey competition model. SIAM Journal on Applied Mathematics, ISSN 0036-1399, 42(1), 27-43 (1982). Referenciado en 13        [ Links ]

5. DR. Wilken. Some remarks on a competing predators problem. SIAM Journal on Applied Mathematics, ISSN 0036-1399, 42(4), 895-902 (1982). Referenciado en 13         [ Links ]

6. GJ. Butler. Competitive predator-prey systems and coexistence, in Population biology proceedings (Edmonton 1982). Lecture notes in biomathematics, 52: Berlin: Springer-Verlag, 210-217 (1983). Referenciado en 13, 15, 39        [ Links ]

7. M. Farkas. Zip bifurcation in a competition model. Nonlinear analysis: Theory, Methods & Applications, ISSN 0362-546X, 8(11), 1295-1309 (1984). Referenciado en 13, 14, 19, 39         [ Links ]

8. M. Farkas. A zip bifurcation arising in population dynamics, in 10th Int. Conf. On, nonlinear oscilations, Varna 1984. Sofia: Bugarian Academy of Science, 150- 155 (1985). Referenciado en 14, 39         [ Links ]

9. M. Farkas, E. Sáez, Szántó. Velcro bifurcation in competition models with generalized holling functional response. Miskolc mathematcal notes, ISSN 1787-2413, 6(2), 185-195 (2005). Referenciado en 14         [ Links ]

10. JD. Ferreira, Luis A. Fernandes de Oliveira. Hopf and zip bifuration in an specfic (n + 1)-competitive system, matematics. Matemáticas: Enseñanza Universitaria, ISSN 0120-6788, XV(1), 33-50 (2007). Referenciado en 14         [ Links ]

11. C. Escobar. Modelo original de tipo exponencial algebraico que exhibe la bifurcación zip. Tesis de maestría, Universidad de Antioquia, 2003. Referenciado en 14         [ Links ]

12. M. Farkas. Competitive exclusión by zip bifurcation in "Dynamical Systems, IIASA Workshop 1985 Sopron". Lecture Notes in Economics and Mathematical Systems, ISSN 0075-8442, 287. Springer-Verlag, 165-178 (1987). Referenciado en 15         [ Links ]

13. Philip Hartman. Ordinary differential equations. John Wiley & Sons, New York, 61-63 (1964). Referenciado en 27, 28, 29.        [ Links ]