Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Accesos
Accesos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares en
SciELO
Similares en
SciELO -
 Similares en Google
Similares en Google
Compartir
Ingeniería y Ciencia
versión impresa ISSN 1794-9165
ing.cienc. v.6 n.12 Medellín ene./jun. 2010
Transformada fraccional de Fourier en el caso de un plano imagen inclinado
Fourier fracional transformar no caso de um plano imagem inclinado
Fraccional Fourier transform in the case of an inclined image plane
C. O. Torres1, L. Mattos2, C. Jiménez3, J. Castillo4 y Y. Torres5
1 Doctor en Ciencias físicas, cesartorres@unicesar.edu.co, docente, grupo LOI, Universidad Popular del Cesar, Valledupar-Colombia.
2 Magíster en Ingeniería electrónica, lorenzo.mattos@gmx.fr, docente, grupo LOI, Universidad Popular del Cesar, Valledupar-Colombia.
3 Magíster en Matemática aplicada, carlosj114@gmail.com, docente, grupo GIMA,Universidad de La Guajira, Riohacha-Colombia.
4 Magíster en Matemática aplicada, jacas68@yahoo.es, docente, grupo GIMA, Universidad de La Guajira, Riohacha-Colombia.
5 Docteur en Optique et Traitement du Signal, ytorres@uis.edu.co, docente investigador, grupo GOTS, Universidad Industrial de Santander, Bucaramanga-Colombia.
(Recepción:13-oct-2009. Modificación:27-abr-2010. Aceptación:27-abr-2010)
Resumen
La conocida fórmula de difracción de Fresnel relaciona la distribución de amplitud compleja de una onda en el plano objeto (campo ondulatorio de entrada) con la distribución de amplitud compleja de la onda en el plano imagen (campo ondulatorio de salida) cuando se trata de propagación en el espacio libre; esto significa que si los planos objeto e imagen son paralelos entre sí, el sistema imagen correspondiente se dice que es un sistema lineal invariante a desplazamiento (LSI). Esta propiedad ventajosa es esencial para el desarrollo de técnicas de imagen sensitivas a fase; sin embargo, si el plano imagen está inclinado con respecto al haz incidente, la distancia efectiva de propagación cambiará sobre el plano imagen, consecuentemente el sistema imagen será no invariante a desplazamiento. En este artículo es propuesta una extensión del formalismo de la difracción de Fresnel al caso de un plano imagen inclinado utilizando la transformada de Fourier de orden fraccional.
Palabras claves: difracción de Fresnel, plano imagen inclinado, transformada fraccional de Fourier.
Resumo
A bem conhecida equação de difração de Fresnel estabelece uma relação entre a distribuição de amplitude complexo de uma onda no plano do objeto (campo de onda de entrada) com a distribuição de amplitude complexa da onda no plano da imagen (campo de onda de saída) no caso da propagação em espaço libre. Isto significa que se os planos objeto e imagen são paralelos uns aos outros, o sistema imagem correspondente é dito ser um sistema linear invariante ao deslocamento (LSI). Esta propriedade vantajosa é essencial para o desenvolvimento de técnicas de imagen sesível á fase, No entanto, se o plano da imagem está inclinada respeito do feixe incidente, a distancia efetiva da propagação mudara sobre o plano imagen, consequentemente o sistema imagem não é invariante ao deslocamento. Neste trabalho uma extensão do formalismo da difração de Fresnel para o caso de um plano imagem inclinado é proposto usando a transformada de Fourier de ordem fracionária.
Palavras chaves: difração de Fresnel, plano de imagem inclinada, Fourier fracionária transformar.
Abstract
The well-known Fresnel integral relates a known complex wave defined in the object plane (the input wave field) to the observable complex wave (the output wave field) defined in the image plane after free-space propagation; this means that if the object and image plane are parallel to each other, corresponding imaging system is said to be linear-shift-invariant (LSI). This advantageous property was essential for the development of phase sensitive imaging techniques; however, if the image plane is inclined with respect to the incident beam, the effective propagation distance will vary over the image plane, consequently, the imaging system is not shiftinvariant. In this paper an extension of the theoretical formalism of Fresnel diffraction to the case of an inclined image plane is proposed using the fractional Fourier transform.
Key words: Fresnel diffraction, inclined image plane, fractional Fourier transform.
1 Introducción
Las mediciones de superficies rugosas de componentes metálicos son consideradas de gran importancia en el campo de maquinado mecánico. Desde 1972, cuando Sprague [1] aplicó técnicas de speckle blanco, muchos investigadores han estudiado este aspecto para realizar mediciones de superficies rugosas, [2, 3, 4, 5, 6, 7, 8]. Los patrones de speckle contienen información sobre las estructuras microscópicas de una superficie rugosa. Para estudiar la relación entre las propiedades estadísticas de los patrones de speckle, formados por superficies rugosas, se debe obtener la distribución de amplitud compleja del campo de speckle. Para lograr este propósito, las ecuaciones correspondientes a la difracción, que describen la propagación de las ondas difractadas de la superficie rugosa al plano de observación, deben ser construidas; en estudios preliminares, las ecuaciones de difracción de Fresnel y Fraunhofer fueron utilizadas para calcular el campo del patrón de speckle [6, 7], con la consideración de que el plano de observación es paralelo al plano del objeto en todos los montajes experimentales, a excepción de la referencia [8]. El propósito de este artículo es derivar las ecuaciones de difracción correspondientes para describir la difracción de una superficie inclinada rugosa reflectiva, bajo iluminación de una onda plana coherente en términos de la transformada fraccional de Fourier. Se considera la diferencia entre el modelo de difracción por superficie reflectiva (RSDM) y el modelo de difracción por transmisión de la apertura (TADM); encontrándose una ecuación general de difracción en términos de la transformada de Fourier de orden fraccional. Aplicando las aproximaciones de campo cercano y de campo lejano a una ecuación general de difracción con consideración de rotación del sistema coordenado, se obtienen las ecuaciones de difracción, tanto para el campo cercano como para el lejano. El significado físico de estas ecuaciones y la obtención como casos particulares de las ecuaciones de Fresnel y Fraunhofer son también presentadas.
2 Integral básica de difracción para una superficie inclinada
2.1 Integral de difracción de Fresnel-Kirchhoff
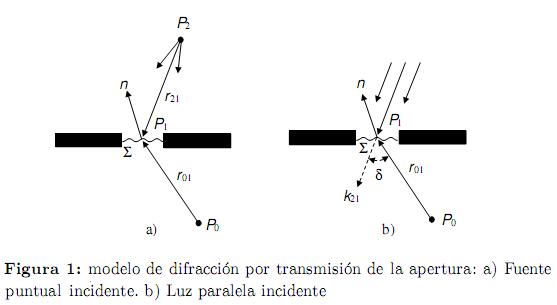
La figura 1 representa el diagrama esquemático del modelo TADM. La figura 1(a) muestra que la luz de una fuente puntual P2 es difractada por transmisión de la apertura, P0 es un punto de observación inicial en la región de difracción.
Luego la integral de difracción de Fresnel-Kirchhoff se puede escribir como
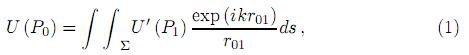
donde Σ es la superficie de la integral y se escoge como una apertura ficticia − curvada. Matemáticamente, U′ (P1) = 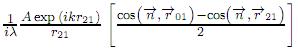 puede ser vista como una fuente puntual secundaria virtual en el punto P1 sobre Σ, r21y r 01son los módulos de los radio vectores
puede ser vista como una fuente puntual secundaria virtual en el punto P1 sobre Σ, r21y r 01son los módulos de los radio vectores  21 y
21 y  0101, respectivamente;
0101, respectivamente; 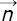 es la normal a Σ en el punto P1. La expresión (1) es únicamente aplicable para el caso de incidencia de fuente puntual (ver figura 1(a)) e inaplicable cuando una onda plana incidente ilumina una apertura de transmisión (ver figura 1(b)). Pero como el término
es la normal a Σ en el punto P1. La expresión (1) es únicamente aplicable para el caso de incidencia de fuente puntual (ver figura 1(a)) e inaplicable cuando una onda plana incidente ilumina una apertura de transmisión (ver figura 1(b)). Pero como el término 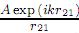 en U′ (P1) es exactamente la distribución del campo luminoso de la superficie de la apertura Σ, y se representa por U (P1), entonces (1) toma la forma
en U′ (P1) es exactamente la distribución del campo luminoso de la superficie de la apertura Σ, y se representa por U (P1), entonces (1) toma la forma
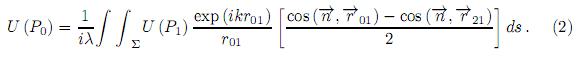
La ecuación (2) puede ser usada en el caso de incidencia de luz paralela, es decir, la fuente de luz puntual P2 está ahora infinitamente alejada de la apertura de transmisión. Visto desde la figura 1 (b), el vector de onda incidente 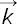 21tiene la misma dirección de
21tiene la misma dirección de 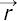 21, luego, (2) se puede reescribir como
21, luego, (2) se puede reescribir como
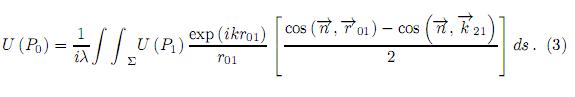
Dando la expresión de U (P1), el campo ondulatorio U (P0) en el punto de observación P0 puede ser obtenido. El ángulo δ en la figura 1 (b) y el término 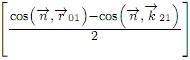 en (3) representa el ángulo de difracción y el factor de inclinación respectivamente para el modelo de difracción por transmisión de la apertura.
en (3) representa el ángulo de difracción y el factor de inclinación respectivamente para el modelo de difracción por transmisión de la apertura.
2.2 Integral básica de difracción de RSDM
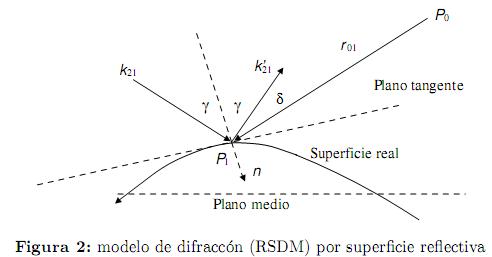
La figura 2 es la ilustración esquemática del modelo RSDM. Una onda plana está incidiendo sobre una superficie que produce scattering débil con un vector de onda 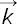 21y es reflejada y difundida.
21y es reflejada y difundida.
El vector de onda reflejado en el punto P1 es 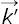 21, comenzando en un punto arbitrario sobre la superficie actual. La atención debe ser puesta sobre el ángulo δ en la figura 2, el cual es definido como el ángulo de difracción para el modelo de difracción por superficie reflectiva, pero es diferente del definido anteriormente en el modelo de difracción por transmisión de la apertura; específicamente, el ángulo δ en la figura 1(b) está definido entre el vector de onda incidente
21, comenzando en un punto arbitrario sobre la superficie actual. La atención debe ser puesta sobre el ángulo δ en la figura 2, el cual es definido como el ángulo de difracción para el modelo de difracción por superficie reflectiva, pero es diferente del definido anteriormente en el modelo de difracción por transmisión de la apertura; específicamente, el ángulo δ en la figura 1(b) está definido entre el vector de onda incidente 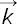 21 y la línea P1P0, mientras que δ, en la figura 2, es el ángulo entre el vector de onda reflejado
21 y la línea P1P0, mientras que δ, en la figura 2, es el ángulo entre el vector de onda reflejado 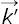 21 y la línea P1P0. Como resultado de esto, el factor de inclinación utilizado para el modelo de difracción por transmisión de la apertura no puede ser directamente usado para el modelo de difracción por superficie reflectiva. Para obtener el factor de inclinación de una difracción por superficie reflectiva, el factor de inclinación
21 y la línea P1P0. Como resultado de esto, el factor de inclinación utilizado para el modelo de difracción por transmisión de la apertura no puede ser directamente usado para el modelo de difracción por superficie reflectiva. Para obtener el factor de inclinación de una difracción por superficie reflectiva, el factor de inclinación 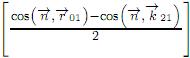 para el modelo de difracción por transmisión de la apertura debe ser reemplazado por
para el modelo de difracción por transmisión de la apertura debe ser reemplazado por 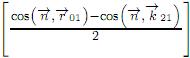 . De la figura 2 se nota que cos (
. De la figura 2 se nota que cos ( ,
,  21) = cos (
21) = cos ( ,
, 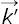 21) donde
21) donde 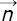 es la normal a la superficie en el punto P1. Combinando con (3), se obtiene la integral de difracción básica para una superficie reflectiva
es la normal a la superficie en el punto P1. Combinando con (3), se obtiene la integral de difracción básica para una superficie reflectiva
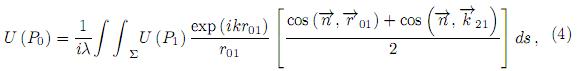
donde (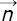 , r01) es el ángulo entre
, r01) es el ángulo entre 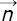 y
y 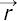 01, (
01, (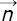 ,
, 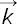 21) es el ángulo entre
21) es el ángulo entre 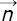 y
y 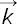 21, r01 es el módulo del radio vector
21, r01 es el módulo del radio vector 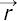 01 y P0 es el punto de observación de la región de difracción.
01 y P0 es el punto de observación de la región de difracción.
3 Ecuación general de la difracción para un plano inclinado
3.1 Distribución de amplitud compleja de una superficie clásica
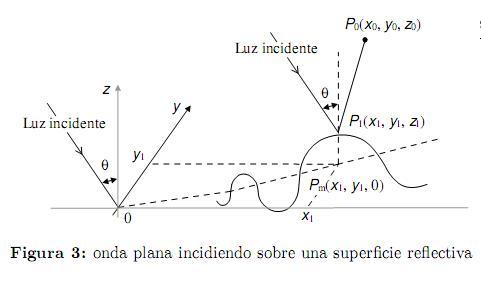
La figura 3 ilustra el caso cuando una onda plana coherente está incidiendo sobre una superficie rugosa reflectiva, con un ángulo θ con respecto al eje z. El plano medio del objeto es representado por el plano coordenado xOy, donde el origen O y Pm (x1, y1, 0) es la proyección de un punto genérico P1 (x1, y1, z1 ) situado sobre la superficie convencional, z1 es una medida de la altura de la superficie en P1. El punto P0(x0, y0, z0) es un punto de observación en el régimen de difracción, sin pérdida de generalidad, asumiendo que la luz incidente tiene amplitud constante A0 y paralela al plano xOz, se nota que es
un objeto de reflexión de pura fase, ignorando la absorción de la luz y otros factores, y haciendo que la fase en el origen O sea cero, se tiene la fase en P1
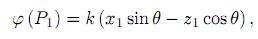
donde k = 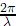 es el número de onda y λ es la longitud de la onda incidente. Aquí se obtiene la distribución de amplitud compleja de la luz de onda incidente sobre la superficie
es el número de onda y λ es la longitud de la onda incidente. Aquí se obtiene la distribución de amplitud compleja de la luz de onda incidente sobre la superficie
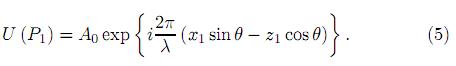
3.2 Cálculo del factor de inclinación
Suponiendo que la superficie es z = h (x, y), donde 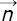 en el punto P1 (x1, y1, z1)
en el punto P1 (x1, y1, z1)
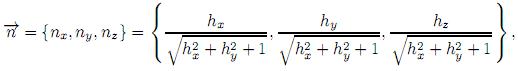
donde hx = 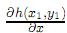 , hy =
, hy = 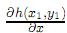 notando que
notando que
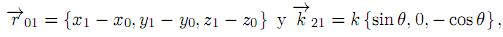
se tiene:
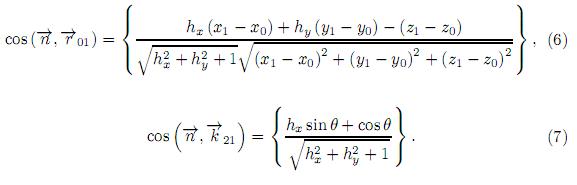
Sustituyendo (6) y (7) en 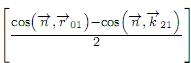 , se obtiene el factor de inclinación del modelo de difracción por superficie reflectiva.
, se obtiene el factor de inclinación del modelo de difracción por superficie reflectiva.
3.3 Ecuación general de la difracción para una superficie inclinada
Se tiene
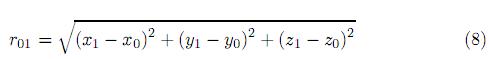
y el elemento de área en (3), en el punto P1,
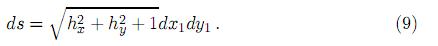
Introduciendo (5) y (6)(9) en (4), se obtiene la ecuación general de la difracción para una superficie inclinada
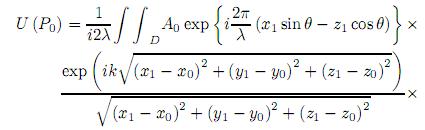
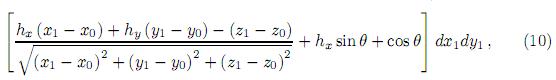
donde D define la región de integración en el plano medio.
4 Ecuación de difracción de campo cercano
4.1 Arreglo geométrico del experimento
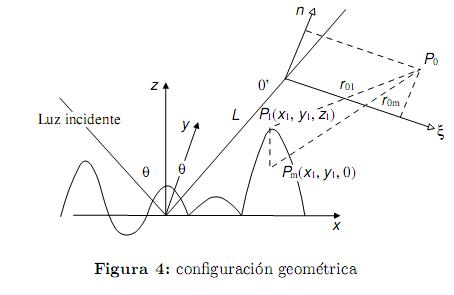
La figura 4 muestra el arreglo geométrico del experimento para el análisis de la difracción de una superficie reflectiva de scattering débil.
4.2 Derivación de la ecuación de difracción de campo cercano
A partir de (10) es difícil calcular la difracción de la luz que debe ser aproximadamente considerada para utilidades prácticas. Todas las aproximaciones son hechas sobre la base de la aproximación paraxial: (1) la distancia L es muy grande comparada con las dimensiones lineales máximas de la región de iluminación, y (2) el punto de observación P0 está cerrado sobre el eje z. Considerando la relación entre el plano de observación y el plano objeto, el factor r01 en el término exponencial exp ikr01 en la ecuación (10) puede ser expandido en serie como
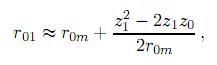
donde el término cuadrático retenido como k es un número grande, mientras los términos de mayor orden son despreciados,
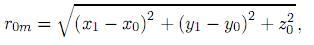
es la distancia entre los puntos P0 y Pm. De acuerdo a la aproximación paraxial (1) y (2), r01 puede ser además refinado por las siguientes tres razonables aproximaciones: (a) ignorando el término pequeño 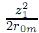 ; (b)
; (b)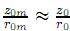 ; (c)
; (c) 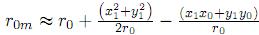 donde
donde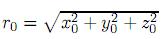 r es la distancia de P0 del origen. Luego r01 en el término exponencial se reduce
r es la distancia de P0 del origen. Luego r01 en el término exponencial se reduce
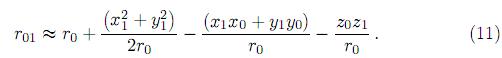
Si se asume que el área de iluminación sobre la superficie del objeto es pequeña, la siguiente desigualdad puede ser utilizada
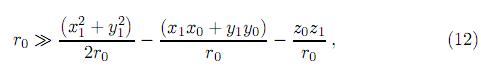
r01 en el denominador de (10) puede ser escrita como
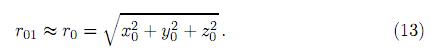
Asumiendo que la superficie de scattering débil satisface la aproximación de equivalentementependiente pequeña, luego las inecuaciones |nx| ≪ | nz |,|ny| ≪ | nz| o equivalente | hx | ≪ 1,| hy | ≪ 1 son válidas. Los términos de la derivación parcial en (10) pueden ser simplificados como
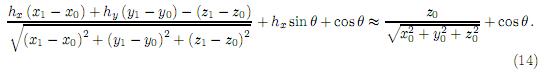
Sustituyendo (11)(14) en (10), se obtiene la expresión aproximada de la ecuación de difracción para una superficie inclinada reflectiva
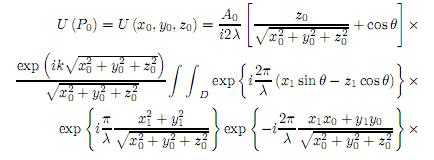
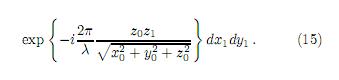
Aplicando la conversión de coordenadas a (15), x0 = L sin θ + ξ cos θ, y0 = η y z0 = L cos θ−ξ sin θ e ser transformada en introduciendo la función apertura P (x, y), (15) puede
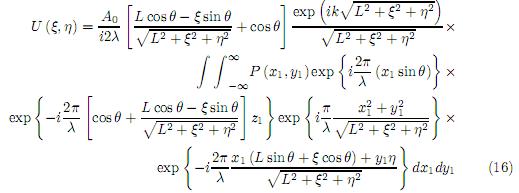
Esta es la ecuación de difracción de campo cercano para una superficie rugosa inclinada.
Si 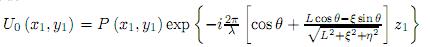 , puede ser reescrita como
, puede ser reescrita como
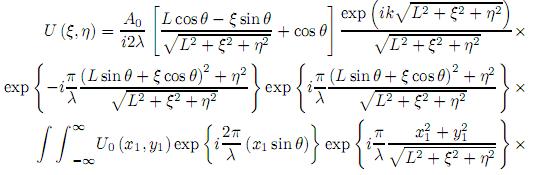
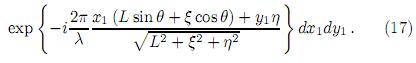
La ecuación (17) corresponde a una transformación fraccional de Fourier de orden α dada por la expresión
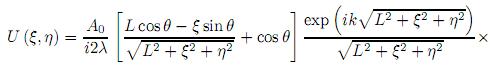
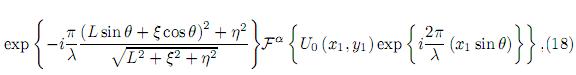
es decir, la función de apertura o pupila se encuentra montada sobre una fase de la forma exp i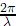 ( x1sin θ) correspondiendo a una onda esférica; y la distribución de amplitudd compleja en el plano de observación corresponde a una transformada fraccional de Fourier de orden fraccional de la distribución de amplitud compleja del plano objeto. Donde
( x1sin θ) correspondiendo a una onda esférica; y la distribución de amplitudd compleja en el plano de observación corresponde a una transformada fraccional de Fourier de orden fraccional de la distribución de amplitud compleja del plano objeto. Donde
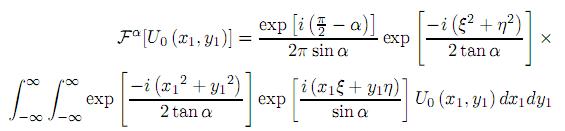
Considerando en (18) las aproximaciones necesarias que permitan describir la difracción de campo cercano, se puede obtener la forma estándar de la ecuación de difracción de Fresnel para una superficie inclinada y reflectiva, es decir,
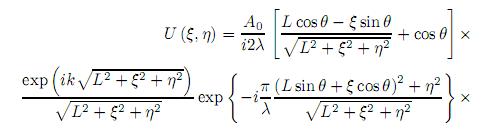
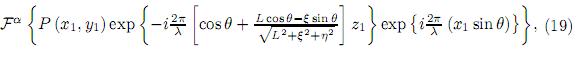
de la misma forma, considerando difracción de campo lejano 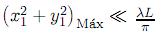 , se llega a la forma estándar de la ecuación difracción de Fraunhofer para una superficie inclinada y reflectiva, es decir,
, se llega a la forma estándar de la ecuación difracción de Fraunhofer para una superficie inclinada y reflectiva, es decir,
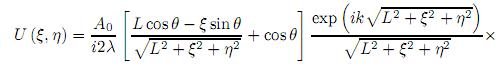
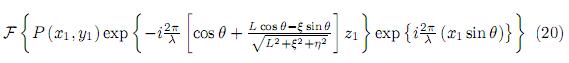
4.3 Comparaciones con las ecuaciones de difracción de Fresnel y Fraunhofer
En el caso especial de incidencia normal, es decir, θ = 00, (19) puede además ser redefinida utilizando las aproximaciones:
(a)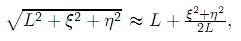 , por el factor exp
, por el factor exp 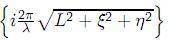 , 19.
, 19.
(b) 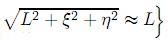 para otros factores en (19).
para otros factores en (19).
Luego, (19) puede ser transformada en
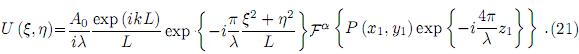
De (20) se obtiene
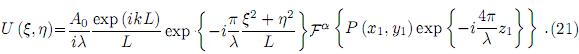
Las ecuaciones (21) y (22) son justamente las expresiones clásicas correspondientes a la difracción de Fresnel y de Fraunhofer para plano de difracción y plano de observación no inclinados.
5 Conclusiones
Partiendo de la integral de Difracción de Fresnel-Kirchhoff, se ha obtenido una integral básica de difracción para una superficie inclinada reflectiva donde la diferencia en el cálculo del factor de inclinación entre el modelo RSDM y el TADM ha sido tenido en cuenta. Como resultado fundamental se ha encontrado una ecuación general de difracción para una superficie inclinada y reflectiva, bajo iluminación de una onda plana coherente, considerando los efectos de rotación del sistema coordenado sobre la aproximación de campo cercano e introduciendo la consideración de inclinaciones pequeñas; la difracción de campo cercano y del campo lejano son obtenidas y presentadas como casos particulares de (8). Por tanto, la expresión derivada es más general que las ecuaciones de difracción clásicas de Fresnel y Fraunhofer. Se debe resaltar que los campos de luz microscópicos emergentes están contenidos en estas ecuaciones de difracción, y hacen referencia a la distribución de altura de la superficie considerada.
Referencias
1. Robert A. Sprague. Surface Roughness Measurement Using White Light Speckle. Applied Optics, ISSN 0003-6935, 11(12), 2811-2816 (1972). Referenciado en 53 [ Links ]
2. PJ. Chandley. Surface roughness measurements from coherent light scattering. Optical and Quantum Electronics, ISSN 0306-8919, 8(4), 323-327 (1976). Referenciado en 53 [ Links ]
3. HM. Pedersen. Object-roughness dependence of partially developed speckle patterns in coherent light. Optics Communications, ISSN 0030-4018, 16(1), 63-67 (1976). Referenciado en 53 [ Links ]
4. H. Fuji, T. Asakura, Y. Shindo. Measurement of surface roughness properties by means of laser speckle techniques. Optics Communications, ISSN 0030-4018, 16(1), 68-72 (1976). Referenciado en 53 [ Links ]
5. Hitoshi Fujii, Toshimitsu Asakura. Roughness measurements of metal surfaces using laser speckle, Journal of the Optical Society of America B, ISSN 0740- 3224, 67(9), 1171-1176 (1977). Referenciado en 53 [ Links ]
6. Ulf. Persson. Real time measurement of surface roughness on ground surfaces using speckle-contrast technique. Optics and Lasers in Engineering, ISSN 0143- 8166, 17(2), 61-67 (1992). Referenciado en 53 [ Links ]
7. Lisa C. Leonard, Vincent Toal. Roughness measurement of metallic surfaces based on the laser speckle contrast method. Optics and Lasers in Engineering, ISSN 0143-8166, 30(5), 433-440 (1998). Referenciado en 53 [ Links ]
8. SL. Toh, HM. Shang, CJ. Tay. Surface-roughness study using laser speckle method. Optics and Lasers in Engineering, ISSN 0143-8166, 29(2- 3), 217-225 (1998). Referenciado en 53 [ Links ]