Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.6 no.12 Medellín Jan./June 2010
Lógicas epistémica y doxástica con restricciones
Lógica epistêmica e doxástica com restrições
Epistemic and doxastic logic with restrictions
Manuel Sierra-A.1
1 Magíster en Ciencias, msierra@eafit.edu.co, profesor, Universidad EAFIT, Medellín- Colombia.
(Recepción: 12-may-2010. Modificación: 06-nov-2010. Aceptación: 06-nov-2010)
Resumen
Se presentan como extensiones del cálculo proposicional clásico las jerarquías de sistemas deductivos LER-n y LDR-n, con n ≥ 1. LER-n es la lógica epistémica con restricciones de profundidad-n, LDR-n es la lógica doxástica con restricciones de profundidad-n. Los sistemas LER-1 y LDR-1 son el cálculo proposicional clásico. El sistema LER-(n + 1) puede ser visto como el resultado de aplicar la regla: de X se infiere +X, una vez a los teoremas del sistema LER-n, además, se restringe la validez de los axiomas +(X → Y ) → (+X → +Y ) y +X → X en términos de la profundidad (complejidad respecto al operador +) de X y de Y, y también se incluyen versiones generalizadas y con restricciones de los axiomas de introspección positiva y negativa. El sistema LER resulta de la reunión de los sistemas de la jerarquía, y puede ser visto como el sistema de lógica modal S5 con diversos tipos de restricciones. cambiando +X → X por +X →∼+∼X se construye la jerarquía LDR-n y el sistema LDR; este último puede ser visto como el sistema de lógica modal KD45 con diversos tipos de restricciones. Los sistemas son caracterizados con semánticas de mundos posibles encajados, con las cuales se le imponen, al problema de la omnisciencia lógica, ciertos límites.
Palabras claves: lógica modal, mundos posibles encajados, lógica doxástica, lógica epistémica, omnisciencia lógica.
Resumo
São apresentadas como extensões do cálculo proposicional clássico as hierarquias dos sistemas dedutivos LDR-n e LER-n, com n ≥ 1. LER-n é a lógica epistêmica com restrições, LDR-n é a lógica doxástica com restrições. Sistemas de LER-1 e LDR-1 são o cálculo proposicional clássico. A LER-(n + 1) sistema pode ser visto como o resultado da aplicação da regra: se X é um teorema de LER-n, então +X é um teorema da LER-(n + 1). Também restringe a validade dos axiomas +(X → Y ) → (+X → +Y ) e +X → X , em termos de profundidade de X e Y, e também inclui limitada versões dos axiomas da introspecção positiva e negativa. O sistema LER é a união do sistemas da hierarquia, e pode ser visto como o sistema de lógica modal S5 com diferentes tipos de restrições. Alterar +X → X por +X →∼+∼X construímos a hierarquia LDR-n e do sistema LDR; este último pode ser visto como o sistema de lógica modal KD45 com diferentes tipos de restrições. Os sistemas são caracterizados com a semântica de mundos possíveis aninhadas, com o qual são impostas, o problema da onisciência lógica, de certos limites.
Palavras chaves: lógica modal, mundos possíveis aninhadas, lógica doxástica, lógica epistêmica, onisciência lógica.
Abstract
Are presented as extensions of classical propositional calculus hierarchies of deductive systems LDR-n and LER-n with n ≥ 1. LER-n is the epistemic logic with restrictions, LDR-n is the doxastic logic with restrictions. The systems LER-1 and LDR-1 are the classical propositional calculus. System LER-(n + 1) can be seen as the result of applying the rule: if X is theorem of LER-n then +X is theorem of LER-(n + 1). Systems also restricts the validity of the axioms +(X → Y) → (+X → +Y) and +X → X, in terms of depth (complexity with respect to the operator +) of X and Y, and also includes restricted versions of the axioms of positive and negative introspection. LER system results from the union of LER-n systems, and can be seen as the S5 modal logic system with different types of restrictions. Changing +X → X by +X →∼+∼X are built LDR-n and the LDR systems. LDR can be seen as the KD45 modal logic system with different types of restrictions. The systems are characterized with a embedded worlds semantics, with which the ‘omniscience logical problem' is limited.
Key words: multi-modal logic, possible worlds embedded, epistemic logic, doxastic logic, logical omniscience.
1 Presentación
Los sistemas deductivos, construidos como extensiones del sistema multi- modal Km utilizando operadores de creencia y conocimiento, los cuales fueron introducidos por Hintikka en Knowledge and Belief [1], son conocidos como lógicas doxásticas y lógicas epistémicas, y son de interés en inteligencia artificial en lo que respecta al modelamiento del razonamiento de agentes inteligentes. Desde el punto de vista semántico, las creencias y el conocimiento de los agentes se caracterizan siguiendo las técnicas desarrolladas por Kripke en Semantical analysis of modal logic [2], con base en un conjunto de mundos posibles y relaciones de accesibilidad entre ellos, donde la fórmula +X será cierta en un mundo posible específico, si X es cierta en cada mundo posible, accesible por el agente asociado al operador +, desde el mundo posible específico.
Como señala Hintikka en Impossible possible worlds vindicated [3], cualquier semántica para estos sistemas deductivos debe justificar como teorema: +(X →
Sim, en Epistemic logic and logical omniscience: a survey [4], muestra cómo, a fin de enfrentar el problema de la omnisciencia lógica, se han construido formalismos alternativos para representar la creencia y el conocimiento. Siguiendo con el modelo de creencia de los mundos posibles, Cresswell en Logic and languajes [5] trabaja con mundos no-clásicos, en los cuales se admiten las inconsistencias, Hintikka en Impossible possible worlds vindicated [3] los llama mundos imposibles, Rescher en The logic of inconsistency [6] los llama mundos no-estándar. Esta aproximación fue seguida por Levesque en A logic of implicit and explicit belief [7], donde un razonador tiene un conjunto relativamente pequeño de creencias explícitas y un conjunto infinito de creencias implícitas, este último incluye las consecuencias lógicas de las creencias explícitas; al operador de creencia implícita se le asocian los mundos estándar y al de creencia explícita los no estándar, resultando una estrecha conexión con la lógica relevante de Anderson y Belnap presentada en Entailment: the logic of relevance and necessity [8]. Lakemeyer en Tractable meta-reasoning in propositional logics of believes [9], diferencia entre creencias objetivas y subjetivas. Fagin y Halpern en Belief, awareness and limited reasoning [10], extienden la lógica de Levesque al razonamiento de múltiples razonadores. La descripción formal del razonamiento parcial hecha por Levesque, es continuada por Schaerf y Cadoli en Tractable reasoning via approximation [11], y a partir de este trabajo, Finger y Wassermann en Logics for approximate reasoning: Approximating classical logic "from above" [12], construyen una familia de lógicas, las cuales son aproximaciones a la lógica clásica. Con base en lo anterior, Rabelloa y Finger, en Approximations of Modal Logics: K and beyond [13], presentan un método para construir aproximaciones a sistemas de lógicas modales, donde el grado de introspección de los razonadores se encuentra limitado por la aproximación a la lógica clásica que se utilice en la construcción. Por otro lado, Konolige en A Deduction Model of belief [14], presenta una alternativa al modelo de creencia de los mundos posibles al representar el razonamiento del agente mediante estructuras de deducción, las cuales constan de un conjunto de fórmulas y un conjunto limitado de reglas de inferencia; en este sistema un razonador cree una fórmula si ésta es una consecuencia del conjunto de fórmulas de la estructura utilizando únicamente reglas de inferencia de la estructura. Gabbay y Woods en Handbook of the History of Logic Vol 7 [15], presentan un panorama muy completo sobre el estado del arte respecto al problema de la omnisciencia en la lógica epistémica.
Sierra, en Sistemas multi-modales de profundidad restringida [16], presenta como extensión del cálculo proposicional clásico, la jerarquía de sistemas deductivos SM M -n, con n ≥ 1. SM M -n es el sistema multi-modal de profundidad-n. El sistema SM M -1 es el cálculo proposicional clásico. El sistema SM M -(n + 1) puede ser visto como el resultado de aplicar la regla de certeza, asociada a los razonadores con suficiente capacidad deductiva, sólo una vez a los teoremas del sistema SM M -n. El lenguaje del sistema SM M - (n+1) es una extensión propia del lenguaje de SM M -n, donde la jerarquía de los lenguajes se encuentra asociada a una jerarquía en la capacidad deductiva de los razonadores. El sistema SM M, sistema multi-modal con restricciones, resulta de la reunión de los sistemas de la jerarquía, y puede ser visto como el sistema de lógica multi-modal Km con restricciones en el lenguaje y en las reglas de certeza, es decir, con razonadores de diferente capacidad de razonamiento.
Continuando parcialmente, con las pautas establecidas en Sistemas multi-modales de profundidad restringida [16], se presentan en este trabajo las jerarquías de sistemas deductivos LER-n y LDR-n, con n ≥ 1. LER-n es la lógica epistémica con restricciones de profundidad-n. En los sistemas LER-n donde n ≥ 2 se restringe la validez del axioma +(X → Y) → (+X → +Y ), así como la aplicación de la regla de certeza, y, por lo tanto, la capacidad deductiva del razonador asociado al operador de certeza + en términos de la profundidad (complejidad respecto al operador +) de X y de Y. En LER-n, con n ≥ 2, también se tienen versiones generalizadas y con restricciones del axioma de conocimiento: +X → X, del axioma de introspección positiva: +1X→ +2 +1X, y del axioma de introspección negativa: ∼ +1X→ +2 ∼ +1X. Los sistemas LER-n son caracterizados con una semántica al estilo Kripke con diversos tipos de restricciones (semántica de mundos posibles encajados). Por ejemplo, la profundidad de un modelo establece la longitud máxima de las cadenas de mundos posibles que figuren en el modelo, resultando que los modelos de profundidad-n se encuentran asociados al sistema deductivo LER-n. El sistema LER resulta de la reunión de los sistemas de la jerarquía, y puede ser visto como una extensión con diversos tipos de restricciones del sistema de lógica modal S5. Las pruebas de validez y completitud de los sistemas de la jerarquía son presentadas de forma detallada, así como las pruebas para la caracterización semántica del sistema LER. cambiando +X → X por +X →∼+ ∼X se construye la jerarquía LDR-n y el sistema LDR. LDR-n es la lógica doxástica con restricciones de profundidad-n, y LDR puede ser visto como el sistema de lógica modal KD45 con diversos tipos de restricciones.
En los sistemas presentados, gracias a las restricciones en el lenguaje (al limitar la aplicabilidad de las reglas de certeza), y a las restricciones en el tipo de los razonadores (al limitar las consecuencias del conocimiento de algunos razonadores), se le imponen al problema de la omnisciencia lógica ciertos límites. Por ejemplo, en el sistema LER-4, un razonador de tipo-2 no siempre puede hacer inferencias cuando se involucran fórmulas de tipo-3, mientras que un razonador de tipo-3 o superior si puede hacerlas, sin embargo, ningún razonador puede hacer inferencias sobre fórmulas de tipo-4.
2 Sistemas deductivos
El lenguaje de todos los sistemas de las jerarquías LER-n y LDR-n, con n ≥ 1, consta de los conectivos binarios →, ∨, ∧, ↔; el conectivo unario ∼; y un conjunto numerable de conectivos unarios u operadores de certeza1 +A, +B, . . . , donde a cada uno de ellos se le asocia un tipo. Cada operador +R de tipo-r se encuentra asociado a un razonador R, y se dice que R es de tipo-r.
El conjunto de fórmulas del cálculo proposicional clásico CP o fórmulas de tipo-1 es generado recursivamente a partir de un conjunto de fórmulas atómicas utilizando los conectivos de la forma:
1. Si P es una fórmula atómica entonces P es una fórmula de tipo-1.
2. Si X es una fórmula de tipo-1 entonces ∼(X) es una fórmula de tipo-1.
3. Si X y Y son fórmulas de tipo-1 entonces (X) → (Y), (X) ↔ (Y), (X) ∧ (Y) y (X) ∨ (Y ) son fórmulas de tipo-1.
En general, para n ≥ 1: si X es una fórmula de tipo-n y + es un operador de certeza, entonces +X es una fórmula de tipo-(n + 1).
Si X es una fórmula de tipo-k, Y es una fórmula de tipo-q y n = máximo {k, q} entonces (X) → (Y), (X) ↔ (Y), (X) ∧ (Y) y (X) ∨ (Y) son fórmulas de tipo-n.
Si X es una fórmula de tipo-n entonces ∼(X) es una fórmula de tipo-n.
Definición 2.1 (Operadores de conocimiento). Si + es el operador de certeza asociado al razonador R, entonces +X denota que la fórmula X es una certeza para el razonador R. La fórmula X es imposible para el razonador R, denotado ¬X, si su negación es una certeza para el razonador R, es decir, ¬X↔ +∼X. La fórmula X es refutable para el razonador R, denotado −X, si no es una certeza para el razonador R, es decir, −X ↔∼ +X. La fórmula X es posible para el razonador R, denotado •X, si no es imposible para el razonador R, es decir, •X ↔∼¬X. Los operadores +, ¬, − y • son llamados operadores de conocimiento para el razonador R2.
Como consecuencia de la definición de los operadores de conocimiento, en la tabla 1 se tienen algunas caracterizaciones de los mismos.
La unión de los conjuntos de fórmulas de tipo-1, tipo-2, . . ., tipo-n determinan el conjunto de fórmulas de profundidad-n, el cual es el lenguaje de los sistemas LER-n y LDR-n.
Los sistemas LER-n, lógica epistémica con restricciones de profundidad-n, se construyen de la forma:
• LER-1 es el cálculo proposicional clásico CP .
• Para n ≥ 1, el sistema LER-(n + 1) se construye a partir del sistema LER-n de la siguiente forma:
-A×CP : los axiomas de CP sobre las fórmulas de profundidad-(n+1) son axiomas de LER-(n + 1).
- MP+<: +(A → B) → (+A → +B) es un axioma de LER-(n + 1), donde A es de tipo-a, B es de tipo-b y 1 ≤ a < b ≤ n.
- MP+=: +(A → B ) → (+A → +B) es un axioma de LER-(n + 1), donde A es de tipo-a, B es de tipo-b y 1 ≤ a = b ≤ n.
- A × R: A → •A es un axioma de LER-(n + 1), donde A es de tipo-a, • es de tipo-r, 1 ≤ a ≤ n y a ≤ r.
- A×T: −2¬1X→ •1X es un axioma de LER-(n + 1), donde +1X es una fórmula de profundidad-n.
- A×E: −1X→ ¬2 +1X es un axioma de LER-(n + 1), donde +1X es una fórmula de profundidad-n.
- A×A×: X es un axioma de LER-(n + 1), donde X es un axioma de LER-n
- A×+: +X es un axioma de LER-(n + 1), donde X es un teorema de LER-n.
Los sistemas LDR-n, lógica doxástica con restricciones de profundidad-n, se construyen de manera similar, cambiando A×R por:
- A×S: +A → •A es un axioma de LDR-(n + 1), donde A es de tipo-a, • es de tipo-r, 1 ≤ a ≤ n y a ≤ r.
- MP : los sistemas LER-(n + 1) y LDR-(n + 1) tienen como única regla de inferencia el modus ponens de tipo-(n + 1), es decir, de X y X → Y se infiere Y, donde X y Y son fórmulas de profundidad-(n + 1).
El lenguaje de LER es la unión de los lenguajes de los sistemas LER-n, con n ≥ 1, por lo que en LER hay fórmulas de profundidad arbitraria. El sistema LER, lógica epistémica con restricciones, tiene como única regla de inferencia primitiva el modus ponens y es axiomatizado de la forma
X es un axioma de LER si y sólo si X es axioma de LER-n para algún n ≥ 1.
De manera análoga se construye el sistema LDR, lógica doxástica con restricciones.
Para cada uno de los sistemas presentados más arriba, se dice que una fórmula X es un teorema del sistema si y solamente si X es la última fórmula de una sucesión finita de fórmulas del sistema, tales que cada una de ellas es un axioma del sistema o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP. Si Γ es un conjunto de fórmulas del sistema, se dice que una fórmula X es un teorema del sistema a partir de Γ, si y solamente si X es la última fórmula de una sucesión finita de fórmulas del sistema, tales que cada una de ellas es un axioma del sistema o un elemento de Γ o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP.
En lo que sigue se utilizaran diversos resultados de CP, se hará referencia a estos resultados simplemente como LCP o leyes lógicas de CP (para detalles de las pruebas en CP ver [17]). Con la notación LR-n (ó LR) se estará haciendo referencia, tanto al sistema LER-n (ó LER), como al sistema LDR-n (ó LDR).
Proposición 2.1 (Conjunción de certezas).
1. Para n ≥ 1, X y Y fórmulas de tipo-t, con t ≤ n. +(X ∧ Y) → (+X ∧ +Y) es un teorema de LR-(n + 1) y de LR.
2. Para n ≥ 1, X y Y fórmulas de profundidad-t, con t ≤ n. (+X ∧ + Y ) → +(X ∧ Y) es un teorema de LR-(n + 1) y de LR.
3. Para n ≥ 1, X y Y fórmulas de tipo-t, con t ≤ n. +(X ∧ Y) ↔ (+X ∧ +Y) es un teorema de LR-(n + 1) y de LR.
Prueba. Para la parte 1, en LR-n se tienen (X ∧ Y) → X y (X ∧ Y) → Y , y por A×+ se afirma que +((X ∧ Y) → X) y +((X ∧ Y) → Y) son axiomas de LR-(n + 1), con n ≥ 1. Utilizando el axioma MP+= y MP se infieren +(X ∧ Y) → +X y +(X ∧ Y) → +Y . Utilizando LCP se infiere +(X ∧ Y ) → (+X ∧ +Y ).
Para la parte 2, por LCP se tiene en LR-n, con n ≥ 1, X → (Y → (X ∧ Y)). Como esta fórmula es de profundidad-t, con t ≤ n, por A×+ se infiere en LR-(n + 1), +(X → (Y → (X ∧ Y))), y el tipo del antecedente es menor o igual que el del consecuente, utilizando uno de los axiomas MP+= ó MP+< y MP resulta +X → +(Y → (X ∧ Y)), como, además, por MP+= ó MP+<, se tiene +(Y → (X ∧ Y)) → (+Y → +(X ∧ Y)), entonces por LCP se obtiene +X → (+Y → +(X ∧ Y)). Utilizando LCP se infiere (+X ∧ + Y ) → +(X ∧ Y).
La parte 3 es consecuencia de las dos anteriores

Proposición 2.2 (Sustitución por equivalencia).
1. Sean X y Y fórmulas de tipo-t, con t ≤ n. Si X ↔ Y es un teorema de LR-n entonces +X ↔ +Y es un teorema de LR-(n + 1) y de LR.
2. Si F (Z ) es una fórmula de profundidad-n en la cual figura la fórmula Z de tipo-t, con 1 ≤ t ≤ n, y F (W) es el resultado de cambiar en F (Z ) alguna ocurrencia de Z por W , donde W es una fórmula de tipo-t, entonces, en LR-n y en LR, de Z ↔ W se infiere F (Z) ↔ F (W).
Prueba. Para la parte 1, supóngase que en LR-n, X ↔ Y, por LCP resulta (X → Y) ∧ (Y → X), la cual es de tipo-t, y por A×+ se infiere en LR-(n + 1), +((X → Y) ∧ (Y → X)), al ser X y Y de tipo-t, por la proposición 2.1, numeral 1, se obtiene +(X → Y) ∧ +(Y → X), utilizando LCP y el axioma MP+= se genera (+X → +Y ) ∧ (+Y → +X), finalmente, utilizando LCP se concluye +X ↔ +Y en LR-(n + 1), y como los axiomas de LR-(n + 1) son axiomas de LR, entonces la prueba de +X ↔ +Y en LR-(n + 1) también es una prueba de +X ↔ +Y en LR (utilizando las definiciones de los operadores de conocimiento, también se siguen •X ↔ •Y, −X ↔ −Y y ¬X↔ ¬Y ).
La parte 2 se sigue de la 1 teniendo en cuenta que la equivalencia se preserva con los demás conectivos, para detalles ver [17].

3 Semántica
Definición 3.1 (n-marco). La terna (S, Ma, RA) es un n-marco (marco de profundidad-n) si y solamente si Ma es un elemento del conjunto S, RA es un conjunto de relaciones binarias sobre S, donde a cada operador de certeza + le corresponde una relación binaria R, la cual es de tipo-r si y sólo si el operador + es de tipo-r. Los elementos de RA son llamados relaciones de accesibilidad, los elementos de S son llamados mundos posibles y el mundo posible Ma es el mundo actual.
Cada mundo posible Np tiene asociado el lenguaje de profundidad-p del sistema LR-p, y se dice que Np es de profundidad-p. En un n-marco (S, Ma, RA), la profundidad de los mundos satisface las siguientes restricciones, para las cuales se tiene que R es la relación de accesibilidad asociada al operador + de tipo-r, 1 ≤ q < a, 1 ≤ p ≤ a − 2, y, además, K, N, D, F (con subíndices) son mundos posibles:
1. RMa (Restricción del mundo actual). Si Ma es el mundo actual entonces 1 ≤ a ≤ n.
2. RE < (Restricción de encaje interno). Si Dq+1 es un mundo posible entonces Dq es un mundo posible. Se dice que Dq está encajado en Dq+1.
3. RA (Restricción de accesibilidad). Las relaciones de accesibilidad son de la forma Nq +1RDq.
4. RAE< (Restricción de accesibilidad encajada interna). Si Np+2RDp+1, Np+1 existe y Dp existe entonces Np+1RDp.
5. (a) RR (Restricción de reflexividad). Para cada Nq+1, si R es de tipo-r y 1 ≤ q ≤ r entonces Nq+1RNq.
6. RE (Restricción de euclidianidad). Si Kp+2R2Np+1 y Kp+1R1Fp entonces Np+1R1Fp.
7. RT (Restricción de transitividad). Si Kp+2R2Np+1, Np+1R1Fp y Kp+1 existe entonces Kp+1R1Fp.
Las anteriores restricciones corresponden a los n-marcos de los sistemas LER-n. Para el caso de los n-marcos de los sistemas LDR-n, basta cambiar la restricción 5(a) RR, por la restricción
5. (b) RS (Restricción de serialidad). Para cada Nq+1, si R es de tipo-r y 1 ≤ q ≤ r entonces existe Dq tal que Nq+1RDq.
Como consecuencia se tiene que ningún mundo accede al mundo actual, los mundos de profundidad-1 no acceden a ningún mundo, y ningún mundo posible accede a sí mismo. Observar que un marco de profundidad-n también es un marco de profundidad-(n + 1).
Definición 3.2 (Cadena). Dado un n-marco (S, Ma, RA), donde Ma, Na−1, . . ., Et+2, Dt+1, Gt son mundos posibles diferentes en S, y Ma es el mundo actual, se dice que C = MaNa−1 . . . Et+2Dt+1Gt es una cadena de profundidad- (a − t + 1) cuando se tienen MaRaNa−1, . . . , Et+2Rt+2Dt+1 y Dt+1Rt+1Gt, donde Ra, . . . , Rt+2 y Rt+1 son elementos de RA.
Observar que una cadena tiene profundidad-t significa que la cadena está formada por t mundos posibles diferentes. En un n-marco la profundidad de las cadenas no puede superar la profundidad del mundo actual, la cual es a lo sumo n.
Definición 3.3 (n-modelo). Sea (S, Ma, RA) un n-marco y Fa el conjunto de las fórmulas de profundidad-a, (S, Ma, RA, V ) es un n-modelo si y solamente si V es una relación funcional3 (valuación) de S × Fa en {0, 1} la cual satisface las siguientes reglas o condiciones: sean P una fórmula atómica, Dk un mundo posible, X y Y fórmulas de profundidad-t, con 1 ≤ t ≤ k ≤ a ≤ n:
Vat. V (Dk, P ) = 1 o V (Dk, P ) = 0.
V∼. V (Dk, ∼X) = 1 ⇔ V (Dk, X) = 0.
V∧. V (Dk, X ∧ Y) = 1 ⇔ V (Dk, X) = 1 = V (Dk, Y).
V∨. V (Dk, X ∨ Y) = 0 ⇔ V (Dk, X) = 0 = V (Dk, Y).
V→. V (Dk, X → Y) = 0 ⇔ V (Dk, X) = 1 y V (Dk, Y) = 0.
V↔. V (Dk, X ↔ Y ) = 1 ⇔ V (Dk, X) = V (Dk, Y ).
V+. V (Dp+1,+Z ) = 1 ⇔ (∀Np ∈ S)(Dp+1RNp ⇒ V (Np , Z) = 1), donde 1 ≤ p < a, y Z es una fórmula de tipo-p.
VP. Si X es una fórmula de tipo-p, con 1 ≤ p ≤ a, entonces para cada t, con p ≤ t ≤ a, si Dt existe entonces V (Dt, X) = V (Dp, X).
Finalmente, los modelos (de profundidad arbitraria) se definen de la misma forma que se definen los n-modelos, eliminando la restricción acerca de la profundidad del marco.
Proposición 3.1 (Caracterización semántica de los operadores de conocimiento). En un n-modelo (S, Ma, RA, V), para 1 ≤ p < a y Z una fórmula de tipo-p.
V ¬. V (Mp+1,¬Z) = 1 ⇔ (∀Np ∈ S)(Mp+1RNp ⇒ V (Np, Z) = 0)
V•. V (Mp+1,•Z) = 1 ⇔ (∃Np∈ S)(Mp+1RNp y V (Np, Z ) = 1).
V −. V (Mp+1,−Z ) = 1 ⇔ (∃Np∈ S)(Mp+1RNp y V (Np, Z) = 0).
Prueba. Consecuencia inmediata de las definiciones de los operadores de conocimiento. 
4 Interpretación canónica
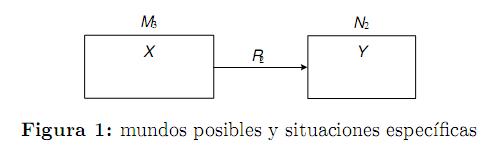
Las intuiciones que motivaron la construcción de los sistemas LR-n corresponden a la siguiente interpretación (ver figura 1): cada mundo posible corresponde a una situación específica y a un razonador, así, el mundo posible M3 de profundidad-3 se interpreta como una situación específica asociada a un razonador-3 de tipo-3. El mundo posible N2 de profundidad-2 se interpreta como una situación específica asociada a un razonador-2 de tipo-2. V (M3, X) se interpreta como información-X (información sobre la veracidad o falsedad de la fórmula X de tipo-3) que el razonador-3 posee en la situación específica M3. M3R2N2 significa que, desde la situación específica M3, el razonador-3 encuentra disponible (puede acceder a) la información-Y , que el razonador-2 posee en la situación específica N2.
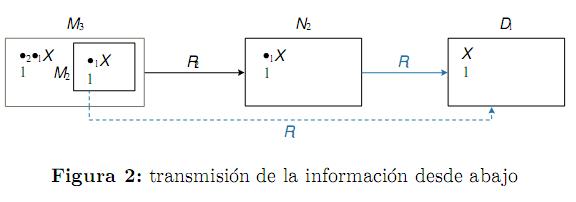
V (M3,•2 •1 X→ •1 X) = 1 se interpreta como (ver figura 2): si desde la situación específica M3, el razonador-3 encuentra disponible la información que el razonador-2 posee en la situación específica N2, y si desde la situación específica N2 el razonador-2 encuentra disponible la información que el razonador-1 posee en la situación específica D1, entonces el razonador-3 encuentra disponible desde M2, la información que el razonador-1 posee en la situación específica D1. Lo anterior significa que el razonador-2 transmite al razonador-3 la información que tiene disponible acerca del razonador-1. Por lo que A×T significa transmisión de la información desde abajo.
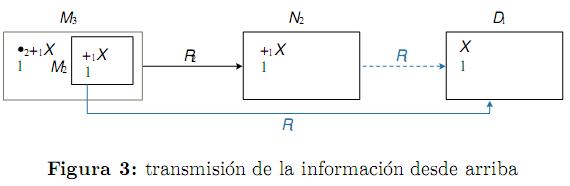
V (M3,•2 +1 X→ +1X) = 1 se interpreta como (ver figura 3): si desde la situación específica M3, el razonador-3 encuentra disponible la información que el razonador-2 posee en una situación específica N2, entonces desde la situación específica N2 el razonador-2 encuentra disponible la información que el razonador-1 posee en cualquier situación específica D1, la cual se encuentre disponible para el razonador-3 desde la situación específica M2. Lo anterior significa que el razonador-3 transmite al razonador-2 la información que tiene disponible acerca del razonador-1. Por lo que A×E significa transmisión de la información desde arriba.
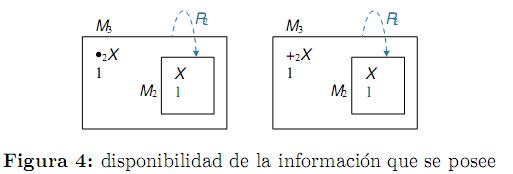
V (M3,+2X→ X) = V (M3, X→ •2X) = 1 se interpreta como (ver figura 4): el razonador-3, en la situación específica M3, encuentra disponible la información-X, de tipo-x, que el razonador-2, de tipo-r, con x ≤ r, posee en la situación específica M2. Lo anterior significa que el razonador-3 encuentra disponible la información que posee como información que el razonador-2 posee. Por lo que A×R significa disponibilidad de la información que se posee si hay un razonador capaz de acceder a ella. Cuando el razonador-2 es el mismo razonador-3, se tiene la llamada autoreflexión del conocimiento.
Observar que en LER-3, la fórmula +1 •2P→ •2P, donde P es atómica, +1 es de tipo-1 y •2 es de tipo-2, es refutada por el modelo que consta de los mundos M1, M2 y M3 , tales que M3R2M2, M2R2M1 y M2R1M1, donde V (M1, P) = 0, puesto que V (M3,+1 •2P) = 1 y V (M2,•2P) = 0.
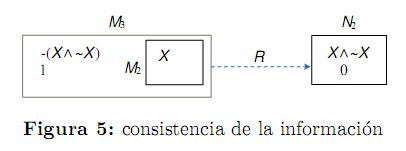
V (M3,+X → •X) = V (M3,−(X∧ ∼ X)) = 1 se interpreta como (ver figura 5): el razonador-3, desde la situación específica M3, puede garantizar que los razonadores de cierto tipo refutan la información inconsistente del mismo tipo o inferior. Por lo que A×S significa consistencia de la información que poseen los razonadores cuando tienen la capacidad de acceder a ella.
Observar que en LDR-3, la fórmula −1(•2P∧∼•2P), donde P es atómica, +1 es de tipo-1 y •2 es de tipo-1, es refutada por el modelo que consta de los mundos N1, M1, M2 y M3, tales que M2R1N1, M2R2N1, M2R2M1 y M2R1M1, donde V (M1, P) = 1 y V (N1, P) = 0.
Observar que la relación entre las profundidades de los mundos, exigida por las reglas y las restricciones, garantizan que la estructura formada por los mundos posibles M3, M2, M1, N2,y N1, tales que únicamente M3R2M2, M2R2M1, M2R1M1, M3R1N2, N2R1N1, N2R2N1, N2R1M1 y N2R2M1, donde V (M1, P) = 1, y V (N1, P) = V (N1, Q) = V (M1, Q) = 0, no es un 3-modelo, el cual refutaría en LR-3 la fórmula +1(P → •2Q) → (+1P→ +1 •2Q) con P y Q atómicas, y +1 de tipo-1, es decir, refutaría el axioma MP +< (para que sea un 3-modelo las restricciones RE < y RAE < implican que M2R1N1, por lo que V (N1, P) = 1, lo cual no es en caso). Observar que en el axioma MP +<: +(X → Y) → (+X → +Y) se pide que la profundidad de Y sea mayor que la profundidad de X, por lo que, para validar este axioma, se requiere la restricción RAE<.
Observar también que la estructura formada por los mundos posibles M3, M2,M1 y N1, tales que únicamente M3R1M2, M2R1M1, M3R2M2, M2R2M1 y M2R1N1, donde V (M1, P) = V (N1, P) = V (M1, Q) = 1 y V (N1, Q) = 0, es un 3-modelo, el cual refuta en LR-3 la fórmula +1 (•2P→ Q) → (+1 •2P→ +1Q) con P y Q atómicas, es decir, refuta la fórmula: +(X → Y) → (+X → +Y) cuando la tipo de X sea mayor que el tipo de Y . La profundidad de los mundos indica el nivel de complejidad de la información, es decir, el tipo de las fórmulas que el razonador posee en una situación específica. Las restricciones RE < y RAE <, las cuales corresponden al axioma MP +<, garantizan que si se accede a información de cierta complejidad, entonces se puede acceder a información de menor complejidad y no necesariamente a información de mayor complejidad.
5 Validez
Definición 5.1 (Validez). Sea X una fórmula de tipo-t. X es verdadera en el n-modelo (S, Ma, RA, V), con t ≤ a ≤ n, si y sólo si V (Ma, X) = 1. X es n-válida si y sólo si X es verdadera en todo n-modelo (S, Ma, RA, V ), con t ≤ a ≤ n. X es verdadera en un modelo (S, Ma, RA, V ) si y solamente si V (Ma, X) = 1, con t ≤ a. X es válida si y solamente si X es verdadera en todo modelo (S, Ma, RA, V ), con t ≤ a.
Tener presente que al hablar de validez, puede ser validez en LER-n o en LDR-n, dependiendo de si son modelos de LER-n o de LDR-n. Esta diferencia será clara en e l contexto.
Observar que cuando se habla de 1-validez, se hace referencia a los 1- modelos, pero en estos modelos no aplica la regla V+, es decir, los 1-modelos son los modelos del cálculo proposicional clásico CP, por lo que 1-validez coincide con validez en CP.
Resulta entonces que una fórmula X de profundidad-t, con t ≤ n, no es n-válida si y solamente si existe un n-modelo M = (S, Ma, RA, V), con t ≤ a ≤ n, en el cual X no es verdadera, es decir, V (Ma, X) = 0. Por lo que si la fórmula X no es n-válida, utilizando las reglas de las valuaciones, a partir de V (Ma, X) = 0, se construye un n-modelo M = (S, Ma, RA, V) que refute la validez de la fórmula X; este modelo es llamado n-modelo refutador. Pero si la fórmula X es n-válida, entonces la construcción del n-modelo refutador fracasará, puesto que, en alguno de los mundos posibles (bien sea Ma o un mundo generado por la aplicación de las reglas) del modelo en construcción, se presentará una inconsistencia. Cuando fracasa la construcción del modelo refutador, entonces se genera una cadena de mundos posibles C = Ma. . . Nk+1Dk tal que Dk es inconsistente, es decir, para alguna fórmula Z, V (Dk, Z) = 1 y V (Dk, Z ) = 0. En este caso se dice que la cadena C es inconsistente.
En resumen, para probar la n-validez de una fórmula X de profundidad-t, con t ≤ n, se supone que la fórmula X no es n-válida, es decir, es falsa en el mundo actual Made un n-modelo, y a partir de esta información se construye el n-modelo refutador. Si tal n-modelo no existe entonces se concluye que la fórmula X es n-válida.
Proposición 5.1 (Preservación de la validez).
1. Sea X de tipo-a, con a ≤ n. Si X es n-válida entonces X y +X son (n + 1)-válidas.
2. Sea X de tipo-a, con a ≤ n. Si X es válida entonces +X es válida.
3. Para A y B fórmulas de profundidad-t, con 1 ≤ t ≤ n. Si A y A → B son n-válidas entonces B también es n-válida.
Prueba. Para la parte 1, supóngase que X de tipo-a es n-válida, por lo que, en la búsqueda constructiva de un n-modelo refutador de la fórmula X, resulta una cadena inconsistente C = Ma. . . Nk+1Dk para algún k tal que 1 ≤ k ≤ a ≤ n. Por lo tanto, en la búsqueda constructiva de un (n + 1)- modelo refutador de la fórmula X, resulta la misma cadena inconsistente C = Ma. . . Nk+1Dk para algún k, 1 ≤ k ≤ a ≤ n + 1. Se concluye entonces que X es (n + 1)-válida.
Supóngase que +X no es (n+1)-válida, por lo que existe un (n+1)-modelo refutador de +X, M O = (S, Ma+1, RA, V), con 1 ≤ a ≤ n, tal que +X no es verdadera en MO, es decir, V (Ma+1,+X) = 0. Por la regla V + resulta que existe un mundo posible Na tal que Ma+1RNa, donde R es la relación asociada a +, y V (Na, X) = 0. El (n+1)-modelo MO se encuentra formado por cadenas consistentes de la forma Ma+1Na . . . Sk, las cuales tienen profundidad a lo sumo a + 1, y, además, en el mundo Ma+1 la fórmula +X toma el valor 0, y en el mundo Na la fórmula X toma el valor 0. A partir del (n + 1)-modelo refutador MO de +X se construye un n-modelo refutador MO′ de la fórmula X de la siguiente manera: se elimina el mundo actual Ma+1 del conjunto S obteniéndose el conjunto S′, y se toma como mundo actual del modelo MO′ el mundo Na; en la relación de accesibilidad del modelo MO se eliminan las relaciones de accesibilidad existentes entre el mundo actual Ma+1 y cualquier otro mundo obteniéndose el conjunto de relaciones RA′, y del dominio de V se excluye el mundo actual Ma+1 obteniéndose V′. Como resultado se obtiene el modelo MO′ = (S′, Na, RA′, V ′), el cual por construcción se encuentra formado por cadenas consistentes Na. . . Sk de profundidad a lo sumo a, con a ≤ n, lo que significa que MO′ es un n-modelo, y, además, en el mundo actual Na la fórmula X toma el valor 0, por lo tanto, MO′ es un n-modelo refutador de la fórmula X, es decir, X no es verdadera en el n-modelo MO′, por lo que X no es n-válida. De lo anterior se concluye que si +X no es (n + 1)-válida, entonces X no es n-válida, es decir, si X es n-válida entonces +X es (n + 1)-válida.
La parte 2 se prueba como la parte 1.
Para la parte 3, sean A de tipo-a y B de tipo-b. Caso 1: a ≤ b, si B no es n-válida entonces existe un n-modelo con mundo actual Mb tal que V (Mb, B) = 0, pero como A → B es n-válida, resulta que V (Mb, A → B) = 1, por la regla V → se infiere que V (Ma, A) = 0, contradiciendo la n-validez de A. Caso 2: a ≥ b, si B no es n-válida entonces A∧B tampoco es n-válida, por lo que existe un n-modelo con mundo actual Matal que V (Ma, A ∧ B) = 0, es decir, V (Ma, A) = 0 ó V (Mb, B) = 0, pero como A es n-válida, entonces V (Mb, B) = 0, como A → B es n-válida, resulta que V (Ma, A → B) = 1, y por la regla V → se infiere que V (Ma, A) = 0, contradiciendo la n-validez de A.

Proposición 5.2 (n-validez de los axiomas). Sea X de profundidad-t, con t ≤ n. Si X es un axioma de LR-n entonces X es n-válida.
Prueba. Supóngase que X es un axioma de LR-n, se probará que X es n-válida haciendo inducción sobre n.
Paso base 1 (n = 1). Se debe probar: si X es un axioma de LR-1 entonces X es 1-válida, lo cual es cierto ya que el sistema LR-1 es el cálculo proposicional clásico CP, 1-validez es validez en CP y utilizando el teorema de validez de CP , presentado en [17], se obtiene que si X es un teorema de CP entonces X es CP-válida.
Paso de inducción. Como hipótesis inductiva 1 se tiene, para cada fórmula Y que, si Y es un axioma de LR-n entonces Y es n-válida. Supóngase que X es un axioma de LR-(n + 1), se debe probar que X es (n + 1)-válida. Al ser X un axioma se deben considerar nueve casos: en el primer caso X es un axioma de LR-n, en el segundo X es de la forma +Y , donde Y es un teorema de LR- n, en el tercer y cuarto caso X es de la forma +(Y → Z) → (+Y → +Z), en el quinto caso X es de la forma Z → •Z , donde el tipo de • es mayor o igual que el tipo de Z , en el sexto caso X es uno de los axiomas de CP, en el séptimo caso X es de la forma −2¬1Z→ •1Z, en el octavo caso X es de la forma −1Z→ ¬2 +1Z, y en el noveno caso X es de la forma +Z → •Z, donde el tipo de + es mayor o igual que el tipo de Z .
En el primer caso, X es un axioma de LR-n; utilizando la hipótesis inductiva resulta que X es n-válida y, por la proposición 5.1, numeral 1, se infiere que X es (n + 1)-válida.
En el segundo caso, X es de la forma +Y , donde Y es un teorema de LR-n. Se probará que Y es n-valida por inducción sobre la longitud L de la demostración de Y en LR-n.
Paso base 2 (L = 1). Si la longitud de la demostración de Y en LR-n es 1, entonces Y es un axioma de LR-n, lo cual, por la hipótesis inductiva 1, significa que Y es n-válida.
Paso de inducción. Como hipótesis inductiva 2 se tiene que para cada fórmula Z , si Z es un teorema de LR-n y la longitud de la demostración de Z tiene longitud menor que L (donde L ≥ 1) entonces Z es n-válida. Si Y es un teorema de LR-n y la longitud de la demostración de Y es L, entonces Y es un axioma de LR-n ó Y es consecuencia de aplicar modus ponens en pasos anteriores de la demostración. En el primer caso se procede como en el caso base. En el segundo caso se tienen en LR-n, para alguna fórmula W, demostraciones de W y de W → Y, donde la longitud de ambas demostraciones es menor que L; utilizando la hipótesis inductiva 2 se infiere que W y W → Y son n-válidas, y por la proposición 5.1, numeral 3, resulta que Y es n-válida.
Con la segunda inducción se ha probado que, si Y es un teorema de LR-n entonces Y es n-válida, y por la proposición 5.1, numeral1, resulta que +Y es (n + 1)-válida, por lo que X es (n + 1)-válida.
En el tercer caso (MP+ =), X es de la forma +(A → B) → (+A → +B ), donde A y B son fórmulas de tipo-a. Si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n + 1)-modelo tal que en el mundo actual Ma+1, V(Ma+1,+(A → B) → (+A → +B)) = 0, lo cual, según la regla V →, significa V (Ma+1,+(A → B)) = 1 y V (Ma+1,+A → +B) = 0, y de nuevo, por la misma regla, se obtienen V (Ma+1,+A) = 1 y V (Ma+1,+B) = 0; de esta última, por la regla V +, se infiere la existencia de un mundo Na tal que Ma+1RNa y V (Na, B) = 0, y como V (Ma+1,+(A → B)) = 1 por V + se infiere V (Na, A → B) = 1, y como V (Ma+1,+A) = 1, por V + se obtiene V (Na, A) = 1, y como ya se tiene V (Na, A → B) = 1, por V → se genera V (Na, B) = 1, pero esto es imposible, ya que V (Na, B) = 0. Por lo tanto, +(A → B) → (+A → +B) es (n + 1)-válida.
En el cuarto caso (MP+ <), X es de la forma +(A → B) → (+A → +B), donde A es de tipo-a, B es de tipo-b y a < b. Si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n + 1)-modelo tal que en el mundo actual Mb+1, V(Mb+1,+(A → B ) → (+A → +B )) = 0, lo cual, según la regla V →, significa V (Mb+1,+(A → B)) = 1 y V (Mb+1,+A → +B) = 0, por la restricción RE < existe la secuencia de mundos encajados Mb+1, Mb, . . . , Ma+1, Ma, . . . , M2, M1, y de nuevo por la regla V → se obtienen V (Ma+1,+A) = 1 y V (Mb+1,+B ) = 0; de esta última, por la regla V+, se infiere la existencia de un mundo Nb tal que Mb+1RNb y V (Nb, B) = 0, y como V (Mb+1,+(A → B)) = 1, también se infiere V (Nb, A → B) = 1. Como Mb+1RNb, entonces, por la restricción RAE<, resulta que MbRNb−1, . . . , Ma+1RNa, y como V (Ma+1,+A) = 1, por V+ se obtiene V (Na, A) = 1, pero, como ya se tiene V (Nb, A → B) = 1, por V → se genera V (Nb, B) = 1, pero esto es imposible, ya que V (Nb, B) = 0. Por lo tanto, +(A → B) → (+A → +B) es (n + 1)-válida.
En el quinto caso X es de la forma Z → •Z (axioma específico de LER-n), donde el tipo de • es mayor o igual que el tipo de Z. Supóngase que Z es de tipo-a y • es de tipo-r, con 1 ≤ a ≤ n y a ≤ r, si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n + 1)-modelo tal que en el mundo actual Ma+1, V(Ma+1, Z→ •Z) = 0, lo cual, según la regla V →, significa V (Ma, Z) = 1 y V (Ma+1,•Z) = 0, es decir, V (Ma+1,∼+∼Z ) = 0, resultando que V (Ma+1,+∼Z ) = 1, utilizando la restricción RR (restricción específica de LER-n) se tiene Ma+1RMa, resultando que V (Ma, ∼ Z) = 1, es decir, V (Ma, Z) = 0, lo cual no es el caso. Por lo tanto, Z → •Z es (n + 1)-válida cuando el tipo de • es mayor o igual que el tipo de Z.
En el sexto caso X es uno de los axiomas de CP , por lo que, utilizando las reglas Vat, V ∼, V ∧, V ∨, V → y V ↔, y procediendo como es habitual para la validez del cálculo proposicional clásico (para detalles del caso clásico ver [17]), se concluye que X es (n + 1)-válida.
En el séptimo caso X es de la forma −2¬1Z→ •1Z. Supóngase que Z es de tipo-a, con 1 ≤ a < n, si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n + 1)-modelo tal que en el mundo actual Ma+2, V(Ma+2,−2¬1Z→ •1Z) = 0, lo cual, según la regla V →, significa V (Ma+2,−2¬1Z) = 1 y V (Ma+1,•1Z) = 0, es decir, V (Ma+1,∼+1∼Z ) = 0 y entonces V (Ma+1,+1∼ Z ) = 1, utilizando la regla V − de la proposición 3.1 resulta que existe un mundo Na+1 tal que Ma+2R2Na+1, y en el cual V (Na+1,¬1Z) = 0, por la regla V ¬ de la proposición 3.1 resulta que existe un mundo Sa tal que Na+1R1Sa, y en el cual V (Sa, Z) = 1, pero por la restricción RT se obtiene Ma+1R1Sa, por lo que se infiere V (Sa, ∼ Z ) = 1, es decir, V (Sa, Z ) = 0, lo cual es imposible, por lo tanto, −2¬1Z→ •1Z es (n + 1)-válida.
En el octavo caso X es de la forma −1Z→ ¬2 +1Z. Supóngase que Z es de tipo-a, con 1 ≤ a < n, si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n+1)-modelo tal que en el mundo actual Ma+2, V(Ma+2,−1Z→ ¬2 +1Z) = 0, lo cual, según la regla V →, significa V (Ma+1,−1Z) = 1 y V (Ma+2,¬2+1Z) = 0, utilizando la regla V − se infiere la existencia de un mundo Na tal que Ma+1R1Na y V (Na, Z) = 0, además, por la regla V ¬, resulta que existe un mundo Sa+1 tal que Ma+2R2Sa+1 y V (Sa+1,+1Z) = 1; utilizando la restricción RE se obtiene Sa+1R1Na resultando que V (Na, Z) = 1, lo cual es imposible, por lo tanto, −1Z→ ¬2+1Z es (n + 1)-válida.
En el noveno caso X es de la forma +Z → •Z (axioma específico de LDR-n), donde el tipo de + es mayor o igual que el tipo de Z . Supóngase que Z es de tipo-a y + es de tipo-r, con 1 ≤ a ≤ n y a ≤ r, si esta fórmula no fuese (n + 1)-válida, entonces existiría un (n + 1)-modelo tal que en el mundo actual Ma+1, V(Ma+1,+Z → •Z ) = 0, lo cual, según la regla V →, significa V (Ma+1,+Z ) = 1 y V (Ma+1,•Z) = 0, utilizando la restricción RS (restricción específica de LDR-n) se tiene la existencia de Natal que Ma+1RNa, lo cual, de acuerdo a las reglas V + y V •, implica que V (Na, Z ) = 1 y V (Na, Z) = 0, lo cual es imposible. Por lo tanto, +Z → •Z es (n+1)-válida cuando el tipo de • es mayor o igual que el tipo de Z.

Proposición 5.3 (Validez de LER-n y LDR-n). Para n ≥ 1 y X una fórmula de profundidad-n. Si X es un teorema de LR-n entonces X es n- válida.
Prueba. Supóngase que X es un teorema de LR-n, se prueba que X es n-válida por inducción sobre la longitud L de la demostración de X es LR-n.
Paso base (L = 1). Si la longitud de la demostración de X en LR-n es uno, entonces X es un axioma de LR-n, lo cual, por la proposición 5.2, significa que X es n-válida.
Paso de inducción. Como hipótesis inductiva se tiene que para cada fórmula Y, si Y es un teorema de LR-n y la longitud de la demostración de Y tiene longitud menor que L (donde L ≥ 1), entonces Y es n-válida. Si X es un teorema de LR-n y la longitud de la demostración de X es L, entonces X es un axioma de LR-n ó X es consecuencia de aplicar modus ponens en pasos anteriores de la demostración. En el primer caso se procede como en el caso base. En el segundo caso se tienen en LR-n, para alguna fórmula Y , demostraciones de Y y de Y → X, donde la longitud de ambas demostraciones es menor que L; utilizando la hipótesis inductiva se infiere que Y y Y → X son n-válidas, y por la proposición 5.1, numeral 3, resulta que X es n-válida.

Proposición 5.4 (Teoremas de LR en LR-n). Para cada fórmula X. X es un teorema de LR si y sólo si existe t ≥ 1 tal que para cada n ≥ t, X es un teorema de LR-n.
Prueba. Supóngase que X es un teorema de LR, por lo que X es consecuencia de un número finito de axiomas de LR, pero los axiomas de LR son los axiomas de los sistemas LR-n, por lo que debe existir un t tal que todos los axiomas utilizados en la prueba de X sean axiomas de LR-t, resultando que X es un teorema de LR-t. Se ha probado que, si X es un teorema de LR entonces X es un teorema de LR-t, y como los axiomas de LR-t son axiomas de LR-n para n ≥ t, se obtiene que, si X es un teorema de LR entonces para cada n ≥ t, X es un teorema de LR-n. Para probar la recíproca, supóngase que X es un teorema de LR-t, lo cual significa que existe una demostración de X a partir de los axiomas de LR-t, y como los axiomas de LR-t son axiomas de LR, entonces la demostración de X en LR-t también es una demostración de X en LR, por lo tanto, X es un teorema de LR.

Proposición 5.5 (Validez de LER y LDR). Para cada fórmula X. Si X es un teorema de LR entonces X es válida.
Prueba. Supóngase que X es un teorema de LR y que X es una fórmula de profundidad-p arbitraria. Por la proposición 5.4 resulta que existe t ≥ 1 tal que para cada n ≥ t, X es un teorema de LR-n, lo cual, según la proposición 5.3, significa que para cada n ≥ t, X es n-válida.
Si X no es válida, entonces existe un modelo M en el cual X es falsa, es decir, V (Ma, X) = 0 donde Ma es el mundo actual, el cual es de profundidad- a, con a ≥ p, por lo que el modelo M es de profundidad-a, resultando que X no es a-válida, y como para cada n ≥ t, X es n-válida, entonces a < t. Pero si a < t entonces todo a-modelo es un t-modelo, resultando que X no es t-válida, lo cual es imposible. Por lo tanto, X es válida.

6 Completitud
Definición 6.1 (Extensión consistente y completa). Una extensión de un sistema deductivo se obtiene alterando el conjunto de axiomas de tal manera que todos los teoremas del sistema sigan siendo teoremas y que el lenguaje de la extensión coincida con el lenguaje del sistema deductivo. Una extensión es consistente si no existe ninguna fórmula X tal que tanto X como ∼X sean teoremas de la extensión. Un conjunto de fórmulas es inconsistente si de ellas se derivan Z y ∼Z para alguna fórmula Z. Una extensión es completa si para toda fórmula X, del lenguaje de la extensión, o bien X o bien ∼X es teorema de la extensión.
Proposición 6.1 (Extensión consistente de LER-n y de LDR-n).
1. Para cada n ≥ 1, LR-n es consistente.
2. LR es consistente.
3. Si E una extensión de LR-n, X es una fórmula de profundidad-n que no es teorema de E, y Ex es la extensión de LR-n obtenida añadiendo ∼X como nuevo axioma a E, en tonces Ex es consistente.
Prueba. Supóngase que LR-n no fuese consistente, por lo que debe existir una fórmula X de profundidad-n tal que tanto X como ∼X sean teoremas. Entonces, por la proposición 5.3, tanto X como ∼X son fórmulas n-válidas, pero esto es imposible, ya que si ∼X es una fórmula n-válida, entonces para todo n-modelo (S, Ma, RA, V ) se tienen V (Ma, ∼X) = 1, es decir, según V∼, V (Ma, X) = 0, por lo que X no puede ser n-válida, lo cual no es el caso. Por lo tanto, LR-n es consistente.
Para la parte 2, si LR no es consistente, entonces existe una fórmula X tal que tanto X como ∼X son teoremas de LR. Pero las demostraciones de X y ∼X en LR son sucesiones finitas de fórmulas, por lo que cada demostración contiene casos particulares de un número finito de axiomas de LR. Por lo que debe existir un n suficientemente grande para que todos estos axiomas utilizados sean axiomas de LR-n, resultando que LR-n es inconsistente, lo cual, según la parte 1, no es el caso. Por lo tanto, LR es consistente.
La parte 3 es un resultado bastante conocido, para detalles ver [16, 17].

Proposición 6.2 (Extensión consistente y completa).4 Si E es una extensión consistente de LR-n (o de LR), entonces existe una extensión consistente y completa de E.
Prueba. Es una construcción estándar conocida como el lema de Lindenbaum, para detalles ver [16, 17].

Proposición 6.3 (Consistencia +-subordinada). Sean Y una fórmula de tipo-t, con t ≤ n, y Z1, . . . , Zk fórmulas de profundidad-a, con a ≤ t. Si {+Z1, . . . , +Zk, •Y } es consistente en LR-(n + 1), entonces {Z1, . . . , Zk, Y } es consistente en LR-n.
Prueba. Supóngase que {Z1 , . . . , Zk, Y} es inconsistente en LR-n, por lo que existe una fórmula W tal que, a partir de {Z1 , . . . , Zk, Y } se infieren W y ∼W en LR-n; utilizando LCP resulta que (Z1 ∧ . . . ∧ Zk∧ Y ) → (W ∧∼W ) es un teorema de LR-n, y, por LCP , en LR-n resulta ∼(Z1∧ . . . ∧ Zk∧ Y), lo cual, por LCP , significa (Z1 ∧. . . ∧Zk) →∼Y . Como esta fórmula es de tipo-t, utilizando A×+ resulta que +((Z1 ∧. . .∧Zk) →∼Y) es derivable en LR-(n+1) como a ≤ t, por MP+< y MP+= se infiere +(Z1 ∧ . . . ∧ Zk) → +∼Y . Como Z1, . . . , Zk son de profundidad-a, con a ≤ n, entonces, por la proposición 2.1, numeral 2, resulta que (+Z1 ∧ . . . ∧ +Zk) → +(Z1 ∧ . . . ∧ Zk) es un teorema de LR-(a + 1) y de LR-(n + 1), por lo que, utilizando LCP, se infiere (+Z1 ∧ . . . ∧ +Zk) → + ∼ Y en LR-(n + 1), lo cual, por LCP y la definición de posibilidad, equivale a ∼ (+Z1 ∧ . . . ∧ +Zk∧ •Y), por lo que {+Z1, . . . , +Zk, •Y} es inconsistente en LR-(n + 1). 
Definición 6.2 (+-subordinado). Para 1 ≤ p ≤ n, si E es una extensión consistente y completa de LR-n, entonces Ep= {X ∈ E : X es de profundidad- p} es un encajado de E, y se dice que Ep es de profundidad-p. Cuando p < n, se dice que Ep es encajado de Ep+1. En se identifica con E.
Sean E y F extensiones consistentes y completas de LR-n, con 1 ≤ p < n. Se dice que Fp es +-subordinado de Ep+1 si y solamente si existe una fórmula Y de tipo-p tal que •Y está en Ep+1, y, además, para cada fórmula Z de tipo-p, tal que +Z está en Ep+1, se tiene que Y y Z están en Fp. Se dice que F es +-subordinado de E cuando Fn−1 es +-subordinado de En.
Proposición 6.4 (Extensión +-subordinada consistente y completa).
1. Para 1 ≤ p ≤ n, si E es una extensión consistente y completa de LR-n, entonces Ep es una extensión consistente y completa de LR-p.
2. Para 1 ≤ p < n, E una extensión consistente y completa de LR-n y X una fórmula de tipo-p, si •X está en Ep+1, entonces existe una extensión consistente y completa F de LR-n tal que X ∈ Fp y Fp+- subordinada de Ep+1.
3. Si 1 ≤ p < n y E una extensión consistente y completa de LR-n, entonces existe una extensión consistente y completa F de LR-n tal que Fp+-subordinada de Ep+1 cuando + es de tipo-r y p ≤ r.
4. Si 1 < n y E una extensión consistente y completa de LR, entonces existe una extensión consistente y completa F de LR tal que Fn−1+- subordinada de En cuando + es de tipo-r y n − 1 ≤ r.
Prueba. Para la parte 1, sea E una extensión consistente y completa de LR-n, y sea Ep un encajado de Ep+1. Si Ep es inconsistente entonces existe una fórmula Z tal que tanto Z como ∼ Z son derivables en Ep, y como Ep está incluido en E, resulta que tanto Z como ∼ Z son derivables en E, es decir, E es inconsistente, lo cual no es el caso. Por lo tanto, Ep es consistente. Sea X una fórmula de profundidad-t, con 1 ≤ t ≤ p, como E es completa entonces X ∈ E ó ∼X ∈ E, al ser X y ∼X de profundidad-t y Ep un encajado de Ep+1, por definición, se infiere que X ∈ Ep ó ∼ X ∈ Ep , es decir, Ep es completa.
Para la parte 2, sea X una fórmula de tipo-p tal que la fórmula •X esté en Ep+1. Sea EX= {X} ∪ {Z : +Z está en Ep+1}, como por la parte 1, Ep+1 es consistente en LR-(p + 1), entonces, por la proposición 6.3, EX también es consistente en LR-p, es decir, la unión de LR-p con EX es una extensión consistente de LR-p. Utilizando la proposición 6.2, se construye una extensión consistente y completa F de LR-p la cual incluye a EX. Como X está en EX, también está en F, y como X es de tipo-p, resulta que X está en Fp. Si W es de tipo-p y +W está en Ep+1, por definición, W está en EX, por lo que W está en F, y al ser W de tipo-p, también está en Fp. Por lo tanto, Fp es +-subordinado de Ep+1.
La parte 3, en el sistema LER-n, es consecuencia de la parte 2, al tener en cuenta que + es de tipo-r y p ≤ r, por A×R, en LER-2 se tiene •(Q → Q), donde Q es una fórmula atómica, y por A×R resulta • • (Q → Q) en LER-3, y continuando de esta manera se construye una fórmula Z de tipo-p tal que •Z está en LER-(p + 1).
La parte 3, en el sistema LDR-n, es consecuencia de la parte 2, al tener en cuenta que, por A×+, en LDR-2 se tiene +(Q → Q), donde Q es una fórmula atómica, y como + es de tipo-r y p 6 r, por A×S, resultaría •(Q → Q), de igual manera resulta • • (Q → Q) en LDR-3, y continuando de esta manera se construye una fórmula Z de tipo-p tal que •Z está en LDR-(p + 1).
La parte 4 se prueba de igual forma que la parte 3.

Proposición 6.5 (Propiedades de la +-subordinación). Para 1 ≤ p < n − 1 y 1 ≤ q ≤ n−1, sean E, F y G extensiones consistentes y completas de LR-n.
1. Si Fp+1 es +2-subordinado de Ep+2y Gp es +1-subordinado de Fp+1, entonces Gp es +1-subordinado de Ep+1.
2. Si Fp+1 es +2-subordinado de Ep+2y Gp es +1-subordinado de Ep+1, entonces Gp es +1-subordinado de Fp+1.
3. Fp es +-subordinado de Fp+1 cuando + es de tipo-r y p ≤ r, y F es una extensión consistente y completa de LER-n
4. Si Gn−1 es +-subordinado de Fn, entonces, para cada q, se tiene que Gq es +-subordinado de Fq+1 cuando + es de tipo-r y 1 ≤ q ≤ r.
5. Para cada E, existe F tal que Fq es +-subordinada de Eq+1 cuando + es de tipo-r y q ≤ r.
Prueba. Para la parte 1 supóngase que Gp es +1-subordinado de Fp+1 y Fp+1 es +2-subordinado de Ep+2. Como Gp es +1-subordinado de Fp+1, entonces existe en Fp+1 una fórmula •1Z tal que Z está en Gp y Z es de tipo-p. Si •1Z no está en Ep+2, entonces al ser una extensión completa, ∼•1Z si debe estarlo, además, por A×T , se tiene que −2¬1Z→ •1Z está en Ep+2, por lo que ∼−2¬1Z, es decir, +2+1∼Z de tipo-(p + 2) también está en Ep+2, y al ser Fp+1 +2 -subordinado de Ep+2 resulta que +1 ∼ Z está en Fp+1, lo cual significa que ∼ •1Z está en Fp+1, pero esto es imposible ya que Fp+1 es consistente. Por lo que •1Zestá en Ep+2, y como •Z es de tipo-(p + 1), entonces también está en Ep+1.
Sea W una fórmula de tipo-p tal que +1W está en Ep+1, es decir, ∼•1 ∼W está en Ep+1 y también en Ep+2; utilizando A×T −2¬1∼W → •1∼W resulta que ∼−2¬1∼W está en Ep+2, por lo que +2+1 W está en Ep+2, y como es +2-subordinado de Ep+2, se infiere que +1W está en, como, además, Gp es +1-subordinado de Fp+1, entonces W está en Gp. En resumen, existe una fórmula •1Z en Ep+1 tal que para cada fórmula +1 W en Ep+1 se tiene que Z y W están en Gp , y, por lo tanto, Gp es +1-subordinado de Ep+1.
Para la parte 2 supóngase que Fp+1 es +2-subordinado de Ep+2 y Gp es +1-subordinado de Ep+1. Como Gp es +1-subordinado de Ep+1, entonces existe en Ep+1 una fórmula •1Z tal que Z está en Gp y Z es de tipo-p. Como •1Z está en Ep+1, es decir, −1 ∼ Z está en Ep+1 y también en Ep+2, utilizando A×E−1∼Z → ¬2+1∼Z resulta que ¬2+1 ∼Z está en Ep+2, lo cual significa que +2 •1Z está en Ep+2, y como Fp+1 es un +2-subordinado de Ep+2, entonces •1Z está en Fp+1.
Supóngase que +1W está en Fp+1 con W de tipo-p. Si +1 W no está en Ep+1, entonces ∼+1W está en Ep+1, es decir, −1W está en Ep+1, y también en Ep+2; utilizando A×E −1W→ ¬2+1 W, se infiere que ¬2+1 W está en Ep+2, o sea que +2∼+1 W está en Ep+2, pero al ser Fp+1+2-subordinado de Ep+2 se tiene que ∼+1W está en Fp+1, lo cual es imposible ya que Fp+1 es consistente, y, por lo tanto, +1W está en Ep+1, y como Gp es +1-subordinado de Ep+1, entonces W está en Gp. Se concluye que, para cada +1W en Fp+1 resulta que W está en Gp. En resumen, existe una fórmula •1Z en tal que para cada fórmula +1W en se tiene que Z y W están en Gp, y, por lo tanto, Gp es +1-subordinado de Fp+1.
Para la parte 3, en el sistema LER-n sea F una extensión consistente y completa de LER-n, y sea X de tipo-p, con p < n − 1, un axioma de CP , por lo que en LER-p se tiene X, y por A×A× en LER-(p + 1) también se tiene X, y como + es de tipo-r y p ≤ r, por A×R, se tiene X → •X, derivándose •X, por lo que X y •X están en F, resultando que •X está en Fp+1 y X está en Fp. Supóngase que +W está en Fp+1, con W de tipo-p, por A×R en Fp+1 se tiene ∼W → •∼W Fp+1, es decir, +W → W , resultando que W también está en Fp+1, y como W es de tipo-p, entonces W está en Fp. Por lo tanto, Fp es +-subordinada de Fp+1.
Para la parte 4, supóngase que Gn−1 es +-subordinado de Fn donde 1 < n, + es de tipo-r y n − 1 ≤ r. Si la conclusión fuese falsa, debe existir un q máximo tal que, q < n − 1 ≤ r y Gq no es +-subordinado de Fq+1.
En el caso del sistema LER-n se sabe que Q → Q, donde Q es una fórmula atómica, está en LER-1, por A×R, •(Q → Q) está en LER-2, resultando que •(Q → Q) está en F2 y Q → Q está en G1, de nuevo por A×R, • • (Q → Q) está en F3 y •(Q → Q) está en G2, y continuando de esta manera se construye una fórmula Z de tipo-q tal que •Z está en Fq+1 y Z está en Gq.
En el caso del sistema LDR-n se sabe que Q → Q donde Q es una fórmula atómica está en LDR-1, por A×+, +(Q → Q) está en LDR-2, y por A×S, •(Q → Q) está en LDR-2, y de nuevo por A×+ y A×S, • • (Q → Q) está en LDR-3 y •(Q → Q) está en LDR-2, y continuando de esta manera se construye una fórmula Z de tipo-q tal que •Z está en LDR-(q + 1) y Z está en LDR-q, concluyéndose que existe una fórmula Z de tipo-q tal que •Z está en Fq+1 y Z está en Gq.
Se tiene entonces que en LR-n existe una fórmula Z de tipo-q tal que •Z está en Fq+1 y Z está en Gq, y como Gq no es +-subordinado de Fq+1, entonces debe existir una fórmula W de tipo-q tal que +W está en Fq+1 yW no esté en Gq. Si +W está en Fq+1, al ser de tipo-(q + 1) +W está en Fq+2, y también por A×T−¬ ∼ W → • ∼ W está en Fq+2, es decir, +W → + + W está en Fq+2, resultando que + + W está en Fq+2; como q es máximo tal que Gq no es +-subordinado de Fq+1, resulta que Gq+1 es +-subordinado de Fq+2, y entonces +W está en Gq+1, y se sabe por la parte 3 que Gq es +-subordinado de Gq+1, por lo que W está en Gq, lo cual no es el caso. Por lo tanto, para cada q, con 1 ≤ q < n, se tiene Gq es +-subordinado de Fq+1, donde 1 < n.
Para la parte 5, en los sistemas LER-n y LDR-n, como se muestra en la parte 4, existe X de tipo-q tal que •X está en Eq+1 cuando + es de tipo- r y q ≤ r; por la proposición 6.4, numeral 2, se infiere la existencia de una extensión consistente y completa F tal que Fq es +-subordinada de Eq+1.

Proposición 6.6 (Construcción de un n-modelo). Si E′ es una extensión consistente de LR-n, entonces existe un n-modelo en el cual todo teorema de E′ es verdadero.
Prueba. Se define el candidato a n-marco (Sn, M En, RA) de la siguiente manera: sean E, F, G, . . ., extensiones consistentes y completas de E′ (En la inicial y las demás subordinadas), presentadas en las proposiciones 6.2 y 6.4. A cada extensión F, es decir, Fn, se le asocia un mundo posible MF, es decir, M Fn, y a cada extensión encajada Fk de F se le asocia un mundo posible encajado M Fk de MF, sean Sn el conjunto de tales mundos posibles y MEn el mundo actual. Las relaciones de accesibilidad R del conjunto RA se construyen así: M Ft+1RM Gt si y solamente si Gt es +-subordinado de Ft+1.
Para afirmar que (Sn, M En, RA) es un n-marco, se deben garantizar las correspondientes restricciones. La restricción RM a se encuentra garantizada por la proposición 6.2, la restricción RE < se encuentra garantizada por la definición de encajado y la proposición 6.4 numeral 1, RA por la definición de +-subordinado, RAE < por la proposición 6.5, numeral 4, RR por la proposición 6.5, numeral 3, RE por la proposición 6.5, numeral 2, RT por la proposición 6.5, numeral 1, y RS por la proposición 6.5, numeral 5.
Asociado al n-marco (Sn, M En, RA) se define el candidato a n-modelo M = (Sn, M En, RA, V) sobre las fórmulas de LR-n haciendo para cada M Fk en Sn y para cada fórmula X de tipo-t donde 1 ≤ t ≤ k ≤ n, V (M Fk, X) = 1 si X está en Fk, y V (M Fk, X) = 0 si ∼X está en Fk, donde Fk es la extensión consistente y completa asociada a M Fk. Nótese que V es una relación funcional por ser Fk consistente y completa. Ahora bien, ya que Fk es consistente, entonces V (M Fk, X) ≠ V (M Fk, ∼X) y, por lo tanto, V (M Fk, X) = 1 ⇔ V (M Fk, ∼ X) = 0, por lo que se satisface la definición V ∼. Para afirmar que M es un n-modelo, se debe garantizar que para cada uno de los conectivos, V satisface la definición de valuación.
Para el caso del condicional, sea X → Y una fórmula de tipo-t donde 1 ≤ t ≤ k ≤ n. Utilizando LCP se tiene la siguiente cadena de equivalencias: V (M Fk, X → Y) = 0, es decir, ∼ (X → Y) está en Fk, o sea que X∧ ∼ Y está en Fk, resultando que X y ∼ Y están en Fk, lo cual significa que V (M Fk, X) = 1 y V (M Fk, Y) = 0, por lo que se satisface la definición V →. Para los demás conectivos binarios se procede de igual forma.
Para el caso de la regla V +, donde 1 ≤ p < n, M es un mundo asociado a Fp+1, MGp es un mundo asociado a Gp y Z es una fórmula de tipo-p. Supóngase que V (M ,+Z) = 1, por lo que +Z está en . Si MFp+1 RM Gp, entonces Gp es subordinada de Fp+1 y Z está en Gp, resultando que V (M Gp, Z ) = 1. Se ha probado de esta manera que V (M ,+Z) = 1 ⇒ (∀M Gp ∈ Sn)(MFp+1 RM Gp ⇒ V (M Gp, Z ) = 1).
Para probar la recíproca, supóngase que (∀M Gp∈ Sn)(MFp+1 RM Gp⇒ V (M Gp, Z) = 1). Si V (MFp+1 ,+Z) = 0, entonces al ser MFp+1 el mundo asociado a la extensión consistente y completa Fp+1 resulta que ∼+Z está en Fp+1, por lo que ∼+∼∼Z, es decir, •∼Z está en Fp+1. Por la proposición 6.4, numeral 2, existe una extensión consistente y completa Gp subordinada de Fp+1 tal que ∼Z está en Gp. Como MGp es el mundo asociado a Gp, entonces MFp+1 RM Gp, lo cual, por el supuesto inicial implica V (M Gp, Z ) = 1, es decir, Z está en Gp, resultando que Gp es inconsistente, lo cual no es el caso. Por lo tanto, V (MFp+1 ,+Z) = 1. Se ha probado de esta manera que (∀M Gp∈ Sn)(MFp+1 RM Gp⇒ V (MGp, Z ) = 1) ⇒ V (MFp+1 ,+Z ) = 1.
Para el caso de la regla VP, sea X una fórmula de profundidad-p, con 1 ≤ p ≤ n, M Fp, el mundo asociado a la extensión Fp, y para cada t, con p ≤ t ≤ n, sea MFt el mundo asociado a la extensión Ft. V (MFp, X) = 1 si y sólo si X está en Fp, como X es de profundidad-p, lo anterior es equivalente a X está en Ft donde p ≤ t ≤ n, pero X está en Ft si y sólo si V (MFt, X) = 1. Por lo tanto, para cada t, con p ≤ t ≤ n, V (MFp, X) = V (MFt, X).
Con base en el análisis anterior, y teniendo en cuenta la forma en que se construye el modelo, se concluye finalmente que V es una valuación, y, por lo tanto, M es un n-modelo.
Para finalizar la prueba, sea X un teorema de E′ , por lo que X está en En. Por lo tanto, utilizando la definición de V , resulta que V (M En, X) = 1, es decir, X es verdadera en el n-modelo M = (Sn, MEn, R, V).

Proposición 6.7 (Completitud de LER-n y de LDR-n). Para cada fórmula X de profundidad-n, con n ≥ 1. Si X es n-válida entonces X es un teorema de LR-n.
Prueba. Sea X una fórmula de LR-n. Si X no es un teorema, entonces, por la proposición 6.1, numeral 3, la extensión E′, obtenida añadiendo ∼X como nuevo axioma, es consistente. Así pues, según la proposición 6.6, existe un n-modelo M tal que todo teorema de E′ es verdadero en M, y como ∼X es un teorema de E′, entonces ∼X es verdadero en M , es decir, X es falso en M, y, por lo tanto, X no es n-válida. Se ha probado de esta forma que, si X no es un teorema de LR-n entonces X no es n-válida, o dicho de otra manera, si X es n-válida entonces X es un teorema de LR-n.

Proposición 6.8 (Completitud de LER y de LDR). Para cada fórmula X, si X es válida entonces X es un teorema de LR.
Prueba. Supóngase que X es válida y que X es de profundidad-p arbitraria, por lo que en la construcción de un modelo refutador de la fórmula X, resulta una cadena inconsistente de mundos posibles C = MaMa−1 . . . Mm para algún m, donde a ≥ p ≥ 1 y Ma es el mundo actual de profundidad-a, lo cual significa que X no puede ser refutada por un a-modelo, es decir, X es a- válida. Por la proposición 6.7 se infiere que X es un teorema de LR-a, y como los axiomas de LR-a son axiomas de LR, se concluye que X es un teorema de LR.
Proposición 6.9 (Caracterización semántica de LER-n, LDR-n, LER, LDR). Sea X una fórmula de profundidad-n.
1. X es n-válida si y solamente si X es un teorema de LR-n.
2. X es válida si y sólo si X es un teorema de LR.
Prueba. La primera parte es consecuencia de las proposiciones 5.3 y 6.7, la segunda se sigue de las proposiciones 5.5 y 6.8.

7 Conclusiones
Cuando el razonador es lo suficientemente fuerte (el tipo de + mayor o igual que el tipo de X), con el axioma A×R se garantiza que las certezas sean verdaderas: +X 7→ X5, que las imposibilidades sean falsas: ¬X 7→∼X, que las verdades sean posibles: X 7→ •X, que las falsedades sean refutables: ∼X 7→ −X, y, además, la contraparte semántica de este axioma, es decir, la restricción RR, permite refutar las recíprocas; con el axioma A×S se garantiza que las certezas sean posibles: +X 7→ •X, que las imposibilidades sean refutables: ¬X 7→ −X, que las contradicciones sean refutables: −(X∧∼ X), y, además, la contraparte semántica de este axioma, es decir, la restricción RS, permite refutar las recíprocas.
En los sistemas LER-n, con el axioma A×T , al cual semánticamente le corresponde la restricción RT , se garantiza que refutar una certeza es una imposibilidad: ¬2 −1 X ↔ +1X, y que la posibilidad de una fórmula imposible es una imposibilidad: ¬2 •1 X ↔ ¬1X. Con el axioma A×E, al cual semánticamente le corresponde la restricción RE, se garantiza que la posibilidad de una fórmula posible es una certeza: +2 •1X↔ •1X, y que refutar una fórmula refutable es una certeza: +2 −1X↔ −1X.
Con el axioma MP+=, al cual semánticamente le corresponde la regla V+, se garantiza que si un condicional y su antecedente son certezas, entonces su consecuente también es una certeza cuando en X → Y el antecedente y el consecuente son del mismo tipo: [+(X → Y) ∧ +X] → +Y; y que si una disyunción es certeza y un disyunto es refutable, entonces el otro disyunto es posible: [+(X ∨ Y ) ∧−X] → •Y cuando los disyuntos son del mismo tipo. Con el axioma MP+<, al cual semánticamente le corresponde la regla V+ y a la restricción RAE <, se garantiza que si un condicional y su antecedente son certezas, entonces su consecuente también es una certeza cuando en X → Y el tipo del antecedente es menor que el tipo del consecuente: [+(X → Y ) ∧ +X] → +Y ; y que si una disyunción es una certeza y el disyunto de tipo superior es refutable, entonces el otro disyunto es posible: [+(X ∨ Y ) ∧ −Y ] → •X.
Tal como lo presenta Chellas en Modal logic: an introduction [20], el sistema de lógica modal S5 puede ser construido adicionando al cálculo proposicional clásico los axiomas A×T y A×E restringidos a un mismo razonador, los axiomas MP +< y A×R sin restricciones y la regla de construcción de certezas, de X se infiere +X, presentada en la proposición 5.1 y el axioma A×+. Por esta razón, los sistemas LER-n, con n ≥ 3 y LER, pueden ser considerados como extensiones del sistema S5 generalizado y con diversos tipos de restricciones, las cuales se reflejan en la semántica de mundos posibles como restricciones en la profundidad de los modelos y de los mundos, es decir, como restricciones en la longitud de las cadenas de mundos posibles, en la relación de accesibilidad entre ellos y en el lenguaje asociado a los mismos. Por otro lado, se sabe que al quitar de S5 algunos de los axiomas restringidos A×R, A×T y A×E, se generan diversos sistemas intermedios conocidos como K, KT, K4, K 5, KT 4, KT 5, K 45; observando la presentación de los axiomas, de las reglas semánticas y la estructura de las pruebas presentadas para los sistemas LER-n, se puede concluir que, asociado a cada uno de estos sistemas intermedios, se encuentra una jerarquía naturalmente obtenida a partir de los sistemas LER-n.
De manera similar, los sistemas LDR-n, con n ≥ 3 y LDR, pueden ser considerados como extensiones del sistema KD45 generalizado y con diversos tipos de restricciones; y también se puede concluir que, asociado a cada uno de los sistemas intermedios KD, KD4 y KD5, se encuentra una jerarquía naturalmente obtenida a partir de los sistemas LDR-n.
Observar que las restricciones en el lenguaje de los sistemas (al limitar la aplicabilidad de las reglas de creencia), y las restricciones en el tipo de los razonadores (al limitar las consecuencias del conocimiento de algunos razonadores), le imponen al problema de la omnisciencia lógica ciertos límites. Por ejemplo, en el sistema LR-4, un razonador de tipo-2 no siempre puede hacer inferencias cuando se involucran fórmulas de tipo-3, mientras que un razonador de tipo-3 o superior si puede hacerlas, sin embargo, ningún razonador puede hacer inferencias sobre fórmulas de tipo-4.
Finalmente, es importante señalar que las restricciones impuestas, por los axiomas MP+< y MP+=, pueden ser relajadas para los razonadores con suficiente capacidad deductiva, es decir, del tipo adecuado, adicionando MP+>: +(A → B) → (+A → +B) es un axioma de LR-(n + 1), donde A es de tipo-a, B es de tipo-b, + es de tipo-r, 1 ≤ b < a ≤ n y a ≤ r; este axioma es validado semánticamente por las restricciones RE>; (restricción de encaje externo): si R es de tipo-r, r > p, Kp+1RFp y Kp+2; existe, entonces existe Fp+1, y RAE> (restricción de accesibilidad encajada externa): si R es de tipo-r, r > p, Kp+1RFp, Kp+2 existe Fp+1y existe, entonces Kp+2RFp+1.
Notas al pie
1 En los sistemas LER-n, + es un operador de certeza en el sentido de saber, mientras que en LDR-n, + es un operador de certeza en el sentido de creer, donde saber es creencia cierta.
2 En lo que sigue se entiende que +, •, − y ¬ son los operadores de conocimiento de tipo-r asociados al razonador R de tipo-r.
3 Sea T una fórmula de tipo-t y Np un mundo de profundidad-p. V (Np, T) no se encuentra definida cuando t > p, es decir, V (Np, T) sólo se encuentra definida si la fórmula T es de profundidad-p. Es en este sentido que cada mundo tiene asociado un lenguaje.
4 Para llegar a las pruebas de completitud en las proposiciones 6.7 y 6.8 se siguen las directrices dadas por Henkin en The completeness of the first order functional calculus [18] y Kaplan en Review of Kripke [19] para probar la completitud de la lógica de primer orden y del sistema modal T .
5 X 7→ Y significa que X → Y , pero no siempre Y → X.
Referencias
1. Jaakko Hintikka, Vincent F. Hendricks, John Symons. Knowledge and Belief - An Introduction to the Logic of the Two Notions, ISBN 9781904987086. College Publications, 2005. Referenciado en 83 [ Links ]
2. Saul A. Kripke. Semantical analysis of modal logic. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, ISSN 0044-3050, 9, 1963. Referenciado en 83 [ Links ]
3. Jaakko Hintikka. Impossible possible worlds vindicated. Journal of Philosophical Logic, ISSN 0022-3611, 4(3), 475-484 (1975). Referenciado en 83 [ Links ]
4. Kwang Mong Sim. Epistemic logic and logical omniscience: a survey. International journal of intelligent systems, ISSN 0884-8173, 12, 57-81 (1997). Referenciado en 83 [ Links ]
5. Max J. Cresswell. Logics and languages, ISBN 0416769500. Egmont Childrens Books, 1973. Referenciado en 83 [ Links ]
6. Nicholas Rescher, Robert Brandon. The logic of inconsistency, ISBN 0631115811. Rowman and Littlefield, 1979. Referenciado en 83 [ Links ]
7. Hector J. Levesque. A logic of implicit and explicit belief, En Proceedings of National Conference on Artificial Intelligence, ISBN 978-0865760806, 198-202 (1984). Referenciado en 83 [ Links ]
8. Ross Anderson, Nuel Belnap. Entailment: The Logic of Relevance and Necessity, ISBN 978-0691071923. Princeton University Press, 1, 1990. Referenciado en 84 [ Links ]
9. Gerhard Lakemeyer. Tractable meta-reasoning in propositional logics of belief. En Proceedings of the 10th international joint conference on Artificial intelligence, 1, 402-408 (1987). Referenciado en 84 [ Links ]
10. Ronald Fagin, Joseph Halpern. Belief, awareness and limited reasoning. Artificial Intelligence, ISSN 0004-3702, 34(1), 1987. Referenciado en 84 [ Links ]
11. Marco Schaerf, Marco Cadoli. Tractable reasoning via approximation. Artificial Intelligence, ISSN 0004-3702, 74(2), 249-310 (1995). Referenciado en 84 [ Links ]
12. Marcelo Finger, Renata Wassermann. Logics for approximate reasoning: Approximating classical logic "from above". En Brazilian Symposium on Artificial Intelligence, ISBN 3-540-00124-7, 2507, 21-30 (2002). Referenciado en 84 [ Links ]
13. Guilherme Rabelloa, Marcelo Finger. Approximations of Modal Logics: K and beyond. Annals of Pure and Applied Logic, ISSn 0168-0072, 152, 2008. Referenciado en 84 [ Links ]
14. Kurt Konolige. A Deduction Model of belief (Research notes in artificial intelligence), ISBN 0934613087. Morgan Kaufmann Publishers Inc, San Francisco, CA, USA , 1986. Referenciado en 84 [ Links ]
15. Dov Gabbay, John Woods. Handbook of the History of Logic, 7, Logic and the Modalities in the Twentieth Century, ISBN 9780444516220. Elsevier, 2006. Referenciado en 84 [ Links ]
16. Manuel Sierra. Sistemas multi-modales de profundidad restringida. Ingeniería y Ciencia, ISSN 1794-9165, 4(8), 175-202 (2008). Referenciado en 84, 85, 103, 104 [ Links ]
17. Walter Carnielli, Claudio Pizzi. Modalities and multimodalities, ISBN 9781402085895. Springer, 2008. Referenciado en 89, 90, 98, 100, 103, 104 [ Links ]
18. Leon Henkin. The completeness of the first order functional calculus. The journal of symbolic logic, ISSN 0022-4812, 14(3), 159-166 (1949). Referenciado en 104 [ Links ]
19. David Kaplan. Review: Saul A. Kripke, Semantical Analysis of Modal Logic I. Normal Modal Propositional Calculi. The journal of symnolic logic, ISSn 0022- 4812, 31(1), 120-122 (1966). Referenciado en 104 [ Links ]
20. Brian F. Chellas. Modal logic: an introduction, ISBN 978-0521295154. Cambridge University Press, Cambridge, 1980. Referenciado en 112 [ Links ]