Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y Ciencia
versão impressa ISSN 1794-9165
ing.cienc. v.6 n.12 Medellín jan./jun. 2010
Dinámica en sistemas de tuberías con movimientos diferentes en sus extremos
Dinâmica nos sistemas das tubulações com movimentos diferentes em suas extremidades
Dynamics in systems of pipes with different movements in its ends
Arnulfo Lúevanos-Rojas1
1 Doctor en Ingeniería, arnulfol 2007@hotmail.com, profesor-investigador, Universidad Juárez del Estado de Durango, Victoria de Durango-México.
(Recepción: 22-feb-2010. Modificación: 10-sep-2010. Aceptación: 22-sep-2010)
Resumen
En este documento se propone un método de análisis dinámico de sistemas de tuberías con movimientos diferentes en los extremos. Esta metodología toma el espectro de respuesta correspondiente a cada uno de los apoyos, y comparado con el método de respuesta simple, que utiliza una envolvente en los espectros de respuesta de los diferentes apoyos que es el clásico, en este último no son conservadores, como se puede notar en la tabla de resultados del problema considerado. Por lo tanto, la práctica usual de considerar la envolvente de espectros no será una solución recomendable. También se propone el empleo de las masas consistentes o distribuidas, y no las discretas o concentradas, como normalmente se hace, y además se apega más a la realidad.
Palabras claves: matriz de influencia, análisis modal, análisis espectral, valores y vectores característicos, factor de participacion modal, aceleración espectral y vector de coordenadas normales máximas.
Resumo
Neste original um método da análise dinâmica dos sistemas de tubulações com movimentos diferentes nas extremidades exps. Esta metodologia toma o fantasma da resposta que corresponde a cada uma das sustentações, e comparado com o método da resposta simples, que usa de cerco nos fantasma da resposta das sustentações diferentes que é clássica, neste último não seja preservativo, como pode ser observado na tabela dos resultados do problema considerado. Conseqüentemente, a prática usual considerar de cerco dos fantasma não será uma solução recommendable. Igualmente o uso das massas consistentes ou distribúıdas exps, e discreto ou concentrado lhes, como é feito normalmente, e além não é tornado unido mas à realidade.
Palavras chaves: matriz da influência, análise modal, análise espectral, valores e vetores característicos, fator da participação modal, aceleração espectral e vetor do normal coordena princípios.
Abstract
In this document a method of dynamic analysis of systems of pipes with different movements in the ends sets out. This methodology takes the response spectrum corresponding to each one of the supports, and to compare it with the method of simple answer, that it uses a surrounding one in the response spectrum of the different supports is the classic one, in this last one they are not preservative, as it is possible to be noticed in the table of results of the considered problem. Therefore, the usual practice to consider the surrounding one of spectrum will not be a recommendable solution. Also the use of the consistent masses or distributed, and not discreet or concentrated them, as normally it is made, and in addition it is become attached but to the reality.
Key words: influence matrix, modal analysis, spectral analysis, characteristic values and vectors, factor of modal participation, spectral acceleration and vector of normal coordinates principles.
1 Introducción
En el análisis de respuesta sísmica-dinámica de sistemas estructurales con apoyos o soportes múltiples sujetos a excitaciones no uniformes en sus apoyos, la literatura es escasa. Haciendo una breve resenã histórica de los avances al respecto, este tipo de sistemas ha sido estudiado por diversos investigadores en el pasado usando básicamente dos métodos para estudiar la respuesta sísmica: análisis de historia en el tiempo y análisis del espectro de respuesta de piso. El primer método consiste en la obtención de la respuesta de la EP (Estructura Principal) sola, en los puntos de contacto de la ES (Estructura Secundaria). Esta respuesta es usada como excitación en la ES en un análisis posterior e independiente, lo cual significa que la interacción entre la EP y la ES no es considerada, este es el caso del trabajo pionero de Kassawara y Peck [1]. El segundo método consiste en conocer el espectro de respuesta en los puntos de conexión entre la EP y la ES usando para esto sólo la respuesta de la EP. Los primeros estudios, entre los que se puede citar a Amin, Hall, Newmark y Kassawara [2]; Shaw [3] y Vashi [4], entre otros, no consideraban tampoco la interacción entre los sistemas. A partir de un trabajo de Lee y Penzien [5], quienes usaron un modelo de proceso estocástico estacionario de terremoto para estimar la participacion de la correlación modal en la respuesta estructural, Der Kiureghian e Igusa [6] estudian la influencia de la configuración entre los modos en la respuesta de sistemas EP+ES considerando además la interacción entre ambos. En este estudio, el autor muestra que, dependiendo de las razones de masa y frecuencia, hay muchas situaciones prácticas donde la interacción entre la EP y la ES puede ser altamente significativo en la respuesta estructural, y, por lo tanto, debe ser incluido en el análisis. El concepto de incluir la interacción es adoptado también por Crandall y Mark [7]; Amin, Hall, Newmark y Kassawara [2]; Pickel [8]; Der Kiureghian, Sackman y Nour Omid [9]. Asfura y Der Kiureghian [10], usando vibraciones estocásticas estacionarias, estudiaron el comportamiento de sistemas EP-ES con configuraciones generalizadas de conexión entre la EP y la ES, determinando un espectro de piso cruzado para los puntos de apoyo del sistema considerando la interacción entre ambos. Estos espectros se usan para el disenõ de la ES. Otros autores, como Suárez y Singh [11, 12, 13], Falsone, Muscolino y Ricciardi [14, 15], han desarrollado técnicas similares a través de análisis completos modelando la EP junto con la ES. Para estimar la respuesta en el tiempo de sistemas complejos de varios grados de libertad que incluyen sistemas EP+ES, Valladares [16] desarrolló un método numérico de obtención de la matriz de correlación cruzada de estructuras sometidas a terremotos simulados como procesos estocásticos. En este estudio se usó un modelo de terremoto no estacionario en amplitud y frecuencia, desarrollado por Aravena y Crempien [17].
En cuanto al disenõ de instalaciones industriales y nucleares, el estudio de su comportamiento sísmico-dinámico constituye una etapa fundamental dentro de su disenõ, puesto que existe la probabilidad de que se presenten excitaciones por efectos sísmicos durante la vida útil de estas plantas, y el danõ causado por dichos efectos puede llegar a ser predominante entre las diversas solicitaciones a considerar para su disenõ. Ello obviamente será mandatorio en aquellas instalaciones que se localicen en zonas de mediana a alta sismicidad, como sucede en varias partes del mundo.
Entre las diversas instalaciones industriales o nucleares es frecuente enfrentarse con sistemas estructurales que presentan apoyos o soportes múltiples a distintas elevaciones y/o son muy extendidos en planta. Esta situación implica que las excitaciones sísmicas en sus apoyos serán distintas, ya sea porque las excitaciones en equipos a elevaciones altas generalmente son mayores que a elevaciones bajas, o bien porque en sistemas estructurales muy largos en planta se presentarían movimientos relativos entre sus apoyos por efecto de la propagación de las ondas sísmicas a través del suelo.
En cuanto a la importancia de que los sistemas de tuberías de plantas industriales y nucleares, constituye un ejemplo típico de aquellos sistemas estructurales que presentan apoyos o soportes múltiples, que a su vez interconectan diversos equipos delicados, los cuales están soportados directamente a piso o sobre estructuras especiales.
Por lo tanto, la práctica común de análisis sísmico dinámico, que usualmente considera un solo movimiento en una dirección actuando simultáneamente en todos sus apoyos y sólo a las estructuras que descansan directamente en el suelo, tratando como "apéndices" a las que se apoyan en ellas; no será confiable y deberán considerarse excitaciones diferentes en sus apoyos.
Las circunstancias anteriores conducen a la necesidad de estudiar el comportamiento sísmico-dinámico estructural con excitación múltiple en sus apoyos, que es el problema que se plantea y se discute en este trabajo, dirigiéndolo específicamente al caso de sistemas de tuberías de instalaciones industriales.
Finalmente, se hace notar que esta técnica puede aplicarse a situaciones en donde las solicitaciones dinámicas sean de naturaleza diferente a la sísmica, como puede ser el caso de excitaciones inducidas por equipo rotatorio o a sistemas de tuberías con excitación múltiple en sus apoyos.
El artículo está organizado así: en la sección 2.1 se describen las ecuaciones de movimiento de un sistema sujeto a excitación múltiple en sus apoyos. La sección 2.2 se dedica a la presentación del Método de espectro de respuesta múltiple, en cuestión. En la sección 2.3 se muestra el Método de espectro de respuesta simple, que es el clásico. En la sección 3 se considera un ejemplo de aplicación que presenta algunos resultados, respecto a la existencia de los movimientos diferentes en los apoyos. En la sección 4 se presenta la conclusión.
2 Desarrollo
2.1 Ecuaciones de movimiento de un sistema sujeto a excitación múltiple en sus apoyos
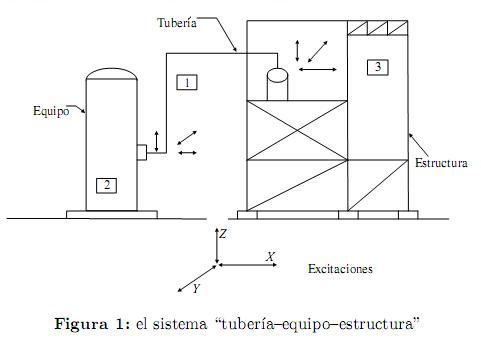
Considérese el sistema "tubería-equipo-estructura" mostrado en la figura 1, en el cual se inducen excitaciones múltiples no uniformes en los soportes de la tubería.
Las ecuaciones generales de movimiento para el sistema de tubería, antes de incluir condiciones de frontera, pueden escribirse en forma matricial como [18]
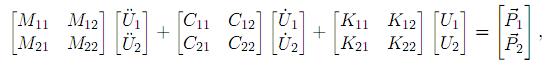
donde:
•U1 es un vector de n × 1 desplazamientos generalizados absolutos (incógnitas), correspondientes a los n grados de libertad no restringidos.
• U2 es un vector de m × 1 desplazamientos generalizados absolutos (nulos o prescritos), correspondientes a los m grados de libertad de los puntos de soporte.
• Mij, Cij, Kij son submatrices de masas, amortiguamiento y rigidez asociadas a los grados de libertad n y/o m, respectivamente.
• 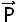 1 es un vector de n × 1 que representa las solicitaciones dinámicas asociadas a los grados de libertad n de los puntos no restringidos.
1 es un vector de n × 1 que representa las solicitaciones dinámicas asociadas a los grados de libertad n de los puntos no restringidos.
• 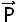 2 es un vector de m × 1 que representa las reacciones (incógnitas) asociadas a los grados de libertad m de los soportes.
2 es un vector de m × 1 que representa las reacciones (incógnitas) asociadas a los grados de libertad m de los soportes.
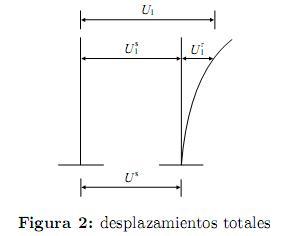
El desplazamiento total U puede expresarse como la suma del desplazamiento relativo Ur y el desplazamiento seudoestático Us que resultaría de un desplazamiento estático del soporte o apoyo según se ve en la figura 2, esto es, U = Ur + Us.
Entonces, U1 = 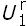 +
+ 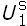 ;
; 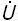 1 =
1 = 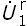 +
+ 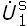 ; Ü1 =
; Ü1 = 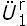 +
+ 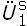 ; U2 =
; U2 = 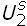 ;
; 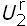 = 0;
= 0; 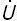 2 =
2 = 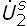 ; Ü2 =
; Ü2 = 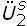 ; siendo
; siendo  la matriz de influencia seudoestática definida por
la matriz de influencia seudoestática definida por  = −
= −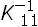 − K12. La componente dinámica de desplazamientos estará definida por
− K12. La componente dinámica de desplazamientos estará definida por 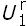 = U1−
= U1− U2. Las ecuaciones de movimiento en términos de la componente de desplazamientos dinámicos exclusivamente, resultando finalmente
U2. Las ecuaciones de movimiento en términos de la componente de desplazamientos dinámicos exclusivamente, resultando finalmente
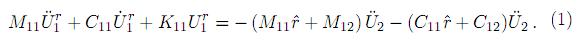
Respecto al amortiguamiento, éste es una combinación lineal de las matrices K y M; la cual implica que el sistema contendrá modos naturales clásicos, que al planear la condición de vibración libre los modos naturales coincidirán con los del sistema amortiguado, si se tienen las mismas características de inercia y rigidez.
Por otra parte, en cuanto al amortiguamiento en la excitación, se demuestra que el segundo término del lado derecho de (1) es muy pequenõ en comparación con el primero, por lo que usualmente se desprecia [19]. Además, al realizar un análisis espectral, el efecto del amortiguamiento de la excitación viene implícito en los espectros [18]. Entonces, tomando en cuenta lo anterior, (1) se puede escribir como
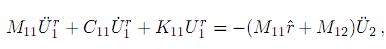
y si se sustituye  = −
= −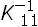 − K12 se tendrá
− K12 se tendrá
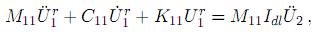
donde Idl = 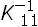 − K12−
− K12−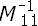 1M12, siendo Idl de orden n × m.Denótese como D a la matriz que resulta del producto M11Idl. La matriz D, de orden n × m, actuá sobre la estructura restringida y tiene un total de m columnas que representan las fuerzas resultantes de las m excitaciones actuando independientemente, con lo cual, el vector de fuerzas efectivas o equivalentes actuando cada uno de los n grados de libertad de la estructura o sistema, estará definido por [
1M12, siendo Idl de orden n × m.Denótese como D a la matriz que resulta del producto M11Idl. La matriz D, de orden n × m, actuá sobre la estructura restringida y tiene un total de m columnas que representan las fuerzas resultantes de las m excitaciones actuando independientemente, con lo cual, el vector de fuerzas efectivas o equivalentes actuando cada uno de los n grados de libertad de la estructura o sistema, estará definido por [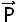 eq]n×1 = [D]n×m[Ü2]m×1. Con esto las ecuaciones de movimiento resultan
eq]n×1 = [D]n×m[Ü2]m×1. Con esto las ecuaciones de movimiento resultan
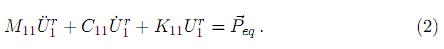
Ahora, para el caso en que el movimiento de todos los puntos de apoyo o soporte sean idénticos y definidos por la aceleración del terreno Üg(t), el vector 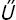 2 resultará
2 resultará
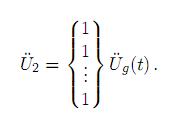
Para el caso en que p puntos de apoyo reciban una excitación aÜg(t) y los otros puntos m − p reciban una excitación bÜg(t), donde a y b son escalares, el vector de acceleraciones de los soportes Ü 2 resultará
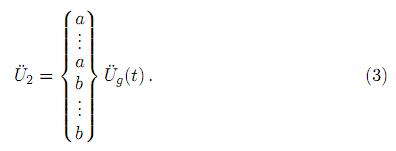
Este procedimiento puede extenderse al caso de m excitaciones arbitrarias Üm(t) en cada uno de los m soportes o apoyos, con lo cual

Con lo cual, de acuerdo a (3) y (4), se tiene
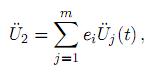
donde cada vector ei es definido unitario para el j-ésimo renglón y cero para los demás.
A partir de cada vector ei, una fuerza equivalente sobre la estructura o sistema queda definida por 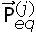 = DeiÜ(t), y la fuerza total estará dada por
= DeiÜ(t), y la fuerza total estará dada por 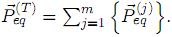
Para cada fuerza equivalente se origina un problema de respuesta dado por
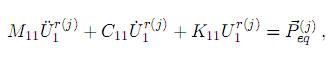
y el desplazamiento relativo (dinámico) se obtendrá a partir de
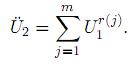
De acuerdo a lo anterior, el problema de determinar la respuesta dinámica de una estructura sujeta a m aceleraciones distintas en los m soportes o apoyos se ha descompuesto en la solución de m problemas, cada uno de los cuales corresponde al de excitación de un solo soporte [19].
Puesto que se está considerando sistemas lineales, en donde existen condiciones de ortogonalidad para matrices de rigideces K, masas M y amortiguamiento C, resulta conveniente diagonalizar el sistema de ecuaciones de movimiento transformado a un sistema de coordenadas normales modales. Para ello, al considerar el sistema (2) bajo la condición de vibración libre sin amortiguamiento, la cual puede existir en la ausencia de cualquier excitación de los soportes, se tiene [20]

Su solución está definida por 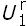 =
= 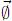 eiωt, donde ω es la frecuencia natural de vibración y
eiωt, donde ω es la frecuencia natural de vibración y 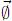 es el vector modal asociado a ω. Los valores de ω y
es el vector modal asociado a ω. Los valores de ω y 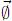 quedan determinados por la solución del siguiente problema de valores característicos
quedan determinados por la solución del siguiente problema de valores característicos

y, usualmente, sólo un número limitado de los modos más bajos del sistema necesitan ser considerados.
Con esto, las ecuaciones de movimiento del sistema, definidas por (2), se pueden diagonalizar si se transforma a un sistema de coordenadas normales modales Yn(t), definidas por
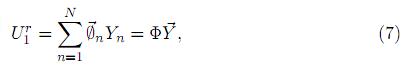
siendo Φ la matriz modal y 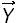 el vector de coordenadas normales.
el vector de coordenadas normales.
Sustituyendo (7) en (2), premultiplicando por la transpuesta del vector modal correspondiente al modo n y aplicando condiciones de ortogonalidad; se logra el desacoplamiento de las ecuaciones de movimiento. Resultando la ecuación correspondiente al modo n la siguiente
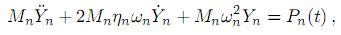
donde ηn es el porciento de amortiguamiento al modo n, siendo:
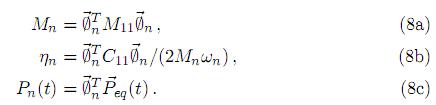
Con lo cual el problema se reduce a resolver n ecuaciones de movimiento desacopladas, similares a las que se tendrían en sistemas de un grado de libertad, cuya solución puede llevarse a cabo analítica o numéricamente.
2.2 Método de espectro de respuesta múltiple
El método de "espectro de respuesta múltiple" se ha planteado para tal efecto donde las excitaciones de cada uno de los soportes se consideran definidas por espectros de respuesta, que representan los valores máximos para los que un sistema de un grado de libertad, con frecuencia de variación y amortiguamiento especificados, responde bajo cierta excitación aplicada en un soporte.
Considerando las ecuaciones de movimiento de acuerdo al procedimiento de superposición para el caso de m excitaciones arbitrarias 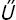 m(t), en cada uno de los m soportes o apoyos, de (2) se tiene para cada excitación
m(t), en cada uno de los m soportes o apoyos, de (2) se tiene para cada excitación
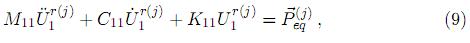
donde 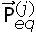 = DeiÜ(t) o bien
= DeiÜ(t) o bien

Ahora, al transformara coordenadas normales modales Yn, del sistema de movimiento (9), se obtiene, para el sistema de n grados de libertad, n ecuaciones de movimiento desacopladas del tipo
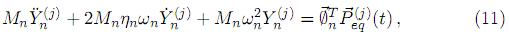
donde Mn y ηn están definidas por (8a) y (8b), siendo ωn y Øn los valores y vectores modales correspondientes al n-ésimo modo. Sustituyendo (10) en (11) y realizando algunas transformaciones se obtiene
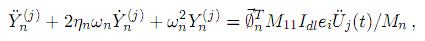
o bien
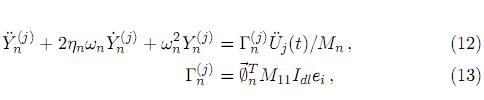
donde 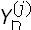 representa la respuesta modal para el n-ésimo nodo debida a la excitación del j-ésimo soporte,
representa la respuesta modal para el n-ésimo nodo debida a la excitación del j-ésimo soporte, 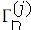 representa el "factor de participación" para el modo n-ésimo y la excitación sísmica en el j-ésimo soporte.
representa el "factor de participación" para el modo n-ésimo y la excitación sísmica en el j-ésimo soporte.
La solución de (12) se puede obtener considerando la primera integral de Duhamel [19], es decir,
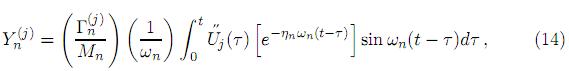
y si se denota
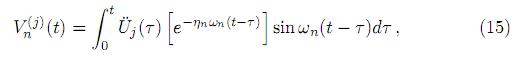
esto es
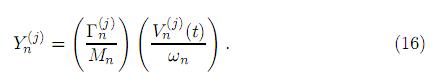
Ahora, de acuerdo al procedimiento, espectro de respuesta sísmica [18], será suficiente determinar únicamente los valores máximos de respuesta y no toda la historia completa. De (14) y (15) se observa que las respuestas máximas quedan definidas al considerar el valor máximo de la función de respuesta Vn(t), denominado "velocidad espectral" 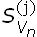 , es decir,
, es decir, 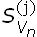 = Vn(j), y al sustituir en (16) resulta
= Vn(j), y al sustituir en (16) resulta
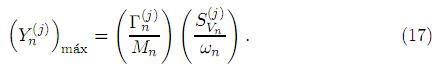
Que en términos de la "acceleración espectral" 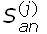 , obtenida para el n-ésimo modo a partir del "espectro de respuesta" correspondiente a la excitación del soporte j-ésimo, se obtiene
, obtenida para el n-ésimo modo a partir del "espectro de respuesta" correspondiente a la excitación del soporte j-ésimo, se obtiene 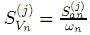 . Que al sustituir en (17) resulta
. Que al sustituir en (17) resulta
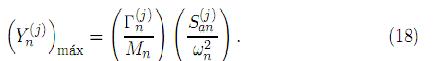
Debido a que las máximas respuestas modales debidas a cada excitación de los soportes pudieran no ocurrir simultáneamente, la respuesta modal máxima total obtenida por simple superposición modal daría una predicción bastante conservadora. Por lo que una respuesta modal máxima, basada en una consideración probabilística, puede obtenerse considerando la "ráız cuadrada de la suma de los cuadrados", procedimiento conocido como el método SRSS [19]; se tiene
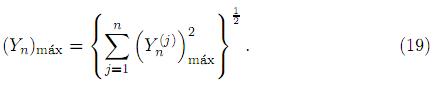
Ahora, conociendo la respuesta modal máxima (coordenada normal máxima) para el modo n-ésimo, la componente máxima de desplazamiento dinámico (relativo) para ese n-ésimo modo está definida por
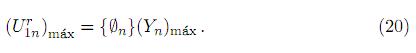
Una vez que han sido obtenidas las respuestas máximas para cada uno de los modos, el máximo de la respuesta total del sistema podrá evaluarse usando el método SRSS superponiendo la contribución de cada una de las respuestas modales, es decir,
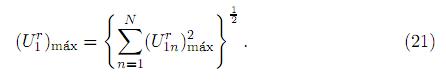
Ahora, la distribución de fuerzas, momentos y/o esfuerzos máximos para el n-ésimo modo, se pueden calcular a través de las propiedades de rigidez de la estructura.
2.3 Método de espectro de respuesta simple
El análisis de un sistema estructural con soportes múltiples, sujeto a excitaciones diferentes en cada apoyo o soporte, usando el método de espectro de respuesta simple, viene a ser el procedimiento de análisis de respuesta estándar; en donde un "espectro de respuesta simple" es similar al análisis de espectro de respuesta convencional, usando un solo espectro de respuesta de entrada, que por lo general es el espectro a la elevación mayor o un espectro amplificado (envolvente), que incluye los espectros de respuesta de todos los apoyos.
Considerando la ecuación de movimiento de acuerdo a este procedimiento, de (2) se obtiene
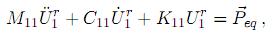
donde [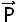 eq] n × 1= [D]n×m[Ü2]m×1.
eq] n × 1= [D]n×m[Ü2]m×1.
Ahora, para el caso en que el movimiento de todos los puntos de apoyo o soporte sean idénticos y definidos por 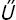 g(t), el vector
g(t), el vector 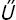 2 resultará
2 resultará
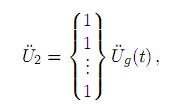
y el vector de fuerzas equivalentes será 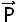 eq = M11 Idl{1}Üg(t), con lo cual, al sustituir en (21), se tiene
eq = M11 Idl{1}Üg(t), con lo cual, al sustituir en (21), se tiene
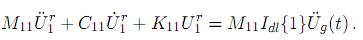
Y al transformar a coordenadas normales modales Yn, para desacoplar las ecuaciones de movimiento, se obtiene
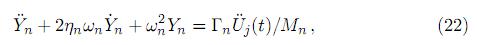
donde

siendo Üg(t) la aceleración de la excitación para todos los apoyos y Γn el factor de participación sísmica.
La solución de (22) quedará definida por la integral de Duhamel como
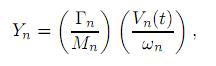
donde Vn(t) es la función de respuesta, es decir,
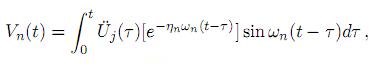
acuerdo al método de espectro de respuesta sísmica, la respuesta modal para valores máximos quedará definida al introducir la velocidad espectral o valor máximo de la función de respuesta; con la cual, de acuerdo con (18), se tendrá
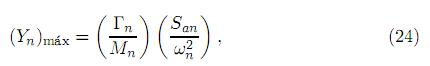
con lo cual
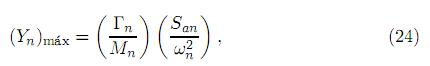
La respuesta máxima unidireccional se obtendrá por el método SRSS superponiendo las respuestas de cada modo, esto es,
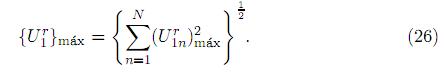
3 Aplicación
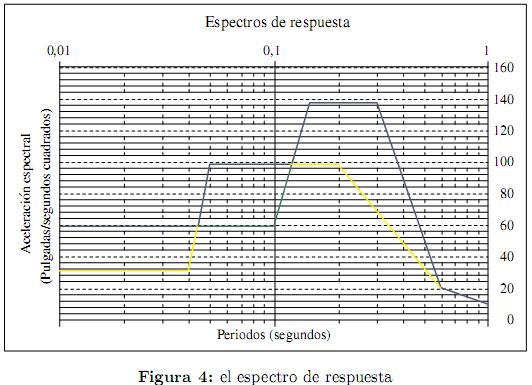
Como una ilustración de la aplicación de los métodos de análisis anteriormente considerados para estudiar el comportamiento de sistemas estructurales sujetos a excitación múltiple en sus apoyos o soportes durante efectos sísmicos, a continuación se presenta el análisis para un sistema de tubería típico, que interconecta a dos equipos a distintas elevaciones que inducen excitaciones distintas en los extremos de la tubería, según se ve en la figura 3; y en la figura 4 se muestra el espectro de respuesta, en tanto que en la tabla 1 se dan la dirección y nodo donde el espectro de excitación es aplicado.

Evaluando la matriz de masas y rigideces de cada una de las barras, posteriormente haciendo el cambio del sistema local al sistema general, y enseguida se realiza el acoplamiento de las matrices de masas y rigideces de cada una de las barras, para conformar el sistema estructural. Luego esta matriz se orga-
niza para separar grados de libertad de la estructura M11 y grados de libertad de los apoyos o soportes M22. Para ello se aplica una "transformación similar" a través de matrices de permutación. Esto se presenta en el anexo.
Despreciando el efecto del amortiguamiento bajo la condición de vibración libre se tiene (5). Siendo 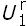 un vector de 9 × 1 de desplazamientos relativos correspondientes a los nueve grados de libertad del sistema de tubería. Posteriormente se encuentra la solución del determinante que resulta de (6), ver anexo, que resultan los valores y vectores característicos.
un vector de 9 × 1 de desplazamientos relativos correspondientes a los nueve grados de libertad del sistema de tubería. Posteriormente se encuentra la solución del determinante que resulta de (6), ver anexo, que resultan los valores y vectores característicos.
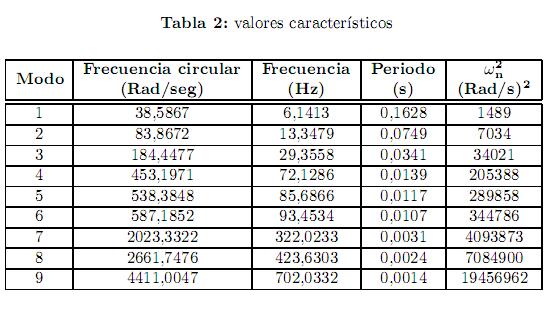
Usando los programas MATLAB 7.1, DERIVE 6 y MAPLE 12 para resolver el determinante, se obtiene el polinomio característico y posteriormente se encuentran las ráıces del polinomio característico; usando el programa MATLAB 7.1, se obtienen los resultados mostrados en la tabla 2.
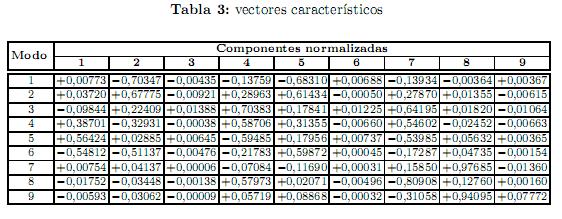
En la tabla 3 se dan los vectores característicos.
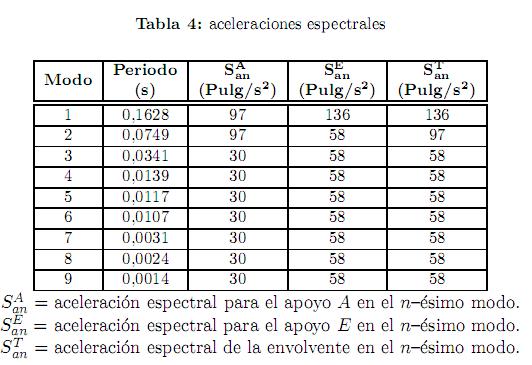
En la tabla 4 se muestran las aceleraciones espectrales para cada apoyo en el n-ésimo modo.
Método de espectro de respuesta múltiple
Los vectores ei para las excitaciones en las boquillas A y E son
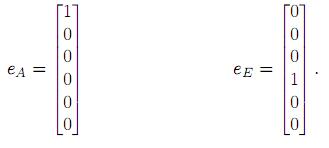
Empleando (8a) se encuentra la masa correspondiente al modo n Mn,de(13) se obtiene los factores de participación 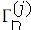 , tanto para el apoyo A como
, tanto para el apoyo A como
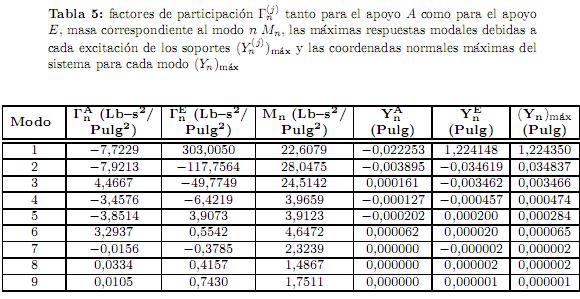
para el apoyo E, las máximas respuestas modales debidas a cada excitación de los soportes (Yn(j))máx se localiza por medio de (18), las coordenadas normales máximas del sistema para cada modo (Yn)máx esobtenidadeacuerdocon(19) y se presentan en la tabla 5. Los vectores correspondientes a las componentes del vector de desplazamientos relativos máximos para cada modo {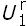 n}máx se encuentra por medio de (20) y finalmente el valor máximo del vector de desplazamientos relativos del sistema de tubería {
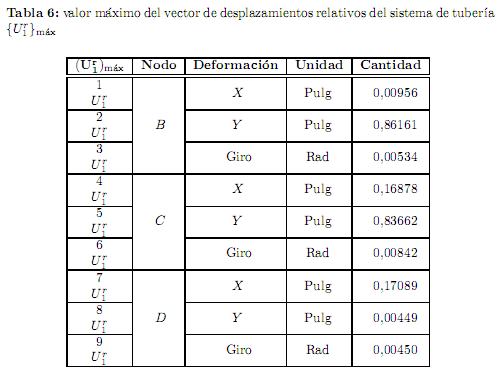
n}máx se encuentra por medio de (20) y finalmente el valor máximo del vector de desplazamientos relativos del sistema de tubería {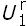 }máx se obtiene por (21). Estos valores se muestran en la tabla 6.
}máx se obtiene por (21). Estos valores se muestran en la tabla 6.
Método de espectro de respuesta simple
Donde al considerar la envolvente de los espectros de excitación se tiene
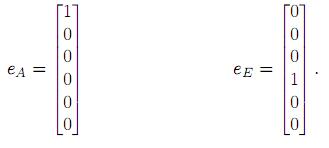
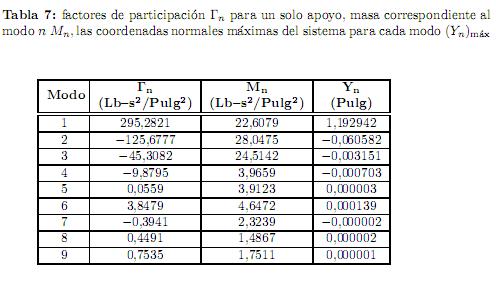
Empleando (8a) se encuentra la masa correspondiente al modo n Mn, de (23) se obtiene los factores de participación Γn para un solo apoyo, las coordenadas normales máximas del sistema para cada modo (Yn)máx es obtenida de acuerdo con (24) y se presentan en la tabla 7. Los vectores correspondientes a las componentes del vector de desplazamientos relativos máximos para cada modo {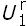 n}máx se encuentran por medio de (25) y finalmente el valor máximo del vector de desplazamientos relativos del sistema de tubería {
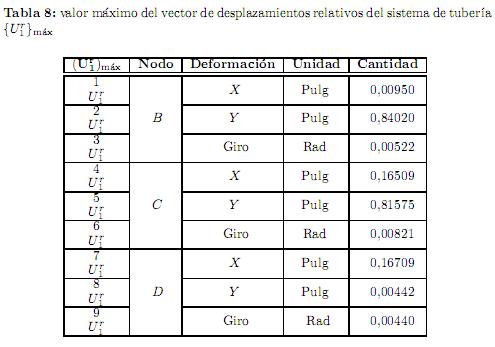
n}máx se encuentran por medio de (25) y finalmente el valor máximo del vector de desplazamientos relativos del sistema de tubería {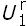 }máx se obtiene por (26). Estos valores se muestran en la tabla 8.
}máx se obtiene por (26). Estos valores se muestran en la tabla 8.
4 Conclusiones
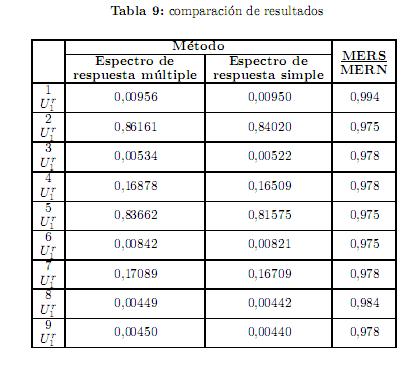
De la aplicación numérica se observa que la diferencia, respecto a operaciones numéricas, entre los métodos de respuesta múltiple y respuesta simple es muy poca, sin embargo, en cuanto a resultados se observa que el método de respuesta múltiple al compararlo con el método de respuesta simple, que es el clásico, en este último son menores que el método propuesto, como se puede notar en la tabla 9 de resultados del problema considerado. Por lo tanto, la práctica usual de considerar la envolvente de espectros no será una solución recomendable. Por lo que tomando en cuenta la aproximación numérica, el método de espectro de respuesta múltiple, resulta ser el método más adecuado para el análisis sísmico-dinámico de sistemas de tuberías sujetos a excitación distinta entre sus apoyos.
Ahora, respecto a la formulación, considerando masa discreta o masa consistente, se observa que en el primer caso se está despreciando el efecto de la masa en las fuerzas de excitación, lo cual definitivamente se reflejará en la respuesta del sistema y no del lado conservador. Por otra parte, al realizar el análisis de frecuencias, se demuestra que considerar masas discretas implica de antemano despreciar ciertas formas modales (modos simétricos y/o antisimétricos) del sistema, que en el caso de excitaciones distintas en los apoyos estarán presentes y deben considerarse, puesto que en algunos casos corresponden a frecuencias relativamente bajas. Lo expuesto anteriormente es porque la matriz de masas discretas tiene valor únicamente sobre la diagonal principal y la matriz de masas consistentes es llena.
En lo que respecta al estado del arte, en el análisis de respuesta sísmica- dinámica de sistemas estructurales con apoyos o soportes múltiples sujetos a excitaciones no uniformes en sus apoyos, es tratado como el método clásico ya mencionado. Al estudiar el comportamiento sísmico-dinámico de instalaciones de plantas nucleares, en donde debido al riesgo que presenta su operación, se
exige un mayor refinamiento en las técnicas de análisis para ser más realistas y tomar en cuenta efectos que en otros casos pueden considerarse de carácter secundario.
Finalmente, dado que es típico encontrar, tanto en la industria petrolera como en la nuclear, sistemas de tuberías sujetas a excitaciones múltiples distintas entre sus apoyos o soportes por los efectos sísmicos, la técnica de análisis a través del método de espectro de respuesta múltiple, viene a ser una práctica simple que debemos considerar como una de las etapas dentro del análisis y disenõ de los sistemas de tuberías.
En este trabajo se hizo un análisis modal y tomando únicamente el espectro de diseño horizontal, que sirve de base para posteriores proyectos de investigación como puede darse el caso en que se tome el espectro de disenõ, tanto el horizontal y el vertical simultáneamente, ya que el método considera la superposición de los efectos, y el método clásico no puede ser posible porque toma la envolvente.
Anexo
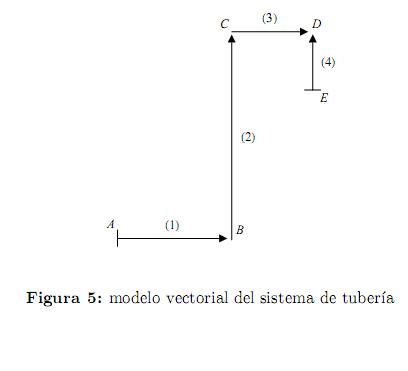
En la figura 5 se muestra el modelo vectorial del sistema de tubería para la obtención de las matrices de masa y rigideces en sistema de coordenadas globales del problema considerado.
Matriz de masas consistentes de un elemento
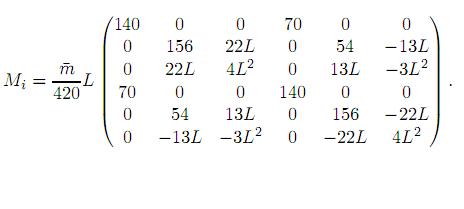
Acoplamiento de masas

Resultando
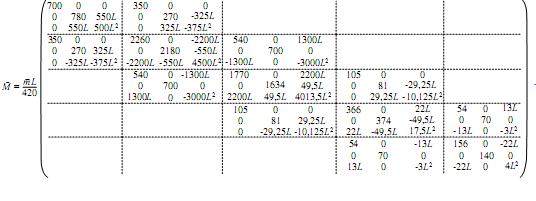
Realizando la transformación similar a través de la matriz de permutación para arreglar los grados de libertad, la matriz de masas resultante se muestra a continuación
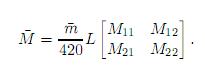
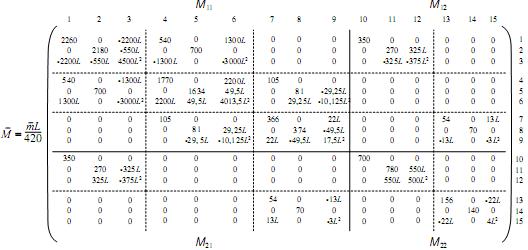
Matriz de rigidez para un elemento en el plano
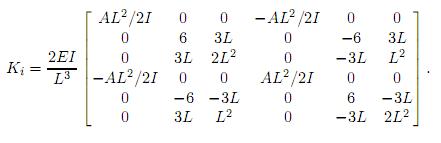
Acoplamiento de rigideces
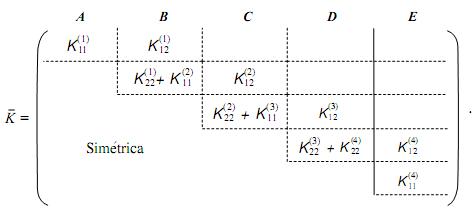
La matriz resultante se muestra a continuación

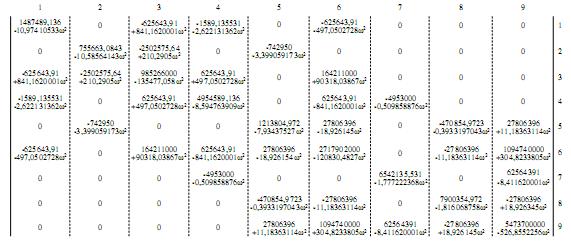
Aplicando la transformación similar a través de la matriz de permutación para arreglar los grados de libertad, se obtiene la matriz de rigideces del sistema de tubería
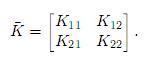

El determinante de K11− ω2M11 resulta de la manera
Referencias
1. RP. Kassawara, DA. Peck. Dynamic analysis of structural systems excited at multiple support locations. ASCE (American Society of Civil Engineers), Second Specialty Conference on Structural Design of Nuclear Plant Facilities, 1-a, 169-187 (1975). Referenciado en 119 [ Links ]
2. M. Amin, WJ. Hall, NM. Newmark, RP. Kassawara. Earthquake response of multiple connected light secondary systems by spectrum method. ASME (American Society of Mechanical Engineers), First National Congress Pressure Vessel and Piping Technical, 1971. Referenciado en 119 [ Links ]
3. DE. Shaw. Seismic structural response analysis for multiple support excitation. SMIRT-3 Conf, 1975. Referenciado en 119 [ Links ]
4. KM. Vashi. Seismic spectral analysis of structural systems subject to nonuni- form excitation at support. ASCE (American Society of Civil Engineers), Second Specialty Conference on Structural Design of Nuclear Plant Facilities, 1-a, 188- 216 (1975). Referenciado en 119
5. MC. Lee, T. Penzien. Stochastic seismic analysis of nuclear power plant structure and piping systems subjected to multiple support excitations. Report N◦UBC/EERC-80/19, Earthquake Engineering Research Center, University of California, 1980. Referenciado en 119 [ Links ]
6. Takeru Igusa, Armen der Kiureghian. Dynamic analysis of multiply tuned and arbitrarily supported secondary systems. Report N◦ UBC/EERC-83/07, Earthquake Engineering Research Center, University of California, 1983. Referenciado en 119 [ Links ]
7. SH. Crandall, WD. Mark. Random vibration of mechanical systems. Academic Press, New York, 1963. Referenciado en 119 [ Links ]
8. TW. Pickel. Evaluation of nuclear system requeriments for accommodating seismic effects. Nuclear Engineering and Design, 20(2), 323-337 (1972). Referenciado en 119 [ Links ]
9. Armen Der Kiureghian, Jerome Sackman, B. Nour-Omid. Dynamic response of light equipment in structures. Report N◦. UBC/EERC-81/05, Earthquake Engineering Research Center, University of California, 1981. Referenciado en 119 [ Links ]
10. Alejandro Asfura, Armen Der Kiureghian. Floor response spectrum method for seismic analysis of multiply supported secondary systems. Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 14(2), 245-265 (1986). Referenciado en 119 [ Links ]
11. Luis Suárez, MP. Singh. Floor response spectra with structure-equipment interaction effects by a mode synthesis approach . Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 15(2), 141-158 (1987). Referenciado en 119 [ Links ]
12. LE. Suárez, MP. Singh. Eigenproperties of non-classically damped primary structure and equipment systems by a perturbation approach. Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 15(5), 565-583 (1987). Referenciado en 119 [ Links ]
13. Mahendra P. Singh, Luis E. Suárez. Seismic response analysis of structure-equipment systems with non-classical damping effects. Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 15(7), 871-888 (1987). Referenciado en 119 [ Links ]
14. G. Falsone, G. Muscolino, G. Ricciardi. Combined dynamic response of primary and multiply connected cascaded secondary subsystems. Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 20(8), 749-767 (1991). Referenciado en 119 [ Links ]
15. G. Falsone, G. Muscolino, G. Ricciardi. Stochastic response of combined primary-secondary structures under seismic input. Earthquake Engineering and Structural Dynamics, ISSN 1096-9845, 21(11), 927-943 (1992). Referenciado en 119 [ Links ]
16. F. Valladares. Análisis dinámico de estructuras con equipos livianos. Memoria para optar al título de Ingeniero Civil. Universidad de Concepción, 1992. Referenciado en 119 [ Links ]
17. J. Crempien, E. Aravena. Análisis dinámico de estructuras con equipos livianos. Revista internacional de métodos numéricos para cálculo y disenõ en ingeniería, ISSN 0213-1315, 8(4), 407-416 (1992). Referenciado en 119 [ Links ]
18. JS. Przemieniecki. Theory of matrix structural analysis, ISBN 0486649482. Mc Graw-Hill, 150-163, 278-287 (1985). Referenciado en 121, 123, 127 [ Links ]
19. RW. Clough, J. Penzien. Dynamics of structures, ISBN 0-07-011392-0. Mc Graw-Hill, 156-167 (1975). Referenciado en 123, 125, 127, 128 [ Links ]
20. José M. Goicolea. Análisis sísmico de estructuras: dinámica estructural. Departamento Mecánica de medios continuos y teoría de estructuras Universidad Politécnica de Madrid, 2003. Referenciado en 125 [ Links ]