Arboles binomiales para la valoración de opciones sobre procesos derivados de la ecuación diferencial estocástica autónoma

Arvore binomial de opção de avaliação processo derivado de equações diferenciais estocásticas autónoma

Binomial tree for option valuation process derived from stochastic autonomous differential equation

Freddy Marín-Sánchez¹

¹ Magíster en Matemáticas aplicadas, fmarinsa@eafit.edu.co, profesor, Universidad EAFIT, Medellín-Colombia.

(Recepción: 04-nov-2009. Modificación: 20-sep-2010. Aceptación: 27-oct-2010)

---

Resumen

En este trabajo se propone una recombinación en árboles binomiales multiplicativa generalizada para la ecuación autónoma, en términos de la condición inicial y del producto entre saltos no constantes hacia arriba y hacia abajo del proceso discretizado. Se presenta de manera formal una técnica para encontrar las probabilidades de transición dinámicas considerando los dos primeros momentos del proceso solución de la ecuación diferencial, los cuales incorporan el factor de crecimiento y la volatilidad en términos de los parámetros y del proceso subyacente a lo largo de su ramificación. Se muestran algunos resultados numéricos experimentales de valoración de opciones Europeas para el proceso log-normal y para los procesos de reversión a la media con ruido aditivo y ruido proporcional para diferentes fechas de expiración.

Palabras claves: ecuaciones diferenciales estocásticas, árboles binomiales, probabilidades de transición, valoración de opciones.

---

Resumo

Neste trabalho, uma recombinação em arvores binomiais multiplicativa generalizada para a equação autônoma é proposta em termos da condição inicial do produto entre saltos não constantes para acima e para abaixo do processo de discretização. Apresenta-se uma técnica formal para encontrar as probabilidades de transição dinâmica considerando as duas primeiras momentos do processo de solução da equação diferencial, que incorporam o fator de crescimento e volatilidade em termos dos parâmetros e dos processos subjacentes ao longo da sua ramificação. São apresentados alguns resultados numéricos experimentais de avaliações Européias para o processo log-normal e do processo de reversão à média com ruído aditivo e ruído proporcional ruído para as diferentes datas de vencimento.

Palavras chaves: equações diferenciais estocásticas, árvores binomiais, probabilidades de transição, avaliação de opções.

---

Abstract

In this paper we propose a multiplicative generalized binomial trees recombination associated with the autonomous equation in terms of the initial condition and the product of non-constant upwards and downwards jumps from the discretized process. We present a formal technique for finding the dynamic transition probabilities involving the first two moments of the solution to the differential equation, which incorporate the factor of growth and volatility in terms of the parameters and the underlying process along its branching. Some experimental numerical results are shown for European option pricing for log- normal process and the processes of mean reversion with additive noise and proportional noise for different expiration dates.

Key words: stochastic differential equations, binomial trees, transition probabilities, pricing of options.

 

---

1 Introducción

El modelo clásico de valoración de opciones de Black-Scholes [1] supone que el activo subyacente tiene un comportamiento dinámico asociado a la ecuación diferencial estocástica lineal homogénea dada por

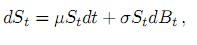
donde µ, σ son constantes y {B_t}_t≥0 es un movimiento browniano estándar unidimensional.

En este modelo se establece que, sin realizar supuestos sobre las preferencias de los inversionistas, se puede obtener una expresión para el valor de las opciones que no depende directamente del rendimiento esperado de la acción subyacente ni de la opción; las hipótesis sobre las que se sustenta configuran un escenario ideal en el que es posible la negociación continua, en unos mercados perfectos en los que la tasa de interés libre de riesgo es constante.

Desde la propuesta inicial de Black y Scholes han surgido numerosos modelos de valoración de opciones más complejos en los cuales se incorporan volatilidad estocástica [2], saltos [3, 4] y otros. Paralelamente, se han propuesto algunos métodos numéricos alternativos para valorar opciones como el de diferencias finitas [5, 6, 7], simulación Monte Carlo [8] y árboles binomiales[9, 10, 11] y trinomiales [10, 12].

En general, las primeras configuraciones de estos métodos están estructuradas bajo el supuesto que el activo subyacente sigue un movimiento browniano geométrico, aunque esta suposición no siempre es cierta. De hecho, existe una clara evidencia de que los precios spot de commodities agrícolas[13] y algunos energéticos pueden ser modelados con procesos asociados a modelos de reversión a la media con parámetros constantes [14], e incluso con modelos más sofisticados que incluyen saltos y parámetros funcionales determinísticos o estocásticos [15, págs. 106-110], [16]. Aunque en [17] se pone en duda está afirmación dado el comportamiento de los precios de petróleo y gas natural en los últimos años, finalmente se propone un modelo de reversión no lineal de tres factores con una marcada tendencia de largo plazo estocástica, incorporando así el crecimiento del consumo mundial y el aumento de incertidumbre en las reservas de petróleo.

Con estas consideraciones, surge una pregunta natural: ¿cómo se valora una opción cuando el activo subyacente no necesariamente sigue un movimiento browniano geométrico? La respuesta a esta pregunta no ha sido clarificada con buen detalle en los textos convencionales de cálculo estocástico aplicado, ni en los textos que hacen referencia a los instrumentos derivados financieros para el caso especial en el que los parámetros son constantes; aunque en [18] se proponen los modelos MRAM y MRRNAM para el proceso de reversión a la media con ruido proporcional. Si bien es cierto que se pueden encontrar fórmulas cerradas para la valoración de opciones, los métodos numéricos juegan un papel importante siempre que su implementación computacional sea más simple que el desarrollo mismo de las soluciones analíticas. Esta es una de las razones por las cuales se plantea el esquema de árboles binomiales para la valoración de opciones sobre la ecuación autónoma.

La primera implementación del modelo binomial para la valoración de opciones fue desarrollada para el proceso log-normal en [9]. Esta formulación, por su construcción misma, condujo a un procedimiento numérico alternativo que es más simple y computacionalmente más eficiente que el método de diferencias finitas. Cabe anotar que el método de árboles binomiales se ha convertido en una herramienta útil y muy popular puesto que su diagramación representa las diferentes posibles trayectorias que pueden ser seguidas por el precio de un activo durante la vida de la opción y a su vez permite obtener muy buenas aproximaciones utilizando resultados matemáticos relativamente simples. Una aproximación más realista para determinar el precio de las opciones, que se conoce como método de árboles binomiales implícito, se discute en [19]. Este modelo se basa en el cálculo de la distribución de probabilidad que utilizan los agentes del mercado para valorar las opciones con un vencimiento común sobre un mismo activo subyacente y en la deducción del proceso seguido por el mismo, bajo un esquema binomial multiplicativo, donde la volatilidad en cada nodo depende del precio del activo. Los precios de las opciones se calculan de igual manera que en los árboles binomiales convencionales. Esta propuesta presenta algunos inconvenientes, pues no se tienen en cuenta las opciones con vencimientos más cortos y, además, se supone que todas las trayectorias que conducen al mismo valor final poseen la misma probabilidad de riesgo neutral.

En [20] se plantea un nuevo enfoque utilizando esta misma técnica teniendo en cuenta opciones con diferentes vencimientos y considerando en cada paso un conjunto de opciones con precios de ejercicio iguales a los precios del subyacente en el nodo anterior y con vencimiento en el momento inmediatamente posterior. El inconveniente de este modelo es que presenta probabilidades negativas y, aunque esta falla se puede corregir, el método se hace más inestable numéricamente a medida que el número de pasos se hace más grande. Otra limitación de este modelo es que sólo se pueden valorar opciones de tipo Europeo, pero en [21] se introduce la posibilidad de valorar opciones Americanas.

Para mejorar la estabilidad del modelo, en [20] se propone en [22] un realineamiento de los nodos centrales del árbol en función de los precios a plazo en lugar de los precios al contado del subyacente, y considerando en cada etapa las opciones con un precio de ejercicio igual al precio a plazo del subyacente, en lugar de su precio al contado. Finalmente, la propuesta presentada en [23] supera las limitaciones observadas en [19] mediante la implementación de los árboles binomiales generalizados en el que se introducen una función de pesos que gobierna el proceso recursivo. Este esquema se puede utilizar para valorar opciones Europeas con un vencimiento anterior al momento correspondiente al último nodo del árbol, e incluso se puede ajustar para valorar opciones Americanas.

La aplicación del modelo binomial clásico [9] para el problema de valoración fue extendida en [10] a un caso más general con tres parámetros que incluye procesos de reversión a la media, pero puede ser ampliado hasta alcanzar la forma estructural de la ecuación autónoma que contiene cuatro parámetros constantes, incorporando así nuevos procesos como, por ejemplo, el ampliamente reconocido proceso de reversión a la media con ruido aditivo o proceso de Ornstein Uhlenbeck. En [9, 10] sólo se estudian procesos con ruido proporcional y en consecuencia los términos de crecimiento, 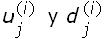en la recombinación multiplicativa, son constantes a lo largo del proceso de ramificación, mientras que de manera natural para la recombinación generalizada que se expone en este trabajo, en la que se incorpora el ruido aditivo, estos términos resultarán ser dinámicos.

2 Primeros momentos de la ecuación autónoma

Los momentos de primer y segundo orden de la ecuación autónoma (1) permiten obtener las probabilidades de transición dinámicas que serán calculadas más adelante. Para este fin, en lugar de hacer este procedimiento con la solución explícita, que es un poco más compleja [24, págs. 100-101], se determinarán los momentos de una manera mucho más simple [25, pág. 113] tomando los valores esperados de la solución en forma integral sobre el intervalo de tiempo [t_i, t_k].

Proposición 2.1. Considere la ecuación diferencial estocástica dada por

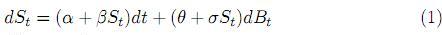
sobre el intervalo de tiempo [t_i, t_k], donde α, β, θ y σ son constantes y {B_t}_t>0 es un movimiento browniano estándar unidimensional. Suponga además que β ≠ 0,2β + σ² ≠ 0,β + σ² ≠ 0 y S_t = S_i. Entonces, el primer y segundo momentos para Stestán dados por:

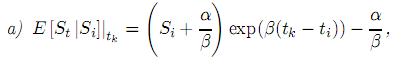
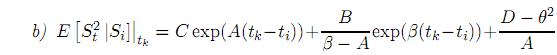, donde 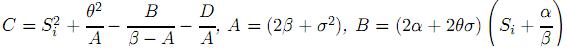y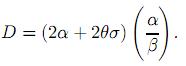

Prueba.

a) La ecuación (1) puede expresarse en forma integral como

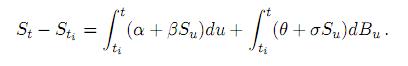
Tomando valor esperado condicional en ambos lados de la ecuación se obtiene

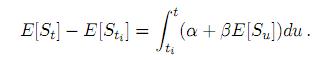
Esta se reduce a la ecuación diferencial ordinaria

donde m(t) = E[S_t]. Note que por simplicidad se tomó E[S_t] para denotar el valor esperado condicional E[S_t][S_i]. La solución explícita para (2) está dada por

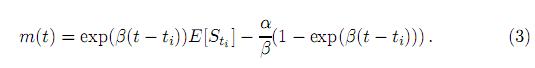
Finalmente,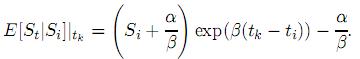

b) Sea g(S_t, t) = 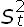, aplicando la fórmula de Ito [24, pág. 32] sobre g se obtiene

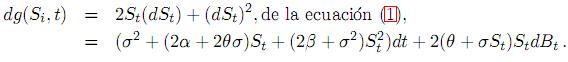
Expresando esta última ecuación en forma integral y tomando valor esperado condicional se sigue que

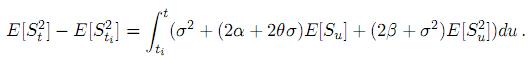
De este modo se obtiene la ecuación diferencial ordinaria

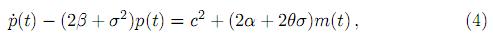
donde p(t) = E[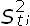]. Sustituyendo m(t) de (3), entonces (4) toma la forma

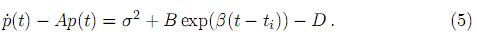
De este modo la solución explícita de (5) está dada por

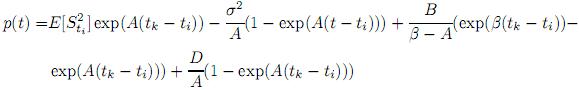
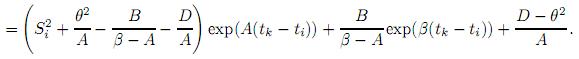
Finalmente, E[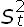|S_i]|_tk =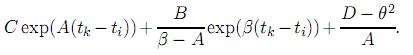

3 Recombinación para procesos discretos

Considere un proceso estocástico S_t modelado discretamente sobre algún intervalo de tiempo. En cada periodo de tiempo i, los posibles estados del proceso están dados por una cantidad finita de vectores S⁽ⁱ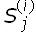⁾ = (), donde j está en un conjunto indexado finito J⁽ⁱ⁾. Así como el flujo de tiempo va del periodo i hasta el i + 1, el nodo discreto 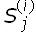puede ir a cualquier 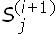, j ∈ J⁽ⁱ⁺¹⁾[10].

El proceso discreto determina una matriz de probabilidades de transición P⁽ⁱ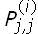⁾ = (), de modo que el elemento 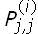representa la probabilidad que 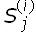, se mueva a 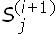. El número de filas en P⁽ⁱ⁾ es el cardinal de J⁽ⁱ⁾ y el número de columnas es el cardinal de J⁽ⁱ⁺¹⁾, tal que para toda Σ_{j∈ J ⁽ⁱ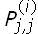⁺¹⁾} = 1.

3.1 Recombinación en árboles binomiales multiplicativa

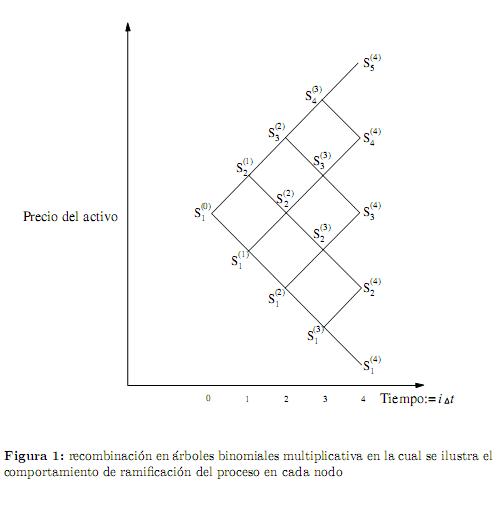
Una recombinación en árboles binomiales para un proceso estocástico Stpuede ser descrita como S⁽ⁱ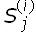⁾ = con j ∈ J⁽ⁱ⁾ = {1, 2, . . . , i + 1}, tal como es mostrado en la figura 1.

Las probabilidades de transición están dadas para cada i por un vector (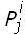), j ∈ J⁽ⁱ⁾ tal que 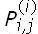está definido como 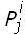si J′ = j + 1, 1 − 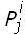si J′ = j, o cero en otro caso.

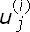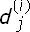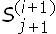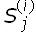
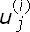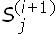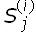
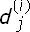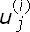
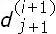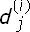
En este proceso multiplicativo se define el tamaño de los saltos hacia arriba y hacia abajo por y , respectivamente, de modo que = y = tal que = 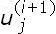; obteniendo la recombinación dada por

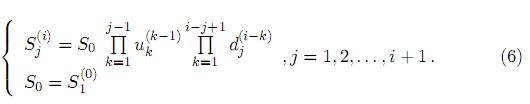
Obsérvese que para el caso especial en el que 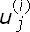= u y 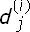= d son constantes, esta recombinación toma la forma 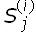= S₀ u^j−1 d^i−j+1 [9, 10],[26, págs. 388-390].

En [10] se presentan otras posibilidades de recombinación multiplicativa utilizando árboles trinomiales para procesos estocásticos de un solo factor, y se muestra un procedimiento similar, con una estructura un poco más compleja, para procesos de dos factores.

3.2 Cálculo de las probabilidades de transición

En esta sección se hará la deducción de las probabilidades de transición dinámicas para (1), la cual contiene implícitamente algunos procesos que han sido muy utilizados para estudiar el comportamiento dinámico de las tasas de interés [27] y otros que han servido como punto de partida para la modelación de los precios spot de algunos energéticos [4, 13, 14, 15]. El análisis que se llevará a cabo para obtener estas probabilidades es similar al propuesto en [10], pero aquí se hace la extensión para el caso más general. Como se expresó anteriormente, una diferencia importante que se establece en este trabajo es que para el cálculo de las probabilidades no se exige que los factores 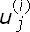y 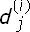sean constantes, sino que se permite, por la naturaleza misma de la recombinación, que ambos factores tengan un comportamiento dinámico a lo largo del proceso de ramificación.

Proposición 3.1. Considere la ecuación diferencial estocástica como en (1) y la recombinación en árboles binomiales multiplicativa S⁽ⁱ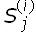⁾ = (). Suponga que t = t_i y S_ti = 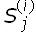. Sobre el intervalo de tiempo [t_i, t_i + ∆t] se denota la esperanza condicional del proceso continuo por E(S_t|S_ti)|_ti+∆t y para el proceso discreto por E_d(S⁽ⁱ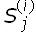⁾|)|_ti+∆t.

El acoplamiento del primer y segundo momentos para estos dos procesos, permite obtener como resultado una recombinación especificada por:

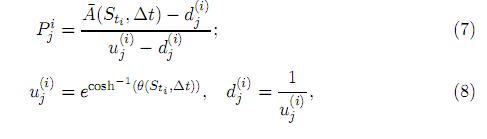
donde

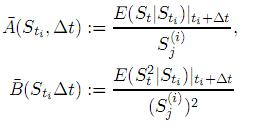y

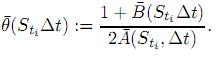
Prueba. La primera parte de la prueba es idéntica a la descrita en [10] (proposición 3). Por otro lado, defina la volatilidad del proceso S_t como la desviación estándar del retorno de S_t en periodo corto de tiempo de longitud ∆t, es decir,

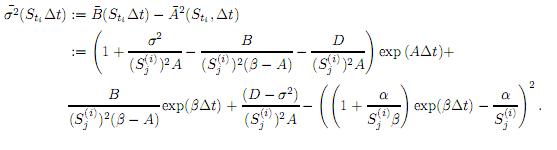
Luego de algunos procedimientos algebraicos se obtiene que

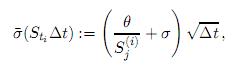
donde los términos de orden superior para ∆t fueron ignorados.

Ahora,

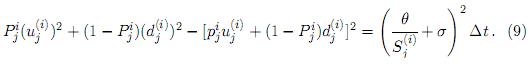
De (7 y 9)

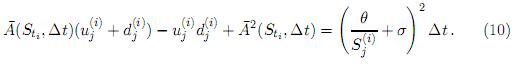
Cuando los términos de orden superior para ∆t son ignorados, una solución para esta ecuación está dada por

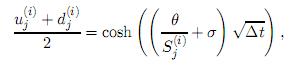
por tanto, 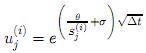y .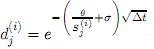

Sustituyendo estos resultados en (10) y despejando la función cosh se sigue que

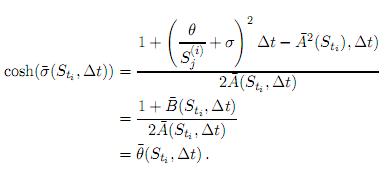
Finalmente, .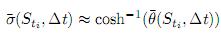

Proposición 3.2. Considere la ecuación diferencial estocástica como en (1) sobre el intervalo de tiempo [t₀, T]. Sea S⁽ⁱ⁾ = (Sj⁽ⁱ⁾) una recombinación en δt. Suponga que existe una cota inferior S_mín > 0 tal que 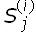> S_mín para toda i, j. Si se hacen coincidir el primero y segundo momento para los procesos discreto y continuo, resulta una recombinación cuya probabilidad de transición está especificada por

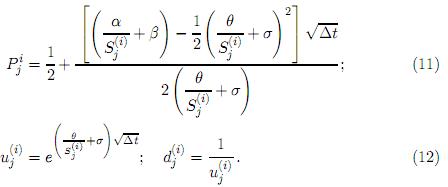
La prueba de esta proposición se basa en la expansión de series de Taylor en ∆t uniformemente con respecto a S_i, considerando los resultados en la proposición 3.1 y es idéntica a la descrita en [10] (Teorema 1. a).

3.3 Probabilidades de transición para algunos procesos derivados

De la ecuación autónoma se derivan algunos procesos muy conocidos que han sido usados en la modelación de tasas de interés y otros que permitieron un primer acercamiento al estudio de precios spot de commodities energéticos; de modo que se presentarán las probabilidades de transición para algunos de ellos.

Considere la ecuación diferencial estocástica con las especificaciones dadas en la proposición 3.2. Este proceso general puede ser discretizado por una recombinación en árboles binomiales multiplicativa en los siguientes casos:

a) Si α = θ = 0, se obtiene el proceso log-normal dS_t = βS_tdt + σS_tdB_t, el cual está especificado por

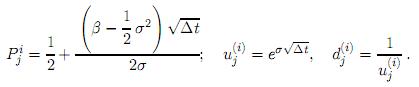
b) Si α = µL, β = −µ y θ = 0, se obtiene el proceso de reversión a la media con ruido proporcional dS_t = µ(L − S_t)dt + σS_tdB_t, el cualestá especificado por

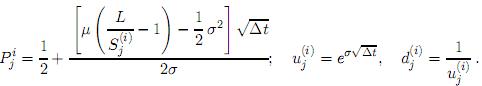
c) Si α = µL, β = −µ y σ = 0, se obtiene el modelo de Vasicek [27], el cual es un proceso de reversión a la media con ruido aditivo dS_t = µ(L − S_t)dt + θdB_t y está especificado por

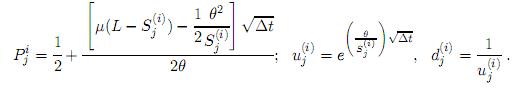
d) Si β = σ = 0, se obtiene el modelo de Merton [27] dS_t = αdt + θdB_t, el cual está especificado por

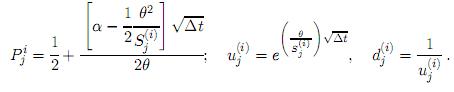
e) Si α = β = θ = 0, se obtiene el modelo de Dothan [27] dS_t = σdtdB_t, el cual está especificado por

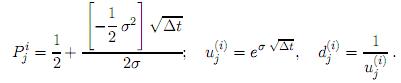
f) Si θ = 0, [10] se obtiene el modelo de Brennan-Schwartz [27] dS_t = (α + βS_t)dt + σS_tdB_t, el cual está especificado por

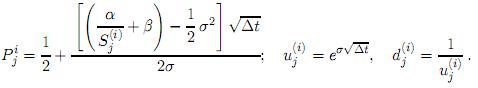
4 Valoración de opciones

En esta sección se hará una breve descripción del método de valoración de opciones call y put del tipo Europeas utilizando la recombinación en árboles binomiales multiplicativa bajo la probabilidad subjetiva P, inmersa en un mundo más riesgoso en el que se pueden presentar oportunidades de arbitraje. A este mundo se le dará el nombre de "mundo real". Así mismo, se presentará un principio importante que da lugar a esta misma valoración en un mundo sin riesgo, que se llamará "mundo de riesgo neutral". Los teoremas y procedimientos bajo los cuales se puede hacer el paso del mundo real al mundo neutral se presentarán en la siguiente sección.

4.1 Una aproximación algebraica

Suponga que la vida de una opción sobre un activo que no paga dividendos, con precio inicial S₀ y precio de ejercicio K, es dividida en N subintervalos de longitud ∆t. Defina 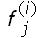como el valor de la opción en el nodo (i, j). Recuerde que el precio del activo en el nodo (i, j) está dado por

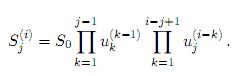
• Para el caso de una opción call Europea, el valor en su fecha de maduración está dada por máx(S_t − K, 0), por tanto,

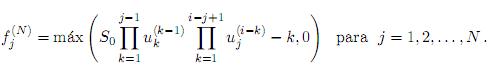
Además, 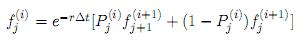para 0 ≤ i ≤ N − 1 y 1 ≤ j ≤ i.

• Para el caso de una opción call Europea, el valor en su fecha de maduración está dada por máx(K − S_t, 0), por tanto,

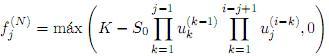para j = 1,2, ..., N.

Además, 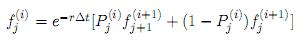para 0 ≤ i ≤ N − 1 y 1 ≤ j ≤ i.

Estas ecuaciones establecen que el valor de la opción hoy es el valor esperado futuro descontado a la tasa de interés libre de riesgo r. En un mundo de riesgo neutral todos los individuos son indiferentes al riesgo, ellos no requieren ninguna compensación por el riesgo, y el retorno esperado de todos los instrumentos es la tasa de interés libre de riesgo. Estas ideas configuran un principio general de vital importancia en la valoración de opciones que se conoce como valoración de riesgo neutral. Este principio establece que cuando se valoran opciones es válido suponer que los agentes que intervienen en el mercado se encuentran en un mundo de riesgo neutral.

4.2 Valoración de riesgo neutral

"Cualquier instrumento derivado dependiente del precio de un activo puede ser valorado suponiendo que el activo se encuentra en un mundo de riesgo neutral" [26, pág. 389]. Para propósitos de valoración de una opción se puede suponer que:

1. El retorno esperado de todos los instrumentos negociados es la tasa de interés libre de riesgo.

2. Los flujos de caja futuros pueden ser valorados descontando sus valores esperados a la tasa de interés libre de riesgo.

De este modo, cuando se quiere hacer el paso del "mundo real" al mundo de riesgo neutral, el retorno esperado del activo experimenta un cambio importante, mientras que su volatilidad sigue siendo la misma. El paso de un mundo Como el valor esperado del pago descontado de un instrumento derivado bajo la probabilidad subjetiva P daría lugar a oportunidades de arbitraje, es necesario construir una única medida de probabilidad P^∗ equivalente a P tal que:

1. El precio descontado a la tasa de interés libre de riesgo r sea una martingala.

2. El valor esperado del pago descontado de un instrumento derivado bajo la probabilidad P^∗ no presente oportunidades de arbitraje.

La medida de probabilidad que se considera en un mundo de riesgo neutral se conoce como medida equivalente de martingala y se describirá a continuación.

5 Medida equivalente de martingala

Sea (Ωi, 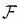,{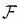_t}_t≥0, P) en espacio de probabilidad completo con una filtración {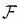_t}P^∗ es una medida sobre (Ω, 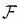) dada por P^∗(A) = ∫_A ƒ (w)dp(w), A ∈ F, entonces dP^∗(w) = ƒ(w)dP^∗(w).

5.1 (Teorema de Cameron-Martin-Girsanov)[24, pág. 270]

Teorema 5.1. Sea{B_t}_{0≤ t≤T} un movimiento browniano standard unidimensional definido sobre un espacio de probabilidad1(Ω, 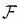, {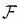_t}_t≥0, P). Sea

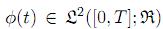. Donde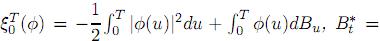

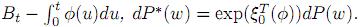
Si P^∗ (Ω) = 1, entonces {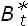}_{0≤ t≤T} es un nuevo movimiento browniano unidimensional definido sobre el espacio de probabilidad (Ω, 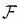, P^∗) con respecto a la misma filtración{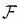_t}.

5.2 (Teorema de Girsanov)[24, pág. 272]

Teorema 5.2. Sea {B_t}_{0≤ t≤T} un movimiento browniano standard unidimensional definido sobre un espacio de probabilidad (Ω, 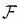,{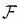_t}_t≥0, P ).

Sea Stun proceso de Ito unidimensional sobre [0, T] dado por

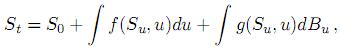
donde .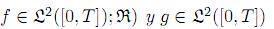

Sea 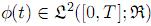. Considere 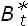y P^∗ definidos como en el teorema entonces 5.1. Si P ∗(Ω) = 1, entonces Stes también un proceso de Ito unidimensional sobre el espacio de probabilidad (Ω, 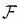, P^∗) con respecto al movimiento browniano 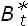, es decir, Stes la solución de la ecuación diferencial estocástica

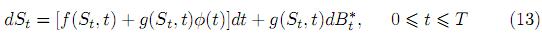
sobre el espacio de probabilidad (Ω, 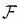, P^∗). Si ƒ (x, t) y 1/g(x, t) son acotados, entonces Φ(t) = −ƒ(S_t, t)/g(S_t, t) y, en consecuencia, (13) se reduce a dS_t = g(St, t)dB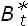, 0 ≤ t ≤ T.

5.3 Incidencia de la valoración de riesgo neutral sobre la ecuación diferencial estocástica autónoma

El precio descontado a la tasa de interés libre de riesgo r es S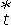 = e^−rt S_t y su diferencial estocástico está dado por

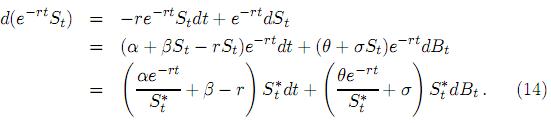
De la solución discretizada de (1) puede observarse que el precio descontado S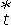 satisface la misma ecuación que S_t, donde el retorno 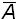(S_ti, ∆t) ha sido remplazado por 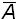(S_ti, ∆t) − e^−rt.

De este modo, el valor esperado bajo la probabilidad subjetiva P, del pago descontado de un instrumento derivado, presentará oportunidades de arbitraje puesto que S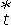 no es una martingala. Para encontrar una medida de probabilidad bajo la cual S 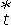constituya una martingala (14) se debe escribir en tal forma que el término de tendencia sea "absorbido" dentro del término de la martingala y así determinar cuál es la sustitución más apropiada sobre los parámetros iniciales.

De los teoremas 5.1 y 5.2,

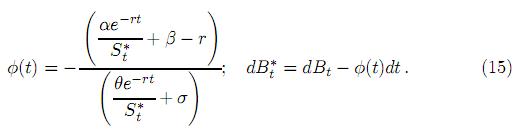
Remplazando en (14) se obtiene dS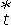= (θ^e−rt + σS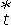)d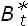, de este modo es fácil observar que 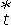S = S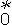 + 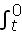(θe^−rt + σS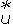)dB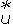 es una martingala.

Al sustituir las ecuaciones obtenidas en (15), la ecuación autónoma (1) en un mundo de riesgo neutral, se reduce a

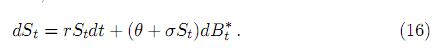
Las probabilidades de transición para (16) se obtienen fácilmente tomando α = 0 y β = r en (11).

6 Resultados numéricos experimentales

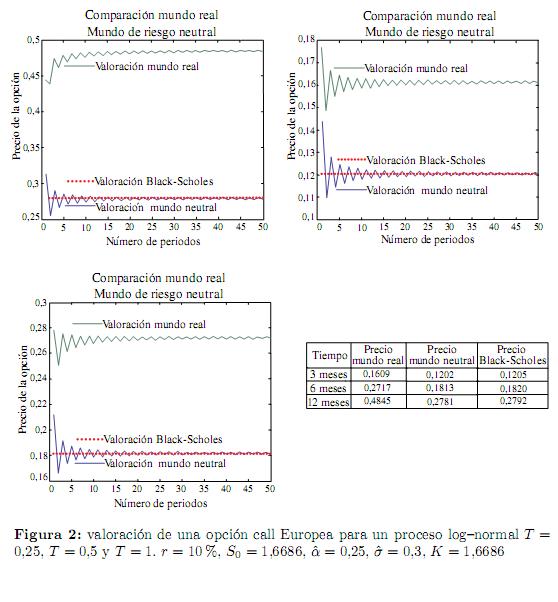
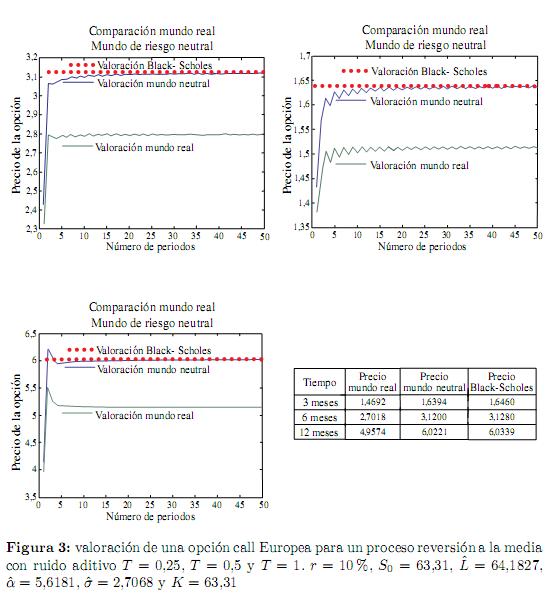
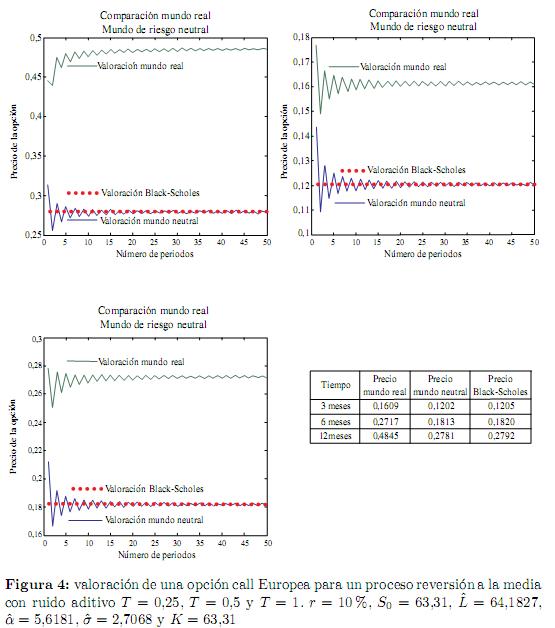
Para efectos ilustrativos del método propuesto en este trabajo, sólo se presentarán algunos resultados numéricos asociados a la valoración de opciones call Europeas en el "mundo real" bajo la probabilidad subjetiva P, y en un mundo de riesgo neutral sobre los procesos log-normal y de reversión a la media con ruido aditivo y ruido proporcional en contraste con resultados que se obtienen al utilizar la fórmula de Black-Scholes. Se debe aclarar que en los mercados financieros la valoración de opciones se lleva a cabo considerando el principio de valoración de riesgo neutral. La valoración bajo la probabilidad subjetiva utilizando los parámetros estimados de los datos históricos es de puro interés teórico.

En las figuras 2, 3 y 4 se observa la rápida convergencia de la recombinación en árboles binomiales multiplicativa generalizada para opciones call Europeas con diferentes fechas de expiración y con un total de 50 períodos.

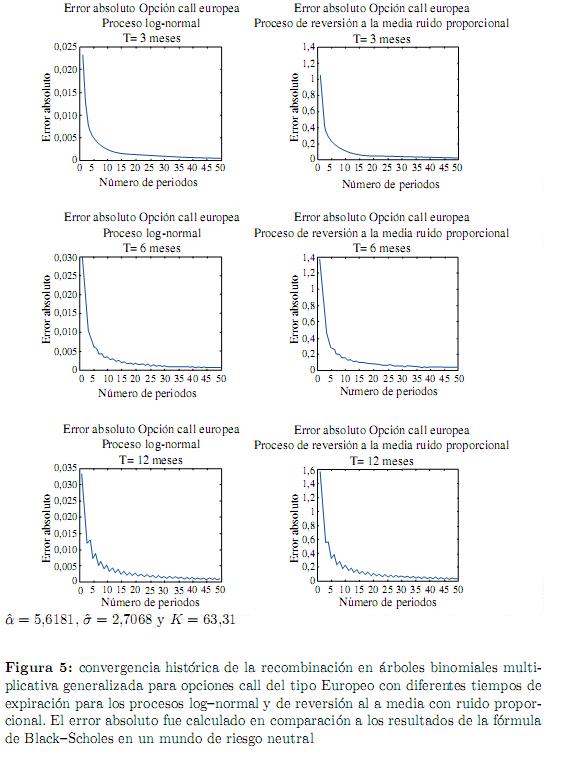
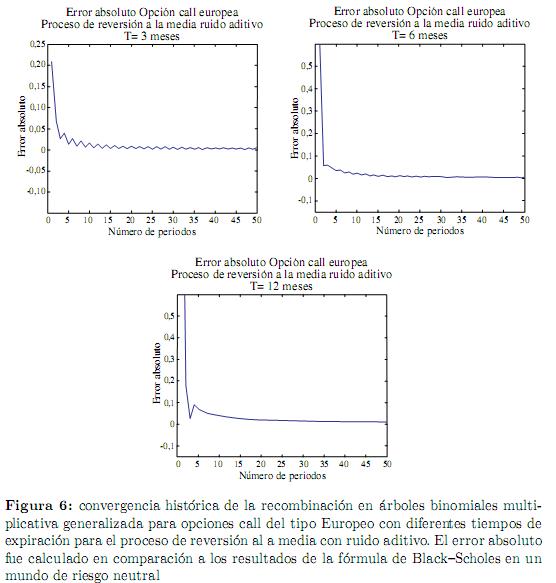
En las figuras 5 y 6 se muestra el comportamiento de las cotas de error absoluto de la recombinación generalizada en comparación con la fórmula de Black-Scholes.

Conclusiones

En el modelo propuesto se obtiene una recombinación multiplicativa generalizada y las probabilidades de transición variables que determinan el comportamiento dinámico de procesos discretizados asociados a la ecuación diferencial autónoma a lo largo del proceso de ramificación, sujeto a unas restricciones apropiadas para los parámetros. Se presenta, además, el esquema de árboles binomiales generalizado como un método numérico alternativo para valorar opciones sobre activos que pueden ser modelados utilizando la ecuación diferencial estocástica lineal general con parámetros constantes o por cualquiera de sus procesos derivados. Se ilustra gráficamente la rápida convergencia del método numérico con sus cotas de error absoluto y los resultados de la valoración de opciones call Europeas para diferentes procesos con distintos tiempos de expiración en el "mundo real" y en un mundo de riesgo neutral. Finalmente, un trabajo posterior permitirá estudiar la velocidad de convergencia del método para opciones call y put Europeas y Americanas. Así mismo, se podrá extender este procedimiento a procesos más generales en los que se consideran parámetros funcionales deterministas inobservables o estocásticos, para sistemas de dos o tres factores e incluso modelos estocásticos más complejos que incluyan saltos, todos ellos basados en la ecuación autónoma con algunas modificaciones y que son usados en la actualidad para modelar el comportamiento dinámico de los precios spot de algunos energéticos.

Referencias

1. Fischer Black, Myron Scholes. The Pricing of Options and Corporate Liabilities. Journal of political economy, ISSN 0022-3808, 81(3), 637-654 (1973). Referenciado en 146         [ Links ]

2. SL. Heston. A closed-form solution for options with stochastic volatility with applications to bonds and currency options. The Review of Financial Studies, ISSN 0893-9454, 6(2), 327-343 (1993). Referenciado en 147         [ Links ]

3. John Cox, Stephen Ross. The valuation of options for alternative stochastic processes. Journal of Financial Economics, ISSN 0304-405X, 3, 145-166 (1976). Referenciado en 147         [ Links ]

4. Shijie Deng. Stochastic models of energy commodity prices and their applications: mean-reversion with jumps and spikes. Working Paper, University of California Energy Institute, Berkeley, October 01, 1999. Referenciado en 147, 153         [ Links ]

5. Michael J. Brennan, Eduardo S. Schwartz. The valuation of American Put options. Journal of Finance, ISSN 0022-1082, 32(2), 449-462 (1977). Referenciado en 147        [ Links ]

6. Georges Courtadon. A More Accurate Finite Difference Approximation for the Valuation of Options. Journal of Financial and Quantitative Analysis, ISSN 0022-1090 17(5), 697-703 (1982). Referenciado en 147         [ Links ]

7. John Hull, Alan White. Valuing Derivative Securities Using the Explicit Finite Difference Method. Journal of Financial and Quantitative Analysis, ISSN 0022-1090, 25(1), 87-100 (1990). Referenciado en 147         [ Links ]

8. Mark Broadie, Paul Glasserman. Estimating Security Price Derivatives Using Simulation. Management Science, ISSN 0025-1909, 42(2), 269-285 (1996). Referenciado en 147         [ Links ]

9. John C. Cox, Stephen A. Ross, Mark Rubinstein. Option Pricing: a Simplified Approach. Journal of Financial Economics, ISSN 0304-405X, 7(3), 229-263 (1979). Referenciado en 147, 148, 149, 153         [ Links ]

10. Ali Lari-Lavassani, Mohamadreza Simchi, Antony Ware. A Discrete Valuation of Swing Options. Canadian Applied Mathematics Quarterly, ISSN 1073- 1849, 9(1), 35-73 (2001). Referenciado en 147, 149, 152, 153, 154, 156, 158         [ Links ]

11. Richard Breen. The Accelerated Binomial Option Pricing Model. Journal of Financial and Quantitative Analysis, ISSN 0022-1090, 26(2), 153-164 (1991). Referenciado en 147         [ Links ]

12. Jaemin Ahn, Minsu Song. Convergence of the trinomial tree method for pricing European/American options. Applied Mathematics and Computation, ISSN 0096-3003, 189(1), 575-582 (2007). Referenciado en 147         [ Links ]

13. Hendrik Bessembinder, Jay Coughenour, Paul Seguin and Margaret Monroe. Mean Reversion in Equilibrium Asset Prices: Evidence from the Futures Term Structure. The Journal of Finance, ISSN 0022-1082, 50(1), 361-375 (1995). Referenciado en 147, 153         [ Links ]

14. Ali Lari-Lavassani, Ali A. Sadeghi, Antony Ware. Mean Reverting Models for Energy Option Pricing, agosto de 2007. Referenciado en 147, 153         [ Links ]

15. Dragana Pilipovic. Energy Risk: Valuing and Managing Energy Derivatives, ISBN 0071485945, McGraw-Hill, New York, 2007. Referenciado en 147, 153         [ Links ]

16. Hélyette Geman, Andrea Roncoroni. A Class of Marked Point Processes for Modelling Electricity Prices, noviembre de 2008. Referenciado en 147         [ Links ]

17. Helyette Geman. Energy Commodity Prices: Is Mean-Reversion Dead? The Journal Of Alternatives Investments, ISSN 1520-3255, 8(2), 31-45 (2005). Referenciado en 147        [ Links ]

18. Anatoliy Swishchuk. Explicit Option Pricing Formula for a Mean-Reverting Asset, diciembre de 2008. Referenciado en 147         [ Links ]

19. Mark Rubinstein. Implied Binomial Trees. The Journal of Finance, ISSN 0022- 1082, 49(3), 771-818 (1994). Referenciado en 148, 149         [ Links ]

20. Emanuel Derman, Iraj Kani. Riding on the smile. Risk, 7, 32-39 (1994). Referenciado en 148         [ Links ]

21. Neil Chriss. Transatlantic trees. Risk, 9, 45-48 (1996). Referenciado en 148         [ Links ]

22. Stanko Barle, Nusret Cakici. How to grow a smiling tree. Journal of Financial Engineering, ISSN 1062-8924, 7(2), 127-146 (1998). Referenciado en 148         [ Links ]

23. Jens Carsten Jackwerth. Generalized binomial trees. Journal of Derivatives, ISSN 1074-1240 , 5(2), 7-17 (1997). Referenciado en 149         [ Links ]

24. Xuerong Mao. Stochastic Differential Equations & Aplications, ISBN 1898563268. Horwood Publishing Limited England, 1997. Referenciado en 149, 151, 160, 161         [ Links ]

25. Peter Kloeden, Eckhard Platen. Numerical Solution of Stochastic Differential Equations, ISBN 0387540628, Springer-Verlag, New York, 1992. Referenciado en 149        [ Links ]

26. John Hull. Options, Futures and Other Derivatives, ISBN 0130224448. Prentice Hall, New Jersey, 2000. Referenciado en 153, 159         [ Links ]

27. Dervis Bayazit. Yield Curve Estimation and Prediction with Vasicek Model, diciembre de 2007. Referenciado en 153, 157, 158        [ Links ]