Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.7 no.13 Medellín Jan./June 2011
Planeación de sistemas secundarios de distribución usando el algoritmo branch and bound
Planejamento de sistemas secundários de distribuição usando um algoritmo de branch and bound
Secondary distribution system planning using branch and bound algorithm
Carlos Javier Tapias-Isaza1 Andrés Alberto Galeano-Ossa2 y Ricardo Alberto Hincapié-Isaza3
1 Ingeniero Electricista, cjtapias@hotmail.com, Universidad Tecnológica de Pereira (UTP), Pereira-Colombia.
2 Ingeniero Electricista, galeo82@hotmail.com, Universidad Tecnológica de Pereira (UTP), Pereira-Colombia.
3 Magíster en Ingeniería Eléctrica, ricardohincapie@utp.edu.co, profesor asistente, Universidad Tecnológica de Pereira (UTP) , Pereira-Colombia.
(Recepción: 13-abr-2010. Modificación: 22-sep-2010. Aceptación: 01-oct-2010 )
Se aceptan comentarios y/o discusiones al artículo
Resumen
En este trabajo se plantea una metodología para la solución del problema del planeamiento de sistemas secundarios de distribución considerando un modelo de programación lineal entero mixto (PLEM), el cual considera la ubicación y dimensionamiento de transformadores de distribución, el dimensionamiento y rutas de circuitos secundarios y sus costos variables. Para la solución del problema se emplea el algoritmo Branch and Bound. Los resultados obtenidos en un sistema de prueba empleado en la literatura especializada muestran la validez y efectividad de la metodología propuesta.
Palabras claves: branch and bound, programación lineal entera mixta, planeamiento de la distribución.
Resumo
Neste trabalho apresenta-se uma metodologia para resolver o problema de planejamento de sistemas de distribuição secundária considerando um modelo de programação linear inteira mista (PLEM). Neste modelo, a localização e dimensionamento dos transformadores de distribuição, o dimensionamento e as rotas de circuitos secundários e os custos variáveis dos circuitos, são variáveis de controle do problema. A técnica de solução usada para resolver o problema é um algoritmo de Branch and Bound. Os resultados obtidos em um sistema de teste utilizado na literatura mostram a validade e a eficácia da metodologia proposta.
Palavras chaves: branch and bound, programação linear inteira mista, planejamento da distribuição.
Abstract
This paper presents a methodology for solving secondary distribution systems planning problem as a mixed integer linear programming problem (MILP). The algorithm takes into account several design issues such as the capacity and location of distribution transformers and secondary feeders. Variable costs of secondary feeders are also considered. The problem is solved using branch and bound algorithm. Numerical results show that the mathematical model and the solution technique are effective for this kind of problems.
Key words: branch and bound, mixed integer linear programming, distribution system planning.
1 Introducción
Debido a la importancia que tiene para el ser humano el consumo de la energía eléctrica, sería poco probable que de acuerdo a las condiciones del mundo actual el hombre pudiera satisfacer sus necesidades sin depender de los sistemas eléctricos. Por eso para garantizar que el ser humano tenga a su disposición energía durante las 24 horas del día es necesario que se consideren diferentes aspectos técnicos, económicos, ambientales y políticos con el fin de abastecer la demanda de potencia exigida por los centros de consumo. La manera como se satisfaga la energía actual y futura, garantizando los aspectos mencionados anteriormente, se conoce como el planeamiento de sistemas secundarios de distribución.
El objetivo principal del planeamiento de un sistema secundario de distribución es abastecer la demanda de potencia garantizando que durante su expansión se cumplan un conjunto de restricciones técnicas impuestas por los sistemas eléctricos, a un precio razonable que beneficie a las empresas distribuidoras de energía y a los usuarios.
En la literatura especializada los trabajos existentes alrededor de esta temática formulan el problema como un problema de programación lineal entero mixto (PLEM) y no lineal entero mixto (PNLEM), donde el objetivo principal es minimizar una función de costos de instalación y operación, sujeta a un conjunto de restricciones técnicas.
Costa et al [1] plantean para solucionar el problema un modelo matemático en el que son considerados la ubicación y capacidad de transformadores de distribución, y la ruta y dimensión de la red secundaria. La metodología usada consiste en dividir el problema en tres etapas. La primera considera la localización de los transformadores de distribución, la segunda realiza el diseño de la red secundaria y la tercera etapa selecciona la ruta adecuada para la red primaria a partir de la red existente. Para resolver las dos primeras etapas los autores emplean un método basado en las p-medianas y relajación lagrangiana. En cuanto a la conexión a la red primaria, emplean el método de árboles generadores mínimos.
En [2] el autor presenta una metodología para el problema del planeamiento de redes secundarias, el cual consiste en minimizar los costos de inversión atendiendo los requerimientos técnicos de la red, y en su solución emplea una técnica heurística. El modelo matemático considera la ubicación de transformadores de distribución y circuitos secundarios. El método propuesto para solucionar el problema consiste en dividirlo en tres etapas. La primera realiza la ubicación y define la capacidad de los transformadores empleando la metodología de las p-medianas. La segunda etapa realiza el diseño de la red secundaria empleando un algoritmo del mínimo camino. Por último, realiza la conexión de los transformadores a la red primaria empleando en el modelamiento un problema de Steiner.
Cossi en [3] plantea el problema del planeamiento de sistemas secundarios de distribución, como un problema de programación no lineal entera mixta (PNLEM). En el modelo planteado el autor considera la función objetivo como la suma de los costos de instalación de nuevos elementos (circuitos secundarios, transformadores, etc.) y los costos de operación de la red proyectados a un año. Las restricciones para el modelo implementado son la primera ley de Kirchhoff, capacidad máxima permitida de transformadores de distribución y circuitos secundarios, límites de tensión para cada uno de los nodos y restricción financiera del proyecto. El método de solución empleado por el autor es un algoritmo evolutivo.
En [4] el autor presenta un modelo matemático no lineal entero mixto para describir el problema, el cual considera el balance de cargas, diseño y ubicación de postes, ubicación y dimensionamiento de transformadores de distribución, diseño de redes primarias y secundarias, y el máximo límite de inversión permitido. Las restricciones consideradas para este modelo son la primera ley de Kirchhoff, los límites de tensión para cada uno de los nodos y la capacidad máxima de los elementos del sistema. Para solucionar el problema emplea un algoritmo de búsqueda tabú.
Marroquín en [5] propone una metodología para solucionar el problema usando un algoritmo basado en colonia de hormigas modelando el sistema como un problema no lineal entero mixto (PNLEM). El autor realiza un balance de cargas y diseña la red secundaria considerando transformadores de distribución y circuitos secundarios. La función objetivo empleada considera el costo de instalación de elementos nuevos, el costo del balance de las cargas y las pérdidas del sistema.
En [6] los autores proponen un modelo matemático general para describir este problema. El modelo propuesto considera la ubicación y dimensionamiento de transformadores de distribución y circuitos secundarios, la repotenciación de alimentadores y transformadores, el balance de fases y los costos de inversión y operación de la red.
Con el fin de solucionar el problema del planeamiento de sistemas secundarios de distribución se propone en este trabajo una metodología empleando como técnica de solución el algoritmo Branch and Bound y considerando un modelo matemático lineal entero mixto, el cual involucra la ubicación y dimensionamiento de transformadores de distribución y alimentadores secundarios. La función objetivo a minimizar tiene en cuenta los costos de instalación de nuevos elementos y los costos de operación de la red.
2 Descripción del problema
El objetivo principal del planeamiento de un sistema secundario de distribución es abastecer la demanda, garantizando que se cumplan un conjunto de restricciones técnicas impuestas por los sistemas eléctricos, a un precio razonable que beneficie a las empresas distribuidoras de energía y a los usuarios. En el planeamiento se debe considerar la localización y el tamaño de nuevos transformadores de distribución, la ruta y el tamaño de nuevos circuitos secundarios, aumento del calibre de los circuitos existentes, cambio de transformadores de distribución existentes, reconfiguración, regulación de la red y el balance de fases.
Un inadecuado planeamiento de estos sistemas se puede ver reflejado en sobrecargas en circuitos secundarios y transformadores de distribución, problemas de regulación, incremento en las pérdidas técnicas del sistema, pérdida de confiabilidad y calidad, sobredimensionamiento de los elementos, sobrecostos en los proyectos de ejecución y desbalance de carga en las fases.
Para evitar que los problemas mencionados anteriormente se presenten en el sistema, se deben explorar diferentes alternativas tanto de inversión como de operación con el fin de encontrar la mejor alternativa posible. Considerar todas las alternativas presentes tomaría bastante tiempo, lo cual se ve reflejado en altos costos para las electrificadoras. Es por esto que es importante encontrar diversas maneras de solución del problema de tal forma que se optimicen los recursos y el tiempo de los ingenieros encargados del planeamiento. Una planificación óptima debe determinar la mejor configuración de la red, qué inversiones deben realizarse y el momento de la instalación de los elementos, con el fin de alcanzar mínimos costos asociados a dicho sistema.
3 Modelamiento matemático
Para solucionar el problema del planeamiento de sistemas secundarios de distribución, se emplea en este trabajo un modelo de programación lineal entero mixto (PLEM), el cual tiene como propósito minimizar una función objetivo, sujeta a un conjunto de restricciones técnicas.
3.1 Consideraciones generales
Para la decisión de instalación de un determinado elemento se emplean variables de tipo binario. Cuando una de estas variables toma el valor de uno, indica que el elemento asociado a dicha variable debe ser instalado. Si esa variable es igual a cero quiere decir que el elemento no será tenido en cuenta. Como existen diversos tipos de circuitos y transformadores, entonces debe haber una variable binaria asociada a cada uno de estos elementos. También existen un conjunto de variables continuas las cuales representan los flujos por las líneas, expresados entre dos nodos i y j. Como el flujo entre estos nodos puede ser en ambos sentidos, entonces deben existir dos variables por cada tramo de red.
Con el fin de facilitar el modelamiento matemático y la solución del problema se emplearon los centros de demanda, los cuales representan un grupo de usuarios y son considerados como un único nodo.
3.2 Nomenclatura empleada en el modelo
• k: tipo o calibre del conductor.
• M : tipo de transformador de acuerdo a su capacidad.
• CFij,k: costo de inversión de un tramo de red tipo k, entre los nodos i-j.
• CFi,M: costo de inversión de un transformador de distribución tipo M, en el nodo i.
• Ckwh: costo de la energía expresada en [$/kWh].
• T : período de planeamiento en horas-año (8760 horas).
• Rij,k: resistencia del conductor tipo k entre los nodos i-j.
• Iij,k: corriente por un conductor tipo k, entre los nodos i-j.
• Iji,k: corriente por un conductor tipo k, entre los nodos j-i.
• Xij,k: potencia que circula por un conductor tipo k, entre los nodos i-j.
• Xji,k: potencia que circula por un conductor tipo k, entre los nodos j-i.
• 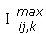 : corriente máxima permitida para un conductor tipo k, entre los nodos i-j.
: corriente máxima permitida para un conductor tipo k, entre los nodos i-j.
• Di: demanda en el nodo i en kVA.
• Si,M: potencia que entrega el transformador de distribución tipo M, ubicado en el nodo i.
• 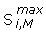 : capacidad nominal del transformador de distribución tipo M, ubicado en el nodo i.
: capacidad nominal del transformador de distribución tipo M, ubicado en el nodo i.
• Vi: voltaje en el nodo i.
• Vimax: máximo voltaje permitido en todos los nodos del sistema.
• Vimin: mínimo voltaje permitido en todos los nodos del sistema.
• ΩAN: conjunto de nuevos tramos de red del sistema.
• ΩA: conjunto de tramos de red nuevos y existentes del sistema.
• ΩTN: conjunto de transformadores nuevos del sistema.
• n: número total de nodos.
• nfex: número de tramos de red existentes.
• ntex: número de transformadores existentes.
• δij,k: variable de decisión binaria para la instalación de un conductor tipo k, entre los nodos i-j.
• δi,M: variable de decisión binaria para la instalación de un transformador tipo M, en el nodo i.
3.3 Función objetivo
La función objetivo a minimizar está dada por (1).
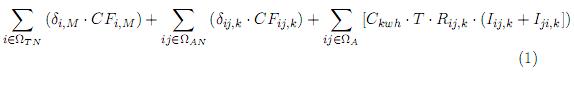
El primer término corresponde a los costos fijos de nuevos transformadores de distribución. Estos costos consideran el valor del transformador, los costos de los elementos como cortacircuitos primarios, transformadores, pararrayos, herrajes, etc., y el valor de su instalación y mano de obra. El siguiente término refleja los costos fijos de nuevos tramos de red. Estos costos tienen en cuenta el valor de cada metro de conductor, los costos de los elementos como aisladores, herrajes, estructuras, etc., y el valor de su instalación y mano de obra. El último término representa los costos variables o de operación de circuitos nuevos y existentes, los cuales consideran el valor de la corriente en forma lineal para el cálculo de las pérdidas de energía.
3.4 Restricciones
El conjunto de restricciones técnicas está compuesto por las ecuaciones (2) a (6).
• Ecuaciones de balance nodal. Considera la aplicación de la primera ley de Kirchhoff a todos los nodos del sistema garantizando de esta forma que todas las demandas sean atendidas y que no queden nodos aislados en la configuración final.
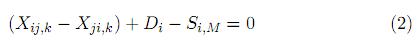
• Máxima capacidad de los transformadores de distribución. Se deben aplicar a todos los transformadores del sistema (nuevos y existentes) para garantizar que en la configuración final no se presenten sobrecargas en estos elementos.

• Máxima capacidad de los circuitos secundarios. Deben considerar todos los circuitos del sistema (nuevos y existentes) para garantizar que en la configuración final no se presenten tramos de red sobrecargados.

• Límites de voltaje. Asegura que los valores de tensión del sistema no sobrepasen unos límites permitidos.

• Restricción de radialidad. Con esta restricción se garantiza que las soluciones encontradas sean radiales.
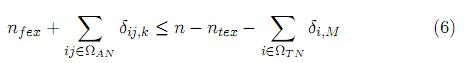
4 Algoritmo branch and bound
El algoritmo Branch and Bound (B&B ) [7], es una metodología que realiza una búsqueda completa de una solución óptima dentro de todo el espacio de búsqueda, pero con la ventaja de ir reduciéndolo a medida que encuentra puntos de infactibilidad y puntos para los cuales se determina una buena solución de la función objetivo.
El algoritmo B&B se basa en dos estrategias: dividir (branching) y explorar (bounding). La división se hace con el fin de disminuir el espacio de búsqueda en espacios de menor tamaño para los cuales encontrar la solución sea más fácil. La división se debe hacer sucesivamente hasta que la solución de cada subespacio sea entera. La exploración consiste en determinar soluciones parciales para cada uno de estos subespacios generados por la división del problema y con cada una de estas soluciones el algoritmo puede ir descartando cada uno de estos espacios. El óptimo global es la mejor solución de las encontradas en cada uno de los subespacios.
Otro aspecto que considera el algoritmo son las pruebas de sondaje por medio de las cuales se realiza la eliminación de nodos infactibles y los nodos para los cuales se obtiene un peor valor de la incumbente (mejor valor obtenido de la función objetivo). Este proceso es el que permite hacer que el espacio de búsqueda sea reducido de manera rápida. A continuación se describen las etapas consideradas por el algoritmo:
• Inicialización: para inicializar el algoritmo se deben introducir todos los datos del problema. Estos datos son la incumbente inicial y la lista de problemas candidatos (PL), o dicho de otra manera, el problema original relajado. Con la obtención de la incumbente inicial se inicia el proceso de sondaje. Si se determina una buena solución inicial el algoritmo podrá sondear una mayor cantidad de nodos y por lo tanto disminuye el espacio de búsqueda de manera más efectiva y por lo tanto el número de PL.
• Resolver el problema original relajando las integralidades y luego solucionar los PL resultantes.
• Selección de la próxima variable a separar. Una de las estrategias más empleadas es los pseudocostos. Estos pueden plantear dos estrategias para la selección de la variable para dividir: MAX-MAX (busca encontrar la variable que produzca la mayor degradación de la función objetivo para que uno de los problemas descendientes sea sondado rápidamente) y MAX-MIN (selecciona una variable cuya menor degradación en la función objetivo sea máxima, por lo tanto se pueden sondar rápidamente los dos subproblemas generados).
• Sondaje: en esta etapa el algoritmo realiza la eliminación de los nodos para los cuales se cumplan cualquiera de las siguientes tres condiciones. La primera es que si la solución del PL encontrada para el nodo es infactible, entonces el nodo es sondado. La segunda condición considera que si la solución determinada para el PL es menor que la incumbente actual, este nodo es sondado, pues las posibles soluciones enteras que se puedan generen a partir de este nodo también tendrán un valor de incumbente menor que la incúmbete actualizada. Finalmente, si la solución del PL es entera para las variables enteras entonces también se considera sondado este nodo.
• Selección del próximo problema a resolver. Cuando se emplea una buena estrategia de selección del próximo subproblema a resolver, la eficiencia computacional aumenta de manera drástica debido que al escoger los mejores subproblemas el espacio de búsqueda puede ser examinado de manera más rápida, ya que para cada uno de estos se obtendrán soluciones de mejor calidad con las cuales el proceso de sondaje se acelera y se reducen el número de PL a resolver. En esta etapa se pueden emplear tres estrategias: la primera es conocida como LIFO (en esta estrategia se escoge el último nodo que ingresa a la lista de PL), la segunda se conoce como FIFO (en esta estrategia se realiza una búsqueda a lo ancho del última es Vest (esta estrategia se basa en la utilización de los pseudocostos para realizar una mejor selección del próximo PL).
• Prueba de convergencia. Para verificar la convergencia se comprueba si el proceso de optimización ha terminado. En caso de haber terminado, entrega la solución encontrada. En caso contrario sigue explorando el espacio de búsqueda. Esta prueba no tiene ninguna implicación para el algoritmo, dado que solo entrega el criterio de parada.
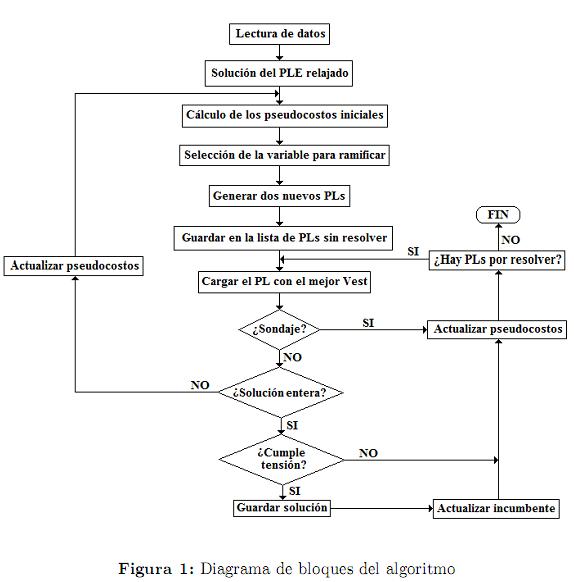
En el diagrama de bloques de la figura 1 se ilustra el algoritmo descrito anteriormente.
5 Aplicación y resultados
Para aplicar la metodología propuesta se empleó el software Matlab [8] en un computador personal con procesador core2duo 2.2Gh, capacidad de memoria de 4Gb y con un sistema operativo Windows Vista 32bit.
El sistema de prueba empleado corresponde a un sistema de distribución usado en la literatura especializada, el cual tiene cincuenta y cuatro nodos, y cincuenta y siete tramos de red propuestos [3]. Para resolver el problema se consideran doce posibles ubicaciones para los transformadores de distribución. El voltaje nominal del sistema es 127 Voltios. La máxima variación de voltaje permitida en todos los nodos del sistema es ±4 %. El valor considerado del kW-h es U S$0, 0345, (1U S$ = $2,000).
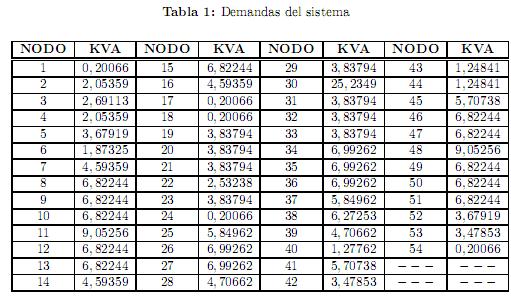
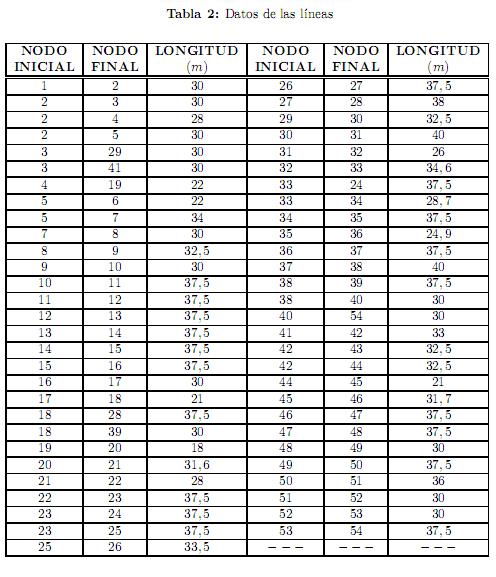
Los valores de las cargas y los datos de las líneas se muestran en las tablas 1 y 2, respectivamente.
La configuración inicial de la red se ilustra en la figura 2, donde los triángulos negros corresponden a las posibles ubicaciones de los transformadores de
distribución (nodos 2, 8, 11, 16, 23, 27, 30, 33, 37, 45, 48, 51), y las líneas punteadas a las rutas propuestas para los tramos de red.
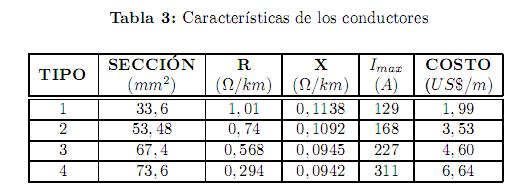
Las especificaciones de los diferentes tipos de conductores considerados se ilustran en la tabla 3. Los conductores son del tipo XLPE reticulado 90oC 600 V con conductor del neutro en aluminio desnudo (ACSR).
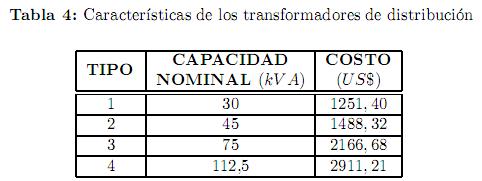
Los diferentes tipos de transformadores de distribución considerados se presentan en la tabla 4. Todos los transformadores son trifásicos, sumergidos en aceite, con conexión DY5 y con una frecuencia de operación de 60 Hz. Cada transformador tiene 13.2 kV en el lado primario y 220/127 voltios en el
lado secundario.
La respuesta encontrada por el algoritmo corresponde a un valor óptimo y tiene un costo de U S$17,458, 44, el cual se obtuvo después de solucionar 1361 PL. El tiempo computacional empleado por el algoritmo fue 102 segundos.
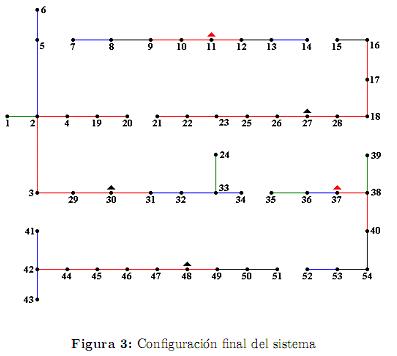
En la figura 3 se muestra la configuración seleccionada por el algoritmo, donde los triángulos rojos corresponden a transformadores de distribución con una capacidad nominal de 45 kVA (nodos 11, 37), y los triángulos en color negro a transformadores de distribución con una capacidad nominal de 75 kVA (nodos 27, 30, 48). Las líneas en color verde, azul, negro y rojo corresponden a líneas del tipo 1, 2, 3 y 4, respectivamente.
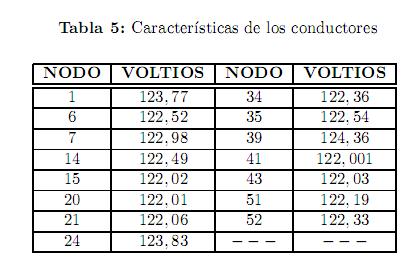
En la tabla 5 se ilustran las tensiones de los nodos terminales en la configuración final.
6 Conclusiones
• En este trabajo se propuso e implementó el algoritmo Branch and Bound aplicado a un modelo matemático lineal entero mixto (PLEM), el cual describe el problema del planeamiento de sistemas secundarios de dis
tribución. El modelo considera en la función objetivo a minimizar, los costos fijos y variables de transformadores de distribución y circuitos secundarios, así como también los costos variables de la red, los cuales consideran las pérdidas del sistema en forma linealizada. El conjun
to de restricciones técnicas involucradas tienen en cuenta la primera ley de Kirchhoff aplicada a todos los nodos del sistema (incluyendo los transformadores de distribución), las restricciones de capacidad máxima permitida de los elementos involucrados en el planeamiento, la radialidad de la red y las caídas máximas de tensión permitidas las cuales se aplicaron a todos los nodos del sistema.
• Algunos trabajos hallados en la literatura especializada proponen dividir el problema en dos etapas: una para la ubicación y dimensión óptima de los transformadores de distribución y la otra para el enrutamiento y dimensión de los circuitos secundarios. En este trabajo se realizó el planeamiento de estos sistemas en una sola etapa, donde las variables asociadas a transformadores y alimentadores se trabajaron en forma conjunta, pues la decisión de considerar uno de estos elementos para su
instalación afecta directamente al otro elemento.
• Los valores obtenidos son de gran calidad, pues se observa que la topología es radial, no se encuentran nodos aislados o cargas sin alimentar, los voltajes nodales al final de los circuitos están dentro de los límites permitidos y no se presentan sobrecargas en los elementos. Adicionalmente al encontrar el algoritmo un valor óptimo, se puede concluir que la metodología propuesta es válida para solucionar este tipo de problemas.
Referencias
1. Costa, A.M., França, P.M. Planejamento de Redes Secundárias de Distribuição de Energia Elétrica, XV Congresso Brasileiro de automática, Natal-RN, 2002. Referenciado en 49 [ Links ]
2. Yoshimoto, E. Planejamento de redes secundárias de distribuição de energía elétrica, Tesis de Maestría, Universidade Estadual de Campinas, Brasil, 2003. Referenciado en 49 [ Links ]
3. Cossi, A. M. Planejamento de circuitos secundários de distribuçao usando algoritmo evolutivo especializado, Tesis de Maestría, Universidade Estadual Paulista, Brasil, 2005. Referenciado en 49, 57 [ Links ]
4. Souza, C.H. Planejamento e projecto de circuitos secundários de distribuição de energía eléctrica utilizando algoritmo busca tabu Tesis de Maestría, Universidade Estadual Paulista, Brasil, 2006. Referenciado en 50 [ Links ]
5. Marroquín, O.A. Planeamiento de redes secundarias de distribución usando un algoritmo de optimización basado en colonia de hormigas, Tesis de Maestría, Universidad Tecnológica de Pereira, 2008. Referenciado en 50 [ Links ]
6 González, J.D., Gallego, R.A., Hincapié, R.A. Modelamiento matemático del problema del planeamiento de sistemas secundarios de distribución Revista Colombiana de Tecnologías de Avanzada, Universidad de Pamplona, 2009. Referenciado en 50 [ Links ]
7. Gallego, R.A., Romero, R.A., Escobar, A.H. Optimización en Sistemas Eléctricos II. Texto guía, Maestría en Ingeniería Eléctrica. Universidad Tecnológica de Pereira. Primera Edición, Capítulo 4. Referenciado en 55 [ Links ]
8. http://www.mathworks.com Referenciado en 57 [ Links ]