Solución de un modelo simplificado de publicidad usando técnicas de control óptimo

Solução de um modelo simplificado de publicidade que usa técnicas de controle ótimo

Solution of a simplified advertising model using optimal control techniques

Ekaterina Tuchnolobova¹, Viktor Terletskii² y Olga Vasilieva³

¹ Licenciada en Economía Matemática, tuchnokaterina@mail.ru, estudiante de doctorado, Universidad Estatal de Irkutsk, Irkutsk-Rusia.

² Ph.D. en Ciencias Físicas y Matemáticas, terletsky@math.isu.ru, profesor asociado, Universidad Estatal de Irkutsk, Irkutsk-Rusia.

³ Doctorado en Ingeniería, Ph.D. en Ciencias Físicas y Matemáticas, olgavas@univalle.edu.co, profesora titular, Universidad del Valle, Cali-Colombia.

(Recepción: 15-sep-2010. Modificación: 12-may-2011. Aceptación: 18-may-2011)

Se aceptan comentarios y/o discusiones al artículo

---

Resumen

En este artículo se presenta una simplificación al modelo distribuido de publicidad, formulándolo como una familia de problemas de control óptimo con parámetros concentrados. Se estudian dos variantes simplificadas: lineal y no lineal. Para el modelo lineal se proporciona una solución analítica derivada del principio de máximo. Para resolver el modelo no lineal se construye un algoritmo numérico basado en dos fórmulas no convencionales del incremento de la funcional objetivo.

Palabras claves: modelo de publicidad, control óptimo, parámetros concentrados, principio de máximo de Pontryagin.

---

Resumo

Neste artigo nós apresentamos uma simplificação do modelo distribuído de publicidade formulando isto como uma família de problemas de controle ótimo com parâmetros concentrados. Nós estudamos duas variantes do modelo simples: linear e não linear. Para o modelo linear fornece uma solução analítica derivada do princípio de máximo. Para resolver o modelo não-linear, nós construímos um algoritmo numérico baseado em duas formas não convencionais de aumentar o funcional objetivo.

Palavras chaves: modelo de publicidade, controle ótimo, parâmetros concentrados, princípio de máximo de Pontryagin.

---

Abstract

In this article we present a simplification of the distributed model of advertising by formulating it as a family of optimal control problems with concentrated parameters. We consider two simplified models: linear and non-linear. Linear model is solved analytically using the maximum principle. To solve non-linear model, we construct a numerical algorithm based on two nonconventional increment formulae for the objective functional.

Key words: advertising model, optimal control, concentrated parameters, Pontryagin maximum principle.

---

1 Introducción

Para tener éxito en ventas, las empresas deben participar en la conformación de la opinión pública acerca de sus servicios y/o productos. Este último se realiza a través de campañas publicitarias y cada empresa debe elegir una estrategia publicitaria óptima con la cual se pueda atraer un mayor número de consumidores de un nuevo producto o servicio.

Está claro que, en primer lugar, los fondos disponibles para inversión a la publicidad, siempre están limitados. En segundo lugar, se busca lograr el máximo efecto de dicha inversión y obtener el máximo beneficio. Existen muchos modelos de optimización dinámica que abordan este tipo de problemas desde el punto de vista de control óptimo [2, 3]. Entre ellos hay una clase bastante limitada de problemas que se formulan en términos de parámetros distribuidos, tomando en cuenta no sólo la dinámica temporal sino también la distribución por edades de los potenciales consumidores. En particular, enfaticemos un modelo formulado en [1] que contiene todas las funciones exógenas de entrada en forma explícita. Dicho modelo describe detalladamente el proceso de persuasión de nuevos consumidores y toma en cuenta un conjunto amplio de factores que pueden influir sobre la dinámica del mismo. No obstante, en [1] solo se formula el problema de optimización del modelo a grandes rasgos y se realizan algunas simulaciones numéricas para adivinar la estructura del control óptimo derivada del principio de máximo en su versión variacional.

El objetivo de este artículo consiste en buscar solución de modelo dinámico distribuido formulado en [1], usando técnicas de control óptimo.

La Sección 2 proporciona el planteamiento del modelo original derivado en [1] y lo formula como un problema de control óptimo con parámetros distribuidos. Dicho problema se reduce luego (Sección 3) a una familia de sub-problemas de control óptimo con parámetros concentrados a los largo de las características del sistema. En la Sección 4 se hace un intento de resolver analíticamente el sub-problema mencionado haciendo linealización del modelo original. Dicha simplificación desmejora considerablemente el modelo original y, para mitigar este efecto negativo, se introduce nuevamente la dependencia no lineal con respecto a la variable de control. En consecuencia, se obtiene un problema con valores en la frontera, resultante de aplicación del principio de máximo de Pontryagin, que resulta insoluble en términos analíticos. Por ende, en la Sección 5 se propone un algoritmo numérico cuya justificación está basada en las fórmulas no convencionales de representación del incremento de la funcional objetivo [4, 5].

2 El modelo y su formulación en términos de control óptimo

En primer lugar vamos a dar una breve descripción del modelo dinámico distribuido formulado en [1]. Se buscan políticas publicitarias de una empresa que le ayuden a vender un nuevo producto o servicio a un mayor número de potenciales consumidores.

Se introducen primero dos variables independientes: sea t ∈ [0, T] la variable temporal donde T >0 marca el período de observación y seas∈ [0, ω] la edad de potenciales consumidores donde ω > 0 denota la edad máxima.

Las variables endógenas del modelo son:

P(t, s) - número de compradores potenciales de edadsen el instante t;

A(t, s) - número de compradores reales (activos) de edad en el instante.

Las variables exógenas y otros parámetros del modelo son:

u = u(t, s) - parámetro de control que indica el monto de dinero que la empresa invierte en publicidad.

µ(t, s, u) - tasa de conversión de compradores potenciales en compradores reales;

a(t, s) - tasa de deserción de los compradores;

φ(s) - distribución de la población de consumidores según sus edades en el momento inicial de tiempo;

κ - tasa de nacimientos de la población (constante).

La variación del número de consumidores con respecto a tiempo se puede describir por medio de ecuaciones (1)(2) con condiciones iniciales (3)(4):

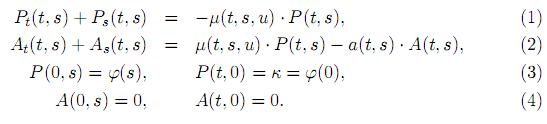
Según (1) y (2), al invertir dinero en la publicidad del producto, en número de compradores potenciales disminuye en µ(t, s, u) ^. P(t, s), mientras que el número de compradores reales (activos) aumenta en esta misma medida. El segundo término del lado derecho de la ecuación (2) expresa la deserción natural de los compradores.

La condición (3) implica que en el momento inicial del período de observación, la población se encuentra distribuida según las edades mediante una función conocida φ(s), y que el número de compradores potencias de edad cero (recién nacidos) es igual a κ.

La condición (4) indica que el número de compradores activos en el momento inicial es cero y que, lógicamente, no hay ningún comprador activo de edad cero en el momento inicial.

Observacion 2.1. En el modelo anterior (1)(4), la población total de edad s en el instantetse considera esencialmente invariante con respecto a s y t, esto es, X(t, h) = X(t + h, s + h) con h > 0 donde X(t, s) = P(t, s) + A(t, s) + R(t, s) siendo R(t, s) el número de personas que no tienen capacidad económica para adquirir producto publicitado y este grupo evoluciona de acuerdo con la ecuación

R_t(t, s) + R_s(t, s) = −a(t, s) ^. A(t, s) ^.

Esta última ecuación no está considera en el modelo ya que su dinámica no depende directamente de la variable de control. En otras palabras, los integrantes de R(t, s) son inmunes a campañas publicitarias.

La política publicitaria de la empresa debe tener la siguiente meta: definir qué monto u(t, s) para la edad s en el momento t se debe invertir en actividades de publicidad (cuyo fin es a convertir los compradores potenciales en compradores reales) y así maximizar las ganancias de venta.

En términos matemáticos, se busca maximizar la funcional objetivo (5) que expresa la ganancia total de las ventas dentro del periodo de observación t ∈ [0, T] y para todas las edadess ∈ [0, ω]:

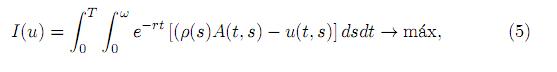
donde

ρ(s) - rendimiento obtenido de un consumidor de la edadsen unidad de tiempo,

r - tasa de descuento,

ω - edad máxima de consumidor,

T - periodo de observación (T > ω).

El parámetro de control u(t, s) debe satisfacer la restricción presupuestaria

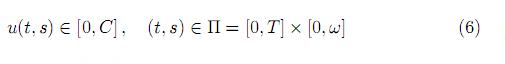
en su dominio Π donde C >0 denomina presupuesto máximo disponible para la inversión en actividades publicitarias.

Así se acaba de formular un problema de control óptimo con parámetros distribuidos: se busca una función de control u(t, s) que satisfaga la restricción (6) y maximice la funcional objetivo (5) sujeto al sistema hiperbólico semilineal (1)(2) con condiciones iniciales (3)(4).

Observacion 2.2. Los autores del modelo [1] han considerado numerosos factores que pueden influir en la dinámica de persuasión de los compradores, logrando así estimar explícitamente las variables exógenas del modelo que aparecen el Apéndice.

3 Reducción a una familia de problemas de control óptimo con parámetros concentrados

Un atributo propio de sistemas hiperbólicos de tipo (1)(2) es la existencia de las llamadas características. Estas son líneas, a lo largo de las cuales existe derivada solamente con respecto a una de las dos variables (parámetro de dicha característica).

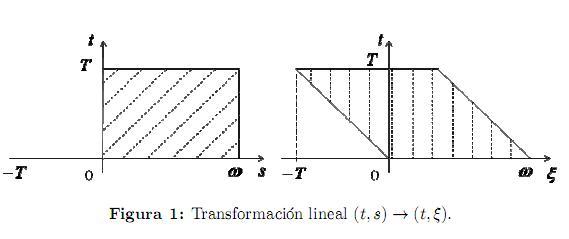
Vamos a introducir un cambio de variables (t, s) → (τ , ξ). Sean ξ = s − t, τ = t. A lo largo de las características ξ = s − t del operador diferencial hiperbólico x_s + x_t, ese operador coincide con el operador diferencial con respecto a la variablet:

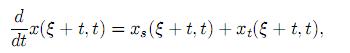
donde el parámetro ξ ∈ [−T , ω] puede verse como “número” de la características = t + ξ.

Entonces las funciones 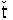(ξ) y 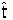(ξ) definen los extremos del intervalo T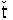(ξ) = (ξ),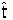(ξ) de la variable t de manera que todos los puntos (t, s) = (t, ξ + t) de la característica s = ξ + t pertenecen al rectángulo Π = [0, T] × [0, ω] si T > ω (Figura 1):

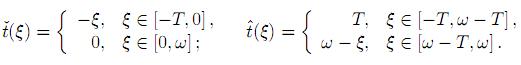
De acuerdo con este razonamiento, el operador diferencial hiperbólico puede verse, a lo largo de su característica ξ ∈ [−T , ω], como operador diferencial (ordinario) con respecto a t.

Usando el mismo cambio de variables podemos reducir la integral doble sobre la región Π a una integral repetida que suma todos los valores de la función integrante a lo largo de las características:

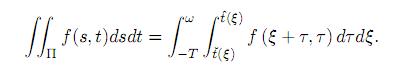
Al completar este paso, podemos formular el problema de control óptimo con parámetros distribuidos (en derivadas parciales) como una familia paramétrica respecto al parámetro ξ ∈ [−T , ω] de problemas de control óptimo con parámetros concentrados (en derivadas ordinarias). Cada uno de estos problemas tiene la siguiente forma:

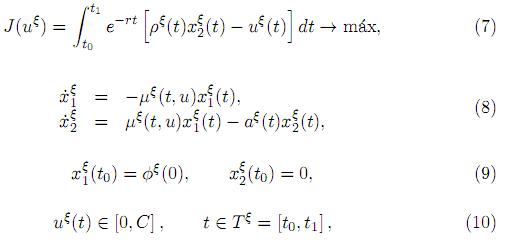
donde

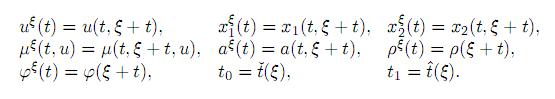
Para cada valor del parámetro ξ ∈ [−T , ω], el problema resultante (7)(10) es equivalente al problema original (1)(6) en el sentido de que cualquier solución (analítica o numérica) de (7)(10) para cada ξ, implicará efectivamente la solución del problema original con parámetros distribuidos (1)(6).

En adelante examinaremos sólo un problema de la familia (7)(10), omitiendo su respectivo superíndice ξ.

4 Solución analítica del problema de control óptimo con parámetros concentrados

Para poder enfrentar el problema (7)(10) en términos analíticos, parece necesario simplificarlo primero. Para este fin, fijemos valores de funciones µ₀(t, s), ρ(s), a(t, s), φ(s) como constantes tomando simultáneamente una aproximación de µ(t, u) = µ₀(t, ξ + t) [13 − 12e−u] (véase el Apéndice) en forma µ(u) = A + Bu(t), A, B = const, A, B > 0.

Por ende, el modelo simplificado será:

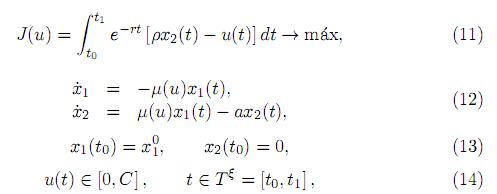
El problema simplificado (11)(14) puede ser solucionado usando el principio de máximo de L. S. Pontryagin como condición necesaria de optimalidad de primer orden. De acuerdo con dicho principio, existen dos multiplicadores (ψ₁, ψ₂ ) como funciones de tiempo t (éstos denominan precios sombra en economía) y la función Hamiltoniana definida por

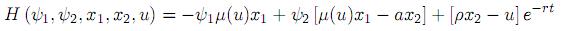
debe alcanzar su valor máximo en un control óptimo con respecto a todo u(t) ∈ [0, C], esto es,

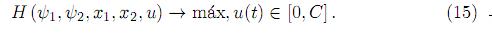
Dichos multiplicadores (ψ₁, ψ₂ ) (también llamados variables de co-estado) obedecen al sistema adjunto

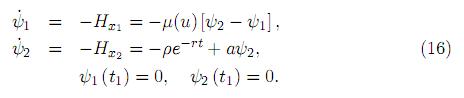
Al realizar el cambio de variables (p₁, p₂) = e^rt(ψ₁, ψ₂), obtenemos:

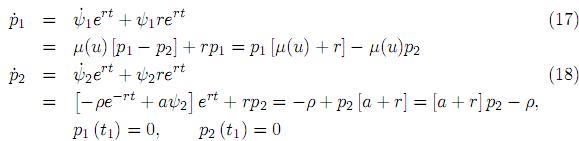
Podemos observar que, de acuerdo con (16), la componente ψ₂ no depende explícitamente de la variable de control u; luego, podemos calcularla sólo una vez como función de t, esto es,

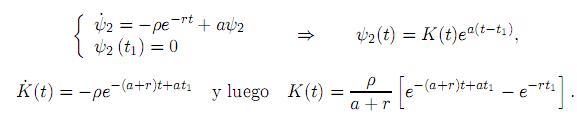
Se obtiene entonces ψ₂(t) = 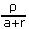[e^−rt − e^{at−(a+r)t₁}] ^. Teniendo en cuenta que p₂(t) = ψ²(t)e^rt, se obtiene también

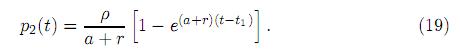
Usando la notación d = x₁[p₂ − p₁] y µ(u) = A + Bu(t), la función Hamiltoniana puede expresarse como

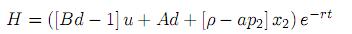
donde solamente el primer término dentro de las paréntesis depende explícitamente de u(t). Podemos entonces omitir los términos que no dependen de u(t) explícitamente y formular el nuevo problema simplificado de maximización equivalente a (15):

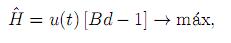
El máximo de 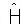ocurre cuando 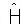_u = Bd − 1 = 0, y es efectivamente

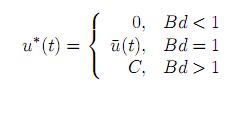
donde 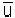(t) puede ser un posible control singular a lo largo del camino Bd = 1. Verifiquemos entonces si este 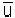(t) existe derivando con respecto atambos lados de la relación Bd = 1:

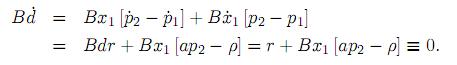
El resultado anterior se obtuvo aplicando las relaciones (12), (17) y (18) y de acuerdo con él tenemos, en vista de (19), que la componente 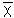₁(t) correspondiente a (t) debe satisfacer

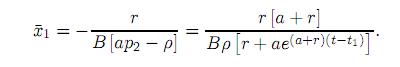
Una vez conocida ₁, podemos encontrar a (t) a partir de (12):

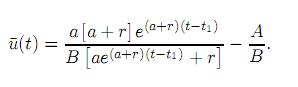
Del (17) se sigue que 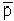₁= 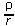e^{(a+r)(t−t₁)} < 0 y si 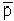₁ < 0, entonces 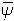₁ < 0. Así llegamos a una contradicción ya que la condición de transversalidad 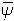₁ (t₁) = 0 será violada en este caso. Por lo tanto, no existe ningún 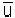(t) tal que Bd = 1; en otras palabras, no existen controles singulares.

Conviene notar que la no existencia de arco singular junto con la linealidad de 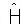con respecto a la variable de control estipulan que sólo habrá a lo más una conmutación.

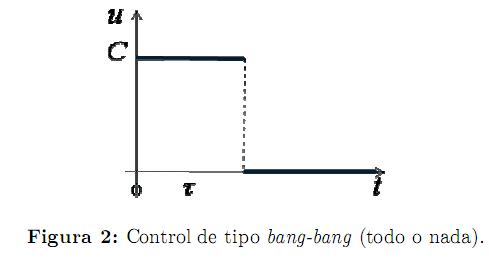
Por ende, la estructura del control óptimo para el modelo simplificado será de tipo “bang-bang” (todo o nada):

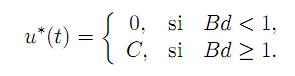
De allí surgen dos variantes:

1. Durante todo el periodo de observación no se invierta nada en la publicidad, esto es,

u*(t) ≡ 0, t∈ [t₀, t₁]

Entonces se tiene que x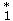(t) = x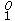e^{−A(t−t₀)} y

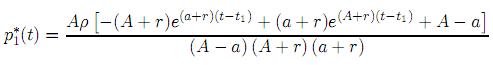
Esto ocurre si Bd < 1 para todo t ∈ T= [t₀, t₁ ] y la condición anterior tendrá lugar siempre y cuando se cumpla

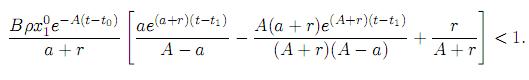
2. Al inicio del periodo de observación se hace la inversión máxima en la publicidad, y después no se invierta nada más hasta el fin del periodo (Figura 2): Entonces debe existir un punto de conmutación τ ∈ [t0, t1] tal que Bd = 1 y se tiene

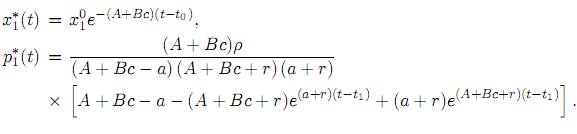
La igualdad Bd = 1 tendrá lugar siempre y cuando

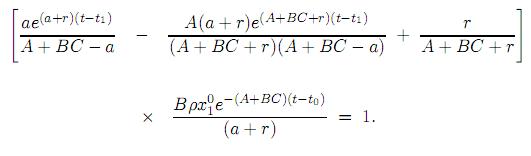
Así, acabamos de dar una solución formal al problema (11)(14); no obstante, las simplificaciones realizadas al modelo original (1)(6) lo empobrecieron drásticamente y esto se reflejó en la trivialidad de la respuesta.

Trataremos aminorar el perjuicio ocasionado por la linealización de µ(u) = A + Bu(t), considerando en su lugar µ(u) = A − Be^−u que se ve más acorde al modelo original (véase la forma de función µ(t, s, u) estimada en [1], que aparece en el Apéndice). Sean

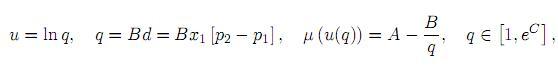
suponiendo que Bx₁ [p₂ − p₁] > 0 (en el caso contrario la condición (15) será insoluble). Entonces se tiene que

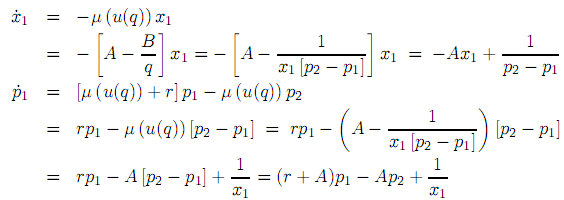
donde p₂ no depende de µ(u) y está dado por (19). Como resultado obtenemos un problema no lineal con valores de frontera:

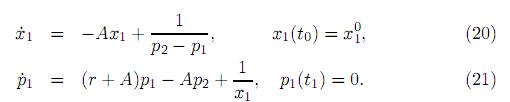
En este problema, p₂(t) está dado por (19) pero no existe método analítico para resolverlo con respecto a x₁(t), p₁(t) con el fin de hallar luego q = Bx₁[p₂ − p₁], y por ende u (t) = ln q.En otras palabras, no se ve posible encontrar una forma explícita para u(t) (como, por ejemplo, de tipo bang-bang).

No obstante, en la Sección 5.2 se justificará la idea de introducir u(t) = ln q como una función de control “intermedia”, derivada del principio de máximo. En consecuencia, será necesario aplicar algún método numérico para resolver tanto problema con valores en la frontera (20)(21) como problema de controlóptimo (7)-(10).

5 Solución numérica del problema de control óptimo con parámetros concentrados

En esta sección se construirá un algoritmo numérico para solución del problema anterior en el caso de µ(u) = A − Be^−u. Dicho algoritmo generará una sucesión de controles admisibles u(k) que cumplen la relación J(u^(k+1)) ≥ J(u^(k)) . Para fundamentarlo, nos serán de utilidad dos fórmulas no convencionales que expresan el incremento de la funcional objetivo [4, 5].

5.1 Representación del incremento de la funcional objetivo

Sean {u, x} y {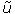,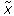} - dos procesos arbitrarios admisibles en el problema (7)(10):

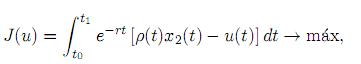
sujeto a = A(u, t)x(t), donde

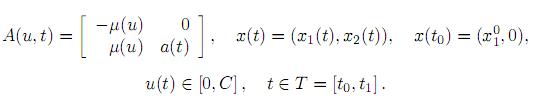
Sea ∆x = 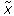− x; y la función Hamiltoniana tiene forma:

Vamos a construir el incremento de la funcional objetivo con respecto a la variable de control, adicionando a la función integrante el llamado “cero axiomático”, esto es,

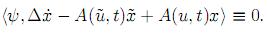
Entonces:

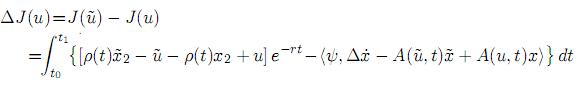
Podemos observar que el término que queda bajo el signo de la integral coincide con el incremento de la función Hamiltoniana:

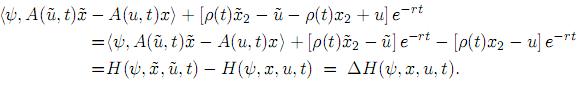
Así, tenemos que

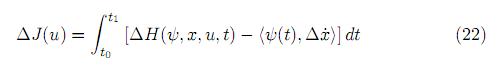
Usando el desarrollo de Taylor, se puede llegar a diversas variantes que representen el incremento de la funcional objetivo ∆J(u).

Consideremos primero el desarrollo habitual (véase, por ejemplo [6]):

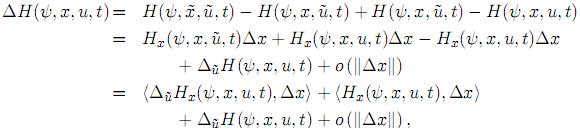
dondeo(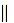∆x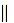) representa el resto de la fórmula de Taylor. Aquí la variable de co-estado ψ obedece al sistema adjunto tradicional 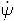= −H_x(ψ, x, u, t), ψ(t₁) = 0. Sustituyéndola junto con la siguiente integración por partes

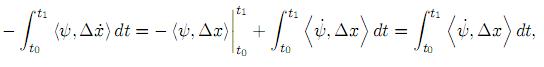
en la Ec. (22), obtenemos que la parte principal del incremento ∆J(u) puede escribirse como

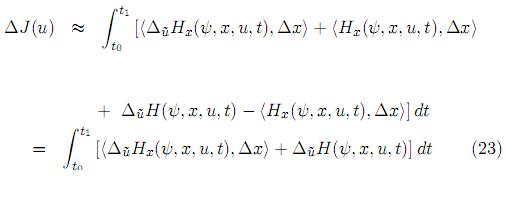
donde ψ, H, H_x están evaluadas en {u, x}.

El enfoque tradicional consiste en separar solamente la parte lineal del incremento ∆J(u) con respecto a la variable de control. Por esta razón, cuando se trata de problemas no lineales, surge inevitablemente un resto más en la fórmula de incremento distinto deo(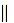∆x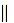). Este último suceso sólo permite construir métodos numéricos basados en búsquedas uniparamétricas.

Existen otras variantes de la presentación de ∆J(u) que no contienen dicho resto (primer término en (23)), entre ellos vamos a revisar brevemente las dos siguientes:

a) Modificación ofrecida en [4]. Se hace

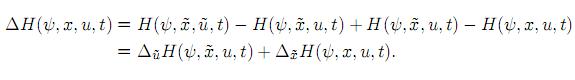
Introduciendo la variable de co-estado de manera tradicional, esto es, 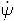= −H_x(ψ, x, u, t), ψ(t₁) = 0, se obtiene:

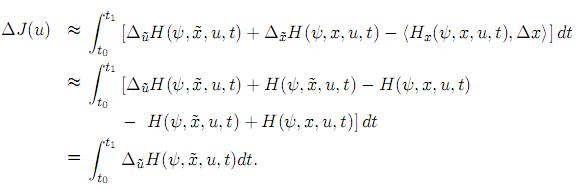
Luego, la parte principal del incremento de la funcional objetivo (22) será representado por

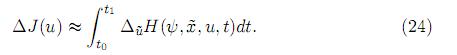
Conviene notar que la variable de co-estado ψ(t) está evaluada en {u, x} pero el incremento ∆J(u) queda evaluado en el estado ya “actualizado” .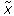

b) Modificación ofrecida [5]. Se hace

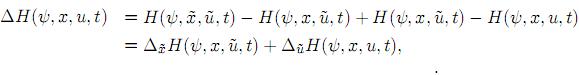
definiendo la variable de co-estado “actualizada”, esto es, 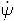= −H_x(ψ, x, 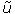, t), ψ(t₁) = 0.

En este caso, el incremento de la funcional objetivo (22) puede escribirse como

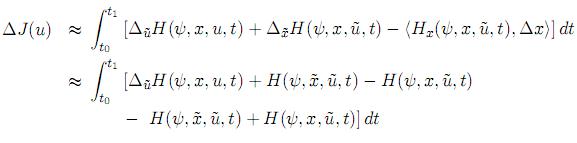
y es equivalente a

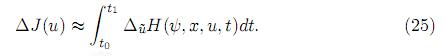
En esta variante, al contrario, ∆J(u) tiene forma tradicional pero la variable de co-estado ψ se evalúa en el proceso “actualizado” .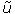

Fórmulas (24) y (25) se consideran “más exactas” que la fórmula tradicional (23) porque permiten evaluar el incremento ∆J(u) con mayor precisión (sin término resto). Por otro lado, hay un “cobro” por dicha exactitud que consiste en el uso de perfiles “actualizados” ψ o 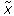correspondientes al nuevo control perturbado 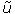.Se debe aclarar que este resultado sólo tiene lugar cuando la función Hamiltoniana depende linealmente de x.

5.2 Condición del máximo de la función Hamiltoniana

Resolver la condición del máximo de la función Hamiltoniana con respecto a la variable de control (que a su vez es la condición necesaria de optimalidad) es esencial para la solución del problema de control óptimo. Dicha condición se formula así:

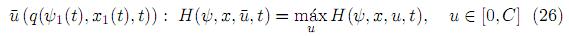
donde la función Hamiltoniana H(ψ, x, u, t) definida por (15) puede escribirse como

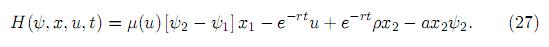
Multiplicándola la por e^rt y omitiendo todos los términos que no dependen de u explícitamente, obtenemos un nuevo problema de maximización simplificado y equivalente a (26):

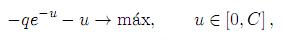
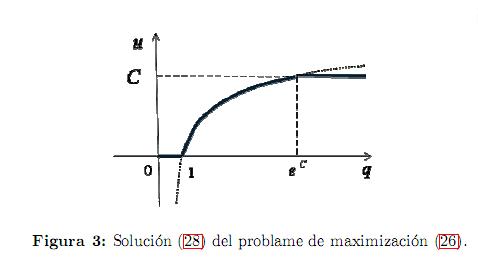
donde q(ψ₁(t), x₁(t), t) = Be^rt [ψ₂− ψ₁]x₁. Su solución en ausencia de restricciones sobre la variable de control (máximo incondicional) es:

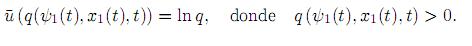
Aplicando la restricciónu∈ u ∈ [0, C], se recortan simplemente las trayectorias que sobresalen los límites admisibles del intervalo [0, C] (véase la Figura 3). Así, la solución de la condición del máximo (26), está dada por:

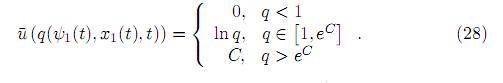
Teniendo en cuenta que 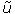depende continuamente de q ( 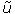en sí es una superposición de funciones ψ₁, x₁ absolutamente continuas de t), podemos concluir que 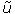es continua con respecto a t. Esta propiedad de continuidad de 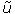respecto a t es bastante esencial para justificar el algoritmo de la solución numérica.

5.3 Esquema del algoritmo numérico

Para finalizar, daremos una descripción esquemática del algoritmo numérico basado en las fórmulas no tradicionales (24) y (25).

Dicho algoritmo generará una sucesión que cumple la propiedad:

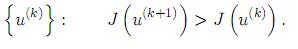
Iteración 0.

Sea k = 0 y defina una función inicial de control u⁽⁰⁾ arbitrariamente. Integre numéricamente (12) para u⁽⁰⁾, almacena el estado correspondiente x⁽⁰⁾ y calcule el valor de J(u⁽⁰⁾). Se hace luego k := k + 1.

Iteración 1 .

Calcule la variable de co-estado ψ⁽⁰⁾como solución de (16). Según lo mencionado anteriormente, 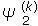no depende de u. Por lo tanto, dicho perfil se evalúa una sola vez y se almacena como función de t solamente. Para evaluar 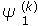, se integra

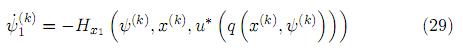
hacia atrás usando la condición terminal ψ^(k)(t₁) = 0. El objetivo de esta integración es encontrar 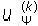haciendo uso de la relación (28), esto es,

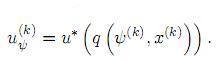
Si el incremento ∆J(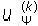 )= J (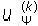) − J(u^(k)) no tendrá sentido realizar más iteraciones. De tal manera, el algoritmo se debe detener cuando para una ζ > 0 (precisión computacional) previamente asignada se cumple

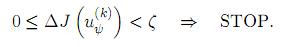
Iteración 2.

Calcule 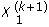mediante integración de

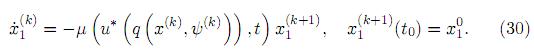
Podemos observar que la componente x₂ no participa en la construcción de u^* ya que q depende efectivamente de ψ₁, x₁ y t. Por lo tanto, no habrá necesidad de evaluarla.

Por ende, construimos la nueva función de control u^(k+1), usando la fórmula

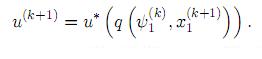
La condición para detener el proceso iterativo es semejante a la de Iteración 1 y está dada por:

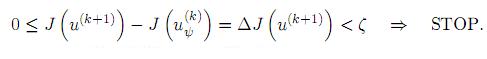
Finalmente se hacek:=k+ 1 para pasar nuevamente a la Iteración 1.

Para llevar a cabo la integración numérica de las ecuaciones (28) y (29) se puede hacer uso de diversas técnicas. Por ejemplo, podemos emplear el método de Euler mejorado (con re-calculación) “hacia atrás” (para la ecuación (29) y “hacia adelante” (para la ecuación (30)).

Para la ecuación diferencial (29) se aplica primero la fórmula explícita de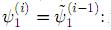

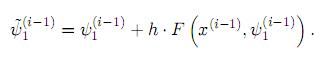
Luego, se usa la fórmula implícita (re-calculación) para evaluar :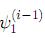

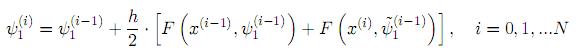
donde h = (t₁ − t₀)/N es el paso de integración y F representa el lado derecho de (29). El mismo esquema se puede usar para integrar la ecuación (30) en modo “hacia adelante”.

De acuerdo con lo mencionado anteriormente, en la solución de la condición del máximo (26), el control óptimo u^* depende continuamente de tiempo t. En el marco del algoritmo descrito, esta propiedad justifica la continuidad de las funciones en los lados derechos de las ecuaciones diferenciales (29) y (30). Esto a su vez garantiza una buena solubilidad referente al proceso de integración. De tal manera, podemos concluir que el algoritmo introducido trabajará continuamente y que en cada iteración (excepto Iteración 0), aumentará el valor de la funcional objetivo.

Conviene notar que los algoritmos habituales basados en el principio de máximo requieren dos integraciones (una hacia adelante y otra hacia atrás) para efectuar el paso de u^(k) a u^(k+1) que cumplan la propiedad de relajación

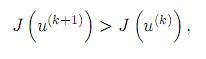
mientras que con el algoritmo presentado en este trabajo se logra realizar una doble actualización de control u^(k) → 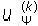→ u^(k+1) efectuando las mismas dos integraciones y garantizando que

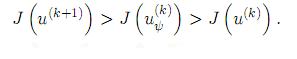
En cuanto a la convergencia del algoritmo, ésta puede ser garantizada en el sentido de que

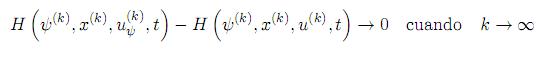
donde 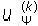se entiende como solución de la condición del máximo (26). Dicho resultado fue comprobado en [4, 5] para un caso más general (x ∈ 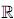ⁿ, u ∈ U ⊂ 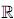^m) bajo las siguientes condiciones:

1. Existe un control óptimo que resuelve la condición (26).

2. La derivada parcial H_x satisface la condición de Lipschitz.

3. La función W (u^(k), t) H (ψ^(k), x^(k), , t) − H (ψ^(k), x^(k), t) satisface la condición de Lipschitz con la misma constante para cada k = 0,1,2, ...

4. La funcional objetivo J(u) es acotada superiormente.

6 Conclusiones

En este trabajo se analizó un modelo de optimización que describe la actividad publicitaria de una empresa que procura vender un nuevo producto a un mayor número de consumidores. El modelo original elaborado en [1] está formulado en términos un sistema hiperbólico semilineal en derivadas parciales con respecto a dos variables independientes - tiempo de observación y la edad de los consumidores. Para resolver dicho modelo con parámetros distribuidos, se llevó a cabo su reducción a una familia de problemas de control óptimo con parámetros concentrados a lo largo de las características del sistema original.

Conviene notar que los autores de [1] se enfocaron principalmente en la estimación parámetros del mismo modelo. Dada la complejidad de las funciones estimadas, nos resultó necesario simplificar el modelo original con el fin de proponer un método adecuado para su solución analítica. Tal simplificación (linealización de µ(u) con respecto a u) empobreció considerablemente el modelo original, lo cual fue evidenciado por la ordinariez de la respuesta obtenida en la Sección 4. Por otro lado, se demostró que si µ(u) depende de u de manera no lineal, la aplicación del principio de máximo de Pontryagin resulta en un sistema con valores en la frontera que es insoluble en términos analíticos. Esta ocurrencia nos señaló la necesidad de construir un algoritmo numérico para su solución.

En la Sección 5, haciendo uso de dos fórmulas no convencionales para el incremento de la funcional objetivo [4, 5] se planteó un método de aproximaciones sucesivas {u^(k)} que cumplen la relación J(u^(k+1)) ≥ J(u^(k)). Por medio de dichas fórmulas se consigue evaluar el incremento ∆J(u) sin términos restantes. La construcción del método resultó posible, en vista del carácter específico del problema de control óptimo examinado (linealidad con respecto a x). Las ventajas del algoritmo propuesto son la continuidad de su funcionamiento y su estructura bifásica (Iteración 1 y Iteración 2), donde en cada fase se realiza una sola integración y con esto se logra mejorar dentro de la misma fase en el valor de la funcional objetivo.

Agradecimientos

Los autores expresan su agradecimiento a dos árbitros anónimos de la revista por sus valiosos comentarios y sugerencias que contribuyeron para mejorar el manuscrito.

Este trabajo fue realizado en el marco del Convenio de Cooperación Académica entre la Universidad Estatal de Irkutsk (Irkutsk, Rusia) y la Universidad del Valle (Cali, Colombia); vigencia 2010-2015.

Referencias

1. E. P. Bokmel'der, A. Y. Gornov and G. Feichtinger. Optimization of advertising activity for initiation for fashionable goods: a distributed model. Optimizaciya, upravlenie, intellekt, ISSN 2218-6250, 6(1), 149-157 (2002) [en ruso, resumen en ingles]. Referenciado en 162, 163, 165, 172, 181, 183        [ Links ]

2. G. Feightinger, R. F. Hartl and S. Sethi. Dynamic optimal control models in advertising: recent developments. Management Science, ISSN 0025-1909, 40(2), 195-226 (1994). Referenciado en 162        [ Links ]

3. S. Sethi. Dynamic optimal control models in advertising: a survey. SIAM Review, ISSN 0036-1445, 19(4), 685-725 (1977). Referenciado en 162        [ Links ]

4. V. A. Srochko and N. V. Mamonova. Iterative pocedures for solving optimal control problems based on quasigradient approximations. Russian Mathematics (Iz. Vuz), ISSN 1066-369X, 45(12), 52-64 (2001). Referenciado en 163, 173, 175, 180, 181        [ Links ]

5. V. A. Srochko. Modernization of gradient-tye methods in optimal control problems. Russian Mathematics (Iz. Vuz), ISSN 1066-369X, 46(12), 64-76 (2002). Referenciado en 163, 173, 176, 180, 181        [ Links ]

6. O. V. Vasiliev. Optimization methods. World Federation Publishers Company, 1996, ISBN 1885978243. Referenciado en 174        [ Links ]

Apéndice.

Los autores del modelo [1], después de haber procesado encuestas suministradas por un supermercado de cadena en Rusia, lograron estimar explícitamente las variables exógenas del modelo distribuido (1)(6):

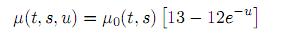
donde µ₀(t, s) denomina la tasa de conversión de compradores potenciales en compradores reales sin hacer campañas publicitarias y se expresa como