Estimación de propiedades mecánicas de roca utilizando inteligencia artificial

Estimativa das propriedades mecânicas da rocha usando a inteligência artificial

Estimation of mechanical properties of rock using artificial intelligence

 

Laura Viviana Galvis Carreño¹, Cesar Augusto Ochoa², Henry Arguello Fuentes³, Jenny Mabel Carvajal Jiménez⁴ y Zuly Himelda Calderón Carrillo⁵

¹ Ingeniera de Sistemas e Informática, laravivis@gmail.com, estudiante Maestría en Ingeniería de Sistemas e Informática, Universidad Industrial de Santander (UIS), Bucaramanga, Colombia.

² Ingeniero de Sistemas e Informática, czar8a@gmail.com, investigador, Universidad Industrial de Santander (UIS), Bucaramanga, Colombia.

³ PhD(c), henarfu@uis.edu.co, Profesor Escuela de Ingeniería de Sistemas e Informática, Universidad Industrial de Santander (UIS), Bucaramanga, Colombia.

⁴ Master en Ingeniería de Petróleos, jenny.carvajal@ecopetrol.com.co, investigador, Instituto Colombiano del Petróleo (ICP), Unidad de Investigación, Piedecuesta, Colombia.

⁵ Doctor en Ingeniería Química, calderon@uis.edu.co, profesor, Universidad Industrial de Santander (UIS), Bucaramanga, Colombia.

(Recepción: 21-sep-2010. Modificación: 27-may-2011. Aceptación: 15-nov-2011)

---

 

Resumen

Este artículo presenta la forma como fueron combinadas dos técnicas de inteligencia artificial, redes neuronales y algoritmos genéticos, para el desarrollo de una herramienta computacional utilizada para la estimación de propiedades mecánicas tales como la resistencia a la tensión, la resistencia a la compresión uniaxial y la resistencia a la compresión triaxial en areniscas, a partir de propiedades petrofísicas utilizando datos de pruebas del Laboratorio de Mecánica de Rocas del Instituto Colombiano del Petróleo – Ecopetrol S.A. como datos de entrenamiento facilitando el diseño de ensayos no destructivos con cierto grado de confianza y dando lugar a una reducción de costos.

Palabras claves: inteligencia artificial, red neuronal artificial, algoritmo genético, propiedades petrofísicas, propiedades mecánicas.

---

 

Resumo

Este artigo discute como duas técnicas foram combinadas de inteligência artificial, redes neurais e algoritmos genéticos para o desenvolvimento de uma ferramenta computacional utilizada para o cálculo das propriedades mecânicas como resistência à tração, resistência à compressão uniaxial e resistência à compressão triaxial em arenitos de propriedades petrofísicas utilizando dados de testes do Laboratório de Mecânica das Rochas da Colômbia Petroleum Institute Ecopetrol SA como dados de treinamento para facilitar o desenho de ensaios não-destrutivos com algum grau de confiança, resultando em redução de custos.

Palavras chaves: inteligência artificial, redes neurais artificiais, algoritmos genéticos, as propriedades petrofísicas, propriedades mecânicas.

---

 

Abstract

This paper discusses how two artificial intelligence techniques were combined, neural networks and genetic algorithms for the development of a computational tool used for the estimation of mechanical properties such as tensile strength, uniaxial compressive strength and triaxial compressive strength in sandstones, from petrophysical properties using data from tests of Rock Mechanics Laboratory of the Colombian Petroleum Institute Ecopetrol SA as training data, to improve the design of non-destructive testing with some degree of confidence and resulting in cost reduction.

Key words: artificial intelligence, artificial neural network, genetic algorithm, petrophysical properties, mechanical properties.

---

 

1 Introducción

La estimación de propiedades o parámetros en diversas áreas de estudio es de interés para los investigadores que trabajan en lograr que sus modelos predigan estos parámetros con un alto grado de certeza y confiabilidad. Según la literatura, la técnica más utilizada para obtener estimaciones de parámetros es el clásico análisis de regresión; sin embargo, la calidad de las estimaciones por medio de esta técnica se ven limitadas cuando se presenta un problema no lineal [1]. Las redes neuronales artificiales constituyen un enfoque fundamentalmente distinto que consiste en aprender y generalizar las interacciones entre las variables de entrada y salida de un conjunto de datos. Debido a esta capacidad de aprender, las redes neuronales presentan un gran potencial en el modelado de comportamientos de rocas a partir de datos experimentales [2] [3]. Sin embargo, el principal obstáculo al utilizar esta técnica, es la determinación de la configuración de las partes de la red neuronal artificial, las cuales pueden ser ordenadas de múltiples formas.

Por otro lado, un algoritmo genético es un algoritmo matemático que transforma un conjunto de individuos o población (colección de objetos matemáticos representando un individuo), cada uno de los cuales tiene asociado un valor de adaptación, en una nueva población utilizando una serie de operadores basados en los principios darwinianos de supervivencia del más adaptado [4]. Este algoritmo es utilizado en este trabajo para dar solución al problema de la determinación de la configuración de la red, optimizando el proceso hasta obtener la configuración de la red neuronal (RN) que mejor se ajuste a los datos de entrenamiento y prueba, que es aquella que presenta los menores porcentajes de error.

Las redes neuronales han sido aplicadas satisfactoriamente en la estimación de propiedades mecánicas como la resistencia a la tensión y la resistencia a la compresión. En la literatura, [5] y [6] aplicaron redes neuronales artificiales para la predicción de resistencia a la compresión sin confinamiento (UCS) en muestras de roca como areniscas y rocas igneas a partir de propiedades como dureza, porosidad, densidad, tamaño de grano e información sobre el tipo de roca, [7] utilizó las RN para predecir tanto resistencia a la compresión sin confinamiento (UCS) como resistencia a la tensión (To) de esquistos o rocas metamórficas, utilizando la composición mineral y propiedades de textura y, [8] y [9] utilizaron las RN para predecir la resistencia a la compresión uniaxial (UCS) y la resistencia a la tensión a partir de velocidades de pulso ultrasónico, densidad, absorción de agua, densidad seca, densidad saturada y densidad aparente. Sin embargo, no se ha documentado en la literatura la estimación de resistencias a partir de propiedades petrofísicas como la porosidad y la permeabilidad, es por esto, que el objetivo principal de este artículo es presentar la herramienta desarrollada para la estimación de propiedades mecánicas en areniscas (resistencias a la tensión y a la compresión) a partir de propiedades petrofísicas utilizando redes neuronales y algoritmos genéticos. Además uno de los aportes de este trabajo es presentar los detalles de desarrollo de una herramienta software que permite encontrar la configuración óptima de red neuronal dado un conjunto de datos disponible.

Se presentan algunos conceptos fundamentales de inteligencia artificial y algoritmos genéticos en las secciones 2 y 3 y del campo de aplicación de este trabajo en la sección 4. También se presenta la herramienta, su diseño y funcionamiento en la sección 6 y, finalmente en la sección 8 se muestran los resultados prácticos obtenidos.

 

2 Redes neuronales artificiales

Las redes neuronales artificiales y su aplicación en diferentes áreas han sido ampliamente difundidas [10] [11] [12], están basadas en la analogía presente en el comportamiento del cerebro humano, principalmente las funciones realizadas por el sistema nervioso compuesto por redes de neuronas que individualmente poseen capacidades de procesamiento bajas, pero que en conjunto y dado las conexiones entre estas presentan altas capacidades cognitivas.

Se ha demostrado que las redes neuronales artificiales pueden usarse de forma individual o combinada con otros métodos [13]. Estas nuevas propuestas han mostrado excelentes resultados al resolver problemas de clasificación, identificación, optimización y predicción [14].

La unidad elemental de una red neuronal artificial es la neurona de comportamiento igual a la del cerebro humano. Un número de estas neuronas componen una capa y a su vez, las capas componen la red; estas neuronas tienen un alto grado de conectividad determinada por unos pesos y el reajuste constante de esos pesos es lo que permite que la red se adapte dinámicamente, es decir que es en las conexiones entre estas unidades donde reside la inteligencia de la red.

La forma como las redes neuronales obtienen conocimiento es mediante ejemplos igual como lo hacen los seres humanos, es decir que no se le indican reglas para llegar a una solución sino que ella misma crea sus propias reglas durante el aprendizaje, modificando su comportamiento en función de la experiencia, alcanzando así una generalización para que luego se le puedan presentar datos diferentes a los ya usados y lograr obtener una solución.

Los problemas a resolver cuando se entrenan redes neuronales son la determinación de los pesos que permitan el ajuste adecuado a los datos de entrenamiento y a valores fuera de este conjunto; y, la determinación de la configuración de red (número de capas, número de neuronas y funciones de activación óptimos para resolver un problema en particular).

 

3 Algoritmos genéticos

El Algoritmo Genético es una técnica computacional desarrollada por John Henry Holland [15] en 1970, él observó el vínculo entre la biología y la computación; y pensó que las máquinas podrían ser capaces de adaptarse a un entorno, de la misma manera que lo pueden hacer los animales.

Este método de análisis de problemas está basado en la teoría de la selección natural de Darwin. El algoritmo inicia con una población conformada por un conjunto de nodos, estos son una combinación de números, letras o cualquier otra forma de codificación que representen una respuesta al problema que se está evaluando, esta población inicial es creada de forma aleatoria. Cada nodo es evaluado por algún método para ver cuáles tienen más éxito. Estos éxitos luego son fundidos en un ”hijo” que tiene una combinación de los rasgos característicos de los padres. En ocasiones también se produce una mutación, alterando aleatoriamente uno de los valores de la codificación, esperando encontrar una respuesta en una zona diferente del espacio de búsqueda. Este proceso es repetido en ciclos llamados generaciones, en los que los hijos, van reemplazando a sus padres generación tras generación, esperando que cada población sea mejor a su predecesora. Para la combinación de nodos (cruce) y el reemplazamiento en la población, existen múltiples técnicas [16].

 

4 Propiedades petrofísicas

Mediante el estudio de la petrofísica, que es el estudio de las propiedades físicas y químicas que describen la incidencia y el comportamiento de las rocas, los sólidos y los fluidos, es posible caracterizar por ejemplo un depósito de petróleo o de gas, para lo que se realizan mediciones tales como resistividad, neutrones y densidad, a partir de las cuales se pueden cuantificar la permeabilidad, las saturaciones y la porosidad efectiva.

 

4.1 Porosidad (∅)

Es la fracción del volumen total de la roca ocupada por su espacio poroso, y representa el porcentaje del espacio total que puede ser ocupado por líquidos o gases. Esta propiedad determina la propiedad de acumulación de las rocas y, generalmente, se expresa como porcentaje o fracción de la unidad [17].

 

4.2 Permeabilidad (k)

Es la capacidad de una roca para permitir el flujo de fluidos, por lo que determina la velocidad a la que se desplaza el fluido que contiene por unidad de tiempo.

Se dice que un material es permeable si deja pasar a través de él una cantidad apreciable de fluido en un tiempo dado, e impermeable si la cantidad de fluido es despreciable.

Para ser permeable un material debe ser poroso, es decir, debe contener espacios vacíos o poros que le permitan absorber fluido. A su vez estos poros deben estar interconectados para que el fluido disponga de caminos a través del material, por lo tanto, hay una relación general entre la porosidad y la permeabilidad [17].

 

5 Propiedades Mecánicas

Cuando una muestra de roca sólida es sometida a grandes esfuerzos lo más seguro es que la roca sea fallada; estas fallas dependerán del estado de esfuerzos, del tipo del material y de la geometría de la muestra. También, la historia de los esfuerzos del espécimen puede ser de gran importancia. Las técnicas sugeridas para determinar la deformabilidad, resistencia y las constantes elásticas son dadas por la ISRM (Sociedad Internacional de Mecánica de Rocas) [18].

Los datos que se obtienen de núcleos de roca son aplicados para evaluar el comportamiento mecánico de una roca in-situ. Estos núcleos permiten las mediciones directas de los parámetros de resistencia y de las propiedades elásticas estáticas.

Diversas pruebas de laboratorio han sido desarrolladas para determinar la resistencia de las formaciones de rocas. El tipo de prueba seleccionada para medir una característica particular de la roca deberá simular lo más cerca posible las condiciones encontradas en el yacimiento. Sin embargo, la manipulación de los diferentes factores que influyen en el valor final de resistencia experimental y la experiencia en su manipulación conlleva a que el laboratorio maneje una tolerancia de error de 20 %.

Se ha demostrado que ninguna técnica actual es capaz de medir in-situ la resistencia de una roca [18]. Por lo tanto se requiere de pruebas de laboratorio estándar, basadas en corazones, que pueden proporcionar esos datos. Sin embargo se debe tener en cuenta que dichos datos no reproducen exactamente las propiedades in situ a gran escala, porque estas propiedades son influenciadas por diaclasas, fallas, heterogeneidades, planos de debilidad y otros factores.

Las pruebas de laboratorio usualmente consisten en experimentos apropiados para la naturaleza de la roca y con estas pruebas se determina información importante como esfuerzos y deformaciones. El hecho de tener que realizar una prueba para obtener el valor de resistencia de una muestra de roca implica contar con la muestra, llevar a cabo la prueba e interpretar los resultados, lo que finalmente conlleva a gastos que se buscan reducir al contar con una nueva forma de estimar estos valores, de aquí la importancia que se le da al trabajo obtenido y al aporte que brinda en el área. Las siguientes son las propiedades mecánicas a estimar a través del trabajo desarrollado:

 

5.1 Resistencia a la tensión (To)

Es el máximo esfuerzo que soporta el material ante la rotura por tracción, se mide a través de la prueba de resistencia a la tensión ó brazilian test y consiste en la compresión en el punto de soporte de una muestra cilíndrica, esto aplicando una carga lineal o compresional a través del diámetro de la muestra de roca [18].

 

5.2 Resistencia a la compresión sin confinamiento (UCS)

Comúnmente llamada resistencia a la compresión uniaxial, es el valor del esfuerzo en el momento en que ocurre la falla en una roca; es decir el máximo esfuerzo que soporta la roca sometida a compresión uniaxial. Uno de los métodos de determinación de esta propiedad es el ensayo de compresión uniaxial que consiste en someter a carga un cilindro recto de muestra de roca con una presión de confinamiento igual a cero hasta que esta falle [18].

 

5.3 Resistencia a la compresión con confinamiento (CCS)

Comúnmente llamada resistencia a la compresión triaxial, es el máximo esfuerzo que soporta la roca sometida a compresión con confinamiento. Uno de los métodos de determinación de esta propiedad es la prueba triaxial, usualmente realizada en el laboratorio incrementando la carga axial y de confinamiento simultáneamente hasta alcanzar el esfuerzo hidrostático recomendado, luego, la presión de confinamiento es mantenida constante mientras la carga axial se va incrementando hasta que la falla ocurra [18].

Para el caso especial de la estimación de resistencia a la compresión con confinamiento, es importante tener en cuenta la presión de confinamiento como factor influyente en el valor de la resistencia, por tal razón esta propiedad forma parte de las variables de entrada de la red neuronal y es definida a continuación.

5.3.1 Presión de Confinamiento (Pc) Suma de la presión litostática (o de carga de todos los materiales que se encuentran situados por todos los lados de la roca) más la presión de fluidos (en poros y rocas), que tiene lugar en rocas permeables que permiten el flujo de fluidos a través de sus poros, grietas o fisuras.

En el caso práctico de los ensayos de laboratorio la cantidad de presión de confinamiento corresponde al valor de carga radial aplicado hidráulica neumáticaticamente sobre la roca.

 

6 Desarrollo de la herramienta

Para el desarrollo de la herramienta se trabajó con los dos métodos computacionales mencionados anteriormente, uno conexionista (Redes Neuronales) y otro evolutivo (Algoritmo Genético).

El algoritmo genético es el encargado de buscar la configuración de red neuronal que obtiene el mejor ajuste y generalización, a partir de la información suministrada. Este problema de encontrar una buena configuración C se logra mediante la optimización de sus parámetros (número de capas, neuronas por capa y funciones de activación), así el problema puede verse como la maximización de la función f dada por la ecuación (1):

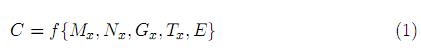
Donde M_x representa el número de capas, N_x el número de neuronas por capa, G_x la función de activación de cada una de las capas, T_x es el algoritmo de entrenamiento y E son los datos de entrenamiento.

El Algoritmo Genético fue desarrollado en la herramienta de simulación MATLAB 7.5, este se encarga de permutar las partes de la red en un proceso evolutivo, generando diferentes configuraciones, que son evaluadas cada vez, esta evaluación guía el proceso de evolución, que finalmente retorna una configuración de red neuronal que presenta un muy buen ajuste y generalización.

Una interfz de usuario fue desarrollada para facilitar la utilización de esta herramienta por otros investigadores. La interfaz del algoritmo genético trae parámetros por defecto pero si el usuario tiene experiencia se permiten ingresar los parámetros necesarios para su ejecución tales como el conjunto de datos de entrenamiento, el tipo de normalización que se utilizará tanto en los datos de entrada como en los de salida, tamaño de población, probabilidad de mutación, probabilidad de cruce, máximo número de capas y de neuronas, número de entrenamientos, algoritmo de entrenamiento, número de generaciones y tolerancia de error.

La duración del proceso de búsqueda de la configuración más apropiada para el conjunto de datos varía dependiendo de los parámetros ingresados al algoritmo genético.

Al finalizar el proceso de búsqueda, la herramienta presenta una interfaz con la lista de redes de la última población, de las que se pueden conocer detalles como gráficas de errores, número de errores, peor error, entre otros y de acuerdo a esto, el usuario selecciona para su posterior utilización la que crea conveniente.

Por su parte, las redes neuronales artificiales, usando la configuración seleccionada mediante el algoritmo genético estiman los valores de resistencia para los cuales fue desarrollado este trabajo.

Para implementar las redes neuronales, se hizo uso del framework JCORTEX [19], con el fin de crear una herramienta en JAVA para que pudiese ser utilizada con gran facilidad y con la menor cantidad de restricciones en cuanto a licenciamiento.

El Framework es una solución completa que permite a los desarrolladores de software crear, entrenar y utilizar redes neuronales artificiales en proyectos Java. Está dividido en dos partes: Framework JCortex, librería para la implementación de redes neuronales y JCortexBuilder, un ambiente gráfico en el que se pueden crear y entrenar redes neuronales.

Para su utilización, se editó el código dejando solo la parte necesaria para cargar las configuraciones escogidas a través de un archivo plano y poder realizar la parte de ejecución de las redes en JAVA.

La ejecución de las redes se realiza mediante una interfaz que permite seleccionar la configuración de entre un conjunto de configuraciones disponibles (aquellas que han sido generadas y almacenadas para su uso) e ingresar los valores de entrada y de esta manera se obtiene de forma rápida el valor estimado por la red neuronal con la configuración escogida.

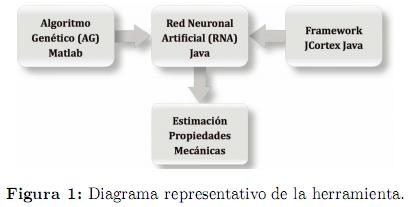
La figura 1 presenta la forma como la red neuronal artificial (RNA) se alimenta con la configuración obtenida a través del algoritmo genético (AG) y mediante el uso del framework Jcortex se crea la herramienta en Java logrando obtener como resultado la estimación de propiedades mecánicas.

 

7 Ejemplo de aplicación

La aplicación para la que se desarrolla este trabajo es la estimación de resistencias de datos tomados del laboratorio de mecánica de rocas, que corresponden a arenas limpias de cuencas sedimentarias Colombianas; para hacerlo se desarrolló la interfaz mencionada anteriormente en la que se implementaron las redes neuronales artificiales y haciendo uso de la configuración seleccionada, el usuario pudiese ingresar los datos y obtener de esta manera resultados.

Para la estimación de resultados de pruebas de laboratorio (resistencias), se hace necesaria la definición de las entradas y las salidas de la red neuronal de manera que entre éstas se encuentre una relación que permita generalizar el proceso de obtención de estos valores y para esto se han definido las siguientes entradas y salidas:

 

7.1 Parámetros de entrada

Como la petrofísica puede describir el comportamiento de las rocas, las variables de entrada que se han definido son propiedades de este tipo:

• Porosidad (expresada en % y representada por ∅)

• Permeabilidad (expresada en md y representada por k)

Para el caso de la resistencia a la compresión triaxial, además de las dos propiedades anteriores, se usa:

• Presión de confinamiento (expresada en PSI y representada por Pc)

 

7.2 Datos de salida

Las características geomecánicas a obtener mediante la simulación de las pruebas son las siguientes respectivamente por tipo de prueba.

 

Prueba Brazilian test

• Resistencia a la tensión (expresada en Kpa y representada por To)

 

Prueba de Compresión Uniaxial

• Resistencia a la compresión sin confinamiento (expresada en PSI y representada por UCS)

 

Prueba de Compresión Triaxial

• Resistencia a la compresión con confinamiento (expresada en PSI y representada por CCS)

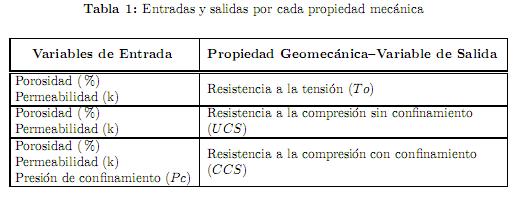
Para cada una de estas características o propiedades mecánicas, las entradas varían de acuerdo a los factores que influyen en su estimación tal como se mencionó en la descripción de los datos de entrada, la tabla 1 muestra claramente las entradas y salidas para cada propiedad.

 

8 Resultados

Los resultados son presentados en esta sección para demostrar el rendimiento de las redes y de la herramienta para su utilización.

Aunque son posibles diferentes configuraciones, utilizando el algoritmo genético se seleccionaron las configuraciones que mostraron el mejor rendimiento entre todas las probadas para hallar la resistencia en cada una de las tres pruebas de laboratorio.

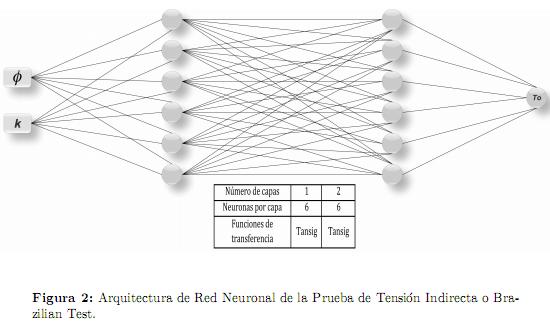
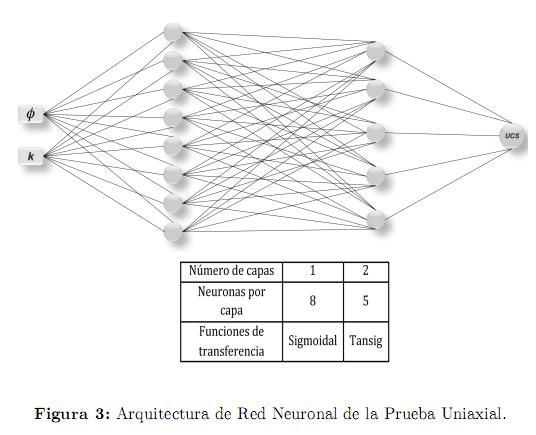
Las figuras 2 y 3 muestran la representación gráfica de las configuraciones seleccionadas por el algoritmo genético teniendo la porosidad y la permeabilidad como datos de entrada. Como datos de salida se obtienen la resistencia a la tensión (To) y la resistencia a la compresión sin confinamiento (UCS) respectivamente. También se presenta por cada configuración de red neuronal una tabla resumen en la que se puede observar el número de capas, el número de neuronas por capa y las funciones de transferencia.

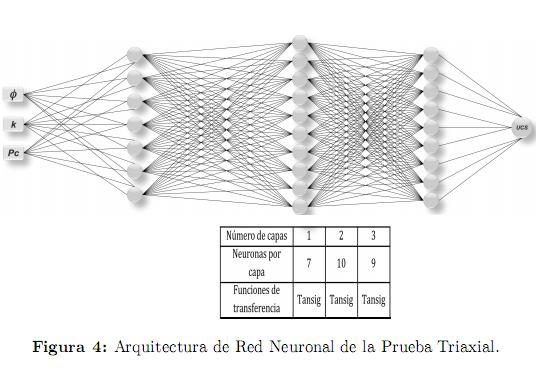
La figura 4 muestra la configuración de red neuronal para la obtención de la resistencia a la compresión con confinamiento (CCS) a partir de la porosidad, la permeabilidad y la presión de confinamiento y su respectiva tabla resumen en la que se observan el número de capas, el número de neuronas por capa y las funciones de transferencia.

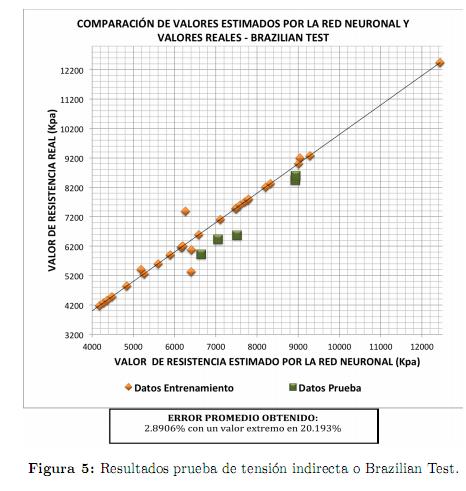
La figura 5 muestra la comparación entre los valores reales de resistencia a la tensión obtenidos en el laboratorio y las estimaciones obtenidas con la red neuronal de manera que se evidencia que se obtuvieron buenos resultados. También se muestra para esta prueba Brazilian test el error promedio obtenido dado por la ecuación 2 y el máximo error que se presentó en alguno de los datos disponibles para este tipo de resistencia.

 

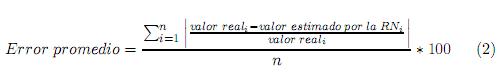
Donde n es el número total de datos disponibles para esta prueba.

Para el caso de la resistencia a la compresión uniaxial, la figura 6 muestra también la comparación entre valores reales y estimados por la RN. Al igual que en el caso anterior se puede observar que los valores estimados por la red neuronal son satisfactorios y además los datos de prueba se ajustan mejor incluso que en el caso anterior a los valores reales. El error promedio obtenido y el máximo error demuestran estos resultados.

 

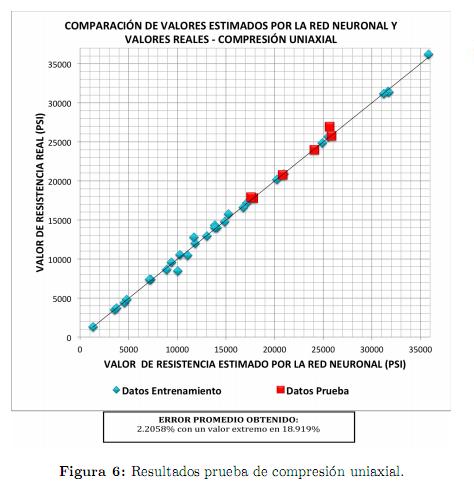
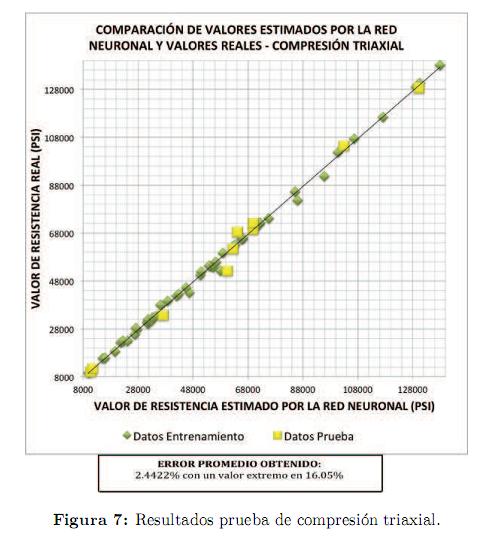
En el caso de la resistencia a la compresión triaxial, en la figura 7 se puede observar que los datos de prueba, estimados mediante la red neuronal, logran seguir el comportamiento de los valores de resistencia real con lo que se demuestra el buen desempeño de la red para esta prueba. Nuevamente el error promedio obtenido y el máximo error obtenido confirman estos resultados.

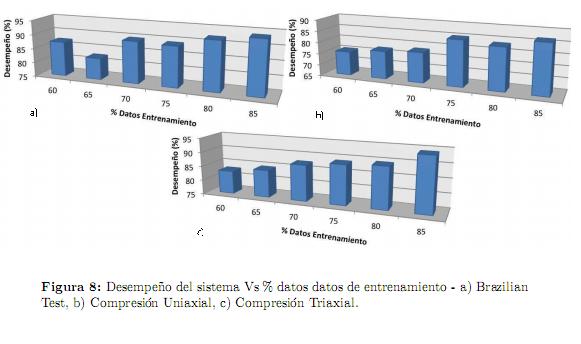
En todos los casos, los datos de entrenamiento fueron seleccionados de forma aleatoria y, para probar la generalización y el hecho de que no solo los resultados son buenos en algunos casos, se presentan mediante la figura 8, los valores promedio de éxito para cada una de las pruebas tomando el 60, 65, 70, 75, 80 y 85 % de los datos como datos de entrenamiento. El restante conjunto de datos se usó para validar la red.

El desempeño de una red neuronal es calculado mediante la ecuación 3:

 

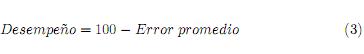
9 Análisis de resultados

Utilizando el algoritmo genético se probaron en promedio 332 diferentes configuraciones de red neuronal por tipo de prueba, buscando las que más se ajustaran al conjunto de datos y, las seleccionadas presentaron errores promedio de 2.8906 %, 2.2058 % y 2.4422 % respectivamente para cada una de las tres pruebas. Estos resultados se encuentran dentro de los margenes de tolerancia de error del laboratorio, por lo que los resultados cumplen con las expectativas.

Los rangos en los que los resultados de la red neuronal son válidos son considerablemente pequeños comparados con el dominio de los valores que se pueden encontrar en estas rocas, esto es debido al escaso número de datos que se lograron recopilar en el Laboratorio de Mecánica de Rocas.

Con las pruebas que se presentaron para diversos conjuntos de datos de entrenamiento, se demuestra cómo realmente se logra una generalización con el modelo propuesto y se facilita con su análisis determinar el número de datos que se hacen necesarios para obtener resultados confiables.

 

10 Conclusiones

Se calcularon propiedades mecánicas de roca (resistencia a la tensión, resistencia a la compresión sin confinamiento y resistencia a la compresión con confinamiento) utilizando métodos propios de la inteligencia artificial, con porcentajes de error permitidos dentro de los límites aceptados por el laboratorio de Mecánica de rocas.

Se logró obtener un buen ajuste en la estimación de resistencias para los tres tipos de pruebas a pesar del escaso volumen de datos que se utilizó.

El modelo de redes neuronales descrito muestra que este puede ser un modelo de confianza para la determinación de las propiedades mecánicas utilizando información de petrofísica y requiriendo un conjunto de datos experimentales obtenidos previamente.

Los resultados obtenidos con este trabajo no pueden ser comparados con los obtenidos por autores como [5], [6], [7],[8] y [9] debido a que el tipo de roca, las características o parámetros de roca utilizados y los rangos en que estos parámetros se encuentran difieren totalmente de un trabajo a otro y por esto el rendimiento se mide con los resultados experimentales obtenidos de las pruebas de laboratorio.

Se logró exportar correctamente la arquitectura de red neuronal de Matlab a Java facilitando la utilización de los modelos de red neuronal pues el único requisito para su uso es la máquina virtual de java versión 1.6.

Es importante resaltar, que de la misma manera como se realizó en esta aplicación, se pueden utilizar datos de otro tipo de rocas y dependiendo del volumen de datos se esperarán encontrar buenos resultados dentro del dominio de los valores utilizados.

 

Referencias

1. A Baykasolu, T Dereli, and S Tani. Prediction of cement strength using soft computing techniques. Cement and concrete research, 34(11):2083–2090, 2004. 85         [ Links ]

2. G. W. Ellis, C. Yao, R. Zhao, and D. Penumadu. Stress-strain modeling of sands using artificial neural networks. 121(5):429–435, 1995. 85         [ Links ]

3. J. H. Garrett Jr. J. Ghaboussi and X. Wu. Knowledge based modeling of material behavior with neural networks. 117(1):132–153, 1991. 85         [ Links ]

4. John R. Koza. Genetic programming: on the programming of computers by means of natural selection. page 819, Jan 1992. 85        [ Links ]

5. F Meulenkamp and M Alvarez. Application of neural networks for the prediction of the unconfined compressive strength (ucs) from equotip hardness. International Journal of rock mechanics and mining sciences, 36:29–39, Feb 1999. 85, 101         [ Links ]

6. F Meulenkamp. Improving the prediction of the ucs, by equotip readings using statistical and neural network models. Memoirs of the Centre for Engineering Geology in the Netherlands, 162:127, 1997. 85, 101         [ Links ]

7. VK Singh, D Singh, and TN Singh. Prediction of strength properties of some schistose rocks from petrographic properties using artificial neural networks. International Journal of Rock Mechanics and Mining Sciences, 38(2):269–284, 2001. 85, 101         [ Links ]

8. A Baykasoglu, H Gullu, H Canakci, and L Ozbakir. Prediction of compressive and tensile strength of limestone via genetic programming. Expert Systems with Applications, 35(1-2):111–123, 2008. 85, 101         [ Links ]

9. Hanifi Çanakci, Adil Baykasoglu, and Hamza Güllü. Prediction of compressive and tensile strength of gaziantep basalts via neural networks and gene expression programming. Neural Comput & Applic, 18(8):1031–1041, Nov 2009. 85, 101         [ Links ]

10. Johann Gasteiger and Jure Zupan. Neural networks in chemistry. Angewandte Chemie International Edition in English, 32(4):503–527, 1993. 86         [ Links ]

11. Constantin von Altrock. Fuzzy logic and neurofuzzy applications explained. Prentice-Hall, Inc., Upper Saddle River, NJ, USA, 1995. 86         [ Links ]

12. T. Dereli and A. Baykasoglu. The use of artificial intelligence techniques in design and manufacturing: a review. Polytech, 3:27–60, 2000. 86         [ Links ]

13. S.K Sinha and F Karray. Classification of underground pipe scanned images using feature extraction and neuro-fuzzy algorithm. Neural Networks, IEEE Transactions on, 13(2):393–401, 2002. 86         [ Links ]

14. I.S Bajwa and M.A Choudhary. A study for prediction of minerals in rock images using back propagation neural networks. Advances in Space Technologies, 2006 International Conference on, pages 185–189. 86         [ Links ]

15. Yuan-Kai Wang and Kuo-Chin Fan. Applying genetic algorithms on pattern recognition: an analysis and survey. Pattern Recognition, 1996., Proceedings of the 13th International Conference on, 2:740–744 vol.2, 1996. 87         [ Links ]

16. U. Maulik. Medical image segmentation using genetic algorithms. Information Technology in Biomedicine, IEEE Transactions on, 13(2):166–173, 2009. 87         [ Links ]

17. K. Miroslav, H. Rafael, and C.J. Oscar. Evaluacion hidrogeológica de pozos a través de registros geofísicos, Fundamentos. Unam, 2005. 88        [ Links ]

18. R. Corzo Rueda y C. Rincón Pabón. Proyecto de grado, Medición y evaluación de la magnitud y dirección de los esfuerzos in-situ en campo. Universidad Industrial de Santander, Colombia, 2004. 88, 89, 90        [ Links ]

19. M. Lara Encabo. Proyecto de grado, Framework para redes neuronales en Java. Universidad Pontificia Comillas ICAI, España, 2006. 92        [ Links ]