Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y Ciencia
versão impressa ISSN 1794-9165
ing.cienc. v.8 n.15 Medellín jan./jun. 2012
ARTÍCULO ORIGINAL
Lógica de las tautologías
Logic of the tautologies
Lógica das tautologias
Manuel Sierra-Aristizábal1
1 Magíster en Matemáticas, msierra@eafit.edu.co, profesor, Universidad EAFIT, Medellín-Colombia.
Recepción: 01-jun-2011. Modificación: 09-abr-2012. Aceptación: 17-abr-2012
Se aceptan comentarios y/o discusiones al artículo
Resumen
Se presenta como extensión del cálculo proposicional clásico, el sistema deductivo LT: lógica de las tautologías. En el sistema LT, se formalizan las nociones meta-lógicas de tautología, contradicción, satisfacible, refutable y contingencia. El sistema LT, es caracterizado con una semántica al estilo Kripke, y puede ser visto como una extensión del sistema de lógica modal S5.
Palabras claves: Tautología, contradicción, contingencia, lógica modal, mundos posibles.
Abstract
Is presented as extension of classical propositional calculus, the deductive system LT: logic of the tautologies. In the LT system, the meta-logical notions of tautology, contradiction, refutable and contingency are formalized. The LT system, is characterized as a Kripke-style semantic, and can be seen as an extension of the modal logic system S5.
Key words: Tautology, contradiction, contingency, modal logic, possible worlds.
Resumo
Apresenta-se como extensão do cálculo propocicional clássico, o sistema dedutivo LT: lógica das tautologias. No sistema LT, formalizam-se as noções meta-lógicas de tautologia, contradição, satisfatível, refutável e contingência. O sistema LT, é caraterizado com uma semántica ao estilo Kripke, e pode ser visto como uma extensão do sistema de lógica modal S5.
Palavras chaves: Tautologia, contradição, contingência, lógical modal, mundos possíveis.
1 Presentación
Con el cálculo proposicional clásico CP, los enunciados que tienen las siguientes estructuras: si lo uno entonces lo otro, lo primero y lo segundo, esto o aquello, eso no, y esto si y solamente si aquello; se formalizan mediante los conectivos lógicos: condicional, conjunción, disyunción, negación y bicondicional respectivamente. Además, CP se encuentra caracterizado por una semántica de valores de verdad, donde cada fórmula es verdadera o falsa pero no verdadera y falsa, y en la cual se da una interpretación precisa de los conectivos, de tal manera que, el valor de verdad de una fórmula se determina a partir de los valores de verdad de sus sub-fórmulas atómicas.
Dada una fórmula, a cada posible combinación de los valores de verdad de las fórmulas atómicas que figuran en ella se le llama una asignación. Se dice que una fórmula es una tautología si y solamente si es verdadera para cada posible asignación, una fórmula es una contradicción si y solamente si es falsa para cada posible asignación, una fórmula es satisfacible si y solamente si es verdadera para alguna asignación, una fórmula es refutable si y solamente si es falsa para alguna asignación, una fórmula es una contingencia si y solamente si es verdadera para alguna asignación y falsa para otra. Resulta que los teoremas del cálculo proposicional clásico son las tautologías y solo ellas. Para detalles ver [1] y [2].
En este trabajo se presenta como extensión del cálculo proposicional clásico, el sistema deductivo LT. LT es la lógica de las tautologías. En el sistema LT, se formalizan las nociones meta-lógicas de tautología, contradicción, satisfacible, refutable y contingencia. El sistema LT, es caracterizado con una semántica al estilo Kripke, y puede ser visto como una extensión del sistema de lógica modal S5(ver [3]). Las pruebas de validez y completitud, son presentadas de forma detallada.
El sistema LT se obtiene a partir de CP, pidiendo que los teoremas de CP sean tautologías, que la conjunción de literales disjuntos (afirmación o negación de formulas atómicas diferentes) sea una contingencia, que la regla de inferencia Modus Ponens preserve las tautologías, y que las tautologías sean verdaderas. Se agregan axiomas que permitan simplificar adecuadamente los anidamientos o secuencias de los operadores de tautología, contradicción, satisfacible, refutable y contingencia. Los modelos para el sistema deductivo LT, son conjuntos de mundos posibles al estilo Kripke (ver [4]), donde del mundo actual (en el cual se determina si una fórmula es tautología, contradicción, satisfacible, refutable, verdadera o falsa), se accede a mundos posibles en los cuales se representan las asignaciones de valores de verdad.
2. Sistema deductivo
El lenguaje del sistema LT, consta de un conjunto enumerable de fórmulas atómicas; de los conectivos binarios  ,
,  ,
,  ,
,  ; el conectivo unario
; el conectivo unario  ; y un conectivo unario + (operador de validez o tautología).
; y un conectivo unario + (operador de validez o tautología).
Definición 2.1 (Literales y operadores de verdad).
Si P es una fórmula atómica, se dice que P y  P son literales (los literales asociados a P). Los literales L y T son asociados si existe una fórmula atómica P tal que L y T son asociados a P. Los literales L1, ..., Ln son disjuntos si para cada i, j tales que 1 ≤ i < j ≤ n, Li y Lj no son asociados.
P son literales (los literales asociados a P). Los literales L y T son asociados si existe una fórmula atómica P tal que L y T son asociados a P. Los literales L1, ..., Ln son disjuntos si para cada i, j tales que 1 ≤ i < j ≤ n, Li y Lj no son asociados.
La fórmula X es una contradicción, denotado ¬ X, si su negación es una tautología, es decir, ¬X  +
+  X. La fórmula X es refutable, denotado -X, si no es una tautología, es decir, -X
X. La fórmula X es refutable, denotado -X, si no es una tautología, es decir, -X  +
+  X. La fórmula X es satisfacible, denotado •X, si no es una contradicción, es decir, •X
X. La fórmula X es satisfacible, denotado •X, si no es una contradicción, es decir, •X 
 ¬X. La fórmula X es una contingencia, denotado *X, si es satisfacible y refutable, es decir, *X
¬X. La fórmula X es una contingencia, denotado *X, si es satisfacible y refutable, es decir, *X  (•X
(•X  -X). Los operadores +, ¬, -, • * y son llamados operadores de verdad.
-X). Los operadores +, ¬, -, • * y son llamados operadores de verdad.
El sistema LT, lógica de de las tautologías, consta de los siguientes axiomas:
Ax•1 •(L1  ...
...  Lk), donde L1 , ... , Ln son literales disjuntos.
Lk), donde L1 , ... , Ln son literales disjuntos.
AxCP Los teoremas del cálculo proposicional clásico CP.
MP+ +(X  Y)
Y)  (+X
(+X  +Y).
+Y).
AxR X  •X.
•X.
AxT -¬X  •X.
•X.
AxE -X  ¬ + X.
¬ + X.
El sistema LT tiene 2 reglas de inferencia:
MP modus ponens, es decir, de X y X  Y se infiere Y.
Y se infiere Y.
R+ regla de validez, es decir, si X es un teorema de LT entonces
+X es un teorema de LT.
Se dice que una fórmula X es un teorema del sistema, si y solamente si X es la última fórmula de una sucesión finita de fórmulas del sistema, tales que cada una de ellas es un axioma del sistema o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP o se infiere de una fórmula anterior utilizando la regla de inferencia R+. Si Γ es un conjunto de fórmulas del sistema, se dice que una fórmula X es un teorema del sistema a partir de Γ, si y solamente si X es la última fórmula de una sucesión finita de fórmulas del sistema, tales que cada una de ellas es un axioma del sistema o un elemento de Γ o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP o se infiere de una fórmula anterior, la cual es un teorema de LT, utilizando la regla de inferencia R+.
En las pruebas de las proposiciones que se presentan más adelante, se utilizaran resultados del cálculo proposicional clásico CP. Se hará referencia a estos resultados simplemente como LCP o leyes lógicas de CP (para detalles de las pruebas en CP ver [1] [2]).
Como consecuencia de la definición de los operadores de verdad, en la tabla 1 se tienen algunas caracterizaciones de los mismos.
Proposición 2.1 (Conjunción de tautologías. +(X  Y)
Y)  (+X
(+X  +Y)).
+Y)).
Prueba 2.1. Por LCP se tienen (X  Y)
Y)  X y (X
X y (X  Y)
Y)  Y, y por R+ se afirma que +((X
Y, y por R+ se afirma que +((X  Y)
Y)  X) y +((X
X) y +((X  Y)
Y)  Y). Utilizando el axioma MP+ y MP se infieren +(X
Y). Utilizando el axioma MP+ y MP se infieren +(X  Y)
Y)  +X y +(X
+X y +(X  Y)
Y)  +Y . Utilizando LCP se infiere +(X
+Y . Utilizando LCP se infiere +(X  Y)
Y)  (+X
(+X  +Y). Para la recíproca, por LCP se tiene A
+Y). Para la recíproca, por LCP se tiene A  (B
(B  (A
(A  B)). Por R+ se infiere +(A
B)). Por R+ se infiere +(A  (B
(B  (A
(A  B))), utilizando MP+ y MP resulta +A
B))), utilizando MP+ y MP resulta +A  +(B
+(B  (A
(A  B)), como además por MP+ se tiene +(B
B)), como además por MP+ se tiene +(B  (A
(A  B))
B))  (+B
(+B  +(A
+(A  B)), entonces por LCP se obtiene +A
B)), entonces por LCP se obtiene +A  (+B
(+B  +(A
+(A  B)). Por lo que se infiere (+A
B)). Por lo que se infiere (+A  +B)
+B)  +(A
+(A  B).
B).
Proposición 2.2 (Sustitución por equivalencia.). Sean F (X) una fórmula en la cual figura X, y F (Y) el resultado de cambiar en F(X) alguna ocurrencia de X por Y.
a. De X  Y se deduce +X
Y se deduce +X  +Y.
+Y.
b. De X  Y se infiere F(X)
Y se infiere F(X)  F(Y).
F(Y).
Prueba 2.2. Para la parte a, supóngase que X  Y, por equivalencia material resulta (X
Y, por equivalencia material resulta (X  Y)
Y)  (Y
(Y  X), y por R+ se infiere +((X
X), y por R+ se infiere +((X  Y)
Y) (Y
(Y  X)), por la proposición 2.1 se obtiene +(X
X)), por la proposición 2.1 se obtiene +(X  Y)
Y)  +(Y
+(Y  X), utilizando LCP y el axioma MP+ se genera (+X
X), utilizando LCP y el axioma MP+ se genera (+X  +Y)
+Y)  (+Y
(+Y  +X), finalmente, utilizando LCP se concluye +X
+X), finalmente, utilizando LCP se concluye +X  +Y . (Utilizando las definiciones de los operadores de verdad, también se siguen •X
+Y . (Utilizando las definiciones de los operadores de verdad, también se siguen •X  •Y, -X
•Y, -X  Y y ¬X
Y y ¬X  ¬Y).
¬Y).
La parte b, se sigue de la parte a, teniendo en cuenta que la equivalencia se preserva con los demás conectivos, para detalles ver [1] [2].
3 Semántica
Definición 3.1 (Marco). La terna (S, M, R) es un marco si y solamente si M es un elemento del conjunto S, R es una relación binaria sobre S. Los elementos de S son llamados mundos posibles, el mundo posible M es el mundo actual, y R es la relación de accesibilidad.
En un marco (S, M, R), para K, N y F elementos de S, se satisfacen las siguientes restricciones:
RR. Para cada K, KRK.
RE. Si KRN y KRF entonces NRF.
RT. Si KRN y NRF entonces KRF.
Definición 3.2 (Modelo). Sea (S, M, R) un marco y F el conjunto de las fórmulas. (S, M, R, V) es un modelo si y solamente si V es una función (valuación) de S x F en {0,1} la cual satisface las siguientes reglas o condiciones: Sean D un elemento de S, P una fórmula atómica, X y Y fórmulas arbitrarias,
Vat. V (D, P) = 1 ó V(D, P) = 0.
V V(D,
V(D,  X) = 1
X) = 1  V (D, X) = 0.
V (D, X) = 0.
V V(D, X
V(D, X  Y) = 1
Y) = 1  V(D, X) = 1 = V (D, Y).
V(D, X) = 1 = V (D, Y).
V V(D, X
V(D, X  Y) = 0
Y) = 0  V (D, X) = 0 = V (D, Y).
V (D, X) = 0 = V (D, Y).
V  V (D, X
V (D, X  Y) = 0
Y) = 0  V (D, X) = 1 y V (D, Y) = 0.
V (D, X) = 1 y V (D, Y) = 0.
V  V (D, X
V (D, X  Y) = 1
Y) = 1  V (D, X) = V (D, Y).
V (D, X) = V (D, Y).
V + V (D, +X) = 1  (
( N
N 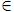 S)(DRN
S)(DRN  V (N, X) = 1).
V (N, X) = 1).
VL Para cada mundo D en S, y para cada secuencia L1, ... , Lk de literales disjuntos, existe un mundo N en S, tal que, DRN y V (N, L1 ...
...  Lk) = 12.
Lk) = 12.
Proposición 3.1. Caracterización semántica de los operadores de verdad. En un modelo (S, M, R, V).
V ¬. V (M, ¬Z) = 1  (
(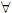 N
N 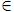 S)(MRN) V (N, Z) = 0).
S)(MRN) V (N, Z) = 0).
V•. V (M, •Z) = 1  (
(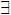 N
N 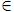 S)(MRN y V (N, Z) = 1).
S)(MRN y V (N, Z) = 1).
V-. V (M, -Z) = 1  (
(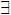 N
N 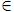 S)(MRN y V (N, Z) = 0).
S)(MRN y V (N, Z) = 0).
V*. V (M, *Z) = 1  (
(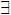 N
N 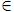 S)(MRN y V (N, Z) = 1) y
S)(MRN y V (N, Z) = 1) y
(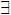 D
D 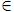 S)(MRD y V (D, Z) = 0).
S)(MRD y V (D, Z) = 0).
Prueba 3.1. De V+ se tiene que, V (M, + Z) = 1
Z) = 1  (
(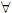 N
N 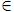 S)(MRN
S)(MRN  V (N,
V (N,  Z) = 1). Utilizando la definición de contradicción y la regla V
Z) = 1). Utilizando la definición de contradicción y la regla V se infiere que V(M, ¬Z) = 1
se infiere que V(M, ¬Z) = 1  (
(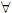 N
N 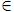 S)(MRN
S)(MRN V (N, Z) = 0), por lo tanto V¬.
V (N, Z) = 0), por lo tanto V¬.
De V+ se tiene que, V (M, +  Z) = 1
Z) = 1  (
(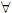 N
N 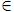 S)(MRN
S)(MRN  V (N,
V (N,  Z) = 1). Por lo que, V (M, +
Z) = 1). Por lo que, V (M, + Z) = 0
Z) = 0  (
(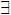 N
N 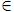 S)(MRN y V (N,
S)(MRN y V (N,  Z) = 0), lo cual por V
Z) = 0), lo cual por V  y la definición de satisfacible significa que V (M, Z) = 1
y la definición de satisfacible significa que V (M, Z) = 1  (
(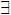 N
N 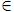 S)(MRN y V (N, Z) = 1), por lo tanto V•.
S)(MRN y V (N, Z) = 1), por lo tanto V•.
De V• se tiene que, V (M, • Z) = 1
Z) = 1  (
(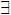 N
N 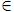 S)(MRN y V (N,
S)(MRN y V (N,  Z) = 1). Lo cual por V
Z) = 1). Lo cual por V y las definiciones de satisfacible y refutable, implica que V (M, -Z) = 1
y las definiciones de satisfacible y refutable, implica que V (M, -Z) = 1  (
(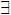 N
N 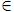 S)(MRN y V (N, Z) = 0), por lo tanto, V-. Finalmente, observar que V* es consecuencia inmediata de V• y V-.
S)(MRN y V (N, Z) = 0), por lo tanto, V-. Finalmente, observar que V* es consecuencia inmediata de V• y V-.
4 Validez
Definición 4.1 (Validez). Sea X una fórmula. X es verdadera en el modelo (S, M, R, V) si y solo si V(M, X) = 1. X es válida si y solo si X es verdadera en todo modelo.
Definición 4.2 (Cadena).
Dado un marco (S, Ma, R), donde Ma, Na-1 ..., Et+2, Dt+1, Gt, son mundos posibles diferentes en S y Ma es el mundo actual. Se dice que C = MaNa-1 ... Et+2Dt+1Gt es una cadena, cuando se tienen MaRNa-1, ..., Et+2RDt+1 y Dt+1RGt.
Resulta entonces que una fórmula X no es válida si y solamente si existe un modelo M = (S, M, R, V), en el cual X no es verdadera, es decir V (M, X) = 0. Por lo que, si la fórmula X no es válida, utilizando las reglas de las valuaciones, a partir de V (M, X) = 0, se construye un modelo M = (S, M, R, V) que refute la validez de la fórmula X, este modelo es llamado modelo refutador. Pero si la fórmula X es válida, entonces la construcción del modelo refutador fracasará, puesto que, en alguno de los mundos posibles (bien sea M o un mundo generado por la aplicación de las reglas) del modelo en construcción se presentará una inconsistencia3. Cuando fracasa la construcción del modelo refutador, entonces se genera una cadena de mundos posibles C = M... N... D tal que en D se presenta una inconsistencia, es decir, para alguna fórmula Z, V (D, Z) = 1 y V (D, Z) = 0. En este caso se dice que la cadena C es inconsistente.
En resumen, para probar la validez de una fórmula X, se supone que la fórmula X no es válida, es decir, es falsa en el mundo actual M de un modelo, y a partir de esta información se construye el modelo refutador. Si tal modelo no existe entonces se concluye que la fórmula X es válida.
Proposición 4.1 (Preservación de la validez).
a. Si X es válida entonces +X es válida.
b. Si X y X  Y son válidas entonces Y también es válida.
Y son válidas entonces Y también es válida.
Prueba 4.1. Para la parte a, supóngase que +X no válida, por lo que existe un modelo refutador de +X, MO = (S, M, R, V) tal que +X no es verdadera en MO, es decir V (M, +X) = 0, por la regla V+ resulta que existe un mundo posible N tal que MRN y V (N, X) = 0. El modelo MO se encuentra formado por cadenas consistentes de la forma MN ... D, y además en el mundo M la fórmula +X toma el valor 0, y en el mundo N la fórmula X toma el valor 0. A partir del modelo refutador MO de +X se construye un modelo refutador MO´ de la fórmula X de la siguiente manera: se toma como mundo actual del modelo MO´ el mundo N, como resultado se obtiene el modelo MO´= (S, N, R, V), el cual por construcción se encuentra formado por cadenas consistentes N ... D, lo que significa que MO´ es un modelo, y además en el mundo actual N la fórmula X toma el valor 0, por lo tanto MO´ es un modelo refutador de la fórmula X, es decir X no es verdadera en el modelo MO´, por lo que X no es válida. De lo anterior se concluye que si +X no es válida entonces X no es válida, es decir, si X es válida entonces +X es válida.
Para la parte b, supóngase que X y X  Y son válidas. Si Y no es válida, entonces existe un modelo tal que, en el mundo actual M, V (M, Y) = 0. Como X y X
Y son válidas. Si Y no es válida, entonces existe un modelo tal que, en el mundo actual M, V (M, Y) = 0. Como X y X  Y son válidas, entonces V (M, X
Y son válidas, entonces V (M, X  Y) = 1 y V (M, X) = 1, por la regla V
Y) = 1 y V (M, X) = 1, por la regla V  de V (M, Y) = 0 y V (M, X
de V (M, Y) = 0 y V (M, X  Y) = 1 resulta V (M, X) = 0 lo cual es imposible. Por lo tanto Y es válida.
Y) = 1 resulta V (M, X) = 0 lo cual es imposible. Por lo tanto Y es válida.
Proposición 4.2 (Validez de los axiomas). Si X es un axioma de LT entonces X es válida.
Prueba 4.2 (Validez de los axiomas). En el primer caso, si X es un teorema de CP, utilizando las reglas Vat, V  , V
, V  , V
, V , V
, V  y V
y V  , y procediendo como es habitual para la validez del cálculo proposicional clásico (para detalles del caso clásico ver [1] [2]), se concluye que X es válida.
, y procediendo como es habitual para la validez del cálculo proposicional clásico (para detalles del caso clásico ver [1] [2]), se concluye que X es válida.
En el segundo caso, X es de la forma +(Y  Z)
Z)  (+Y
(+Y  +Z). Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, +(Y
+Z). Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, +(Y  Z)
Z)  (+Y
(+Y  +Z)) = 0, lo cual según la regla V
+Z)) = 0, lo cual según la regla V  significa V (M, +(Y
significa V (M, +(Y  Z)) = 1 y V (M, +Y
Z)) = 1 y V (M, +Y  +Z) = 0, y de nuevo por la misma regla se obtienen V (M, +Y) = 1 y V (M, +Z) = 0, de esta última por la regla V+ se infiere la existencia de un mundo N, tal que MRN y V (N, Z) = 0, y como V (M, +(Y
+Z) = 0, y de nuevo por la misma regla se obtienen V (M, +Y) = 1 y V (M, +Z) = 0, de esta última por la regla V+ se infiere la existencia de un mundo N, tal que MRN y V (N, Z) = 0, y como V (M, +(Y  Z)) = 1, por V+ se infiere V (N, Y
Z)) = 1, por V+ se infiere V (N, Y  Z) = 1, y como V (M, +Y) = 1, por V+ se obtiene V (N, Y) = 1, y como ya se tiene V (N, Y
Z) = 1, y como V (M, +Y) = 1, por V+ se obtiene V (N, Y) = 1, y como ya se tiene V (N, Y  Z) = 1, por V
Z) = 1, por V  se genera V (N, Z) = 1, pero esto es imposible. Por lo tanto, +(Y
se genera V (N, Z) = 1, pero esto es imposible. Por lo tanto, +(Y  Z)
Z)  (+Y
(+Y  +Z) es válida.
+Z) es válida.
En el tercer caso X es de la forma Z  •Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, Z
•Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, Z  •Z) = 0, lo cual según la regla V
•Z) = 0, lo cual según la regla V  significa V (M, Z) = 1 y V (M, •Z) = 0, es decir V (M,
significa V (M, Z) = 1 y V (M, •Z) = 0, es decir V (M, +
+  Z) = 0, resultando que V (M, +
Z) = 0, resultando que V (M, + Z) = 1, utilizando la restricción RR se tiene MRM, resultando que V (M,
Z) = 1, utilizando la restricción RR se tiene MRM, resultando que V (M, Z) = 1, es decir V (M, Z) = 0, lo cual no es el caso. Por lo tanto, Z
Z) = 1, es decir V (M, Z) = 0, lo cual no es el caso. Por lo tanto, Z  •Z es válida.
•Z es válida.
En el cuarto caso X es de la forma -¬Z  •Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, -¬Z
•Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, -¬Z  •Z) = 0, lo cual según las regla V
•Z) = 0, lo cual según las regla V  significa V (M,-¬Z) = 1 y V (M, •Z) = 0, es decir V (M,
significa V (M,-¬Z) = 1 y V (M, •Z) = 0, es decir V (M, +
+  Z) = 0 y entonces V (M, +
Z) = 0 y entonces V (M, +  Z) = 1, utilizando la regla V- resulta que existe un mundo N, tal que MRN , y en el cual V (N, ¬Z) = 0, por la regla V¬ resulta que existe un mundo S, tal que NRS, y en el cual V (S, Z) = 1, pero por la restricción RT se obtiene MRS, por lo que se infiere V (S,
Z) = 1, utilizando la regla V- resulta que existe un mundo N, tal que MRN , y en el cual V (N, ¬Z) = 0, por la regla V¬ resulta que existe un mundo S, tal que NRS, y en el cual V (S, Z) = 1, pero por la restricción RT se obtiene MRS, por lo que se infiere V (S,  Z) = 1, es decir V (S, Z) = 0, lo cual es imposible, por lo tanto, -¬Z
Z) = 1, es decir V (S, Z) = 0, lo cual es imposible, por lo tanto, -¬Z  •Z es válida.
•Z es válida.
En el quinto caso X es de la forma -Z  ¬ + Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, -Z
¬ + Z. Si esta fórmula no fuese válida, entonces existiría un modelo tal que en el mundo actual M, V (M, -Z  ¬ + Z) = 0, lo cual según la regla V
¬ + Z) = 0, lo cual según la regla V  significa V (M, -Z) = 1 y V (M, ¬+Z) = 0, utilizando la regla V- se infiere la existencia de un mundo N, tal que MRN y V (N, Z) = 0, además por la regla V¬ resulta que existe un mundo S, tal que MRS y V (S, +Z) = 1, utilizando la restricción RE se obtiene SRN resultando que V (N, Z) = 1, lo cual es imposible, por lo tanto, -Z
significa V (M, -Z) = 1 y V (M, ¬+Z) = 0, utilizando la regla V- se infiere la existencia de un mundo N, tal que MRN y V (N, Z) = 0, además por la regla V¬ resulta que existe un mundo S, tal que MRS y V (S, +Z) = 1, utilizando la restricción RE se obtiene SRN resultando que V (N, Z) = 1, lo cual es imposible, por lo tanto, -Z  ¬ + Z es válida.
¬ + Z es válida.
Finalmente, en el sexto caso X es de la forma •(L1 ...
...  Lk) donde L1, ... , Lk son literales disjuntos. Si X no es válida, entonces existe un modelo, tal que en el mundo actual M, V (M, •(L1
Lk) donde L1, ... , Lk son literales disjuntos. Si X no es válida, entonces existe un modelo, tal que en el mundo actual M, V (M, •(L1  ...
...  Lk)) = 0. Por la regla VL, existe un mundo N, tal que MRN, y en el cual V (N, L1
Lk)) = 0. Por la regla VL, existe un mundo N, tal que MRN, y en el cual V (N, L1 ...
... Lk) = 1, pero como MRN y V (M, •(L1
Lk) = 1, pero como MRN y V (M, •(L1  ...
...  Lk)) = 0, por la regla V• resulta que V (N, L1
Lk)) = 0, por la regla V• resulta que V (N, L1  ...
...  Lk) = 0, lo cual no es el caso. Por lo tanto, •(L1
Lk) = 0, lo cual no es el caso. Por lo tanto, •(L1  ...
...  Lk) es válida.
Lk) es válida.
Proposición 4.3 (Validez de LT). Si X es un teorema de LT entonces X es válida.
Prueba 4.3. Supóngase que X es un teorema de LT, se prueba que X es válida por inducción sobre la longitud L de la demostración de X en LT. Paso Base L = 1. Si la longitud de la demostración de X en LT es 1 entonces, X es un axioma de LT, lo cual por la proposición 4.2 significa que X es válida. Paso de inducción. Como hipótesis inductiva se tiene que para cada fórmula Y , si Y es un teorema de LT y la longitud de la demostración de Y tiene longitud menor que L (donde L > 1) entonces Y es válida. Si X es un teorema de LT y la longitud de la demostración de X es L entonces, X es un axioma de LT, o X es consecuencia de aplicar MP en pasos anteriores de la demostración o X es consecuencia de aplicar la regla R+ en un paso anterior de la demostración. En el primer caso se procede como en el caso base. En el segundo caso se tienen en LT, para alguna fórmula Y, demostraciones de Y y de Y  X, donde la longitud de ambas demostraciones es menor que L, utilizando la hipótesis inductiva se infiere que Y y Y
X, donde la longitud de ambas demostraciones es menor que L, utilizando la hipótesis inductiva se infiere que Y y Y  X son válidas, y por la proposición 4.1b, resulta que X es válida. En el tercer caso basta utilizar la proposición 4.1a.
X son válidas, y por la proposición 4.1b, resulta que X es válida. En el tercer caso basta utilizar la proposición 4.1a.
5 Completitud
Definición 5.1 (Extensión consistente y completa). Una extensión de un sistema deductivo, se obtiene alterando el conjunto de axiomas de tal manera que, todos los teoremas del sistema sigan siendo teoremas, y que las reglas de inferencia de la extensión coincidan con las del sistema deductivo. Específicamente, una extensión E de LT, se obtiene añadiendo como nuevos axiomas un conjunto de fórmulas Γ, donde, una fórmula X es un teorema de E, si y solamente si, X es la última fórmula de una sucesión finita de fórmulas, tales que, cada una de ellas es un axioma de LT o un elemento de Γ o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP o se infiere de una fórmula anterior, la cual es un teorema de LT, utilizando la regla de inferencia R+ (en consecuencia los teoremas de LT son teoremas de E). O de manera equivalente, una extensión E de LT, tiene como axiomas a los teoremas de LT junto con un conjunto de fórmulas Γ, las cuales no son teoremas de LT, donde, una fórmula X es un teorema de E, si y solamente si, X es la última fórmula de una sucesión finita de fórmulas, tales que, cada una de ellas es un teorema de LT o un elemento de Γ o se infiere de dos fórmulas anteriores utilizando la regla de inferencia MP (no se utiliza la regla de inferencia R+). Una extensión es consistente si no existe ninguna fórmula X tal que tanto X como  X sean teoremas de la extensión. Un conjunto de fórmulas es inconsistente si de ellas se deriva una contradicción, es decir, si se deriva Z
X sean teoremas de la extensión. Un conjunto de fórmulas es inconsistente si de ellas se deriva una contradicción, es decir, si se deriva Z
 Z para alguna fórmula Z. Una extensión es completa si para toda fórmula X, del lenguaje de la extensión, o bien X o bien
Z para alguna fórmula Z. Una extensión es completa si para toda fórmula X, del lenguaje de la extensión, o bien X o bien  X es teorema de la extensión.
X es teorema de la extensión.
Para llegar a la prueba de completitud en la proposición 5.7, se siguen las directrices dadas por Henkin en The completeness of the first order functional calculus [5], por Kripke en Semantical analysis of modal logic [4] y por Kaplan en Review of Kripke [6], para probar la completitud de la lógica de primer orden y del sistema modal T.
Proposición 5.1. Extensión consistente de LT.
a. LT es consistente.
b. Sea E una extensión consistente de LT. E 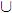 {X} es consistente o E
{X} es consistente o E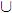 {
{ X} es consistente.
X} es consistente.
c. Si E es una extensión de LT, X no es teorema de E y Ex= E 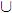 {
{ X}, entonces, Ex es consistente.
X}, entonces, Ex es consistente.
Prueba 5.1. Para la parte a, supóngase que LT no fuese consistente, por lo que debe existir una fórmula X tal que tanto X como  X sean teoremas. Entonces por la proposición 4.3, tanto X como
X sean teoremas. Entonces por la proposición 4.3, tanto X como  X son fórmulas válidas, pero esto es imposible, ya que si
X son fórmulas válidas, pero esto es imposible, ya que si  X es una fórmula válida, entonces para todo modelo (S, M, R, V), se tienen V (M, X) = 1, es decir, según V
X es una fórmula válida, entonces para todo modelo (S, M, R, V), se tienen V (M, X) = 1, es decir, según V  , V (M, X) = 0, por lo que X no puede ser válida, lo cual no es el caso. Por lo tanto, LT es consistente.
, V (M, X) = 0, por lo que X no puede ser válida, lo cual no es el caso. Por lo tanto, LT es consistente.
Para la parte b. Sea E = TLT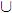 Γ, donde TLT es el conjunto de teoremas de LT y Γ es un conjunto de no teoremas de LT. Si E
Γ, donde TLT es el conjunto de teoremas de LT y Γ es un conjunto de no teoremas de LT. Si E 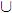 {X} es inconsistente entonces de E = TLT
{X} es inconsistente entonces de E = TLT 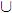 Γ
Γ 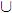 {X} se deduce Y
{X} se deduce Y 
 Y para alguna fórmula Y, por lo que existen A1, ... , An, en Γ, tales que de TLT
Y para alguna fórmula Y, por lo que existen A1, ... , An, en Γ, tales que de TLT 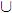 {A1, ... , An}
{A1, ... , An} 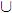 {X} se deduce Y
{X} se deduce Y 
 Y , es decir, de TLT
Y , es decir, de TLT 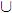 {A1, ... , An, X} se deduce Y
{A1, ... , An, X} se deduce Y 
 Y , lo cual por LCP significa que de TLT se deduce
Y , lo cual por LCP significa que de TLT se deduce  (A1
(A1  ...
...  An
An  X), es decir, en LT se tiene que
X), es decir, en LT se tiene que  (A1
(A1  ...
...  An
An  X), donde A1, ... , An están en E. De manera similar, si E
X), donde A1, ... , An están en E. De manera similar, si E 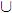 {
{ X} es inconsistente, entonces existen B1, ... , Bk en E, tales que en LT se tiene
X} es inconsistente, entonces existen B1, ... , Bk en E, tales que en LT se tiene  (B1
(B1  ...
...  Bn
Bn
 X). De estos resultados se infieren (A1
X). De estos resultados se infieren (A1  ...
...  An)
An) 
 X y (B1
X y (B1  ...
...  Bk)
Bk)  X, por lo que se deduce
X, por lo que se deduce  (A1
(A1  ...
...  An
An  B1 ...
B1 ...  Bk), y como A1, ... , An, B1, ... , Bk están en E, se concluye que E es inconsistente.
Bk), y como A1, ... , An, B1, ... , Bk están en E, se concluye que E es inconsistente.
Para la parte c, si Ex= E 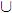 {
{ X} es inconsistente, entonces existen A1, ... , An en E, tales que en LT
X} es inconsistente, entonces existen A1, ... , An en E, tales que en LT  (A1
(A1  ...
...  An
An 
 X), es decir, (A1
X), es decir, (A1  ...
...  An)
An)  X, y como A1, ... , An, están en E, se concluye que X es teorema de E.
X, y como A1, ... , An, están en E, se concluye que X es teorema de E.
Proposición 5.2 (Extensión consistente y completa). Si E es una extensión consistente de LT entonces existe una extensión consistente y completa de E.
Prueba 5.2. Sea X0, X1, X2, ... una enumeración de todas las fórmulas de LT. Se construye una sucesión J0, J1, J2, ... de extensiones de E como sigue:
Sea J0 = E. En general, dado t ≥ 1, para construir Jta partir de Jt-1, se procede de la siguiente manera: si Jt-1 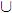 {Xt-1} es consistente entonces Jt= Jt-1
{Xt-1} es consistente entonces Jt= Jt-1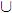 {Xt-1}, y si Jt-1
{Xt-1}, y si Jt-1 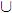 {Xt-1} es inconsistente entonces Jt= Jt-1
{Xt-1} es inconsistente entonces Jt= Jt-1 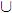 {
{ Xt-1}.
Xt-1}.
Se tiene que E es consistente, es decir, J0 es consistente. Dado t ≥ 1, si Jt-1 es consistente, entonces, por la proposición 5.1b, Jt es consistente. Así pues, por inducción, todo Jt es consistente. Se define ahora J, como aquella extensión de E, la cual tiene como axiomas a aquellas fórmulas que son axiomas de al menos uno de los Jt.
Se probará que J es consistente. Supóngase lo contrario, por lo que, existe una fórmula X tal que, tanto X como  X son teoremas de J, ahora bien, las demostraciones de X y
X son teoremas de J, ahora bien, las demostraciones de X y  X en J son sucesiones finitas de fórmulas, de modo que cada demostración solamente puede contener casos particulares de un número finito de axiomas de J, por lo que, debe existir un t suficientemente grande, para que todos estos axiomas utilizados sean axiomas de Jt, se deduce que tanto X como
X en J son sucesiones finitas de fórmulas, de modo que cada demostración solamente puede contener casos particulares de un número finito de axiomas de J, por lo que, debe existir un t suficientemente grande, para que todos estos axiomas utilizados sean axiomas de Jt, se deduce que tanto X como  X son teoremas de Jt, lo cual es imposible ya que Jt es consistente. Por lo tanto J es consistente.
X son teoremas de Jt, lo cual es imposible ya que Jt es consistente. Por lo tanto J es consistente.
Para probar que J es completo, sea X una fórmula de LT, por lo que X debe aparecer en la lista X0, X1 , X2, ... supóngase que X es Xk. Si Jk 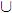 {Xk} es consistente entonces Xk está en Jk+1, y por lo tanto también está en J, y si Jk
{Xk} es consistente entonces Xk está en Jk+1, y por lo tanto también está en J, y si Jk 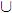 {
{ Xk} es consistente entonces
Xk} es consistente entonces  Xk está en Jk+1, y por lo tanto también está en J. Se concluye que J es completo.
Xk está en Jk+1, y por lo tanto también está en J. Se concluye que J es completo.
Proposición 5.3 (Consistencia subordinada). Si {+Z1, ... , +Zk, •Y} es consistente entonces {Z1, ... , Z k, Y} es consistente.
Prueba 5.3. Supóngase que {Z1, ... , Zk, Y} es inconsistente, por lo que  (Z1
(Z1  ...
...  Z k
Z k  Y), lo cual por LCP significa, (Z1
Y), lo cual por LCP significa, (Z1  ...
...  Z k)
Z k) 
 Y . Utilizando R+ resulta que +((Z1
Y . Utilizando R+ resulta que +((Z1 ...
... Z k)
Z k) 
 Y), por MP+ se infiere +(Z1
Y), por MP+ se infiere +(Z1  ...
... Z k)
Z k)  +
+  Y, por la proposición 2.1 se obtiene (+Z1
Y, por la proposición 2.1 se obtiene (+Z1 ...
...  +Z k)
+Z k)  +
+  Y , lo cual, por LCP y la definición de satisfacible equivale a
Y , lo cual, por LCP y la definición de satisfacible equivale a  (+Z1
(+Z1  ...
...  +Zk
+Zk  •Y), por lo que {+Z1, ... , +Zk, •Y} es inconsistente.
•Y), por lo que {+Z1, ... , +Zk, •Y} es inconsistente.
Definición 5.2 (Subordinado). Sean E y F extensiones consistentes y completas de LT. Se dice que F es subordinado de E si y solamente si existe una fórmula Z tal que, •Z en E y Z está en F, y además para cada fórmula W, si +W está en E entonces W está en F.
Proposición 5.4 (Extensión subordinada consistente y completa).
a. Para E una extensión consistente y completa de LT, si •X está en E, entonces, existe una extensión consistente y completa F de LT tal que X 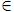 F y F subordinada de E.
F y F subordinada de E.
b. Si E una extensión consistente y completa de LT, entonces, existe una extensión consistente y completa F de LT tal que F subordinada de E.
Prueba 5.4. Para la parte a, sea X una fórmula tal que •X está en E. Sea EX= {X} 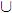 {Z : +Z está en E}, entonces por la proposición 5.3, EX también es consistente. Al adicionar a EX los axiomas de LT y todas sus consecuencias, se obtiene una extensión de LT que incluye a EX, utilizando la proposición 5.2, se construye una extensión consistente y completa F de LT la cual incluye a EX. Como X está en EX , también está en F. Si +W está en E, por definición W está en EX, por lo que W está en F. Por lo tanto, F es subordinado de E.
{Z : +Z está en E}, entonces por la proposición 5.3, EX también es consistente. Al adicionar a EX los axiomas de LT y todas sus consecuencias, se obtiene una extensión de LT que incluye a EX, utilizando la proposición 5.2, se construye una extensión consistente y completa F de LT la cual incluye a EX. Como X está en EX , también está en F. Si +W está en E, por definición W está en EX, por lo que W está en F. Por lo tanto, F es subordinado de E.
La parte b, es consecuencia de la parte a, al tener en cuenta que, por LCP y AxR, en LT se tiene •(P  P).
P).
Proposición 5.5 (Propiedades de la subordinacion). Para E, F y G extensiones consistentes y completas de LT.
a. Si F es subordinado de E, y G es subordinado de F, entonces G es subordinado de E.
b. Si F es subordinado de E, y G es subordinado de E, entonces G es subordinado de F.
c. F es subordinado de F.
Prueba 5.5. Para la parte a, supóngase que G es subordinado de F y F es subordinado de E. Como G es subordinado de F entonces existe en F una fórmula •Z tal que Z está en G. Si •Z no está en E, entonces al ser una extensión completa,  •Z sí debe estarlo, además por AxT se tiene que —¬Z
•Z sí debe estarlo, además por AxT se tiene que —¬Z  •Z está en E, por lo que
•Z está en E, por lo que  —¬Z, es decir ++
—¬Z, es decir ++ Z también está en E, y al ser F subordinado de E resulta que +
Z también está en E, y al ser F subordinado de E resulta que + Z está en F, lo cual significa que
Z está en F, lo cual significa que  •Z está en F, pero esto es imposible ya que F es consistente. Por lo que, •Z está en E.
•Z está en F, pero esto es imposible ya que F es consistente. Por lo que, •Z está en E.
Sea W una fórmula, tal que +W está en E, es decir  •
• W está en E, utilizando AxT —¬
W está en E, utilizando AxT —¬ W
W  •
• W, resulta que
W, resulta que  —¬
—¬ W está en E, por lo que ++W está en E, y como F es subordinado de E, se infiere que +W está en F, como además, G es subordinado de F, entonces W está en G. En resumen, existe una fórmula •Z en E tal que para cada fórmula +W en E se tiene que Z y W están en G, y por lo tanto, G es subordinado de E.
W está en E, por lo que ++W está en E, y como F es subordinado de E, se infiere que +W está en F, como además, G es subordinado de F, entonces W está en G. En resumen, existe una fórmula •Z en E tal que para cada fórmula +W en E se tiene que Z y W están en G, y por lo tanto, G es subordinado de E.
Para la parte b, supóngase que F es subordinado de E y G es subordinado de E. Como G es subordinado de E entonces existe en E una fórmula •Z tal que Z está en G. Como •Z está en E, es decir — Z está en E, utilizando AxE —
Z está en E, utilizando AxE — Z
Z  ¬+
¬+ Z, resulta que ¬+
Z, resulta que ¬+ Z está en E, lo cual significa que +•Z está en E, y como F es un subordinado de E entonces •Z está en F.
Z está en E, lo cual significa que +•Z está en E, y como F es un subordinado de E entonces •Z está en F.
Supóngase que +W está en F. Si +W no está en E, entonces  +W está en E, es decir —W está en E, utilizando AxE —W
+W está en E, es decir —W está en E, utilizando AxE —W  ¬ + W , se infiere que ¬+W está en E, o sea que +
¬ + W , se infiere que ¬+W está en E, o sea que + +W está en E, pero al ser F subordinado de E se tiene que
+W está en E, pero al ser F subordinado de E se tiene que  +W está en F, lo cual es imposible ya que F es consistente, y por lo tanto, +W está en E, y como G es subordinado de E entonces W está en G. Se concluye que, para cada +W en F resulta que W está en G. En resumen, existe una fórmula •Z en F tal que para cada fórmula +W en F se tiene que Z y W están en G , y por lo tanto, G es subordinado de F
+W está en F, lo cual es imposible ya que F es consistente, y por lo tanto, +W está en E, y como G es subordinado de E entonces W está en G. Se concluye que, para cada +W en F resulta que W está en G. En resumen, existe una fórmula •Z en F tal que para cada fórmula +W en F se tiene que Z y W están en G , y por lo tanto, G es subordinado de F
Para la parte c, sea X la fórmula P  P, por lo que en LT se tiene X, y como por AxR se tiene X
P, por lo que en LT se tiene X, y como por AxR se tiene X  •X, resulta •X, por lo que X y •X están en F. Supóngase que +W está en F, por AxR en F se tiene
•X, resulta •X, por lo que X y •X están en F. Supóngase que +W está en F, por AxR en F se tiene  W
W  •
• W, es decir +W
W, es decir +W  W, resultando que W también está en F. Por lo tanto, F subordinada de F.
W, resultando que W también está en F. Por lo tanto, F subordinada de F.
Proposición 5.6 (Construcción de un modelo). Si E´es una extensión consistente de LT, entonces existe un modelo en el cual todo teorema de E´es verdadero.
Prueba 5.6. Se define el marco (S, M E, R) de la siguiente manera: sean E, F , G , ..., extensiones consistentes y completas de E´(E la inicial y las demás subordinadas), presentadas en las proposiciones 5.2 y 5.4. A cada extensión F, se le asocia un mundo posible MF, sean S el conjunto de tales mundos posibles y M E el mundo actual. La relación de accesibilidad R se construye así: MFRMG si y solamente si G es subordinado de F.
Asociado al marco (S, M E, R), se define el candidato a modelo M = (S, M E, R, V) sobre las fórmulas de LT haciendo para cada MF en S y para cada fórmula X, V (M F, X) = 1 si X está en F, y V (M F , X) = 0 si  X está en F, donde F es la extensión consistente y completa asociada a M F . Nótese que V es una función, por ser F consistente y completa. Ahora bien, ya que F es consistente, entonces V (M F, X) ≠ V (M F,
X está en F, donde F es la extensión consistente y completa asociada a M F . Nótese que V es una función, por ser F consistente y completa. Ahora bien, ya que F es consistente, entonces V (M F, X) ≠ V (M F,  X) y por lo tanto, V (M F , X) = 1
X) y por lo tanto, V (M F , X) = 1  V (M F ,
V (M F ,  X) = 0, por lo que se satisface la definición V
X) = 0, por lo que se satisface la definición V  . Para afirmar que M es un modelo, se debe garantizar que para cada uno de los conectivos, V satisface la definición de valuación.
. Para afirmar que M es un modelo, se debe garantizar que para cada uno de los conectivos, V satisface la definición de valuación.
Para el caso del condicional, se tiene la siguiente cadena de equivalencias: V (M F , X  Y) = 0, es decir
Y) = 0, es decir  (X
(X  Y) está en F, o sea que X
Y) está en F, o sea que X 
 Y está en F, resultando que X y
Y está en F, resultando que X y  Y están en F, lo cual significa que V (M F , X) = 1 y V (M F , Y) = 0, por lo que se satisface la definición V
Y están en F, lo cual significa que V (M F , X) = 1 y V (M F , Y) = 0, por lo que se satisface la definición V 
Para el caso de la conjunción, se tiene la siguiente cadena de equivalencias: V (M F , X  Y) = 1, es decir X
Y) = 1, es decir X  Y está en F, por lo que X y Y están en F, lo cual significa que V (M F , X) = 1 y V (M F , Y) = 1, por lo que se satisface la definición V
Y está en F, por lo que X y Y están en F, lo cual significa que V (M F , X) = 1 y V (M F , Y) = 1, por lo que se satisface la definición V  .
.
Para el caso de la disyunción, se tiene la siguiente cadena de equivalencias: V (M F , X Y) = 0, es decir
Y) = 0, es decir  (X
(X Y) está en F, o sea que
Y) está en F, o sea que  X
X
 Y está en F, de donde
Y está en F, de donde  X y
X y  Y están en F, es decir V (M F , X) = 0 y V (M F , Y) = 0, por lo que se satisface la definición V
Y están en F, es decir V (M F , X) = 0 y V (M F , Y) = 0, por lo que se satisface la definición V .
.
Para el caso del bicondicional, se tiene la siguiente secuencia de equivalencias: V (M F , X  Y) = 1, es decir X
Y) = 1, es decir X  Y está en F, por lo que (X
Y está en F, por lo que (X  Y)
Y)  (
( X
X
 Y) está en F, lo que significa V (M F, (X
Y) está en F, lo que significa V (M F, (X  Y)
Y)  (
( X
X
 Y)) = 1, o de otra forma V (M F, X
Y)) = 1, o de otra forma V (M F, X  Y) = 1 o V (M F,
Y) = 1 o V (M F,  X
X
 Y) = 1, es decir, V (M F , X) = V (M F , Y) = 1 o V (M F , X) = V (M F , Y) = 0, o dicho de otra manera V (M F , X) = V (M F , Y), por lo que se satisface la definición V
Y) = 1, es decir, V (M F , X) = V (M F , Y) = 1 o V (M F , X) = V (M F , Y) = 0, o dicho de otra manera V (M F , X) = V (M F , Y), por lo que se satisface la definición V  .
.
Para el caso de la regla V+, donde M F es un mundo asociado a F, MG es un mundo asociado a G. Supóngase que V (M F , +Z) = 1, por lo que +Z está en F. Si MFRMG, entonces G es subordinada de F y Z está en G, resultando que V (M G , Z) = 1. Se ha probado de esta manera que V (M F , +Z) = 1) ( MG
MG 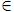 S)(MFRMG
S)(MFRMG  V (MG , Z) = 1).
V (MG , Z) = 1).
Para probar la recíproca, supóngase que ( MG
MG 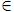 S)(MFRMG
S)(MFRMG  V (MG,Z) = 1). Si V (M F , +Z) = 0, entonces al ser M F el mundo asociado a la extensión consistente y completa F resulta que
V (MG,Z) = 1). Si V (M F , +Z) = 0, entonces al ser M F el mundo asociado a la extensión consistente y completa F resulta que  +Z está en F, por lo que •
+Z está en F, por lo que • Z está en F. Por la proposición 5.4 existe una extensión consistente y completa G subordinada de F tal que
Z está en F. Por la proposición 5.4 existe una extensión consistente y completa G subordinada de F tal que  Z está en G. Como MG es el mundo asociado a G, entonces MFRMG, lo cual, por el supuesto inicial implica V (MG, Z) = 1, es decir Z está en G, resultando que G es inconsistente, lo cual no es el caso. Por lo tanto, V (M F , +Z) = 1. Se ha probado de esta manera que (
Z está en G. Como MG es el mundo asociado a G, entonces MFRMG, lo cual, por el supuesto inicial implica V (MG, Z) = 1, es decir Z está en G, resultando que G es inconsistente, lo cual no es el caso. Por lo tanto, V (M F , +Z) = 1. Se ha probado de esta manera que ( MG
MG 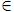 S)(MFRMG
S)(MFRMG  V (MG,Z) = 1) = 1)) V (M F , +Z) = 1.
V (MG,Z) = 1) = 1)) V (M F , +Z) = 1.
Para el caso de la regla VL, sea MF un mundo, y sea F la extensión consistente y completa de LT asociada. Si L1, ... , Lkes una secuencia de literales disjuntos, por Ax•. se tiene que •(L1  ...
...  Lk) está en F, lo cual por la proposición 5.4 implica que existe G una extensión consistente y completa de LT tal que, L1
Lk) está en F, lo cual por la proposición 5.4 implica que existe G una extensión consistente y completa de LT tal que, L1  ...
...  Lkestá en G y G es subordinada de F, resultando que MFRMG donde MG es el mundo asociado a G, y como L1
Lkestá en G y G es subordinada de F, resultando que MFRMG donde MG es el mundo asociado a G, y como L1  ...
...  Ln está en G entonces V (MG , L1
Ln está en G entonces V (MG , L1 ...
...  Lk) = 1.
Lk) = 1.
Con base en el análisis anterior, y teniendo en cuenta que las reglas RR, RE y RT, se encuentran garantizadas por la proposición 5.5 y la forma en que se construye el modelo, se concluye finalmente que V es una valuación, y por lo tanto, M es un modelo.
Para finalizar la prueba, sea X un teorema de E´, por lo que X está en E. Por lo tanto, utilizando la definición de V resulta que V (M E, X) = 1, es decir, X es verdadera en el modelo M = (S, M E, R, V).
Proposición 5.7 (Completitud de LT). Si X es válida entonces X es un teorema de LT.
Prueba 5.7. Sea X una fórmula de LT. Si X no es un teorema, entonces, por la proposición 5.1c, la extensión E´, obtenida añadiendo  X como nuevo axioma, es consistente. Así pues, según la proposición 5.6, existe un modelo M tal que todo teorema de E´es verdadero en M, y como
X como nuevo axioma, es consistente. Así pues, según la proposición 5.6, existe un modelo M tal que todo teorema de E´es verdadero en M, y como  X es un teorema de E´, entonces
X es un teorema de E´, entonces  X es verdadero en M, es decir, X es falso en M, y por lo tanto, X no es válida. Se ha probado de esta forma que, si X no es un teorema de LT entonces X no es válida, o dicho de otra manera, si X es válida entonces X es un teorema de LT.
X es verdadero en M, es decir, X es falso en M, y por lo tanto, X no es válida. Se ha probado de esta forma que, si X no es un teorema de LT entonces X no es válida, o dicho de otra manera, si X es válida entonces X es un teorema de LT.
Proposición 5.8 (Caracterización semántica de LT). X es válida si y solamente si X es un teorema de LT.
Prueba 5.8. Consecuencia de las proposiciones 4.3 y 5.7.
6 Interpretación canónica
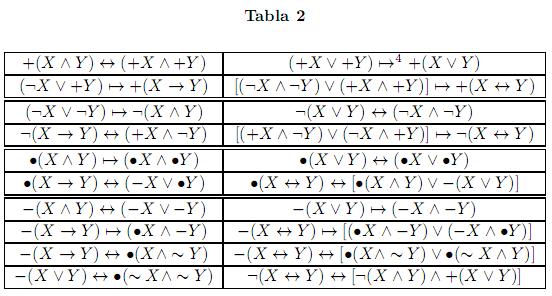
En la tabla 2, se presenta el comportamiento de los operadores de verdad con los conectivos binarios usuales en LT. Observar que los resultados satisfacen plenamente la interpretación canónica de los operadores de verdad (la forma como se prueban estos resultados se ilustra en la proposición 6.1).
Proposición 6.1 (Disyunción de tautologías).
a. (+X  +Y)
+Y) 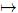 +(X
+(X  Y) y (X
Y) y (X  Y)
Y) 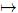 (—X
(—X  Y) son teoremas de LT.
Y) son teoremas de LT.
b. Si L y T son literales disjuntos entonces (+L  +T)
+T)  +(L
+(L  T) y —(L
T) y —(L  T)
T)  (—L
(—L  T) son teoremas de LT.
T) son teoremas de LT.
Prueba 6.1. Para el primer enunciado de la parte a, por LCP se tienen X  (X
(X  Y) y Y
Y) y Y  (X
(X  Y), por R+ resultan, +(X
Y), por R+ resultan, +(X  (X
(X  Y)) y +(Y
Y)) y +(Y  (X
(X  Y)), utilizando MP+ y MP se infieren +X
Y)), utilizando MP+ y MP se infieren +X  +(X
+(X  Y) y +Y
Y) y +Y  +(X
+(X  Y), y por LCP resulta que (+X
Y), y por LCP resulta que (+X  +Y)
+Y)  +(X
+(X  Y).
Y).
Para refutar el recíproco, sean X = P y Y =  P (donde P es una fórmula atómica). Por LCP se tiene P
P (donde P es una fórmula atómica). Por LCP se tiene P 
 P, y por R+ resulta +(P
P, y por R+ resulta +(P 
 P), además, por Ax• se tienen •P y •
P), además, por Ax• se tienen •P y • P, por lo que se obtienen
P, por lo que se obtienen  +P y
+P y  +
+  P, y como LT es consistente, no se pueden tener ni +P ni +
P, y como LT es consistente, no se pueden tener ni +P ni +  P, por lo tanto, +(P
P, por lo tanto, +(P
 P)
P)  (+P
(+P  +
+  P) no es un teorema. Esta fórmula es refutada por el modelo con mundos M y D donde el mundo actual M accede a M y a D, y V (D, P) = 0 y V (M, P) = 1.
P) no es un teorema. Esta fórmula es refutada por el modelo con mundos M y D donde el mundo actual M accede a M y a D, y V (D, P) = 0 y V (M, P) = 1.
Para el segundo enunciado de la parte a, basta notar que (+X  +Y)
+Y) 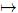 +(X
+(X  Y) es equivalente a
Y) es equivalente a  +(X
+(X  Y)
Y) 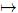
 (+X
(+X  +Y), por LCP equivale a
+Y), por LCP equivale a  +(X
+(X  Y)
Y) 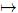 (
( +X
+X 
 +Y), lo cual según la definición de refutable significa —(X
+Y), lo cual según la definición de refutable significa —(X  Y)
Y) 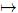 (—X
(—X  —Y).
—Y).
Para la parte b, en la cual L y T son literales disjuntos. Supóngase que +(L  T)
T)  (+L
(+L  +T) es inválida, se construye el modelo refutador de +(L
+T) es inválida, se construye el modelo refutador de +(L  T)
T)  (+L
(+L  +T) de la siguiente manera: Sea M el mundo actual de un modelo que refuta +(L
+T) de la siguiente manera: Sea M el mundo actual de un modelo que refuta +(L T)
T)  (+L
(+L +T), si V (M, +(L
+T), si V (M, +(L T)
T)  (+L
(+L +T)) = 0 entonces, por V
+T)) = 0 entonces, por V  resultan V (M, +(L
resultan V (M, +(L T)) = 1 y V (M, +L
T)) = 1 y V (M, +L +T) = 0, lo cual por V
+T) = 0, lo cual por V  significa que V (M, +L) = 0 y V (M, +T) = 0. Como V (M, +L) = 0, por V+ se infiere la existencia de un mundo N, tal que MRN y V (N, L) = 0, como además V (M, +(L
significa que V (M, +L) = 0 y V (M, +T) = 0. Como V (M, +L) = 0, por V+ se infiere la existencia de un mundo N, tal que MRN y V (N, L) = 0, como además V (M, +(L  T)) = 1, entonces por V+ resulta V (N, L
T)) = 1, entonces por V+ resulta V (N, L  T) = 1, y aplicando V
T) = 1, y aplicando V  se obtiene V (N, T) = 1. Como V (M, +T) = 0, por V+ se infiere la existencia de un mundo D, tal que MRD y V (D, T) = 0. Como además V (M, +(L
se obtiene V (N, T) = 1. Como V (M, +T) = 0, por V+ se infiere la existencia de un mundo D, tal que MRD y V (D, T) = 0. Como además V (M, +(L  T)) = 1, entonces por V+ resulta V (D, L
T)) = 1, entonces por V+ resulta V (D, L  T) = 1, y aplicando V
T) = 1, y aplicando V  se obtiene V(D, L) = 1. Observar que como L y T son literales disjuntos, entonces por la regla VL, además de los mundos N y D, debe existir otro mundo E, tal que MRE, y V (E, L) = V (E, T) = 0, es decir V (E, L
se obtiene V(D, L) = 1. Observar que como L y T son literales disjuntos, entonces por la regla VL, además de los mundos N y D, debe existir otro mundo E, tal que MRE, y V (E, L) = V (E, T) = 0, es decir V (E, L  T) = 0, resultando que V (M, +(L
T) = 0, resultando que V (M, +(L  T)) = 0, lo cual no es el caso, y por lo tanto +(L
T)) = 0, lo cual no es el caso, y por lo tanto +(L  T)
T)  (+L
(+L  +T) no puede ser refutada, cuando L y T son literales disjuntos.
+T) no puede ser refutada, cuando L y T son literales disjuntos.
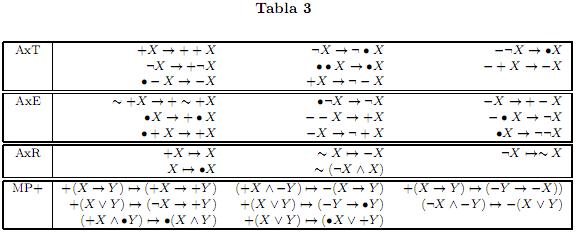
Como consecuencia de la definición de los operadores de verdad, en la tabla 3 se tienen diversas presentaciones de los axiomas:
En la tabla 4 se presenta el comportamiento de los operadores de verdad con los literales disjuntos en LT (la forma como se prueban estos resultados se ilustra en la proposición 6.2).
Proposición 6.2 (Literales contingentes). La conjunción y la disyunción de literales disjuntos son satisfacibles, refutables y contingencias.
Prueba 6.2. Si L y T son literales disjuntos, por Ax• se obtiene •(L  T). Si L y T son literales disjuntos, también lo son
T). Si L y T son literales disjuntos, también lo son  L y
L y  T, por Ax• resulta •(
T, por Ax• resulta •( L
L  T), lo cual por LCP significa •
T), lo cual por LCP significa • (L
(L  T), es decir —(L
T), es decir —(L  T). Supóngase que •(L
T). Supóngase que •(L  T) no es válido, por lo que existe un modelo con mundo actual M tal que, V (M, •(L
T) no es válido, por lo que existe un modelo con mundo actual M tal que, V (M, •(L  T)) = 0, como L es un literal entonces, por VL existe un mundo N, tal que MRN y V (N, L) = 1. Pero de V (M, •(L
T)) = 0, como L es un literal entonces, por VL existe un mundo N, tal que MRN y V (N, L) = 1. Pero de V (M, •(L T)) = 0, por V• resulta que V (N, L
T)) = 0, por V• resulta que V (N, L  T) = 0, y por V
T) = 0, y por V  se obtiene V (N, L) = 0, lo cual es imposible, y por lo tanto, •(L
se obtiene V (N, L) = 0, lo cual es imposible, y por lo tanto, •(L  T) es válido. Observar que al ser L y T literales disjuntos, también lo son
T) es válido. Observar que al ser L y T literales disjuntos, también lo son  L y
L y  T, y como se acaba de probar, resulta •(
T, y como se acaba de probar, resulta •( L
L 
 T), es decir, •
T), es decir, • (L
(L  T), o sea —(L
T), o sea —(L  T). Al ser la conjunción y la disyunción satisfacibles y refutables, resulta que son contingencias.
T). Al ser la conjunción y la disyunción satisfacibles y refutables, resulta que son contingencias.
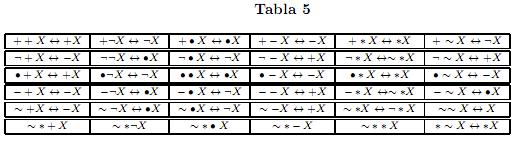
En la tabla 5 se presenta el comportamiento de los operadores de verdad con ellos mismos (reducciones) en LT (la forma como se prueban estos resultados se ilustra en la proposición 6.3)
Proposición 6.3 (Reducción de operadores de verdad).
a. + + X  +X
+X
b. ¬ + X  —X
—X
c. •—X  —X
—X
d.——X  +X
+X
e.  *—X
*—X
Prueba 6.3. Para la parte a, observar en la tabla 3 que + + X  +X corresponde a AxR, y que la recíproca corresponde a AxT. Observar que la parte b, por la definición de los operadores de verdad es equivalente a +
+X corresponde a AxR, y que la recíproca corresponde a AxT. Observar que la parte b, por la definición de los operadores de verdad es equivalente a + +X
+X 
 +X, de la tabla 3 resulta que la implicación directa corresponde a AxR, y la recíproca corresponde a AxE. De la parte a, se infiere
+X, de la tabla 3 resulta que la implicación directa corresponde a AxR, y la recíproca corresponde a AxE. De la parte a, se infiere  ++X
++X 
 +X, lo cual por LCP implica
+X, lo cual por LCP implica  +
+
 +X
+X 
 +X, y por la definición de operadores de verdad resulta •—X
+X, y por la definición de operadores de verdad resulta •—X  —X, es decir, la parte c. Ya se obtuvo +
—X, es decir, la parte c. Ya se obtuvo +  +X
+X 
 +X, es decir
+X, es decir  +
+ +X
+X  +X, y por la definición de operadores de verdad resulta la parte d. Supóngase que *—X, por definición resultan ——X y •—X, utilizando las partes d y c, se infieren +X y —X, es
+X, y por la definición de operadores de verdad resulta la parte d. Supóngase que *—X, por definición resultan ——X y •—X, utilizando las partes d y c, se infieren +X y —X, es
 +X, lo cual es imposible, por lo tanto,
+X, lo cual es imposible, por lo tanto,  *—X.
*—X.
7 Conclusiones
Con el axioma Ax• se está garantizando que las fórmulas atómicas sean contingencias, además la contraparte semántica de este axioma, es decir la regla VL, garantiza que en los modelos, para cada asignación de valores de verdad, exista un mundo posible en el cual, la asignación se encuentra representada, lográndose de esta manera que las fórmulas asociadas a las asignaciones sean satisfacibles. Con el axioma AxR se garantiza que las tautologías sean verdaderas: +X 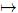 X, que las contradicciones sean falsas: ¬X
X, que las contradicciones sean falsas: ¬X 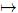
 X, que las verdades sean satisfacibles: X
X, que las verdades sean satisfacibles: X 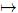 •X, que las falsedades sean refutables:
•X, que las falsedades sean refutables:  X
X 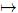 —X, y además, la contraparte semántica de este axioma, es decir la restricción RR, permite refutar las recíprocas. Con el axioma AxT, al cual semánticamente le corresponde la restricción RT, se garantiza que refutar una tautología es una contradicción: ¬ —X
—X, y además, la contraparte semántica de este axioma, es decir la restricción RR, permite refutar las recíprocas. Con el axioma AxT, al cual semánticamente le corresponde la restricción RT, se garantiza que refutar una tautología es una contradicción: ¬ —X  +X, y que satisfacer una contradicción es una contradicción: ¬ •X
+X, y que satisfacer una contradicción es una contradicción: ¬ •X  ¬X. Con el axioma AxE, al cual semánticamente le corresponde la restricción RE, se garantiza que satisfacer una fórmula satisfacible es una tautología: +•X
¬X. Con el axioma AxE, al cual semánticamente le corresponde la restricción RE, se garantiza que satisfacer una fórmula satisfacible es una tautología: +•X  •X, y que refutar una fórmula refutable es una tautología: +— X
•X, y que refutar una fórmula refutable es una tautología: +— X  —X. Con el axioma MP+, al cual semánticamente le corresponde la regla V+, se garantiza que si un condicional y su antecedente son tautologías entonces su consecuente también es tautología: [+(X
—X. Con el axioma MP+, al cual semánticamente le corresponde la regla V+, se garantiza que si un condicional y su antecedente son tautologías entonces su consecuente también es tautología: [+(X  Y)
Y)  +X]
+X]  +Y, y que si una disyunción es tautología y un disyunto es refutable entonces el otro disyunto es satisfacible: [+(X
+Y, y que si una disyunción es tautología y un disyunto es refutable entonces el otro disyunto es satisfacible: [+(X  Y)
Y)  —X]
—X]  •Y. Finalmente, cuando se construye el sistema LT, se pide que +X sea teorema si X es un teorema, lo cual garantiza que los teoremas de CP sean tautologías, y en general que todos los teoremas de LT sean tautologías. Lo anterior, reforzado por los resultados presentados en las tablas 1 a 5, permite conjeturar que las interpretaciones de tautología, contradicción, satisfacible, refutable, contingencia, verdadero y falso, son adecuadas para los conectivos +, ¬, •, —, *, — y
•Y. Finalmente, cuando se construye el sistema LT, se pide que +X sea teorema si X es un teorema, lo cual garantiza que los teoremas de CP sean tautologías, y en general que todos los teoremas de LT sean tautologías. Lo anterior, reforzado por los resultados presentados en las tablas 1 a 5, permite conjeturar que las interpretaciones de tautología, contradicción, satisfacible, refutable, contingencia, verdadero y falso, son adecuadas para los conectivos +, ¬, •, —, *, — y  , en el sistema LT.
, en el sistema LT.
Se sabe que el sistema de lógica modal S5 , puede ser construido (para detalles ver [3]), adicionando al cálculo proposicional clásico, los axiomas MP+, AxR, AxT, AxE y la regla R+. Por esta razón, LT es una extensión del sistema S5. Cuando se analiza la estructura de las pruebas presentadas, se puede afirmar que los sistemas resultantes de la eliminación de uno o varios de los axiomas AxR, AxT, AxE o Ax•, se encuentran caracterizados, por la semántica que resulta al eliminar las restricciones correspondientes.
Referencias
1. Xavier Caicedo. Elementos de lógica y calculabilidad, ISBN 0824703367. Universidad de Los Andes, 1990. Referenciado en 98, 100, 101, 105 [ Links ]
2. A. Hamilton. Lógica para matemáticos, ISBN 8428311013. Paraninfo. Madrid, 1981. Referenciado en 98, 100, 101, 105 [ Links ]
3. Brian F . Chellas. Modal Logic: An Introduction, ISBN 0521295157. Cambridge University Press, 1980. Referenciado en 99, 118 [ Links ]
4. Saul Kripke. Semantical analysis of modal logic, Zeitschrift für Mathematische Logik und Grundlagen der Mathematik, ISSN 0044-3050, 9, 67-96 (1966). Referenciado en 99, 107 [ Links ]
5. Leon Henkin. The completeness of the first order functional calculus, The Journal of Symbolic Logic, ISSN 0022-4812, 14(3), 159-166 (1949). Referenciado en 107 [ Links ]
6. David Kaplan. Review of Kripke. The Journal of Symbolic Logic, ISSN 00224812, 31, 120-122 (1966). Referenciado en 107 [ Links ]
Notas
1Esto tiene como consecuencia que, si P es una fórmula atómica entonces •P y —P son axiomas de LT. También se tiene como consecuencia que —(L1 ...
...  Lk) es un teorema de LT.
Lk) es un teorema de LT.
2 Esto tiene como consecuencia que, para cada fórmula atómica Q y para cada mundo K en S, existen mundos N y D en S, tales que, KRN, KRD, V (N, Q) = 1 y V (D, Q) = 0.
3 La forma como se construye el modelo refutador, puede ser apreciada en la prueba de la proposición 4.2.
4 A 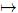 B significa que A
B significa que A  B es un teorema pero B
B es un teorema pero B  A no es un teorema.
A no es un teorema.