Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.8 no.16 Medellín July/Dec. 2012
ARTÍCULO ORIGINAL Some Exact Solutions for a Klein Gordon Equation Algunas soluciones exactas para una ecuación de Klein Gordon H. H. Ortíz Álvarez1 F. N. Jiménez-García2 A. E. Posso Agudelo3 1 MSc. en Enseñanza de la Matemática, hugo.ortiz@ucaldas.edu.co, Profesor Asistente, Universidad de Caldas, Manizales–Colombia. Profesor Asociado, Universidad Nacional de Colombia, Manizales–Colombia. 2 Doctora en Ingeniería, fnjimenezg@unal.edu.co, Profesora Titular, Universidad Autónoma, Manizales–Colombia. Profesor Titular, Universidad Nacional de Colombia, Manizales–Colombia. 3 Doctor en Matemática, possoa@utp.edu.co, Profesor Titular, Universidad Tecnológica, Pereira–Colombia. Received: 20-jun-2012, Acepted: 12-sep-2012 Available online: 30-nov-2012 MSC: 35A30
Abstract
In solving practical problems in science and engineering arises as a direct consequence differential equations that explains the dynamics of the phenomena. Finding exact solutions to this equations provides importan information about the behavior of physical systems. The Lie symmetry method allows to find invariant solutions under certain groups of transformations for differential equations.This method not very well known and used is of great importance in the scientific community. By this approach it was possible to find several exact invariant solutions for the Klein Gordon Equation uxx — utt = k(u). A particular case, The Kolmogorov equation uxx — utt = k1u + k2un was considered. These equations appear in the study of relativistic and quantum physics. The general solutions found, could be used for future explorations on the study for other specific K(u) functions.
Key words: Lie simmetries, Klein Gordon equation, invariant solutions
Resumen
En la solución de problemas prácticos de las ciencias y la ingeniería surgen como consecuencia directa ecuaciones diferenciales que dan razón de la dinámica de los fenómenos. El encontrar soluciones exactas a estas ecuaciones proporciona información importante sobre el comportamiento de sistemas físicos. El método de las simetrías de Lie permite encontrar soluciones invariantes bajo ciertos grupos de transformaciones para ecuaciones diferenciales. Mediante este método fue posible encontrar familias de soluciones exactas invariantes para la ecuación de Klein Gordon uxx — utt = k(u): En particular, se consideró la ecuación de Kolmogorov uxx — utt = k1u + k2un. Estas ecuaciones aparecen en el estudio de la física relativista y cuántica. Las soluciones generales encontradas podrían emplearse en futuros desarrollos en el estudio para otro tipo de funciones k(u).
Palabras claves: Simetrías de Lie, Ecuacion de Klein Gordon, soluciones invariantes.
1 Introduction
It is remarkable how two areas of apparently so different have reached such synergy on the solution of differential equations, as it is the case of Group and Differential Geometry theories. In the late eighteen century Sophus Lie made use of transformation groups in an effort to bring the results of Evarist Galois on polinomial equations to the differential equations theory. It was just the beginning and Sophus Lie already foresaw the monumental work that he had proposed to himself. The dedication of a whole life established the corner stone of this huge theory. It was Cartan who for the first time stated the concept of manifold in relation with transformation groups, building the bridge that allowed to relate the results on groups to the differential geometry theory and vice versa. The first fundamental theorem of Lie estates the correspondence between a Lie group and its infinitesimal representation also called Lie algebra or the symbol of the transformation. Such relation makes it possible to study differential equations not from the group action on submanifolds but from its infinitesimal representation. This fact conduced to a remarkable simplification on the understanding of the problem of how to identify transformations under which a differential equation remained invariant or equivalently according to Lie's theory, to find transformations (Symmetries) or new coordinates that allowed an easier approximation to the solution of this kind of equations [2].
The second fundamental Lie's theorem deals with the construction of a local Lie group from its Lie algebra. The above is very important in seeking new solutions from known ones. Through a complete classification of transformation groups, Lie could identify all possible ordinary differential equation order reductions. According to Olver [8], although most of Lie's work was concerned with first order linear differential equation systems, he also studied the problem of determining the symmetries of second order partial differential equations in two independent and one dependent variables; in particular, Lie found the heat equation symmetries, a case that has been taken for several authors as a key example for the description of the method. After a period of little work on the theory, the inspiring work of Birkoff on the application of group methods to differential equations of mathematical physics, favored a new beginning in the exploration of this area, worth to mention Ovsiannikov e Ibragimov in the soviet school and Bluman and Cole in occident in the decades of 1950' and 1960'. More recently, among many other authors is remarkable the rigorous treatment and the general formulation found in the Olver's book Application of Lie Groups to Differential Equations ([8]). From then on, this field has become one of the mathematical areas of more progress and development, wich can be seen from the large number of papers reporting new solutions of differential equations and other topics based on this method [3], [11].
Roughly speaking, if a one-parameter group of symmetries of a partial differential equation is known, then it can be used to reduce in one unit the number of independent variables. In particular if the equation has two independent variables then it can be transformed in an ordinary differential equation, moreover if an ordinary differential equation is also invariant under an one-parameter group, then its order can be reduced in one, in the case of first order ordinary equations, the symmetry group can be used to find a solution in terms of cuadratures by two very well known methods, canonical coordinates and the Lie integrating factor.
According to [8], and [9], in the last four decades the range of application of Lie theory deals among others with the following topics: algorithmic determination of differential system symmetry groups, determination of explicit solutions for nonlinear partial differential equations, conservation laws, classification of integrable systems, numeric methods and solution stability [5].
This article will focus on the application of the Lie group theory to the Klein-Gordon equation

a very important hyperbolic equation that appears in the study of relativistic or quantum mechanics particles.
2 The Method
In general a second order partial differential equation takes the form:
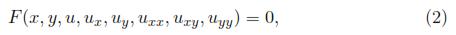
where the equation is seen as a submanifold in a space isomorphic to  8. An element of this space is the octuple (x, y, u, ux, uy, uxx, uxy, uyy):
8. An element of this space is the octuple (x, y, u, ux, uy, uxx, uxy, uyy):
2.1 Function Prolongation
Definición 2.1. Given a smooth function
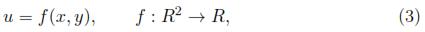
there is an induced function f(2) = Pr(2)f(x, y) called the second prolongation of f defined as
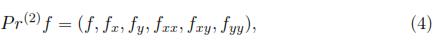
a solution of (2), will be understood as a smooth function u = f(x, y), such that
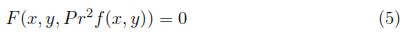
whenever (x, y) is in the domain of definition of f.
2.2 Group Prolongation Action
Let suppose G is a local group of transformations acting on an open subset of  2 ×
2 ×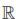 , there is an induced local action of G on the prolonged space of the variables,
, there is an induced local action of G on the prolonged space of the variables,
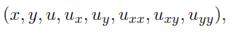
called the second prolongation of G, denoted Pr(2)G, defined in such a way, that it transforms the derivatives of (3) in the corresponding derivatives of the function transformed by the group.
2.3 Symbol Group Prolongation
Definición 2.2. Let M be an open subset of 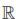 2 ×
2 × 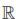 and suppose v is an infinitesimal generador of a group G = exp(αv), then, the second prolongation of v, denoted Pr(2)v, is defined as the infinitesimal generador of the second prolongation of G, Pr(2)[exp(αv)], that is,
and suppose v is an infinitesimal generador of a group G = exp(αv), then, the second prolongation of v, denoted Pr(2)v, is defined as the infinitesimal generador of the second prolongation of G, Pr(2)[exp(αv)], that is,
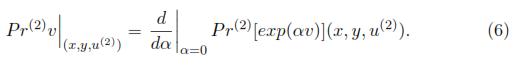
For a group action in an open subset M ⊂ 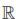 2 ×
2 ×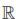 , the symbol has the form:
, the symbol has the form:
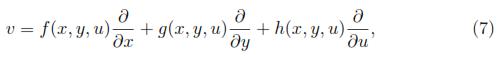
and the first and second prolongation of v are:
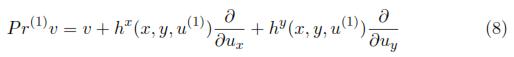
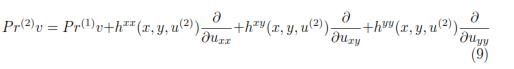
where,
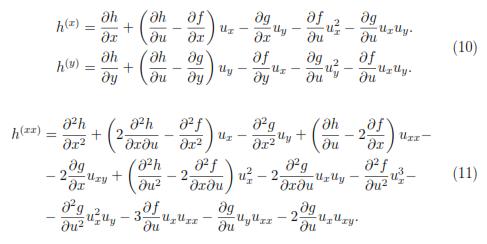
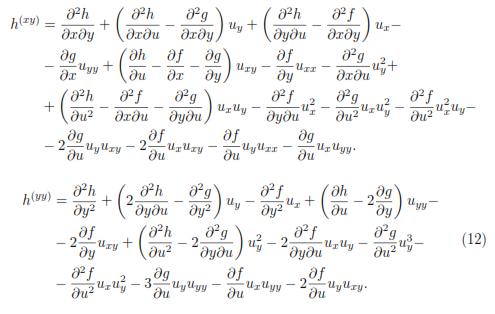
See [8]. Now it will be stated the condition that must be satisfied in order that a differential equation be invariant under a transformation group or, equivalently, what is needed to transform the solutions of a differential equation in solutions of the transformed equation.
Teorema 2.1. Suppose
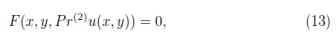
is a second order differential equation of maximal rank defined on an open subset M ⊂ 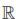 2 ×
2 × 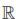 . If G is a local group of transformations acting on M, and
. If G is a local group of transformations acting on M, and
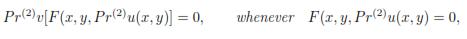
for every infinitesimal generator v of G, then G is a symmetry group of the differential equation [8], [1].
2.4 Computing Symmetry Groups
The above theorem with the prolongation formula (6), defines an effective way to calculate the symmetries of a second order differential equation in two independent and one dependent variables. Formulation that can be generalized for higher orders.
When applying the theorem (2.1) to a differential equation, it is obtained an equation equal to zero, which can involve x, y and u and its partial derivatives to the second order and also functions f, g, h of the symmetry group with their partial derivatives to the second order with respect to x, y and u. After replacing in this equation the condition given by the differential equation, that is, F(x, y Pr2u(x, y)) = 0, collecting the coefficients of u and its derivatives, and equating these coefficients to zero, it results a system of partial differential equations called the determining equations that very often can be solved by elementary methods, giving in this way the most general form of the infinitesimal symmetry of the equation.
3 The Klein-Gordon Equation
For the Klein-Gordon equation

it is observed that its jacobian matrix
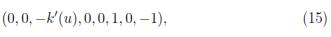
never vanishes, so the submanifold defined for the differential equation in  8 is of maximal rank, that means, this submanifold has no singularities.
8 is of maximal rank, that means, this submanifold has no singularities.
Applying the theorem (2.1) and the prolongation formula (6), to the differential equation (14),
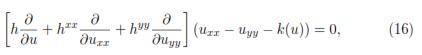
It follows that,
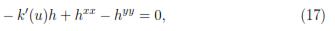
After replacing hxx and hyy of expressions (11) and (12) and substituting uxx = utt + k(u) whenever it occurs in (17) and then collecting terms of each one of the derivatives of u, equating their coefficients to zero and solving the resulting determining system for the functions f, g and h, the following vectors or symbols of the symmetry group are found
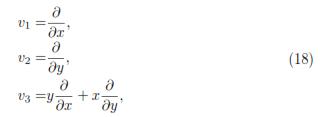
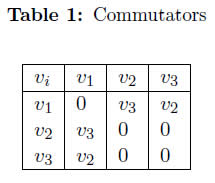
where v1; v2 y v3, constitute a basis for the Lie algebra of the group of symmetries. As it is expected by the theory of algebras, the Lie bracket is a closed operation between these generators (see table (1)).
The corresponding one-parameter transformation groups found by exponentiation of (18) are respectively:
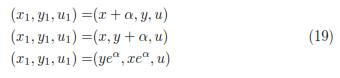
3.1 Invariant Solutions
Since a partial differential equation is invariant under a group of transformations, if their solutions are transformed in solutions under the action of the group, it is reasonable the possibility that some solutions of the equation also be invariant under the group. In this work it is explored this possibility that indeed is the way to find reductions in the number of independent variables and the construction of explicit solutions.
Let see: A function f invariant under the group with generator v1, must satisfy the condition

the very well known characteristics method [7] assures that (20) is equivalent to the system

that has, as solution, the invariant functions y = t and ν = u; taking

that is, u only depends on y, it follows:

replacing (23) in the Klein-Gordon equation (1), results de ordinary equation

In similar form, for the symmetry v2 we obtain:

the ordinary equation of cases (24) and (25)

can be transformed through canonical coordinates [4], X = w, Y = t; into equation
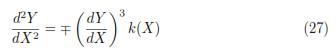
the change of variable ν = 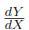 , gives the reduced equation,
, gives the reduced equation,

or after integration,
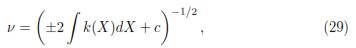
in terms of the original variables
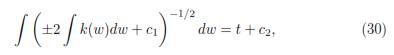
that implicitly defines w as a function of t, where u = w(t) is an invariant solution of equation (14) under the group given by the exponentiation of v1.
The results for the other generators and for the possible linear combinations between them are shown in table (2).
It follows from the groups (19) and their property of transforming solution on solutions, that:
If u = w(x, y) is a solution of (1), then, other solutions for the same equation are:
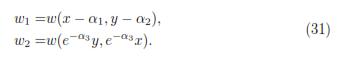
Nota 3.1. An equivalent solution to the one found for v3 generator appears reported at: http://eqworld.ipmnet.ru/en/solutions/npde/npde2107.pdf
3.2 A particular form of k(u)
Considering particular cases of k(u), it could be obtained more specific invariant solutions; by instance, for the equation,

that appears in heat conduction, mass transfer, biology and ecology [10],
after integrating the equation wtt = λ(k1w + k2wn); that includes the reduced ordinary differential equations corresponding to the generators v1 and v2;
for k1 = 0 , it is found the solution:
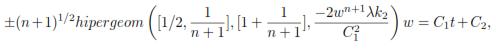
for k2 = 0
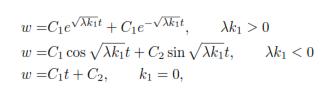
similarly for solution in table (3.1) corresponding to generator av1 + bv2, the integration with c1 = c2 = 0, k1 > 0; k2 > 0 and λ = 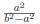 , gives the solution
, gives the solution
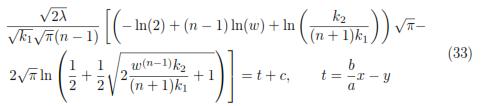
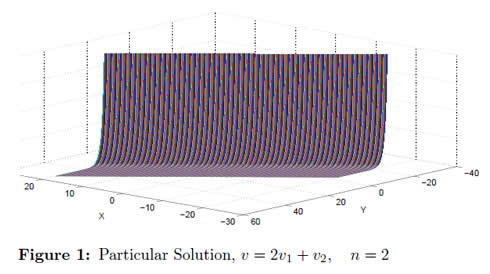
The integral surface defined by equation (33) for the particular values a = 1, b = 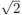 , k1 = 1, k2 = 1, n = 2 y c = 0 is shown in figure 1.
, k1 = 1, k2 = 1, n = 2 y c = 0 is shown in figure 1.
4 Conclusions
1. The Klein-Gordon Equation is invariant under a Lie group generated by three vector fields. From each vector field, it was possible to obtain invariant solutions and from each group construct new solutions from known ones.
2. The more particular nonlinear case k(u) = k1u + k2un, was considered, being possible to find several solutions.
3. The method of Lie groups applied to differential equations gives an explicit and algorithmic way to compute invariant solutions for a wide range of equations. In the nonlinear case, these solutions could be the only at hand, being very important for modelling physical situations or to compare with numerical solutions as well. Now a day, there are a number of specialized software packages that make it easier the time consuming job of computing symmetries, and should be taken in account for a more practical use of the theory, mainly for equations of higher order or in working with differential equation systems. It is strongly recommended the Hereman review of symbolic software [6].
Acknowledgements
The assitance of Dr. Guillermo Calvo Mahé of the Universidad Autónoma de Manizales in translation of this article is gratefully acknowledged.
Referencias
1. G. Bluman, S. Kumei. Symmetries and Differential Equations, 2nd. Edition, Springer Verlag. Springer Verlag, 1989. [ Links ] Referenciado en 63
2. Abraham Cohen. An Introduction to the Lie Theory of one Parameter Groups, Kessinger Publishing, 2007. [ Links ] Referenced in 59
3. R. Cherniha, V. Davydovych. ''Conditional symmetries and exact solutions of the diffusive Lotka-Volterra system''. Mathematical and Computer Modellling, vol. 54, no 5-6, 1238-1251, 2011. [ Links ] Referenced in 59
4. G. Emanuel. Solution of Ordinary Differential Equations by Continuous Groups, Chapman and Hall/CRC, 2000. [ Links ] Referenced in 66
5. Liu Hanze, Li Jibin. ''Lie symmetry analysis and exact solutions for the short pulse equation. Nonlinear Analysis''. Nonlinear Analysis: Theory, Methods and Application, vol. 71, no5-6, pp. 2126-2133, 2009. [ Links ] Referenced in 60
6. W. Hereman. ''Review of Symbolic Software for Lie Symmetrie Analysis''. Mathematical and Computer Modelling, vol. 25 no8-9, pp. 115-132, 1997. [ Links ] Referenced in 69
7. Robert C. McOwen. Partial Differential Equations: Methods and Applications, Prentice Hall, 2002. [ Links ] Referenced in 65
8. Peter J. Olver. Application of Lie Groups to Differential Equations, Springer Verlag, 1993. [ Links ] Referenced in 59, 60, 62, 63
9. L. Ovsiannikov. Group Analysis of Differential Equations, Academic Press, 1978. [ Links ] Referenced in 60
10. Andrei D. Polyanin, V. Zaitsev. Handbook of Nonlinear Partial Differential Equations, Chapman and Hall/CRC, 2004. [ Links ] Referenced in 67
11. Nikolay Sukhomlin, Jan Marcos Ortiz. ''Equivalence and new exact solutions to the Black-Scholes and diffusion equations''. Applied Mathematics E-Notes, vol. 7, no 2, pp. 206-213, 2007. [ Links ] Referenced in 59