Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.9 no.17 Medellín Jan./June 2013
ARTÍCULO ORIGINAL
Class Schedule Assignment Based on Students Learning Rhythms Using A Genetic Algorithm
Asignación de horarios de clase basado en los ritmos de aprendizaje de los estudiantes usando un algoritmo genético
Victor F. Suarez Chilma1, Omar D. Castrillón Gomez2 and Álvaro Guerrero Aguirre3
1 Magister in Industrial Engineering, vfsuarezc@unal.edu.co, Universidad Nacional de Colombia, Manizales, Colombia
2 PhD in Bioengineering with an emphasis on Bioelectronics, odcastrillong@unal.edu, Universidad Nacional de Colombia, Manizales, Colombia.
3 Electronic Engineer, aguerreroa@unal.edu.co, Universidad Nacional de Colombia, Manizales, Colombia.
Received: 25-07-2012, Acepted: 15-02-2013 Available online: 22-03-2013
MSC:49-00, 90B06
Abstract
The objective of this proposal is to implement a school day agenda focused on the learning rhythms of students of elementary and secondary schools using a genetic algorithm. The methodology of this proposal takes into account legal requirements and constraints on the assignment of teachers and classrooms in public educational institutions in Colombia. In addition, this proposal provides a set of constraints focused on cognitive rhythms and subjects are scheduled at the most convenient times according to the area of knowledge. The genetic algorithm evolves through a process of mutation and selection and builds a total solution based on the best solutions for each group. Sixteen groups in a school are tested and the results of class schedule assignments are presented. The quality of the solution obtained through the established approach is validated by comparing the results to the solutions obtained using another algorithm.
Key words: learning rhythms, genetic algorithm, class schedule, optimization, logistic.
Highlights
• The computational model presented is a genetic algorithm. • The methodology developed achieves an improvement of 12% (based on the rhythms as cognitive) than traditional algorithms generate schedules. • The algorithm shows high stability in the found solutions, ensuring an effieciency over 92% in the result obtained in each cycles.
Resumen
El objetivo de esta propuesta es implementar un horario escolar que tenga en cuenta los ritmos de aprendizaje en los estudiantes de educación primaria y secundaria, utilizando un algoritmo genético. La metodología considera los requerimientos legales y las restricciones necesarias para la asignación de maestros y aulas en instituciones educativas públicas de Colombia. Adicionalmente, se establecen un conjunto de restricciones relacionadas con el enfoque en los ritmos cognitivos, determinando las horas de la jornada en las que es más conveniente la ubicación de ciertas materias de acuerdo al área del conocimiento al que pertenecen. El algoritmo genético evoluciona mediante un proceso de mutación y selección, a través del cual se construye una solución completa a partir de la búsqueda de las mejores soluciones por grupo. Se presentan los resultados de las pruebas realizadas para la asignación de una institución con 16 grupos. La calidad de las soluciones obtenidas de acuerdo al enfoque establecido es validada mediante la comparación de los resultados obtenidos con las soluciones de otro algoritmo.
Palabras clave: ritmos de aprendizaje, algoritmos genéticos, horario de clase, optimización, logística.
1 Introduction
School day is the time that primary and secondary schools establish for teaching and learning activities. The assignment of class schedules must meet the standards of current legal requirements, the institutional educational project and also the curriculum of the school. In general, the planning of the school day is based on the availability of teachers and classrooms and takes into account some special conditions of each school and the overlapping of class assignments. However, the assigning of class schedules must also consider the academic performance of students. Many schools fail to see the importance of academic performance when assigning class schedules, thus the learning rhythms of the students are not taken into account. The mental activity of human beings is subject to cycles of greater or lesser degree of accuracy when performing tasks, which vary in frequency. So, students do not always have the cognitive capacity to assimilate certain knowledge or to carry out certain learning activity at any given time of the day. There has been a lot of research done on the learning rhythms of students, also known as circadian rhythms (periods between 20 and 28 hours), which facilitate the analysis of performance according to factors such as characteristics of the task (complexity, motor component), individual differences (age, sex, chronotype, cognitive style, level of motivation) and socio-cultural factors (urban, rural) [1].
The school day (morning or afternoon) is a continuous program divided into predetermined time periods for teaching and learning activities of a number of subjects. These subjects are associated with a specific grade level, and are taken by a group of students not by choice, as university courses, but as mandatory courses. Class arrangements take into consideration the conditions of the school facilities and classrooms are permanently assigned to the same group, systematically favoring the rotation of teachers among classrooms. Multi-purpose classrooms or classrooms for special purposes can also be considered when assigning class schedules as these may turn into permanent classrooms for any of the groups at any given time. Moreover, the assigning of schedules must ensure that a teacher is not placed in two different groups at the same time, or that the weekly schedule assignment for each teacher does not exceed a preset number of hours of supervised work.
In a high proportion of institutions, the class schedule is manually made, which additionally of taking either days or weeks of work, does not allow to set certain types of restrictions that optimize the use of oth resources human and infrastructure, as well as give errors for subjects overlaps and the teachers' assignation (Flores Pichardo, 2011). wever, at the investigative level this proposal is not beyond the scope of previous work in which a wide variety of techniques have een applied to solve scheduling problem [2] based on models such integer programming [3],[4] linear programming [5], Backtraking [6],[7] multi objectives scheduling [8] evolutionary algorithms [9],[10],[11] metaheuristics [12], mathematical models based on polynomial reduction [13], taboo search [14] and expert systems [15] among others [16],[17],[18].
Nevertheless, this research establishes a class schedule structure that embraces not only the constraints of infrastructure and general capacity of the school, but also includes an approach to a pedagogical practice that considers the times of the day that are more conducive to the learning of certain subjects. The questions of when to teach, or what is the best time to carry out certain academic activities become an important focal point. There are difierent approaches specifically addressing three types of lines: the first refers to the implementation of a double shift school day or a split shift [19]; the second refers to the duration of the school day [20]; and the third refers to the best time of the day to carry out specific learning actions [1].
The approach of this proposal deals with the most appropriate time of the day for teaching and the considerations made by Hederich [1] were adapted and adjusted to the general parameters of public educational institutions in Colombia, where the school day is continuous and lasts six hours. Three instances of time in which attention and cognitive activity are more conducive to certain types of subjects were determined. The chosen schedule, which attempts to concentrate the most difficult subjects in the middle of the day is presented in the methodology section and is identified as the time window in which students have a greater attention span and a better cognitive disposition.
The computational model presented in this paper is a genealgorithm, which although it has been used repeatedly to solve the traditional approach to the problem [21],[22],[23], has properties that allow to cover comprehensively the multiple needs presented, including the set of constraints associated with cognitive rhythms, which increase the complexity of the problem.
In summary, the assigning of class schedules will be focused on the learning rhythms of the students. This is done through the use of a genetic algorithm which seeks to solve and optimize a class schedule in which the location of subjects will depend on constraints of the activities planned, so that these match the time of the day when the cognitive ability of the students is more suitable. These optimization criteria are not compatible with optimization criteria commonly used in school planning, because the above are not always focused on the student.
2 Methodology
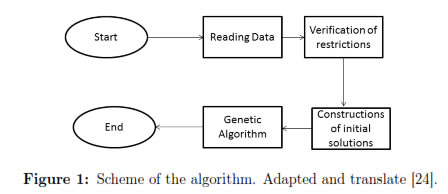
Figure 1 generally describes the methodology developed for the solution of the problem in this research:
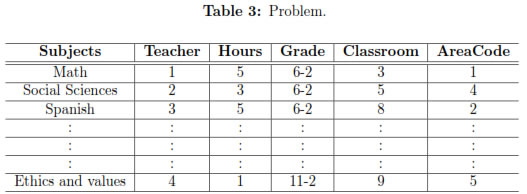
Basic information such name of the subjects, identification codes for each subject (regardless of group), names of the teachers teaching each subject, identification codes for each teacher, current weekly hours per subject, name of the group taking each subject, area identification codes for the area of each subject (this code is an identifier of the area of knowledge in which a subject is located, for example, subjects like math, calculus, and geometry belong to the area of sciences), and identification numbers for the classrooms where each subject is to be taught, was taken into account to structure class schedules
Since this is a program focused on the characteristics of educational public institutions, the information provided must adhere to two basic conditions, which are previously verified before giving way to finding a solution [25]: a) Each group must take 30 hours of class a week. b) A total of 22 hours of class will be assigned to a teacher each week.
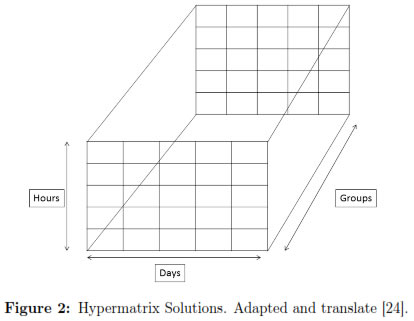
Once the data is validated, initial solutions are structured and these correspond to four hipermatrices1 (final solutions) in which the information of each group concerning subjects, teachers, codes of knowledge area, and code of classrooms are randomly added. Figure 2 shows the arrangement in which such hipermatrices are constructed.
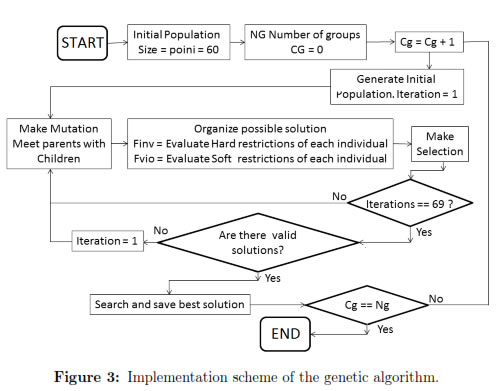
The initial solutions provide the input for the implementation of the genetic algorithm, which is described in Figure 3.
The first step of the algorithm is to determine the initial population size (vector named Parents - chromosome). The dimension must be between L and 2 * L, where L is the size of the input vector, which in this case is 30 positions corresponding to each class hour to be scheduled in each group. The next step is to specify the number of groups (NG) and the counter begins (cg) shifting the group on which the algorithm is applied. This mechanism allows the best solutions for each group and not just an overall optimal solution.
The initial solution is taken in each group. Other solutions are randomly generated using the elements of this initial solution, until the size determined in the initial population is reached. The maximum size of the initial population, that is 2 * L, was considered in order to cover a wider solution space and to allow the attaining of a more optimal solution. The counting of the iterations was then reset to zero, which represents the number of generations to be found before evaluating whether or not there are any valid solutions. For this case, a parameter of 70 iterations was chosen, which was found experimentally by selecting the average value at which the algorithm guarantees at least one valid solution for the group.
The next step is to apply mutation (3%) to each individual in the initial population in order to find new individuals (Children). Two random positions within the vector (named Parents) of each individual are determined, and the sub-vector contained within those two positions is inversed. This particular genetic algorithm does not perform crossover as the genetic content of the individuals would be altered by using this coding method, resulting in invalid solutions. In some cases, a solution might never be found.
Once the parents and children are obtained, they are gathered in one community to further evaluate the hard and soft constraints and thus verify the validity and level of optimization of the solutions. Hard constraints take into consideration general conditions of the school scheduling problem and are as follows: a) No more than 2 hours on the same subject matter should be taught in one single day. b) A block should be scheduled when two hours on the same subject are to be taught in one day. c) A teacher cannot teach 2 subjects at the same time of day. d) Two classes cannot be scheduled at the same time in the same classroom.
These constraints are evaluated in the Hypermatrix of subjects, teachers and classrooms. The solution is invalidated when there is not full compliance with these constraints. Soft constraints refer to learning rhythms and its evaluation determines the quality of the solutions, according to the location of each subject during the time of day. Taking into account the information in Table 1.
These constraints are evaluated in the hypermatrix of knowledge area codes. Using the evaluation function in Equation (1):
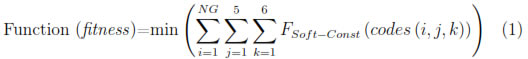
Where:
i = variable to traverse the total number of groups to be programmed;
j = variable to traverse the days of the week;
k = variable to traverse the hours of the day.
FSoft-Const(codes(i, j, k) = Evaluation function of soft constraints in the hypermatrix of the knowledge area codes. Depending on the knowledge area code, only one constraint per iteration is evaluated.
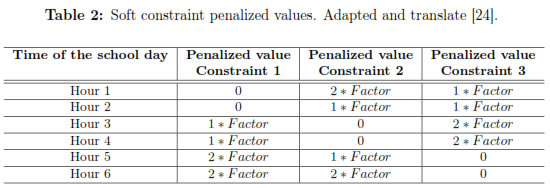
Table 2 shows the penalized low grade values held by each constraint according to the location of each subject at a certain time of the school day. A greater penalty is given to the subject located the farthest from its ideal position (Table 1)
Where, Factor = 3.
The selection of new individuals takes place once the constraints described above are evaluated and the results are stored in their respective variables. Therefore, a vector that describes pairs with individuals of the community is generated in order to confront each other in a duel in which one of them is rejected and the other is selected for the next generation, thus: a) The solutions to be confronted are taken according to the vector of pairs. b) The values of verification of the soft constraints are compared and the lowest (preferably zero) is chosen. If both are of the same value, the next step is taken. c) The values of verification of the soft constraints are compared in each solution and the lowest is chosen. If both solutions are of the same value, one is randomly chosen, since they are considered genetically equal. The above process is repeated until 70 iterations are completed, and then it is corroborated whether valid solutions are found in the last selected population. That is to say, the verification vector of the hard constraints has at least one zero (0), if not the count is reset and another 70 iterations are completed. If the result is positive, the best result is selected and the process continues for the next group. Upon completion of all groups, the final chosen solution is shown.
3 Experimentation
The previous methodology was tested for the assigning of class schedules in a high school2 in the city of Manizales. This particular school has 16 groups between sixth and eleventh grade. There are three groups per level in sixth, seventh, eighth and ninth grade, and two groups per level in tenth and eleventh grades. The algorithm was implemented during 4 cycles, and 10 solutions to the problem were found in each cycle. The Initial data were registered in an excel file, using the information of Table 3.
4 Results and Discussions
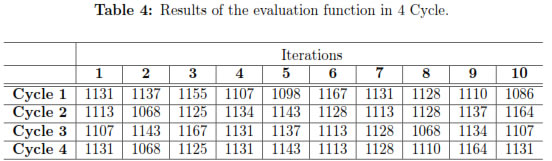
The Table 4 presents the results of the evaluation function of the 10 total solutions of the problem in each of the four cycles. The best solution found during the 40 iterations corresponds to a value of 1068 in its evaluation function.
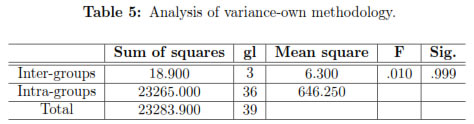
The solutions' values were compared in each cycle using ANOVA analysis, in order to establish whether there are significant differences among them (Table 5).
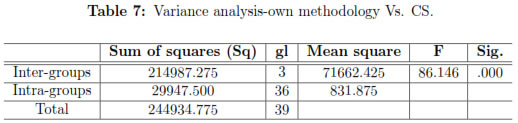
The variance analysis in Table 5 shows that the significance value is higher than 5%(p ≥ 0.05), and consequently it can be said that the results obtained are statistically equal, which proves the stability of the algorithm.
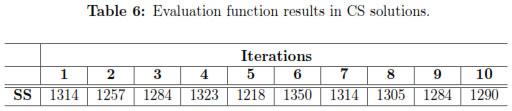
Subsequently, another variance analysis was performed to determine if both methods have significant differences (Table 7) using the solutions generated in cycles 1 to 3 of Table 3 and also 10 values of the evaluation function of the solutions found by the commercial software (CS) used for the generation of class schedules (Table 6) Another variance analysis was performed (Table 6) to determine if there were significant differences between the optimization levels for the methodology proposed and the CS results (Table 7).
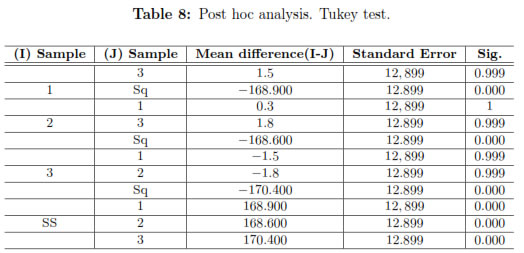
Table 7 shows that the significance of the test is less than 5%(p ≤ 0.05), therefore there are statistical differences between the means of the results obtained. The Tukey test was applied to confirm that the difference are between the samples of the own model and the CS (Table 8) It was found in the contrast tests that the results obtained of the evaluation function in the execution cycles always showed significant differences with the CS, being always less for the results of the proposed algorithm.
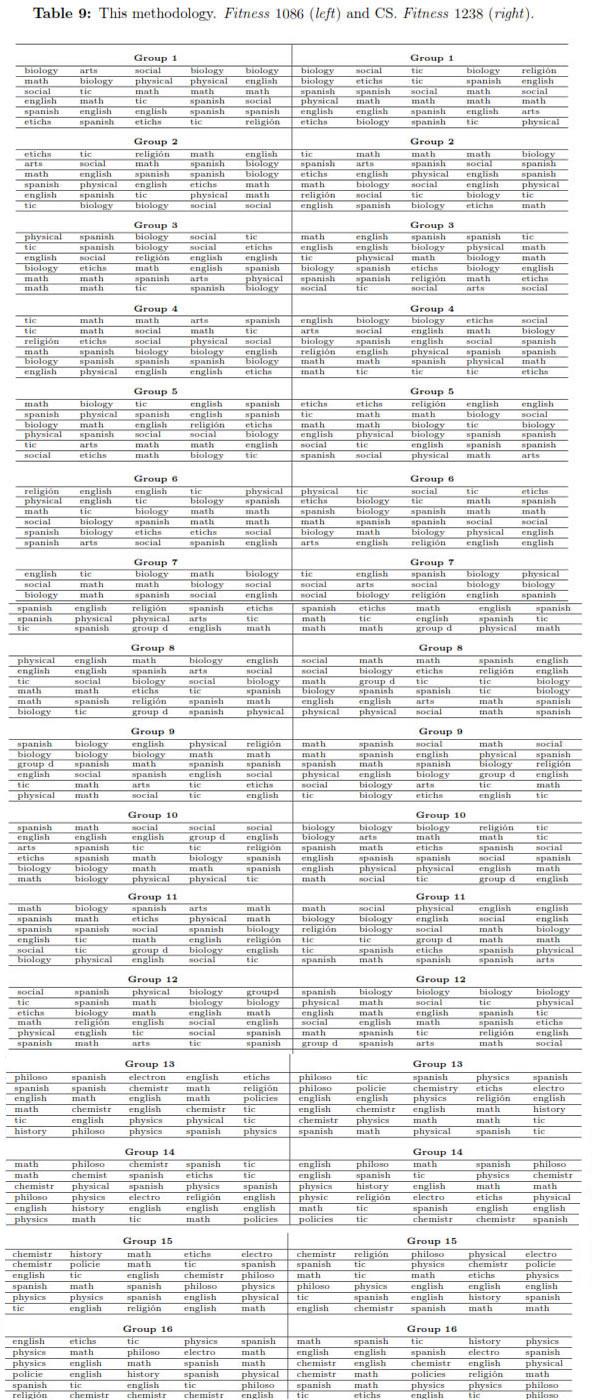
Finally in this point two real solutions are illustrated. The first solution represents this methodology (Table 9 left) Fitness 1086 and the second solution represents the CS methodology (Table 9 right) Fitness 1238.
5 Conclusions
The results show that the methodology developed achieves an improvement of 12.3% in the assigning of class schedules based on the model of student learning rhythms when compared to the CS, program currently used by the school under study. Additionally, the algorithm shows high stability in the found solutions, ensuring an efficiency of over 92%, (Tables 4 and 5) in the results obtained in each cycles. Finally, this methodology is to be implemented as a future line of research in a large number of schools in order to analyze its impact.
Acknowledgements
This article is part of the Project entitled ''Disminución de la mortalidad académica en instituciones de educación básica y media mediante el empleo de Técnicas Inteligentes en la asignación de horarios'', funded by the Universidad Nacional de Colombia, Manizales. This proyect was developed between 2010 and 2012 by the authors of this article.
1 Three-dimensional matrix
2 Educational Institution San Jorge School.
References
[1] C. Hederich Martinez, A. Camargo Uribe, and M. Reyes Cuervo, Ritmos cognitivos en la escuela. Bogotá: Universidad Pedagógica Nacional, 2004. [ Links ] 79 80
[2] D. De Werra, ''An introduction to timetabling,'' European Journal of Operational Research, vol. 19, pp. 151-162, 1985. [ Links ] 80
[3] S. Daskalaki, T. Birbas, and E. Housos, ''An integer programming formulation for a case study in university timetabling,'' European Journal of Operational Research, vol. 153, no. 1, pp. 117-135, 2004. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0377221703001036 80
[4] S. Daskalaki and T. Birbas, ''Efficient solutions for a university timetabling problem through integer programming,'' European Journal of Operational Research, vol. 160, no. 1, pp. 106-120, 2005. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0377221703005046 80
[5] N. Boland, B. D. Hughes, L. T. G. Merlot, and P. J. Stuckey, ''New integer linear programming approaches for course timetabling,'' Computers & Operations Research, vol. 35, no. 7, pp. 2209-2233, 2008. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0305054806002784 80
[6] J. Patterson, F. Brian Talbot, R. Slowinski, and J. Weglarz, ''Computational experience with a backtracking algorithm for solving a general class of precedence and resource-constrained scheduling problems,'' EuropeanJournal of Operational Research, vol. 49, pp. 68-79, 1990. [ Links ]
[7] N. Sadeh, K. Sycara, and Y. Xiong, ''Backtracking techniques for the job shop scheduling constraint satisfaction problem,'' Artificial Intelligence, vol. 76, no. 1-2, pp. 455-480, 1995. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/000437029500078S 80
[8] E. K. Burke and S. Petrovic, ''Recent Research Directions in Automated Timetabling,'' European Journal of Operational Research, vol. 140, pp. 266-280, 2002. [ Links ]
[9] M. Granada, E. Toro Ocampo, and J. Baquero Franco, ''Programación óptima de horarios de clase usando un algoritmo memético,'' Scientia et Technica, vol. 1, no. 30, 2006. [Online]. Available: http://revistas.utp.edu.co/index.php/revistaciencia/article/view/6531 80 [ Links ]
[10] N. Pillay and W. Banzhaf, ''An informed genetic algorithm for the examination timetabling problem,'' Applied Soft Computing, vol. 10, no. 2, pp. 457-467, 2010. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1568494609001331 80
[11] J. M. Mejía Caballero and C. Paternina Arboleda, ''Asignación de horarios de clases universitarias mediante algoritmos evolutivos,'' Educación en Ingeniería, no. 9, pp. 140-149, 2010. [ Links ]
[12] P. D. Causmaecker, P. Demeester, and G. V. Berghe, ''A decomposed metaheuristic approach for a real-world university timetabling problem,'' European Journal of Operational Research, vol. 195, no. 1, pp. 307-318, 2009. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0377221708001665 80
[13] J. Studenovsky, ''Polynomial reduction of timeâ''space scheduling to time scheduling,'' Discrete Applied Mathematics, vol. 157, no. 7, pp. 1364-1378, 2009. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0166218X08004708 80
[14] Z. Lüand J.-K. Hao, ''Adaptive Tabu Search for course timetabling,'' European Journal of Operational Research, vol. 200, no. 1, pp. 235-244, 2010. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/ S0377221708010394 80
[15] C.-C. Wu, ''Parallelizing a CLIPS-based course timetabling expert system,'' Expert Systems with Applications, vol. 38, no. 6, pp. 7517-7525, 2011. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S095741741001479X 80
[16] H. Turabieh and S. Abdullah, ''An integrated hybrid approach to the examination timetabling problem,'' Omega, vol. 39, no. 6, pp. 598-607, 2011. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S030504831100003X 80
[17] C. Soza, R. L. Becerra, M. C. Riff, and C. A. C. Coello, ''Solving timetabling problems using a cultural algorithm,'' Applied Soft Computing, vol. 11, no. 1, pp. 337-344, 2011. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S1568494609002373 80
[18] J.-K. Hao and U. Benlic, ''Lower bounds for the ITC-2007 curriculum- based course timetabling problem,'' European Journal of Operational Research, vol. 212, no. 3, pp. 464-472, 2011. [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0377221711001500 80
[19] R. Feito Alonso, ''Tiempos escolares: El debate sobre la jornada escolar continua y partida,'' Cuadernos de pedagogía, vol. 365, 2007. [ Links ] 80
[20] Banco Mundial., La calidad de la educación en Colombia: Un análisis y algunas opciones para un programa de política. Bogotá: Banco Internacional de Reconstrucción y Fomento / Banco Mundial Misión residente en Colombia, 2009. [ Links ] 80
[21] A. Colorni, M. Dorigo, and V. Maniezzo, ''A Genetic Algorithm To Solve The Timetable Problem,'' 1993. [Online]. Available: http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.49.3342 81 [ Links ]
[22] W. Erben and J. Keppler, ''A genetic algorithm solving a weekly course- timetabling problem,'' in Practice and Theory of Automated Timetabling, ser. Lecture Notes in Computer Science, E. Burke and P. Ross, Eds. Springer Berlin Heidelberg, 1996, vol. 1153, pp. 198-211. [Online]. Available: http://dx.doi.org/10.1007/3-540-61794-9_60 81 [ Links ]
[23] P. Mendoza Crisostomo, I. Flores Trujillo, and D. Morales Genis, ''Algoritmo Evolutivo para generar cargas académicas en TIC-SI,'' in 4to Simposio Internacional en Sistemas Inteligentes y Organizaciones Inteligentes, México D.F., 2009. [ Links ] 81
[24] V. F. Suárez, A. Guerrero, and O. D. Castrillón, ''Programación de Horarios Escolares basados en Ritmos Cognitivos usando un Algoritmo Genético de Clasificación No-dominada, NSGA-II,'' Inf. tecnol., vol. 24, no. 1, pp. 103-114, 2013. [ Links ] 81, 82, 86
[25] G. Beligiannis, S. Moschopoulos, and C Likothanassis, ''A genetic algorithm approach to school timetabling,'' Journal of the Operational Research Society, vol. 60, pp. 23-42, 2009. [ Links ] 82
[26] G. Peñalara, ''Generador de horarios para centros de enseñanza,'' 2008. [Online]. Available: http://www.penalara.com/ 88 [ Links ] Arial, Helvetica, sans-serif" size="2">