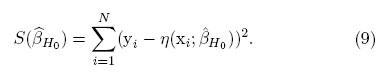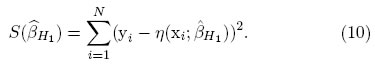ARTÍCULO ORIGINAL

Elección de la constante de ponderación en diseños óptimos compuestos: Diseños cD-óptimos

Choosing the Weighting Constant in Compound Optimal Designs: cD-optimal Designs

César Flórez–Restrepo¹ y Víctor Ignacio López–Ríos²

1 M. Sc. Ciencias-Estadística, florezrestrepo@gmail.com, Universidad Nacional de Colombia, Medellín Colombia.

2 Ph. D. en Estadística, vilopez@unal.edu.co, Universidad Nacional de Colombia, Medellín-Colombia.

Recepción: 25-01-2013, Aceptación: 24-04-2013 Disponible en línea: 05-11-2013

MSC:62K05, 62K99

Resumen

Se proponen dos metodologías alternativas para la elección de la constante de ponderación en diseños cD-óptimos. Las metodologías están basadas en el cálculo de la potencia de las pruebas de hipótesis asociadas tanto a la significancia de los parámetros del modelo bajo estudio como a la función no lineal de interés. Se describen las dos metodologías junto con la metodología existente en la literatura del cálculo de las eficiencias de los diseños individuales. Con un ejemplo se exhibe la búsqueda de la constante de ponderación con las dos metodologías propuestas y se compara con la metodología de las eficiencias, obteniendo diseños cD-óptimos con potencias altas y errores relativos pequeños, e incluso mejores que el diseño obtenido con la metodología existente.

Palabras clave: diseños experimentales óptimos; matriz de información; eficiencia; D-optimalidad; c-optimalidad; diseño óptimo compuesto; potencia de una prueba; error relativo.

Aspectos relevantes

• Se aplica una metodología existente y dos metodologías propuestas para seleccionar el valor de la constante de ponderación en el criterio compuesto, involucrando dos criterios, D-optimalidad y c-optimalidad. • Los diseños obtenidos dan la potencia más alta con relación a la prueba de significancia de los parámetros y de la función no lineal considerada o proporcionan los diseños con los errores relativos menores.

Abstract

Two alternative methods for choosing the weighting constant in cD-optimal designs are proposed. The methods are based on power hypothesis testing associated with both the significance of model parameters under study as the significance of a nonlinear function of interest. The two methodologies and the existing methodology in the literature (efficiencies methodology) are described. With an example, the weighting constant is found with methodologies proposed and is compared with the methodology of efficiencies. cD-optimal designs with higher powers, small relative errors and even better than the optimal designs with the efficiencies methodology are obtained.

Key words: optimal experimental designs; information matrix; Efficiency; D-optimality; c-optimality; compound optimal design; power test; relative error.

1 Introducción

La teoría clásica de los diseños óptimos tiene como uno de sus principales objetivos determinar las condiciones experimentales (asociadas a las combinaciones de los tratamientos) que minimizan algún funcional de la matriz de información y, por tanto, generan una mejor estimación de los parámetros del modelo bajo estudio, en el sentido de minimizar la varianza de los estimadores[1],[2],[3].

La experimentación, en algunos problemas de aplicación, se realiza con el propósito de satisfacer dos objetivos; la estimación de los parámetros y la estimación en forma óptima de una función lineal o no lineal de éstos. Entre los trabajos realizados en esta dirección están los de Huang & Wong (1998) [4] quienes realizan un análisis de costo y beneficio y un análisis de dosis efecto en el área de farmacocinética; Wei & Wong (1998) [5] muestran una aplicación referente a la toxicidad de una droga en la sangre; y Dette et al. (2009) [6] proponen diseños óptimos para el análisis del efecto-dosis en estudios de toxicidad. Otros trabajos son reportados en [7],[8],[9]. Una forma de lograr estos objetivos es mediante la construcción de los diseños óptimos compuestos que buscan el diseño que maximice una combinación convexa de dos criterios de optimalidad, Φ_D y Φ_c, (D-optimalidad, coptimalidad, respectivamente) expresados mediante la relación, [10]:

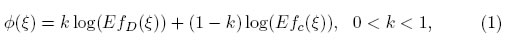
donde ξ denota el diseño conformado por los puntos de soporte y las respectivas frecuencias, ver sección 2.2 para la definición formal. Además Ef_D(ξ) y Ef_c(ξ) denotan las eficiencias del diseño ξ calculadas a partir de los criterios D- y c- optimalidad respectivamente. Para 0 < k < 1, ξ_k denota el diseño que maximiza la función dada en la ecuación (1).

En la literatura, para elegir la constante de ponderación más adecuada, se reporta una técnica basada en el cálculo de las eficiencias de cada uno de los diseños óptimos compuestos, ξ_k, con respecto a cada criterio de optimalidad involucrado, D- y c- optimalidad. Para cada valor de k (k ∈ (0,1)), se encuentra el diseño compuesto ξ_k que maximiza la relación (1). Luego, se calculan las eficiencias Ef_D(ξ_k) y Ef_c(ξ_k), obteniendo funciones monótonas para k ∈ (0, 1). El valor de k donde se cortan las dos funciones estará asociada con el diseño óptimo ξ_cD [11].

En este artículo se propone una solución alternativa para la elección de la constante de ponderación mediante dos metodologías: Cálculo de los errores relativos asociados a los parámetros y a la función no lineal de interés y el análisis de la potencia de las pruebas de hipótesis asociada a los parámetros.

Las metodologías propuestas buscan aquellos diseños óptimos compuestos que proporcionan una potencia alta en las pruebas de hipótesis de los parámetros y de la función no lineal a estimar, o dan aquellos diseños que minimizan los errores relativos tanto en la estimación de los parámetros como de la función no lineal que se desee estimar.

Las tres metodologías son ampliamente detalladas e ilustradas a partir de un modelo no lineal de uso en el área de farmacocinética para el estudio de la concentración de Teofilina presente en la sangre de un potro.

El artículo comprende las siguientes secciones: En la sección 2 se dan algunos conceptos preliminares de la teoría de diseños óptimos. En la sección 3 se describen las metodologías propuestas y en la sección 4 se ilustran las tres metodologías a partir de un ejemplo de aplicación.

2 Preliminares

2.1 Formulación general del modelo

En diversas áreas de investigación, se pretende explicar una variable respuesta en términos de M variables explicativas, x^T = [x₁, x₂, . . . , x_M] definidas en un conjunto compacto χ ⊆ R^M, conocido como el rango de regresión, mediante la relación [2]:

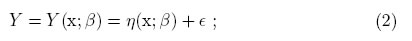
donde: β ∈ R^p es un vector de p parámetros desconocidos, η(x; β) es una función lineal o no lineal en los parámetros, ϵ es el término de error aleatorio y representa la información que no alcanza a ser explicada por el modelo y se asume que se distribuye normal con media cero y varianza constante σ². Además, los errores se supone son independientes para diferentes repeticiones del experimento.

2.2 Diseño experimental

En la experimentación es importante tener claridad sobre los tratamientos (puntos experimentales) y el número de réplicas donde se deben hacer las mediciones con el fin de obtener resultados óptimos. La teoría de los diseños óptimos proporciona una forma de determinar tanto los puntos de experimentación como las frecuencias. En este artículo, un diseño se denota por ξ y se define como una medida de probabilidad sobre el conjunto de Borel B de χ que incluye todos los conjuntos unitarios; tal que ξ tiene soporte finito [2], y se expresa por:

donde: ξ(x_i) = w_i, indica que en el punto x_i se deben realizar una fracción w_iN de réplicas, los puntos x_i, i = 1, . . . , n, son los puntos de soporte del diseño, y además se debe cumplir que: 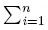w_i = 1. El conjunto de todos los diseños definidos sobre χ se denota por Ξ.

2.3 Matriz de información

La forma de cuantificar la información aportada por el diseño y la media del modelo, η(x; β), con respecto al vector de parámetros β, es a través de la matriz de información. Para el caso de los modelos no lineales la matriz de información, es definida por [3]:

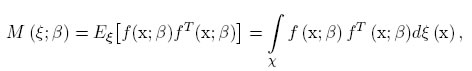
donde f (x; β) = 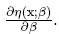Esta matriz depende del vector de parámetros, β, y por tanto para hallar los diseños óptimos se necesita un valor local o apriori para el vector de parámetros. Los diseños resultantes se denominan diseños óptimos locales. El valor local se obtiene de diversas fuentes, entre ellas, por la experiencia del investigador, estudios similares o con un estudio preliminar.

2.4 Criterios de optimalidad

La forma como se cuantifica la información suministrada por un diseño es a partir de funcionales de valor real de la matriz de información, denominados criterios de optimalidad. En la práctica estos criterios se implementan analíticamente o, algunas veces, mediante algoritmos para encontrar los puntos y los pesos asociados al diseño óptimo donde se deben hacer las mediciones. Los criterios de optimalidad se denotan por: Φ[M(ξ)] o también Φ(ξ) [12], donde Φ es una función diferenciable convexa definida en el conjunto M =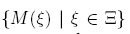 siendo M un conjunto compacto [13]. Lo anterior garantiza que el mínimo de Φ[M(ξ)] existe y por tanto el problema de optimización tiene solución.

Definición 2.1. Diseño Φ-óptimo

Se dice que un diseño ξ^* es Φ-óptimo, si verifica

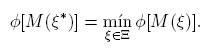
Algunos de los funcionales convexos más conocidos se mencionan a continuación:

Definición 2.2. D-optimalidad (Criterio del determinante)

Este criterio viene definido por el siguiente funcional:

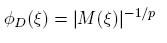
Es un criterio utilizado para hallar diseños que permitan estimar en forma óptima el vector de parámetros. Los diseños que minimicen este criterio serán aquellos que minimicen el volumen del elipsoide generado por el espacio p-dimensional asociado al vector de parámetros [12], y se denominarán diseños D-óptimos.

Definición 2.3. c-optimalidad

El funcional asociado está dado por:

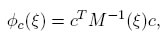
en este caso el diseño que minimiza Φ_c(ξ) se denomina c-óptimo y es aquel diseño que minimiza la varianza del estimador de mínimos cuadrados de la combinación lineal c^T β. En el caso de la estimación de una función no lineal de β, el vector c representa el gradiente de la función no lineal evaluada en el valor local de β.

En la literatura existen otros criterios de optimalidad, que no se mencionan en este artículo [12].

Con el fin de encontrar un diseño óptimo y/o de verificar si un diseño dado en efecto es D o c-óptimo se usan los siguientes dos teoremas de equivalencia:

Teorema 2.1. Sea M(ξ) una matriz definida positiva. Un diseño ξ es Dóptimo si y sólo sí:

• D(x;M(ξ)) := f^T (x)M^-1(ξ)f(x) − p ≤ 0 para todo x ∈ χ.

• La igualdad se cumple en los puntos de soporte del diseño ξ, es decir, D(x_j ;M(ξ)) = 0, para xj un punto de soporte de ξ.

El teorema anterior se conoce con el nombre de teorema de equivalencia de Kiefer y Wolfowitz [1].

Teorema 2.2. Sea M(ξ) una matriz definida positiva. Un diseño ξ es cóptimo si y sólo sí:

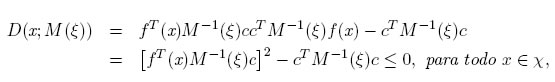
y la igualdad se cumple en los puntos de soporte del diseño ξ, es decir, D(x_j ;M(ξ)) = 0, para x_j un punto de soporte de ξ.

La demostración de estos resultados se encuentra en [14].

Una medida que permite cuantificar el grado de separación de un diseño con relación al diseño óptimo, es mediante el cálculo de la eficiencia. A continuación se define este concepto para los dos criterios de interés en este artículo, D-optimalidad y c-optimalidad.

2.5 D-Eficiencia y c-Eficiencia

Si ξ_D, es un diseño D-óptimo, entonces la D-eficiencia, denotada por Ef_D(ξ), de cualquier otro diseño ξ, relativa al diseño óptimo se define como [15]:

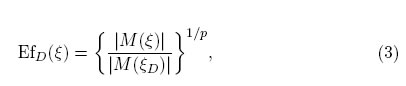
donde p es el número de parámetros del modelo.

Para D-optimalidad una eficiencia de 0.5, significa que el diseño obtenido necesita el doble de réplicas para obtener la misma información que el diseño D-óptimo (Zhu et al. 1998) [16].

La c-eficiencia del diseño ξ, denotado por Ef_c(ξ) relativa al diseño c-óptimo, ξ_c, se define como:

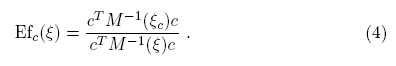
Intuitivamente valores cercanos a uno indican que el diseño ξ ofrece una información muy similar a la del diseño óptimo con el que se está comparando, y si la eficiencia de un diseño ξ con relación al diseño óptimo ξ^* es exactamente 1, entonces el diseño ξ es equivalente al óptimo ξ^*.

3 Metodologías propuestas para la elección de la constante de ponderación

La elección de la constante de ponderación es un problema al que se enfrenta el investigador cuando usa diseños óptimos compuestos. En ssta sección se presentan las dos propuestas para la determinación de dicha constante, cuando se tiene una combinación convexa de los criterios D- y c-optimalidad. Inicialmente se considera la combinación convexa de los logaritmos de las eficiencias asociadas a ambos criterios, es decir, se considera la siguiente función, [12]

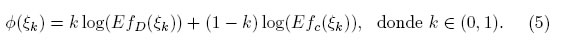
La expresión dada en (5) resulta de calcular el logaritmo de la media geométrica de las dos funciones de eficiencia consideradas. Para un valor de k dado, el diseño que maximice Φ(ξ_k) se denomina diseño cD-óptimo, obteniendo tantos diseños como valores posibles de k ∈ (0, 1) sean considerados, representados en el siguiente conjunto

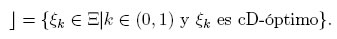
De la ecuación 5 surge la siguiente pregunta ¿existe alguna forma de determinar el valor de la constante de ponderación, k, en una situación experimental y de esta forma tener un diseño óptimo compuesto (ξ_cD)?. La respuesta a esta pregunta aparece por primera vez en [11], quiénes proponen una metodología mediante el cálculo de las eficiencias del diseño compuesto para un valor fijo de k, con relación a los diseños (individuales) ξ_D y ξc- óptimos, y luego encontrar el valor de la constante más adecuado. En este artículo se da solución a este interrogante proponiendo dos metodologías, usando simulación,

• el cálculo de los errores relativos de los parámetros y

• el estudio de la potencia de la prueba asociada a los parámetros.

Observación 3.1. Se puede mostrar que el problema de maximizar el criterio dado en la ecuación (5), es equivalente a maximizar, [17]

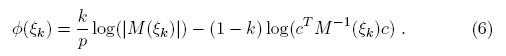
Teorema 3.1. Sea M(ξ) una matriz definida positiva. Un diseño ξ es cDóptimo compuesto si y sólo sí:

• D(x;M(ξ)) := −1 ≤ 0 para todo x ∈ χ y

• La igualdad se cumple en los puntos de soporte del diseño ξ, es decir, D(x_j;M(ξ)) = 0, para x_j un punto de soporte de ξ.

A continuación se detallan las tres metodologías mencionadas.

3.1 Metodología mediante el cálculo de las eficiencias

Para la elección de la constante de ponderación se realiza el siguiente procedimiento, para k ∈ (0, 1):

• Se calcula el diseño óptimo compuesto ξ_k , cD-óptimo, diseño que maximiza la expresión dada en (6).

• Se calcula la D- y c-eficiencia del diseño ξ_k (ver expresiones (3) y (4))

• Las eficiencias obtenidas anteriormente se grafican en función de k.

• Se elige el valor de k donde se cortan ambas curvas. Para ampliar el procedimiento [18].

En las siguientes secciones se exponen las dos metodologías propuestas en este artículo para la elección de k.

3.2 Metodología alternativa 1. Cálculo del error relativo

Se propone comparar los diseños óptimos compuestos para los diferentes valores de k mediante el cálculo de la magnitud de los errores relativos (ver definición 3.1) asociados tanto a los parámetros individuales como al vector de parámetros usando simulación.

Definición 3.1 (Error relativo). Sea β ∈ R^p un vector de p parámetros desconocidos y β⁰ ∈ R^p un vector de valores conocidos. Se define el error relativo de β con respecto a β⁰, denotado por ERR_β, como una aplicación, ERR : R^p → R dada por:

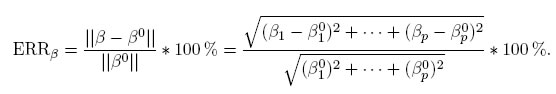
En forma análoga se define el error relativo para cada componente del vector de parámetros β,

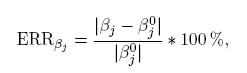
y el error relativo asociado a la estimación de una combinación lineal del vector de parámetros, c^T β:

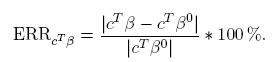
La expresión anterior también se usará para cuantificar el error en la estimación de una función no lineal del vector de parámetros, g(β), al considerar la versión linealizada de ésta, y en este caso: c = 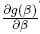evaluada en el valor local β⁰.

Se propone determinar el valor o posibles valores de k tal que el diseño óptimo compuesto, ξ_k, dé una estimación óptima tanto de los parámetros, β, como de una función no lineal de interés, g(β), a partir de la minimización de los respectivos errores relativos. Para ello se usa en lugar de β, los estimadores de mínimos cuadrados no lineales, 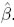. Será denotado por β⁰. A continuación se expone el procedimiento usado para obtener los errores relativos para el ejemplo presentado en la sección 4. Se fija el número de corridas experimentales, N; una rejilla de valores para la constante de ponderación, k, con incrementos fijos en el intervalo [0.1,0.9]. Se obtiene con k = 0 el diseño c-óptimo y con k = 1 el diseño D-óptimo. Ninguno de estos dos diseños, individualmente, estiman en forma conjunta tanto los parámetros como la función no lineal de interés.

a. Se fija k = 0.1.

b. Se maximiza la relación dada en (6) y se aplica el teorema 3.1 para verificar la optimalidad del diseño hallado.

c. Se convierte el diseño aproximado a un diseño exacto usando la propuesta presentada en Pukelsheim [19].

d. Se generan N-errores aleatorios, ϵi, de la distribución N(0, σ²), para σ² se usa la media cuadrática del error (MSE) obtenido de un ajuste previo. Luego con cada xi y el respectivo número de réplicas, n_i = w_i * N, se determinan los valores y_i a partir del modelo (2), usando los valores simulados de los errores:

e. Con los datos simulados, {(x_i, y_i), i = 1, 2, . . . ,N}, se ajusta el modelo (2) usando el método de los mínimos cuadrados no lineales y se obtiene una estimación para el vector de parámetros, denotada por

f. Se calculan los errores relativos asociados a los parámetros tanto individuales como en forma conjunta, dados en la definición 3.1.

g. Se repiten los pasos d., e. y f. un número fijo de simulaciones, nsim.

h. Se calcula el promedio (o mediana) de los nsim-errores relativos.

i. Se incrementa k y se repite el procedimiento anterior.

Observación 3.2. Se elige el valor de k^* donde el diseño asociado ξ_k^* proporcione errores relativos menores con relación a aquellos asociados a los otros diseños óptimos compuestos ξ_k.

3.3 Metodología alternativa 2. Análisis de la potencia de la prueba de hipótesis

En esta sección se propone escoger el valor de k tal que el diseño óptimo compuesto ξ_k presente la mayor potencia para realizar inferencias tanto para el vector de parámetros como para una función de ellos. Se busca maximizar la potencia del siguiente par de pruebas de hipótesis:

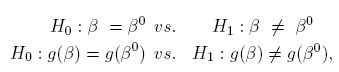
donde g(β) es una función lineal o no lineal en los parámetros de interés. El estadístico de prueba, S_L;k para probar las hipótesis anteriores se obtiene a partir del estadístico de razón de verosimilitudes dado en [20]:

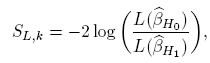
donde L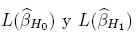 denota el máximo de la función de verosimilitud bajo H₀ y H₁ respectivamente. Para N grande, S_L converge a una distribución χ². Sin embargo, para propósitos prácticos, el número de corridas experimentales, N, usualmente es pequeño. Para este caso, se halla inicialmente la distribución de dicho estadístico, simulando observaciones bajo H₀, y calculando los respectivos cuantiles simulados de la distribución de S_L. A continuación se describe el procedimiento realizado, ver literales d. al i. Los tres primeros pasos (a., b. y c.) coinciden con los descritos en la metodología anterior. Para ambas pruebas de hipótesis se realizan los siguientes pasos adicionales:

d. Se generan N-errores aleatorios N(0, σ²), ϵ_i, con σ² el MSE obtenido al ajustar el modelo con observaciones previas. Luego, con cada xi y el respectivo número de réplicas, n_i = w_i * N, se halla los valores simulados para yi a partir del modelo (2)

siendo β^* el vector de valores verdaderos de los parámetros bajo H₀, es decir, para la primera hipótesis, β^* = β⁰.

e. Con los datos simulados, {(x_i, y_i), i = 1, 2, . . . ,N} se hallan las sumas de cuadrados de los errores obtenidas bajo H₀ y H₁, las cuales se describen a continuación:

• Bajo las restricciones de los parámetros dadas en H₀ (si las hay, caso de la segunda hipótesis), se reajusta el modelo (2), hallando una estimación del vector de parámetros, denotada por _H0 y se calcula la suma cuadrática del error bajo H₀, es decir

• En forma análoga se procede con H₁ y se obtiene un estimador para β, denotado por _H1 . Se calcula la siguiente suma cuadrática del error bajo H₁:

f. Se calcula el estadístico S_L;k.

g. Se repiten los pasos d., e. y f. un número dado de simulaciones, por ejemplo, 500 simulaciones.

Potenciak = P(S_L;k > C_α|H₁ es verdadera),

P₁ Se considera el siguiente modelo

donde β^* es el valor de los parámetros restringido a los puntos considerados en H₁ (se denotará como β¹). Se realizan los pasos a. al f. con el fin de calcular el estadístico S_L,k.

P₂ Se compara el S_L,k del paso P₁ con el cuantil 0.975, C_0:975, o con el cuantil 0.025, C_0:025 del estadístico S_L,k hallados en el paso i.

P₃ Se repiten los dos pasos anteriores (P₁ y P₂) un número de veces y se calcula el porcentaje de veces donde se cumple S_L,k > C_0:975 o S_L,k < C_0:025. De esta forma se obtiene la potencia por cada punto de la región definida por H₁.

j. Se incrementa k, y se repite el procedimiento anterior.

Observación 3.3. Por cada punto simulado bajo H₁ y con el diseño exacto ξ_k, se halla la potencia de la prueba de hipótesis y se escoge el diseño ξ_k que tenga las potencias más altas en ambas pruebas de hipótesis en comparación con los otros diseños dados por las diferentes elecciones de k.

4 Resultados

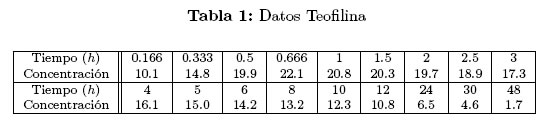
A continuación se ilustra las metodologías anteriores con un ejemplo aplicado en el área de la farmacocinética. Es de anotar que el modelo a considerar también tiene aplicaciones en otras áreas. A un caballo se le suministra una dosis de 15mg/Kg de teofilina en la sangre, y se registra la concentración del medicamento presente en el organismo en muestras de sangre extraídas en diferentes tiempos. Los datos fueron reportados en Fresen (1986), referenciado en Atkinson et al. (2007) [12] y se presentan en la Tabla 1:

Inicialmente se ajusta el modelo compartimental, cuya concentración promedio está dada por:

se obtiene los siguientes estimadores de mínimos cuadrados para los parámetros del modelo: , estimaciones obtenidas con el paquete estadístico R project [21]. Con la ayuda del paquete estadístico R se hallan los diseños óptimos locales, y se implementan los procedimientos descritos en la sección anterior. El diseño encontrado, con el cual se puede alcanzar una estimación óptima de los parámetros (D-óptimo), se muestra a continuación:

Este diseño le indica al experimentador que debe obtener muestras de sangre en los siguientes tiempos: 0.23, 1.39, 18.40 horas con el fin de determinar la concentración de teofilina en la sangre y con el mismo número de réplicas.

Además se halla el diseño óptimo para estimar el tiempo donde se alcanza la concentración máxima, parámetro de interés en el área de farmacocinética, cuya expresión analítica está dada por:

obteniendo el siguiente diseño:

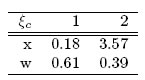
En este caso, el mayor esfuerzo experimental (61%) se debe realizar en el tiempo 0.18 horas y el resto (aproximadamente 39%) en el tiempo 3.57 horas, con el fin de estimar en forma óptima Tmáx. Note que este diseño no es adecuado para estimar los tres parámetros del modelo, ya que tiene sólo dos puntos de soporte. De acuerdo con la observación anterior se encuentra, en las siguientes subsecciones, uno o más diseños óptimos que estiman en forma óptima tanto los parámetros del modelo como el tiempo para la concentración máxima.

4.1 Metodología mediante eficiencias

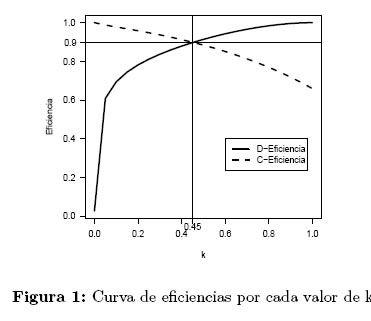
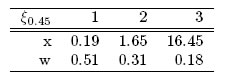
Al aplicar el procedimiento descrito en la sección 3.1 se obtiene la curva de eficiencias del diseño óptimo compuesto (ξk) con respecto a los diseños individuales, D-óptimo (ξ_D) y c-óptimo (ξ_c), Figura 1.

Las eficiencias del diseño compuesto con respecto a cada diseño óptimo individual coinciden en el valor k = 0.45, dando como diseño óptimo compuesto aquel donde el 51%, 31% y 18% del esfuerzo experimental se debe realizar en los tiempos 0.19, 1.65 y 16.45 horas respectivamente.

4.2 Metodología alternativa 1: Cálculo del error relativo

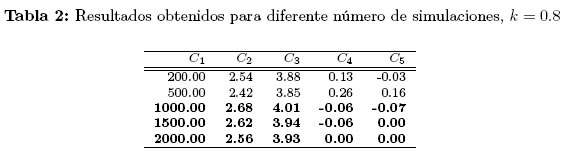
Se siguen los pasos a. hasta el f. descritos en la sección 3.2, tomando N = 10 corridas experimentales. Para determinar el número apropiado de simulaciones se fijó un valor de k = 0.8, se halla diseño óptimo ξ_0.8, y con diferente número de simulaciones: 50, 100, 200, 1000, 1500, 2000, se calculan los errores relativos. Los resultados obtenidos se listan en la Tabla 2, para el caso de 200, 1000, 1500 y 2000 simulaciones. En cada columna se tiene: número de simulaciones, C₁; medianas de los errores relativos del vector de parámetros, C₂; medianas del error relativo asociado al tiempo de máxima concentración, C₃; diferencias consecutivas entre las medianas reportadas en C₂, C₄; y diferencias consecutivas entre las medianas reportadas en C₃; C₅.

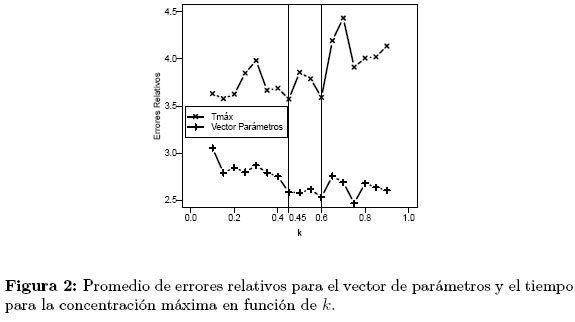
A partir de 1000 simulaciones se detectan leves diferencias en las medianas de los errores relativos asociados tanto a los parámetros del modelo como al Tmáx. Por esta razón se fija el número de simulaciones en 1000 y se realizan los pasos h. e i. (Figura 2) usando incrementos fijos de 0.05 para el valor de k.

Los errores relativos asociados al vector de parámetros tiende a decrecer mientras que los asociados al tiempo para la concentración máxima tiende a crecer levemente a medida que el valor de k aumenta, Figura 2. Existen dos posibles valores de k en donde simultáneamente los errores relativos son pequeños, k = 0.45 y k = 0.60, los diseños óptimos compuestos asociados a estos dos valores garantizan una estimación óptima tanto del vector de parámetros del modelo como del tiempo para la concentración máxima. Esta metodología aporta un diseño óptimo adicional al obtenido por el método de las eficiencias. Los diseños asociados se encuentran en la Tabla 3.

4.3 Metodología alternativa 2: Análisis de la potencia de la prueba de hipótesis

Se consideran las pruebas de hipótesis presentadas en la sección 3.3. Para este ejemplo β = (β₁,β₂,β₃), y como valor local se tomó β⁰ = (4.29, 0.0589, 21.8). Además, g(β) = Tmáx = 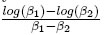y g(β⁰) = Tmáx⁰ = 1.02.

Cálculo de la potencia de la prueba de hipótesis 1.

Después de realizar los pasos a. al i. descritos en la sección 3.3. se obtiene algunos cuantiles simulados del estadístico S_L;k bajo H₀. Luego se realizan los pasos P₁ −P₃, considerando como valores de β aquellos que resultan de perturbar los valores locales del vector de parámetros, denotados por β¹, valor de β bajo la hipótesis alternativa.

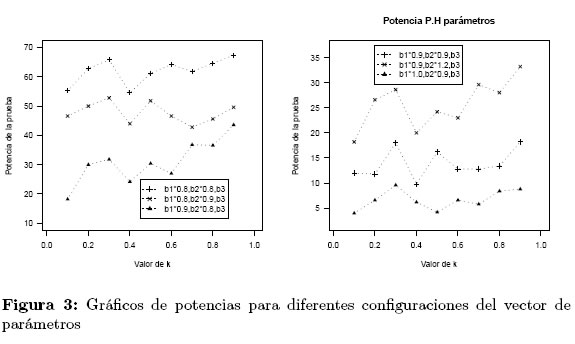
Según la Figura 3, no se observa una tendencia clara en el gráfico de las potencias en función de la constante de ponderación, y como el cálculo depende de que configuración para β1 fue usada, se opta por reportar las potencias promedio en las 24 configuraciones de valores de β1 para cada valor de k (Tabla 4).

El mayor valor de la potencia promedio se obtiene para k = 0.3 y k = 0.9 alcanzando una potencia promedio por encima del 32%, y depende de los valores de β que fueron usados en la hipótesis alternativa, es posible que este valor sea más alto en la medida que se tengan en cuenta valores de β considerablemente distantes del valor local usado, es decir, al considerar perturbaciones de órdenes mayores para los tres parámetros. Con los resultados obtenidos hasta este momento no hay una conclusión contundente acerca del valor apropiado para k que dé una mayor potencia para la prueba de hipótesis.

Cálculo de la potencia de la prueba de hipótesis 2.

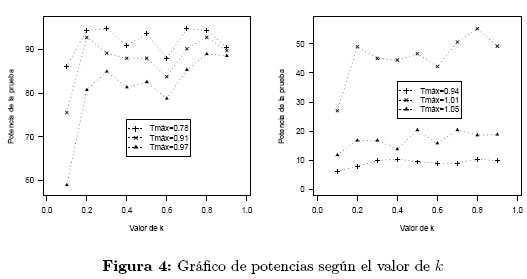
Se razona de forma análoga a la prueba de hipótesis 1. En este caso la región de rechazo está determinada por los siguientes valores en Tmáx, Tmáx = 0.78, 0.85, 0.88, 0.91, 0.94, 0.97, 1.01, 1.05, que corresponden a un porcentaje de perturbación de 23.5%, 16.6%, 13.7%, 10.7%, 8%, 5% y 1% por debajo del valor local Tmáx⁰ y del 3% por encima de ese valor, respectivamente.

En la Figura 4 se muestra las potencias para seis configuraciones del Tmáx en función de la constante de ponderación. En general, no se observa una tendencia clara en el gráfico de las potencias en función de la constante de ponderación, se opta por reportar las potencias promedio en las ocho configuraciones de valores de β¹ para cada valor de k (Tabla 5).

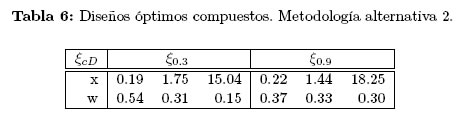
Si un valor razonable para la potencia de la prueba es al menos del 65%, entonces se tienen como valores factibles para k = 0.2, 0.3, 0.7, 0.8, 0.9, y el máximo se alcanza en k = 0.8. El valor de esta potencia depende de los valores para el Tmáx usados en la hipótesis H1, notándose potencias de al menos el doble de las obtenidas en el caso anterior. Bajo los escenarios realizados en ambas pruebas de hipótesis y usando los promedios de las potencias para ambas pruebas de hipótesis se pueden recomendar los siguientes dos diseños obtenidos con k = 0.3 y k = 0.9, presentados en la Tabla 6. Se observa que para k = 0.45, valor obtenido mediante el cálculo de las eficiencias, la potencia promedio está alrededor del 64%.

5 Discusión

Cada metodología empleada es adecuada según su propósito: diseño óptimo eficiente, el diseño que minimiza los errores relativos, y el diseño que maximiza la potencia de las pruebas de hipótesis asociada a los parámetros y al tiempo de máxima concentración. Los diseños óptimos compuestos encontrados en esta aplicación son: eficiencia: ξ_0:45; error relativo ξ_0:45 y ξ_0:6; potencia: ξ_0:30 y ξ_0:9. En esta aplicación los dos primeros métodos dan el mismo diseño óptimo compuesto, un diseño más eficiente y el de menor error relativo con relación a sus valores de referencia. Los diseños óptimos encontrados con el cálculo de la potencia de la prueba dependen de los valores escogidos en la hipótesis alternativa para los parámetros involucrados, además del número de simulaciones realizadas y en algunas ocasiones puede que no proporcione un diseño óptimo con alta potencia.

Es necesario investigar otras posibles regiones para el vector de parámetros, β consideradas en la hipótesis alternativa, posiblemente valores más distantes del valor local considerado, y estudiar las variaciones en los cálculos de las potencias.

6 Conclusiones

En este artículo se aplicó una metodología existente en la literatura [11] y dos metodologías propuestas, con el fin de seleccionar el valor de la constante de ponderación en el criterio compuesto, donde se involucran dos criterios, D-optimalidad y c-optimalidad. Cada una de las metodologías estudiadas, aplicadas a situaciones prácticas, puede que no proporcionen diseños únicos y por tanto se tiene una variedad de posibilidades para la realización de la experimentación.

Las dos metodologías propuestas con relación a la metodología del cálculo de las eficiencias, tienen la ventaja que los diseños obtenidos dan la potencia más alta con relación a la prueba de significancia de los parámetros y de la función no lineal considerada o proporcionan los diseños con los errores relativos menores.

7 Agradecimientos

Este trabajo fue realizado en el marco del proyecto de investigación: Investigación de diversos tópicos en diseños óptimos, de la Facultad de Ciencias y adscrito al grupo de investigación en Estadística de la Escuela de Estadística Universidad Nacional de Colombia, sede Medellín, cuya fecha de aprobación fue 20 de junio del 2011 y de finalización el 24 de enero del 2013.

Referencias

[1] J. Kiefer, ''Optimum experimental designs (with discussion)'', Journal Royal Statistical Society, vol. 21, no. 2, pp. 272–319, 1959.         [ Links ] [Online]. Available: http://www.jstor.org/stable/2983802 108, 113

[2] V. López Ríos and R. Ramos Quiroga, ''Introducción a los diseños óptimos'', Revista Colombiana de Estadística, vol. 30, no. 1, pp. 37–51, 2007.         [ Links ] [Online]. Available: http://www.emis.de/journals/RCE/V30/V30-1-37LopezRamos.pdf 108, 110

[3] A. C. Atkinson, ''The usefulness of optimum experimental design'', Journal of the Royal Statistical Society. Serie B (Methodological), vol. 58, no. 1, pp. 59–76, 1996.         [ Links ] [Online]. Available: http://www.jstor.org/stable/2346165 108, 111

[4] Y. C. Huang and W. K. Wong, ''Multiple-objective optimal designs'', Journal of Biopharmaceutical Statistics, vol. 8, no. 4, pp. 635–643, 1998.         [ Links ] [Online]. Available: http://dx.doi.org/10.1080/10543409808835265 109

[5] Z. Wei and W. K. Wong, ''Multiple-objective designs in a dose response experiment'', Lecture Notes Monograph Series, vol. 34, pp. 73–82, 1998.         [ Links ] [Online]. Available: http://www.jstor.org/stable/4356063 109

[6] H. Dette, A. Pepelyshev, and W. K. Wong, ''Optimal designs for dose-finding experiments in toxicity studies'', Bernoulli, vol. 15, pp. 124–145, 2009.         [ Links ] [Online]. Available: 10.3150/08-BEJ152 109

[7] A. Biswas and P. Chaudhuri, ''An efficient design for model discrimination on parameter estimation in linear models'', Biometrika, vol. 89, no. 3, pp. 709–718, 2002.         [ Links ] [Online]. Available: http://biomet.oxfordjournals.org/content/89/3/709.short 109

[8] Y. C. Huang and W. K. Wong, ''Sequential construction of multiple-objective optimal designs,'' Biometrics, vol. 54, pp. 1388–1397, 1998. 109

[9] T. E. O´Brien and J. O. Rawlings, ''A nonsequential design procedure for parameter estimation and model discrimination in nonlinear regression models'', Journal of Statistical Planning and Inference, vol. 55, no. 1, pp. 77–93, 1996.         [ Links ] [Online]. Available: http://www.sciencedirect.com/science/article/pii/0378375895001824 109

[10] A. Atkinson and A. Donev, Optimal Design of Experiments. New York: Oxford, 1992.         [ Links ] 109

[11] D. R. Cook and W. K. Wong, ''On the equivalence of the constrained and compound optimal design'', Journal of the American Statistical Association, vol. 89, no. 426, pp. 687–692, 1994.         [ Links ] [Online]. Available: http://www.jstor.org/stable/2290872 109, 115, 127

[12] A. Atkinson, A. Donev, and R. Tobias, Optimum Experimental Designs, with SAS. New York: Oxford, 2007.         [ Links ] 111, 112, 114, 120

[13] R. Martín Martín, ''Construcción de diseños óptimos para modelos con variables no controlables'', Tesis de Doctorado, Universidad de Castilla-La mancha, España, 2006. [Online]. Available: https://ruidera.uclm.es/xmlui/handle/10578/972 112        [ Links ]

[14] V. López Ríos, ''Diseños óptimos para discriminación y estimación en modelos no lineales'', Tesis de Doctorado, CIMAT, México, 2008. [Online]. Available: http://probayestadistica.cimat.mx 113        [ Links ]

[15] W. K. Wong and M. Moerbeek, ''Multiple objetive optimal designs for the hierarchical linear model'', Journal of Official Statistics, vol. 18, no. 2, pp. 291–303, 2002.         [ Links ] [Online]. Available: http://igitur-archive.library.uu.nl/fss/2010-0607-200156/UUindex.html 113

[16] W. Zhu, H. Ahn, and W. K. Wong, ''Multiple-objective optimal designs for the logit model'', Communications in Statistics - Theory and Methods, vol. 27, no. 6, pp. 1581–1592, 1998.         [ Links ] [Online]. Available: http://dx.doi.org/10.1080/03610929808832178 114

[17] C. Flórez, ''Una alternativa para elegir la constante de ponderación en diseños Óptimos compuestos'', Tesis de Maestría, Escuela de Estadística Universidad Nacional de Colombia-Medellín, Colombia, 2012. [Online]. Available: http://www.bdigital.unal.edu.co/8509/ 115        [ Links ]

[18] I. Lorens and W. K. Wong, ''A graphical method for finding maximin efficiency designs'', Biometrics, vol. 56, no. 1, pp. 113–117, 2000.         [ Links ] [Online]. Available: http://www.jstor.org/stable/2677110 116

[19] F. Pukelsheim, Optimal Design of Experiments. New York: John Wiley and Sons, 1993.         [ Links ] 117

[20] S. Huet, A. Bouvier, M. Poursat, and E. Jolivet, Statistical Tools for Nonlinear Regression: A practical Guide with S-Plus and R- Examples. New York: Springer, 2004.         [ Links ] 118

[21] R Development Core Team, R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, 2011, ISBN 3-900051-07-0. [Online]. Available: http://www.R-project.org/ 121        [ Links ]