Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.9 no.18 Medellín July/Dec. 2013
ARTÍCULO ORIGINAL
Relativistic models of thin disks immersed in a Robertson-Walker type spacetime
Modelos relativistas de discos delgados inmersos en un espacio-tiempo tipo Robertson-Walker
Gonzalo García Reyes1 y Edwin García-Quintero2
1 PhD. en Ciencias Naturales, ggarcia@utp.edu.co, Universidad Tecnológica de Pereira, Pereira, Colombia.
2 PhD. en Tecnología Eléctrica, materiales, generación y distribución, egarcia@udea.edu.co, Universidad de Antioquía, Medellín, Colombia.
Received: 19-11-2012, Acepted: 07-08-2013 Available online: 05-11-2013
MSC: 83C22, PACS:04.40Nr
Abstract
Using the well known ''displace, cut and reflect'' method used to generate disks from given solutions of Einstein field equations, we construct some relativistic models of time dependent thin disks of infinite extension made of a perfect fluid based on the Robertson-Walker metric. Two simple families of models of disks based on Robertson-Walker solutions admitting Matter and Ricci collineations are presented. We obtain disks that are in agreement with all the energy conditions.
Key words: general relativity; thin disks; exact solutions; robertsonwalker metric.
Highlights
• We construct time dependent disks of infinite extension made of a perfect fluid based on the well known Robertson-Walker metric. • The models are interpreted as a disk-like matter distribution made of a perfect fluid with negative pressure or tension immersed in a Robertson-Walker type cosmological model. • The solutions satisfy all the energy conditions.
Resumen
Usando el método de ''desplazamiento, corte y reflexión'' se construyen algunos modelos relativistas exactas de soluciones que representan discos delgados de extensión infinita, dependientes del tiempo y hechos de un fluido perfecto, basados en la métrica de Robertson-Walker. Se presentan dos familias simples de modelos de discos basados sobre el espacio tiempo de Robertson-Walker que admiten colineaciones de Ricci y de materia. Se obtienen modelos de discos que satisfacen todas las condiciones de energía.
Palabras clave: relatividad general; discos delgados; soluciones exactas; métrica de robertson-walker.
1 Introduction
Exact solutions of Einstein field equations describing relativistic thin disks are of great astrophysical importance since they can be used as models of certain stars, galaxies and accretion disks. Solutions for static thin disks without radial pressure were first studied by Bonnor and Sackfield [1], and Morgan and Morgan [2], and with radial pressure by Morgan and Morgan [3]. Also disks with radial tension were considered by González and Letelier [4]. Several classes of exact solutions of the Einstein field equations corresponding to static thin disks with or without radial pressure have been obtained by different authors [5]–[6].
Thin rotating disks that can be considered as a source of the Kerr metric were presented in [7], while rotating disks with heat flow were studied in [8]. Also thin disks in presence of electromagnetic field have been discussed as sources for Kerr-Newman fields [9], magnetostatic axisymmetric fields [10], and conformastationary metrics [11]. The nonlinear superposition of a disk and a black hole was first obtained by Lemos and Letelier [5].
In all the above cases, the disks are obtained by an ''inverse problem'' approach, called by Synge the ''g-method'' [12]. The method works as follows: a solution of the vacuum Einstein equations is taken, such that there is a discontinuity in the derivatives of the metric tensor on the plane of the disk, and the energy-momentum tensor is obtained from the Einstein equations. The physical properties of the matter distribution are then studied by an analysis of the surface energy-momentum tensor so obtained. Another approach to generate disks is by solving the Einstein equations given a source (energy-momentum tensor). Essentially, they are obtained by solving a Riemann-Hilbert problem and are highly nontrivial [13]. A review of this kind of disks solutions to the Einstein-Maxwell equations was presented by Klein in [14].
The purpose of this paper is to consider time dependent thin disk of infinite extension made of a perfect fluid, i.e., with radial pressure equal to tangential pressure, immersed in a Robertson-Walker type cosmological model. These models can be important in the study of the evolution of some planar astrophysical objects such as galaxies or accretion disks. The inclusion of the time to the disks add for example a more degree of reality to the geometric models of galaxies since even though in first approximation the galactic disks can be considered independent of time (stationary or static) which can be true on small time scales compared with the average age of the galaxies, in reality its structures were several billion years ago especially when we observe them to large distances, and consequently its physical properties also must have changed over time. So in more realistic models the time need be considered. On the other hand, even though realistic disklike sources have thickness, in first approximation these astrophysical objects can be considered to be very thin, e.g., in our Galaxy the radius of the disk is 10 kpc and its thickness is 1 kpc. Moreover, even though the disks are of infinite extension, the solutions might lead to useful local disk models, describing the spacetime in a vicinity of a disk.
The method used to generate the field of such disks is the well known ''displace, cut and reflect'' method which was used first by Kuzmin and Toomre [15] to constructed Newtonian models of disks, and later extended to general relativity [6]–[11]. The method is an adaptation of the method of images of electrostatic and consists of the following steps. First, choose a surface that divide the usual space in two parts, one with no singularities or sources and the other with the sources. Second, disregard the part of the space with singularities. Third, use the surface to make an inversion of the nonsingular part of the space. The jump in the normal derivatives of the resulting potentials induces a matter distribution in the disk. The procedure is mathematically equivalent to make the transformations  , with z0 constant.
, with z0 constant.
The paper is structured as follows. In Sec. 2 we present a summary of the procedure to obtain models of relativistic thin disks using the well known ''displace, cut and reflect'' method and we apply it to the Robertson- Walker metric. We also compute the main physical variables associated with the disks and we analyses its physical properties. In Sec. 3 two simple families of models of disks based on Robertson-Walker solutions admitting Matter and Ricci collineations [16] are presented which satisfy all the energy conditions. Finally, in Sec. 4, we summarize our main results.
2 Relativistic thin disks
The Robertson-Walker metric in stereographic coordinates is [17]

where S is an arbitrary (non-zero) function of t, k = 0,±1 and ρ2 = x2 + y2 + z2. The same metric in cylindrical coordinates (t, φ, r, z) reads

The procedure above mentioned applied to the metric (2) gives us
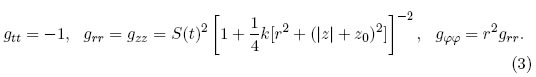
This metric can be named Robertson-Walker type metric and the spacetime is not homogeneous nor isotropic [18]. Now assuming that the components of the metric tensor are continuous across the disk but with discontinuous first derivatives in the direction normal to the disks, the Einstein equations in geometric units such that 8πG = 1 give us

where Tab is the momentum-energy tensor in the exterior of the disk, δ(z) is the usual Dirac function with support on the disk and

is the distributional energy-momentum tensor of the disk. bab denote the jump of the normal derivatives of the metric tensor on the plane z = 0

and other quantities are also evaluated at z = 0. This procedure in principle can be applied to any solution of the Einstein field equations with or without source (momentum-energy tensor). So for example its application to the Einstein-Maxwell equations yield a matter distribution with electric current density. On the other hand, these disks are essentially of infinite extension. Finite disks can be obtained introducing oblate spheroidal coordinates, which are naturally adapted to a disk source, and imposing appropriate boundary conditions. These solutions, in the vacuum and static case, correspond to the Morgan and Morgan solutions [2]. A more general class of solutions representing finite thin disks can be constructed using a method based on the use of conformal transformations and solving a boundary-value problem [3, 4, 19].
For the metric (2), the nonzero components of Qab are
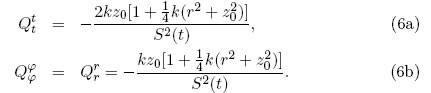
The ''true'' surface energy-momentum tensor (SEMT) of the disk, Sab, can be obtained through the relation

where dsn =  dz is the ''physical measure'' of length in the direction normal to the disk.
dz is the ''physical measure'' of length in the direction normal to the disk.
Thus the surface energy density σ and radial and azimuthal pressures or tensions P in the disk read

with non-zero S(t). We will now analyses the physical properties of the disks for the models k = 0,±1. When k = 1 Eq. (8) shows that the surface energy density is positive in agreement with the weak energy condition. The strong energy condition ϱ = ϵ + Pφ + Pr ≥ 0, where ϱ is the effective Newtonian density, is also satisfied. This last condition characterizes a disk made of matter with the usual gravitational attractive property. Furthermore, P < σ and so the disks also satisfy the dominant energy condition. Accordingly these solutions satisfy all the energy conditions everywhere on the disks, however the disks present tension (negative pressure) rather pressure. Therefore these disks can be interpreted as made of a perfect fluid with negative pressure or tension immersed in a Robertson-Walker type cosmological model. When k = —1 obtains the opposite case, that is disks with positive stress (pressure) but with negative energy density in violation of the weak energy condition. When k = 0 the metric (3) is the same that the Robertson-Walker metric and no infinitely extended thin disk can be allowed to exist from the homogeneity and isotropy. Nonetheless, finite disks could exist for the model k = 0 since this model which is based on cosmological principle applies on very large spatial scale (on scales of tens of Mpc and in the case, e.g., of our Galaxy the radius of the disk is 10 kpc). The models k = 1 and k = —1 could be possible in an anisotropic and inhomogeneous spacetime.
3 Disks from Robertson-Walker solutions admitting Matter and Ricci Collineations
As an example of the above presented formalism, we consider the thin disk models obtained by means of the ''displace, cut and reflect'' method applied to Robertson-Walker solutions admitting Matter and Ricci collineations. We consider the standard Robertson-Walker model with vanishing cosmological constant and comoving observers  , t being the standard cosmic time. For these observers the energy-momentum tensor has a perfect fluid form i.e. Tab = (ρ+p)uaub +pgab, where ρ, p are the energy density and the isotropic pressure in the exterior region of the disk measured by the observers ua. Note that the spacetime (3) implies two types of pressure. P denote the stresses (pressure or tension) in the disk, Eq. (8), and p the pressure of the matter where is inmmersed the disk, Eq. (9). Thus, p could be zero (a dust fluid) but not necessarily the stress in the disk as shown by Eq. (8). Thus using the Einstein field equations we obtain
, t being the standard cosmic time. For these observers the energy-momentum tensor has a perfect fluid form i.e. Tab = (ρ+p)uaub +pgab, where ρ, p are the energy density and the isotropic pressure in the exterior region of the disk measured by the observers ua. Note that the spacetime (3) implies two types of pressure. P denote the stresses (pressure or tension) in the disk, Eq. (8), and p the pressure of the matter where is inmmersed the disk, Eq. (9). Thus, p could be zero (a dust fluid) but not necessarily the stress in the disk as shown by Eq. (8). Thus using the Einstein field equations we obtain

Since there remains one variable free, S(τ ), we need one additional condition in order to solve the model. One possibility is a geometric equations of state defined by requirement of existence of Matter or Ricci collineations. Thus two possible forms of the scale factor S(t) for Robertson-Walker models with k = ±1 which admit Matter and Ricci collineations are [16]
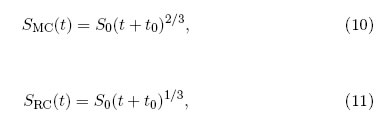
where S0 and t0 are constants of integration. So for disks generate from Robertson-Walker spacetimes with k = 1 admitting Matter collineations we have

where  Equally for disks generate from Robertson-Walker spacetimes also with k = 1 which admit Ricci collineations we obtain
Equally for disks generate from Robertson-Walker spacetimes also with k = 1 which admit Ricci collineations we obtain

where again 
In order to study the behavior of previous physical quantities in Fig. 1 we have plotted the surface energy density σ and the tension P for disks with α = 1, 2, 3, and 4, as functions of 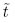 . We see that at
. We see that at 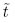 = 0 the energy density presents its maximum value and then decreases with the time
= 0 the energy density presents its maximum value and then decreases with the time 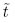 , being always a positive quantity in agreement with the weak energy condition. We also see that the energy density initial is greater as the parameter α is increased. Finally, we observe that the tension P presents the behavior opposite.
, being always a positive quantity in agreement with the weak energy condition. We also see that the energy density initial is greater as the parameter α is increased. Finally, we observe that the tension P presents the behavior opposite.
4 Conclusions
Using the well-known ''displace, cut and reflect'' method used to generate disks from given solutions of Einstein field equations, we constructed time dependent disks of infinite extension made of a perfect fluid based on the well known Robertson-Walker metric. As far we know these are the first disk models of this kind in the literature.
When k = 1 we obtained disks which satisfy all the energy conditions, however these disks present tension (negative pressure) rather pressure. Therefore these disks can be interpreted as made of a perfect fluid with negative pressure or tension immersed in a Robertson-Walker type cosmological model. When k = —1 obtains the opposite case, that is disks with positive stress (pressure) but with negative energy density in violation of the weak energy condition. Two simple families of models of disks based on Robertson-Walker spacetimes with k = 1 admitting Matter and Ricci collineations were presented. We found that initially the surface energy density presents its maximum value and then decreases with the time, being always a positive quantity in agreement with the weak energy condition, whereas the tension presents a behavior opposite. Finally, more realistic models like thick disks, finite disks based on this same metric, and disks based on other time dependent metrics are being considered.
References
[1] W. A. Bonnor and A. Sackfield, ''The interpretation of some spheroidal metrics,'' Commun. Math. Phys., vol. 8, pp. 338-344, Apr. 1968. [ Links ] 132
[2] T. Morgan and L. Morgan, ''The Gravitacional Field of a Disk,'' Phys. Rev., vol. 183, pp. 1097-1101, Apr. 1969. [ Links ] 132, 135
[3] L. Morgan and T. Morgan, ''Gravitational Field of Shells and Disks in General Relativity'', Phys. Rev. D, vol. 2, pp. 2756 - 2761, Apr. 1970. [ Links ] 132, 135
[4] G. A. Gonzalez and P. S. Letelier, ''Relativistic static thin discs with radial stress support,'' Class. Quantum Grav., vol. 16, pp. 479-494, Apr. 1999. [ Links ] 132, 135
[5] J. P. S. Lemos and P. S. Letelier, ''Superposition of Morgan and Morgan discs with a Schwarzschild black hole,'' Class. Quantum Grav., vol. 10, pp. L75 - L78, Apr. 1993. [ Links ] 132
[6] J. Bicák, D. Lynden-Bell, and J. Katz, ''Relativistic disks as sources of static vacuum spacetimes,'' Phys. Rev. D, vol. 47, pp. 4334-4343, Apr. 2003. [ Links ] 132, 133
[7] J. Bicák and T. Ledvinka, ''Relativistic disks as sources of the Kerr metric,'' Phys. Rev. Lett., vol. 71, pp. 1669-1672, Apr. 1993. [ Links ] 132
[8] G. A. Gonzalez and P. S. Letelier, ''Rotating relativistic thin disks,'' Phys. Rev. D, vol. 62, 064025, pp. 1 - 8, Apr. 2000. [ Links ] 132
[9] T. Ledvinka, J. Bicák, and M. .Zofka, ''Relativistic discs as sources of Kerr-Newman fields,'' in Proc. 1999 of 8th Marcel-Grossmann Meeting in General Relativity, edited by T. Piran, World Scientific, Singapore, pp. 339-341. [ Links ] 132
[10] C. H. García-Duque and G. García-Reyes, ''General magnetized Weyl solutions: disks and motion of charged particles,'' Gen. Relativ. Gravit., vol. 43, pp. 3001-3032, Apr. 2011. [ Links ] 132
[11] J. Katz, J. Bicák, D. Lynden-Bell, ''Disc sources for conformastationary metrics,'' Class. Quantum Grav., vol. 16, pp. 4023-4034 , Apr. 1999. [ Links ] 132, 133
[12] J. L. Synge, Relativity: The General Theory. Amsterdam: North-Holland publishing company, 1966. [ Links ] 132
[13] C. Klein, ''Exact relativistic treatment of stationary black-holedisk systems,'' Phys. Rev. D, vol. 68, 027501, pp. 1-4, Apr. 2003. [ Links ] 133
[14] C. Klein, ''On explicit solutions to the stationary axisymmetric Einstein- Maxwell equations describing dust disks,'' Annalen der Physik, vol. 12, pp. 599-639, Apr. 2003. [ Links ] 133
[15] J. Binney and S. Tremaine, Galactic Dynamics. Princeton, New Jersey: Princeton University Press, 1987, pp. 43. [ Links ] 133
[16] P. S. Apostolopoulos and M. Tsamparlis, ''Geometric Equations of State in Friedmann-Lemaître Universes Admitting Matter and Ricci Collineations,'' Gen. Rel. Grav. Vol. 36, pp. 277-292, Apr. 2004. [ Links ] 134, 137
[17] H. Stephani, D. Kramer, M. McCallum, C. Hoenselaers and E. Herlt, Exact Solutions of Einstein's Field Equations. England: Cambridge University Press, 2003, pp. 211. [ Links ] 134
[18] Ray d'Inverno, Introducing Einstein's Relativity: Clarendon Press, Oxford, 1998, pp.. 313-314. [ Links ] 134
[19] G. García-Reyes and G. A. González, ''Electrovacuum Static Counterrotating Relativistic Dust Disks,'' Phys. Rev. D, vol. 70, 104005, pp.1-6, Apr. 2004. [ Links ] 135














