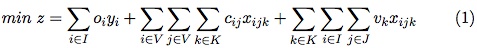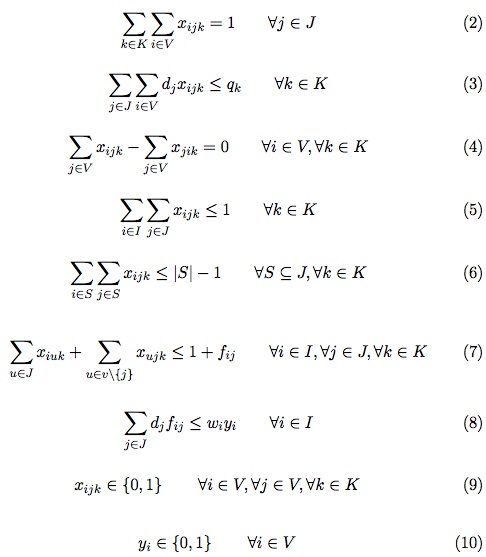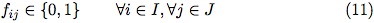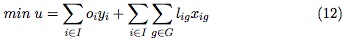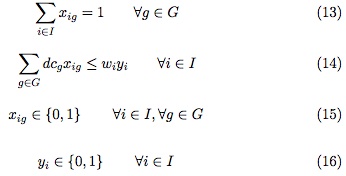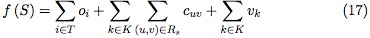Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO -
 Access statistics
Access statistics
Related links
-
 Cited by Google
Cited by Google -
 Similars in
SciELO
Similars in
SciELO -
 Similars in Google
Similars in Google
Share
Ingeniería y Ciencia
Print version ISSN 1794-9165
ing.cienc. vol.10 no.19 Medellín Jan./June 2014
ARTÍCULO ORIGINAL
Un algoritmo metaheurístico para el problema de localización y ruteo con flota heterogénea
A Metaheuristic Algorithm for the Location Routing Problem with Heterogeneous Fleet
Rodrigo Linfati1 , John Willmer Escobar2 y Gustavo Gatica3
1 Ph. D. in Operations Research, rlinfati@ubiobio.cl, Universidad del Bío-Bío, Chile.
2 Ph. D. in Operations Research, jwescobar@javerianacali.edu.co, Pontificia Universidad Javeriana, Cali, Colombia.
3 Candidato a Doctor en Ciencias de la Ingeniería USACH, ggatica@unab.cl, Universidad Andrés Bello, Santiago, Chile.
Recepción: 04-06-2013, Aceptación: 26-09-2013
Disponible en línea: 30-01-2014
PACS:68Qxx, 68W40
Resumen
Este artículo considera el problema de localización y ruteo con flota heterogénea (LRPH, por sus siglas en inglés), en el cual se busca determinar los depósitos a ser abiertos, los clientes a ser asignados a cada depósito, y las rutas a ser construidas para satisfacer las demandas de los clientes, considerando una flota de vehículos con capacidad diversa y costos de utilización asociados. El objetivo es minimizar la suma de los costos asociados con la apertura de depósitos, los costos de los vehículos utilizados, y los costos variables directamente relacionados con las distancias recorridas. En este artículo, se propone un algoritmo metaheurístico basado en una búsqueda tabú granular para la resolución del problema. Experimentos computacionales en instancias adaptadas de la literatura, muestran que el algoritmo propuesto es capaz de obtener, en tiempos computacionales razonables, soluciones de alta calidad demostrando su efectividad.
Palabras clave: Problema de Localización y Ruteo; Flota Heterogénea; Búsqueda Tabú Granular; Algoritmos Metaheurísticos.
Abstract
This paper considers the Location-Routing Problem with Heterogeneous Fleet (LRPH), in which the aim is to determine the depots to be opened, the customers to be assigned to each open depot, and the routes to be performed to fulfill the demand of the customers by considering a heterogeneous fleet with different capacities and associated costs. The objective is to minimize the sum of the cost of the open depots, of the used vehicle costs, and of the variable costs related with the distance traveled by the performed routes. In this paper, it is proposed a metaheuristic algorithm based on a granular tabu search to solve the LRPH. Computational experiments on adapted benchmark instances from the literature show that the proposed approach is able to obtain, within short computing times, high quality solutions illustrating its effectiveness.
Key words: Location Routing Problem; Heterogeneous Fleet; Granular Tabu Search; Metaheuristic Algorithms.
1 Introducción
La logística tiene como misión, proveer los productos o servicios apropiados, en el lugar correcto, en el momento adecuado, en la condición deseada, a un precio competitivo, contribuyendo a la obtención de la máxima utilidad y proporcionando el mayor nivel de servicio [1]. La logística comprende la integración de las actividades de abastecimiento, producción, transporte, distribución, inventario, almacenamiento, manipulación de materiales y empaque, así como el flujo de información entre ellas, convirtiéndose en uno de los factores fundamentales para alcanzar y mejorar las posiciones competitivas de las compañías.
La logística considera tres niveles de planeación de acuerdo con el horizonte de tiempo del proceso de toma de decisiones: estratégico, táctico y operacional; con horizontes superiores a un año, menor a un año y otras escalas de menor tiempo, es decir, semanas, días e incluso horas, respectivamente. Uno de los problemas abiertos en la literatura, corresponde al ruteo de vehículos, que puede dividirse en aquellos con flota heterogénea (LRPH, por sus siglas en inglés) y aquellos que utilizan flotas homogéneas [2]. El presente artículo está enfocado en el desarrollo de un algoritmo metaheurístico para la solución de la problemática de integración de decisiones de localización de instalaciones (decisión estratégica) y ruteo de vehículos (decisión operacional) considerando flota heterogénea.
El LRPH es un problema nuevo y nuestro objetivo es atraer a otros investigadores a considerar su estudio. El único trabajo cercano a la problemática es propuesto por [3], quienes presentan una formulación matemática y un algoritmo de búsqueda de vecindario variable para el problema de ruteo de vehículos con múltiples depósitos (MDHVRP, por sus siglas en inglés). Sin embargo, en el trabajo presentado por [3] no se consideran decisiones de apertura y cierre de depósitos. Debido a lo anterior, no se cuentan con instancias reales, razon por la cual se han realizado pruebas computacionales con set de instancias adaptadas de la literatura.
En la práctica la problemática de localización y ruteo han sido estudiadas de manera independientes. Sin embargo, recientemente se han publicado algunos trabajos que demuestran que la integración de estas decisiones proporciona mejores resultados en términos de eficiencia en la cadena de suministro ([4], [5],[6] y [7]). Numerosos trabajos han considerado la problemática conjunta de localización y ruteo con flota homogénea, a pesar de ser inusual en la práctica ([2]).
El problema de localización de instalaciones está asociado a decisiones de apertura, ubicación y asignación de clientes a depósitos. Por otro lado, el ruteo de vehículos, responde al desarrollo de un conjunto de rutas, minimizando el costo de la distancia recorrida para satisfacer la demanda de los clientes. El problema de Localización y Ruteo (LRP, por sus siglas en inglés) integra ambas problemáticas. Algoritmos exactos han sido capaces de demostrar optimalidad para instancias pequeñas (menos de 100 clientes) para el LRP. Por esta razón algoritmos heurísticos y metaheurísticos han sido propuestos para resolver instancias de mayor tamaño, como las consideradas en este trabajo ([7]). En [2] se define una clasificación para el LRP de acuerdo a diferentes criterios como son la función objetivo, método de solución y periodo de planeación.
Para la mayoría de problemas de localización y ruteo de vehículos, el número de vehículos es variable considerando una flota homogénea. De ahí que la literatura es escasa en cuanto a problemas con flota heterogénea y con decisiones de localización y ruteo simultáneamente. Algunas consideraciones de flota heterogénea son propuestas por [8], [9], [10], [11] y [12].
En [8] se aplica una descomposición Bender para dividir el LRP en dos subproblemas: localización-asignación y ruteo, se considera una flota heterogénea. Ambos subproblemas son resueltos de manera óptima en un esquema interactivo.
En [9] se considera un algoritmo de dos fases. En la fase de localización se consideran como entrada todas las posibles parejas de clientes. En la función objetivo se considera la longitud de los tours como costo un costo variable relacionado con la distancia recorrida. Estos costos son ajustados considerando una flota heterogénea de vehículos. En la fase de localización se utilizan movimientos de inserción y swap. Mientras que la fase de ruteo considera una heuristica multinivel. El método propuesto en [10] es similar al anterior, excepto que ambas fases son resueltas en un algoritmo combinado de búsqueda tabú y simulado recocido considerando un solo vecindario.
En [11] se considera un problema LRP de 4 niveles, donde el nivel 1 son las plantas de fabricación, el nivel 2 los centros de distribución, el nivel 3 los puntos de transferencia y el nivel 4 los clientes finales. En este problema se incluyen decisiones de inventario con una flota heterogénea de vehículos. El problema es formulado como un modelo de programación entera mixta el cual es resuelto de manera óptima para instancias pequeñas utilizando software comercial, entre los cuales podemos nombrar CPLEX® de IBM®, y GUROBI®. Finalmente, en [12] se considera un problema de traslado desde hubs hasta clientes, considerando una flota heterogénea para realizar viajes cortos y largos.
El problema de localización y ruteo con flota heterogénea (LRPH) es considerado un problema NP-Hard [13] debido a que corresponde a una generalización del problema de localización y ruteo con restricciones de capacidad (CLRP, por sus siglas en inglés) y el problema de ruteo de vehículos con múltiple depósitos, considerando flota heterogénea (HMDVRP, por sus siglas en inglés). En este artículo se propone un algoritmo metaheurístico basado en una búsqueda tabú granular para resolver el LRPH. La descripción del LRPH es detallada y el marco general del algoritmo propuesto es presentado en la Sección 2. La Sección 3 muestra los resultados computacionales en instancias adaptadas de la literatura. Finalmente, se presentan las conclusiones.
2 Metodología Propuesta
2.1 Formulación del problema
El LRPH puede ser formalizado como: Sea G = (V, E) un grafo no dirigido donde V = {1,..., m + n } corresponde al conjunto de vértices y E al conjunto de arcos. Los vértices J = 1,..., m corresponden a los clientes con demanda dj y los vértices I = m + 1,..., m + n corresponden a los depósitos potenciales, cada uno con capacidad wi y costo de apertura oi. Un costo cij es asociado a cada par de nodos (i, j)  E. Un conjunto de vehículos heterogéneos K, cada uno con capacidad qk está disponible en cada depósito i
E. Un conjunto de vehículos heterogéneos K, cada uno con capacidad qk está disponible en cada depósito i  I. Asimismo, cada vehículo cuando realiza una ruta genera un costo fijo vk.
I. Asimismo, cada vehículo cuando realiza una ruta genera un costo fijo vk.
El objetivo principal del LRPH es minimizar los costos totales de logística, los cuales incluyen costo fijo de apertura de depósitos, costo variable asociado a rutas establecidas y costo fijo de uso de los vehículos. El problema LRPH es mono objetivo, con restricciones, y discreto. Una solución para el LRPH es factible si las siguientes restricciones son satisfechas: i) cada ruta debe comenzar y terminar en el mismo depósito, ii) cada cliente debe ser visitado exactamente una vez por una sola ruta, iii) la suma de las demandas de los clientes visitados por cada vehículo k, no puede exceder su capacidad qk, iv) la suma de las demandas de los clientes asignados a cada depósito abierto i  I, no debe exceder su capacidad wi, y v) no se permite flujo entre depósitos.
I, no debe exceder su capacidad wi, y v) no se permite flujo entre depósitos.
Se propone un modelo de programación lineal entera mixta de tres índices para el LRPH. El modelo extiende la formulación presentada por [4] para el problema de localización y ruteo con restricciones de capacidad y vehículos homogéneos (CLRP, por sus siglas en inglés), incluyendo las consideraciones de vehículos heterogéneos presentada en [9]. La formulación utiliza las variables binarias:
yi = 1 si el depósito es abierto
fij = 1 si el cliente j  J es asignado al depósito i
J es asignado al depósito i  I
I
xijk = 1 si se utiliza el arco desde i  V a j
V a j  V en la ruta asignada al vehículo k
V en la ruta asignada al vehículo k  K
K
Sujeto a:
Note que el modelo no permite el flujo entre depósitos, por lo tanto, el costo de transporte cij no está definido para (i, j)  I x I. La función objetivo (1) minimiza la suma de tres costos distintos, el primero asociado a los depósitos abiertos, el segundo tiene relación con los arcos visitados por las rutas y el último con los costos fijos asociados al uso de los vehículos. Los términos de la función objetivo (1) son una extensión de los costos considerados en el CLRP por [4]. El grupo de restricciones (2) garantiza que cada cliente j
I x I. La función objetivo (1) minimiza la suma de tres costos distintos, el primero asociado a los depósitos abiertos, el segundo tiene relación con los arcos visitados por las rutas y el último con los costos fijos asociados al uso de los vehículos. Los términos de la función objetivo (1) son una extensión de los costos considerados en el CLRP por [4]. El grupo de restricciones (2) garantiza que cada cliente j  J debe ser atendido por un solo depósito i
J debe ser atendido por un solo depósito i  I en una ruta asignada a un solo vehículo k
I en una ruta asignada a un solo vehículo k  K. El grupo de restricciones (3) y (8) son asociadas con las capacidades de los vehículos y los depósitos respectivamente. Restricciones (4) y (5) aseguran la continuidad de cada ruta y determina que cada una de ellas inicie y termine en el mismo depósito. La eliminación de los subtours es satisfecha a través del conjunto de restricciones (6). La restricción (7) especifica que un cliente puede ser asignado a un depósito solamente si existe una ruta que lo une. Finalmente, las restricciones (9), (10) y (11) representan las variables binarias usadas en el modelo matemático. Más detalle acerca de la notación usada en esta formulación puede ser encontrada en [14] y [15].
K. El grupo de restricciones (3) y (8) son asociadas con las capacidades de los vehículos y los depósitos respectivamente. Restricciones (4) y (5) aseguran la continuidad de cada ruta y determina que cada una de ellas inicie y termine en el mismo depósito. La eliminación de los subtours es satisfecha a través del conjunto de restricciones (6). La restricción (7) especifica que un cliente puede ser asignado a un depósito solamente si existe una ruta que lo une. Finalmente, las restricciones (9), (10) y (11) representan las variables binarias usadas en el modelo matemático. Más detalle acerca de la notación usada en esta formulación puede ser encontrada en [14] y [15].
Al intentar resolver el modelo de manera óptima utilizando algún software comercial como CPLEX® se puede incurrir en elevados tiempo computacionales, y el consumo de memoria crecerá de forma exponencial con el número de nodos, dada la dificultad del problema [16]. Lo anterior afirma que desde el punto de vista computacional, el uso de modelos matemáticos, sin el uso de técnicas de descomposición, o algoritmos de ramificación y acotamiento, es prohibitivo. En ese sentido, aparecen las heurísticas y metaheurísticas como alternativa para la solución del LRPH. Dado que el problema considerado es relativamente nuevo, los resultados obtenidos por la metaheurística propuesta se han comparado con la solución obtenida del modelo (1) - (11), relajando las restricciones de eliminación de subtour (6). De esta forma, estas restricciones solo son añadidas en cada nueva solución entera encontrada durante el proceso de Branch-Cut desarrollado en CPLEX®.
2.2 Descripción del algoritmo propuesto
En esta sección, se presenta el algoritmo propuesto para resolver el LRPH. El algoritmo propuesto extiende la idea de búsqueda tabú granular (GTS, por sus siglas en inglés), introducida por [17] para el problema capacitado de ruteo de vehículos con un solo depósito, al problema LRPH. La idea general de la GTS es encontrar soluciones de gran calidad en tiempos computacionales reducidos, para ello se define una implementación efectiva de una lista de candidatos, la cual contiene los mejores vecindarios a visitar, reduciendo el tiempo computacional al utilizar solo vecindades que pueden ser examinados en un tiempo menor al requerido en la forma tradicional, preservando la calidad de las soluciones de una búsqueda tabú tradicional. En particular, buenos vecindarios son visitados, acotando la región de búsqueda mediante el descarte de una gran cantidad de soluciones vecinas ''no prometedoras'' y explorando sólo un subconjunto que contiene soluciones vecinas ''prometedoras''.
En el algoritmo propuesto, se construye una solución inicial factible mediante un procedimiento híbrido que combina técnicas de clústeres con métodos exactos. El procedimiento inicial está fundamentado en la generación de clústeres de clientes con asignación de vehículos aleatoriamente, que permite obtener una solución factible con un tiempo de cómputo reducido. De esta manera se reduce el espacio de búsqueda del algoritmo propuesto de un problema de localización y ruteo con flota heterogénea, a un problema de múltiple depósitos con vehículos heterogéneos. El procedimiento de búsqueda tabú propuesto no considera decisiones de cierre y apertura de centros de distribución. Cuando el algoritmo es atrapado en un óptimo local por un número determinado de iteraciones, un procedimiento de perturbación es aplicado. Un óptimo local para un vecindario se alcanza cuando no existe una solución mejor que la actual, es decir, no se puede realizar una mejora moviéndose a otra solución dentro del mismo vecindario, según lo expresado por [18]. A continuación se describe el pseudocódigo del Algoritmo 1 propuesto.
2.3 Espacio de búsqueda granular
El grafo original G se sustituye por un grafo que considera todos los arcos que tienen un costo menor a un umbral de granularidad 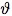 , los arcos incidentes a los depósitos y los arcos que pertenecen a la mejor solución encontrada durante la búsqueda. Sea
, los arcos incidentes a los depósitos y los arcos que pertenecen a la mejor solución encontrada durante la búsqueda. Sea 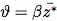 donde
donde 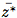 es el costo promedio de los arcos que pertenecen a las mejores soluciones encontradas y β un factor de esparsificación que controla los mecanismos de diversificación e intensificación de la búsqueda tabú. Valores grandes de β inducen procesos de diversificación, mientras que valores pequeños de β permiten procesos de intensificación.
es el costo promedio de los arcos que pertenecen a las mejores soluciones encontradas y β un factor de esparsificación que controla los mecanismos de diversificación e intensificación de la búsqueda tabú. Valores grandes de β inducen procesos de diversificación, mientras que valores pequeños de β permiten procesos de intensificación.
2.4 Procedimiento de solución inicial
En primera instancia se construye un tour del vendedor viajero (TSP, por sus siglas en inglés) para todos los clientes utilizando la heurística Lin Kernighan (LKH, por sus siglas en inglés) ([19],[20]), que permite resolver el TSP de manera efectiva mediante la aplicación de diferentes estrategias de búsqueda local. A partir de dicho tour, se procede a determinar grupos de clientes (clústeres) que pueden ser atendidos en una misma ruta por un vehículo determinado. Dado el inicio con flota finita y heterogénea, el tour gigante es divido en diferentes grupos de clientes de acuerdo a las capacidades de los vehículos disponibles mediante los siguientes pasos:
1. Seleccionar un vehículo libre k  K de manera aleatoria para atender a un grupo de clientes (clúster).
K de manera aleatoria para atender a un grupo de clientes (clúster).
2. Determinar un primer cliente para ser asignado a dicho vehículo k  K.
K.
3. Agregar uno a uno clientes nuevos siguiendo la trayectoria del TSP.
4. Una vez completada la capacidad del vehículo k  K , se reinicia el proceso con el paso 1 hasta asignar todos los clientes a un vehículo de la flota disponible.
K , se reinicia el proceso con el paso 1 hasta asignar todos los clientes a un vehículo de la flota disponible.
Luego para cada depósito i  I y cada clúster g
I y cada clúster g  G, se aplica nuevamente el procedimiento LKH para determinar la longitud del tour (lig) al asignar el depósito i al clúster g. Finalmente, los depósitos se asignan a los grupos de clientes mediante la solución del modelo de programación lineal entera mixta correspondiente al problema de localización de instalaciones con restricciones de single sourcing (FLPS, por sus siglas en inglés) ([21] y [22]). En este problema se consideran los siguientes conjuntos de variables binarias:
G, se aplica nuevamente el procedimiento LKH para determinar la longitud del tour (lig) al asignar el depósito i al clúster g. Finalmente, los depósitos se asignan a los grupos de clientes mediante la solución del modelo de programación lineal entera mixta correspondiente al problema de localización de instalaciones con restricciones de single sourcing (FLPS, por sus siglas en inglés) ([21] y [22]). En este problema se consideran los siguientes conjuntos de variables binarias:
xig = 1 Si el depósito i  I es asignado al clúster g
I es asignado al clúster g  G
G
yi = 1 Si se abre el depósito i  I
I
Donde G, corresponde al conjunto de clústeres resultantes de dividir el tour gigante en subtours y dcg a la demanda global del clúster g, es decir, la suma de las demandas de los clientes asignados a g  G. Así, el FLPS se puede formular mediante el modelo (12)-(16):
G. Así, el FLPS se puede formular mediante el modelo (12)-(16):
Sujeto a:
La función objetivo (12), corresponde a la suma de los costos totales de apertura de los depósitos y los costos de la distancia recorrida al asignar los depósitos a los clústeres. El grupo de restricciones (13) garantiza que cada grupo de clientes sea asignado exactamente a un solo depósito. El grupo de restricciones (14) determina la capacidad de cada uno de los depósitos. Por último, las restricciones (15) y (16) determinan el conjunto de variables binarias usadas en el modelo. Note que el procedimiento inicial es repetido n veces (donde n es el número de clientes), considerando cada cliente como inicio para la división del TSP tour. En este procedimiento la mejor solución factible es conservada.
2.5 Movimientos
La cardinalidad de vecindarios es la cantidad de soluciones vecinas a la solución S. En [17] se menciona que el tiempo de ejecución de cada iteración de un algoritmo de búsqueda local es proporcional a la cardinalidad de los vecindarios y al tiempo necesario para verificar factibilidades y evaluar costos de las nuevas soluciones. En la mayoría de los casos el tiempo de cada iteración está asociado a una función que depende del tamaño de la instancia. El número de iteraciones a ser ejecutadas para alcanzar un mínimo local puede ser grande, dependiendo directamente del tamaño de la instancia dado por el número nodos.
Una forma de reducir el tiempo computacional es restringir la búsqueda a ciertas vecindades ''prometedoras'', que normalmente pertenecen a las mejores soluciones encontradas para el problema de ruteo de vehículos (VRP, por sus siglas en inglés), denominadas ''vecindarios granulares''. El algoritmo propuesto utiliza los siguientes vecindarios:
• Shift: Un cliente es transferido desde su posición actual a otra posición, ya sea en la misma ruta o en una ruta diferente (que pertenece al mismo depósito o a otro diferente).
• Swap: Dos clientes de la misma o de diferente ruta intercambian su posición, ya sea en la misma ruta o en una ruta diferente (que pertenece al mismo depósito o a otro diferente).
• Double-Shift: Dos clientes consecutivos son transferidos de sus actuales posiciones a otras posiciónes diferentes, manteniendo el arco que los conecta. Los clientes pueden ser insertados en su ruta actual o en una diferente (que pertenece al mismo depósito o a otro diferente).
• Double-Swap: Este movimiento es una extensión del Swap, obtenido considerando dos pares de clientes consecutivos. El arco que conecta a cada par de clientes es mantenido. Este movimiento es ejecutado entre dos rutas diferentes que pertenecen al mismo depósito o a otro diferente.
Los movimientos de cada una de las vecindades son ejecutados solo si los nuevos arcos se encuentran en la lista de candidatos.
2.6 Procedimiento de Búsqueda Tabú Granular
La solución inicial S0 obtenida por el procedimiento descrito en la sección 2.4 es mejorada mediante un procedimiento de búsqueda tabú granular, en el cual no se consideran vecindarios que modifiquen los depósitos abiertos. En ese sentido se busca mejorar las rutas determinadas por el procedimiento de solución inicial, permitiendo durante la Búsqueda Tabú soluciones infactibles con respecto a las capacidades de los depósitos y de los vehículos, utilizando las vecindades descritas en la Sección 2.5 y el espacio de búsqueda descrito en la Sección 2.3. La lista tabú está compuesta por los arcos eliminados de la ruta actual, permaneciendo 7 iteraciones antes de ser descartados de la lista tabú. Los vecindarios son explorados de forma secuencial, seleccionando el mejor vecino entre todos los vecindarios.
La búsqueda tabú granular considera dos estrategias de diversificación. La primera, está relacionada con la diversificación granular. Inicialmente el factor de esparsificación β es ajustado a un valor pequeño β0. Si la mejor solución factible encontrada no ha sido actualizada durante Nimp iteraciones, el valor de β se incrementa a un valor β n. De esta manera una nueva lista de candidatos es calculada. Luego, después de Nback iteraciones, el valor del factor de esparsificación β se restablece al valor inicial de β0 y la búsqueda continua desde la mejor solución factible encontrada. Los valores de β0, Nimp, βn y Nback son parámetros dados en el desarrollo del algoritmo los cuales se pueden observar en la 3. La segunda estrategia de diversificación, se basa en un enfoque de penalización propuesto por [23] y [24] para el problema de ruteo de vehículos (VRP). En particular, para cada solución S se considera un conjunto de rutas R1,..., Rk. Cada ruta Rs, s  {1,..., K}, puede ser denotada por (vs0, vs1, v s2, ..., vs0),donde vs0 representa el depósito asignado a la ruta, y cada vsj , j
{1,..., K}, puede ser denotada por (vs0, vs1, v s2, ..., vs0),donde vs0 representa el depósito asignado a la ruta, y cada vsj , j  J, representan los clientes visitados. Note que la solución S puede ser factible o infactible con respecto a la capacidad de los vehículos o la capacidad de los depósitos. Sea T el subconjunto de depósitos abiertos y Di el conjunto de clientes asignados al depósito i; la siguiente notación es usada: v
J, representan los clientes visitados. Note que la solución S puede ser factible o infactible con respecto a la capacidad de los vehículos o la capacidad de los depósitos. Sea T el subconjunto de depósitos abiertos y Di el conjunto de clientes asignados al depósito i; la siguiente notación es usada: v  Rs, si un cliente v pertenece a la ruta Rs y (u; v)
Rs, si un cliente v pertenece a la ruta Rs y (u; v)  Rs, si u y v son dos vértices consecutivos de la ruta Rs. La siguiente función objetivo f (S) está asociada a cada solución factible S:
Rs, si u y v son dos vértices consecutivos de la ruta Rs. La siguiente función objetivo f (S) está asociada a cada solución factible S:
De igual manera la ecuación (18), indica la función objetivo g (S) asociada con cualquier solución infactible S:
Donde [x]+ = max (0, x), γd y γr son dos pesos positivos utilizados para incrementar el valor de la solución S, adicionando la suma de los excesos de carga de los depósitos y la suma de los excesos de demanda en las rutas, respectivamente.
Los dos pesos son calculados de la siguiente forma: γd = αd x f (S0) y γr = αr x f (S0), donde f (S0) es el valor de la función objetivo de la solución inicial obtenida mediante el procedimiento descrito en la sección 2.4 y αd y αr son dos parámetros ajustados durante la búsqueda tabú granular dentro del rango [αmin, αmax]. En particular, si no se han encontrado soluciones infactibles respecto a la capacidad de los depósitos durante Nsearch iteraciones, el valor de αd se establece como max {αmin, αd x ip}, donde 0 < ip < 1. Por otro lado, si las soluciones encontradas durante Nsearch iteraciones son infactibles, entonces el valor de αd se establece como min {αmax, αd x rp}, donde rp > 1. Una regla similar se aplica para modificar el valor de αr, αmin, αmax, Nsearch, ip y rp son parámetros dados.
Finalmente, en la selección del mejor movimiento infactible para una solución S se considera el siguiente criterio: Si el valor de g (S) es menor que el costo de la mejor solución encontrada, se asigna un valor h (S) = g (S). De lo contrario, como estrategia de diversificación se introduce una penalidad extra al valor de g (S) igual a Δmax x t x √k. Δmax corresponde a la diferencia absoluta entre dos valores sucesivos de la función objetivo g (S), t es un factor de escala y k es igual al número de rutas de la solución S. De esta manera se define h (S) = g (S)+ Δ max x t x √k. Note que si la solución S es factible h (S) = f (S). El movimiento con el menor valor de h (S) es ejecutado.
2.7 Procedimiento de perturbación
El algoritmo propuesto aplica el procedimiento propuesto en [7] para el CLRP, utilizando ''distancia entre rutas'' como medida de proximidad. La evaluación de la ''distancia entre rutas'' depende de las características de las instancias consideradas. En este nuestro caso, cada vértice del grafo G es asociado con un punto en el plano Cartesiano y el costo cij es calculado para el nodo (i, j) como la distancia Euclidiana entre los puntos asociados con los vértices i y j. Dado lo anterior, para medir la cercanía entre las rutas se utiliza sus ''Centros de Gravedad''.
En particular si después de Npert iteraciones el algoritmo está atrapado en un óptimo local, es aplicado el siguiente procedimiento:
• Seleccionar una primera ruta k1 aleatoriamente;
• Seleccionar la ruta más cercana a k1(k2);
• Seleccionar la ruta más cercana a k2 (k3), donde k1 ≠ k3;
• Seleccionar un cliente de la ruta k1(i1) y un arco de la ruta k2 (h2, j2) de acuerdo con el mínimo costo de insertar i 1 en (h2, j2);
• Seleccionar un cliente de la ruta k2(i2) y un arco de la ruta k3 (h3, j3) de acuerdo con el mínimo costo de insertar i 2 en (h3, j3). En este caso i2 ≠ h2 y i2 ≠ j2;
• Obtener una nueva solución S realizando los siguientes pasos:
- Remover el cliente i1 de la ruta k1 e insertar entre los vértices (h2, j2) de la ruta k2.
- Remover el cliente i2 de la ruta k2 e insertar entre los vértices (h3, j3) de la ruta k3.
3 Resultados
El algoritmo propuesto ha sido implementado en C++, en ambiente Windows 7 Professional. Los experimentos computacionales han sido ejecutados en un Intel Core i5 (2.80 GHz) con 8 GB de memoria RAM.
Para probar la efectividad del algoritmo propuesto se han utilizado dos conjuntos de instancias adaptadas de la literatura. El primer conjunto, corresponde a instancias de [25] para el problema de ruteo de vehículos con flota heterogénea (HFVRP, por sus siglas en inglés). En HFVRP todos los depósitos son considerados para determinar el número de rutas que permitan satisfacer la demanda de los clientes. Por el contrario, en LRPH los depósitos son considerados como ''potenciales'' y por ende se debe decidir cuáles depósitos se deben abrir y qué clientes se deben asignar a cada uno de ellos.
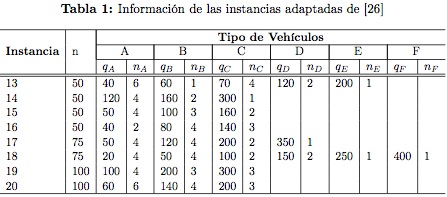
El primer conjunto de 8 instancias tiene las siguientes características: el número de depósitos potenciales m toma valores entre 5 y 10, el número de clientes n es de 50, 75 o 100. Las demandas y coordenadas fueron originalmente tomadas de [26], la demanda de los clientes es uniformemente distribuida entre [1, 40] y la capacidad (qk) de los vehículos usados, el costo de uso de los vehículos (vk) y el número de vehículos k es un parámetro determinado en [25]. La Tabla 1 muestra el número de clientes, el número de vehículos de cada tipo y la capacidad de cada uno de ellos.
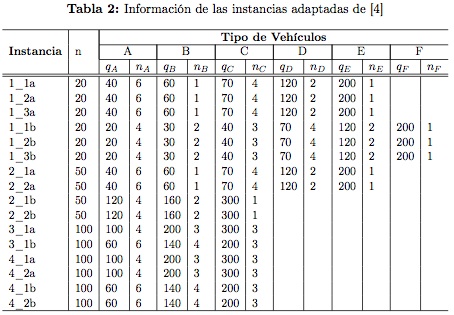
El segundo conjunto de instancias ha sido adaptado de [4] para el CLRP. En particular se ha cambiado las características de la flota homogénea (capacidad y costo de uso del vehículo) por las características de los vehículos propuestos en [25]. Este grupo considera 16 instancias con las siguientes características: el número de depósitos potenciales toma valores de 5 y 10, el número de clientes es 20, 50 o 100, la demanda de los clientes presenta una distribución uniforme entre [11, 20] y la capacidad (qk) de los vehículos usados, el costo de uso de los vehículos (vk) y el número de vehículos k es un parámetro adaptado de [25]. La Tabla 2 muestra el número de clientes, el número de vehículos de cada tipo y la capacidad de cada uno de ellos.
3.1 Ajuste de parámetros
El éxito del algoritmo propuesto depende directamente de los parámetros utilizados, es por ello que al cabo de una sintonización fina de ellos, se ha
logrado establecer que los valores presentes en la Tabla 3, permiten resolver todas las instancias consideradas en esta investigación. Los parametros βo y βn permiten al algoritmo alternar entre fases de intensificación y diversificación respectivamente. El proceso de intensificación se realiza durante Nimp iteracciones, mientras que el proceso de diversificación se realiza durante Nback iteracciones. Los parametros αd, αr, γmin, 1/F1(S0), γmax, N search, ip, rp y t, estan relacionados con el esquema de penalización que permite considerar soluciones infactibles durante la busqueda. Finalmente, el parametro Npert ayuda al algoritmo a escapar de óptimos locales. El proceso para la sintonización fina de parámetros se ha realizado de acuerdo al procedimiento propuesto en [27]. El algoritmo ha sido ejecutado por un número máximo de iteraciones igual a 10 x n.
3.2 Resultados sobre el conjunto de instancias
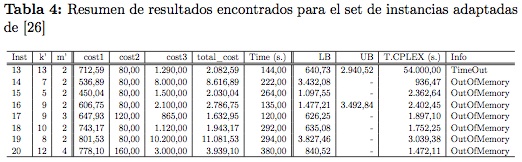
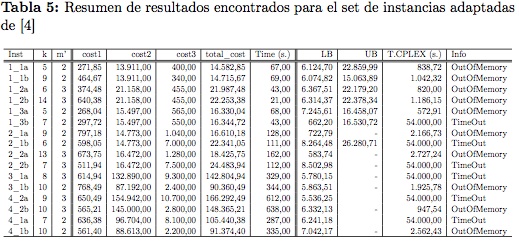
En las Tablas 4 y 5, se presentan los resultados computacionales con ambos conjuntos de instancias, la primera columna indica el problema analizado,
las columnas sucesivas describen el número de rutas obtenido en la solución final (k'), el número de depósitos abiertos (m'), el costo de la distancia recorrida por las rutas (cost1), el costo de los depósitos abiertos (cost2) y el costo de los vehículos usados (cost3). De igual manera se describe el costo total (total_cost) y el tiempo de ejecución (CPU time) en segundos empleado por el algoritmo propuesto (time), respectivamente. Adicionalmente se reporta los resultados obtenidos mediante CPLEX® para el modelo relajado (1)-(11) dados por la cota inferior de la función objetivo (LB), la cota superior o mejor solución factible (UB), el tiempo de ejecución (T.CPLEX) con un límite de 15 horas y la información sobre el estado de CPLEX® al terminar (Info). TimeOut significa que no fue posible para CPLEX®encontrar la solución óptima dentro del límite de tiempo establecido, OutOfMemory significa que CPLEX®agotó la memoria disponible y termino antes del tiempo límite sin encontrar la solución óptima. Las cifras no reportadas corresponden a instancias donde CPLEX® no fue capaz de encontrar una cota, ya sea por agotamiento de la memoria o por exceso del límite de tiempo establecido.
4 Conclusiones
En este artículo se propone un algoritmo efectivo basado en la metaheurística búsqueda tabú granular para el problema de localización y ruteo con restricciones de capacidad usando una flota heterogénea (LRPH). En particular, el algoritmo propuesto utiliza dos estrategias de diversificación, diversos vecindarios y un algoritmo de perturbación cuando se obtiene un óptimo local en un número determinado de iteraciones.
El algoritmo propuesto ha sido evaluado considerando instancias adaptadas de la literatura. Los experimentos computacionales muestran que el algoritmo propuesto es capaz de obtener, dentro de razonables tiempo de computación, soluciones de gran calidad. Los resultados obtenidos sugieren que el algoritmo propuesto podría ser aplicado a otros problemas de logística similares como son: el problema de ruteo con múltiples depósitos con flota heterogénea (HMDVRP, por sus siglas en inglés), el problema de localización y ruteo con restricciones de periodicidad considerando flota heterogénea (HPLRP, por sus siglas en inglés). Como trabajo futuro, se sugiere la implementación de procedimientos de busqueda local considerando movimientos que permitan abrir o cerrar instalaciones, de manera que se pueda explorar de mejor forma el espacio de solución del LRPH.
Agradecimientos
El trabajo de investigación ha sido parcialmente soportado por el MIUR (Ministero Istruzione, Università e Ricerca), Italia, la Pontificia Universidad Javeriana Cali, Colombia y las Universidades del Bío-Bío y Andrés Bello, Chile. Los autores agradecen enormemente a los referees por sus valiosos comentarios.
Referencias
[1] R. H. Ballou, Business Logistics/Supply Chain Management. Prentice Hall, 2004. [ Links ] 56
[2] G. Nagy and S. Salhi, ''Location-routing: Issues, models and methods,'' European Journal of Operational Research, vol. 177, no. 2, pp. 649-672, 2007. [ Links ] 57
[3] S. Salhi, A. Imran, and N. A. Wassan, ''The multi-depot vehicle routing problem with heterogeneous vehicle fleet: Formulation and a variable neighborhood search implementation,'' Computers & Operations Research, 2013. [ Links ] 57
[4] C. Prins, C. Prodhon, A. Ruiz, P. Soriano, and R. W. Calvo, ''Solving the capacitated location-routing problem by a cooperative lagrangean relaxationgranular tabu search heuristic,'' Transportation Science, vol. 41, no. 4, pp. 470-483, 2007. [ Links ] 57, 59, 61, 70, 71, 73
[5] C. Duhamel, P. Lacomme, C. Prins, and C. Prodhon, ''A GRASP x ELS approach for the capacitated location-routing problem,'' Computers & Operations Research, vol. 37, no. 11, pp. 1912-1923, 2010. [ Links ] 57
[6] V. F. Yu, S.-W. Lin, W. Lee, and C.-J. Ting, ''A simulated annealing heuristic for the capacitated location routing problem,'' Computers & Industrial Engineering, vol. 58, no. 2, pp. 288-299, 2010. [ Links ] 57
[7] J. Willmer Escobar, R. Linfati, and P. Toth, ''A two-phase hybrid heuristic algorithm for the capacitated location-routing problem,'' Computers & Operations Research, vol. 40, no. 1, pp. 70-79, 2013. [ Links ] 57, 68
[8] J. H. Bookbinder and K. E. Reece, ''Vehicle routing considerations in distribution system design,'' European Journal of Operational Research, vol. 37, no. 2, pp. 204-213, 1988. [ Links ] 58
[9] S. Salhi and M. Fraser, ''An integrated heuristic approach for the combined location vehicle fleet mix problem,'' Studies in Locational Analysis, vol. 8, pp. 3-21, 1996. [ Links ] 58, 59
[10] T.-H. Wu, C. Low, and J.-W. Bai, ''Heuristic solutions to multi-depot location-routing problems,'' Computers & Operations Research, vol. 29, no. 10, pp. 1393-1415, 2002. [ Links ] 58
[11] D. Ambrosino and M. Grazia Scutellà, ''Distribution network design: New problems and related models,'' European Journal of Operational Research, vol. 165, no. 3, pp. 610-624, 2005. [ Links ] 58
[12] H. Gunnarsson, M. Rönnqvist, and D. Carlsson, ''A combined terminal location and ship routing problem,'' Journal of the Operational Research Society, vol. 57, no. 8, pp. 928-938, 2005. [ Links ] 58
[13] M. T. C. S. JIS, Computers and intractability A Guide to the Theory of NP-Completeness. WH Freeman and Company, 1979. [ Links ] 58
[14] G. Laporte, ''The vehicle routing problem: An overview of exact and approximate algorithms,'' European Journal of Operational Research, vol. 59, no. 3, pp. 345-358, 1992. [ Links ] 61
[15] P. Toth and D. Vigo, The vehicle routing problem. Siam, 2002, vol. 9. [ Links ] 61
[16] C. H. Papadimitriou and K. Steiglitz, Combinatorial optimization: algorithms and complexity. Courier Dover Publications, 1998. [ Links ] 61
[17] P. Toth and D. Vigo, ''The granular tabu search and its application to the vehicle-routing problem,'' INFORMS Journal on Computing, vol. 15, no. 4, pp. 333-346, 2003. [ Links ] 62, 65
[18] C. Blum and A. Roli, ''Metaheuristics in combinatorial optimization: Overview and conceptual comparison,'' ACM Computing Surveys (CSUR), vol. 35, no. 3, pp. 268-308, 2003. [ Links ] 62
[19] S. Lin and B. W. Kernighan, ''An effective heuristic algorithm for the traveling-salesman problem,'' Operations research, vol. 21, no. 2, pp. 498- 516, 1973. [ Links ] 64
[20] K. Helsgaun, ''An effective implementation of the lin-kernighan traveling salesman heuristic,'' European Journal of Operational Research, vol. 126, no. 1, pp. 106-130, 2000. [ Links ] 64
[21] J. Barceló and J. Casanovas, ''A heuristic lagrangean algorithm for the capacitated plant location problem,'' European Journal of Operational Research, vol. 15, no. 2, pp. 212-226, 1984. [ Links ] 64
[22] J. G. Klincewicz and H. Luss, ''A lagrangian relaxation heuristic for capacitated facility location with single-source constraints,'' Journal of the Operational Research Society, pp. 495-500, 1986. [ Links ] 64
[23] M. Gendreau, A. Hertz, and G. Laporte, ''A tabu search heuristic for the vehicle routing problem,'' Management science, vol. 40, no. 10, pp. 1276- 1290, 1994. [ Links ] 67
[24] É. Taillard, ''Parallel iterative search methods for vehicle routing problems,'' Networks, vol. 23, no. 8, pp. 661-673, 1993. [ Links ] 67
[25] B. Golden, A. Assad, L. Levy, and F. Gheysens, ''The fleet size and mix vehicle routing problem,'' Computers & Operations Research, vol. 11, no. 1, pp. 49-66, 1984. [ Links ] 69, 70
[26] N. Christofides and J. E. Beasley, ''A tree search algorithm for the p-median problem,'' European Journal of Operational Research, vol. 10, no. 2, pp. 196- 204, 1982. [ Links ] 70, 73
[27] S. P. Coy, B. L. Golden, G. C. Runger, and E. A. Wasil, ''Using experimental design to find effective parameter settings for heuristics,'' Journal of Heuristics, vol. 7, no. 1, pp. 77-97, 2001. [ Links ] 71