Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO -
 Acessos
Acessos
Links relacionados
-
 Citado por Google
Citado por Google -
 Similares em
SciELO
Similares em
SciELO -
 Similares em Google
Similares em Google
Compartilhar
Ingeniería y Ciencia
versão impressa ISSN 1794-9165
ing.cienc. vol.10 no.20 Medellín jul./dez. 2014
ARTÍCULO ORIGINAL
Monte Carlo Simulation of Ferroelectric Behavior in PZT Films by Using a Stress Dependent DIFFOUR Hamiltonian
Simulación Monte Carlo del comportamiento ferroeléctrico de películas de PZT empleando un Hamiltoniano DIFFOUR dependiente de la presión
E. Restrepo-Parra1, H. H. Ortíz Álvarez2 , C. M. Bedoya-Hincapié3
1 Doctora en Ingeniería, erestrepopa@unal.edu.co, Universidad Nacional de Colombia, Manizales, Colombia.
2 Cand.Doctorado en Ingeniería, MSc. Ed. Matemática, hugo.ortiz@ucaldas.edu.co, Universidad de Caldas, Universidad Nacional de Colombia, Manizales, Colombia.
3 Ingeniera Física, MSc. Materiales y Procesos cmbedoyahi@unal.edu.co, Universidad Nacional de Colombia,Universidad Santo Tomás, Bogotá, Colombia.
Received: 27-09-2013, Acepted: 09-05-2014 Available online: 01-07-2014
PACS:77.55.hj
Abstract
In this work the polarization and hysteresis response of Lead Zirconate Titanate (PZT) ferroelectric thin films was studied in relation to the variation on temperature, stress, electric field and the content of non-ferroelectric impurities by using a Monte Carlo simulation. The simulation was based on a DIFFOUR Hamiltonian that takes into account the effect of uniaxial stress, in addition to the nearest neighbor dipoles interaction and the effect of an external electric field. The obtained results for hysteresis loops and polarization curves correspond with reported experimental data for this material.
Key words: Monte Carlo; simulation; ferroelectrics; DIFFOUR; PZT.
Resumen
En este trabajo se estudió la respuesta de polarización y de histéresis en películas delgadas de titanato zirconato de plomo (PZT) a la variación de temperatura, presión, campo eléctrico y contenido de impurezas no ferroeléctricas, mediante simulación Monte Carlo. La simulación se basó en un Hamiltoniano DIFFOUR, que tiene en cuenta el efecto de un esfuerzo uniaxial, además de la interacción entre dipolos vecinos y el efecto de un campo eléctrico externo. Los resultados obtenidos para ciclos de histéresis y curvas de polarización se ajustan a los datos experimentales reportados para este material.
Palabras clave: Monte Carlo; simulación; ferroeléctricos, DIFFOUR, PZT.
1 Introduction
Ferroelectrics and their characteristic of piezoelectricity have attracted the interest from the scientific community. In recent years a considerable effort has been accomplished in the development of technological application based on these phenomena. The piezoelectric devices, include, among others: cantilever actuators, [1],[2], probes for atomic force microscopy [3], ultrasonic micromotors [4],[5],[6], micropumps [7], ultrasonic transducers [8],[9] and actuators for suppression of mechanical vibrations in buildinglike structures [10].
The study of variables that directly affect domain formation and the quality response of these materials under the influence of electric fields have been of wide interest, because of their potential use in the design of non-volatile memories [11] and the development of multiferroic complex perovskites from the mixture of ferroelectric and ferromagnetic simple perovskites [12]. A big amount of experimental data reports the behavior of several ferroelectric materials such as Lead Zirconate Titanate (PZT) and Bismuth Titanate (BIT) [13], considering effects of temperature, stress and dopants, among other variables in relation with polarization and hysteresis. Experimentally, Wondsamnern [14] characterized ferroelectric hysteresis loops of PZT ceramics, observing the influence of external stress and temperature in an inverse relation of these variables with the hysteresis area. As important as those analysis that we mentioned before are research proposals trying to contribute to a better understanding of these materials through a theoretical modeling approach. Recently Laosiritaworn et al. [15] studied by Monte Carlo technique, PZT thin films by proposing a uniaxial stress dependent Hamiltonian. They simulated the dynamic response of a ferroelectric thin film, identifying changes in the energy dissipation from hysteresis loops with the stress variation.
In this research, the response of polarization, susceptibility and hysteresis of ferroelectric thin films to the variation of temperature, stress, electric field and the content of non-ferroelectric impurities was addressed through a Monte Carlo simulation. For this purpose, a DIFFOUR Hamiltonian was proposed to model ferroelectric properties in PZT thin films, one of the most studied ferroelectrics nowadays.
2 Simulation Methodology
PZT is a piezoelectric ceramic material in the form of a solid solution of PbZrO3 and PbT iO3 with formula Pb(ZrxTi1−x)O3 0 ≤ x ≤ 1. This material exhibits different stoichiometries according to Zr/Ti composition ratio, which directly affects its properties as it is evident from its phase diagram [16]. When the Ti content is higher than 0.47, PZT transforms from cubic structure to tetragonal structure at temperatures ranging from 370 to 490°C. When the Ti content is lower than 0.47, there is a cubic to rhombohedral transition with Curie-temperatures ranging from 230 to 370 °C [17]. The sample construction for simulation takes into account the transition expected for a thin film with a Ti content, x = 0.5, in which the perovskite geometry of the cell can be closely associated with a cubic structure (lattice parameter a ≈ c ≈ 4.07A°)[18]. This reduces to six the number of possible electric dipole orientations for each cell (−x,+x,−y,+y,−z, z), to be consistent with 90° or 180° experimentally observed polarization domain switching. In this manner for the model, an electric dipole associated to a PZT cell is assigned to each point of the cubic lattice, with one of the above orientations.
A single-spin movement Monte Carlo algorithm was used for obtaining equilibrium thermodynamic properties [19]. The lattice for simulation was designed with a thin film geometry of LxLxd dimensions. Periodic boundary conditions in the transverse directions (x-y plane or in-plane) and free along the perpendicular direction z of the film (out-of-plane) were employed. A linear dimension of L = 40 and a thickness of d = 5 (lattice units) were considered. Simulations for larger sizes of L were computed, giving no significant variation for the parameters and variables under consideration.
The system began with a random electric dipole configuration, corresponding to a high disordered or a high temperature system. We used Monte carlo simulation and Metropolis Algorithm as well as a DIFFOUR Hamiltonian [20],[21], Equation (1), to simulate the ferroelectric behavior (looking for a Transition temperature or Curie's temperature) of the system, with a variation range temperature from a high temperature up to a low temperature that correspond to a high ordered system.
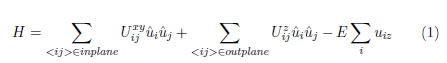
In this hamiltonian 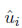 is the polarization unit vector at site i,uiz is the z component of polarization vector at site i, Uij is the magnitud of ferroelectric interaction between pairs of nearest pairs of dipoles and E is the electric field applied in the z direction. The first summation for inplane interactions, the second for out-of-plane interactions and the last one considers the electric field action over dipoles in z direction. For this model, we proposed that the stress dependent interaction intensity took the form of a Lennard-Jones potential:
is the polarization unit vector at site i,uiz is the z component of polarization vector at site i, Uij is the magnitud of ferroelectric interaction between pairs of nearest pairs of dipoles and E is the electric field applied in the z direction. The first summation for inplane interactions, the second for out-of-plane interactions and the last one considers the electric field action over dipoles in z direction. For this model, we proposed that the stress dependent interaction intensity took the form of a Lennard-Jones potential:
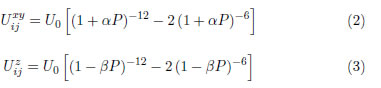
here, U0 stands for the magnitud of ferroelectric interaction associated to zero strain, P is the uniaxial compressive stress in the out of plane direction. The quantities 1+αP and 1−βP are proportional to the augmented and reduced length of distances in xy plane and z axis respectively under the action of P, counting for strain-polarization intensity relationship. That means, α and β values depend on the specific effect of mechanical stresses on the ferroelectric material and parameters to be adjusted with reported experimental data . A particular case, for α = 1/Y and β = ϵ/Y (Young modulus Y, and Poisson ratio ϵ) gives the Hamiltonian previously studied by Laosiritaworn et al. [15].
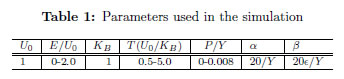
For simulations U0 was set as 1, re-defining the unit of temperature T as (U0/KB) (being KB the Boltzmann constant), the electric field E was considered in units of U0 and stress introduced through the dimensionless ratio P/Y . The parameters used in the simulation are listed in Table 1. The updating procedure for electrical displacement at any site is done as follow: For a given temperature and starting from a random lattice site, a new random orientation is assigned to ui among the six possible directions, then the Hamiltonian is calculated and the Metropolis algorithm is used to update the electric displacement in the site [22]. This procedure is repeated for all sites in the lattice(One Monte Carlo step (MCS)), and repeated as many times as necessary to reach the relaxation of the system. We used 10.000 Monte Carlo steps (MCS) for the relaxation of the system and 5.000 MCS more, to determine the average for polarization along the z direction and susceptibility, Equations (4) and (5); N is the total number of dipoles in the sample. The same algorithm was used to obtain the hysteresis loops, but in this case the electric field was varied instead of the temperature.
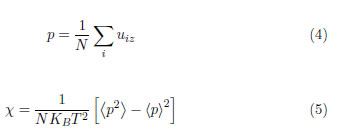
3 Results and Discussion
The phase transition from paraelectric to ferroelectric and the hysteresis phenomena were studied. First by varying the adimentional ratio (P/Y ) 0 to 0.008, secondly considering an electrical field variation in the out-ofplane direction from 0 to 2.0 U0 units, finally considering non-ferroelectric impurities (sites in the lattice without dipole) from 0 to 100% concentration.
The susceptibility curves as a function of temperature are shown for various stress values in Figure 1.
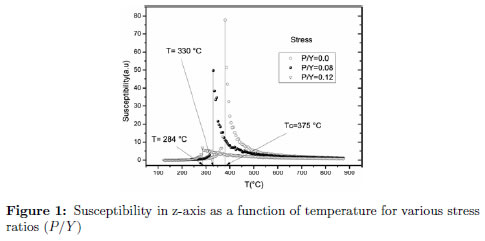
The temperature was reported in Celsius units by fitting the transition temperature obtained in the simulation (in arbitrary units) with the corresponding experimental transition temperature for the material. By using the adimentional ratio H/(KBT) at this critical temperature (where H is the energy given by the Hamiltonian), it was posible to compute U0 = 20.2 mev. This allowed to simulate the Hamiltonian in real units.
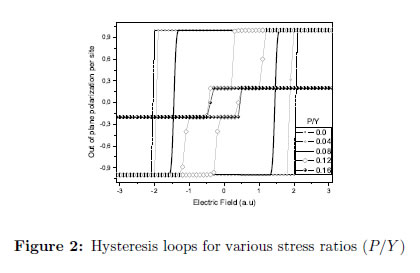
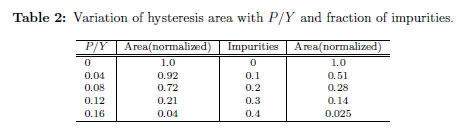
A decrease in intensity and critical temperature with increase of stress can be observed.This could be explained considering that in the Hamiltonian, the stress in the out-of-plane direction favored the dipole flipping into the in-plane, becoming z a hard axis of polarization and then reducing the formation of domains in the out-of-plane direction. The LGD (Landau- Ginzburg-Devonshire) theory estimates that for this kind of ferroelectric, a 100 MPa stress will shift the transition temperature by about 20 °C. In this matter, a systematic study of the ferroelectric properties of PZT nanowires was done by Hong and Fang [23] considering this thermodynamic approach. Two competing mechanisms had been proposed to explain this transition temperature shift. One, the uniaxial stress causes a distance diminution between dipoles and consequently an increase in ferroelectric coupling intensity leading to higher transition temperatures. On the other hand, uniaxial stress causes a movement of the Zr/Ti cation to a more symmetric position in the cell, reducing the dipole magnitude and the ferroelectric coupling in the out of plane direction, favoring in this way, the shift to lower transition temperatures. This is closely related to the variation of hysteresis loops with the applied stress, Figure 2. A reduction in their area with the increase of stress, and thereby, a decrease in the coercive field can be observed due to non easy alignment in z direction, Table 2. Experimental data on ferroelectrics and in particular on PZT systems coincide reasonable well with this simulated behavior [24],[25],[26],[27].
On the other hand, the observed effect of an increasing field in the out-of-plane direction is the horizontal shift of the polarization curves, accompanied with higher values of polarization and minor deviating slopes, meaning a less defined critical temperature peaks for the corresponding susceptibility curves, Figure 3. The presence of the electrical field E term in the Hamiltonian Equation (1) favors the flipping of dipoles in the outof- plane direction, converting z in an easy axis of polarization. The abovee explains the formation of z-domains in a larger range of temperatures.
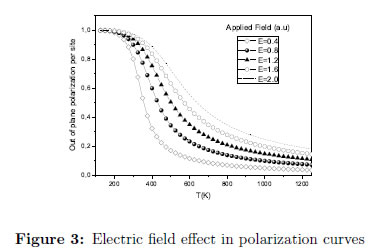
Figure 4 shows hysteresis loops at different non-ferroelectric impurity percentages from 0 to 40%. The increased presence of these impurities in the lattice, causes a transition temperature reduction and the decrease on the hysteresis loop areas Table 2. This is due to the fact that less states of polarization for the system are available with the impurities. Therefore, less dipole-dipole interaction and domain formation results. The effect of these defects in the sample is notorious, becoming an important parameter to control these ferroelectric properties.
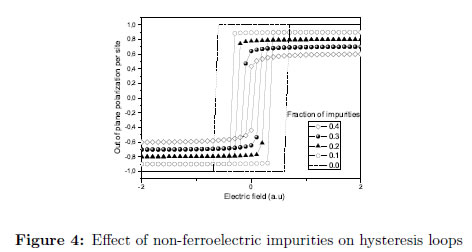
At higher percentages of non-ferroelectric impurities the simulated sample presented critical temperatures very close to absolute zero and insignificant hysteresis areas, meaning a paraelectric behavior. In an experimental way, the hysteresis area can be changed with the influence of dopants on the electrical performance of these materials, including imprint effects due to pinned dipoles and material fatigue [28].
4 Conclusions
Monte Carlo simulation of the ferroelectric phenomenon on PZT thin films was carried out. The effect of outstanding variables on the ferroelectric performance as the stress, electric field and content of non-ferroelectric impurities were evaluated by proposing a DIFFOUR Hamiltonian with a stress dependent ferroelectric coupling coefficient. The results showed a significant influence of these variables in the hysteresis loops and polarization curves. The stress effect in ferroelectric sample, leads to a change in the probability of dipole switching along its axis of application. An increase in stress in the out-of-plane direction diminishes the number of domains in this axis, favoring dipole switching to the in-plane direction. All of the above means, that rising the stress causes lower values in the susceptibility peaks and a shift of them toward lower temperature values. Besides, this out-of-plane domain diminution (also caused by non-ferroelectric impurities) yields to a reduction in the hysteresis area. These effects correspond with the qualitative behavior in the experimental reports observed.
Acknowledgements
The authors gratefully acknowledge to the Universidad Nacional de Colombia sede Manizales and Universidad de Caldas for the financial support given during this research.
References
[1] S. Watanabe, T. Fujiu, and T. Fujii, ''Effect of poling on piezoelectric properties of lead zirconate titanate thin films formed by sputtering,'' Applied Physics Letters, vol. 66, no. 12, pp. 148-150, 1995. [ Links ] 66
[2] P. Luginbuhl, G.-A. Racine, P. Lerch, B. Romanowicz, K. G. Brooks, N. F. de Rooij, P. Renaud, and N. Setter, ''Piezoelectric cantilever beams actuated by {PZT} sol-gel thin film,'' Sensors and Actuators A: Physical, vol. 54, no. 1-3, pp. 530-535, 1996. [ Links ] 66
[3] Y. Miyahara, M. Deschler, T. Fujii, S. Watanabe, and H. Bleuler, ''Noncontact atomic force microscope with a {PZT} cantilever used for deflection sensing, direct oscillation and feedback actuation,'' Applied Surface Science, vol. 188, no. 3-4, pp. 450-455, 2002. [ Links ] 66
[4] P. Muralt, M. Kohli, T. Maeder, A. Kholkin, K. Brooks, N. Setter, and R. Luthier, ''Fabrication and characterization of {PZT} thin-film vibrators for micromotors,'' Sensors and Actuators A: Physical, vol. 48, no. 2, pp. 157-165, 1995. [ Links ] 66
[5] M. Dubois and P. Muralt, ''PZT thin film actuated elastic fin micromotor,'' Ultrasonics, Ferroelectrics and Frequency Control, IEEE Transactions on, vol. 45, no. 5, pp. 1169-1177, 1998. [ Links ] 66
[6] A. M. Flynn, L. S. Tavrow, S. F. Bart, R. A. Brooks, D. Ehrlich, K. R. Udayakumar, and L. E. Cross, ''Piezoelectric micromotors for microrobots,'' Microelectromechanical Systems, Journal of, vol. 1, no. 1, pp. 44-51, Mar. 1992. [ Links ] [Online]. Available: http://dx.doi.org/10.1109/84.128055 66
[7] P. Luginbuhl, S. D. Collins, G.-A. Racine, M.-A. Gretillat, N.-F. de Rooij, K. G. Brooks, and N. Setter, ''Microfabricated Lamb wave device based on PZT sol-gel thin film for mechanical transport of solid particles and liquids,'' Microelectromechanical Systems, Journal of, vol. 6, no. 4, pp. 337-346, 1997. [ Links ] 66
[8] P. Muralt, ''Ferroelectric thin films for micro-sensors and actuators: a review,'' Journal of Micromechanics and Microengineering, vol. 10, no. 2, pp. 136-146, 2000. [ Links ] 66
[9] G. Haertling, Piezoelectric and electrooptic ceramics, 1st ed., ser. Materials engineering, R. Buchanan Dekker, Ed. New York: Taylor & Francis, 1986. [ Links ] 66
[10] M. Rios Gutierrez and G. Silva, ''Control de vibraciones en estructuras tipo edificio usando actuadores piezoeléctricos y retroalimentación positiva de la aceleración,'' DYNA, vol. 80, no. 179, pp. 116-125, Jun. 2013. [ Links ] [Online]. Available: http://dx.doi.org/10.15446/dyna.v80n179.30733 66
[11] M. Strikha, ''Non-volatile memory and IR radiation modulators based upon graphene-on-ferroelectric substrate. A review,'' Ukrainian Journal of Physical Optics, vol. 13, no. 3, pp. s15-s12, 1995. [ Links ] 66
[12] D. Landínez Tellez, G. Peña Rodríguez, F. Fajardo, J. Rodríguez, and J. Roa Rojas, ''Structural, magnetic, multiferroic, and electronic properties of Sr2TiMnO6 double perovskite,'' DYNA, vol. 79, no. 171, pp. 111-115, 2012. [ Links ] [Online]. Available: http://dx.doi.org/10.15446/dyna.v79n171.18104 66
[13] C. Bedoya Hincapié, M. Pinzón Cárdenas, J. Alfonso Orjuela, and E. Restrepo Parra, ''Propiedades fisicoquímicas del bimuto y óxidos de bismuto: síntesis, caracterización y aplicaciones,'' DYNA, vol. 79, no. 176, pp. 139-148, 2012. [ Links ] 66
[14] N. Wongdamnern, N. Triamnak, A. Ngamjarurojana, Y. Laosiritaworn, S. Ananta, and R. Yimnirun, ''Comparative studies of dynamic hysteresis responses in hard and soft {PZT} ceramics,'' Ceramics International, vol. 34, no. 4, pp. 731-734, 2008. [ Links ] 66
[15] Y. Laosiritaworn, S. Ananta, J. Poulter, and R. Yimnirun, ''Monte Carlo investigation of hysteresis properties in ferroelectric thin-films under the effect of uniaxial stresses,'' Ceramics International, vol. 35, no. 1, pp. 181-184, 2009. [ Links ] 67, 69
[16] B. Jaffe, W. R. Cook, and H. L. Jaffe, Piezoelectric ceramics, ser. Nonmetallic solids. Academic Press, 1971. [ Links ] 67
[17] Y. J. Song, Y. Zhu, and S. B. Desu, ''Low temperature fabrication and properties of sol-gel derived (111) oriented Pb(Zr1-xTix)O3 thin films,'' Applied Physics Letters, vol. 72, no. 21, pp. 2686-2688, 1998. [ Links ] [Online]. Available: http://dx.doi.org/10.1063/1.121099 67
[18] N. Tohge, S. Takahashi, and T. Minami, ''Preparation of PbZrO3-PbTiO3 Ferroelectric Thin Films by the Sol-Gel Process,'' Journal of the American Ceramic Society, vol. 74, no. 1, pp. 67-71, 1991. [ Links ] 67
[19] S. r. F. Jarner and E. Hansen, ''Geometric ergodicity of Metropolis algorithms,'' Stochastic Processes and their Applications, vol. 85, no. 2, pp. 341-361, 2000. [ Links ] [Online]. Available: http://dx.doi.org/10.1016/S0304-4149(99)00082-4 68
[20] T. Janssen and J. A. Tjon, ''One-dimensional model for a crystal with displacive modulation,'' Phys. Rev. B, vol. 24, no. 4, pp. 2245-2248, 1981. [ Links ] [Online]. Available: http://link.aps.org/doi/10.1103/PhysRevB.24.2245 68
[21] J.-M. Liu, W. M. Wang, Z. G. Liu, H. L. Chan, and C. L. Choy, ''Dynamic hysteresis in ferroelectric systems: experiment and Monte Carlo simulation,'' Applied Physics A, vol. 75, no. 4, pp. 507-514, 2002. [ Links ] [Online]. Available: http://dx.doi.org/10.1007/s003390101012 68
[22] Y.-Z. Wu, D.-L. Yao, and Z.-Y. Li, ''Monte-Carlo simulation of the switching behavior in ferroelectrics with dipolar defects,'' Solid State Communications, vol. 122, no. 7-8, pp. 395-400, 2002. [ Links ] 69
[23] J. Hong and D. Fang, ''Systematic study of the ferroelectric properties of Pb(Zr0.5Ti0.5)O3 nanowires,'' Journal of Applied Physics, vol. 104, no. 6, pp. -, 2008. [ Links ] [Online]. Available: http://dx.doi.org/10.1063/1.2982090 71
[24] R. Yimnirun, Y. Laosiritaworn, and S. Wongsaenmai, ''Effect of uniaxial compressive pre-stress on ferroelectric properties of soft PZT ceramics,'' Journal of Physics D: Applied Physics, vol. 39, no. 4, p. 759, 2006. [ Links ] [Online]. Available: http://stacks.iop.org/0022-3727/39/i=4/a=025 71
[25] W. Smiga and B. Garbarz-Glos, ''Studies of the influence of uniaxial pressure on the electric behaviour of Li0.015Na0.985NbO3 ceramics,'' Ukrainian Journal of Physical Optics, vol. 13, no. 4, p. S27, 2012. [ Links ] [Online]. Available: http://dx.doi.org/10.3116/16091833/13/1/s27/2012 71
[26] M. D. Nguyen, M. Dekkers, E. Houwman, R. Steenwelle, X. Wan, A. Roelofs, T. Schmitz-Kempen, and G. Rijnders, ''Misfit strain dependence of ferroelectric and piezoelectric properties of clamped (001) epitaxial Pb(Zr0.52,Ti0.48)O3 thin films,'' Applied Physics Letters, vol. 99, no. 25, pp. -, 2011. [ Links ] [Online]. Available: http://dx.doi.org/10.1063/1.3669527 71
[27] J. Suchanicz, N. T. H. Kim-Ngan, K. Konieczny, I. Jankowska-Sumara, D. Sitko, D. Goc-Jaglo, and A. G. Balogh, ''Influence of combined external stress and electric field on electric properties of 0.5% Fe-doped lead zirconate titanate ceramics,'' Journal of Applied Physics, vol. 106, no. 9, pp. 94 104- 94 109, 2009. [ Links ] [Online]. Available: http://dx.doi.org/10.1063/1.3234394 71
[28] D. Guo, K. Cai, L. Li, and Z. Gui, ''Investigation of the additive induced doping effects in gelcast soft lead zirconate titanate ceramics,'' Journal of Applied Physics, vol. 106, no. 5, p. 054104, 2009. [ Links ] [Online]. Available: http://dx.doi.org/10.1063/1.3190549 72













